Abstract
The limited field of view, cumulative inter-frame jitter, and dynamic parallax interference in handheld video stitching often lead to misalignment and distortion. In this paper, we propose an end-to-end, unsupervised deep-learning framework that jointly performs real-time video stabilization and stitching. First, collaborative optimization architecture allows the stabilization and stitching modules to share parameters and propagate errors through a fully differentiable network, ensuring consistent image alignment. Second, a Markov trajectory smoothing strategy in relative coordinates models inter-frame motion as incremental relationships, effectively reducing cumulative errors. Third, a dynamic attention mask generates spatiotemporal weight maps based on foreground motion prediction, suppressing misalignment caused by dynamic objects. Experimental evaluation on diverse handheld sequences shows that our method achieves higher stitching quality, lower geometric distortion rates, and improved video stability compared to state-of-the-art baselines, while maintaining real-time processing capabilities. Ablation studies validate that relative trajectory modeling substantially mitigates long-term jitter and that the dynamic attention mask enhances stitching accuracy in dynamic scenes. These results demonstrate that the proposed framework provides a robust solution for high-quality, real-time handheld video stitching.
1. Introduction
With the widespread adoption of smartphones, sensor resolutions have steadily improved. However, due to the limitations of built-in consumer-grade lenses, the field of view (FoV) of cameras remains restricted [1]. Video stitching technology combines multiple video sequences from moving cameras into a single frame with a wider FoV and higher resolution, thereby enhancing the user’s immersive visual experience. This technology has been widely applied in video surveillance [2], drone inspections [3], and autonomous driving [4]. However, low-quality or failed video stitching not only compromises the visual experience but also reduces the accuracy of downstream video analysis tasks such as object detection and tracking [5,6,7].
In handheld camera video stitching, common distortions can be categorized into two main types: natural shaking (Shaky), caused by camera motion, and visual inconsistency (Jitters), arising from insufficient consideration of temporal continuity during frame stitching. Traditional solutions often rely on additional hardware to impose constraints on camera motion for video stabilization, but these methods are costly and inconvenient. In contrast, algorithm-based video stitching and stabilization methods offer greater flexibility and cost-effectiveness.
Conventional video stabilization techniques typically involve three steps: camera trajectory estimation, trajectory smoothing, and motion compensation. Camera trajectory estimation relies on feature point extraction and tracking, approximating camera motion through homography matrices or motion vectors [8,9,10]. However, in scenes with sparse textures, severe occlusions, or intense motion, these methods often suffer from feature matching failures and cumulative errors, affecting stabilization performance [11]. Moreover, reliance on handcrafted features limits robustness under varying illumination and scene conditions, and the iterative nature of RANSAC-based outlier removal can lead to increased computational latency. These shortcomings make it challenging for traditional pipelines to maintain real-time performance and high-quality stabilization in complex, dynamic environments.
Image and video stitching techniques have been extensively studied in computer vision and multimedia fields, with homography estimation being the core challenge. Traditional methods typically rely on feature point detection algorithms such as SIFT, SURF, and ORB for matching, followed by robust estimation algorithms like RANSAC to eliminate outliers and compute the transformation matrix. Additionally, flexible transformation models such as grid-based transformations and thin-plate splines (TPSs) have been introduced to mitigate parallax errors while incorporating shape-preserving constraints to improve stitching quality. Deep learning-based approaches have also emerged, using end-to-end networks to directly regress homography transformation parameters, demonstrating better adaptability and robustness in complex scenes. Nevertheless, handcrafted feature-based stitching still exhibits poor handling of low-texture regions and repetitive patterns, leading to visible seam artifacts. Even deep learning regressors can fail in extreme parallax or illumination changes due to insufficient training diversity, and the lack of explicit geometric constraints may result in nonphysical warping artifacts.
For trajectory smoothing, early methods primarily employed signal processing techniques such as low-pass filtering, Kalman filtering, and polynomial interpolation to suppress camera shake and optimize trajectory smoothness. More recently, deep learning-based approaches, including StabNet, optical flow-based optimization, and adversarial learning networks, have further enhanced video stability, allowing trajectory smoothing to adapt more effectively to complex scenarios. However, signal processing-based filters often introduce temporal lag or over-smoothing that distorts rapid camera movements. Deep learning-based smoothers, while more flexible, require extensive labeled data for supervised training or risk mode collapse in adversarial setups. Additionally, many end-to-end smoothing networks do not explicitly enforce global trajectory consistency, leading to accumulated drift over long sequences.
To address the aforementioned challenges, some researchers have attempted to jointly optimize video stitching and stabilization tasks to produce globally smooth and stabilized videos [1,3]. However, these methods typically require designing joint optimization functions for overall camera trajectory modeling and performing multiple offline iterations, making them unsuitable for real-time applications. Stabstitch [12] proposed an unsupervised online video stabilization and stitching method primarily targeting inter-frame discontinuities after image stitching, assuming that the original video does not contain natural camera shake. Despite this, Stabstitch’s reliance on post hoc smoothing limits its ability to correct misalignments introduced during stitching, and the assumption of negligible camera shake restricts its applicability to highly dynamic handheld conditions.
To tackle the challenges of both natural camera shake and inter-frame discontinuities introduced by stitching, this paper presents a novel end-to-end online video stabilization and stitching framework based on unsupervised deep learning. The proposed method employs a recurrent neural network (RNN) with dual inputs—historical stabilized frames and original unstable frames—to achieve real-time video stitching and stabilization. During training, the overall network jointly optimizes three key modules: camera trajectory estimation, stitching trajectory estimation, and trajectory smoothing. This ensures both smooth trajectory generation and high-quality stitching. To mitigate cumulative errors caused by absolute coordinate modeling, a relative coordinate representation strategy is adopted, effectively reducing video distortion. Additionally, a dynamic attention mask mechanism is introduced, generating spatiotemporal weight maps based on foreground motion prediction to suppress interference from dynamic objects. The proposed method enables high-quality stitching and stabilization of multi-source handheld videos in real time, providing an efficient and cost-effective solution for video enhancement technology.
2. Methodology
2.1. Camera Trajectory Estimation
To address motion estimation issues in handheld videos caused by jitter and dynamic foreground interference, this paper proposes an unsupervised end-to-end method based on grid motion fields. This method directly estimates local motion information from consecutive frames and constructs the overall camera trajectory. Unlike traditional feature point matching-based approaches, this method leverages deep neural networks to model motion at the grid level, enabling finer capture of both local and global motion while enhancing robustness against non-ideal motion disturbances. The overall network architecture is illustrated in Figure 1.
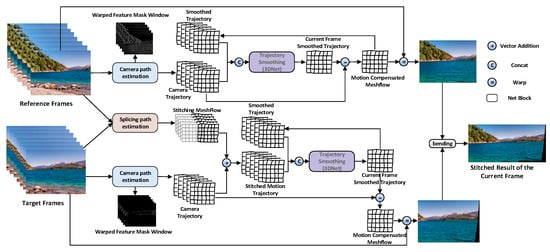
Figure 1.
Overall network architecture.
Figure 1 presents the overall architecture of the proposed unsupervised end-to-end video stabilization and stitching network, which is composed of three key modules: camera trajectory estimation, stitching trajectory estimation, and trajectory smoothing. The camera trajectory estimation module analyzes the sparse motion field (meshflow) between adjacent frames to estimate the global transformation induced by camera motion. This provides a foundational motion representation for downstream processing. The stitching trajectory estimation module refines alignment across overlapping views by optimizing homographies within a temporal window, minimizing photometric inconsistency. To ensure temporal coherence and reduce cumulative drift, the trajectory smoothing module introduces a relative coordinate–based Markov smoothing strategy, which incrementally models motion and applies historical constraints. Together, these modules enable real-time processing with high stability and stitching accuracy in an unsupervised learning framework.
To begin with, consider two consecutive frames, and . This study defines the function Stab(⋅) to directly estimate the motion vectors of grid nodes between the two frames:
where i and j represent the row and column indices of the grid, respectively. Compared to pixel-level motion estimation, grid-level estimation provides a more stable representation of the overall motion trend within local regions, thereby mitigating the interference caused by dynamic foreground objects.
To further enhance the accuracy and robustness of motion estimation, we follow the approach of Liu et al. [13] and design a multi-scale and content-aware feature extraction module, which consists of the following four components:
- (1)
- Multi-scale feature extraction: A feature extractor, f(⋅), is employed to extract multi-scale feature maps from the input image :
The first two scales are utilized for coarse alignment, while the remaining three scales capture fine details and contextual information, thereby providing rich semantic support for subsequent motion estimation.
- (2)
- Context-aware feature extraction: To integrate contextual information across adjacent frames, multi-scale contextual features are extracted from , , and using the context-aware feature extractor ccl(⋅):
These features help compensate for information loss that may occur when using single-scale features in dynamic scenes, thereby improving the overall accuracy of motion estimation.
- (3)
- Inlier mask prediction: Since dynamic foregrounds and noisy regions may negatively impact homography estimation, we introduce a mask predictor m(⋅) to generate an inlier probability mask :
This mask is then applied to the corresponding scale feature maps, producing weighted features:
where denotes the element-wise multiplication operation. This strategy emphasizes regions beneficial for motion estimation while suppressing noise and irregular motion effects.
- (4)
- Grid motion field estimation: Based on the weighted feature maps and contextual features , the grid motion field estimator computes the motion vectors at each grid node from frame to frame :
Subsequently, these local motion vectors are transformed into homography matrices corresponding to each grid region using the classical Direct Linear Transformation (DLT) method:
where h and w represent the row and column indices of the grid, respectively.
Once local motion estimation between consecutive frames is obtained, accumulate sequential transformation matrices to construct the global camera motion trajectory. Specifically, given that represents the local transformation matrix from time t−1 to t, the camera trajectory at time t, denoted as , is expressed as
where represents the absolute motion relative to the first frame. Absolute trajectory representation is employed to capture the overall motion trend, while in the subsequent trajectory smoothing module, it is converted into a relative path representation to mitigate cumulative errors and reduce geometric distortion.
In summary, the proposed camera trajectory estimation method integrates multi-scale feature extraction, contextual information fusion, inlier mask generation, and grid motion field estimation to accurately capture local motion across consecutive frames. By accumulating transformations over time, a global camera trajectory is constructed. This approach demonstrates high robustness in dynamic and noisy environments, laying a solid foundation for subsequent video stitching and stabilization applications.
2.2. Stitching Trajectory Estimation
The stitching trajectory estimation module aims to determine the relative motion between frames captured by different cameras at the same timestamp, enabling precise stitching of video frames across cameras. This module first estimates the initial motion by computing the local motion field (meshflow) between the reference and target frames at the same moment. Subsequently, the previously obtained camera trajectory information is integrated to refine the local motion, generating the final stitching trajectory. The computation process is illustrated in Figure 2.

Figure 2.
Computation of meshflow between the reference and target frames.
In the first stage, due to the potentially limited overlapping regions between frames from different cameras, direct local feature matching often fails to provide stable motion estimation. To address this, our method adopts a network structure similar to the camera trajectory estimation module, while incorporating a context-aware module at a larger feature scale to enhance long-range matching capability between images. Specifically, for the same timestamp t, let and denote the reference and target frames, respectively. The local motion field in the reference frame coordinate system can be expressed as
where represents the motion vector at the i-th row and j-th column of the mesh grid. This design captures long-range correlations between images, mitigating the issue of motion information loss caused by insufficient overlap between frames.
During stitching trajectory generation, the reference frame’s motion trajectory has already been computed via the camera trajectory estimation module and serves as a global baseline. The motion of the target frame, however, is determined by combining its temporal continuity with the local motion information obtained from the stitch meshflow in the spatial domain. Defining and as the local motion vectors obtained from temporal sequence analysis and spatial matching, respectively, the overall motion of the target frame in the reference frame coordinate system can be expressed as
where captures the temporal motion trend of the target frame, while supplements the spatial motion information that may be difficult to capture due to insufficient frame overlap.
Following the approach used for constructing camera trajectories, the stitching trajectory of the target frame is computed based on the camera trajectory of the reference frame and the estimated homography matrix for stitching, as follows:
where represents the position of the target frame at timestamp t in the reference frame coordinate system. This formulation ensures that the final stitching trajectory not only inherits the global motion information of the reference frame but also incorporates fine-grained corrections from local motion estimation, leading to more precise stitching results.
The proposed stitching trajectory estimation method enhances long-range image matching by introducing contextual correlation mechanisms at a large feature scale. Additionally, by integrating both temporal and spatial motion information, this approach accurately determines the target frame’s position in the reference coordinate system. It demonstrates high robustness against challenges such as insufficient overlap regions and motion discontinuities, laying a solid foundation for subsequent video stitching and stabilization.
2.3. Trajectory Smoothing
The trajectory smoothing module aims to eliminate discontinuities in motion trajectories caused by camera shake and complex environmental conditions while maintaining consistency in smoothness across different scene layouts and depth conditions. Traditional methods such as meshflow [10] and RTVSASP [14] typically apply Gaussian filtering or Kalman filtering to smooth global trajectories, using the first video frame as an absolute reference coordinate. However, these approaches are prone to cumulative errors over time, leading to deviations in the final stitched result. To address this issue and achieve real-time video stabilization, this study adopts the concept of DUTnet [15] and proposes a CNN-based online trajectory smoothing method. The core idea is to establish a mapping relationship between the raw camera trajectory of the current frame and the historical smoothed trajectory using a dual-input network structure. The network framework is illustrated in Figure 3.
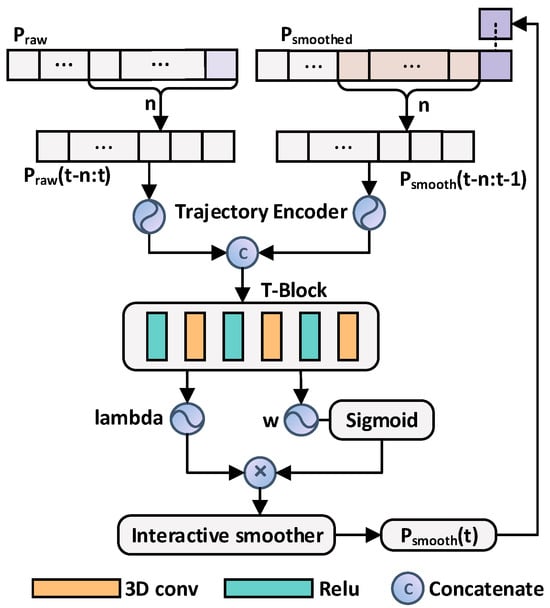
Figure 3.
Network architecture of trajectory smoothing.
To integrate trajectory information over time, a sliding window strategy is adopted. Let represent the raw camera trajectory from time t−n to t, with a dimension of [2,n,M,N], where M and N denote the number of grid rows and columns in each video frame, respectively. Similarly, let denote the historical smoothed trajectory of the preceding n−1 frames, with a dimension of [2,n−1,M,N]. To fully utilize both sources of information, the method first maps the 2D trajectory features into a 64-dimensional feature space through independent embedding layers:
Subsequently, a concatenation operation is performed to fuse the two embedded features into a unified feature tensor:
This fused feature tensor contains information from both the current raw trajectory and the historical smoothed trajectory, facilitating the network’s ability to capture local temporal and spatial variations.
A 3D convolutional layer is then applied to extract features from . The 3D convolution has a receptive field in both spatial and temporal dimensions, enabling it to capture continuous trajectory variations over time. After multiple layers of 3D convolution, the network ultimately outputs a set of parameters θt, which include smoothing weights wk and offset values bk, collectively defining the mapping relationship from the raw trajectory to the smoothed trajectory. Given a local smoothing window radius l (typically set to l = 3), the smoothed trajectory at time t is updated as follows:
By restricting accumulation to a finite time window, this approach effectively reduces error propagation while enhancing the stability and real-time performance of online smoothing.
The proposed trajectory smoothing method integrates raw trajectory and historical smoothed trajectory information using a dual-input network structure and extracts spatiotemporal features via 3D convolutional layers. The final smoothing weights and offsets ensure real-time trajectory smoothing. Additionally, the relative path accumulation strategy significantly minimizes cumulative errors, ensuring a more robust and accurate video stabilization process while maintaining computational efficiency.
2.4. Loss Function
The proposed unsupervised end-to-end method implements joint training across all modules, with a loss function designed to simultaneously optimize camera trajectory estimation, stitching motion estimation, and trajectory smoothing.
2.4.1. Loss for Trajectory Estimation and Stitching Motion Estimation
Both the camera trajectory estimation and stitching motion estimation modules adopt an image registration strategy. The trajectory estimation module employs a feature mask to filter out dynamic regions, which is directly applied in the stitching motion estimation module. To mitigate the interference introduced by dynamic regions, a triplet loss is introduced to optimize the homography estimation. This loss aims to ensure that the masked and warped image pairs become more similar while constraining the inconsistency between the forward and backward homography matrices. The loss function is formulated as follows:
where Ia′ and Ib′ represent the images after inlier mask weighting and warping, while Hab and Hba denote the forward and inverse homography matrices between images Ia and Ib. The hyperparameters ξ and μ are used to balance the relative importance of different terms.
Given the significant viewpoint variations in stitching scenarios, relying solely on the triplet loss may lead to slow convergence or even divergence. To enhance robustness in low-overlap regions, optical flow information is incorporated during training. Specifically, the optical flow loss is formulated based on the discrepancy between the actual optical flow OF obtained from PWC-Net and the feature flow FF estimated from network-based feature matching:
where Mβ represents the inlier probability mask (ranging from 0 to 1), and Fβ denotes feature similarity. The hyperparameter λ controls the contribution of the mask to the loss.
To ensure spatial continuity of the grid motion vectors computed via the function , a continuity loss function Lcont is introduced. This loss constrains the motion vector differences between adjacent grid points in both vertical and horizontal directions, preserving the smoothness of the motion field. It is formally defined as follows:
Combining the above components, the total loss function for trajectory estimation and stitching motion estimation is expressed as
where the hyperparameters λ and β balance the impact of each component. The weight λ is selected so that the flow consistency term effectively suppresses inter-frame jitter without dominating the triplet alignment term; if λ is too small, motion artifacts persist, whereas if λ is too large, fine alignment deteriorates. Likewise, β is chosen to enforce long-range temporal coherence while preserving local stitching accuracy: a small β permits cumulative drift over extended sequences, while a large β over-smooths local alignment. In practice, λ and β are adjusted to equilibrate the gradient magnitudes of their respective loss components, and their values are confirmed through validation set metrics that jointly measure alignment fidelity and stability.
To facilitate early convergence while ensuring fine alignment in later stages, the parameter λ decays with the training epoch t as follows:
where λ0 is the initial value, and γ is the decay factor.
2.4.2. Trajectory Smoothing Loss
For trajectory smoothing in video stabilization, a composite loss function is designed to integrate three key aspects: local smoothness, path fidelity, and historical continuity. Additionally, an alignment loss is introduced to ensure consistency of the motion-compensated images.
- (1)
- Local smoothness loss: This term enforces smooth and gradual transitions in the trajectory over a given time window, preventing abrupt changes. Let represent the smoothed trajectory at time t. The local smoothness loss is defined aswhere l denotes the local smoothness window radius, n is the sliding window length, and α is a weighting parameter that adjusts the contribution of this term.
- (2)
- Path fidelity loss: To prevent excessive smoothing that may distort the motion path, the path fidelity loss encourages the smoothed trajectory to remain as close as possible to the original, unsmoothed trajectory Praw(t):where β is a parameter controlling the importance of this term.
- (3)
- Historical continuity loss: To maintain coherence between past smoothed trajectories and the current computation, particularly at sequence boundaries, the historical continuity loss is defined aswhere Psmooth(t) represents the previously computed smoothed trajectory, and γ controls the influence of this term.
- (4)
- Alignment loss: To ensure proper alignment after motion compensation and image warping, an alignment loss is designed as follows:where It,warp1 and It,warp2 represent the images warped through stabilization and stitching, respectively. N is the total number of pixels, xi denotes pixel positions, and λs is a weighting factor.
Combining these components, the total trajectory smoothing loss function is given:
This comprehensive loss function design ensures the realism of video content while effectively smoothing the camera motion trajectory. It minimizes unnatural jumps introduced by the smoothing process, thereby improving overall video stability and visual consistency. Through the multi-level loss function design, the model not only learns to transform unstable videos into stabilized outputs but also effectively handles parallax effects and fast-moving objects in dynamic scenes. This enables superior overall stabilization performance under a multi-task joint optimization framework.
3. Experimental Results and Analysis
3.1. Experimental Parameter Settings
In this study, experiments were conducted using the StabStitch-D video stitching dataset provided in [12]. This dataset consists of 100 videos categorized into four groups based on scene characteristics: Regular (RE), Low-Texture (LT), Low-Light (LL), and Fast-Moving (FM). Among these, the Fast-Moving category features rapid and irregular camera motions, making it particularly valuable for research. To maintain computational efficiency while ensuring experimental diversity, all videos were uniformly resized to a resolution of 360 × 480. The datasets employed are limited in diversity—most contain predominantly daytime, outdoor scenes with moderate motion—thus they do not fully represent challenging conditions such as extreme low-light environments, heavy occlusions, or highly dynamic indoor footage.
Regarding parameter settings and evaluation metrics, the hyperparameters of the triplet loss in the trajectory estimation module were set to ξ = 2 and μ = 1. For the overall loss function, the initial weight λ0 was set to 3, and the weight of the stitching motion loss β was set to 5. In the trajectory smoothing module, the respective weights of different loss components were assigned as αs = 20, βs = 10, and γs = 30. The grid vertex partition was configured as (6 + 1) × (8 + 1). Within the sliding window framework, the lengths of the historical and original paths were set to 6 and 8, respectively. For evaluation metrics, the image alignment quality was assessed using PSNR and SSIM, consistent with StabStitch. Additionally, the video stability and distortion rates were evaluated following the methodology of RTVSASP [14], ensuring a fair comparison with state-of-the-art methods.
The values of ξ = 2.0 and μ = 0.01 are adopted following the settings in [13], where these hyperparameters were extensively validated for content-aware unsupervised deep homography estimation and shown to achieve superior robustness and accuracy. In our framework, which uses a similar loss formulation and network backbone, these values have also been confirmed through preliminary sensitivity tests to provide stable convergence and consistent performance across diverse scene conditions.
Considering that unsupervised learning in image registration tasks is prone to nonlinearities and local optima, direct end-to-end training often faces convergence challenges. To address this issue, a staged training strategy was designed. Initially, in the independent training phase, the camera trajectory estimation module and stitching parameter estimation module were trained separately using temporal and spatial data, respectively. Their inference results were saved as initialization parameters for subsequent optimization. Next, during the sliding window optimization phase, historical path information was incorporated for further refinement. In each iteration, the network simultaneously computed trajectory estimation loss and stitching motion loss, while the trajectory smoothing loss was computed every 8 iterations to ensure both global continuity and local consistency. The training was performed on an RTX 4090 Ti GPU manufactured by NVIDIA in the United States (Santa Clara, CA, USA) in an Ubuntu 18.04 environment. The Adam optimizer was employed with an initial learning rate of 0.00001 and momentum parameters set to β1 = 0.9 and β2 = 0.99. A StepLR strategy was applied to reduce the learning rate by 50% every 10 epochs, with the entire training process lasting for 50 epochs.
3.2. Quantitative Results and Analysis
To comprehensively evaluate the proposed method, we conducted extensive comparisons with state-of-the-art unsupervised image and video stitching approaches. Specifically, for image quality assessment, we compared our method against the traditional image stitching approach LPC [16], learning-based image stitching methods UDIS [17] and UDIS++ [18], and the learning-based video stitching method StabStitch. The quantitative comparison results are presented in Table 1, where “·/·” represents PSNR/SSIM values, and “-” indicates failure cases for the corresponding category. The experimental results are summarized in Table 1.

Table 1.
Quantitative comparisons with image stitching methods on StabStitch-D dataset.
The proposed method outperforms existing approaches with clear numerical advantages. As shown in Table 1, it achieves an average PSNR/SSIM improvement of 17.07%/7.20% over UDIS and 15.07%/3.12% over UDIS++. Additionally, in terms of video stability (Table 2), it surpasses StabStitch by 5.3% on average, and in distortion reduction (Table 3), it shows a marginal yet consistent improvement over StabStitch++.

Table 2.
Stability comparison between StabStitch and the proposed method across four scenarios.

Table 3.
Distortion comparison between StabStitch and the proposed method across four scenarios.
The quantitative experimental results demonstrate that the proposed method outperforms current state-of-the-art unsupervised image and video stitching methods in both image quality and video stability. In the comparison experiments, our method was compared with traditional image stitching methods like LPC, learning-based methods such as UDIS and UDIS++, and the video stitching method StabStitch. The experimental data show that, in Regular, Low-Light, and Low-Texture scenes, our method achieves or surpasses other methods in terms of PSNR and SSIM. In the Fast-Moving scene, where rapid and irregular camera movements are present, our method exhibits higher alignment accuracy and stability, significantly outperforming StabStitch. This can primarily be attributed to the proposed end-to-end training approach and relative path computation strategy, which effectively reduces cumulative errors and maintains high image alignment precision.
Upon inclusion of StabStitch++ in the comparative evaluation, it is observed that despite enhancements such as adaptive motion confidence weighting and refined smoothing filters, StabStitch++ continues to depend on absolute trajectory estimations during its stabilization phase. As a result, residual drift persists in extended video sequences. Measured PSNR and SSIM values for StabStitch++ in Low-Light and Fast-Moving scenarios remain inferior to those achieved by our framework. Moreover, the iterative post hoc adjustment of stitching parameters in StabStitch++ cannot rectify alignment errors introduced earlier in the processing pipeline, whereas the end-to-end joint training mechanism of the proposed method inherently corrects misalignments at each stage of the network.
In terms of video stability assessment, the proposed method was evaluated based on the stability of target frames. The results indicate that the proposed framework surpasses StabStitch in stability rate, owing to the utilization of historical smoothed trajectories as input. Furthermore, relative coordinate computation facilitates smoother transitions between newly generated output frames and previously stabilized frames, thereby markedly reducing cumulative errors. With respect to distortion rate, the proposed method exhibits clear advantages in most scenes, with only a marginal difference observed in the Low-Texture scenario. In summary, the proposed method not only preserves the authenticity of the video content but also attains superior stability and alignment accuracy through end-to-end joint training, rendering it a competitive solution for real-time video enhancement.
When comparing video stability metrics with StabStitch++, it becomes evident that the incremental improvements introduced by StabStitch++’s smoothing algorithm do not surmount the inherent limitation of decoupling stitching and stabilization. Despite StabStitch++’s enhanced motion consistency checks, residual wobble remains evident in prolonged sequences, particularly under rapid viewpoint changes. In contrast, the relative coordinate-based Markov smoothing strategy employed by the proposed framework inherently maintains temporal coherence over arbitrary sequence lengths. Consequently, although StabStitch++ demonstrates slight gains over StabStitch in stability rate, its performance remains significantly inferior to that of the proposed framework.
3.3. Visual Effect Comparison
To visually demonstrate the advantages of the proposed method in video stitching and stability, we selected representative cases and compared them with the popular StabStitch method. Since StabStitch often sacrifices the accuracy of early-stage stitching for smoothness in the path estimation phase, it is difficult to visually reflect its flaws in PSNR/SSIM metrics. Therefore, we specifically visualized part of the stitching results, as shown in Figure 4 and Figure 5.

Figure 4.
Experiment 1: Qualitative comparison experiment.

Figure 5.
Experiment 2: Qualitative comparison experiment.
In the comparison images, it is evident that in the overlapping region between the reference and target frames, the stitched image generated using StabStitch contains noticeable artifacts, which are highlighted by red boxes. The generation of these artifacts can mainly be attributed to the large compensation required in the target frame for a smooth transition during fast camera movements, while the reference frame fails to synchronize with effective compensation. This results in a clear misalignment in the overlapping area. In contrast, our method applies motion compensation between both the target and reference frames and uses L1 photometric loss in the overlapping region to align the image content. This not only ensures video stability but also significantly improves the alignment accuracy of the overlapping region, resulting in a more natural and coherent visual effect.
3.4. Ablation Experiments
To further explore the contribution of each module and strategy to overall system performance, we conducted a series of ablation experiments. In the experiments, “original stitching” refers to stitching each frame individually without employing the joint smoothing strategy. “Single-input smoothing” involves using the original unstable path as input in the trajectory smoothing module, while “dual-input smoothing” uses both the original and historical smoothed paths as inputs. Table 4 presents the ablation experimental results on alignment, distortion, and stability metrics.

Table 4.
Ablation studies on alignment, distortion, and stability. (“↑” means higher values are better for the metric).
The results indicate that, while maintaining image stitching quality and a low distortion rate, the introduction of historical smoothed trajectories as additional input significantly improves the overall stability rate. This demonstrates that historical smoothing information plays a critical role in transitioning between newly generated frames and previously stable frames, effectively reducing cumulative errors and enhancing the overall stability of the video.
Moreover, to evaluate the impact of the relative path and absolute path strategies on system performance, we conducted a comparative experiment, with the results shown in Table 5.

Table 5.
Ablation studies on alignment, distortion, and stability. (“↑” means higher values are better for the metric).
The experimental results reveal that the relative path calculation method can significantly reduce cumulative errors while ensuring alignment accuracy, further improving video stability. Specifically, in terms of alignment and distortion rates, both path strategies perform similarly. However, the relative path method shows a more significant advantage in stability metrics, proving its effectiveness in suppressing error accumulation during the stabilization of long-sequence videos.
To comprehensively evaluate the impact of key hyperparameters on model performance, we conducted a series of ablation and sensitivity experiments. Specifically, we analyzed the influence of trajectory smoothing coefficients (αs, βs, and γs) by independently varying each parameter while keeping the others fixed at their default values. The experimental results, presented in Table 6, Table 7 and Table 8, indicate that lower values of αs lead to insufficient smoothing and noticeable jitter artifacts, while overly large values introduce excessive smoothing that compromises structural consistency and increases distortion. Similarly, increasing βs enhances the fidelity of the estimated paths but may introduce slight reductions in temporal stability. Adjusting γs affects the temporal coherence, particularly near sequence boundaries; however, excessive values can lead to performance degradation in overall visual quality. These observations highlight the importance of careful tuning to maintain a balanced trade-off among visual stability, spatial alignment, and minimal distortion.

Table 6.
Ablation study on the selection of parameter αs (“↑” means higher values are better for the metric).

Table 7.
Ablation study on the selection of parameter βs. (“↑” means higher values are better for the metric).

Table 8.
Ablation study on the selection of parameter γs. (“↑” means higher values are better for the metric).
In addition, a sensitivity analysis was conducted on the weighting parameters λ0 and β, which control the influence of photometric alignment and temporal consistency, respectively. By systematically varying λ0 while fixing β, and vice versa, we observed that improper values can significantly affect convergence behavior and alignment accuracy. The results, summarized in Table 9 and Table 10, confirm that the selected default values strike an optimal balance between training efficiency and reconstruction quality. These findings reinforce the robustness of the proposed framework across a range of parameter settings.

Table 9.
Ablation experiments on the selection of parameter λ0.

Table 10.
Ablation experiments on the selection of parameter β.
Based on the above ablation experiment results and the visual effect comparison, it is evident that our method outperforms existing advanced methods in all metrics through the overall end-to-end training strategy, dual-input smoothing module, and relative path calculation mechanism. This not only verifies the rationality of each module design but also further proves the feasibility and superiority of achieving efficient video stitching and stabilization in dynamic and complex scenes.
4. Conclusions
This paper addresses the challenges of limited field of view, jitter accumulation, and dynamic interference in online video stitching by proposing an end-to-end unsupervised deep learning framework that achieves the collaborative optimization of both stability and stitching tasks. The specific conclusions are as follows:
- (1)
- End-to-End collaborative optimization architecture: To tackle the alignment degradation caused by phase-wise optimization, we propose an end-to-end collaborative optimization framework. By constructing a differentiable network to jointly learn stitching and stability parameters and utilizing an error backpropagation mechanism to synchronize the optimization of both tasks, we solve the imbalance between stitching quality and stability caused by independent optimization in traditional methods. This validates the effectiveness of end-to-end joint training.
- (2)
- Relative coordinate-based Markov smoothing strategy: To address the cumulative error flaw in absolute trajectory modeling, we design a relative coordinate-based Markov smoothing strategy. By incrementally modeling motion and applying historical path constraints, the motion relationship between adjacent frames is transformed into a relative coordinate optimization problem, significantly reducing error accumulation in long sequences and effectively ensuring the spatiotemporal continuity of the video.
- (3)
- Dynamic attention mask mechanism: To mitigate the disparity interference caused by dynamic objects, we propose a dynamic attention mask mechanism. By combining foreground motion prediction to generate spatiotemporal weight maps and using L1 photometric loss to dynamically suppress misalignment interference in dynamic regions, the robustness of stitching in complex scenes is significantly improved.
This study advances the state of online video stitching and stabilization by integrating three core innovations: end-to-end collaborative optimization architecture, a relative coordinate-based Markov smoothing strategy, and a dynamic attention mask mechanism. These contributions address shortcomings in prior phase-wise approaches and enable high-quality, low-distortion stitching under strong camera shake and dynamic content. Future efforts will focus on expanding the training set to encompass a wider variety of scene types (e.g., low-light and underwater), exploring lightweight model variants for deployment on mobile and embedded hardware and refining dynamic mask generation using more sophisticated semantic segmentation or depth cues. Such extensions aim to further enhance the generalization and real-time applicability of our framework, paving the way for seamless integration into AR/VR platforms and next-generation consumer video applications.
A brief ethical consideration is warranted, as real-world use in video surveillance or drone operations may capture identifiable individuals without consent. High-quality stabilization and stitching can enable unauthorized tracking or profiling. To mitigate this, practitioners should anonymize sensitive data (e.g., blur faces or license plates), comply with applicable privacy regulations, and implement clear data governance policies. Such measures help ensure responsible deployment of the proposed framework.
Author Contributions
Conceptualization, P.W., P.Q. and J.Z.; methodology, P.W. and R.C.; software, P.W.; validation, P.W. and B.H.; formal analysis, P.W. and P.Z.; investigation, P.W.; resources, P.Q.; data curation, P.W. and B.H.; writing—original draft preparation, P.W.; writing—review and editing, P.W., P.Q. and Z.C.; visualization, P.W.; supervision, P.Q., J.Z. and R.C; project administration, P.Q.; funding acquisition, P.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Major Science and Technology Project of Shanxi Province, China (Shanxi Provincial Department of Science and Technology, Grant No. 202101010101018), and the “Unveiling the Leader” Project: Key Technologies and Demonstration for the Construction of a Green Airport and Intelligent Management and Control Platform, funded by the Changzhi Municipal Bureau of Science and Technology (No funding number).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The code for the method and original data can be accessed through the following websites: Code URL: https://anonymous.4open.science/r/E2E_OVStitch-06DE (13 March 2025); StabStitch-D dataset URL: https://github.com/nie-lang/StabStitch (15 July 2024); DeepStab dataset URL: https://opendatalab.org.cn/OpenDataLab/DeepStab (15 April 2024); NUS dataset URL: https://www.modelscope.cn/datasets/zcmaas/NUS_video-stabilization/files (7 March 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nie, Y.; Su, T.; Zhang, Z.; Sun, H.; Li, G. Dynamic video stitching via shakiness removing. IEEE Trans. Image Process. 2017, 27, 164–178. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Yu, S. Parallax-robust surveillance video stitching. Sensors 2015, 16, 7. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Liu, S.; He, T.; Zhu, S.; Zeng, B.; Gabbouj, M. Joint video stitching and stabilization from moving cameras. IEEE Trans. Image Process. 2016, 25, 5491–5503. [Google Scholar] [CrossRef] [PubMed]
- Lai, W.S.; Gallo, O.; Gu, J.; Sun, D.; Yang, M.H.; Kautz, J. Video stitching for linear camera arrays. arXiv 2019, arXiv:1907.13622. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardo, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H. Fully-convolutional Siamese networks for object tracking. In Computer Vision–ECCV 2016 Workshops: Amsterdam, The Netherlands, October 8–10 and 15–16, 2016, Proceedings, Part II 14; Springer: Cham, Switzerland, 2016; pp. 850–865. [Google Scholar]
- Zhang, J.; Tao, D. Empowering things with intelligence: A survey of the progress, challenges, and opportunities in artificial intelligence of things. IEEE Internet Things J. 2020, 8, 7789–7817. [Google Scholar] [CrossRef]
- Bradley, A.; Klivington, J.; Triscari, J.; van der Merwe, R. Cinematic-L1 video stabilization with a log-homography model. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 1041–1049. [Google Scholar]
- Liu, S.; Yuan, L.; Tan, P.; Sun, J. Bundled camera paths for video stabilization. ACM Trans. Graph. (TOG) 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Liu, S.; Tan, P.; Yuan, L.; Sun, J.; Zeng, B. Meshflow: Minimum latency online video stabilization. In Lecture Notes in Computer Science, Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part VI 14; Springer International Publishing: Cham, Switzerland, 2016; pp. 800–815. [Google Scholar]
- Roberto e Souza, M.; Maia, H.A.; Pedrini, H. Survey on digital video stabilization: Concepts, methods, and challenges. ACM Comput. Surv. (CSUR) 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Nie, L.; Lin, C.; Liao, K.; Zhang, Y.; Liu, S.; Ai, R.; Zhao, Y. Eliminating Warping Shakes for Unsupervised Online Video Stitching. In Lecture Notes in Computer Science, Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer Nature: Cham, Switzerland, 2024; pp. 390–407. [Google Scholar]
- Liu, S.; Ye, N.; Wang, C.; Luo, K.; Wang, J.; Sun, J. Content-aware unsupervised deep homography estimation and its extensions. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 2849–2863. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Wan, G.; Bai, H.; Kong, X.; Tang, B.; Wang, F. Real-time Video Stabilization Algorithm based on SuperPoint. IEEE Trans. Instrum. Meas. 2023, 73, 1–13. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Maybank, S.J.; Tao, D. Dut: Learning video stabilization by simply watching unstable videos. IEEE Trans. Image Process. 2022, 31, 4306–4320. [Google Scholar] [CrossRef] [PubMed]
- Jia, Q.; Li, Z.; Fan, X.; Zhao, H.; Teng, S.; Ye, X.; Latecki, L.J. Leveraging line-point consistence to preserve structures for wide parallax image stitching. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 12186–12195. [Google Scholar]
- Nie, L.; Lin, C.; Liao, K.; Liu, S.; Zhao, Y. Unsupervised deep image stitching: Reconstructing stitched features to images. IEEE Trans. Image Process. 2021, 30, 6184–6197. [Google Scholar] [CrossRef] [PubMed]
- Nie, L.; Lin, C.; Liao, K.; Liu, S.; Zhao, Y. Parallax-tolerant unsupervised deep image stitching. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 7399–7408. [Google Scholar]
- Nie, L.; Lin, C.; Liao, K.; Zhang, Y.; Liu, S.; Zhao, Y. StabStitch++: Unsupervised Online Video Stitching with Spatiotemporal Bidirectional Warps. IEEE Trans. Pattern Anal. Mach. Intell. 2025; early access. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).