Whole-Body Motion Generation for Balancing of Biped Robot
Abstract
:1. Introduction
- A novel method for generating arm motions via optimization, designed to minimize whole-body angular momentum and improve balance in the presence of disturbances.
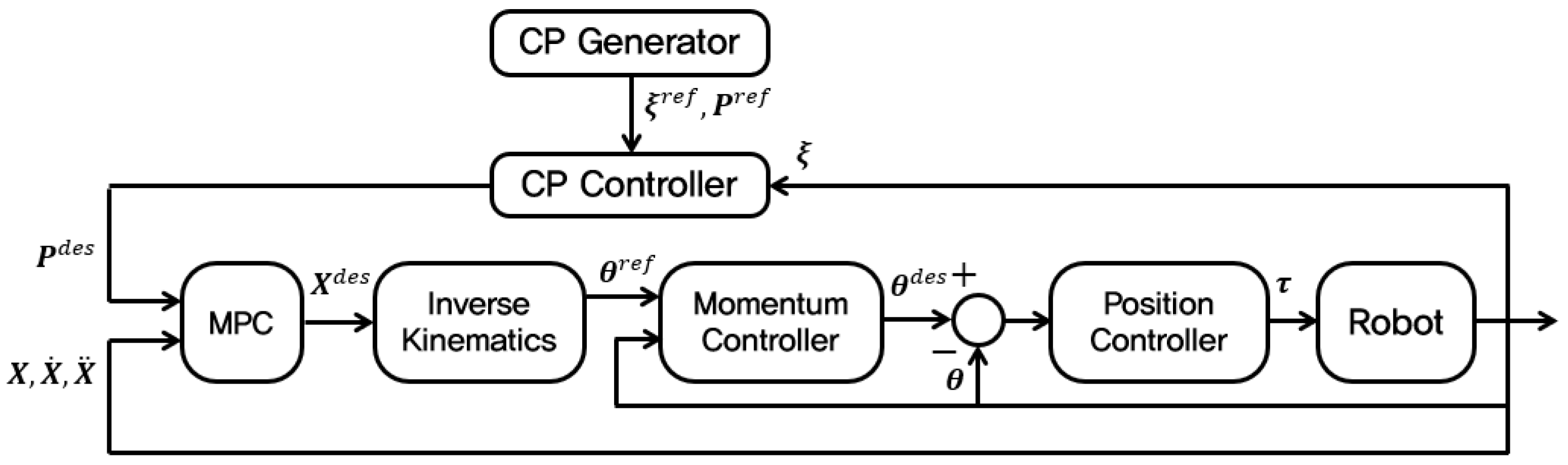
- An integrated whole-body motion generation framework that combines CP control, MPC, and momentum control. This extended and unified modular design improves stability and adaptability, particularly where lower-body-only control is insufficient.
2. Walking Pattern Generation
2.1. Linear Inverted Pendulum Model
2.2. Capture Point
2.3. Capture Point Reference Generation for Constant ZMP
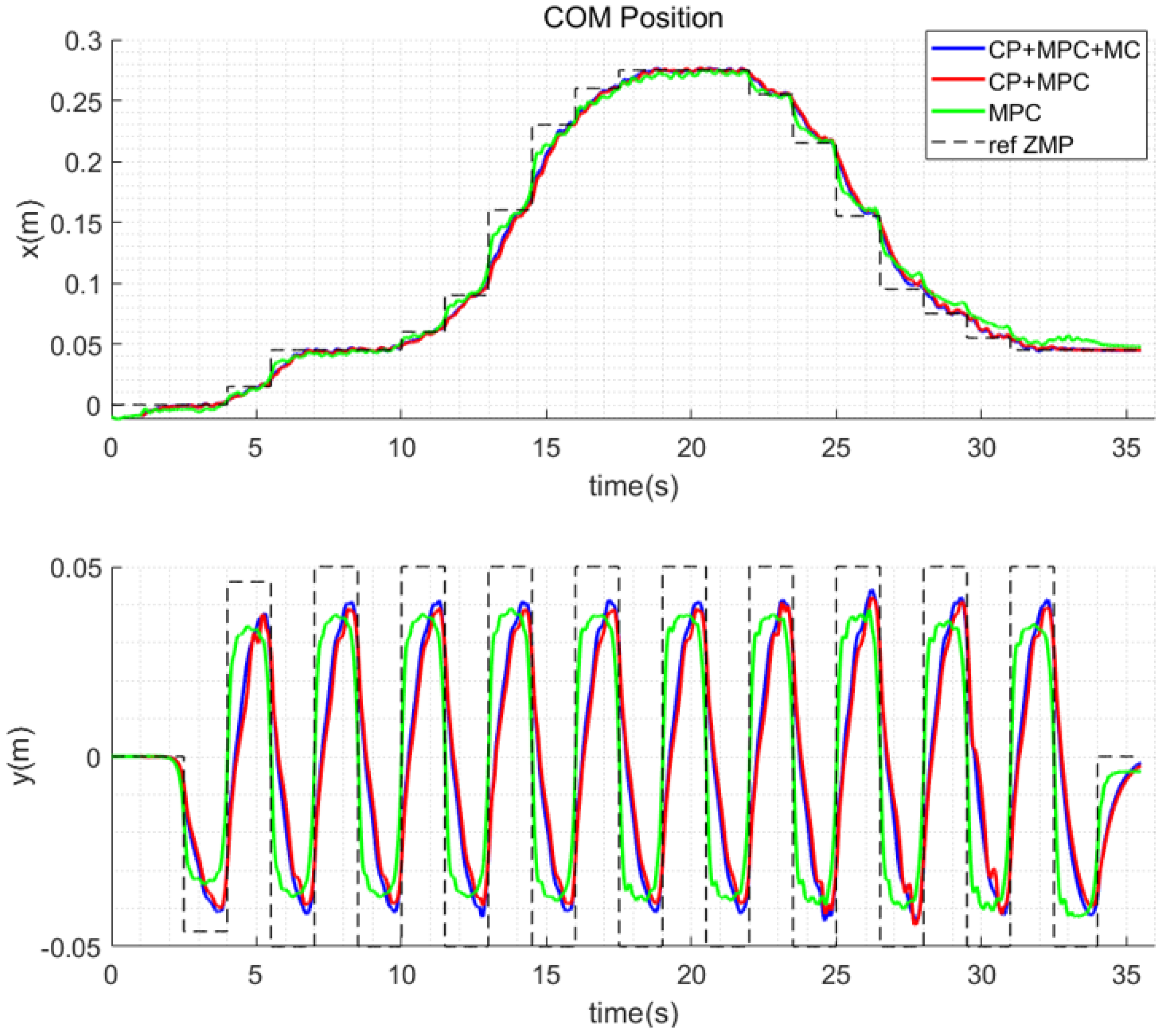
3. Generation of COM Trajectory
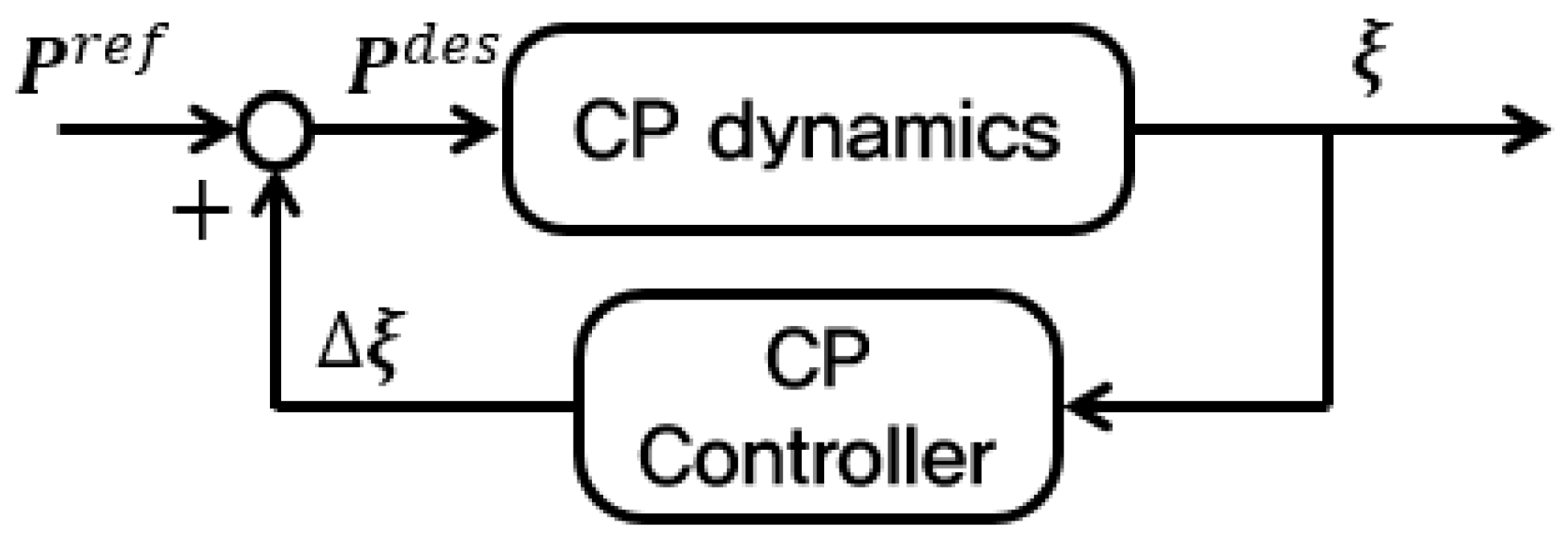
3.1. ZMP Modification Through CP Control
3.2. COM Trajectory Generation Using MPC
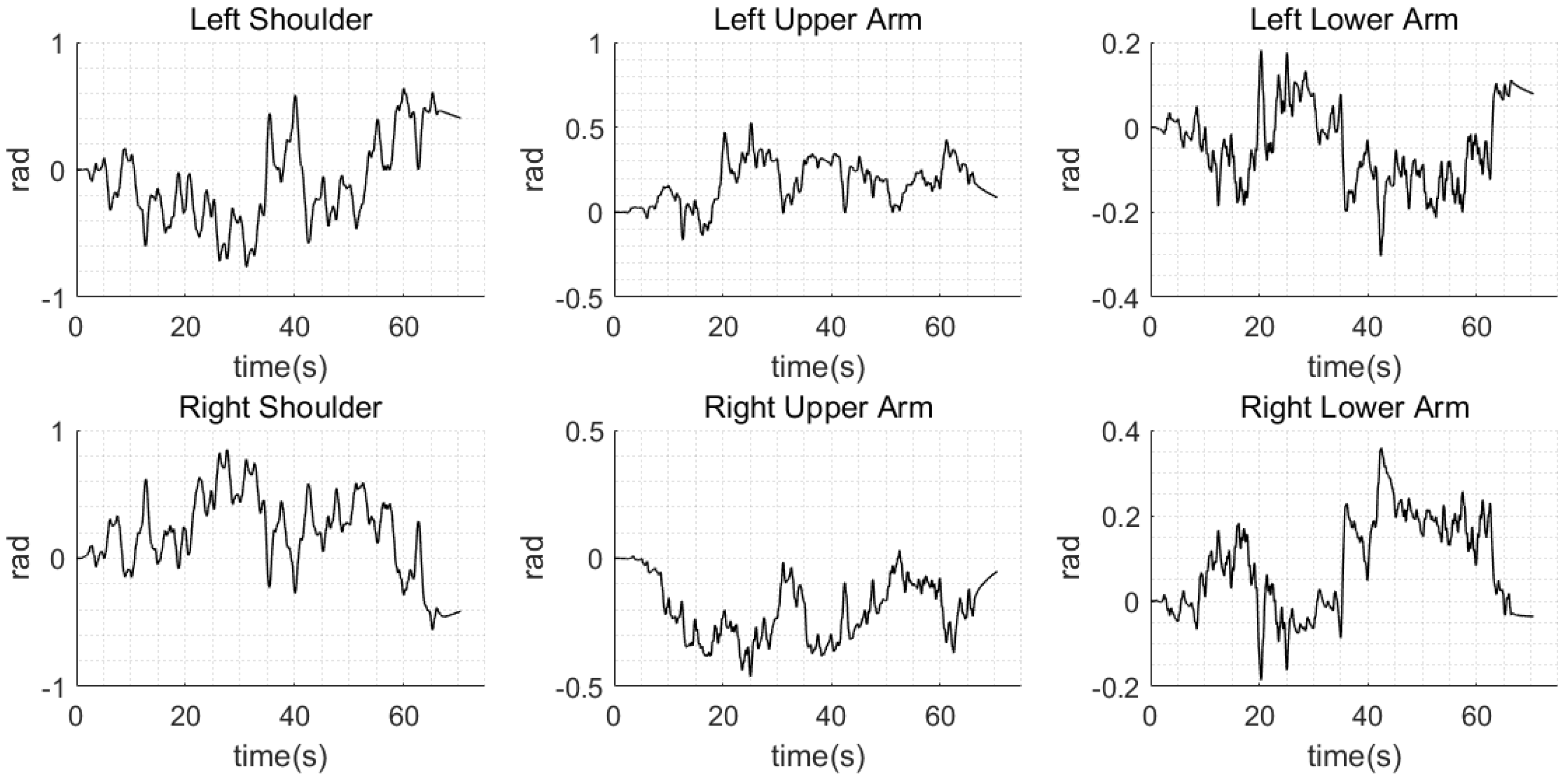
4. Generation of Arm Motion
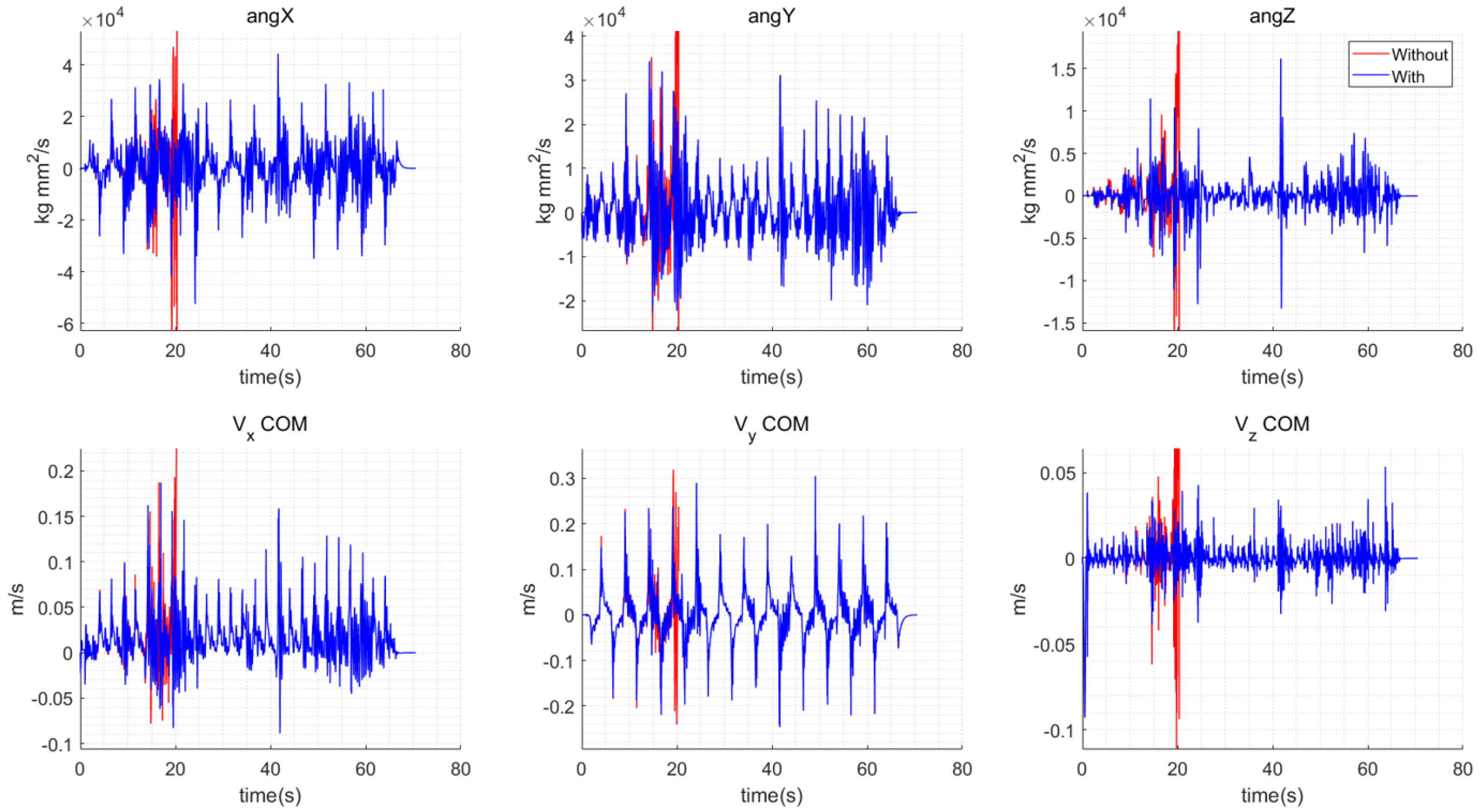
4.1. Momentum Equation
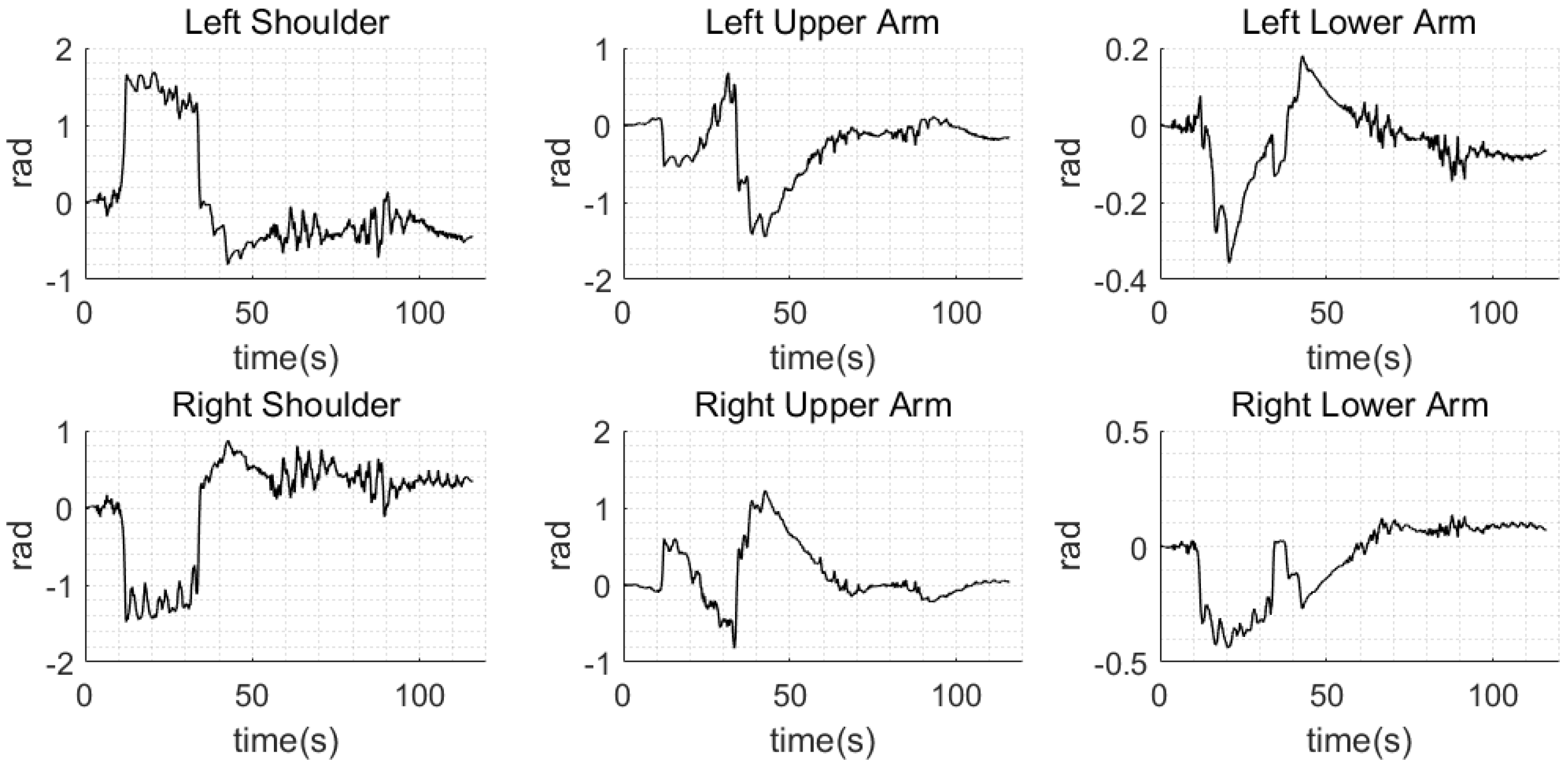
4.2. Momentum Control Using Optimization
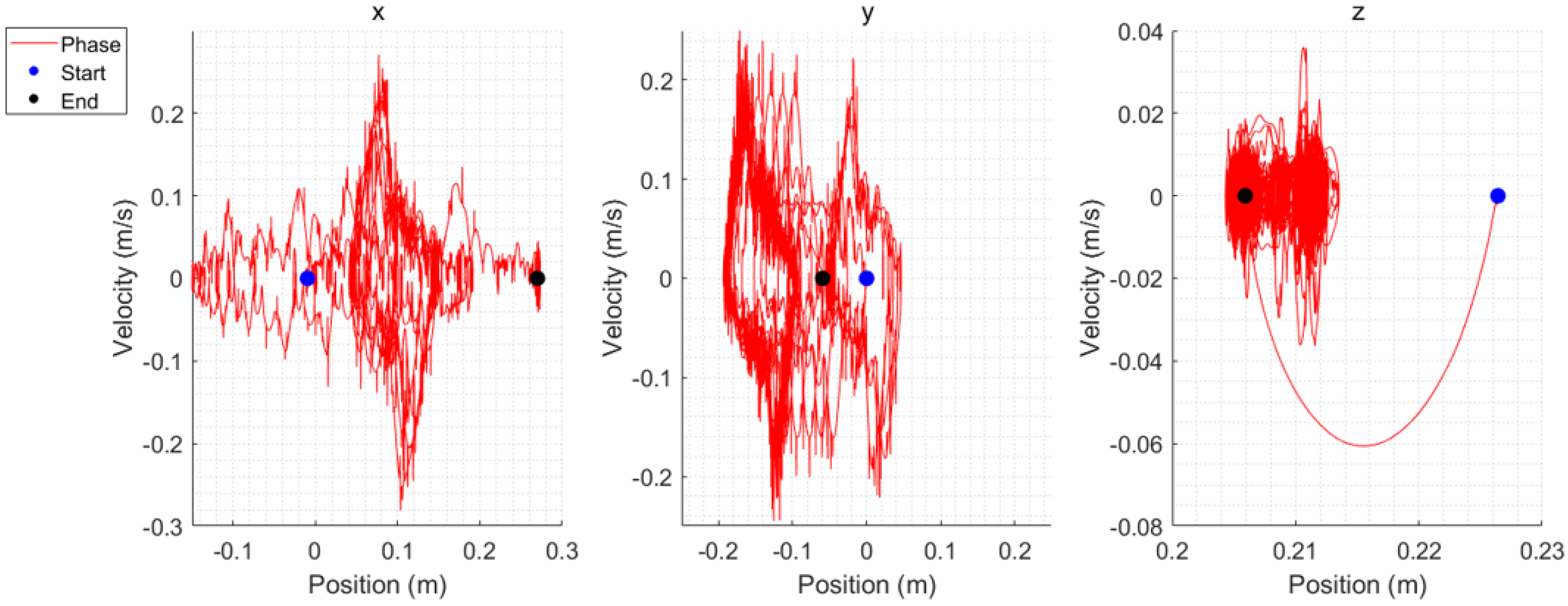
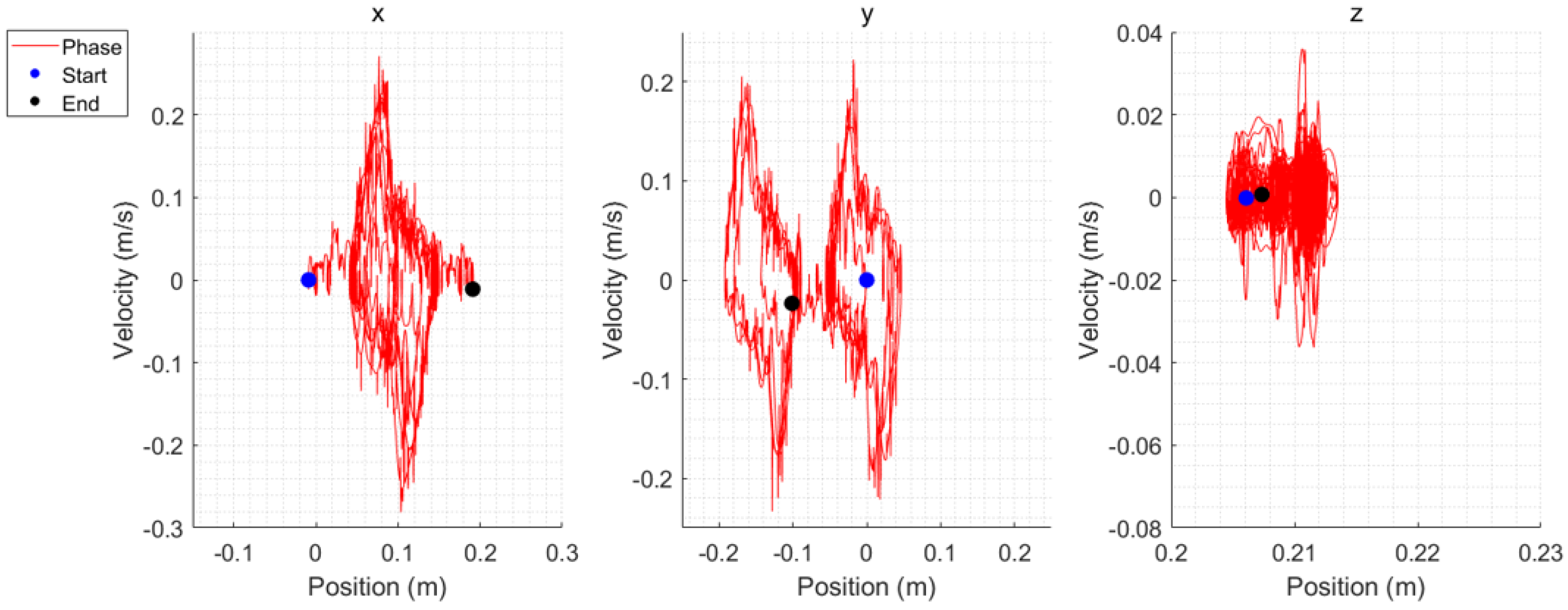
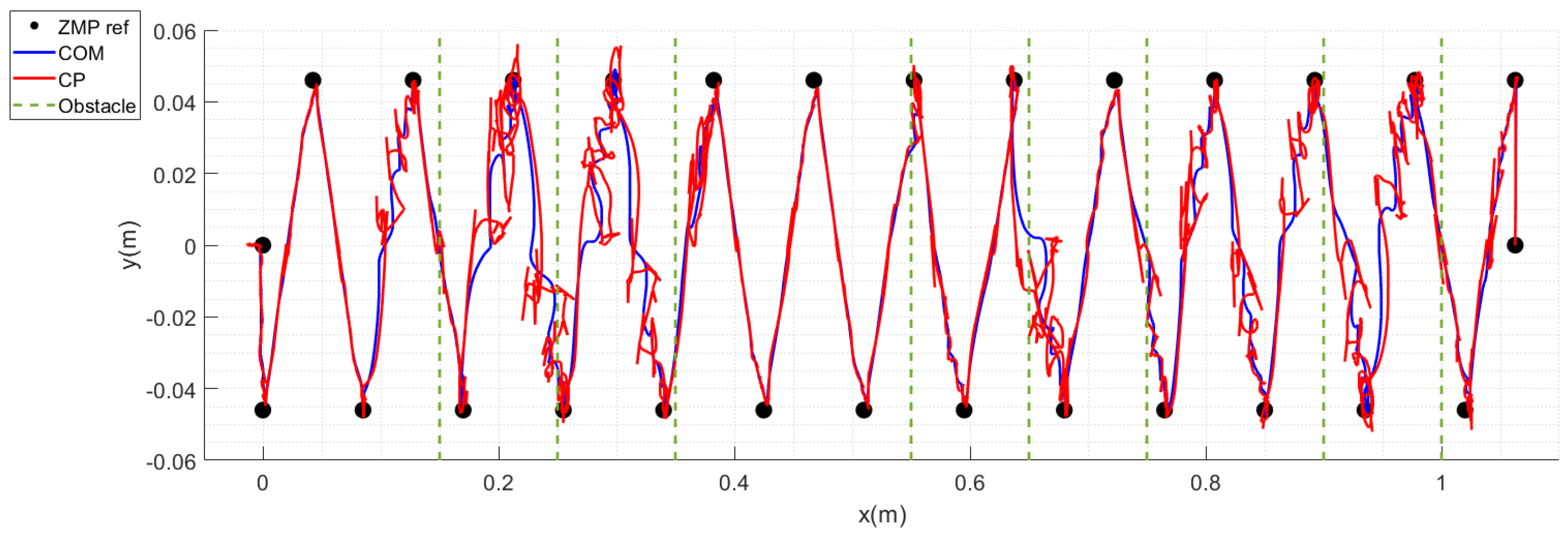
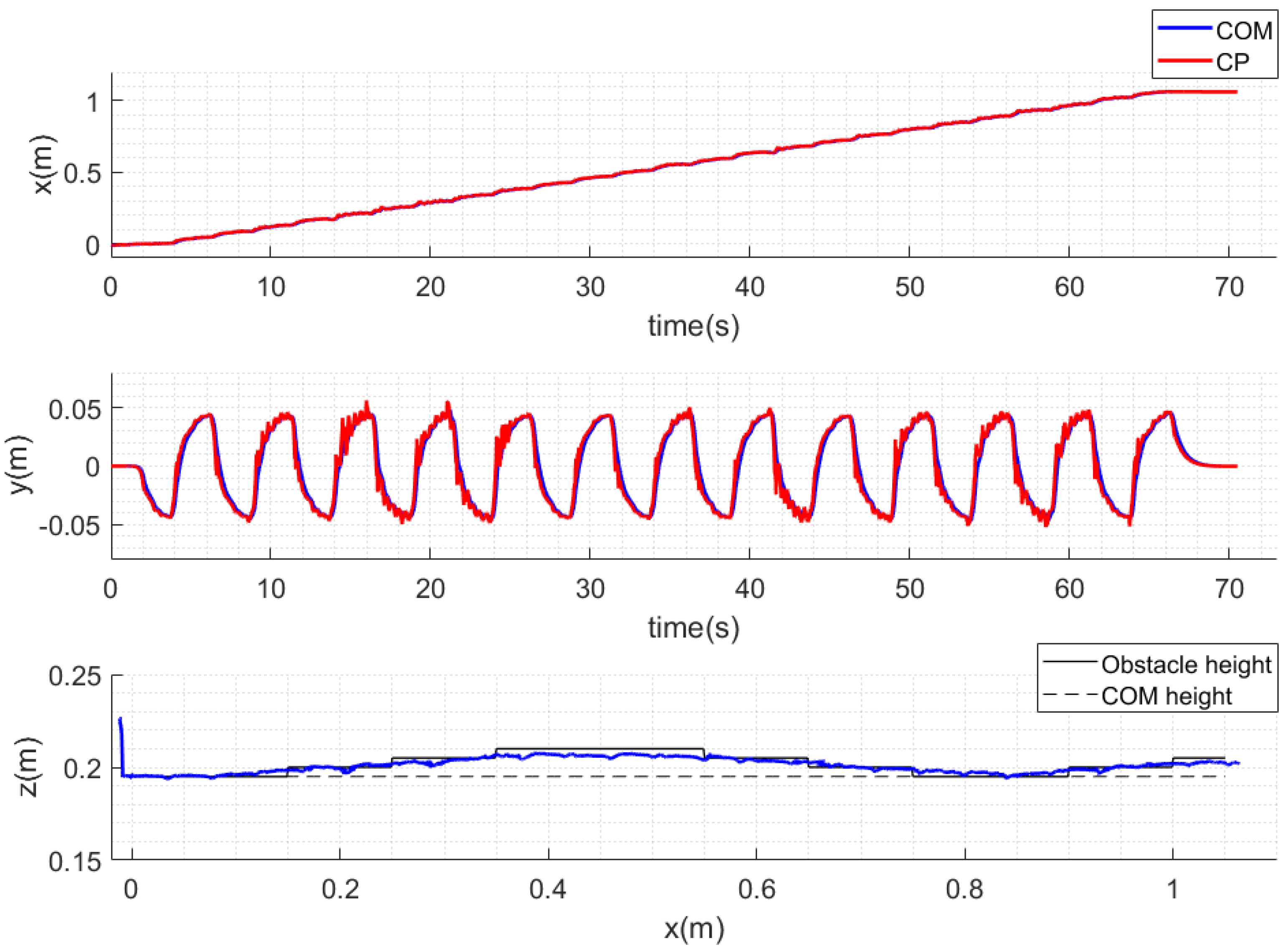
5. Simulation
5.1. Simulation Environment
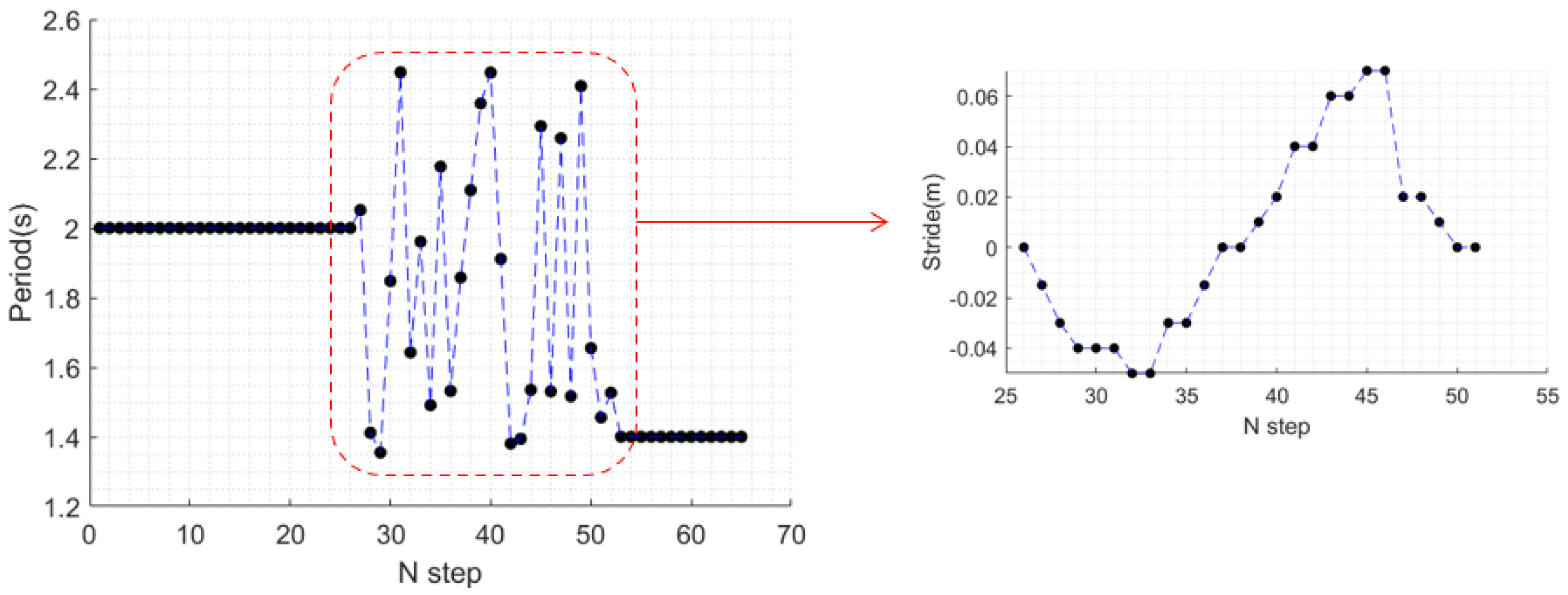
5.2. Variable Stride and Step Period
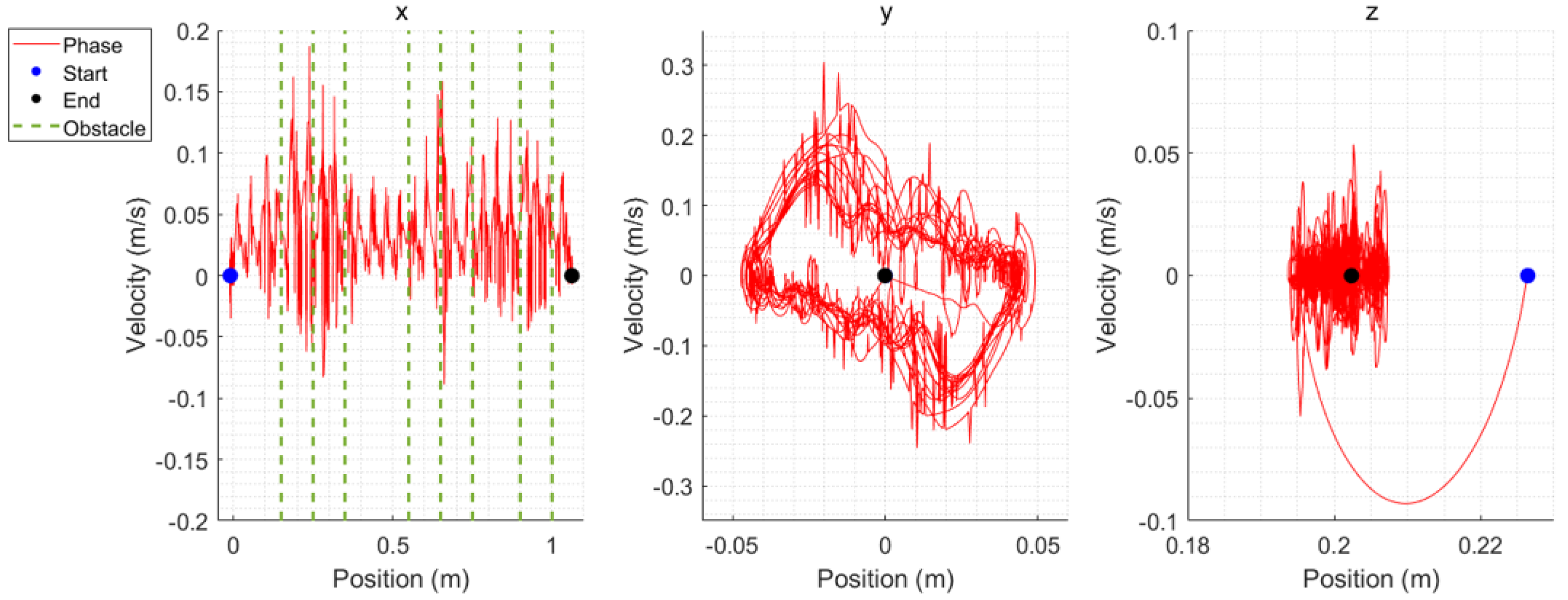
5.3. Unexpected Obstacles
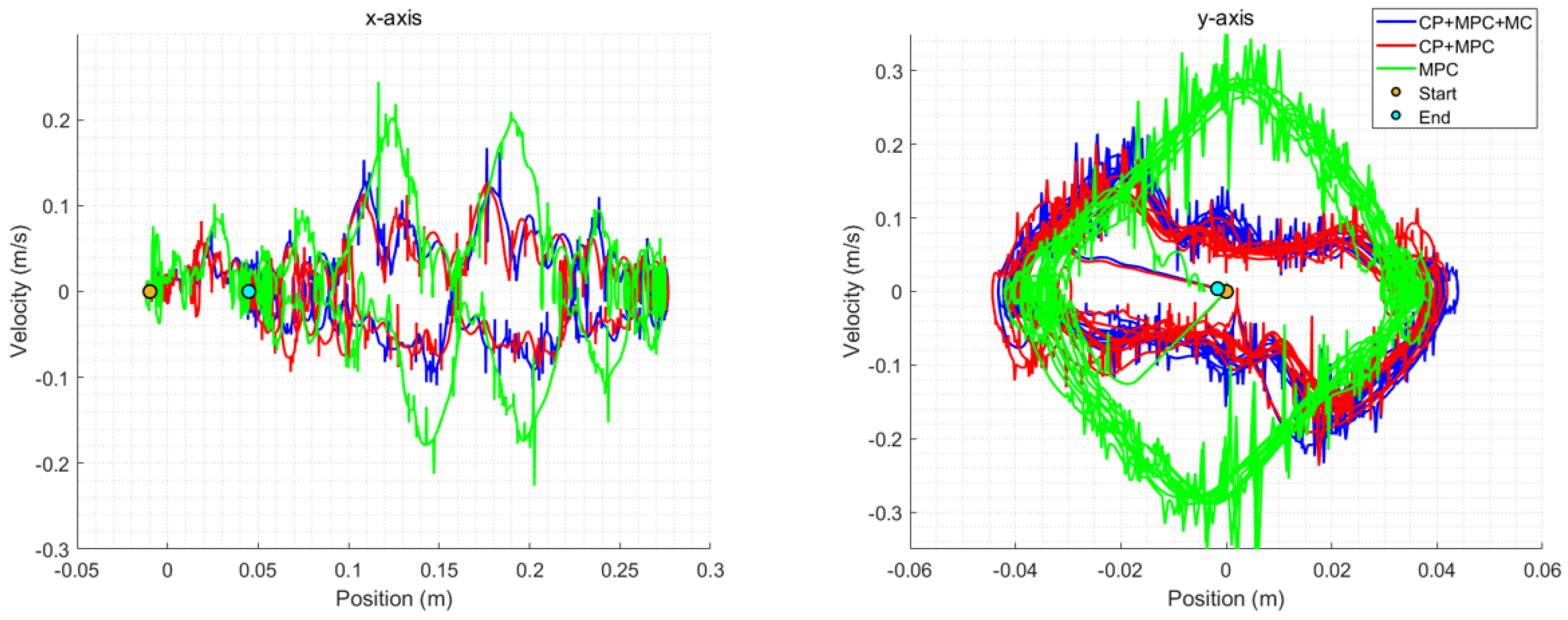
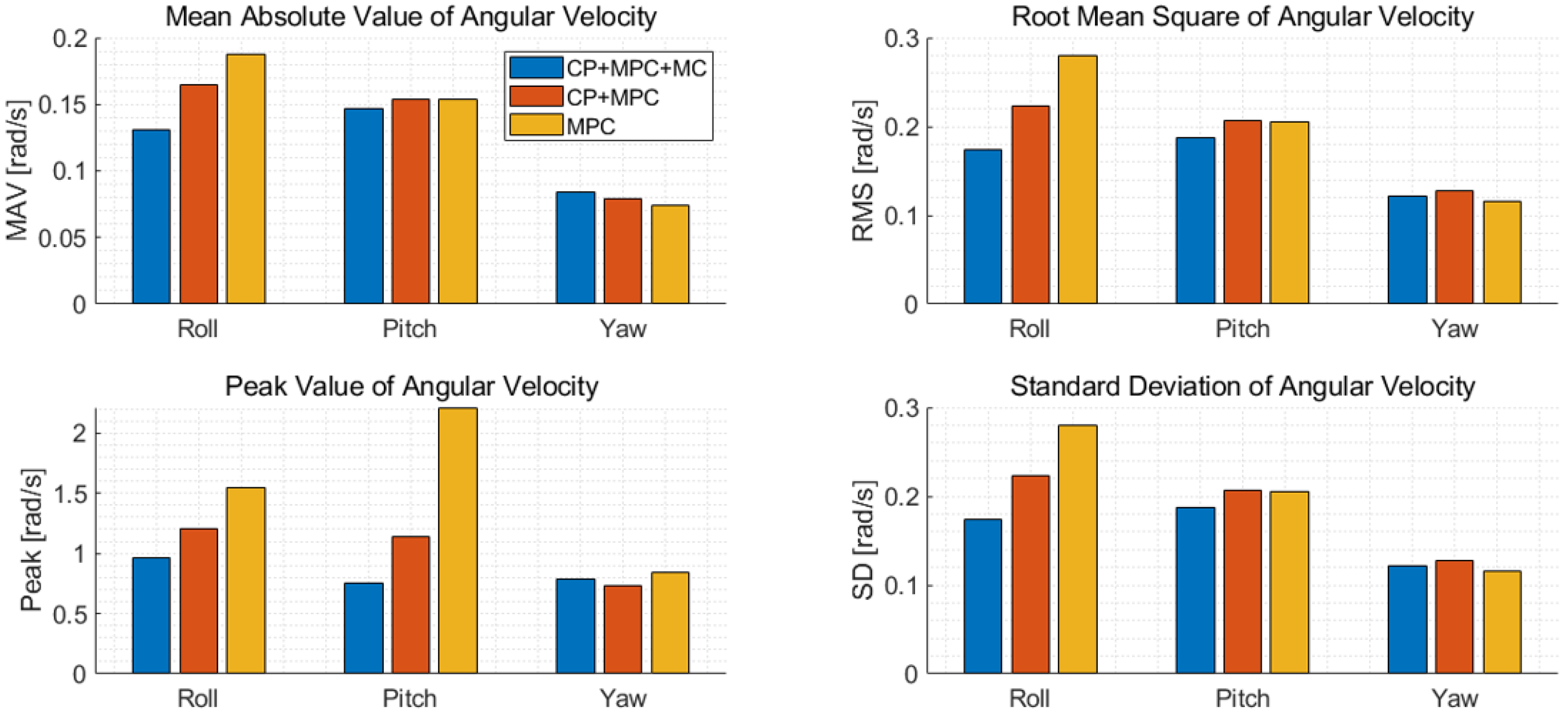
5.4. Comparative Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tong, Y.; Liu, H.; Zhang, Z. Advancements in humanoid robots: A comprehensive review and future prospects. IEEE/CAA J. Autom. Sin. 2024, 11, 301–328. [Google Scholar] [CrossRef]
- Huang, H.; Liu, S.Q. Are consumers more attracted to restaurants featuring humanoid or non-humanoid service robots? Int. J. Hosp. Manag. 2022, 107, 103310. [Google Scholar] [CrossRef]
- Song, C.S.; Kim, Y.K. The role of the human-robot interaction in consumers’ acceptance of humanoid retail service robots. J. Bus. Res. 2022, 146, 489–503. [Google Scholar] [CrossRef]
- Darvish, K.; Penco, L.; Ramos, J.; Cisneros, R.; Pratt, J.; Yoshida, E.; Ivaldi, S.; Pucci, D. Teleoperation of humanoid robots: A survey. IEEE Trans. Robot. 2023, 39, 1706–1727. [Google Scholar] [CrossRef]
- Vianello, L.; Penco, L.; Gomes, W.; You, Y.; Anzalone, S.M.; Maurice, P.; Thomas, V.; Ivaldi, S. Human-humanoid interaction and cooperation: A review. Curr. Robot. Rep. 2021, 2, 441–454. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3D linear inverted pendulum mode: A simple modeling for a biped walking pattern generation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001. [Google Scholar]
- Park, J.H.; Kim, K.D. Biped robot walking using gravity-compensated inverted pendulum mode and computed torque control. In Proceedings of the IEEE International Conference on Robotics and Automation, Leuven, Belgium, 20–20 May 1998. [Google Scholar]
- Cho, J.; Park, J.H. Model predictive control of running biped robot. Appl. Sci. 2022, 12, 11183. [Google Scholar] [CrossRef]
- Nakaura, S.; Sampei, M. Balance control analysis of humanoid robot based on ZMP feedback control. In Proceedings of the International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped walking pattern generation by using preview control of zero-moment point. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003. [Google Scholar]
- Katayama, S.; Murooka, M.; Tazaki, Y. Model predictive control of legged and humanoid robots: Models and algorithms. Adv. Robot. 2023, 37, 298–315. [Google Scholar] [CrossRef]
- Wieber, P.B. Trajectory free linear model predictive control for stable walking in the presence of strong perturbations. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Genoa, Italy, 4–6 December 2006. [Google Scholar]
- Herdt, A.; Perrin, N.; Wieber, P.B. LMPC based online generation of more efficient walking motions. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Osaka, Japan, 29 November–1 December 2012. [Google Scholar]
- Pratt, J.; Carff, J.; Drakunov, S.; Goswami, A. Capture point: A step toward humanoid push recovery. In Proceedings of the IEEE–RAS International Conference on Humanoid Robots, Genoa, Italy, 4–6 December 2006. [Google Scholar]
- Hof, A.L.; Gazendam, M.G.J.; Sinke, W.E. The condition for dynamic stability. J. Biomech. 2005, 38, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Takenaka, T.; Matsumoto, T.; Yoshiike, T. Real-time motion generation and control for biped robot—1st report: Walking gait pattern generation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009. [Google Scholar]
- Hof, A.L. The ‘extrapolated center of mass’ concept suggests a simple control of balance in walking. Hum. Mov. Sci. 2008, 27, 112–125. [Google Scholar] [CrossRef] [PubMed]
- Englsberger, J.; Ott, C.; Roa, M.A.; Albu-Schäffer, A.; Hirzinger, G. Bipedal walking control based on capture point dynamics. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Kamioka, T.; Kaneko, H.; Takenaka, T.; Yoshiike, T. Simultaneous optimization of ZMP and footsteps based on the analytical solution of divergent component of motion. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar]
- Herdt, A.; Diedam, H.; Wieber, P.B.; Dimitrov, D.; Mombaur, K.; Diehl, M. Online walking motion generation with automatic footstep placement. Adv. Robot. 2010, 24, 719–737. [Google Scholar] [CrossRef]
- Shafiee-Ashtiani, M.; Yousefi-Koma, A.; Shariat-Panahi, M. Robust bipedal locomotion control based on model predictive control and divergent component of motion. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017. [Google Scholar]
- Joe, H.M.; Oh, J.H. Balance recovery through model predictive control based on capture point dynamics for biped walking robot. Robot. Auton. Syst. 2018, 105, 1–10. [Google Scholar] [CrossRef]
- Luo, X.; Xia, D.; Zhu, C. Planning and control of biped robots with upper body. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, South Korea, 9–14 October 2016. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Resolved momentum control: Humanoid motion planning based on the linear and angular momentum. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Kajita, S.; Nagasaki, T.; Kaneko, K.; Hirukawa, H. ZMP-based biped running control. IEEE Robot. Autom. Mag. 2007, 14, 63–72. [Google Scholar] [CrossRef]
- Lee, S.H.; Goswami, A. A momentum-based balance controller for humanoid robots on non-level and non-stationary ground. Auton. Robot. 2012, 33, 399–414. [Google Scholar] [CrossRef]
- Otani, T.; Hashimoto, K.; Miyamae, S.; Ueta, H.; Sakaguchi, M.; Kawakami, Y.; Lim, H.O.; Takanishi, A. Angular momentum compensation in yaw direction using upper body based on human running. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017. [Google Scholar]
- Kim, S.; Kim, C.; Park, J.H. Human-like arm motion generation for humanoid robots using motion capture database. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3486–3491. [Google Scholar]
- Yang, A.; Chen, Y.; Naeem, W.; Fei, M.; Chen, L. Humanoid motion planning of robotic arm based on human arm action feature and reinforcement learning. Mechatronics 2021, 78, 102630. [Google Scholar] [CrossRef]
- Khazoom, C.; Kim, S. Humanoid arm motion planning for improved disturbance recovery using model hierarchy predictive control. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 6607–6613. [Google Scholar]
- Englsberger, J.; Ott, C. Integration of vertical com motion and angular momentum in an extended capture point tracking controller for bipedal walking. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Osaka, Japan, 29 November–1 December 2012. [Google Scholar]
- Englsberger, J.; Ott, C.; Albu-Schäffer, A. Three-dimensional bipedal walking control using divergent component of motion. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Kumar, S.; Rajeevlochana, C.G.; Saha, S.K. Realistic modeling and dynamic simulation of kuka kr5 robot using recurdyn. In Proceedings of the 6th Asian Conference on Multibody Dynamics, Shanghai, China, 26–30 August 2012. [Google Scholar]
- Gummer, A.; Sauer, B. Modeling planar slider-crank mechanisms with clearance joints in RecurDyn. Multibody Syst. Dyn. 2014, 31, 127–145. [Google Scholar] [CrossRef]















| Part | Mass (kg) |
|---|---|
| Body | |
| Head | |
| Neck | |
| Shoulder (2) | |
| Upper arm (2) | |
| Lower arm (2) | |
| Pelvic (2) | |
| Thigh (2) | |
| Tibia (2) | |
| Ankle (2) | |
| Foot (2) | |
| Total |
| Gain | Value |
|---|---|
| 30 | |
| 600 | |
| Location (mm) | Height (mm) |
|---|---|
| 150∼250 | 5 |
| 250∼350 | 10 |
| 350∼550 | 15 |
| 550∼650 | 10 |
| 650∼750 | 5 |
| 900∼1000 | 5 |
| 1000∼1200 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, Y.; Park, J.H. Whole-Body Motion Generation for Balancing of Biped Robot. Appl. Sci. 2025, 15, 5828. https://doi.org/10.3390/app15115828
Cho Y, Park JH. Whole-Body Motion Generation for Balancing of Biped Robot. Applied Sciences. 2025; 15(11):5828. https://doi.org/10.3390/app15115828
Chicago/Turabian StyleCho, Yonghee, and Jong Hyeon Park. 2025. "Whole-Body Motion Generation for Balancing of Biped Robot" Applied Sciences 15, no. 11: 5828. https://doi.org/10.3390/app15115828
APA StyleCho, Y., & Park, J. H. (2025). Whole-Body Motion Generation for Balancing of Biped Robot. Applied Sciences, 15(11), 5828. https://doi.org/10.3390/app15115828







