Structural Design of Segmented Linings for High-Pressure CAES in Underground Workings: Method and Case Study
Abstract
1. Introduction
2. Materials and Methods
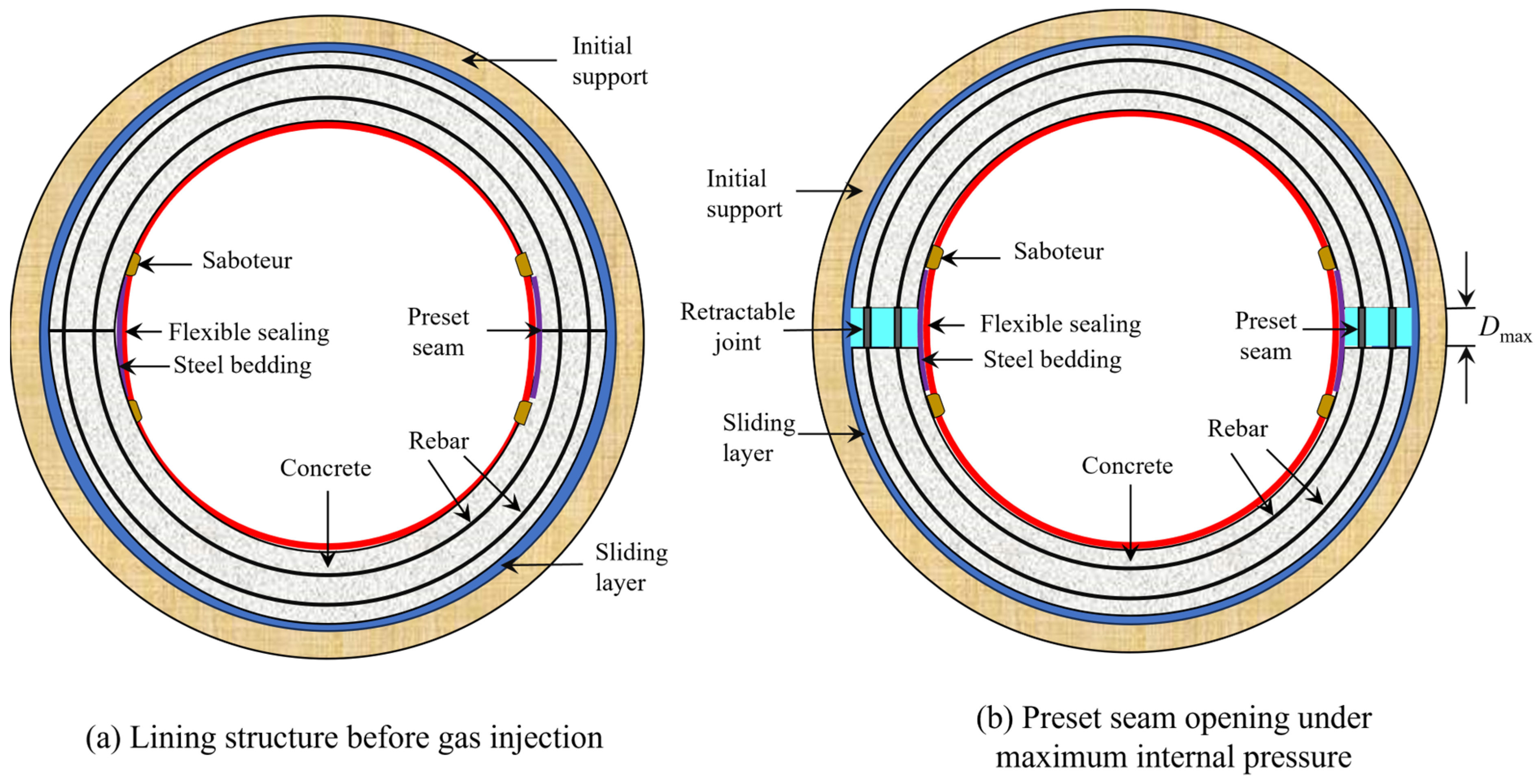
2.1. Governing Equations for Segmented Linings
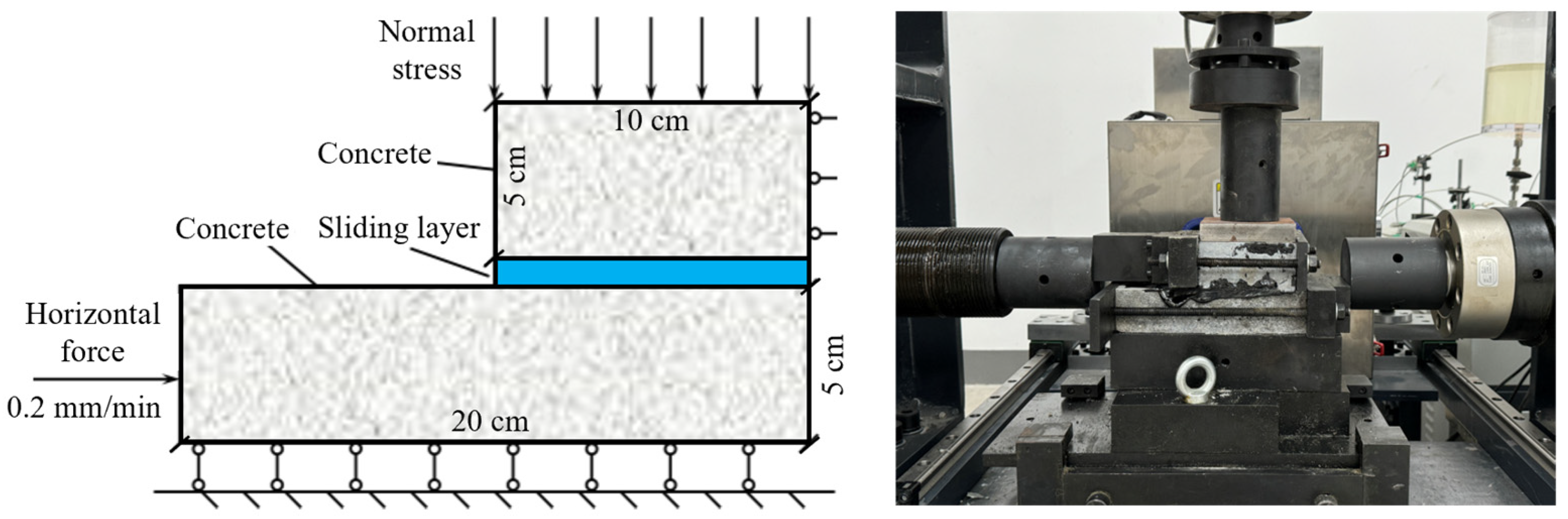
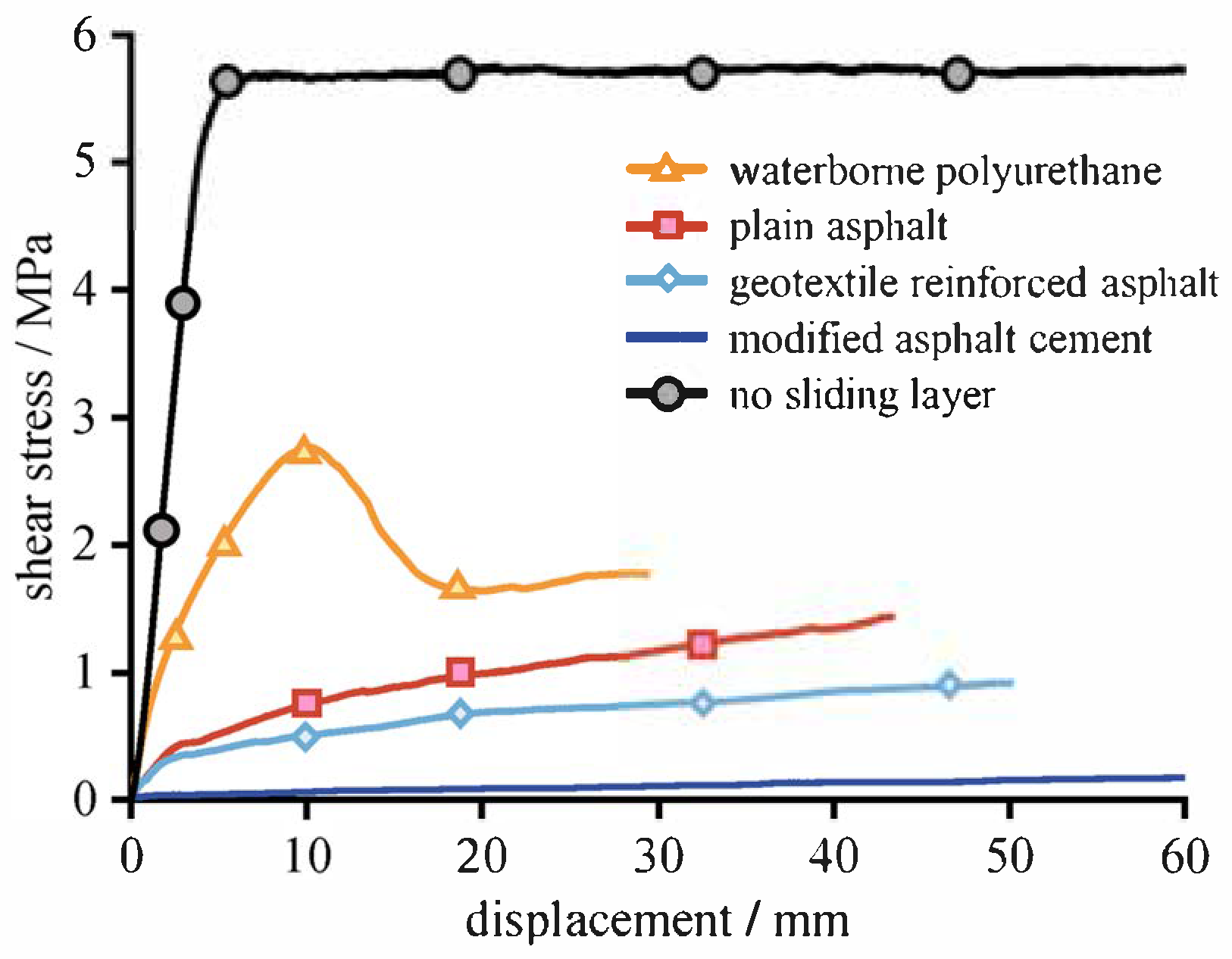
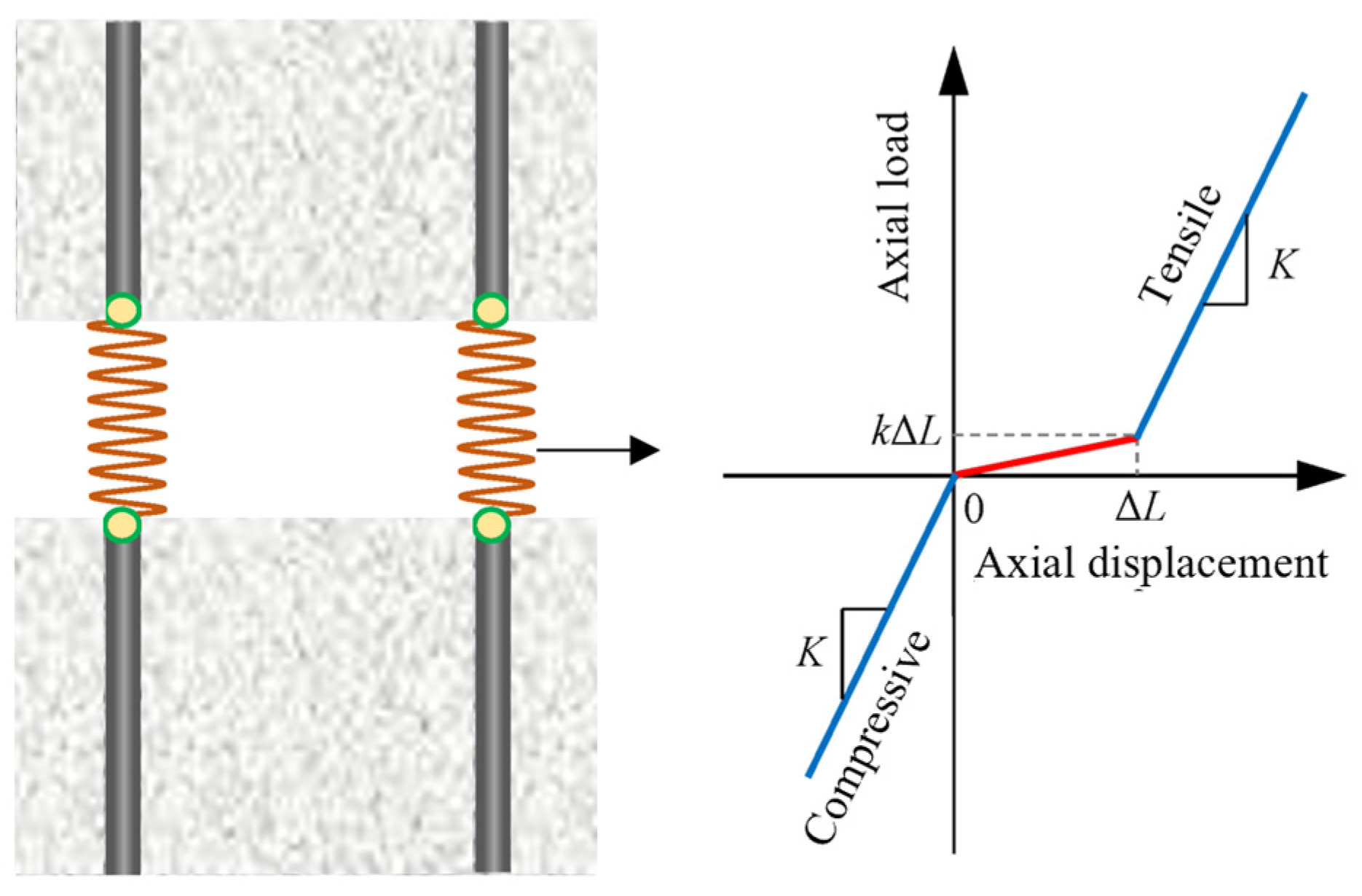
2.2. Mechanical Behavior of Sliding Layers
2.3. Calculation for the Maximum Crack Width of Segmented Linings
2.4. Implementation
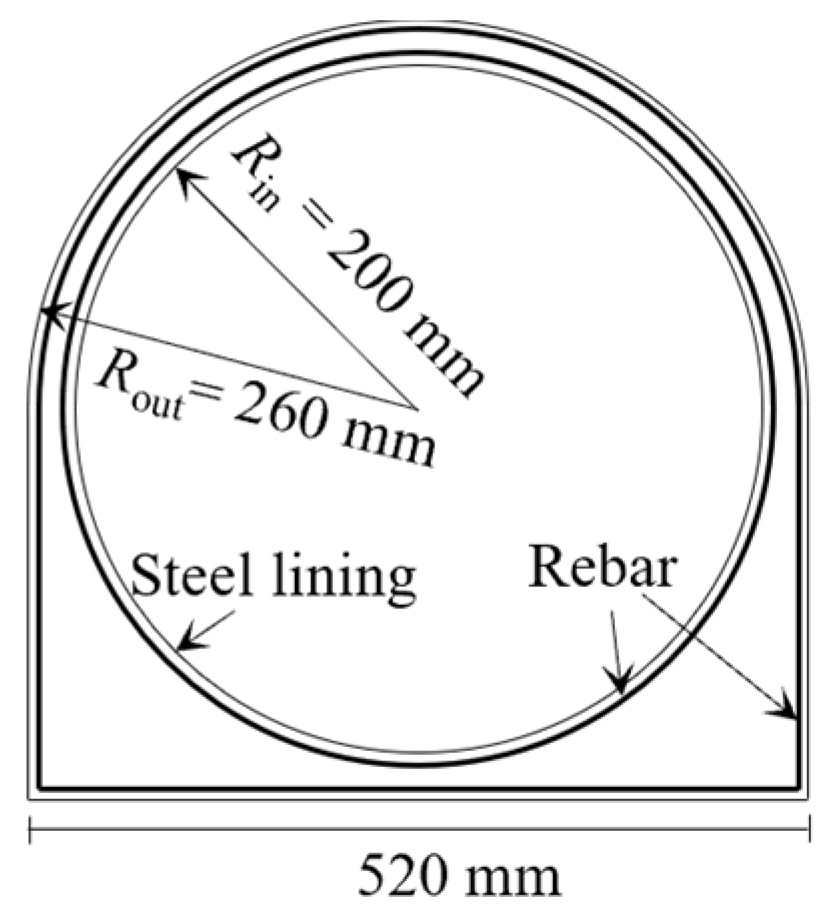
3. Validation
4. Case Study
4.1. Case Background
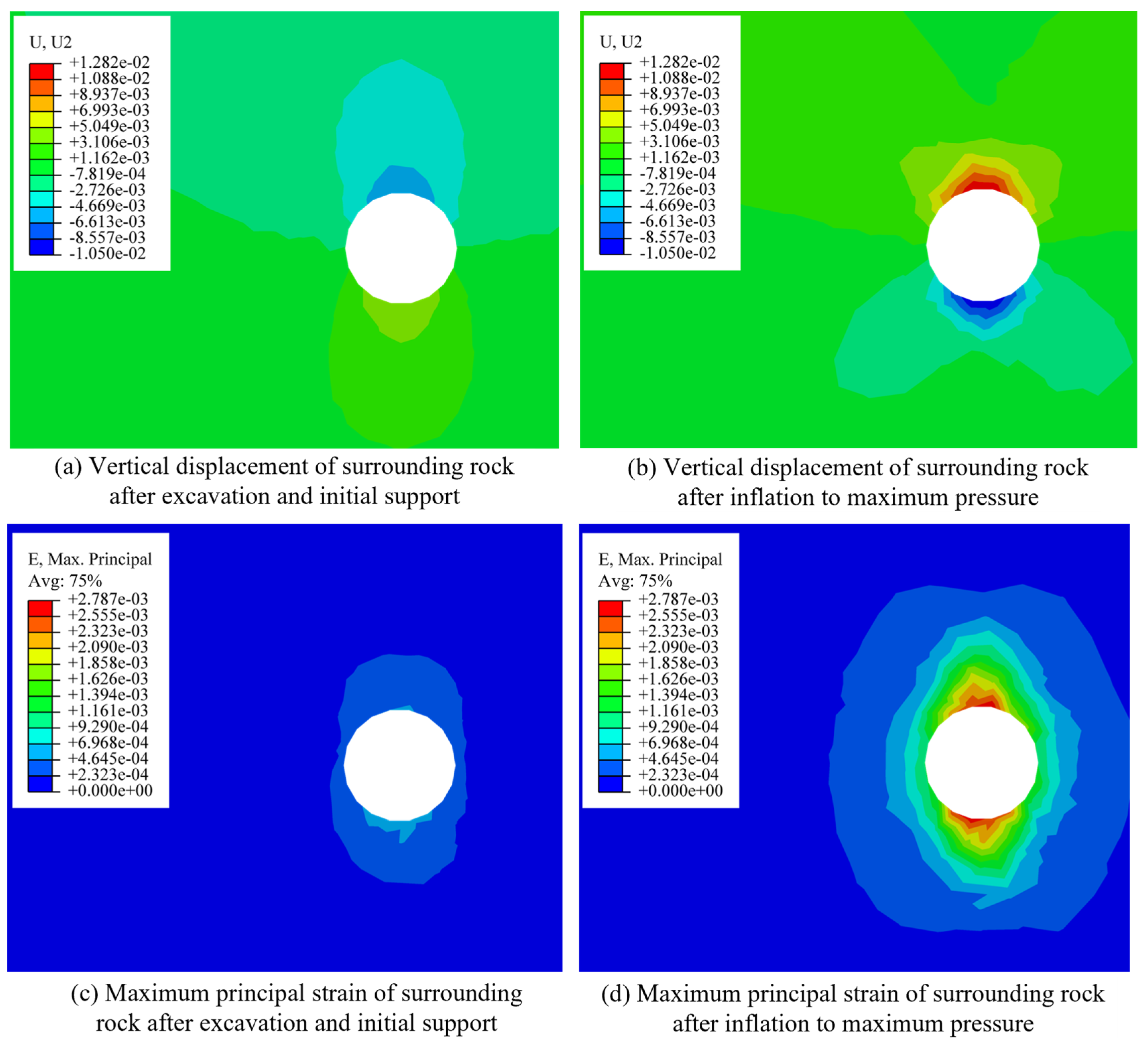
4.2. Mechanical Response of the Surrounding Rock
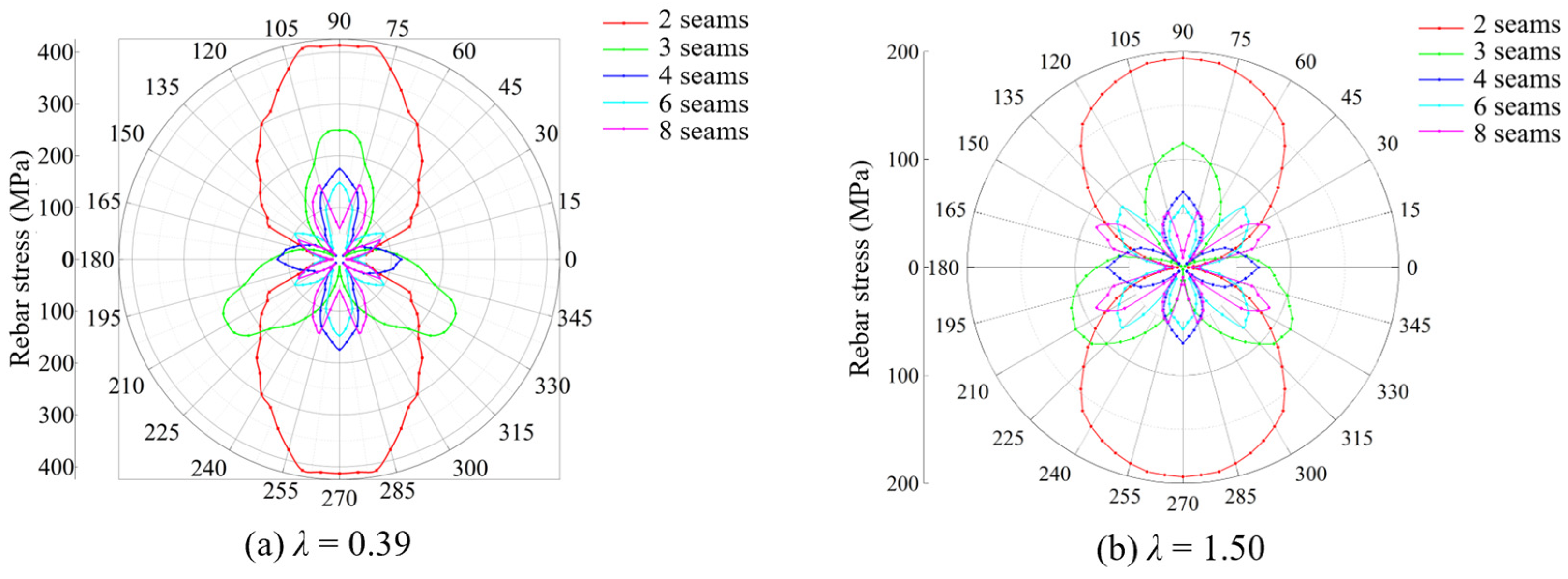
4.3. Design of the Number of Preset Seams
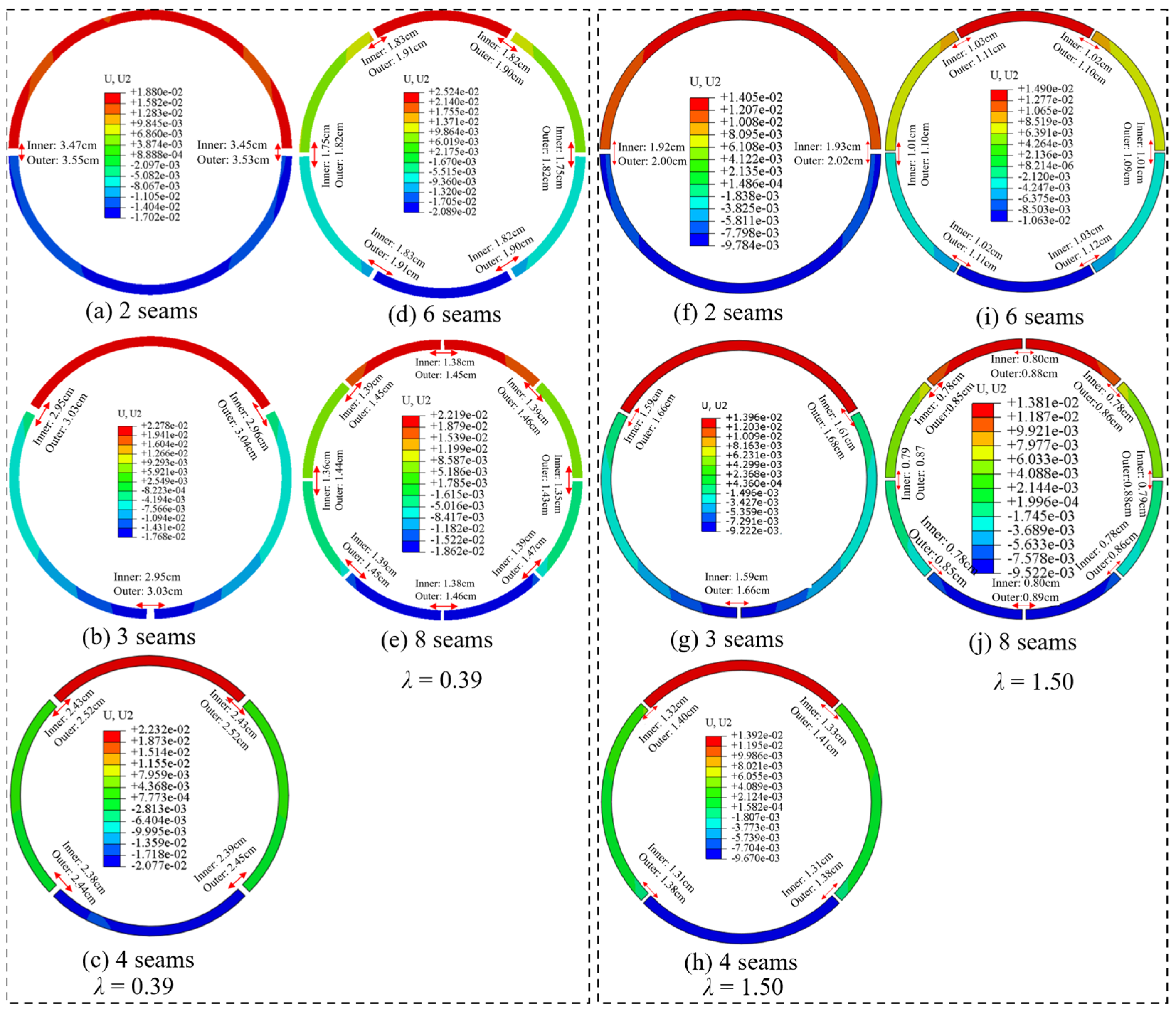
4.3.1. Lateral Pressure Coefficient Less than One
4.3.2. Lateral Pressure Coefficient Greater than One
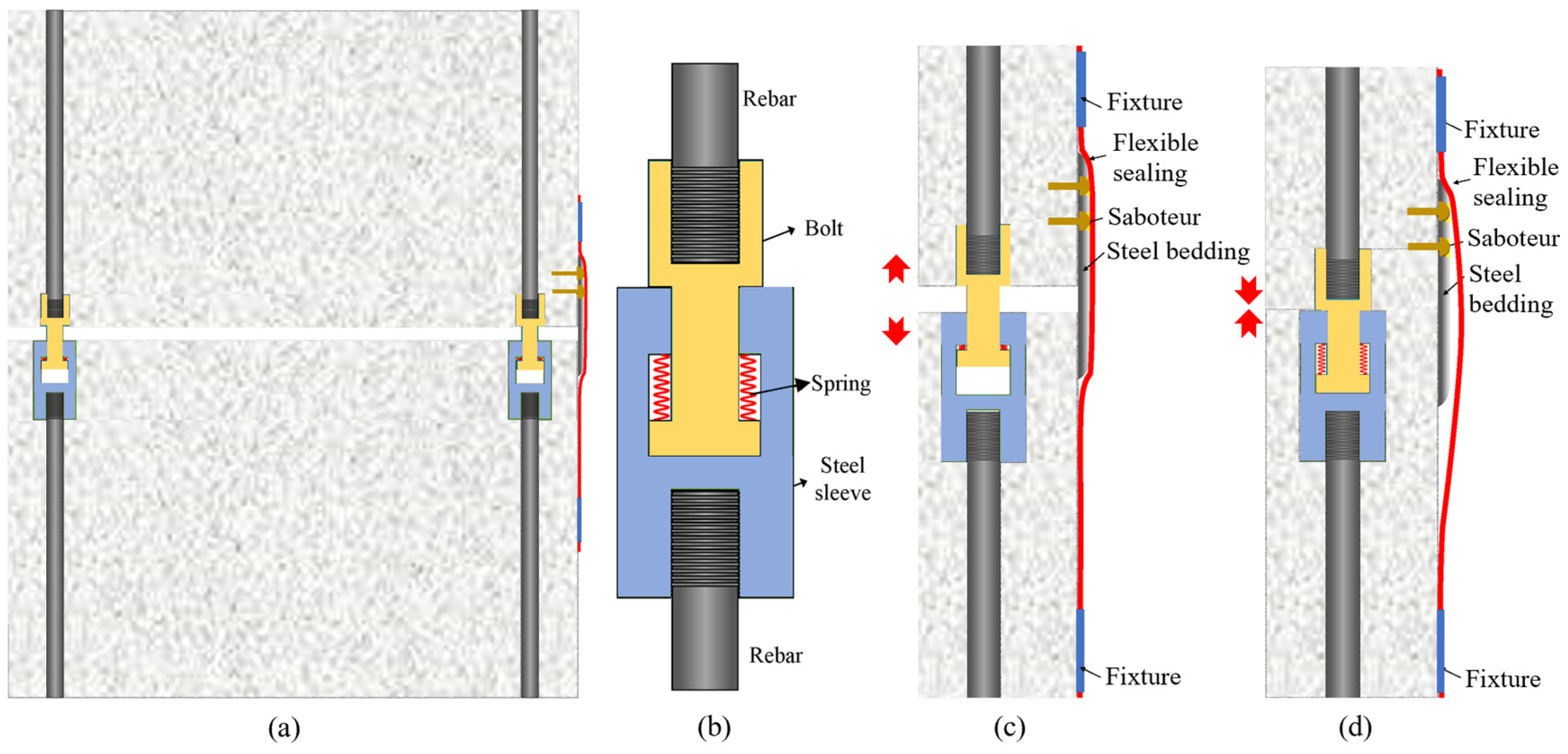
4.4. Design of Retractable Joints
4.5. Design of Reinforcement Ratio
5. Discussion
5.1. Maximum Crack Width of the Lining
5.2. Maximum Seam Opening Displacement of the Lining
5.3. Generalizability of the Proposed Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, A.; Li, P.; Fan, L.; Yi, Z.; Tang, X.; Fei, W. Influence of drainage system on the stability of underground CAES gas storage under different lateral pressure coefficients. Tunn. Undergr. Space Technol. 2025, 159, 106444. [Google Scholar] [CrossRef]
- Prado, L.Á.D.; Menéndez, J.; Bernardo-Sánchez, A.; Galdo, M.; Loredo, J.; Fernández-Oro, J.M. Thermodynamic analysis of compressed air energy storage (CAES) reservoirs in abandoned mines using different sealing layers. Appl. Sci. 2021, 11, 2573. [Google Scholar] [CrossRef]
- Liang, W.; Yang, D.; Bian, H. Mechanical properties of rubber sealing material in lined rock cavern for compressed air energy storage considering thermo-mechanical coupling effect. Constr. Build. Mater. 2025, 458, 139494. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, Z.; Shi, Z.; Mao, Q.; Liao, J.; Tian, X. Mechanical performance of polyurethane polymer mortar—A novel sealing material for CAES man-made caverns. J. Energy Storage 2025, 106, 114845. [Google Scholar] [CrossRef]
- Qin, S.; Xia, C.; Zhou, S. Air tightness of compressed air storage energy caverns with polymer sealing layer subjected to various air pressures. J. Rock Mech. Geotech. Eng. 2023, 15, 2105–2116. [Google Scholar] [CrossRef]
- Damasceno, D.R.; Spross, J.; Johansson, F. Rock mass response for lined rock caverns subjected to high internal gas pressure. J. Rock Mech. Geotech. Eng. 2023, 15, 119–129. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Yang, C.; Zhang, Z.; Chen, W. Numerical simulation on cavern support of compressed air energy storage (CAES) considering thermo-mechanical coupling effect. Energy 2023, 282, 128916. [Google Scholar] [CrossRef]
- Shatskyi, I.P.; Makoviichuk, M.V.; Shcherbii, A.B. Equilibrium of cracked shell with flexible coating. In Shell Structures: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2017; Volume 4, pp. 165–168. [Google Scholar]
- Shatskyi, I.P.; Makoviichuk, M.V.; Shcherbii, A.B. Influence of flexible coating on the limit equilibrium of a spherical shell with meridional crack. Mater. Sci. 2020, 55, 484–491. [Google Scholar] [CrossRef]
- PCNECL. Design Specification for Hydraulic Concrete Structures; China Water and Power Press: Beijing, China, 2009. [Google Scholar]
- Li, P.; Kang, H.; Zhu, Q.; Wu, Y.; Zhang, J.; Fan, L.; Wang, Z. Numerical and experimental investigations of concrete lined compressed air energy storage system. J. Clean. Prod. 2023, 390, 136153. [Google Scholar] [CrossRef]
- Yu, Z.; Shen, S.; Li, M.; Zhang, M.; Tian, L.; Hua, G. An improved rock damage model from a cyclic temperature–triaxial loading experiment for compressed air energy storage caverns. Eng. Geol. 2025, 344, 107857. [Google Scholar] [CrossRef]
- Aghababaei, F.; Sedaee, B. Underground compressed air energy storage (CAES) in naturally fractured depleted oil reservoir: Influence of fracture. Geoenergy Sci. Eng. 2025, 244, 213496. [Google Scholar] [CrossRef]
- Hu, B.; Yu, L.; Mi, X.; Xu, F.; Li, S.; Li, W.; Wei, C.; Zhang, T. Comparative analysis of thermodynamic and mechanical responses between underground hydrogen storage and compressed air energy storage in lined rock caverns. Int. J. Min. Sci. Technol. 2024, 34, 531–543. [Google Scholar] [CrossRef]
- Zhou, S.W.; Xia, C.C.; Zhao, H.B.; Mei, S.H.; Zhou, Y. Numerical simulation for the coupled thermo-mechanical performance of a lined rock cavern for underground compressed air energy storage. J. Geophys. Eng. 2017, 14, 1382–1398. [Google Scholar] [CrossRef]
- Wan, F.; Jiang, Z.; Tian, X.; Konietzky, H.; Xiao, Z. A thermo-hydro-mechanical damage model for lined rock cavern for compressed air energy storage. J. Energy Storage 2024, 78, 110186. [Google Scholar] [CrossRef]
- Monte, F.L.; Harmon, J.; Andrade, J.; Ferrara, L. Fiber-Reinforced Concrete for an Innovative Energy Storage Plant: From the Experimental Investigation to the Structural Design. In RILEM-fib International Symposium on Fibre Reinforced Concrete; Springer Nature: Cham, Switzerland, 2024; pp. 252–259. [Google Scholar]
- Xiang, Y.; Zhang, G.; Wang, X.; Zhang, G.; Xiong, F.; Tang, Z.; Hua, D. Load-sharing characteristics of lined rock caverns of compressed air energy storage system: A theoretical analysis. Appl. Energy 2025, 388, 125626. [Google Scholar] [CrossRef]
- Ma, Y.; Rao, Q.; Huang, D.; Liu, Z.; Yi, W.; Li, P. Gas-mechanical coupled crack initiation analysis for local air-leakage of compressed air energy storage (CAES) cavern with consideration of seepage effect. Theor. Appl. Fract. Mech. 2023, 125, 103827. [Google Scholar] [CrossRef]
- Li, Y.; Xue, P.; Liu, Y.; Wang, J.; Yin, W. Modeling underground performance of compressed air energy storage in a practical flat aquifer: Insights on the permeability effects. Energy 2025, 332, 135592. [Google Scholar] [CrossRef]
- Hori, M.; Goda, Y.; Onishi, H. Mechanical behaviour of surrounding rock mass and new lining structure of air-tight pressure cavern. In Proceedings of the 10th ISRM Congress, Sandton, South Africa, 8–12 September 2003; p. ISRM-10CONGRESS-2003-088. [Google Scholar]
- Ishihata, T. Underground compressed air storage facility for CAES-G/T power plant utilizing an airtight lining. News J. Int. Soc. Rock Mech. 1997, 5, 17–21. [Google Scholar]
- Nishimoto, Y.; Tobase, T.; Hori, M.; Sawada, T. In-situ chamber tests for underground compressed-air storage facilities. In Proceedings of the ISRM International Symposium—EUROCK 96, Turin, Italy, 2–5 September 1996; p. ISRM-EUROCK-1996-124. [Google Scholar]
- Gasanzade, F.; Bauer, S. Approximating coupled power plant and geostorage simulations for compressed air energy storage in porous media. Appl. Energy 2025, 380, 125070. [Google Scholar] [CrossRef]
- Wu, K.; Song, J.; Zheng, X.; Zhao, N.; Shao, Z.; Chu, Z. The deformation coordination-dominated design of yielding supports applied in large deformation tunnels. Acta Geotech. 2024, 19, 2499–2513. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, G.; Xia, C.; Du, S. Mechanical behavior of a new segmented lining for underground rock caverns with high internal pressure. Comput. Geotech. 2024, 167, 106100. [Google Scholar] [CrossRef]
- Zhang, G.C.; Xu, C.; Xia, C.C. Mechanical properties of composite segmented lining for high-pressure gas storage cavern considering shear deformation. Comput. Geotech. 2024, 45, 3533–3544. [Google Scholar]
- Qiu, K.; Li, S.; Wang, Z.; Wan, Z.; Zhao, S. Research on influence patterns of fault activation on lining structures in lined rock caverns for underground hydrogen energy storage. Int. J. Hydrogen Energy 2024, 58, 605–620. [Google Scholar] [CrossRef]
- Zhang, D.M.; Zhou, W.D.; Bu, X.H.; Jiang, Y.; Jia, K.; Yang, G.H. Failure mechanism and stiffness degradation of double lining with inner R/FRC lining subjected to internal water pressure. Tunn. Undergr. Space Technol. 2022, 130, 104737. [Google Scholar] [CrossRef]
- Damasceno, D.R.; Spross, J.; Johansson, F. Effect of rock joints on lined rock caverns subjected to high internal gas pressure. J. Rock Mech. Geotech. Eng. 2023, 15, 1625–1635. [Google Scholar] [CrossRef]
- PCCECL. Code for Design of Hydraulic Tunnel; China Water and Power Press: Beijing, China, 2020. [Google Scholar]
- Yang, T.W. Research on Calculation Model of Crack Width of Steel Lined Reinforced Concrete Penstocks; Hubei University of Technology: Wuhan, China, 2020. [Google Scholar]
- JTG/T D70—2010; Design Guidelines for Highway Tunnels. China Communications Press: Beijing, China, 2010. (In Chinese)







| αc | αt | fc,r/MPa | ft,r/MPa | εc,r/10−3 | εt,r/10−5 |
|---|---|---|---|---|---|
| 1.94 | 1.25 | 19.1 | 1.71 | 1.79 | 9.5 |
| Material Types | Plain Asphalt | Geotextile-Reinforced Asphalt | Modified Asphalt Cement | Waterborne Polyurethane | No Sliding Layer |
|---|---|---|---|---|---|
| Shear stiffness Kn (MPa·m−1) | 33.1 | 18.2 | 2.6 | 98.5 | 943.2 |
| Normal Stresses (MPa) | 8 | 10 | 12 | 15 |
|---|---|---|---|---|
| Shear stiffness Kn (MPa·m−1) | 20.1 | 33.1 | 118.2 | 147.3 |
| Retractable Joint | Maximum Stress in Inner Reinforcement (MPa) | Maximum Stress in Outer Reinforcement (MPa) | Maximum Crack Width of Linings (mm) | Maximum Seam Opening Displacement (cm) | Reinforcement Ratio | Reinforcement Design |
|---|---|---|---|---|---|---|
| Without joints | 145.3 | 60.8 | 0.12 | 1.91 | 2.0% | Inner: Φ25@100 mm Outer: Φ25@100 mm |
| With joints | 240.6 | 212.3 | 0.27 | 1.00 | 2.0% | Inner: Φ25@100 mm Outer: Φ25@100 mm |
| Rock Quality | Elastic Modulus (GPa) | Cohesion (MPa) | Friction Angle (°) | Density (kg/m3) | Poisson’s Ratio |
|---|---|---|---|---|---|
| Extremely hard | 34.0 | 2.2 | 61 | 2800 | 0.19 |
| Very hard | 25.0 | 1.8 | 55 | 2700 | 0.23 |
| Hard | 15.0 | 1.3 | 47 | 2500 | 0.25 |
| Medium quality | 9.0 | 0.9 | 41 | 2400 | 0.28 |
| Fair | 5.0 | 0.6 | 37 | 2300 | 0.30 |
| Poor | 3.0 | 0.4 | 33 | 2200 | 0.32 |
| Very poor | 2.0 | 0.3 | 28 | 2100 | 0.34 |
| Extremely poor | 1.3 | 0.2 | 22 | 2000 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Gao, M.; Xia, C. Structural Design of Segmented Linings for High-Pressure CAES in Underground Workings: Method and Case Study. Appl. Sci. 2025, 15, 5782. https://doi.org/10.3390/app15105782
Wang S, Gao M, Xia C. Structural Design of Segmented Linings for High-Pressure CAES in Underground Workings: Method and Case Study. Applied Sciences. 2025; 15(10):5782. https://doi.org/10.3390/app15105782
Chicago/Turabian StyleWang, Sheng, Mengfan Gao, and Caichu Xia. 2025. "Structural Design of Segmented Linings for High-Pressure CAES in Underground Workings: Method and Case Study" Applied Sciences 15, no. 10: 5782. https://doi.org/10.3390/app15105782
APA StyleWang, S., Gao, M., & Xia, C. (2025). Structural Design of Segmented Linings for High-Pressure CAES in Underground Workings: Method and Case Study. Applied Sciences, 15(10), 5782. https://doi.org/10.3390/app15105782






