Abstract
Multi-Key Fully Homomorphic Encryption (MKFHE) offers a powerful solution for secure multi-party computations, where data encrypted under different keys can be jointly computed without decryption. However, existing MKFHE schemes still face challenges such as large parameter sizes, inefficient evaluation key generation, complex homomorphic multiplication processes, and limited scalability in multi-hop scenarios. In this paper, we propose an enhanced multi-hop MKFHE scheme based on the Brakerski-Gentry-Vaikuntanathan (BGV) framework. Our approach eliminates the need for an auxiliary Gentry-Sahai-Waters (GSW)-type scheme, simplifying the design and significantly reducing the public key size. We propose novel algorithms for evaluation key generation and key switching that simplify the computation while allowing each party to independently precompute and share its evaluation keys, thereby reducing both computational overhead and storage costs. Additionally, we combine the tensor product and key switching processes through homomorphic gadget decomposition, developing a new homomorphic multiplication algorithm and achieving linear complexity with respect to the number of parties. Furthermore, by leveraging the Polynomial Chinese Remainder Theorem (Polynomial CRT), we design a ciphertext packing technique that transforms our BGV-type MKFHE scheme into a batched scheme with improved amortized performance. Our schemes feature stronger multi-hop properties and operate without requiring a predefined maximum number of parties, offering enhanced flexibility and scalability compared to existing similar schemes.
1. Introduction
The increasing adoption of big data and cloud computing has driven the need for secure outsourced computation. While cloud platforms enable efficient processing of large-scale data, they also introduce significant privacy risks, as sensitive data is often handled by untrusted servers. Fully Homomorphic Encryption (FHE), first proposed by Gentry in 2009 [1], provides a transformative cryptographic solution by allowing arbitrary computations on encrypted data without decryption. This powerful capability makes FHE particularly valuable in ciphertext retrieval [2], privacy-preserving data analytics [3], secure cloud computing, and confidential machine learning [4], where sensitive information must be processed without exposure. Since its inception, several highly influential single-key fully homomorphic encryption (SKFHE) schemes have been developed, including BGV [5], BFV [6,7], GSW [8], CKKS [9], and TFHE [10]. These schemes are renowned for their distinct advantages in functionality, computational efficiency, and adaptability to various application scenarios.
In cloud-based applications, especially in secure multi-party computation (MPC) protocols, multiple independent entities need to compute on their encrypted data collaboratively. However, SKFHE is not well-suited for multi-party settings, as it requires all plaintexts to be encrypted under the same secret key. This results in an authority concentration issue, where the entity holding the secret key can access and control all data, thereby potentially violating the privacy of other parties.
To address this limitation, Multi-Key Fully Homomorphic Encryption (MKFHE) [11,12,13,14,15,16,17,18,19,20] was introduced, enabling homomorphic operations on ciphertexts encrypted under different keys. Unlike SKFHE, MKFHE allows computations across independently encrypted data without requiring a shared secret key, making it a crucial cryptographic tool. Furthermore, MKFHE supports on-the-fly MPC [11], where the circuit to be evaluated can be dynamically chosen after the data providers upload their encrypted data. This feature allows computations to be carried out by a public server without requiring data owners to be online, significantly enhancing the flexibility and efficiency of real-time collaborative secure computing.
1.1. Related Works
The first MKFHE scheme was introduced by López-Alt et al. in 2012 [11]. Their construction enabled homomorphic evaluations over ciphertexts encrypted under different keys, with the computation results jointly decrypted by all participating parties. This approach addressed the challenge of collaborative encrypted computation across multiple users. However, this scheme relied on a non-standard security assumption related to NTRU [21] and suffered from exponential complexity growth with the number of participants, making it impractical for large-scale applications. In 2015, Clear et al. [12] extended the GSW scheme [8] to support a multi-identity (multi-key) setting, constructing the first MKFHE scheme based on the Learning with Errors (LWE) problem [22], thereby establishing its security under a standard security assumption. This work laid the foundation for subsequent optimizations and extensions of MKFHE. Mukherjee et al. [13] later simplified the scheme in [12] and proposed a new ciphertext extension algorithm, allowing for a single-round distributed decryption process for multi-key ciphertexts. This optimization enabled the construction of two-round MPC protocols. However, similar to [12], their scheme was limited to single-hop, meaning that the number of participants in the homomorphic computation had to be predefined. Furthermore, it did not support dynamic joining—once the homomorphic computation was performed, the resulting ciphertexts could not be further computed with ciphertexts from newly added participants.
To address this limitation, Peikert et al. [14] proposed a multi-hop MKFHE scheme based on the GSW framework, eliminating the need for prior knowledge of parties. The multi-hop nature of the scheme allows the output ciphertexts to continue being computed with ciphertexts from newly joined parties, enabling real-time, dynamic participation. Compared to [13], their approach also significantly reduced ciphertext size, though it still imposed a limitation on the maximum number of participants. Shortly thereafter, Brakerski and Perlman [15] proposed a fully dynamic MKFHE scheme based on the LWE assumption, allowing parties to dynamically join homomorphic computations without requiring a predefined number of participants. Their scheme supported an arbitrary polynomial number of parties and unlimited-depth homomorphic evaluations, with the spatial complexity of ciphertext extension and homomorphic operations growing only linearly with the number of parties. However, it relied on bootstrapping for ciphertext extension, and the generation of bootstrapping keys still required extending encrypted secret keys, significantly degrading efficiency.
In 2017, Chen et al. [16] proposed a batched multi-hop MKFHE scheme based on the BGV scheme [5], with security under the standard Ring Learning with Errors (RLWE) assumption [23]. Their scheme allowed ring elements to be encrypted as plaintexts, achieving higher computational efficiency. Additionally, they introduced methods for constructing two-round MPC protocols and threshold decryption protocols. In 2019, Li et al. [17] optimized the construction in [16], reducing the length of the extended ciphertext by nearly half. They also introduced a directed decryption protocol, enabling extended ciphertexts to be decrypted by specific designated users. This enhancement removed the limitation that only participating parties in the homomorphic evaluation could decrypt the result, thereby giving data owners greater control over access to decrypted information. In the same year, Chen et al. [18] constructed a TFHE-type MKFHE scheme, leveraging the low-latency homomorphic encryption techniques from TFHE [10]. They achieved a reduced concrete complexity, but their scheme did not support the packing technique, thereby resulting in a large expansion rate similar to TFHE. Later, Chen et al. [19] designed multi-key variants of BFV [6,7] and CKKS [9], optimizing the relinearization (key switching) process in batched MKFHE. They demonstrated the practicality of their work by applying it to oblivious neural network inference. In 2023, Kim et al. [20] introduced a homomorphic gadget decomposition technique, which can reduce the number of gadget decompositions required in MKFHE schemes. Furthermore, they proved that the gadget decompositions used in advanced FHE schemes [5,6,7,9,16,17,19] can support the homomorphic properties they proposed. As an attempt to explore different design approaches for multi-key variants, Zhou et al. [24] proposed a MKFHE scheme based on an accumulation-style key structure, inspired by the threshold FHE approach introduced in [25]. Their construction achieves more compact extended ciphertexts and enables more efficient homomorphic operations. However, similar to threshold FHE schemes, it also introduces certain inherent drawbacks, such as the use of more complex and diverse parameters, as well as increased frequency and complexity of interactions among the participating parties.
1.2. Motivations
The BGV-type scheme, as a representative of leveled FHE schemes, offers several advantages over other types of schemes, such as flexible noise management, the ability to avoid expensive bootstrapping by predefining the homomorphic evaluation depth for any polynomial size, and not relying on unreliable circular security assumptions. However, existing mainstream BGV-type MKFHE schemes still have some drawbacks. First, these schemes only support basic multi-hop features, requiring a predefined maximum number of participating parties during the initialization phase. Second, the tensor product in homomorphic multiplication results in further expansion of the dimensions of the extended ciphertext. After this tensor product, a key switching process is necessary to convert the expanded ciphertext back into a standard extended ciphertext. Due to the special and complex structure of the evaluation keys needed for key switching in a multi-party setting, existing BGV-type MKFHE schemes require an embedded extendable auxiliary ring-GSW scheme (which can be regarded as a separate GSW-type MKFHE scheme) to compute the evaluation key generation materials. These materials are then used to extend a large joint evaluation key at each level, and any change in the set of participating parties necessitates the recalculation of these joint evaluation keys. In simple terms, the presence of this auxiliary scheme leads to redundant and complex computations as well as significant storage overhead. Moreover, after eliminating the bootstrapping procedure, the tensor product and key exchange process become the new performance bottlenecks, introducing a square-level complexity related to the number of parties.
Additionally, the most efficient FHE schemes today are those that support batch techniques and allow SIMD (Single Instruction, Multiple Data) style operations. By utilizing ciphertext packing, such schemes pack multiple plaintexts into an equal number of independent “slots” within the plaintext space. However, existing mainstream MKFHE schemes [16,17,19] that theoretically support batching only make a simple claim that their schemes inherit the batch-processing capability of basic SKFHE schemes, without providing a detailed explanation of how to design ciphertext packing techniques to aggregate multiple plaintexts or how to specifically construct a batched MKFHE scheme.
1.3. Our Contributions
In this paper, we address the main issues present in existing works and propose an improved multi-hop BGV-type MKFHE scheme along with its batch-processing scheme.
First, we optimize the design of the multi-key variant of BGV by developing a simpler and more natural construction that eliminates the need for an additional auxiliary GSW-type MKFHE scheme. This innovation also enables a significant reduction in the size of the public key.
Next, we present novel evaluation key generation and key switching algorithms that allow each party to precompute and securely share its evaluation keys independently, without requiring the computation of evaluation key generation materials or the derivation of joint evaluation keys, and without needing to obtain or verify any information from other parties. These approaches substantially reduce both computational and storage costs, yielding performance improvements over existing mainstream MKFHE schemes.
Moreover, by adopting homomorphic gadget decomposition, we combine the tensor product and key switching processes, redesigning the homomorphic multiplication algorithm. This further improves the computational performance of our scheme and achieves linear complexity with respect to the number of participating parties.
Finally, drawing inspiration from the single-key construction in [26], we design a novel ciphertext packing technique based on Polynomial Chinese Remainder Theorem (Polynomial CRT) for a multi-party setup. We provide a detailed construction that transforms our BGV-type MKFHE scheme into a batched MKFHE scheme with superior amortized performance. Our schemes both exhibit a stronger multi-hop property, as they do not require a predefined upper bound on the number of participating parties, thereby offering increased flexibility and scalability compared to previous schemes.
2. Preliminaries
2.1. Notation
In this paper, we employ standard cryptographic notations. Vectors are denoted in bold, like , and matrices are written in upper-case bold, like . For a positive integer , let be the -th cyclotomic polynomial, whose degree is , where is the Euler’s totient function. We work over the polynomial ring and the corresponding residue ring for some integer modulus . In , each polynomial has coefficients in the interval . We use the security parameter , and denote a negligible function with respect to as . For a distribution , indicates that is sampled according to . When referring to the uniform distribution over a finite set , we use . For a polynomial in , we define as the standard -norm of its coefficient vector. All logarithms in this paper are taken to base 2 unless otherwise specified.
2.2. Ring Learning with Errors
The Ring Learning with Errors (RLWE) assumption [23] with parameter is a central cryptographic assumption used in lattice-based encryption schemes. Given a set of polynomially many samples , where is uniformly sampled from , and both (the secret) and (the noise) are drawn from an error distribution over , the RLWE assumption asserts that it is computationally hard to distinguish the ’s from uniformly random elements of .
In standard RLWE-based constructions, the error distribution is defined as the spherical discrete Gaussian distribution over the ring , where is the -th cyclotomic polynomial and denotes its degree. In the context of RLWE, this degree is also referred to as the dimension of the RLWE assumption. The distribution is -bounded, meaning that with overwhelming probability, the -norm of a sampled element—viewed as a coefficient vector in —is at most a fixed bound , where . Specifically, each element sampled from is represented as a polynomial in whose coefficients are independently drawn from the same one-dimensional discrete Gaussian distribution with mean zero and some standard deviation .
2.3. Polynomial Chinese Remainder Theorem
Polynomial operations are fundamental to many cryptographic constructions, especially in the context of lattice-based schemes. In this section, we introduce the Polynomial Chinese Remainder Theorem, which facilitates the decomposition and reconstruction of polynomial residues under modular constraints.
Definition 1.
(Polynomial Chinese Remainder Theorem (Polynomial CRT) [26]). Consider a set of polynomials that are pairwise relatively prime. Let , and let represent any given polynomial. Then, there exists a unique polynomial such that for . The unique solution to this system of congruences is given by:
where and is the modular inverse of modulo , i.e., .
2.4. Multi-Key Fully Homomorphic Encryption (MKFHE)
MKFHE is a cryptographic scheme that extends traditional FHE by enabling computations on ciphertexts encrypted under different keys. In contrast to single-key FHE, which requires all data to be encrypted under the same secret key, MKFHE allows encrypted data from multiple parties, each using its own secret key, to be processed together. This makes MKFHE a more flexible and scalable solution for privacy-preserving computations in multi-party settings.
An MKFHE scheme consists of five probabilistic polynomial-time (PPT) algorithms: , , , , and . These algorithms are described as follows:
- Setup: . The setup algorithm takes the security parameter as input and outputs the public parameters . These public parameters are implicitly used by other algorithms in the scheme.
- Key Generation: . The key generation algorithm takes the public parameters as input and generates a public key and a secret key for each participating party. Each party holds its own secret key while sharing the public key.
- Encryption: . The encryption algorithm takes a message and the corresponding public key as inputs, encrypting the message to produce a ciphertext .
- Evaluation: . The evaluation algorithm allows for computations on multiple ciphertexts , each encrypted under a (possibly repeated) public key from the set , where denotes the number of distinct public keys involved. It performs homomorphic operations on these ciphertexts based on a given circuit , producing a new ciphertext that is the encrypted result of the computation.
- Decryption: . The decryption algorithm takes a ciphertext and the corresponding secret keys for the participating parties as input, decrypting the ciphertext to recover a plaintext message .
Each MKFHE ciphertext implicitly contains references to the public keys associated with it. Initially, a ciphertext corresponds to a single key, but as computations proceed with ciphertexts encrypted under different keys, the reference set expands. When decrypting a ciphertext, all associated secret keys must be used.
Correctness and security: An MKFHE scheme is correct if, for any set of ciphertexts , the decryption of the result obtained from the homomorphic evaluation matches the result of applying the circuit to the decrypted inputs with an overwhelming probability, i.e.,
An MKFHE scheme is IND-CPA secure if, for any pair of messages , the distributions of ciphertexts and are computationally indistinguishable.
2.5. Gadget Decomposition
Gadget decomposition, originally introduced by [27], is a fundamental technique extensively employed in FHE schemes (e.g., [5,6,7,8,9,10,15,16,17,18,19]) to mitigate the escalation of noise during homomorphic evaluations and bootstrapping. Intuitively, it expresses a ring element as a vector of polynomials with relatively small coefficients, thereby facilitating key switching and other noise-control procedures.
Formally, let be a positive integer, and consider the ring . We define a gadget vector . The gadget decomposition function maps each element to a vector such that: . In this decomposition, the parameter is a positive integer referred to as the decomposition degree. The resulting vector is typically constrained to have a small -norm, i.e., , where is a predetermined bound significantly smaller than . For and , the external product is defined as , where denotes the inner product between two vectors.
Over the years, multiple gadget decomposition variants have been employed in FHE schemes tailored to diverse design needs and constructions, including bit decomposition [5,6], residue-number-system (RNS)-oriented decomposition [28,29], base decomposition [10,30], and homomorphic gadget decomposition [20].
2.6. IND-CPA Security
A foundational security notion for modern public-key encryption schemes, including SKFHE schemes and MKFHE schemes, is indistinguishability under chosen plaintext attack (IND-CPA). This notion guarantees that any PPT adversary, even with access to an encryption oracle, cannot distinguish between the ciphertexts of any two messages of their choice with non-negligible advantage.
Definition 2.
(IND-CPA Security [31]). Let be a public-key encryption scheme, and let denote the security parameter. Let denote the message space. We say that is IND-CPA secure if for every PPT adversary , there exists a negligible function such that:
where the experiment is defined as follows:
- 1.
- The challenger runs , and sends the public key to .
- 2.
- sends two equal-length messages to the challenger.
- 3.
- The challenger samples a uniform bit , computes the challenge ciphertext , and sends to .
- 4.
- outputs a guess bit . The experiment outputs 1 if , and 0 otherwise.
A scheme is IND-CPA secure if the adversary’s advantage in distinguishing from based on is bounded by a negligible function with respect to . For FHE schemes, IND-CPA security is typically established under the RLWE assumption, ensuring that ciphertexts do not leak any partial information about the underlying plaintexts against passive adversaries.
3. New Multi-Key Variant of BGV
In this section, we present a novel multi-hop BGV-type MKFHE scheme. Unlike those in [16,17], our construction does not rely on a separately tailored auxiliary GSW-type MKFHE scheme. We then introduce new algorithms for evaluation key generation and key switching, which deliver superior performance compared to recent mainstream methods [16,17,19]. Moreover, by incorporating techniques introduced in [20], we redesign both the homomorphic multiplication and key switching procedures, thereby achieving further improvements in overall computational efficiency.
3.1. Improved Multi-Key BGV
Throughout this work, we adopt the standard convention used in leveled FHE schemes, where the evaluation of the input circuit proceeds from the highest level (the initial input level) down to level 0 (the final output level). Accordingly, the index variable , which denotes the level index, ranges from high to low, and operations involving —such as evaluation key generation, key switching, modulus switching, and homomorphic evaluation—are only performed at levels , and are not invoked at level 0.
In this section, we focus on presenting the overall structure of our scheme and provide an outline of the full homomorphic evaluation procedure. The formal algorithms for evaluation key generation and key switching— and —will be described in detail in Section 3.2.
- : For a given , , and , where denotes the RLWE dimension, is a bound on the circuit depth, and is the security parameter, define a sequence of ciphertext moduli recursively as for , where each is an integer. Specifically, the largest modulus is . Let the error distribution be a -bounded spherical discrete Gaussian distribution over the ring , where the bound satisfies . Let be the plaintext modulus, chosen such that is coprime with every . Let be a gadget decomposition function associated with the gadget vector . For each level , uniformly sample a random vector . Output the public parameters .In practical deployments, the algorithm is executed once in a trusted setup phase, during which the public parameters are generated. This setup may be performed by a trusted third party (e.g., a cloud service provider) or collaboratively via a distributed multi-party protocol. Once established, the public parameters remain fixed and publicly known.
- : The key generation algorithm is executed independently by each party without requiring any interaction or coordination with others. For each level (from down to 0) and for the -th party, the secret key is sampled as , ensuring that is invertible in . A noise vector is drawn as . The public key is then computed by , where . Thus, the key generation algorithm outputs pairs for each party .As detailed in [23,32], efficient algorithms exist to verify whether an element in is invertible and to compute its inverse. Moreover, when setting , elements that belong to are invertible with overwhelming probability. We point out that since is a distribution over , and is defined as , the sampled secret key is naturally an element of [5,33].
- : The encryption algorithm is performed locally by each data owner. For a plaintext , sample a random element , and noise . Then, for party at level , compute the ciphertext as .Here, and denote the first component of the vectors and , respectively.
- : The ciphertext extension algorithm is performed by the evaluator, such as a cloud server or another computation entity. Suppose is a ciphertext at level associated with parties. To extend this ciphertext to support parties (with ), construct and output an extended ciphertextby setting and for , while for all satisfying . This construction guarantees thatThus, the extended ciphertext encrypts the same underlying plaintext at the same level while now being associated with parties.
- : The decryption algorithm is jointly executed by all involved parties. Given an -key ciphertext at level associated with parties, along with the corresponding secret keys , the plaintext is recovered by computing
- : The modulus switching algorithm is executed by the evaluator. Given a ciphertext at level , computefor , where denotes the rounding operation, and output the ciphertext at level .In BGV-type schemes, reducing the inner modulus from to decreases the internal noise by roughly the factor . The modulus switching technique ensures that the resulting ciphertext can still be decrypted under the same secret key without affecting the correctness of the underlying plaintext, enabling continued homomorphic computations at the lower level. A detailed correctness proof for modulus switching can be found in [5].
- : The homomorphic evaluation algorithm is executed by the evaluator. Let denote the circuit provided as input for homomorphic evaluation on ciphertexts . Each ciphertext (where ) is at a particular level and was originally encrypted under a subset of the parties’ keys. The algorithm proceeds as follows:
- If any ciphertexts are at higher levels than others, apply the necessary key switching or modulus switching procedures so that all ciphertexts are converted to a common level .
- For each ciphertext , invoke the ciphertext extension algorithm to extend into an extended ciphertext that is related to the union of all parties involved across these ciphertexts. This step ensures that all input ciphertexts are associated with the same set of parties.
- For each involved party , compute its level- evaluation key .
- To evaluate the circuit gate by gate, simply apply the homomorphic operations and (detailed immediately below) on the extended ciphertexts.
- After processing all gates in , output the final ciphertext , which encrypts the result of on the original plaintexts under the secret keys of all involved parties.
- : For two ciphertexts and in , output their component-wise sum .
- : Given ciphertexts and in along with the public keys and evaluation keys , compute the tensor product with components for all . Then, compute , and finally output .
Security: The security and correctness of our scheme derive from the inherent properties of both the RLWE assumption (with parameters ()) and the basic BGV scheme.
As in most mainstream FHE schemes [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], we consider a static, passive adversarial model, in which an adversary may corrupt an arbitrary subset (possibly large but not all) of parties before the setup phase but cannot adaptively corrupt parties during the computation. The adversary can observe all public parameters, public keys, and ciphertexts throughout the execution, but cannot access the secret keys of honest parties. Furthermore, all parties are assumed to honestly follow the specified steps of the scheme.
In our scheme, elements and vectors are independently and randomly sampled from discrete Gaussian or uniform distributions, such as , and . This includes, for example, the secret keys , noise vectors and random vectors . These distributions ensure sufficient entropy and unpredictability in parameter generation, thereby satisfying the security requirements under the RLWE assumption.
For each level , a public key for party is , where , , and . Because negating remains within the same error distribution and multiplying by merely rescales the noise, still constitutes an RLWE sample. Therefore, by the RLWE assumption, is computationally indistinguishable from a uniform random vector in . A ciphertext at level similarly has a form where and . Here, and each can be viewed as an RLWE sample with secret , in which contains a plaintext in an otherwise random encryption of zero. Hence, is computationally indistinguishable from a random pair in under the RLWE assumption.
To formally prove the IND-CPA security of our scheme under the RLWE assumption, we construct a hybrid argument consisting of two experiments: Hybrid 0 (the real IND-CPA experiment) and Hybrid 1 (an indistinguishable variant), and then argue their computational indistinguishability. The experiments are defined according to Definition 2 and aim to show that no PPT adversary can distinguish between the encryptions of any two chosen plaintexts with non-negligible advantage.
Hybrid 0: Let denote the number of participating parties. The experiment proceeds as follows:
- For each party , the challenger generates key pairs , and sends the public keys to the adversary .
- The adversary selects two plaintexts , and specifies a public key to be used for encryption.
- The challenger samples a uniform bit , and returns the ciphertext to .
- outputs a guess bit . The experiment outputs 1 if , and 0 otherwise.
Let this experiment be denoted by .
Hybrid 1: This experiment is identical to Hybrid 0, except that the challenger encrypts the other message, i.e., , instead of . The same public key specified by the adversary is used.
- All key generation and public key disclosure steps remain unchanged.
- The adversary submits the same two plaintexts and public key as in Hybrid 0.
- The challenger samples the same bit , but now computes , and returns it to .
- outputs a guess bit . The experiment outputs 1 if , and 0 otherwise.
Let this experiment be denoted by .
In Hybrid 0, the challenge ciphertext is generated as , while in Hybrid 1, the ciphertext is constructed as . As analyzed earlier, both ciphertexts and are computationally indistinguishable from uniformly random pairs in under the RLWE assumption. Since both ciphertexts are independently computationally indistinguishable from uniform, they are also computationally indistinguishable from each other. It follows that Hybrid 0 and Hybrid 1 are computationally indistinguishable from the perspective of any PPT adversary. Formally, we have:
In Hybrid 1, the adversary has no advantage beyond random guessing, and hence:
By combining the above, we conclude that the adversary’s distinguishing advantage in the real IND-CPA experiment is negligible:
A similar analysis holds for extended ciphertexts. As a result, neither the secret keys nor the plaintexts are revealed by the public keys or ciphertexts, ensuring IND-CPA security for .
Correctness: At level , a ciphertext is decrypted as , where denotes the secret key of party at level . As long as , the reduction modulo and modulo correctly recover the plaintext . Regarding the correctness of homomorphic evaluation, consider two ciphertexts and at the same level . Their homomorphic sum is defined as component-wise modulo . Decryption then yields . In homomorphic addition, the noise components of the two ciphertexts are added linearly. Similarly, their homomorphic multiplication is computed as and decryption of yields , which simplifies to . In homomorphic multiplication, the noise components combine multiplicatively, and additional noise from cross-terms is introduced. However, with proper noise management techniques—such as gadget decomposition and modulus switching—the overall noise remains within the decryption threshold, ensuring that the correct product of the original plaintexts is recovered.
3.2. Novel Methods for Evaluation Key Generation and Key Switching
In this section, we present our scheme’s approach for generating evaluation keys and performing key switching .
- : For a party at level , sample a random element , a random vector , and noise vectors . Compute , , and . Then, output the evaluation key .
We can observe that the evaluation key generation algorithm’s input depends solely on the public parameters and the parties’ own keys. Therefore, each party can generate its evaluation keys independently, and these evaluation keys in our scheme can be precomputed prior to encryption or homomorphic evaluation, and may even be stored publicly for potential future evaluations, irrespective of any changes in the set of participating parties.
- : The key switching algorithm is executed by the evaluator. Consider a tensored ciphertext with each , which is associated with the secret keys , and a set of public keys together with evaluation keys for . To produce a standard ciphertext at level that is associated with the secret keys , perform the following steps:
- Set the first component as , and for each , assign .
- For each , update .
- For each , compute , and subsequently update .
- For the intermediate ciphertext , set and for each , compute .
- Output the resulting ciphertext .
Security: The security proofs for our evaluation key generation and key switching algorithms are essentially identical to the ciphertext security proofs presented in Section 3.1. Specifically, since , , and are random vectors, and is computationally indistinguishable from a random vector in (making it pseudorandom), replacing , , and by random vectors is computationally indistinguishable under the same RLWE assumption with parameters and the corresponding secrets , or . Consequently, the distribution of each evaluation key is computationally indistinguishable from .
Correctness: To demonstrate the correctness of the key switching procedure, it suffices to show that the standard ciphertext output in the last step decrypts to the original plaintext under the new secret keys. Formally, we need to ensure . We first examine the intermediate ciphertext generated in Step 3 of the algorithm. One can verify that
Using the relations and , it follows that
Thus, the intermediate ciphertext is normalized and correctly decryptable using the original secret keys. Next, we consider the final ciphertext . By design, we have
Hence, we obtain the desired equality which is exactly the intended decryption condition. This confirms the correctness of the key switching algorithm.
Performance: As an informal overview, our proposed evaluation key generation and key switching algorithms already provide superior parameter sizes and practical efficiency compared to the mainstream approaches in [16,17,19]. In [16,17], for each level, each party must run an additional GSW-type MKFHE protocol to generate its own evaluation key generation materials, and the public keys and associated materials of all participating parties must be combined to produce a large shared evaluation key. In contrast, our scheme achieves the same multi-party functionality without incurring these burdens. Moreover, in each key switching procedure, our evaluation key size is only , whereas [16,17] require and , respectively. Compared to [19], our algorithm leverages a precomputation of in Step 3 so that, when updating , only external products are required, instead of the external products needed in their procedure. A more detailed performance analysis and comparison is presented in Section 5.
3.3. Redesigning Homomorphic Multiplication
Although our key switching algorithm exhibits improved performance, we recognize that our MK-BGV scheme still offers substantial potential for further optimization. In particular, homomorphic multiplication remains the most expensive component, both in our construction and in existing batched MKFHE frameworks. We observe that the most complex parts of this operation are the tensor product and the ensuing key switching process, which require, respectively, ring multiplications and gadget decompositions. Consequently, these steps introduce a square-level complexity tied to the number of participating parties, significantly affecting the overall efficiency. In [20], a novel concept called homomorphic gadget decomposition is introduced. In essence, a homomorphic gadget decomposition function not only satisfies the basic properties described in Section 2.5 but also allows arithmetic operations to be performed directly on the decomposed polynomials.
Definition 3.
(Homomorphic Gadget Decomposition [20]). A function is called a homomorphic gadget decomposition if, for any , it satisfies the following properties:
where denotes the component-wise product, and is the fixed gadget vector.
Inspired by this technique, we observe that and can serve as effectively bounded substitutes for and , since and . Leveraging this property, we redesign the homomorphic multiplication algorithm in our scheme by merging the tensor product and key switching steps into a single process, thereby reducing the overall complexity from to ring multiplications and gadget decompositions. As a result, our new homomorphic multiplication algorithm achieves a linear complexity in terms of the number of participating parties.
- : Consider two ciphertexts and in , together with a set of public keys and evaluation keys for . To produce the multiplied ciphertext at level that is associated with the secret keys , proceed as follows:
- Set the first component as , and for each , assign .
- Compute and .
- For each , update .
- For each , update .
- For the intermediate ciphertext , set and for each , compute .
Finally, output the resulting ciphertext .
Performance: In previous versions of the homomorphic multiplication algorithm, each component of a tensored ciphertext was computed as , which led to computational complexity. By applying the homomorphic gadget decomposition, we substitute with the component-wise product of decompositions . Equally significant, the component-wise product operation is commutative and can be reordered without affecting the correctness of the inner product, thereby enabling further simplifications. Specifically, we can rewrite the expressions in Steps 2 and 3 of the algorithm as:
and similarly,
Note that is independent of index , and similarly, is independent of index . Thus, once computed, these values can be reused repeatedly for each subsequent external product computation, significantly reducing computational overhead. As a result, this optimization substantially decreases the number of required ring multiplications and gadget decompositions, both of which are scaled down to .
Correctness: To demonstrate the correctness of our new homomorphic multiplication algorithm, it suffices to show that the multiplied ciphertext from the multiplication of two -key ciphertexts and decrypts correctly under the new secret keys . Formally, we need to verify that:
We begin by analyzing the intermediate ciphertext generated in Step 4 of the algorithm. The expression for expands as:
Using the homomorphic properties of the gadget decomposition and the relation
the term becomes:
Similarly, using the relation , we obtain:
Combining all terms together, we arrive at:
This shows that the intermediate ciphertext is correctly normalized and decryptable under the original secret keys. The process in the subsequent Step 5, along with its correctness, is entirely consistent with Step 4 of the algorithm described in Section 3.2. Consequently, we obtain the desired equality:
This confirms the correctness of our new homomorphic multiplication algorithm. The algorithm can be directly used to replace the algorithm in our scheme if we replace the gadget decomposition with the homomorphic gadget decomposition , achieving improved performance.
4. Batched MK-BGV Scheme
In this section, we provide a detailed construction of the ciphertext packing technique based on the Polynomial CRT introduced in Section 2.3, and demonstrate how it can be employed to convert our scheme into an efficient batch processing scheme.
4.1. Ciphertext Packing Based on Polynomial CRT
Recall from Section 3.1 that for a given integer , the input plaintext in the scheme is structured based on the algebraic structure , where both addition and multiplication are defined modulo and . Let represent a finite field with as its characteristic. The polynomial can be decomposed modulo into distinct irreducible factors , such that , where each factor has degree , with , and . This decomposition enables multiple plaintext values to be mapped into a single plaintext element via the Polynomial CRT, which is then encrypted into a ciphertext supporting slot-wise SIMD operations. We then have the following isomorphism for :
In this representation, is isomorphic to copies of , each corresponding to a message in . Here, each factor is referred to as a “plaintext slot”. This allows us to represent plaintext elements of as a single element in . By Definition 1, algebraic operations (addition and multiplication) in can be viewed as parallel operations across all slots, where each slot corresponds to a separate message. This enables us to perform homomorphic computations on input values simultaneously, which forms the foundation for efficient batch homomorphic computations. The above isomorphisms are explicitly manifested through the following mappings and :
where , .
Hence, , where denotes function composition, forms a mapping that is an isomorphism from to . Since this mapping is a ring isomorphism, it is bijective and structure-preserving by Definition 1, which guarantees the existence of its inverse mapping . This inverse uniquely recovers the original slot-wise representation in from any ring element in , enabling slot-level access and decomposition when needed.
Let and be two plaintext vectors consisting of independent slots, where each component represents one plaintext message. Let and be their encoded representations in the plaintext ring via the Polynomial CRT-based packing. Then, the ring homomorphism properties of imply the following identities:
where all additions and multiplications on the right-hand side are component-wise over .
4.2. Improved Batched Multi-Key BGV
Building upon the scheme introduced in Section 3 and the ciphertext packing technique presented in Section 4.1, we now explicitly construct our final batched multi-hop BGV-type MKFHE scheme, termed . The typical application model of is shown in Figure 1.
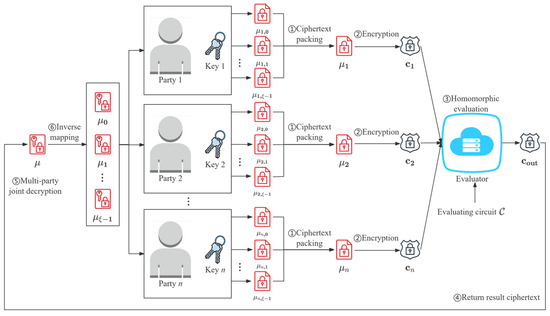
Figure 1.
Multi-party privacy-preserving computation model of the scheme.
- : For a given , , and , where denotes the RLWE dimension, is a bound on the circuit depth, and is the security parameter, define a sequence of ciphertext moduli recursively as for , where each is an integer. Specifically, the largest modulus is . Let the error distribution be a -bounded spherical discrete Gaussian distribution over the ring , where the bound satisfies . Let be the plaintext modulus, chosen such that is coprime with every . Let be a homomorphic gadget decomposition function associated with the gadget vector . The mappings and are isomorphisms between and . For each level , uniformly sample a random vector . Output the public parameters .
- : For each level (from down to 0) and for the -th party, output secret-public key pairs .
- : For a plaintext vector , compute the aggregate plaintext . Then, for party at level , compute the ciphertext as .
- : Suppose is a ciphertext at level associated with parties. To extend this ciphertext to support parties (with ), construct and output an extended ciphertext .
- : Given an -key ciphertext at level associated with parties, along with the corresponding secret keys , the aggregate plaintext is recovered by computing . Subsequently, the complete set of plaintext messages across the slots is obtained via the inverse mapping
- : Let denote the circuit provided as input for homomorphic evaluation on ciphertexts . Each ciphertext (where ) is at a particular level and was originally encrypted under a subset of the parties’ keys. To produce the output ciphertext, compute , where every invocation of the homomorphic multiplication is replaced by our new multiplication algorithm .
By employing batch processing, all participating parties can concurrently perform joint homomorphic evaluations on sets of encrypted data under the scheme. The use of ciphertext packing and batching does not compromise the IND-CPA security inherited from the underlying framework. Furthermore, the correctness of naturally follows from the correctness of , Definition 1, and the ciphertext packing technique.
5. Parameter and Performance Analysis and Comparison
In this paper, the settings for parameters such as the RLWE assumption parameters , the plaintext modulus , and the decomposition degree for the gadget decompositions can follow the classical choices used in advanced schemes such as [5,16,17,19,23], as no modifications have been made to these parameters. Table 1 and Table 2 present a comparison of our schemes with several prominent recent MKFHE schemes. Schemes [16,17] are BGV-type MKFHE schemes of the same type as ours, while Scheme [19] is a BFV(CKKS)-type MKFHE scheme, which is of a similar type to ours. For our batched scheme , we focus on its amortized performance.

Table 1.
Comparison of parameter sizes (in bits) and properties of recent mainstream schemes. Here, represents the number of parties, is the dimension of the (R)LWE assumption, is the decomposition degree, is the ciphertext modulus, is the torus precision, is the raising modulus factor, is the circuit depth, and denotes the number of packed plaintexts.

Table 2.
Comparison of homomorphic multiplication and key switching (relinearization) algorithm performance between recent efficient MKFHE schemes. The notation is consistent with Table 1.
A notable aspect that is difficult to display in tables is that the input ciphertexts in and , as well as and , can either be fresh or intermediate results from any homomorphic operations. This demonstrates the multi-hop property of our schemes. Unlike the schemes in [16] and [17], which also support multi-hop capabilities, their designs require a predefined upper bound on the number of parties (keys) in the system, whereas our schemes impose no such limitation. Therefore, our schemes are actually closer to the stronger “fully dynamic” property as proposed in [15], but unlike [15], we do not require the introduction of the expensive bootstrapping procedure. However, due to the level-based BGV-type design, our schemes do require predefined maximum computation depths , which can be of arbitrary polynomial magnitude. Nonetheless, the size of the extended ciphertexts in our schemes increases only linearly with the number of parties, the same as in [15].
Additionally, in [16,17], each public key is set to a very large size to accommodate their auxiliary GSW-type MKFHE schemes. Their designs also involve storing repeated random samples of vectors , where , in both the public parameters and the public keys, which results in redundant storage overhead. Our schemes optimize these issues, reducing the public key size to approximately one-quarter of that in [16,17] for non-batch scenarios. Compared to [19], our scheme has slightly larger public key and evaluation key sizes, which is due to the fact that in BFV(CKKS)-type schemes, each party uses the same secret key across all circuit levels. However, this introduces the need for an additional circular security assumption, which poses the risk of leaking secret keys of the participants. Since this circular security assumption has not been rigorously proven, our scheme avoids this potential security issue by rotating the secret keys for all parties at each circuit level.
Scheme [24] adopts an accumulation-style key technique from threshold FHE, achieving extended ciphertexts and evaluation keys whose sizes are independent of the number of participating parties. Furthermore, the number of ring multiplications required in the tensor product operation is independent of the number of parties. However, this design also inherits structural complexities and limitations similar to those observed in threshold FHE constructions. Specifically, their scheme requires the computation of additional types of intricate parameters—such as joint public keys, joint evaluation public keys, and refreshing keys—none of which are required in either of our constructions. As in [16,17], each party in [24] must locally generate its own evaluation key generation materials (referred to as partial switching keys), which are then aggregated to derive joint evaluation keys. In their scheme, a key distinction is that any change in the set of participating parties necessitates the recomputation of not only the joint evaluation key but also all of the aforementioned parameters. This design leads to even higher interaction frequency and complexity, as well as greater computational and storage overheads for each party, compared to [16,17], which highlights the efficiency advantages of our design in minimizing coordination, computation, and storage overheads. Moreover, each ciphertext extension in [24] requires the use of refreshing keys and key switching, whereas our ciphertext extension algorithms— and —complete this operation using only lightweight assignment operations, making our method significantly more efficient than that of [24].
6. Conclusions
In this paper, we propose an enhanced multi-hop BGV-type MKFHE scheme that optimizes key aspects of existing schemes. By removing the need for an auxiliary GSW-type scheme, we simplify the multi-key variant design and significantly reduce public key sizes. We introduce novel algorithms for evaluation key generation and key switching that minimize computational overhead and storage requirements while enabling each party to independently and securely precompute and share its evaluation keys. Additionally, we combine tensor products with key switching through homomorphic gadget decomposition, improving homomorphic multiplication efficiency and achieving linear complexity in terms of the number of parties. We also leverage the Polynomial CRT to design a ciphertext packing technique, transforming our BGV-type MKFHE scheme into a batched version with superior amortized performance. Our schemes support multi-hop computations without a predefined upper bound on the number of parties, offering enhanced flexibility and scalability compared to existing similar schemes.
Author Contributions
Conceptualization, L.Z. and R.H.; methodology, L.Z.; validation, L.Z., R.H. and B.W.; formal analysis, L.Z.; investigation, L.Z. and B.W.; writing—original draft preparation, L.Z.; writing—review and editing, L.Z. and R.H.; supervision, R.H.; funding acquisition, R.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Guangxi Key Research and Development Program, Project No. AB24010340.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We sincerely thank the editors for their kind and efficient support. We are also grateful to the anonymous reviewers for their insightful comments and valuable suggestions, which have greatly improved the quality of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 169–178. [Google Scholar]
- Hamlin, A.; Shelat, A.; Weiss, M.; Wichs, D. Multi-key searchable encryption, revisited. In Proceedings of the Public-Key Cryptography–PKC 2018: 21st IACR International Conference on Practice and Theory of Public-Key Cryptography, Rio de Janeiro, Brazil, 25–29 March 2018; Proceedings, Part I. Springer International Publishing: Berlin/Heidelberg, Germany; pp. 95–124. [Google Scholar]
- Froelicher, D.; Troncoso-Pastoriza, J.R.; Raisaro, J.L.; Cuendet, M.A.; Sousa, J.S.; Cho, H.; Berger, B.; Fellay, J.; Hubaux, J.P. Truly privacy-preserving federated analytics for precision medicine with multiparty homomorphic encryption. Nat. Commun. 2021, 12, 5910, Erratum in Nat. Commun. 2021, 12, 6649. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Graepel, T.; Lauter, K.; Naehrig, M. ML confidential: Machine learning on encrypted data. In Proceedings of the International Conference on Information Security and Cryptology, Seoul, Republic of Korea, 28–30 November 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–21. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) fully homomorphic encryption without bootstrapping. ACM Trans. Comput. Theory (TOCT) 2014, 6, 13. [Google Scholar] [CrossRef]
- Brakerski, Z. Fully homomorphic encryption without modulus switching from classical GapSVP. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 868–886. [Google Scholar]
- Fan, J.; Vercauteren, F. Somewhat practical fully homomorphic encryption. Cryptology ePrint Archive 2012. Available online: https://eprint.iacr.org/2012/144 (accessed on 4 April 2025).
- Gentry, C.; Sahai, A.; Waters, B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In Proceedings of the Advances in Cryptology–CRYPTO 2013: 33rd Annual Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2013; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2013; pp. 75–92. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Proceedings of the Advances in Cryptology–ASIACRYPT 2017: 23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2017; pp. 409–437. [Google Scholar]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachene, M. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds. In Advances in Cryptology–ASIACRYPT 2016: 22nd International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 4–8 December 2016; Proceedings, Part I; Springer: Berlin/Heidelberg, Germany, 2016; pp. 3–33. [Google Scholar]
- López-Alt, A.; Tromer, E.; Vaikuntanathan, V. On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 19–22 May 2012; pp. 1219–1234. [Google Scholar]
- Clear, M.; McGoldrick, C. Multi-identity and multi-key leveled FHE from learning with errors. In Proceedings of the Advances in Cryptology—CRYPTO 2015: 35th Annual Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2015; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2015; pp. 630–656. [Google Scholar]
- Mukherjee, P.; Wichs, D. Two round multiparty computation via multi-key FHE. In Proceedings of the Advances in Cryptology—EUROCRYPT 2016: 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2016; pp. 735–763. [Google Scholar]
- Peikert, C.; Shiehian, S. Multi-key FHE from LWE, revisited. In Proceedings of the Theory of Cryptography Conference, Beijing, China, 1–3 November 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 217–238. [Google Scholar]
- Brakerski, Z.; Perlman, R. Lattice-based fully dynamic multi-key FHE with short ciphertexts. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 190–213. [Google Scholar]
- Chen, L.; Zhang, Z.; Wang, X. Batched multi-hop multi-key FHE from ring-LWE with compact ciphertext extension. In Proceedings of the Theory of Cryptography: 15th International Conference, TCC 2017, Baltimore, MD, USA, 12–15 November 2017; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2017; pp. 597–627. [Google Scholar]
- Li, N.; Zhou, T.; Yang, X.; Han, Y.; Liu, W.; Tu, G. Efficient multi-key FHE with short extended ciphertexts and directed decryption protocol. IEEE Access 2019, 7, 56724–56732. [Google Scholar] [CrossRef]
- Chen, H.; Chillotti, I.; Song, Y. Multi-key homomorphic encryption from TFHE. In Proceedings of the Advances in Cryptology–ASIACRYPT 2019: 25th International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 8–12 December 2019; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2019; pp. 446–472. [Google Scholar]
- Chen, H.; Dai, W.; Kim, M.; Song, Y. Efficient multi-key homomorphic encryption with packed ciphertexts with application to oblivious neural network inference. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 395–412. [Google Scholar]
- Kim, T.; Kwak, H.; Lee, D.; Seo, J.; Song, Y. Asymptotically faster multi-key homomorphic encryption from homomorphic gadget decomposition. In Proceedings of the 2023 ACM SIGSAC Conference on Computer and Communications Security, Copenhagen, Denmark, 26–30 November 2023; pp. 726–740. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Proceedings of the International Algorithmic Number Theory Symposium, Portland, OR, USA,, 21–25 June 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 267–288. [Google Scholar]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM (JACM) 2009, 56, 34. [Google Scholar] [CrossRef]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On ideal lattices and learning with errors over rings. J. ACM (JACM) 2013, 60, 43. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, L.; Che, X.; Liu, W.; Zhang, Z.; Yang, X. Multi-key Fully Homomorphic Encryption Scheme with Compact Ciphertexts. Cryptology ePrint Archive 2021. Available online: https://eprint.iacr.org/2021/1131 (accessed on 4 April 2025).
- Asharov, G.; Jain, A.; López-Alt, A.; Tromer, E.; Vaikuntanathan, V.; Wichs, D. Multiparty computation with low communication, computation and interaction via threshold FHE. In Proceedings of the Advances in Cryptology—EUROCRYPT 2012: 31st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Proceedings 31. Springer: Berlin/Heidelberg, Germany; pp. 483–501. [Google Scholar]
- Gentry, C.; Halevi, S.; Smart, N.P. Fully homomorphic encryption with polylog overhead. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Micciancio, D.; Peikert, C. Trapdoors for lattices: Simpler, tighter, faster, smaller. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bajard, J.C.; Eynard, J.; Hasan, M.A.; Zucca, V. A full RNS variant of FV like somewhat homomorphic encryption schemes. In Proceedings of the International Conference on Selected Areas in Cryptography, St. John’s, NL, Canada, 10–12 August 2016; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Halevi, S.; Polyakov, Y.; Shoup, V. An improved RNS variant of the BFV homomorphic encryption scheme. In Proceedings of the Topics in Cryptology-CT-RSA 2019: The Cryptographers’ Track at the RSA Conference 2019, San Francisco, CA, USA, 4–8 March 2019; Proceedings. Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Ducas, L.; Micciancio, D. FHEW: Bootstrapping homomorphic encryption in less than a second. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Goldwasser, S.; Micali, S. Probabilistic encryption. J. Comput. Syst. Sci. 1984, 28, 270–299. [Google Scholar] [CrossRef]
- Stehlé, D.; Steinfeld, R. Making NTRU as secure as worst-case problems over ideal lattices. In Proceedings of the Advances in Cryptology—EUROCRYPT 2011: 30th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tallinn, Estonia, 15–19 May 2011; Proceedings 30. Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Fully homomorphic encryption from ring-LWE and security for key dependent messages. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).