A Meta-Learning-Based Recognition Method for Multidimensional Feature Extraction and Fusion of Underwater Targets
Abstract
1. Introduction
- 1.
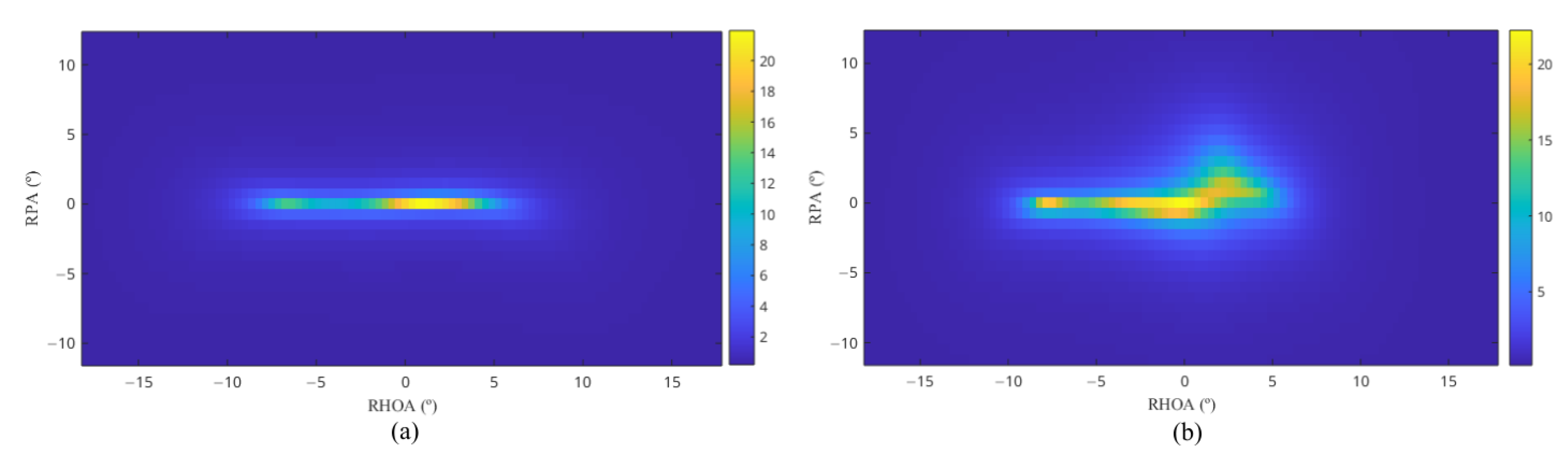
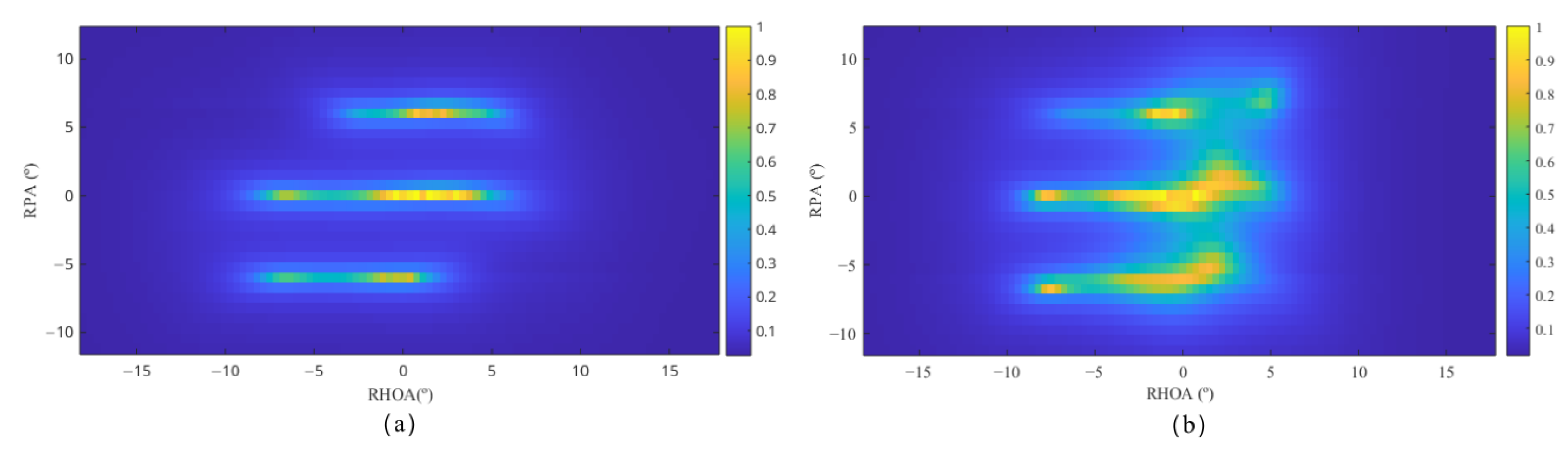
- Based on the generalized MUSIC algorithm, a pseudo-three-dimensional spatial feature was constructed by integrating range–dimension information, thereby enhancing the adaptability of the algorithm to the relative attitudes of the targets. The pseudo-WVD time–frequency spectrum was filtered and smoothed using the time–frequency function of the transmitted signal, which improved the resolution for distinguishing between targets and interferences. A method for extracting the Doppler frequency shift distribution feature of underwater moving targets was proposed, demonstrating excellent identification capabilities for moving targets. This feature is complementary to the posture adaptability provided by the time–frequency spectrum.
- 2.
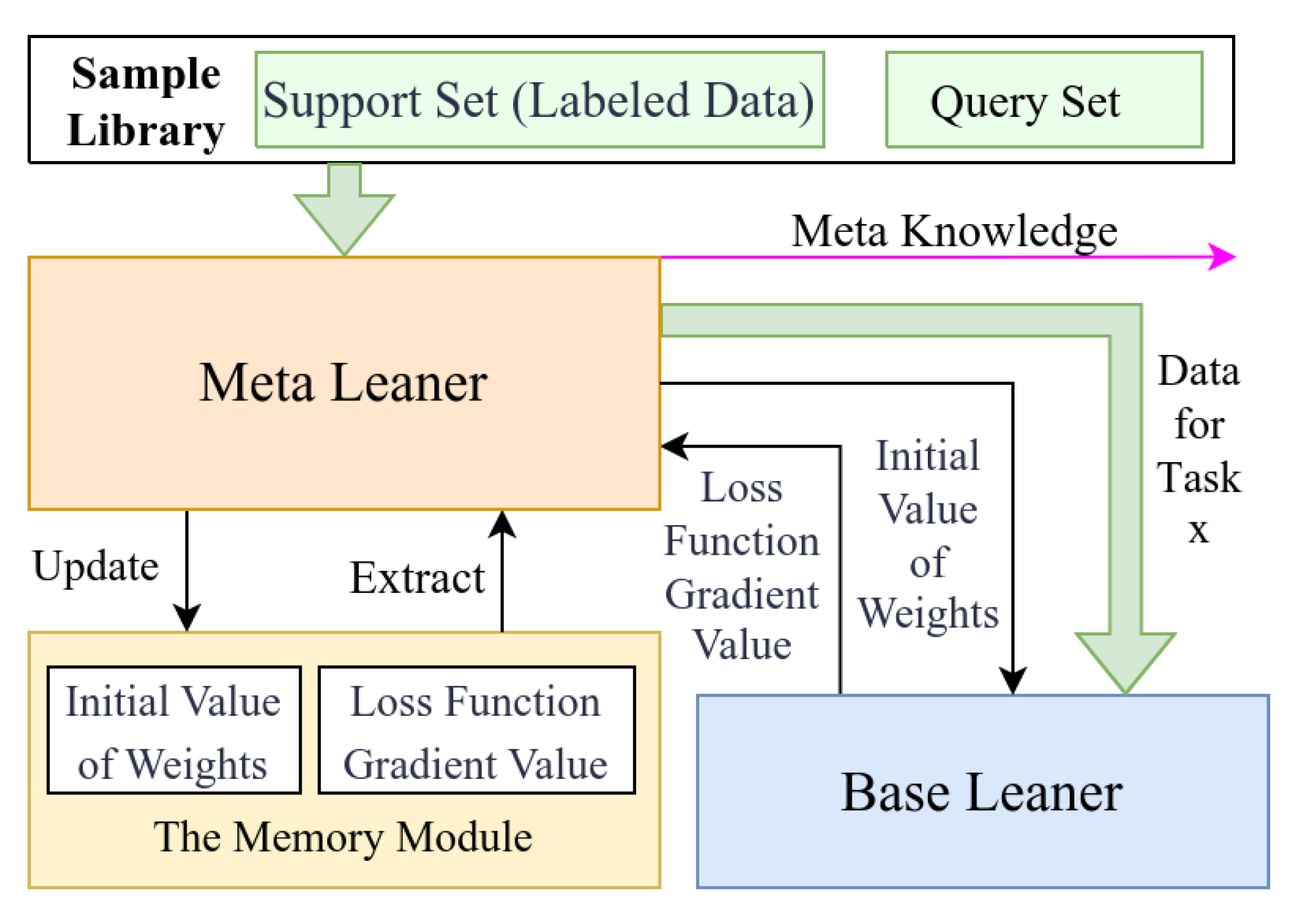
- Inspired by meta-learning network structures such as MAML [21,22], a multidimensional feature information fusion network model based on meta-learning was developed. This model consists of three base learners, a meta-learner, a target task network, and a multidimensional feature fusion classifier. In accordance with the characteristics of spatial, time–frequency, and Doppler feature spectra, three concise base learners were specifically designed to mitigate overfitting and non-convergence issues in small-sample scenarios.
- 3.
- The designs of the meta-learning task space and the network training methodology were refined. A meta-learning sample library based on simulation data was constructed. A target task learning sample library was established by integrating experimental data with simulation-enhanced data. The training and testing results demonstrate that the meta-learning feature-level information fusion network model developed significantly outperforms the data-level information fusion approaches implemented in four lightweight networks, such as EfficientNetB0.
2. Methods
2.1. Extraction of Multidimensional Features for Underwater Targets
2.1.1. Pseudo-Three-Dimensional Spatial Features
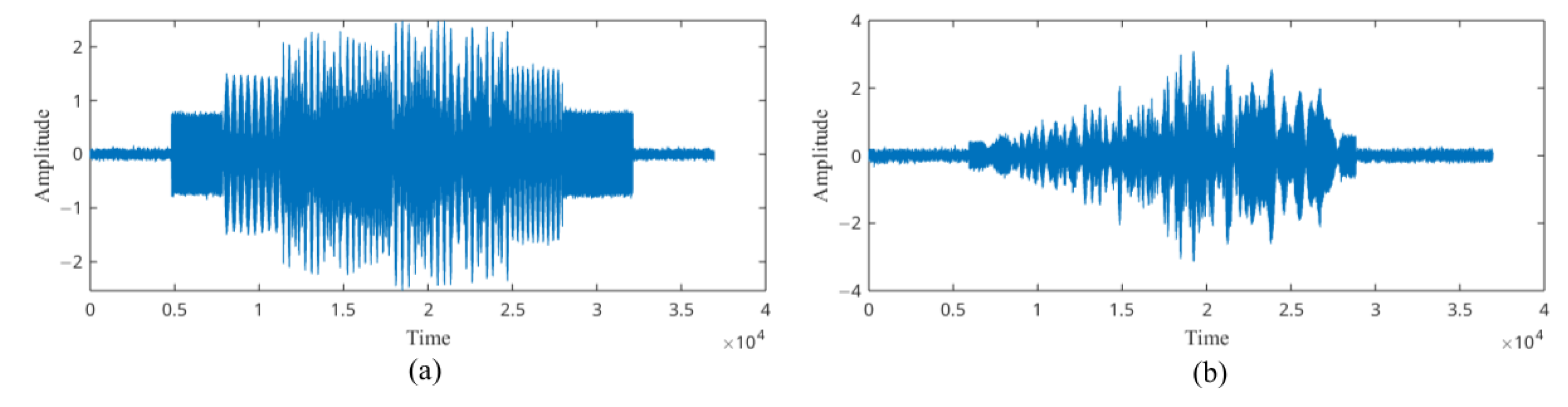
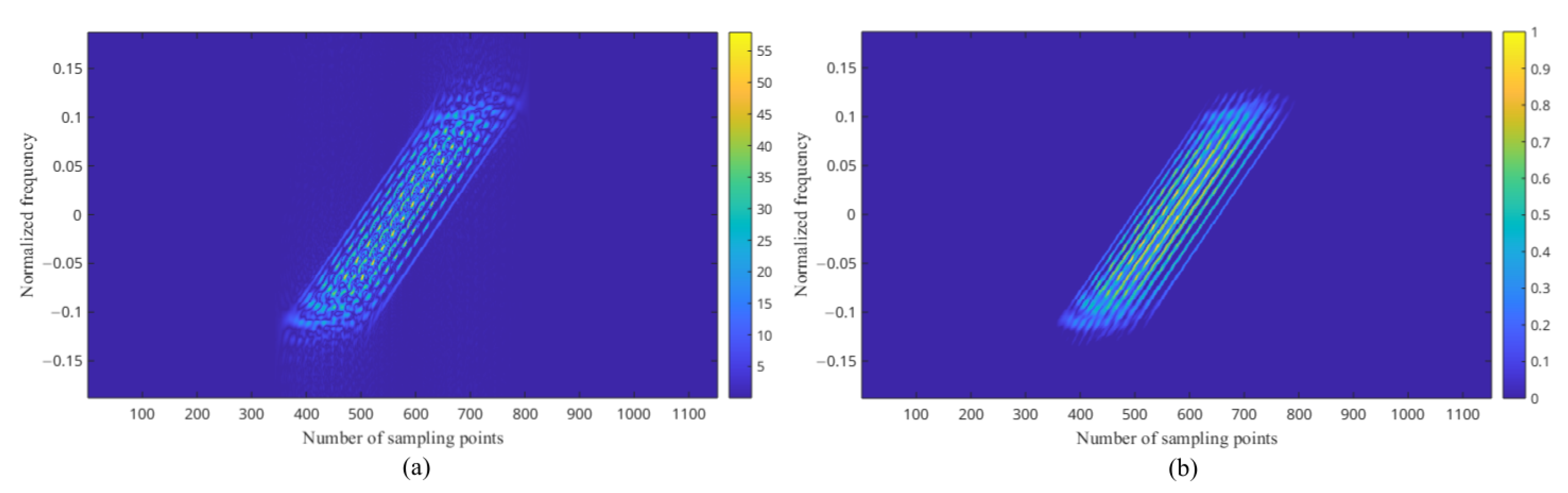
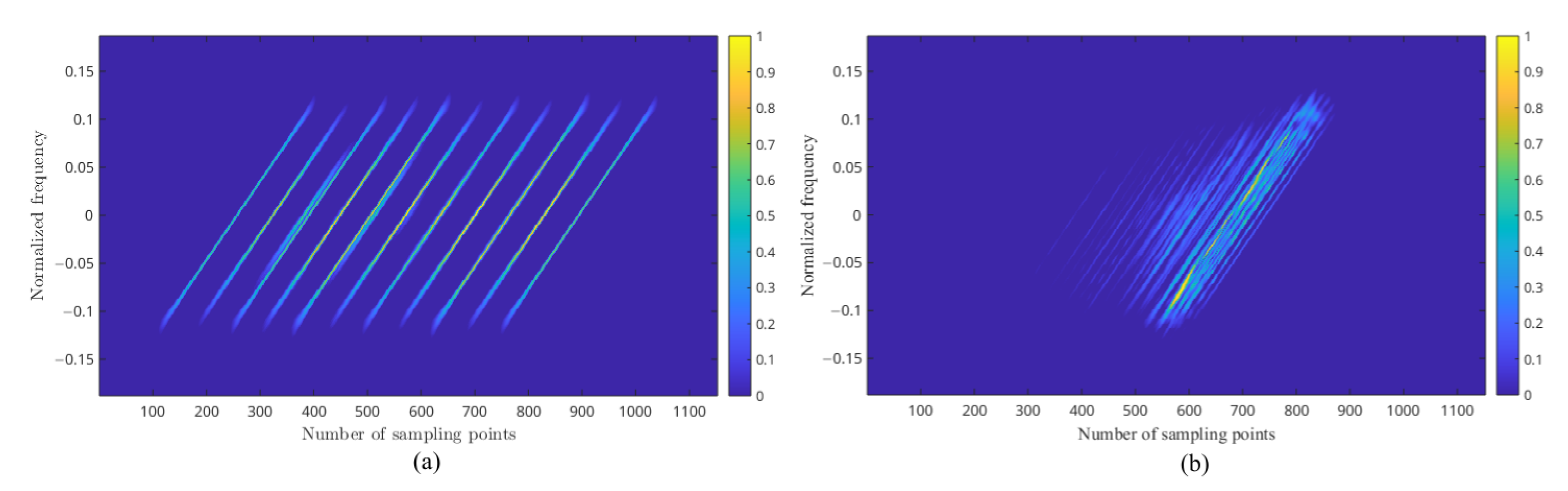
2.1.2. The Enhanced PWVD Time–Frequency Features
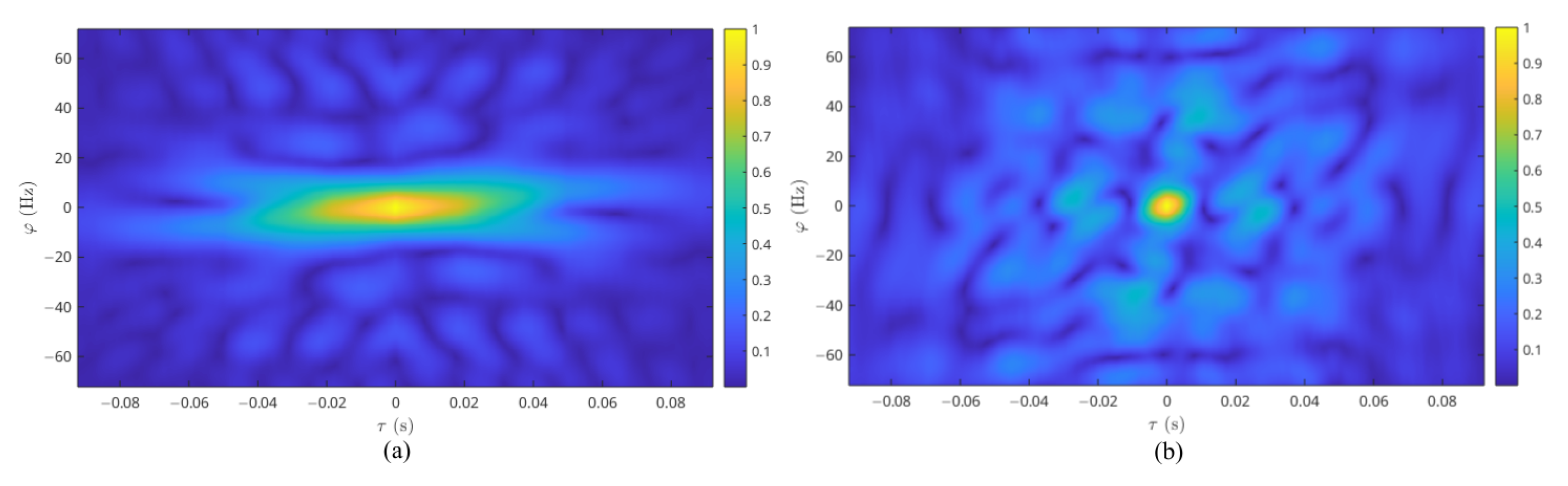
2.1.3. Distribution of Doppler Frequency Shift
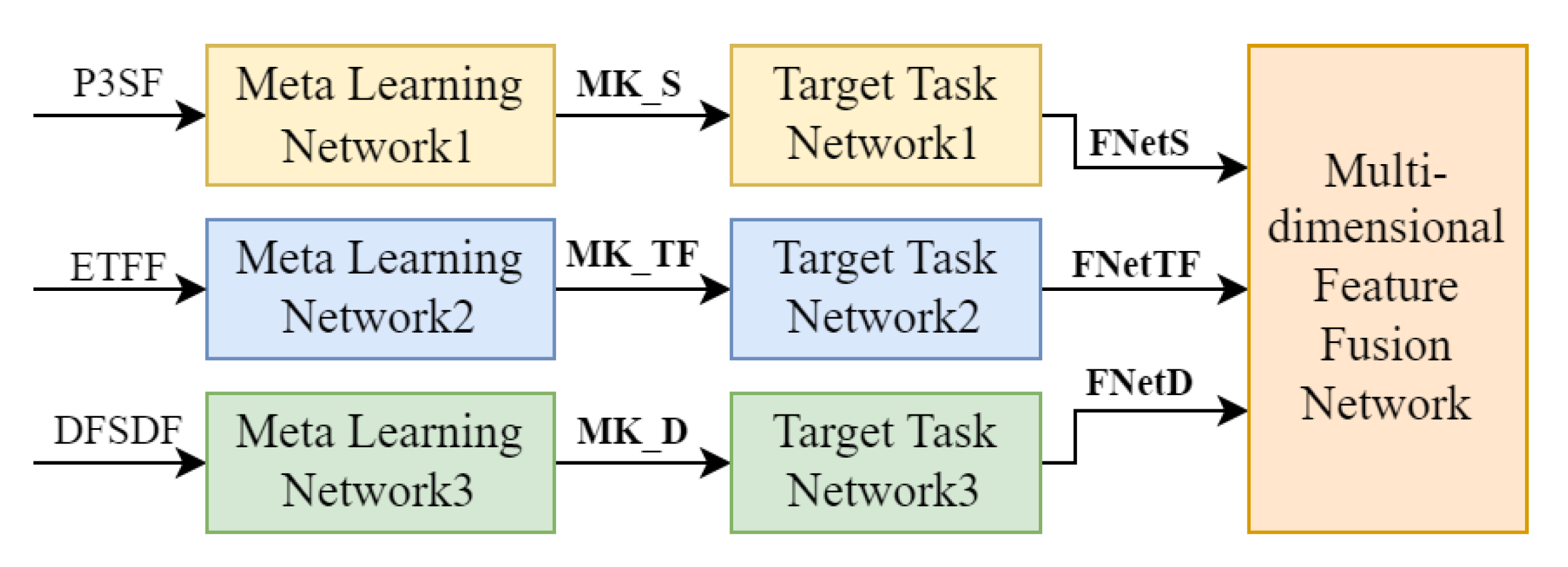
2.2. Development of the Meta-Learning-Based Feature Fusion Network
2.2.1. Network Framework
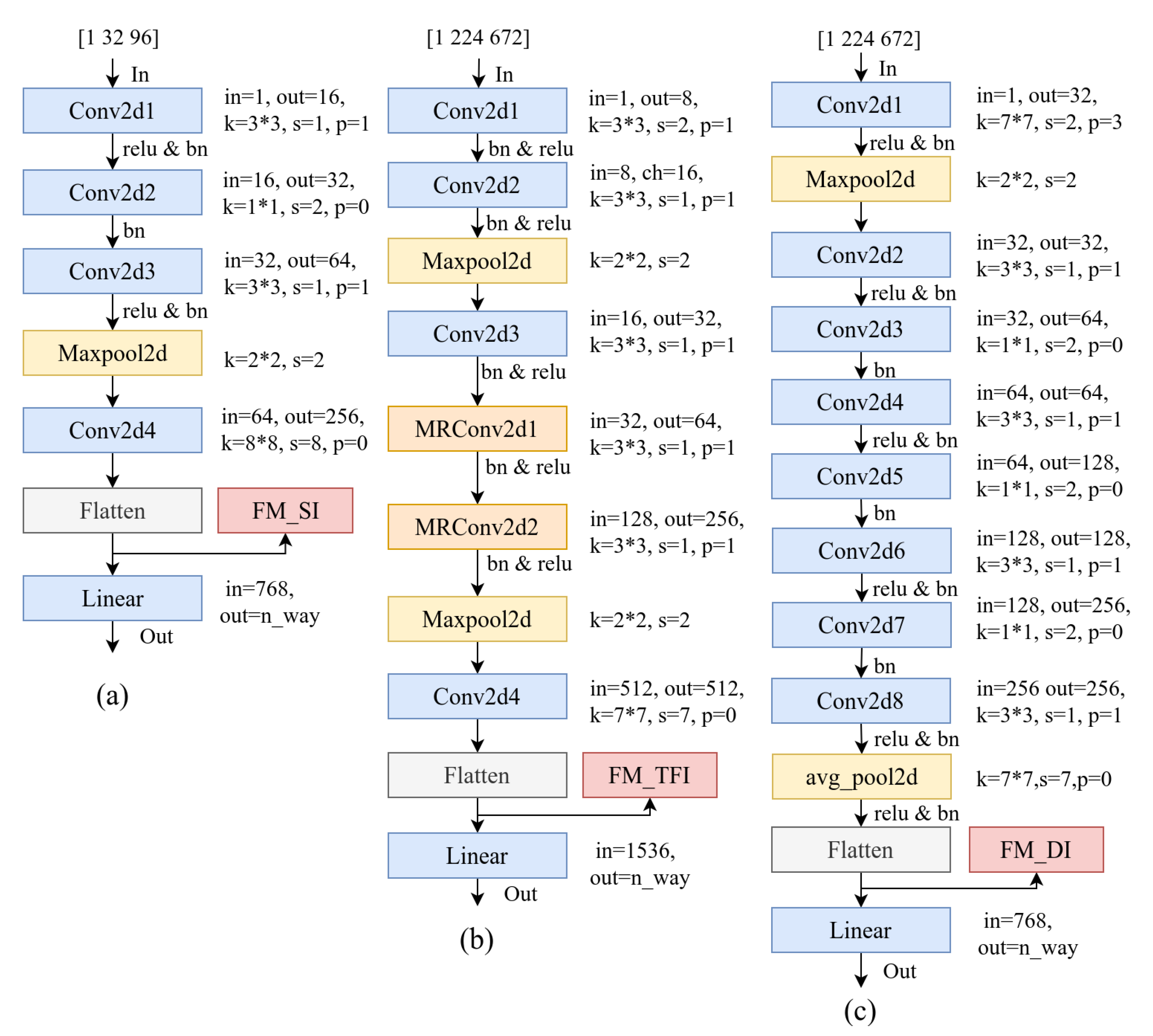
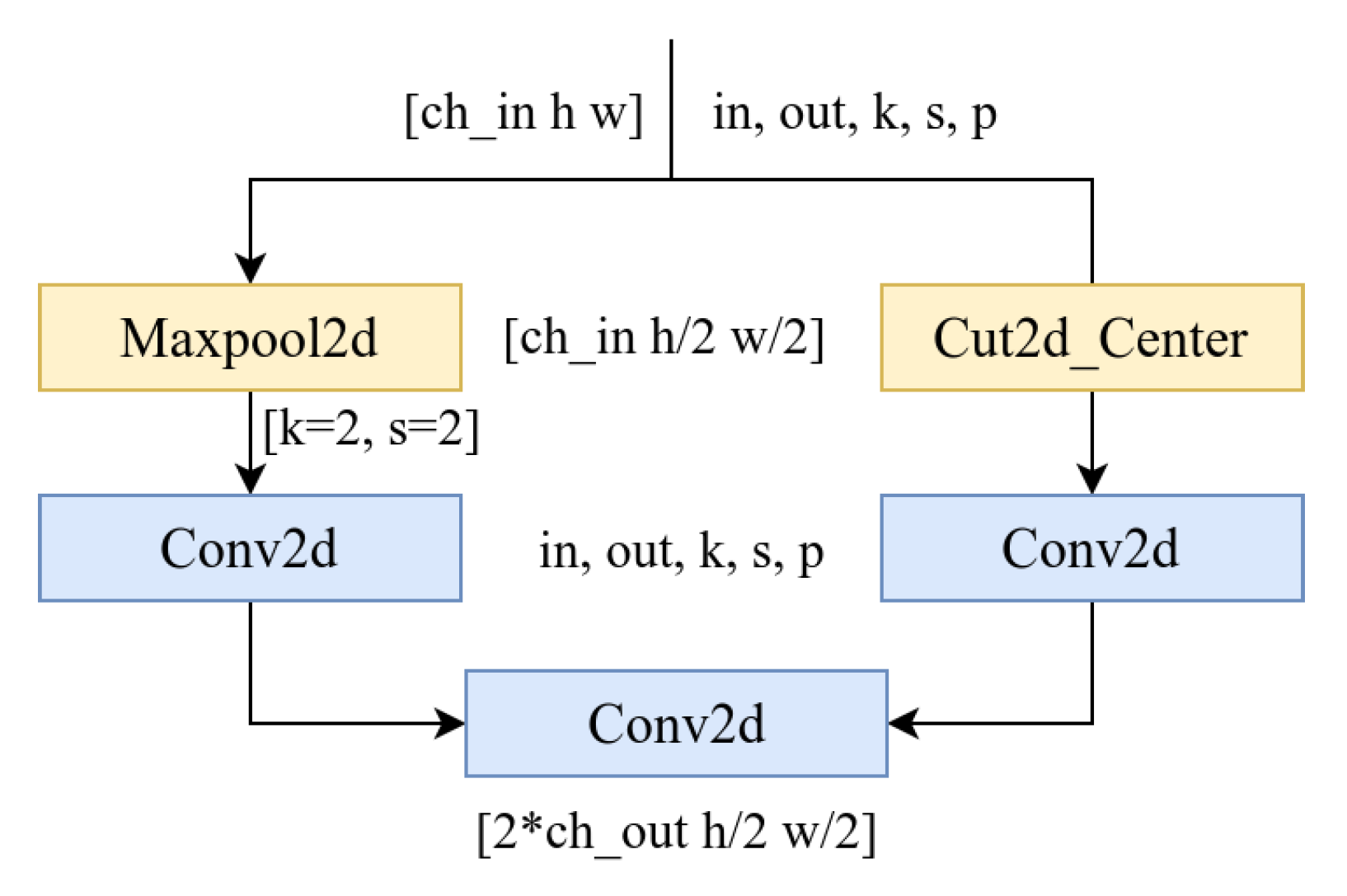
2.2.2. Design of Base Learners
2.2.3. Design of the Meta-Leaner
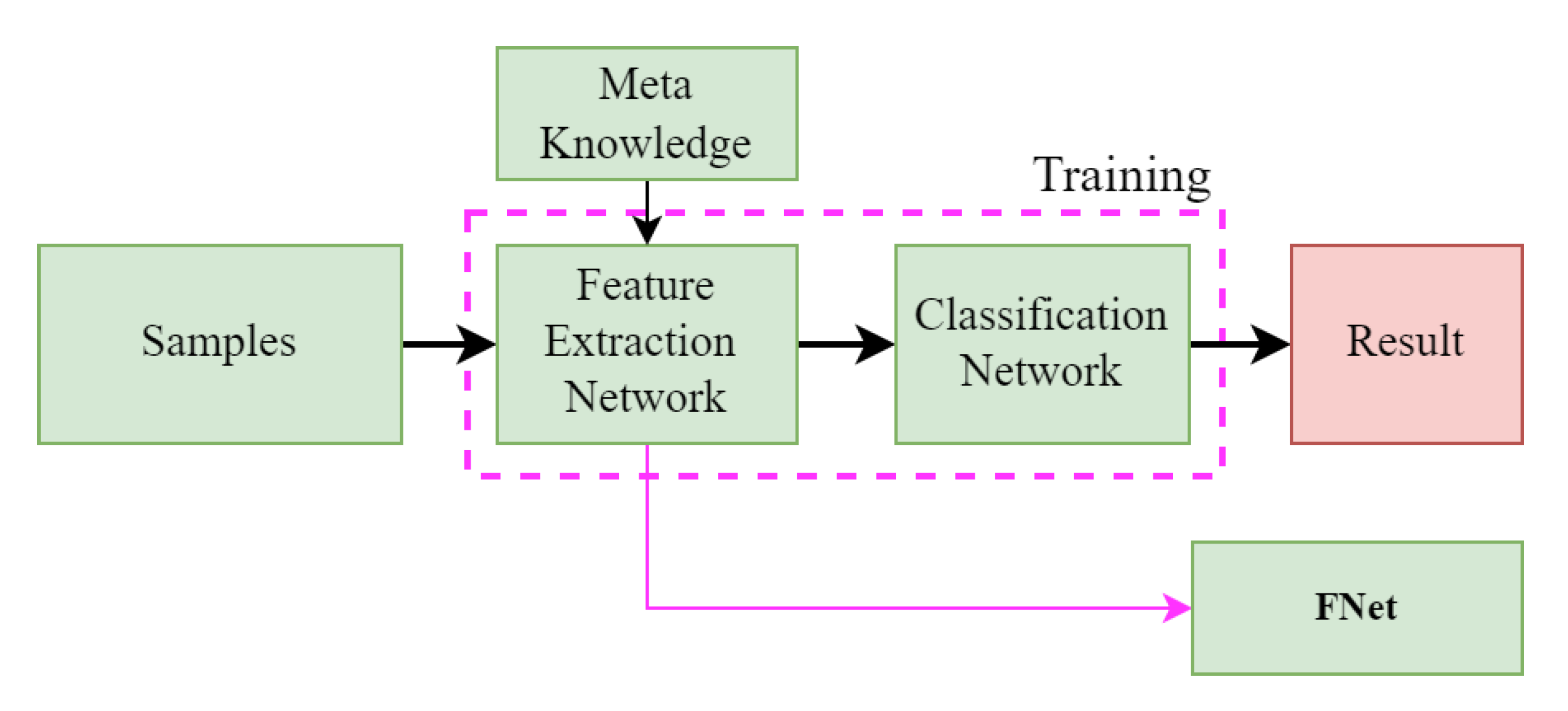
2.2.4. Structure of the Target Task Network
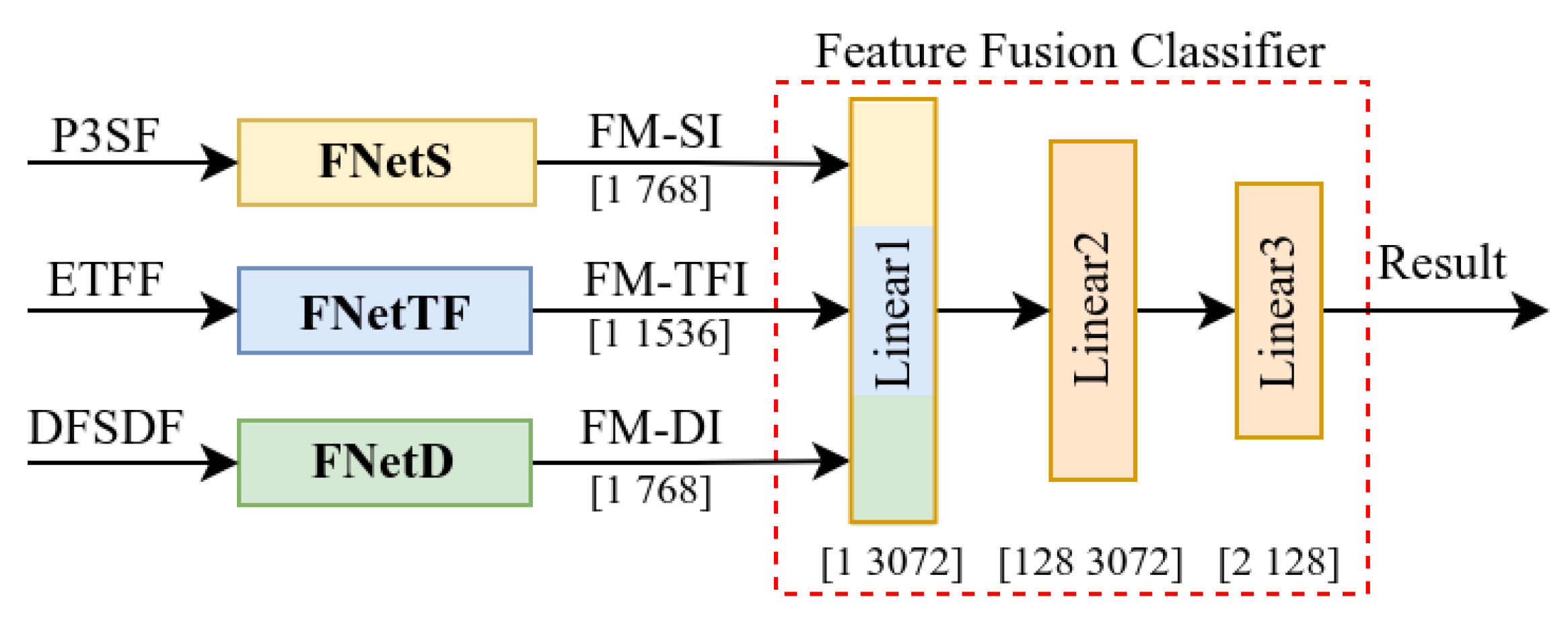
2.2.5. Multidimensional Feature Fusion Network
3. Results
3.1. Dataset
3.2. Evaluation Metrics
3.3. Results and Analysis
3.3.1. Overview of the Verification Process
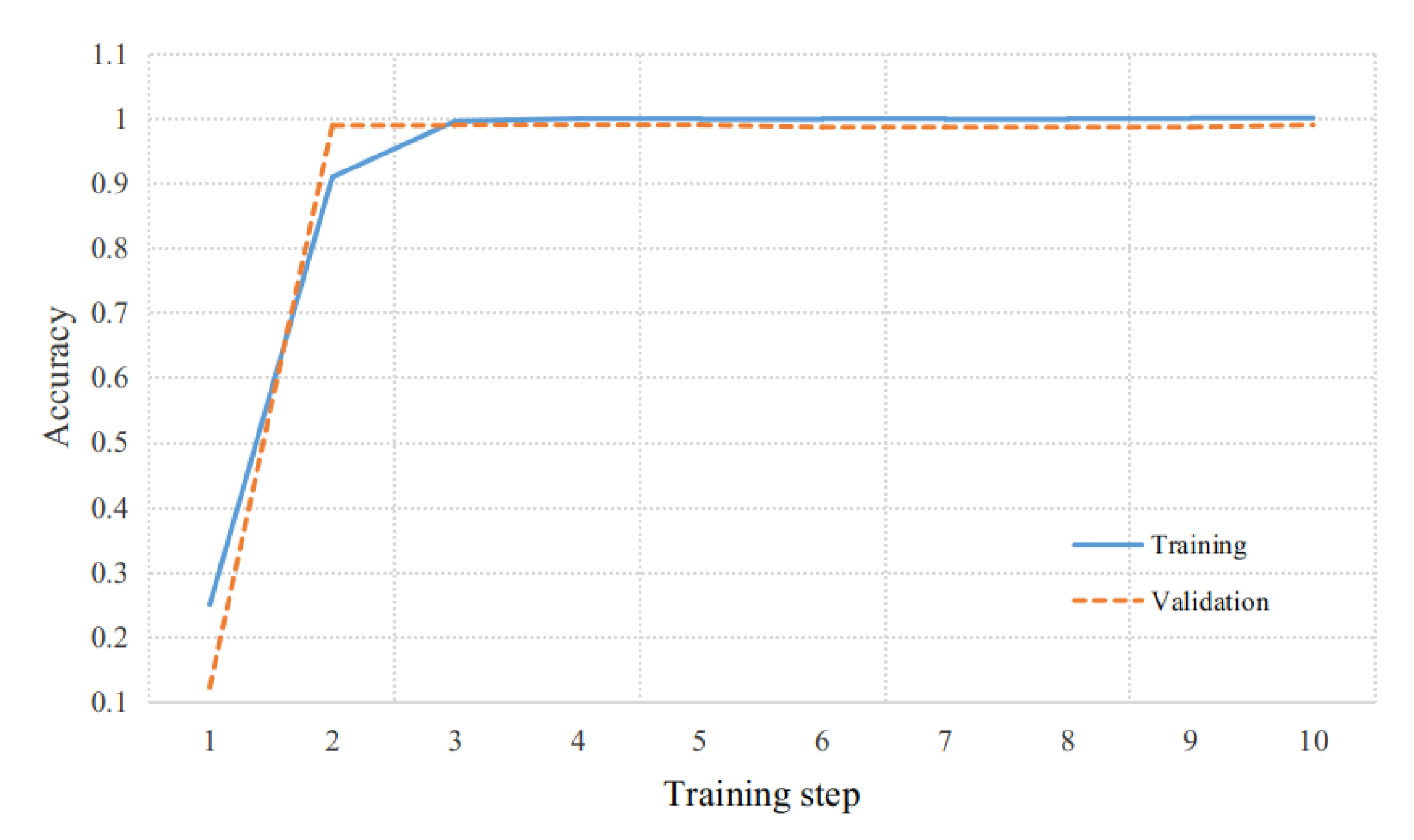
3.3.2. Meta-Learning Training
3.3.3. Training and Testing of the Target Task Network
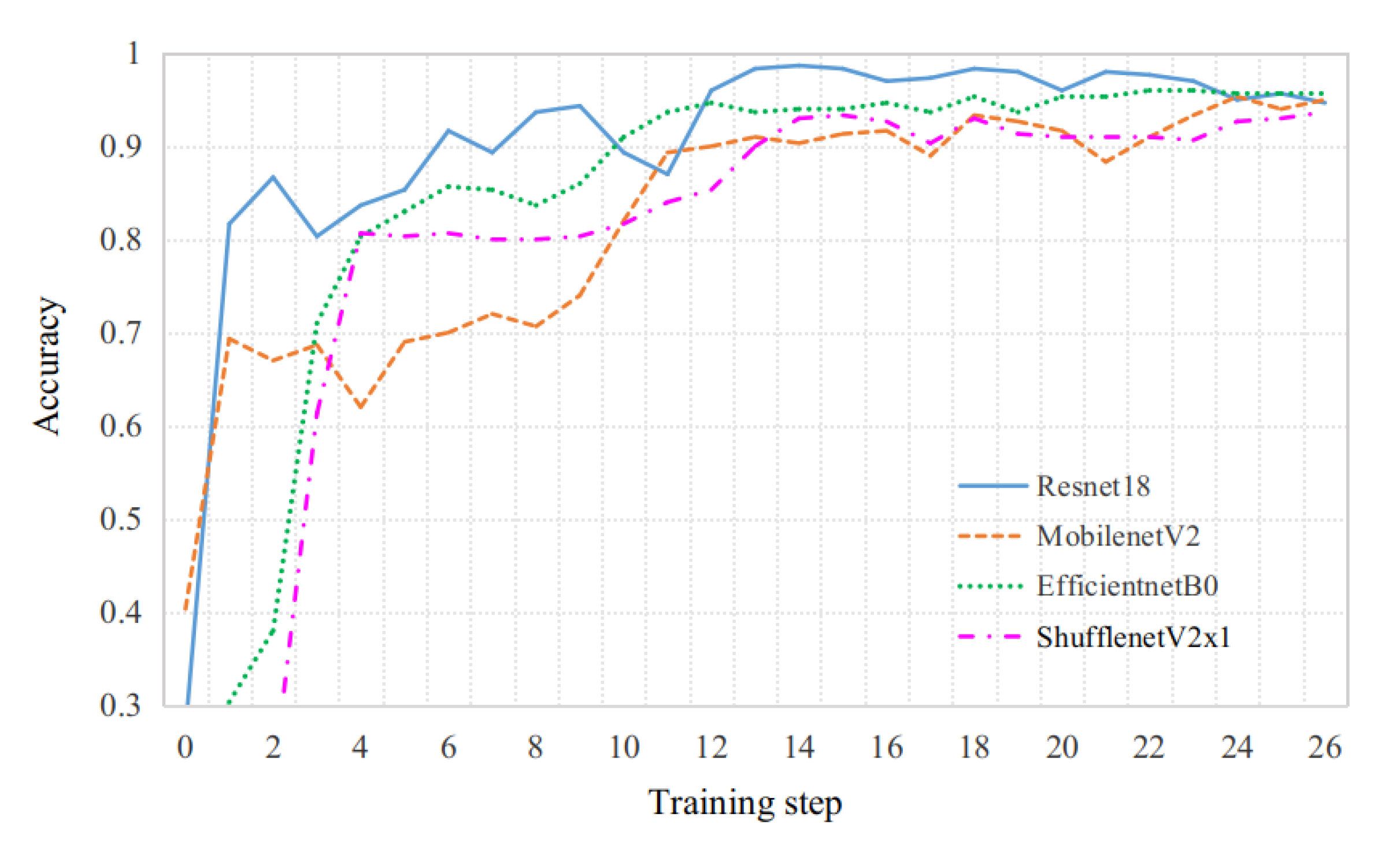
3.3.4. Training and Testing of MFasNetV1
3.3.5. Ablation Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFSDF | Doppler frequency shift distribution feature |
| DOA | direction of arrival |
| ETFF | enhanced time–frequency feature |
| FFC | feature fusion classifier |
| MSI | multi-source interference |
| MUSIC | multiple signal classification |
| P3SF | pseudo-three-dimensional spatial feature |
| PC | parameter configuration |
| RHOA | relative horizontal orientation angle |
| RPA | relative pitch angle |
| STFT | short-time Fourier transform |
| WVD | Wigner–Ville distribution |
| SVM | support vector machine |
References
- Yu, L.; Cheng, Y.; Li, S.; Liang, Y.; Wang, X. Tracking and Length Estimation of Underwater Acoustic Target. Electron. Lett. 2017, 53, 1224–1226. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, J.; Wang, H.; Hao, Y.; Wang, H. A Torpedo Target Recognition Method Based on the Correlation between Echo Broadening and Apparent Angle. Appl. Sci. 2022, 12, 12345. [Google Scholar] [CrossRef]
- Xu, Y.; Yuan, B.C.; Zhang, H.G. An Improved Algorithm of Underwater Target Feature Abstracting Based on Target Azimuth Tendency. Appl. Mech. Mater. 2012, 155–156, 1164–1169. [Google Scholar] [CrossRef]
- Xia, Z.; Li, X.; Meng, X. High Resolution Time-Delay Estimation of Underwater Target Geometric Scattering. Appl. Acoust. 2016, 114, 111–117. [Google Scholar] [CrossRef]
- Rui, L.; Junying, A.; Gang, C. Target Geometric Configuration Estimation Based on Acoustic Scattering Spatiotemporal Characteristics. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Li, X.; Xu, T.; Chen, B. Atomic Decomposition of Geometric Acoustic Scattering from Underwater Target. Appl. Acoust. 2018, 140, 205–213. [Google Scholar] [CrossRef]
- Palomeras, N.; Furfaro, T.; Williams, D.P.; Carreras, M.; Dugelay, S. Automatic target recognition for mine countermeasure missions using forward-looking sonar data. IEEE J. Ocean. Eng. 2022, 47, 141–161. [Google Scholar] [CrossRef]
- Zhang, B.; Zhou, T.; Shi, Z.; Xu, C.; Yang, K.; Yu, X. An underwater small target boundary segmentation method in forward-looking sonar images. Appl. Acoust. 2023, 207, 109341. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Yang, X.; Liu, L.; Shi, L.; Li, Y.; Liu, J. Zero-Shot Learning-Based Recognition of Highlight Images of Echoes of Active Sonar. Electronics 2024, 13, 457. [Google Scholar] [CrossRef]
- Ou, H.H.; Au, W.W.L.; Syrmos, V.L. Underwater Ordnance Classification Using Time-Frequency Signatures of Backscattering Signals. In Proceedings of the OCEANS 2010 MTS/IEEE SEATTLE, Seattle, WA, USA, 20–23 September 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Wu, Y.; Li, X.; Wang, Y. Extraction and Classification of Acoustic Scattering from Underwater Target Based on Wigner-Ville Distribution. Appl. Acoust. 2018, 138, 52–59. [Google Scholar] [CrossRef]
- Kubicek, B.; Sen Gupta, A.; Kirsteins, I. Feature Extraction and Classification of Simulated Monostatic Acoustic Echoes from Spherical Targets of Various Materials Using Convolutional Neural Networks. J. Mar. Sci. Eng. 2023, 11, 571. [Google Scholar] [CrossRef]
- Shang, J.; Liu, Z.L. Research on Feature Extraction and Classification Recognition of Underwater Small Target Active Sonar. In Proceedings of the 2023 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Zhengzhou, China, 14–17 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Q.; Du, S.; Wang, F.; Chen, Y. Underwater Target Recognition Method Based on Multi-Domain Active Sonar Echo Images. In Proceedings of the 2021 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 17–19 August 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, V.C. Advances in Applications of Radar Micro-Doppler Signatures. In Proceedings of the 2014 IEEE Conference on Antenna Measurements & Applications (CAMA), Antibes Juan-les-Pins, France, 16–19 November 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, J.; Guo, J.; Shao, X.; Wang, K.; Fang, X. Road Targets Recognition Based on Deep Learning and Micro-Doppler Features. In Proceedings of the 2018 International Conference on Sensor Networks and Signal Processing (SNSP), Xi’an, China, 28–31 October 2018; pp. 271–276. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, Y.; Wei, Q.; Wang, W.; Ren, Y.; Wang, C. A High-Resolution Radar Automatic Target Recognition Method for Small UAVs Based on Multi-Feature Fusion. In Proceedings of the 2022 IEEE 25th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Hangzhou, China, 4–6 May 2022; pp. 775–779. [Google Scholar] [CrossRef]
- LeNoach, J.; Lexa, M.; Coraluppi, S. Feature-Aided Tracking Techniques for Active Sonar Applications. In Proceedings of the 2021 IEEE 24th International Conference on Information Fusion (FUSION), Sun City, South Africa, 1–4 November 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Li, W.; Yi, W.; Teh, K.C.; Kong, L. Adaptive Multiframe Detection Algorithm With Range-Doppler-Azimuth Measurements. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5119616. [Google Scholar] [CrossRef]
- Wu, Y.; Luo, M.; Li, S. Measurement and Extraction of Micro-Doppler Feature of Underwater Rotating Target Echo. In Proceedings of the OCEANS 2022—Chennai, Chennai, India, 21–24 February 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; PMLR 70. pp. 1126–1135. [Google Scholar] [CrossRef]
- Zeng, Z.; Gu, D.; Sun, J.; Han, Z.; Wang, Y.; Hong, W. SAR Few-Shot Recognition Based on Inner-Loop Update Optimization of Meta-Learning. In Proceedings of the 2023 8th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Bali, Indonesia, 23–27 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Mulinde, R.; Attygalle, M.; Aziz, S.M. Pre-Processing-Based Performance Enhancement of DOA Estimation for Wideband LFM Signals. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, NSW, Australia, 6–10 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, P.; Black, A.W.; Anumanchipalli, G.K. A Fast and Accurate Pitch Estimation Algorithm Based on the Pseudo Wigner-Ville Distribution. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Hague, D.A.; Buck, J.R. The Generalized Sinusoidal Frequency-Modulated Waveform for Active Sonar. IEEE J. Ocean. Eng. 2017, 42, 109–123. [Google Scholar] [CrossRef]
- Brazdil, P.; Van Rijn, J.N.; Soares, C.; Vanschoren, J. Metalearning: Applications to Automated Machine Learning and Data Mining, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 113–121. [Google Scholar] [CrossRef]
- Song, Z.; Lanrui, L.; Xinhua, Z.; Dawei, Z.; Mingyuan, L. Simulation of Backscatter Signal of Submarine Target Based on Spatial Distribution Characteristics of Target Intensity. In Proceedings of the 2021 OES China Ocean Acoustics (COA), Harbin, China, 14–17 July 2021; pp. 234–239. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Hu, Y.; Yang, X.; Li, Y.; Xiao, L. Data Augmentation Based on Highlight Image Models of Underwater Maneuvering Target. Xibei Gongye Daxue Xuebao/J. Northwestern Polytech. Univ. 2024, 42, 417–425. [Google Scholar] [CrossRef]
- Liggins, M., II; Hall, D.; Llinas, J. Handbook of Multisensor Data Fusion: Theory and Practice, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 7–8. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, B.; Yan, Y.; Zhou, A.; Ye, Y.; Zhu, X. Multi-Features Fusion for Underwater Acoustic Target Recognition Based on Convolution Recurrent Neural Networks. In Proceedings of the 2022 8th International Conference on Big Data and Information Analytics (BigDIA), Guiyang, China, 24–25 August 2022; pp. 342–346. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, H.; Li, H.; Song, S. A Lightweight Time-Frequency-Space Dual-Stream Network for Active Sonar-Based Underwater Target Recognition. IEEE Sens. J. 2025, 25, 11416–11427. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. arXiv 2018, arXiv:1807.11164. [Google Scholar] [CrossRef]
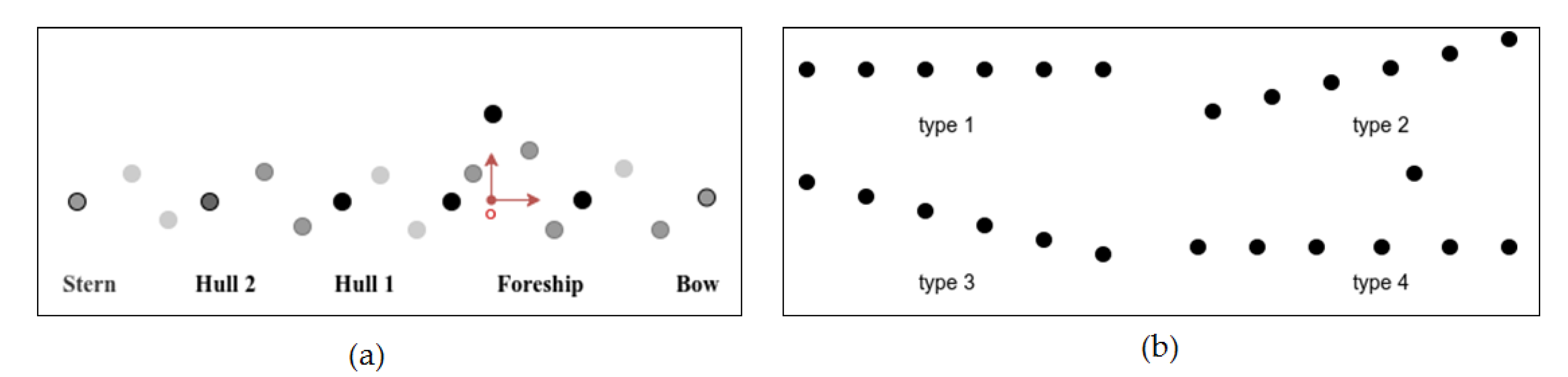
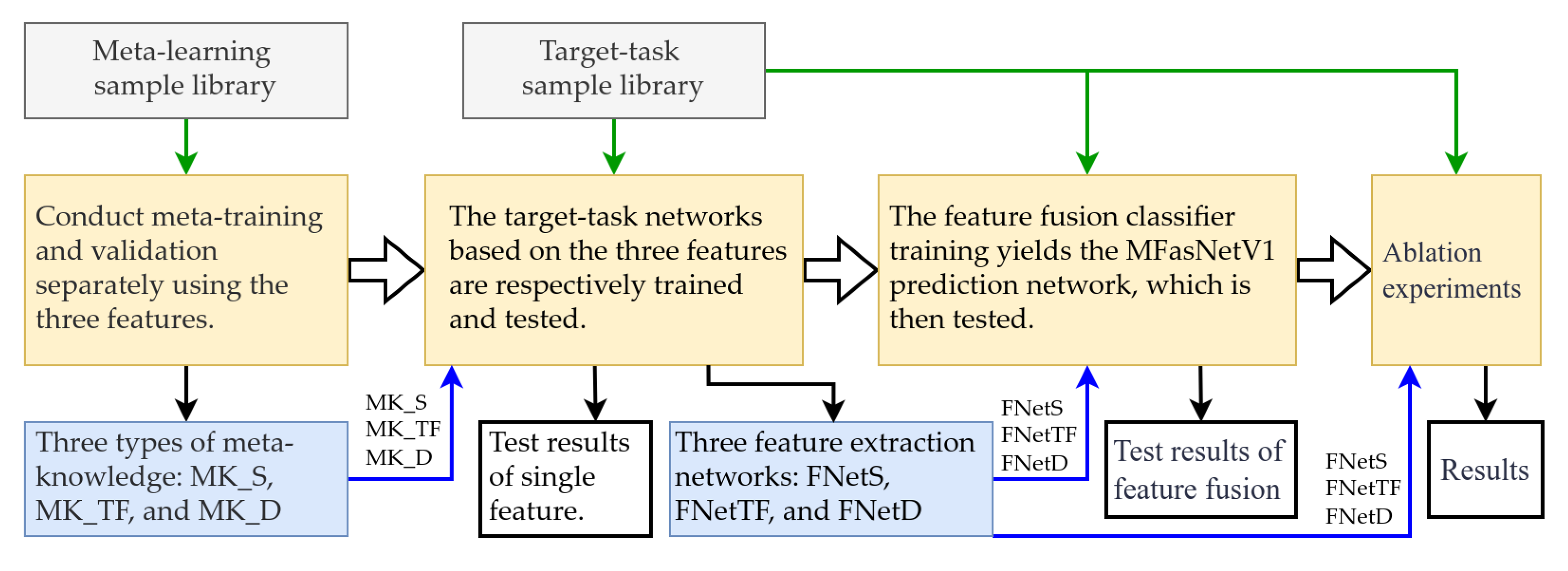
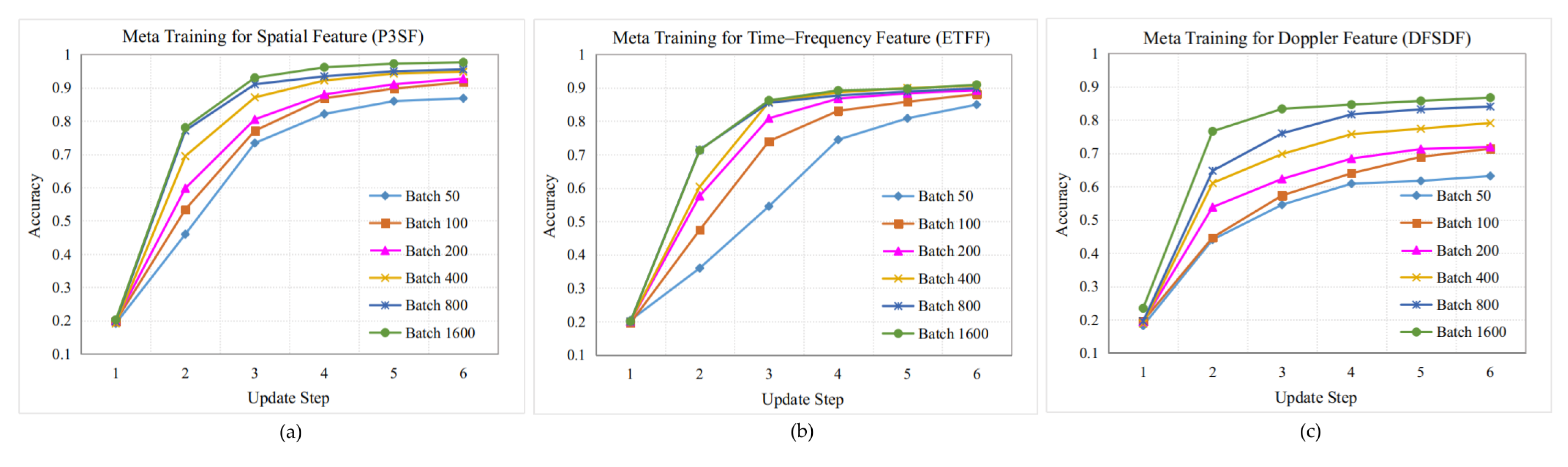

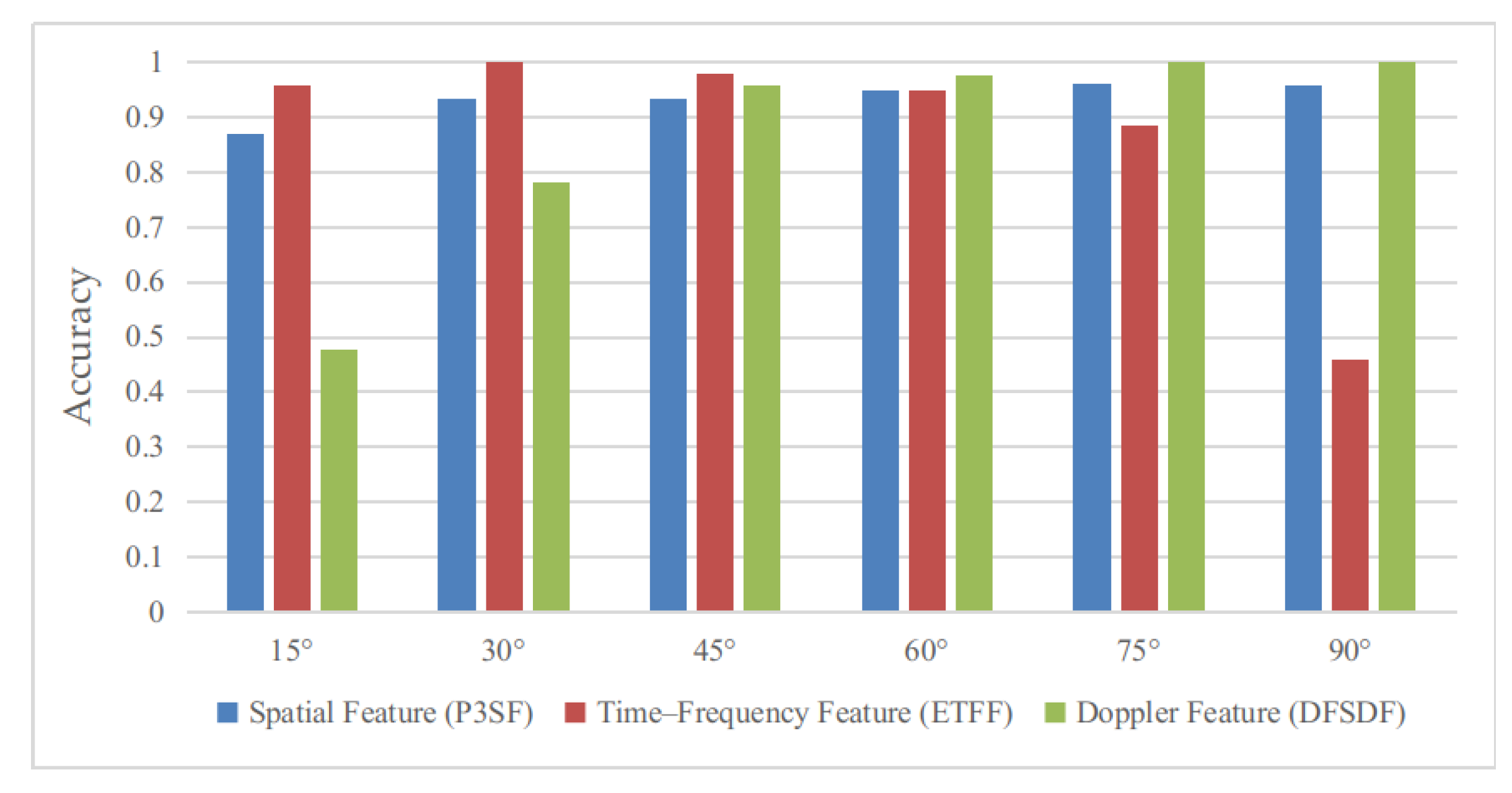
| Algorithm Type | Limitations or Unresolved Challenges |
|---|---|
| Parameter estimation algorithms | These algorithms exhibits limited environmental adaptability, restricted interference discrimination capability, and relatively low recognition accuracy. |
| Target scale-recognition algorithms | Research on the fine scattering characteristics of targets has primarily concentrated on static targets and has not yet been applied to the recognition of moving targets. Highlight-based image recognition algorithms exhibit sensitivity to the relative attitude of targets. |
| Time–frequency feature recognition algorithms | Algorithm verification predominantly depends on pool experiments or simulation data. A few researchers have utilized experimental data to validate the classification between moving targets and static objects. Nevertheless, the limitations regarding the algorithm’s applicability to the relative attitude of targets have not been adequately addressed. |
| Doppler feature recognition algorithms | Micro-Doppler features in the radar domain have been extensively utilized for target recognition. In contrast, in the sonar domain, Doppler features are primarily employed for target detection and velocity estimation, whereas the acquisition of micro-Doppler signatures remains challenging. |
| Target Type | Relative Horizontal Orientation Angles (°) | Relative Pitch Angle (°) |
|---|---|---|
| Underwater vehicle | 15, 30, 45, 60, 75, 90 | 1.5 |
| Type I interference | 15, 30, 45, 60, 75, 90 | 1.5 |
| Type II interference | 15, 30, 45, 60, 75, 90 | 1.5 |
| Type III interference | 15, 30, 45, 60, 75, 90 | 1.5 |
| Type IV interference | 15, 30, 45, 60, 75, 90 | 1.5 |
| Sample Set Type | Experimental Data | Simulation Data (PC3) | Simulation Data (PC4) | Total |
|---|---|---|---|---|
| Training set | 100 | 160 | 0 | 260 |
| Validation set | 65 | 0 | 140 | 205 |
| Test set | 205 | 0 | 0 | 205 |
| Data Type | Classification Results | Recall Rate | |
|---|---|---|---|
| Interference | Underwater Vehicle | ||
| Type I interference A | 32 | 0 | 100 % |
| Type I interference B | 31 | 1 | 96.9% |
| Type II interference | 25 | 0 | 100% |
| Type III interference | 24 | 1 | 96.0% |
| Type IV interference | 24 | 1 | 96.0 % |
| Underwater vehicle | 3 | 63 | 95.4% |
| Test Type | Spatial Feature P3SF | Time– Frequency Feature ETFF | Doppler Feature DFSDF | Accuracy |
|---|---|---|---|---|
| P3SF | ✓ | 93.6% | ||
| ETFF | ✓ | 90.2% | ||
| DFSDF | ✓ | 87.8% | ||
| P3SF and ETFF | ✓ | ✓ | 96.6% | |
| P3SF and DFSDF | ✓ | ✓ | 95.6% | |
| ETFF and DFSDF | ✓ | ✓ | 96.1% | |
| All | ✓ | ✓ | ✓ | 97.1% |
| Module | Parameters (M) | FLOPs (M) | Accuracy (%) | |
|---|---|---|---|---|
| MFasNetV1 | HasNet-5 | 1.06 | 11.1 | 97.1 |
| TFasNet-7 | 3.56 | 324.5 | ||
| DasNet-9 | 0.84 | 428.4 | ||
| FFC | 0.39 | 0.4 | ||
| ResNet18 | 11.68 | 1824.0 | 94.1 | |
| MobileNetV2 | 3.51 | 327.6 | 93.2 | |
| EfficientNetB0 | 5.29 | 412.8 | 92.7 | |
| ShuffleNetV2x1 | 1.26 | 146.0 | 91.2 | |
| Stage of Fusion | Module | Accuracy (%) |
|---|---|---|
| Data-level | ResNet18 | 94.1 |
| MobileNetV2 | 93.2 | |
| EfficientNetB0 | 92.7 | |
| ShuffleNetV2x1 | 91.2 | |
| Feature-level | MFasNetV1 | 97.1 |
| Decision-level | MFasNetV1 | 94.1 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Yang, Y.; Hu, Y.; Yang, X.; Liu, L.; Shi, L.; Liu, J. A Meta-Learning-Based Recognition Method for Multidimensional Feature Extraction and Fusion of Underwater Targets. Appl. Sci. 2025, 15, 5744. https://doi.org/10.3390/app15105744
Liu X, Yang Y, Hu Y, Yang X, Liu L, Shi L, Liu J. A Meta-Learning-Based Recognition Method for Multidimensional Feature Extraction and Fusion of Underwater Targets. Applied Sciences. 2025; 15(10):5744. https://doi.org/10.3390/app15105744
Chicago/Turabian StyleLiu, Xiaochun, Yunchuan Yang, Youfeng Hu, Xiangfeng Yang, Liwen Liu, Lei Shi, and Jianguo Liu. 2025. "A Meta-Learning-Based Recognition Method for Multidimensional Feature Extraction and Fusion of Underwater Targets" Applied Sciences 15, no. 10: 5744. https://doi.org/10.3390/app15105744
APA StyleLiu, X., Yang, Y., Hu, Y., Yang, X., Liu, L., Shi, L., & Liu, J. (2025). A Meta-Learning-Based Recognition Method for Multidimensional Feature Extraction and Fusion of Underwater Targets. Applied Sciences, 15(10), 5744. https://doi.org/10.3390/app15105744






