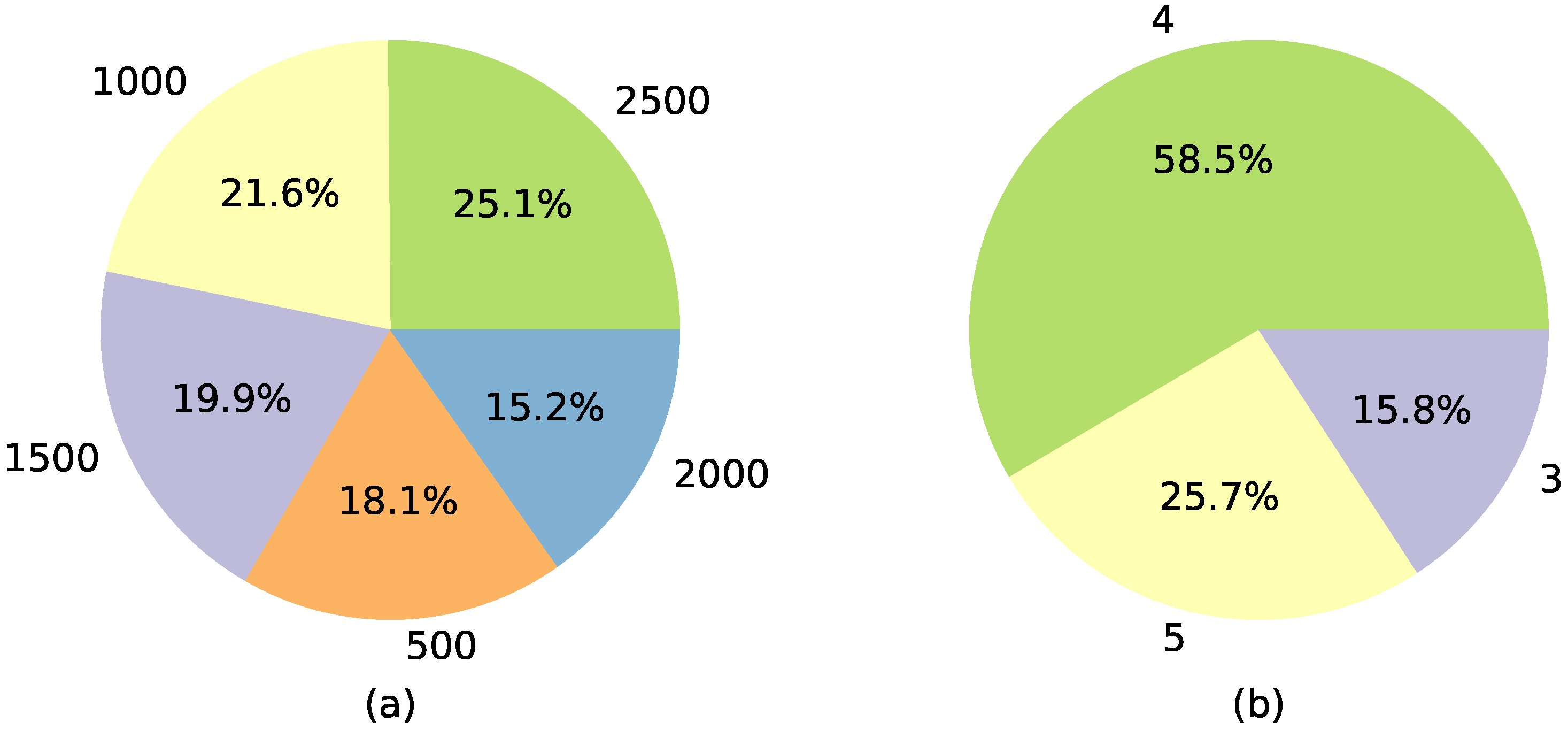1. Introduction
The Chase is a popular TV quiz show licensed by ITV Global Entertainment Limited. On each episode, four contestants, who have just met for the first time, aim to beat the chaser (a professional quiz player) and win a specific amount of money. The show has been broadcast in the United Kingdom since 2009, with numerous international versions produced, including the Croatian version, which has been broadcast by Croatian Radiotelevision (Hrvatska radiotelevizija, abbreviated as HRT) since 2013. Because of the show’s immense popularity, several spin-off versions have been created, such as celebrity specials (The Chase: Celebrity Special), for charitable purposes, The Family Chase, where four family members compete together, and, ultimately, Beat the Chasers. The latter, which is the focus of this paper, immediately gained popularity in all markets because of its pronounced dynamics and suspense. The main premise of the show is the inversion of the original concept. Although in The Chase, a team of contestants faces one chaser, in Beat the Chasers, a single contestant faces a team of chasers. The show began airing in 2023.
Although the rules of the game will be explained in detail in
Section 3, it is important to mention the offers as one of the main concepts of the quiz. After the initial part of the game (the so-called cash builder), where a contestant answers a maximum of five questions, they challenge a team of up to five chasers, usually professional quizzers, with respect to the offers given by the host. Each offer balances risk and reward, varying in prize money, time advantage, and the number of chasers. During the airing time, it was observed that sometimes the contestants received vastly different offers, despite answering the same number of questions in the first phase of the game (i.e., in the cash builder). Some offers differ significantly in the prize money or the time allocated to the chasers, while others vary only in the order of the chasers.
The motivation behind this study stems from a desire to understand how contestants make decisions regarding the offers presented to them, specifically, how their demographic data and personal traits (i.e., contestants’ profiles) influence their choices and, ultimately, shape the outcome. By applying artificial intelligence methods, deeper insights into the decision-making process could be uncovered, ultimately contributing to a more strategic and informed approach for both the contestants and the show’s producers. From the producers’ perspective, a better understanding of these dynamics could lead to a more engaging show, while contestants could benefit from improved preparation and a more predictable decision-making framework.
The study of human decision making falls within the domain of psychology and has been under extensive research for several decades. Among the most influential contributors to this field are Kahneman and Tversky, whose development of prospect theory fundamentally reshaped the understanding of decision making under risk. One of the key insights of prospect theory is the certainty effect, wherein individuals tend to underweight outcomes with low probabilities and overweight outcomes that are certain [
1]. This leads to loss aversion, the principle that losses have a greater psychological impact than equivalent gains, which manifests as risk aversion in scenarios involving potential gains and risk-seeking behavior when faced with potential losses. Additionally, their work highlights that choices are typically evaluated relative to a reference point, rather than in absolute terms [
2], and that individuals often ignore elements common to all the alternatives, a tendency known as the isolation effect. Prospect theory was later refined and extended by the same authors [
3]. Complementary to this work is their research on human risk assessment [
4], which further supplements the complete decision-making picture. On the other hand, Gigerenzer’s approach is similar but different. Together with Goldstein, Gigerenzer introduced a family of fast and frugal heuristics that deliberately ignore a part of the available information and avoid complex integration processes yet often yield effective results in real-world contexts [
5]. Gigerenzer argues that the uncertainty and incompleteness, both inherent in heuristic processes, can be advantageous and ultimately lead to better decisions [
6]. One of the key insights from this research is the less-is-more effect, which suggests that using fewer cues or less information can sometimes lead to better decisions than more complex approaches. This forms the basis of Gigerenzer’s model of
Homo heuristicus, a cognitive agent that features a biased mind and purposefully ignores a part of the available information. Such an agent often performs more efficiently and robustly in uncertain environments than a theoretically unbiased agent relying on exhaustive, resource-intensive methods [
7]. Although this is prospective for a study of this kind, we opted not to proceed in that direction, as these aspects are beyond the scope of the present work. Properly addressing psychological factors, such as human decision making, would require more advanced tools, an expanded research framework, and collaboration with experts in other applicable fields.
Instead, this paper aims to investigate several artificial intelligence methods used to predict the course of the game. This research is divided into two main goals: The first part (
Section 5.2) seeks to identify which offer a contestant will select based on (1) the contestant’s profile, (2) the contestant’s profile and the cash builder result, and, finally, (3) the contestant’s partial profile (gender, age group, hometown size, and NUTS 2 region). Cases (1) and (2) are separated to determine whether the cash builder results significantly influence contestants’ choices, while case (3) came out as one of the combinations that yielded the best prediction results.
The second part (
Section 5.3) of the analysis aims to predict the game’s outcome based on six different feature combinations (i.e., scenarios). The first scenario aims to do so based on only (1) the contestant’s profile, while the second adds (2) the cash builder result, all the offers, and specific chasers within the selected offer alongside the contestant’s profile. The third scenario explores the influence of the contestant’s profile on the outcome by removing the profile from the second scenario, yielding a feature set comprising (3) the cash builder result, all the offers, and specific chasers within the selected offer. The fourth, fifth, and sixth scenarios completely disregard the concepts of a profile and an offer and aim to predict the outcome based on (4) the selected number of chasers and the cash builder result, (5) the selected number of chasers and the chasers’ time in the selected offer, and (6) the selected number of chasers, cash builder result, and chasers’ time in the selected offer.
To sum up, this paper makes the following contributions:
- 1.
A publicly available dataset for the Croatian version of the Beat the Chasers TV quiz [
8];
- 2.
Tuned machine-learning models for predicting the offers that a contestant is the most likely to select;
- 3.
Tuned machine-learning models for the game’s outcome prediction;
- 4.
The identification of the key factors that influence both the selected offer and the game’s outcome prediction.
The rest of the paper is organized as follows. First, in
Section 2, we provide a brief overview of the respective field. We then proceed to explain the core rules and propositions of the game in
Section 3. The collected dataset is introduced and thoroughly described in
Section 4. In
Section 5, we describe the methodology and present and discuss the results obtained by applying several machine-learning classifiers for both goals. Finally, the paper is concluded in
Section 6.
2. Related Work
In this section, we provide a brief review of the field in terms of data mining and knowledge extraction on quiz-based games and shows. To the best of our knowledge, there has been no published scientific work on either The Chase or Beat the Chasers quizzes. We thus focus on other cases of knowledge extraction in a quizzing context. Because of the limited scientific literature specifically targeting quizzes, we also consider not only the adjacent fields of students’ academic performance and the prediction of sports’ outcomes but also the application of artificial intelligence in consumer behavior analysis, marketing, and gamification.
First, we consider various TV quiz shows. For a show named
The Price is Right, Kvam [
9] considered various strategies to maximize the winning probability based on the players’ bidding order. They considered the preceding bids of the other players and finally analyzed how confidence can affect the winning probability of a player. Frazen and Pointner analyzed the determinants of successful participation on a popular TV quiz show
Who Wants to Be a Millionaire? [
10]. The analysis was based on the German instance of the quiz. The authors tested the assumed advantage of social capital in terms of personal networks and human capital in terms of participants’ education. The same TV quiz show was the topic of research of Molino et al. [
11,
12]. They developed a virtual player for the game, which used various natural language-processing techniques to rank the answers according to several lexical, syntactical, and semantic criteria. These sources also implicitly affirm that the application of the techniques available under the artificial intelligence umbrella to TV quizzes has existed for a not-so-brief period. On the other hand, the authors in [
13] explored the use of crowdsourcing and lightweight machine-learning techniques to create a player for the same game. Their system collected answers from a crowd of mobile users and aggregated these responses using various algorithms, including majority voting and confidence-weighted voting. The results demonstrated that by effectively combining crowdsourced data with machine learning, even difficult questions could be answered with a high degree of accuracy, suggesting the feasibility for building a “super player” for question answering. To sum up, research on TV quiz shows so far has primarily focused either on analyzing factors that contributed to or have led to successful participation or on building virtual players, whereas our study concentrates on predicting both in in-game decision making and the final games’ outcomes.
One of the most complete approaches we found involving a contestant’s profile was related not to the TV quiz show but to a reality show. In [
14], Lee et al. trained three machine-learning models on demographic and other profile-related data extracted from aired episodes, trying to predict the winner of
The Bachelor. The authors stated that they found clear consistency across all three models, which enabled them to pinpoint the specific demographic (e.g., exact age, race, or home region) and in-show achievement parameters that influence the probability of progressing far in the show. The approach taken by the authors in that study to some extent resembles the approach we took in this paper, mainly in terms of the game’s outcome prediction using contestants’ profiles.
Significant work has been conducted within the context of predicting students’ performance. Ofori et al. [
15], in their literature-based review of machine-learning algorithms for the prediction of students’ performance, stated contentious results with respect to the selection of a model that best predicts performance. They stated that varying prediction levels may be a result of differences in socioeconomic status or other types of students’ backgrounds, which were not considered when assessing the accuracy of the models. Alhothali et al. [
16] performed a survey that examined online learners’ data to predict their outcomes, using machine- and deep-learning techniques. They stated that most studies in the field utilized statistical features, such as the number of downloaded materials and the total time spent on course-related video watching in a given time period. Wu et al. [
17] reviewed 83 studies, finding that ensemble-learning models achieved the highest accuracy rate (87.7%), followed by the support-vector-machine (84.3%) approach.
Demographic, academic, and behavioral factors were significant predictors of academic achievement. Rebai et al. [
18] applied machine-learning techniques (regression trees and random forests) to Tunisian secondary schools, identifying school size, competition, class size, parental pressure, and the proportion of girls as key performance factors. Random forests additionally revealed the significant roles of the proportion of girls and the school size in improving predictive accuracy and, hence, could influence school efficiency. Similarly, Agyemang et al. [
19] found random forests to be the best-performing algorithm for predicting students’ performance, with an accuracy rate of 85.4%. The authors also emphasized challenges such as the lack of standardization in performance metrics, limited model generalization abilities, and potential bias in training data. Finally, Suaza-Medina et al. [
20] combined machine-learning algorithms and Shapley values to analyze factors influencing Colombian students’ academic performance. The results showed that the best accuracy was achieved with extreme gradient boosting. Furthermore, according to the Shapley values, the socioeconomic level index, gender, age, region, and school location were identified as key predictors. As shown in related studies on students’ performance in academic contexts, authors typically base their analyses on various subsets of demographic data (as we do in our study), as well as on non-demographic and environmental factors.
The authors in [
21] suggested a multilevel heterogeneous predictive model, which yielded an ensemble-learning model for predicting students’ performance and assessments. The authors claimed a predictive accuracy rate of 99.5%. Abiodun and Andrew [
22] investigated the prediction of students’ academic performance using ensemble machine-learning algorithms, specifically, random forest, k-nearest neighbors, XGBoost, and a stacked ensemble approach. Their results demonstrated that the stacked ensemble model achieved the best performance. This study builds upon previous work, such as that by Yagci [
23] and Ababneh et al. [
24], by demonstrating the effectiveness of ensemble methods for improving the accuracy of student performance predictions. Similar to the authors of these studies, we also employed ensemble methods (voting classifiers), which yielded solid, though not the best, results in our case.
Finally, the authors of a review study [
25] stated that individuals tend to validly use different multiple-machine-learning models to solve the problems related to predicting students at risk and assessing their performance. Multiple authors have tackled the problem of predicting degree completion with various approaches in terms of machine-learning models and the underlying type of the used data [
26,
27,
28]. The authors in [
29] focused on demographic data as predictors of learners’ performance. In this study, we adopted a similar approach by evaluating multiple models to determine which would yield the best results, as we did not have a prior indication of which model might perform optimally.
Machine learning and artificial intelligence have, in general, gained significant traction in the fields of marketing and consumer behavioral analysis. The authors in [
30] demonstrated that AI-driven marketing strategies, such as targeted ads and chatbots, significantly improved outcomes, with increases in click-through rates and general improvements in customer satisfaction. That study also highlighted ethical concerns and the challenges of AI adoption in developing markets. The authors in [
31] emphasized the transformative role of generative AI in consumer engagement and decision making through personalized recommendations and interactive experiences, offering valuable insights for future research and policymaking. When it comes to neuromarketing, the authors in [
32] presented neural networks as a cost-effective alternative to traditional neuromarketing tools, employing them to examine the predictive consumer-buying behavior of an effective advertisement. This field relates to our research by highlighting a parallel: Just as marketing seeks to persuade consumers to buy a product, the production team could aim to influence the contestant to select a specific offer.
Artificial intelligence has also become a powerful enabler of gamification, enhancing user engagement and motivation through personalization and adaptive experiences. The authors in [
33] outlined how AI optimizes gamification by tailoring interactions to individual user preferences and performance. Within the context of education, Rosunally [
34] introduced a framework that supports educators in designing and implementing engaging learning experiences by leveraging generative artificial intelligence, especially when expertise or resources are limited. Kok et al. [
35] further explored the integration of AI with gamification and immersive learning, demonstrating its potential to transform educational environments through dynamic and effective experiences. Geleta et al. [
36] presented Maestro, an effective open-source game-based platform that contributes to the advancement of robust AI education. Additionally, You et al. [
37] proposed a novel approach to AI explainability using LLM-powered narrative gamification, enabling non-technical users to interact with visualizations and derive insights through conversational gameplay.
Other possible applications of machine-learning methods related to our work include the prediction of the contestants’ outcomes in competitive programming [
38] and the prediction of the outcomes of sports matches. In [
39], Gifford and Bayrak used a decision tree and a binary logistic regression model to forecast outcomes in the NFL (National Football League, a professional American football league in the US). Similarly, Wong et al. [
40] developed machine-learning models for the prediction of the outcomes of soccer matches. Partially related to the sports domain, machine learning has a proven application record in the betting industry [
41,
42], with a systematic review available in [
43]. The researchers in [
44] proposed a framework for the outcome predictions of ongoing chess matches. The achieved prediction accuracies were nearly 66%, with most of the correct predictions made with nine or more moves before the game ended. In [
45], Keerthana and Mary Valantina explored chess game-winning predictions using AlexNet and stochastic gradient descent (SGD). Their study trained both classifiers on chess game data, using features derived from previous moves to identify players’ skills and strengths. The results indicated that AlexNet achieved a significantly higher accuracy rate of 99.9% in predicting winning ratios, compared to SGD’s accuracy rate of 96.6%.
3. Game Rules
In this section, we introduce a subset of the core rules and propositions of the Beat the Chasers quiz, which are necessary for understanding the purpose of this research [
46].
The TV quiz show Beat the Chasers consists of two phases. In the first phase of the game (the cash builder), the player answers up to five multiple-choice questions (each with three options and one correct answer) until they make a mistake. In the Croatian version of the quiz, each correct answer is worth EUR 500, implying that the maximum amount that can be earned in this phase is EUR 2500. If the player answers the first question incorrectly, they are immediately eliminated and cannot continue the game. At the end of the cash builder, the contestant faces the chasers and receives four offers. The offers differ in the number of chasers, the prize money for winning the second phase, and the time allocated to the chasers in the second phase. The time part of the offer implies the time allocated to the chasers in a direct head-to-head contest. Although the contestant is given 60 s, the chasers’ time varies depending on the offer selected by the contestant.
The first offer always consists of the money earned in the cash builder, two non-deterministically assigned chasers, and the time allocated to the chasers, which varies among the contestants. Each subsequent offer adds a chaser and usually increases both the prize money and the time allocated to the chasers. The order of the chasers is non-deterministic; thus, different players may face different chasers for the same offer. Before advancing to the second phase, the contestant must select one of the four offers.
Table 1 shows an example of four possible offers given to the contestant, with varying numbers of chasers, times allocated to the chasers, and prize monies.
The second phase of the game is a competition between the contestant and the chasers. As stated before, the contestant has a total of 60 s to answer the questions, while the chasers have the amount of time specified in the offer selected by the contestant. The host alternately asks questions to the contestant and the chasers. The respective time on both sides runs downward until they do not answer the host’s question correctly. The first one to answer is the contestant, and their time starts as soon as the host starts reading the first question. If the contestant answers a question incorrectly or skips a question (colloquially, “passes” a question), the host moves on to the next question while the contestant’s time is still running down. If the contestant answers correctly, their time stops, and the host switches to the chasers. The same rules apply to the chasers: Their time starts running as soon as the first question is asked and continues until they provide a correct answer. The only difference is that a chaser must press the buzzer before they can answer a question, or their response will not be accepted. The game ends when either the contestant or the chasers run out of time. If the chasers run out of time before the contestant, the contestant wins and receives the prize money determined by the selected offer. Conversely, if the contestant runs out of time, they lose the game and receive no monetary reward.
4. Dataset
In this section, we present the dataset [
8] extracted from the first two seasons of the publicly aired Croatian version of the show. We constructed the dataset manually by watching all the aired episodes of the quiz and transcribing the relevant information into a spreadsheet. First, we consider ethical issues, and then, we describe the encodings we used for the qualitative types of the set. In the final subsection, we describe the dataset in terms of descriptive statistics.
4.1. Ethical Responsibility
All the data used as a part of this research were publicly available. The information about the contestants and the offers was collected from publicly aired episodes of the TV quiz show and converted to numerical values (i.e., coded in the way described in
Section 4.2). The data were anonymized by dropping contestants’ names and by grouping explicit values, e.g., contestants’ ages were translated to age groups and occupations to fields of work. The data were additionally shuffled with the aim of obscuring the mapping between the appearance of contestants on the show and their data in the dataset. To ensure the anonymity of the chasers, they were assigned IDs, which were used consistently throughout the dataset. The analysis was conducted exclusively for academic and research purposes. Furthermore, both Convention 108 of the Council of Europe [
47] and the GDPR state that personal data that have been rendered as anonymous in such a way that the individual is no longer identifiable are not considered as personal data [
48].
4.2. Dataset Description and Preparation
In the first step, we discarded the entries representing the contestants who did not manage to successfully answer the first question in the cash builder, which disqualified them from facing the chasers. Thereafter, using all the available information about the contestants, we identified eight features that comprised the contestants’ profiles. Those features were as follows:
- 1.
Gender;
- 2.
Age group;
- 3.
Level of education;
- 4.
Field of work;
- 5.
Hometown size;
- 6.
NUTS 2 region;
- 7.
Intended use of the prize money;
- 8.
Whether the chasers recognized them from other quizzes.
All the information about the contestants was encoded as numerical values according to the rules defined below. Like the dataset collection, the encoding was also performed manually, thus inherently ensuring data quality and validation. To begin with, we assigned the gender according to the contestant’s language-based self-presentation, as Croatian is a gender-specific language. We assigned 0 for men and 1 for women. Next, the contestants were divided into age groups, as defined in
Table 2. The groups were defined according to the United Nations’ Provisional Guidelines on Standard International Age Classifications [
49], with a minor adjustment: The boundary between the first two groups was lowered from 19 to 18 because the Croatian population typically enters higher education at the age of 19.
The contestants were then categorized by their level of education according to the Croatian Qualifications Framework [
50] (an instance of the European Qualifications Framework [
51]), as shown in
Table 3. The contestants’ fields of work were recorded based on the Croatian Regulation on Scientific and Artistic Areas, Fields, and Branches [
52], which defines seven scientific and artistic areas and two interdisciplinary areas, as presented in
Table 4. For a few contestants who completed graduate studies in different fields, we retained the field they stated they were currently working in. In cases where the contestant was still a high school student, the field of work was recorded as zero (0).
For each contestant, the host stated the city where they currently reside (i.e., their hometown). From this information, two values were derived. The first value was the size of the city and the second was the second-level statistical region (HR NUTS 2) in which the city is located. Cities were categorized by population into large, medium, and small, as shown in
Table 5. The large cities’ category contained the five largest Croatian cities, which are Zagreb, Split, Rijeka, Osijek, and Zadar. The second group consisted of all cities with a population of between 10,000 and 70,000, such as Velika Gorica, Pula, Slavonski Brod, Karlovac, Varaždin, and others. The third group included all the Croatian cities with fewer than 10,000 inhabitants.
The NUTS classification [
53] is a statistical standard used to divide a country’s territory (in this case, the Republic of Croatia) into spatial units for regional statistical analysis. The application of the NUTS classification began when Croatia joined the European Union, dividing its territory into three levels. The lowest level (HR NUTS 3) consists of administrative units, which are 21 counties in the case of Croatia. The next level (HR NUTS 2) comprises four non-administrative (regional) units depicted in
Figure 1, created by county grouping. The highest level (HR NUTS 1) encompasses the entire territory of the Republic of Croatia as a single administrative unit. For our dataset, we chose the second-level division (NUTS 2) for further analysis, as it provided additional information about the contestants without overburdening the models with too many possibilities, as would be the case with the county-level division. Additionally, although not all the counties were represented by contestants in the quiz, all four non-administrative regions were.
Table 6 shows the region codes used according to the NUTS 2 classification.
Most of the contestants were asked by the host about their plans for spending the prize money in case they managed to win on the show. Despite the wide variety of answers, we defined four categories of the intended use of the prize money, as presented in
Table 7. The first category included intentions that we identified as basic life expenses, such as car purchases, money savings, or real estate investments. The second category, titled “Extravagant purposes” included all the unusual ideas for spending money, such as “buying shoes”, “participating just for fame”, “presidential election campaign”, “giving money to a spouse”, or simply stating “it does not matter”. The third category consisted of travel, wellness activities, treating friends, or other common hobbies, such as sports or music. The final category included noble uses of the prize money, such as funding one’s education (e.g., a PhD degree or driving lessons), publishing a novel, or donating money to a charity. Some contestants mentioned multiple intended uses for the prize money. In such cases, the first-mentioned purpose was selected.
The final feature describing the contestants was whether the chasers recognized them from previous TV shows or pub quizzes. When the host announced the contestant’s name, the camera usually focused on the team of chasers, revealing their reaction to the upcoming contestant. In cases where they were familiar with the contestant, they usually made a brief comment about their past performance in other quizzes or their reputation on the quiz scene. Whether the chasers were already familiar with the contestant was encoded with a value of 1 if true and 0 otherwise.
In addition to the contestant-related data, the offers also had to be converted to purely numerical values. The prize money and time were already expressed as numbers, but it was also important to consider the order in which the chasers appeared in the offers. To preserve the chaser’s anonymity, their names were replaced with the assigned identifier numbers (from Chaser #1 to Chaser #5), which remained consistent across all the instances. A column was added for each chaser to indicate the offer in which they appeared. For example, if Chaser #2 and Chaser #3 appeared in the first offer, Chaser #5 joined them in the second, Chaser #4 in the third, and Chaser #1 in the fourth, the record for that contestant would look as presented in
Table 8. As mentioned in the Introduction (
Section 1), we also analyzed two scenarios where we only considered the information about which chasers participated in the second phase of the game, regardless of their order of appearance. For this purpose, we introduced five additional columns (Chaser #1’s participation–Chaser #5’s participation). Each column indicated whether the respective chaser participated in the second phase of the game. Because this involved binary possibilities, a value of 1 was recorded if the respective chaser participated and 0 if not. This way, when predicting the game’s outcome, the order in which a chaser appeared in the offers is disregarded, focusing solely on the fact that they participated in the final chase.
To achieve optimal performance, the dataset required some additional processing. Apart from removing the names of the contestants who did not progress to the second phase of the game and converting all the values to numerical ones, missing values for other contestants, such as the field of work or level of education, were filled with the mean value for all the other contestants for the corresponding attribute. If a contestant did not specify their age, an estimated age group was assigned. In addition, all the values, except for the selected offer (i.e., the selected number of chasers), were scaled to a range between 0 and 1 to ensure that the magnitude of individual features would not influence their final importance. Without scaling, monetary offers ranging from several hundred to tens of thousands of euros would have a greater impact than the time advantage over the chasers, which is on the scale of several tens of seconds. Scaling ensured equality among different attributes, thereby improving the performance of various models.
4.3. Dataset Properties
As mentioned in the previous subsection, in the first step, we excluded entries corresponding to contestants who failed to correctly answer the first question in the cash builder because they were, thus, disqualified from the second phase. Apart from this initial filtering, we did not explicitly remove outliers from the dataset. Because of the relatively small sample size and the subjective human elements influencing the gameplay, it was challenging to define clear outlier criteria. For instance, contestants with similar profiles and comparable offers might experience different outcomes, making it difficult to objectively determine which cases deviate meaningfully from the norm, given the dataset’s size. After this preliminary filtering, the final dataset comprised 171 contestants, 53 of whom ultimately won their games.
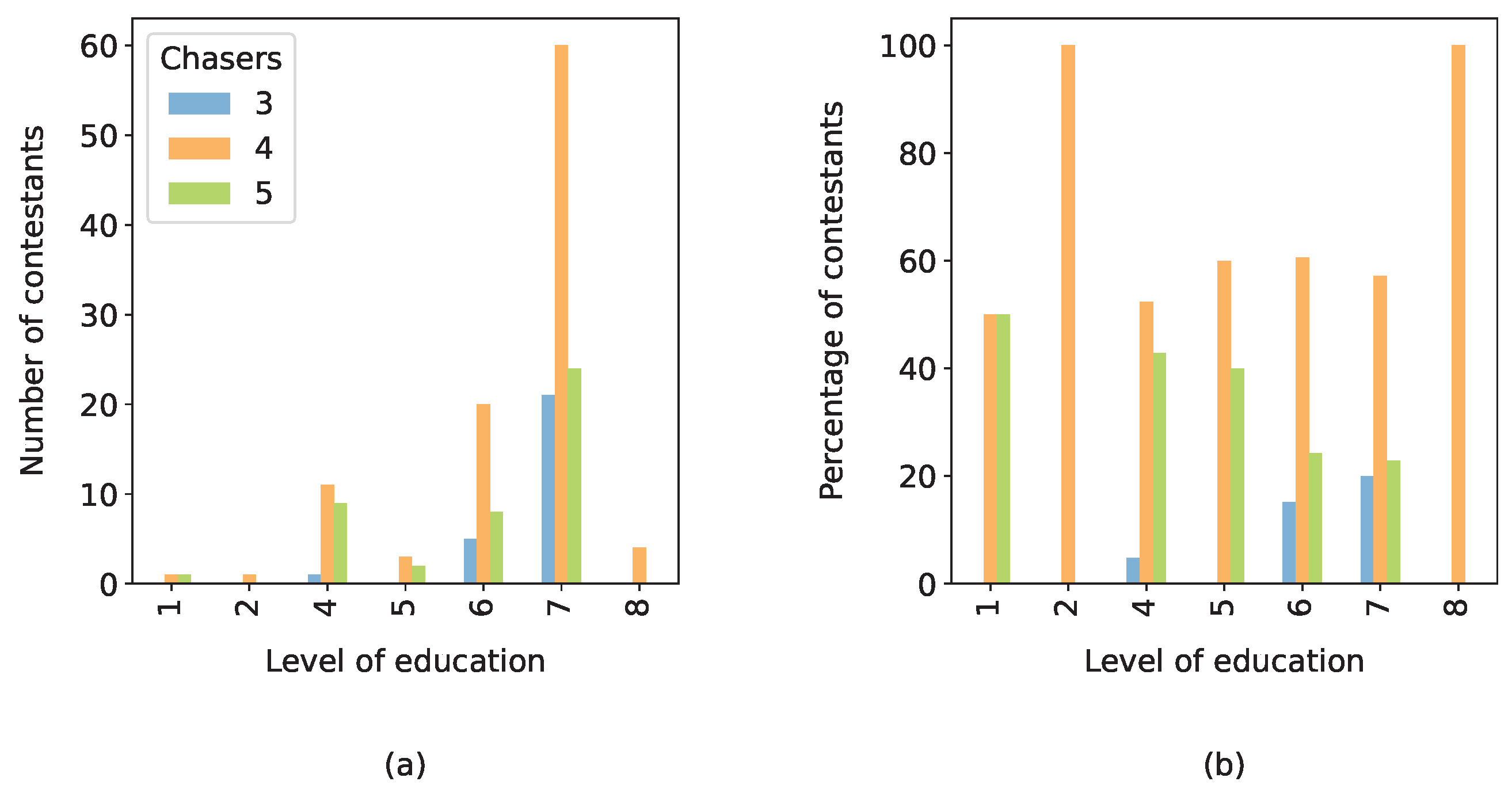
Appendix A presents a detailed statistical analysis of the whole dataset, while in this subsection, we highlight the most important insights. The left-hand-side graph in
Figure 2 shows the breakdown of the contestants’ cash builder results, while the right-hand-side graph indicates the distribution of the selected offer. The success in the cash builder was relatively evenly distributed across all five options, with a slight prevalence of five correct answers in the cash builder (EUR 2500). A significant portion of the contestants (58.5%) opted to compete against four chasers, while none has ever selected to compete against two.
We noticed that as the age group increases, the percentage of contestants selecting the offer with four chasers rises, while the number of those selecting the offer with five chasers decreases. The only age group that did not choose to face four chasers most frequently was the second one (from ages 19 to 24), where as many as 47.6% of the contestants selected the offer with all five chasers. On average, older contestants tended to select offers with lower monetary prizes but a greater time advantage over the chasers than the younger ones did. An interesting observation is that younger contestants with lower results in the cash builder, on average, selected offers with more chasers compared to those of the older contestants with the same results.
Both men and women most often selected the offer with four chasers. Women selected the offer with three and five chasers with equal frequency (22%), whereas men tended to choose five chasers (27.3%) more often than three (13.2%). On average, women selected offers with EUR 1725 less prize money and a 2.3 s longer time advantage over the chasers than men did. An unexpected statistical finding was that the contestants who were recognized by the chasers from their previous participation on quiz shows or in local pub quizzes, on average, selected offers with fewer chasers and less prize money than those who were not, regardless of their cash builder result. Contestants from large cities, on average, selected offers with more chasers. Those from smaller cities competed for approximately EUR 1500 more prize money compared to that by those from middle-sized cities. Notably, 70% of the contestants from Pannonian Croatia selected the offer with four chasers.
Regarding the intended use of the prize money, the contestants who planned to spend their winnings on education or donations selected the offer with four chasers in 70% of the cases, while those who intended to use the money for entertainment did so in 60% of the cases.
When looking into the cash builder results, we observed that compared to the other contestants, those with the lowest scores for EUR 500 and EUR 1000 were more likely to select the offer with five chasers.
It is important to note that although all the contestants receive four offers, the offers are purely non-deterministic, i.e., the contestants usually receive different offers with respect to the amount of prize money, time allocated to the chasers, and the chasers themselves, making the prediction of their choice a more complex challenge than it might have initially seemed. We observed that the offers in the first season were not only significantly more generous in terms of the prize money but also more challenging regarding the amount of time allocated to the chasers. Although the contestant’s risk–reward preferences influence the selected offer, predicting the game’s outcome depends on a broader range of factors. These include not only the contestant’s profile but also the current psychological state of both the contestant and the chasers, such as stage fright or lack of concentration, which are, in this context, impossible to quantify and include in the dataset.
Only 31% of the contestants managed to win the prize money by beating the chasers in the second phase of the game. The most successful age group was the fourth one (from ages 35 to 44), where 42% of the contestants were victorious, while the least successful was the sixth (from ages 55 to 64) with only 10% of the victories. Regarding gender, both men and women were equally successful in about 31% of the games. Their highest winning rate was after earning EUR 1000 in the cash builder.
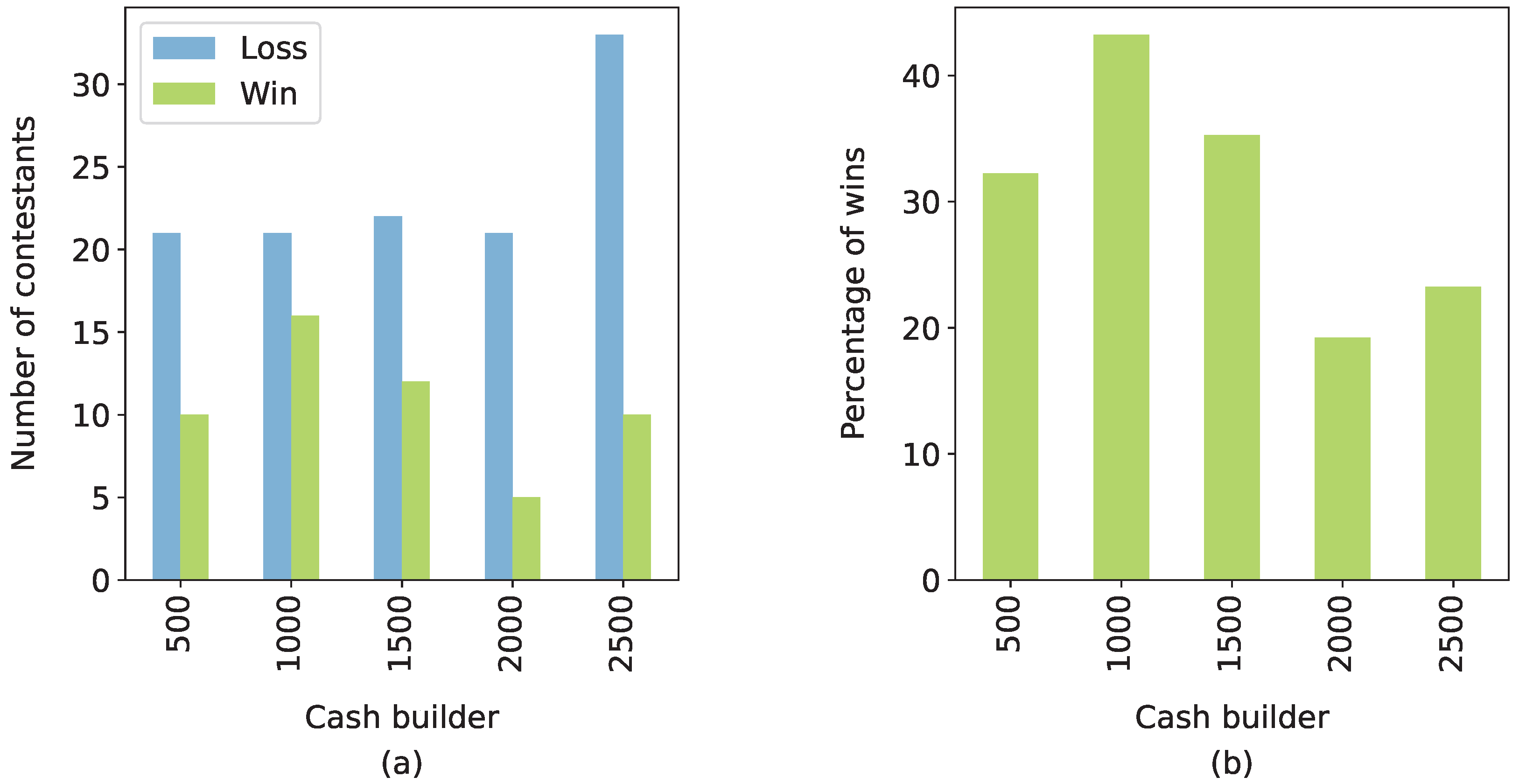
Figure 3 shows the relationship between the contestants’ wins and the number of chasers who participated in the final chase. In the right-hand-side graph, it is evident that as the number of chasers increases, the percentage of winners decreases, which aligns with the game’s main premise that it is harder to beat a higher number of chasers. The same can be seen in the left-hand-side graph, as the discrepancy between losses and wins increases with the number of chasers.
An analysis of the number of victories and the results in the cash builder revealed that contestants with weaker results in the first phase of the game performed better in the second phase.
Figure 4 depicts the relationship between the number of victories and the cash builder results.
The thorough analysis of the dataset’s statistics revealed various interesting patterns, which prompted us to apply artificial intelligence to investigate the interactions between different features and attempt to predict the course of the game. Despite the relatively small dataset size, we aimed to leverage all the collected information to predict both the offer that a contestant would select and their success in the second phase of the game, using various machine-learning methods.
6. Conclusions
In this section, we conclude the paper with a brief overview of the results, a discussion of this study’s limitations, and the provision of future work perspectives.
6.1. Result Overview
In this paper, we presented an in-depth analysis of the Beat the Chasers TV game show. Initially, we described the game with its rules and propositions, followed by the first contribution of the paper: the dataset obtained by extracting data from publicly aired episodes of the first two seasons of the Croatian version of the show. The dataset was studied from the perspectives of descriptive and semantic statistical analyses. As the main contribution of the paper, we applied several machine-learning methods to the data in two separate contexts.
First, we aimed to identify which offer a contestant would select based on the following information:
- 1.
The contestant’s profile;
- 2.
The contestant’s profile paired with the cash builder result;
- 3.
The contestant’s partial profile (gender, age group, hometown, and NUTS 2 region).
Predicting the contestant’s choice was a challenging task not only because of the different contestant profiles but also because of the variety of offers. Despite the same performance in the cash builder, the contestants received different offers in terms of the amount of the prize money, the amount of time allocated to the chasers, and the chaser lineup for specific offers.
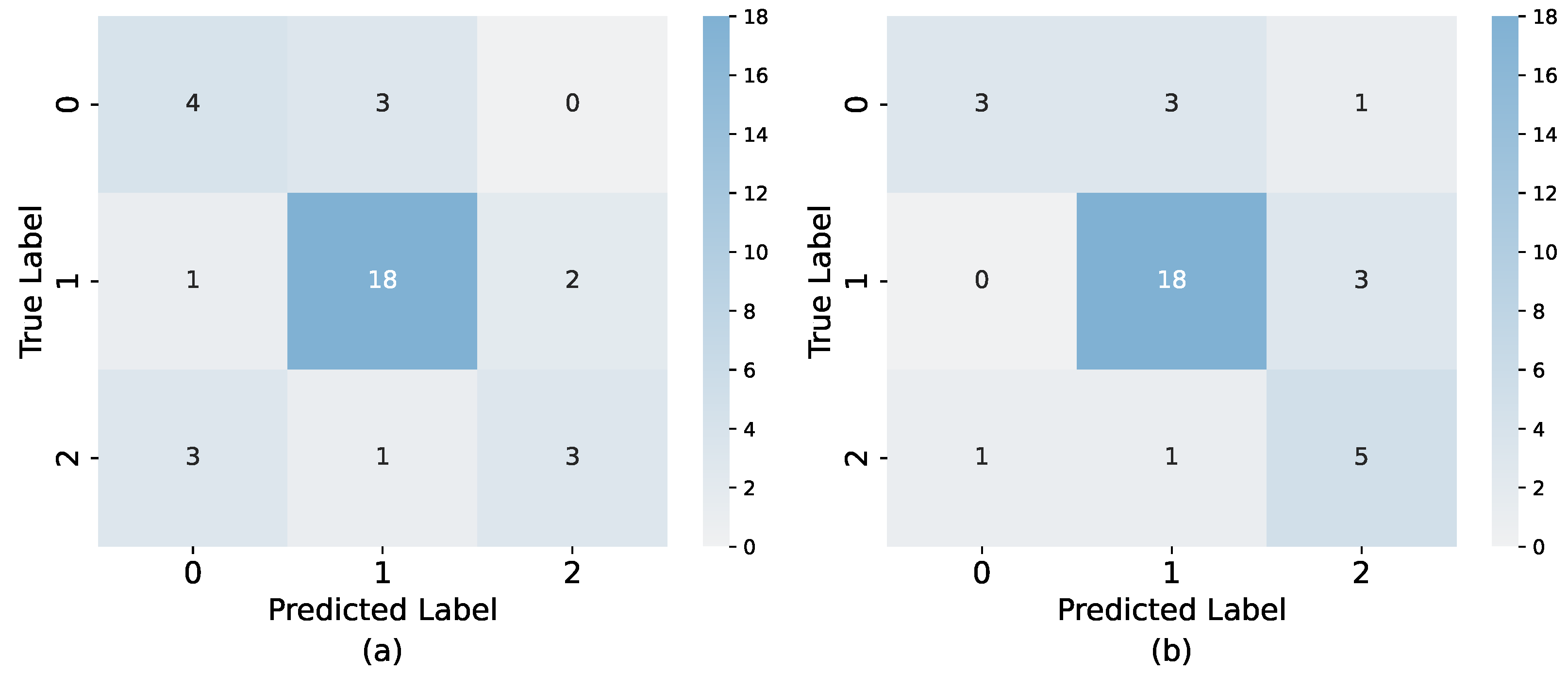
Table 18 sums up the results of all the models for all the scenarios described in
Section 5.2, including the model parameters and the use of SMOTE oversampling. The voting classifier yielded the best results in all three scenarios, with the contestant’s partial profile (third scenario) achieving an F1-score as high as 73.6%. Only in the first scenario did the k-nearest-neighbor model manage to match the performance of the voting classifier. By looking at
Table 18, we can notice that all the models reached their best performances in the third scenario, where we only used the features that were explicitly extracted from the show and that did not have any missing values. Regarding the first two scenarios, the results showed that adding the cash builder result degraded the performances of all the tested models, which might lead to a suspicion that the contestants’ cash builder results do not influence their choices and that the contestants usually come to the show with a forethought about the offer they would select.
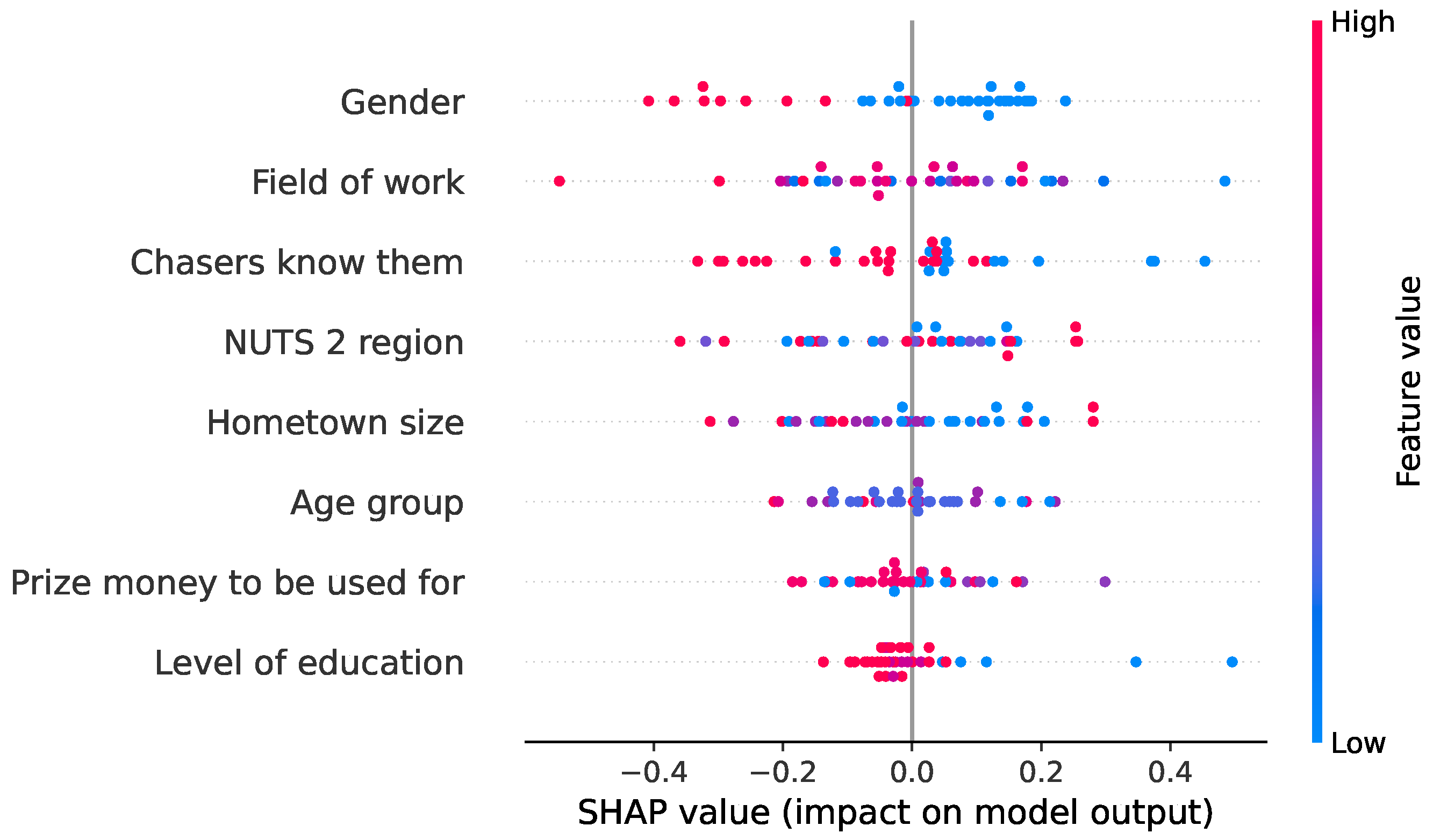
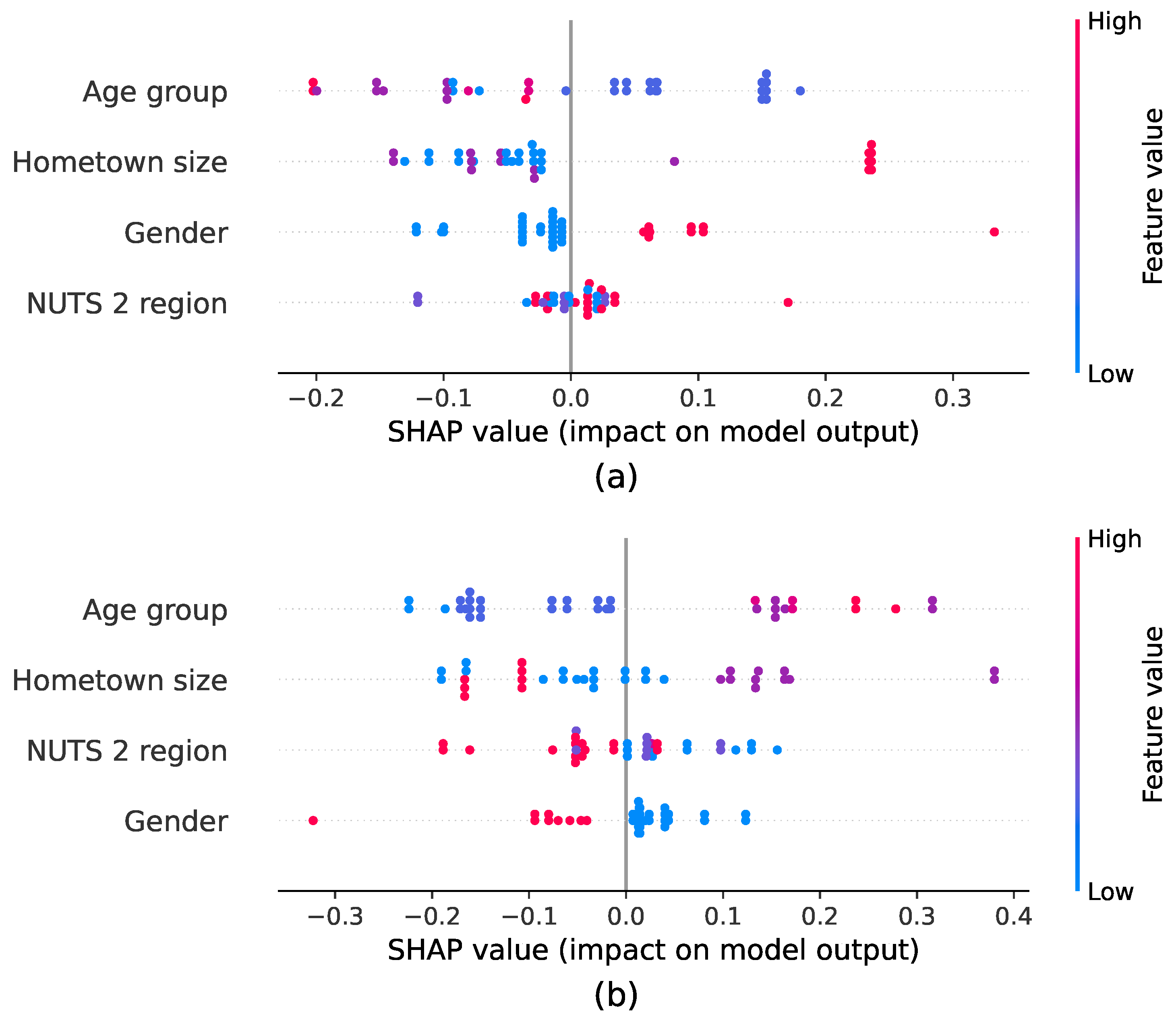
To assess the impacts of individual features on the models’ outputs, we utilized SHAP values for all the applicable models (with the exception of the voting classifier). In the first two reported scenarios, we identified the field of work as the most impactful feature. The contestants’ gender and whether the chasers recognized them also played significant roles in both scenarios. The second scenario included the cash builder result and the particular offers in the feature set. It highlighted the importance of the cash builder result, with lower values pushing the model’s output to higher values (i.e., the offers with more chasers). However, as previously mentioned, this approach degraded the models’ performances. In the final scenario, with the best overall performance, the hometown size was the most impactful and gender was the least impactful feature in most of the models. Lower values for the gender, age group, hometown size, and education level but higher values for the NUTS 2 region and chasers not recognizing the contestant tended to shift the model’s predictions toward higher-value offers. In contrast, higher values for the field of work, gender, education level, and whether the chasers recognized the contestant pushed predictions toward offers involving fewer chasers.
Regarding the binary classification problem of outcome predictions, we focused on several combinations of features with the goal of maximizing the prediction abilities of the used models. The feature combinations (scenarios) that we took under deeper consideration were as follows:
- 1.
The contestant’s profile;
- 2.
The contestant’s profile, the cash builder result, all the offers, and specific chasers within the selected offer;
- 3.
The cash builder result, all the offers, and specific chasers within the selected offer;
- 4.
The selected number of chasers and the cash builder result;
- 5.
The selected number of chasers and the chasers’ time in the selected offer;
- 6.
The selected number of chasers, the cash builder result, and the chasers’ time in the selected offer.
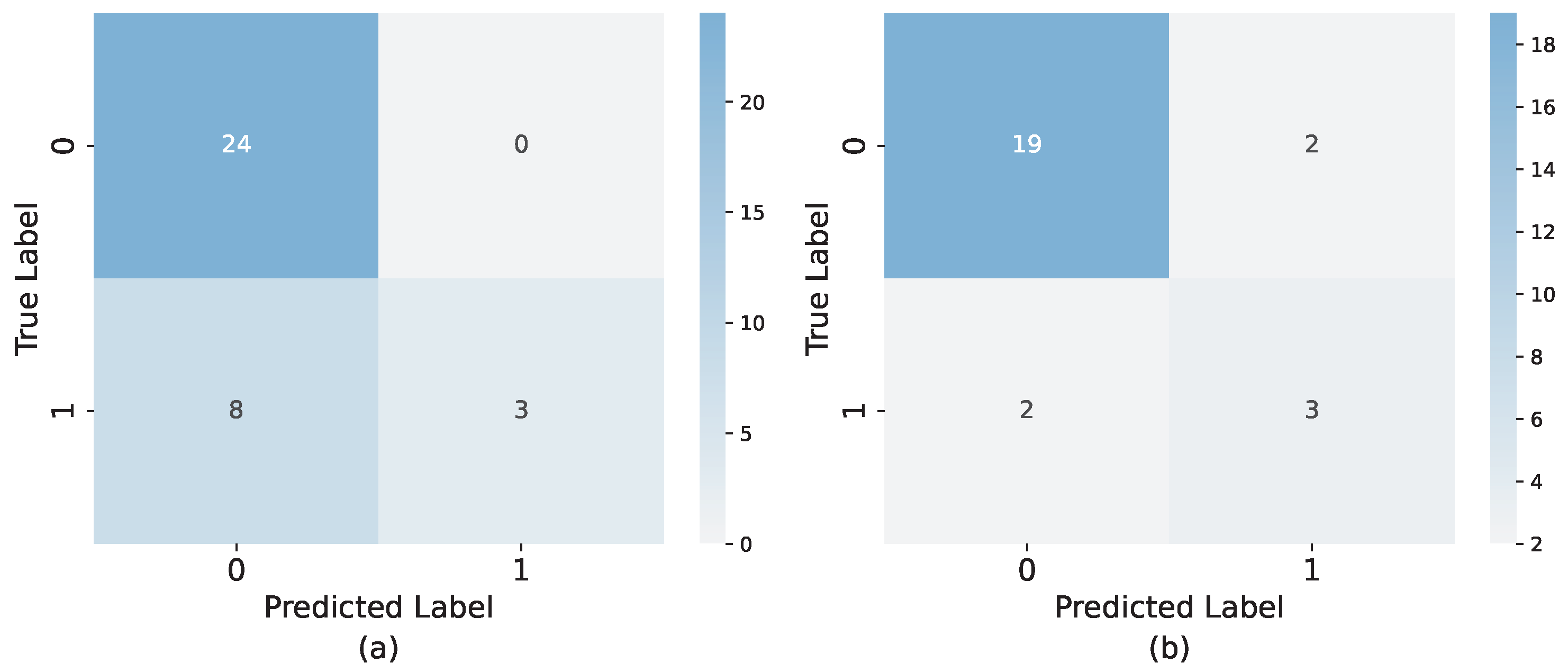
The results, parameters, and use of SMOTE in all the models and scenarios are summarized in
Table 19. In the majority of the scenarios, the neural network yielded the best result, reaching a prediction accuracy of as high as 84.6% for the combination of the number of chasers and the chasers’ time in the selected offer (5). On average, the best performance was reached when also including the cash builder result (6).
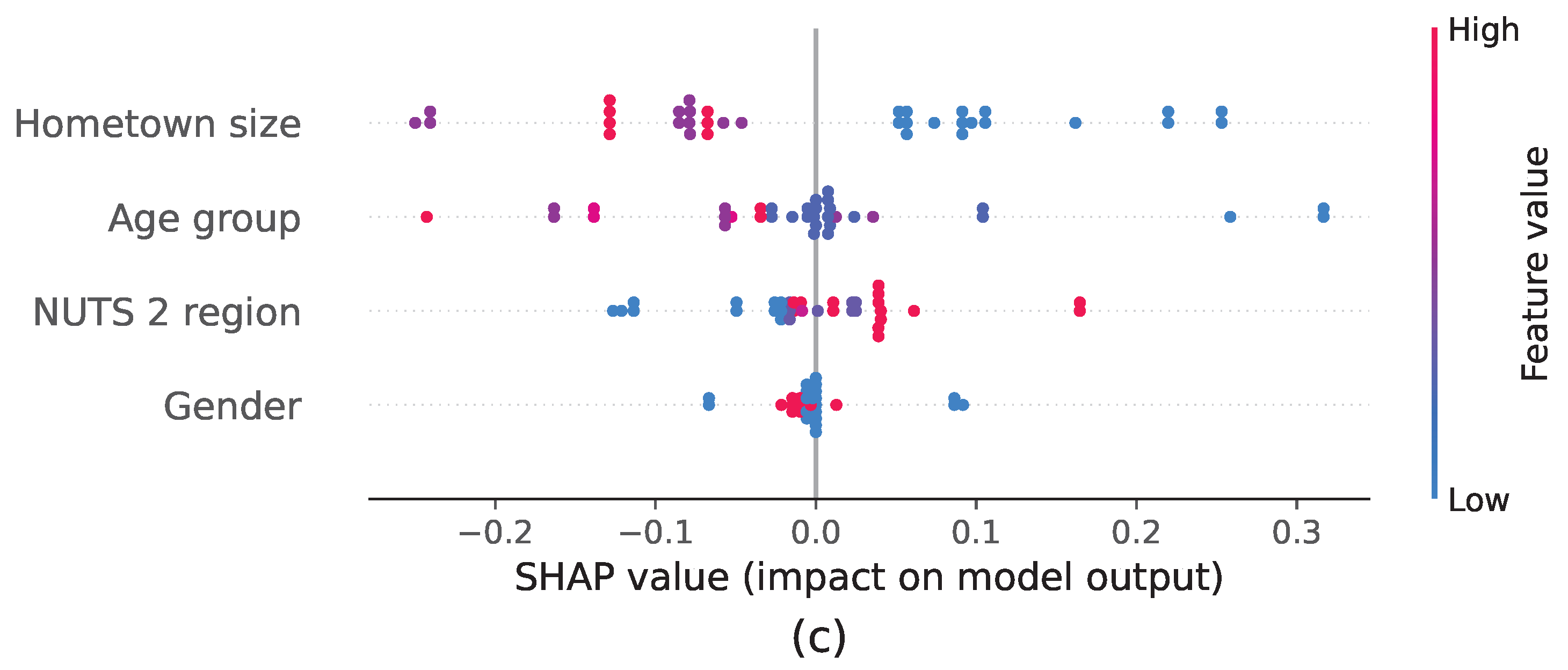
We also utilized SHAP values to interpret the models’ decisions in the outcome prediction task. As the best-performing models were the ones in the last three scenarios, which used only the selected number of chasers, the cash builder result, and the chasers’ time in the selected offer, we emphasize these features as the most impactful ones. In most cases, higher values for these features led the models to predict that the contestant would lose the game, while lower values pushed the models’ outputs to decide the opposite. The best-performing model in almost all the cases, the neural network, was the only model where the mid-range value for the cash builder result pushed the model’s output toward predicting that a contestant would win, while its lower values shifted the model’s prediction toward a negative outcome for the contestant. Regarding the other features, the participation of Chaser #4, the contestant’s gender, and whether the chasers recognized the contestant were the most impactful features. In the best-performing model (the neural network), a higher value for gender and not being recognized by the chasers led the model’s outputs to predict that a contestant would win the game. The participation of Chaser #4 was also considered as important by several models, with their participation shifting the model’s output to lower values.
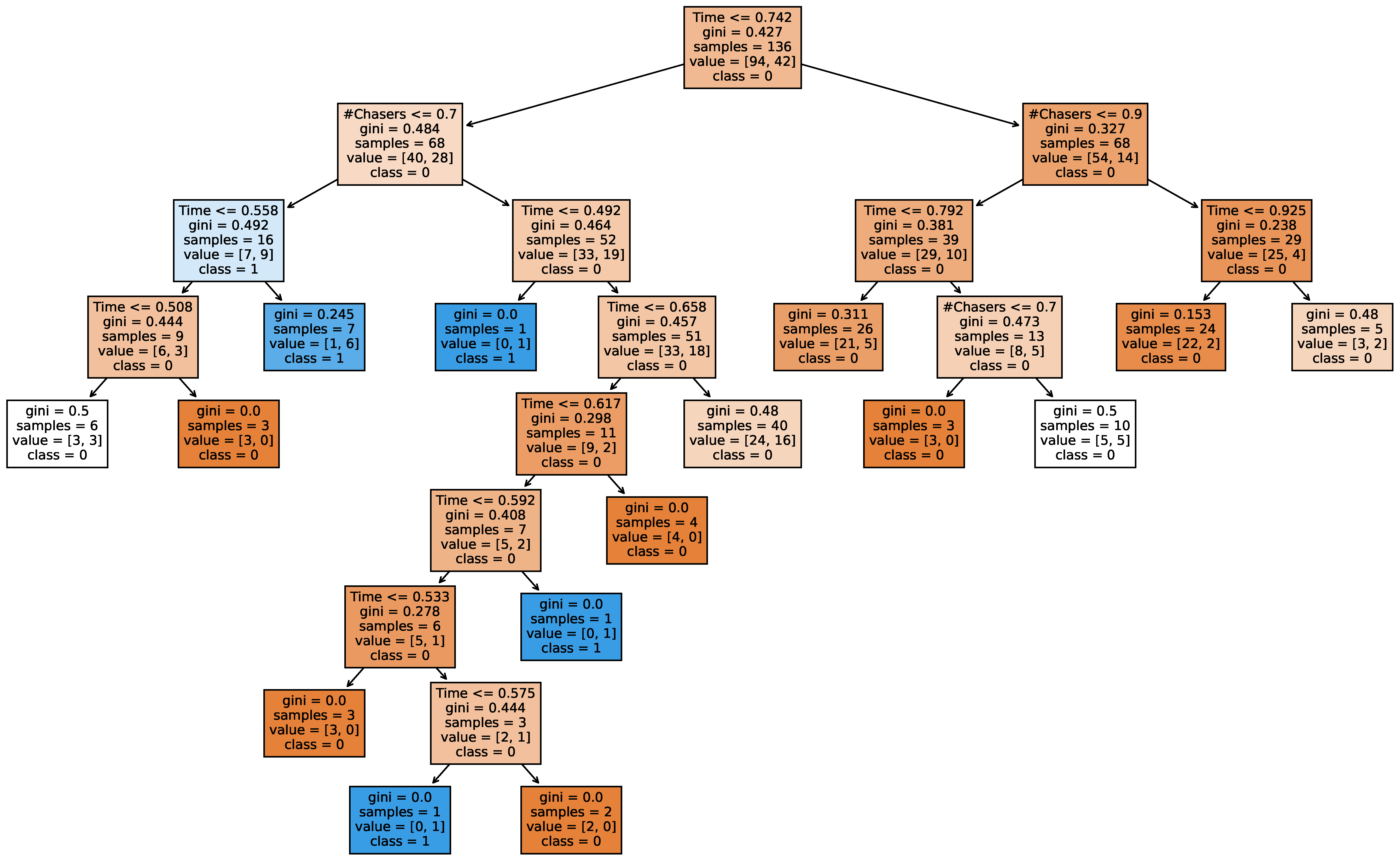
Although the voting classifier stood out as the best-performing model in several scenarios, the other models are generally preferred in cases where they achieve a similar performance level. By applying SHAP to these models, we were able to clarify the decision process and justify the final classification. In contrast, the voting classifier lacked clear reasoning, making its decisions challenging to explain. In the best-performing scenarios, for both the selected offer and the outcome prediction, we presented a pruned decision tree, which visualized the decision process (
Figure 6 and
Figure 10), making the model classification interpretable.
These results have shown that the selected offer depended more on the contestant’s profile rather than their cash builder result or particular offers. In contrast, the game’s outcome was more dependent on the game-specific features, like the number of chasers, the cash builder result, and the amount of time the chasers received in the second phase of the game, rather than the contestant’s profile. These results can help both the show’s producers and the contestants. The show’s producers can use the information about a contestant for personalized offer tailoring, making the show more suspenseful. The contestants can benefit from this research by predicting their performance in the second phase of the game, which would help them in selecting the optimal offer.
Although this study focuses exclusively on the Croatian version of Beat the Chasers, the question of generalizability to other versions of the show, or even other TV quiz shows, arises naturally. We tend to be of the opinion that cultural and socioeconomic factors may influence contestants’ behaviors. For instance, one might hypothesize that contestants from less affluent regions are more motivated by potential financial gain, while those from wealthier areas may primarily participate for fun or experience. However, such interpretations are purely speculative and cannot be confirmed or refuted within the scope of this study.
In this study, we do not specifically address cultural factors, and although we acknowledge that contestants’ behaviors may, indeed, be culturally specific, our current data and methodology do not allow for definitive conclusions. The features and methods used in our models are appropriate for the Croatian context but may not transfer directly to other countries without model retraining and feature reselection, as different cultural or structural dynamics could render other variables as more relevant. For example, Croatia is highly centralized around its capital, Zagreb, with relatively few large urban centers. This centralization may influence contestants’ representation and behaviors in ways that differ significantly from those in countries with more evenly distributed populations and multiple major cities. Therefore, although some insights may be broadly applicable, we refrain from asserting that our conclusions hold universally.
6.2. Limitations
It is important to mention that even though the dataset provided as a part of this paper can be considered as being relatively wide feature-wise, it is still far from complete. A large amount of data that could significantly influence the prediction models is not publicly available. For starters, we lack the data from the contestants’ application forms, in which the contestants explicitly provide information on their personal traits. Additionally, we do not have any information describing a contestant’s quizzing skill level, which could be a key factor for accurate predictions. To compensate for this, we used data on the cash builder result and included whether the chasers recognized the contestant, assuming they were more familiar with skilled individuals. Furthermore, for both the selected offer prediction and the outcome prediction, deriving simple rules using tree-based methods was not feasible. This was primarily because of the complexity of the generated trees and, more importantly, the relatively small size of our dataset, which limited the rule extraction.
Although the total number of samples in the dataset is relatively low for machine-learning tasks, the dataset provided sufficient information for the models to perform well. To prevent overfitting during the model training, we used cross-validation for the neural networks and pruning of the decision trees. The built-in bootstrapping mechanism helped to reduce overfitting in random forests.
Although some of the limitations presented in this subsection could conceivably be mitigated by increasing the dataset size, we are currently unable to do so. For the Croatian version of the show, all the available episodes that are a part of complete seasons were included in the analysis at the time of the publication of this paper. In contrast, international versions of the show are not directly applicable to this study for several reasons. Primarily, we are not able to make categorical claims about the influences of cultural differences on the findings of this study, as such differences may, indeed, play different roles. In addition, other versions of the show can differ significantly in terms of the rules and propositions of the game. For example, the British version features different chasers across seasons and even varies in the number of chasers (some seasons include six). The German version features seven chasers; the Australian version, four chasers; and the Finnish version, only three chasers. International versions with five chasers might be applicable to our research (e.g., the Czech or Dutch versions), but it still remains unclear whether the offers in various versions of the show are commensurate with those in the Croatian version in terms of the prize money and chasers’ time, and whether contestants’ strategies or preferences are influenced by cultural factors.
Many contestants also mentioned the amount of money they would be satisfied with. This information could play a significant role in the offer-tailoring process but was excluded because of a high number of missing values. Furthermore, some of the age groups, educational levels, or fields of work lack higher representability. Although we were able to draw valid conclusions from the dataset used in this research, one could easily claim that the set itself contains a relatively low number of samples (171) for further and more advanced analyses. Despite these limitations, the dataset serves as a strong starting point for further research, providing valuable insights and establishing a foundation for future studies with more comprehensive data.
Another factor that could play a key role in the further improvement of the models’ performances is the psychological state of the contestants. People react to stress differently. Potential anxiety, stage fright, or an adrenaline rush could lead to cognitive blocks or impulsive reactions that could result in poor performance. Unfortunately, this information is impossible to obtain accurately by observing the contestants. To gather such information, the contestants should undergo an appropriate psychodiagnostic assessment or wear a device, such as a smartwatch or a fitness tracker, that can assess the stress level by measuring the heart rate variability, pulse, respiratory rate, and activity.
We can also freely assume that the production team has a predefined budget, which could induce the intra-show dependency in a way that the offers depend on the success of the other contestants in the quiz. On the other hand, we cannot exclude cross-show dependency because TV productions usually share a budget at the level of the entertainment program, which could mean that the success of other TV quiz shows produced by the same broadcasting company could influence the offers in this show.
6.3. Future Work
There are several directions for possible future work. The first step is to update the dataset with the information on the contestants and the offers from the upcoming seasons. These data could be used for further model testing or retraining in a larger dataset. Different neural network architectures could also be investigated, as the tested architectures were fairly simple. Future work could involve incorporating other international versions of the quiz rather than limiting the analysis to the Croatian version.
A major potential extension of this research would involve examining the human behavioral factors of the contestants, including not only decision making but also other psychological factors, such as stage pressure, performance anxiety, and stage fright, as well as individual personality traits. Conducting such a study would require involving experts in psychology to ensure appropriate the methodology and result interpretation.
Beyond the immediate context of TV quiz shows, the methods and paradigms presented in this study could be used in other contexts and applications. Machine-learning models capable of predicting users’ decisions based on users’ profiles and in the absence of more detailed contextual data could influence the development of personalized recommendation systems. Similarly, the approach presented in this study could be extended to simulate users’ behaviors in gamified environments, enabling tailored user engagement strategies and more adaptive game designs. On the other hand, the ability to predict decisions and their outcomes from a limited set of inputs might also influence predictive marketing, where the anticipation of users’ choices can offer better customer targeting. The aforementioned application highlights the value of data-driven behavioral modeling within the contexts in which the decisions are influenced by personal traits.
Another possible research direction we aim to take is to investigate the offers more deeply. A quantitative metric of an individual offer remains an open question. By validly defining such a metric, claims regarding the fairness of the offers could be made. After collecting a sufficiently large dataset, another option could be the prediction of the specific offers that the production staff would propose to a particular contestant according to their profile and cash builder result. Another possible research direction is the prediction of the optimal offer, which balances the winning probability and the prize money with risks, such as the number of chasers and their allocated time. This way, each contestant could be advised on which offer to select to beat the chasers.