Optimizing Container Placement in Data Centers by Deep Reinforcement Learning

Abstract

As our society becomes increasingly digitized, the demand for computing power provided by data centers continues to grow; consequently, operating costs are increasing exponentially. Data centers supply virtualized servers to customers, primarily in the form of lightweight containers. Since the number of containers to be allocated is fixed, they should be optimally placed on physical servers to minimize the number of required servers and reduce costs. However, current data center operations do not prioritize reducing the number of physical servers through optimized container placement. Instead, containers are distributed across existing servers primarily to maintain stability. Therefore, costs associated with servers, auxiliary facilities, and electricity consumption have increased. To address this issue, we propose an optimization method that ensures economic efficiency without compromising system stability. Specifically, we utilize deep reinforcement learning (DRL), which has been widely applied in various fields, to optimize container placement. Our approach outperforms traditional heuristic algorithms and offers the additional advantage of handling fixed-size inputs, enabling flexible operation regardless of the number of containers. Using DRL in container placement has further reduced the number of servers and operating costs while enhancing overall system flexibility.

1. Introduction

Data centers are facilities that house servers providing computing power. These servers are installed in rack units alongside network and security equipment that facilitates connectivity. In addition, power supply systems and temperature- and humidity-control facilities are essential for maintaining optimal server operation.

Data centers are increasingly becoming an important component of digital infrastructure because of rapid advancements in cloud computing [1]. With the continuous emergence of artificial intelligence (AI)-driven applications, this demand is expected to increase even further.

The operating costs of data centers increase exponentially with the number of servers used. Purchasing additional servers increases direct server costs and also escalates expenses related to network and security equipment, power consumption, and cooling systems. Particularly, energy efficiency is an important issue in data centers [2,3]. Therefore, reducing the number of active servers is important for reducing overall data center costs.

To enhance efficiency, data centers are rapidly transitioning to cloud-based architectures using virtual machines and containers that leverage virtualization technology. Virtualization is considered one of the pioneering concepts initiating modern clouds [4]. Virtual machine technology is the execution environment used in cloud computing, whereas a container is a lightweight virtualization technology that provides an isolated virtual environment [5].

Given the increasing need for agility, lightweight containerized servers are gaining popularity [6]. However, containers are often not deployed in an optimized manner. Currently, data centers tend to scale resources up and down during periods of high and low traffic, respectively, leading to inefficient resource utilization, particularly of physical servers. Optimizing container placement on physical servers can mitigate resource wastage. By strategically allocating containers, unused servers can be switched to idle mode, serving as spares, thereby reducing unnecessary server purchases and improving overall operational efficiency [7].

Operational practices in data centers often allocate more resources than necessary. Operators tend to feel relieved when resource levels are significantly above their immediate requirements. Additionally, the business models of some orchestration software makers, which may involve licensing costs tied to the number of physical servers, can incentivize the deployment of software on more servers. This can lead to over-provisioning relative to actual demand.

However, as long as operational stability is guaranteed, it is essential to minimize resource consumption for economic operations. Consequently, applying optimization algorithms to container placement is a critical strategy as they can determine the minimum number of required servers, allowing the surplus servers to be transitioned to an idle state, thereby enhancing overall efficiency.

Placing multiple containers on each physical server presents a key challenge: the complexity of finding an optimal solution as the number of possible combinations increases exponentially. For instance, even in a relatively simple case of placing 13 containers on five servers, there are 2380 possible overlapping combinations. This problem can be expressed as a variant of the bin-packing problem, which is considered to be an NP-hard problem [8].

To address this, various optimization methods, such as heuristic, meta-heuristic, and deep reinforcement learning methods, have been explored in previously reported studies [1]. However, these studies have primarily focused on improving algorithmic efficiency rather than achieving effective placements. Furthermore, the inherent complexity of meta-heuristic and deep reinforcement learning methods can make them difficult to implement, and their application in real-world environments may be limited owing to an incomplete understanding of the containerized server systems.

Given the critical importance of stability in server operations, data centers currently maintain numerous spare resources to ensure reliability. Thus, there is a pressing need for an optimized container placement method that can be practically implemented while maintaining operational stability.

In this paper, we propose an optimal container placement method for managing large-scale server infrastructures, such as data centers. Our approach aims to enhance economic efficiency by reducing the number of active physical servers while ensuring the stability required for data center operations.

The remainder of this paper is organized as follows: Section 2 discusses related work, Section 3 explains container placement models, Section 4 introduces the proposed container placement optimization algorithms, Section 5 discusses the experiments and results, and Section 6 concludes the paper and presents directions for future research.

2. Related Work

There have been many studies on optimal placement algorithms for items and cloud resources, such as virtual machines and containers. Several detailed surveys explore them [9,10]. In this section, we discuss these efforts in more detail.

2.1. Heuristic Methods

Traditional bin-packing algorithms are commonly used to address item placement problems, such as container placement. The bin-packing problem involves arranging n items into the smallest possible number of bins, given a fixed bin capacity.

Common heuristic methods for solving this problem include next fit, first fit, and best fit. Next fit sequentially fills items into a bin and moves to the next bin once the current one is full. First fit, however, always checks for available space in bins starting from the first one and places the item in the first bin that has room. Best fit follows a similar approach but prioritizes placing new items in the bin with the least remaining space among those with available room [11].

2.2. Meta-Heuristic Methods

Meta-heuristic is a high-level, problem-independent algorithmic framework used to solve complex optimization problems where exact methods are impractical due to time or computational constraints. Using this framework, many algorithms are introduced to optimally deploy items or cloud resources.

The grouping Harmony Search (HS) algorithm, introduced by Kim et al., is an optimization technique inspired by the harmony formation process in jazz improvisation. This paper proposes a Virtual Machine Consolidation (VMC) method that focuses on transitioning physical servers to idle mode via virtual machine migration, significantly reducing power consumption in data centers. The primary objective of VMC is to maximize the number of servers transitioned to idle mode while minimizing the number of migrations to ensure server stability. To solve this optimization problem, the paper proposes the HS algorithm, with performance enhancements achieved by applying a grouping representation method based on physical servers rather than a virtual machine-based permutation [7].

The ACO algorithm was proposed by Hussein et al. ACO is an optimization technique inspired by the foraging behavior of ant colonies. This paper presents an optimal method for placing virtual machines on physical servers and containers within those virtual machines. The goal of this placement strategy is to minimize the number of active physical servers and instantiated virtual machines. To achieve this, the best-fit algorithm was employed to instantiate additional virtual machines when necessary, while the ACO algorithm was utilized for optimal placement. The ACO algorithm enhanced resource utilization across physical servers and virtual machines, outperforming both the best-fit and maximum-fit algorithms [5].

The Firefly algorithm was proposed by Katal et al. This paper proposes two enhanced versions of the Firefly algorithm: Discrete Firefly (DFF) and Discrete Firefly with Local Search (DFFLSM). Compared with existing placement algorithms, such as first fit and ACO, the proposed algorithm reduces energy consumption by up to 40.85% and the number of active physical machines by up to 21.89%. This approach is shown to be effective in both homogeneous and heterogeneous environments [12].

2.3. Deep Reinforcement Learning (DRL) Methods

DRL is a powerful AI technique that combines reinforcement learning and deep learning. It trains agents to make optimal decisions by interacting with an environment to maximize rewards using deep neural networks to approximate complex functions. It is used to optimally allocate items or cloud resources in various studies.

DRL algorithm for general bin-packing problems was proposed by Laterre et al. This self-adjusting training mechanism ensures that the agent consistently learns at an appropriate level, ultimately leading to an optimized placement strategy. Unlike previous heuristic methods, which require manual adaptation to specific problems, this approach leverages reinforcement learning to generalize across different optimization scenarios. The proposed algorithm has been shown to outperform Monte Carlo tree searches, heuristic algorithms, and integer-programming solvers [13].

Another DRL algorithm for container placement was proposed by Li et al., who introduced an improved Q-Learning strategy that incorporates eligibility traces and dynamic ε-greedy exploration. Eligibility traces accelerate learning by updating Q-values for both the current state-action pair and related past pairs. The dynamic ε-greedy exploration strategy begins with a high exploration rate, gradually shifting toward exploitation while retaining some exploration to mitigate the risk of converging to local optima. The proposed method outperforms baseline algorithms, including First-Fit Host Selection, Least-Full Host Selection, and traditional Q-Learning. The results demonstrated that the resulting container allocation consumed less energy and featured a reduced service level agreement violation rate, confirming the effectiveness of the algorithm [14].

A novel approach named CARL, which means Cost-optimized placement using Adversarial Reinforcement Learning, was proposed by Vinayak et al. CARL employs Adversarial Reinforcement Learning (ARL) to solve the online container placement problem. ARL learns policies through the interaction between reinforcement learning agents and adversarial agents and thus presents placement strategies for various scenarios. In evaluation using workloads traces from Google Cloud and Alibaba Cloud, it demonstrated high throughput, cost reduction, and adaptability. It processed approximately 1900 container placement requests per second across 8900 candidate VMs and achieved up to 16% lower VM costs compared to existing heuristic methods. It also maintained performance despite changes in the workload [15].

Although the heuristic algorithms above are simpler to implement and have faster convergence, they are prone to fall into local optimal solutions and are difficult to approach the global optimum. The meta-heuristic algorithms are highly flexible and easy to obtain the optimal solution, but it has more parameters, which are more difficult to adjust and may not perform well in complex problems. And although the deep learning-based allocation strategies are more suitable for dealing with complex problems, they require a large amount of data for training and are difficult to adapt to the real cluster container allocation environment [14].

3. Problem Formulation

Data centers house numerous physical servers on which virtualized servers are deployed. Virtualization allows a single physical resource to be separated into multiple logical or physical resources, which can then be combined into a single logical entity. The most common form of virtualization is server virtualization, which enables a single physical server to operate as multiple virtualized servers. Server virtualization includes virtual machines (VMs), where a separate operating system is installed on each instance, and containers, which share a host operating system without requiring separate OS installations. Compared to VMs, containers offer greater speed, flexibility, and efficiency by enabling rapid deployment, scalability, and lightweight operation while running only essential software. Due to these advantages, containers are becoming the dominant form of server virtualization in data centers [4].

As the number of physical servers in a data center increases, the corresponding costs increase proportionally. Since the number of containers to be operated is fixed, it is important to minimize costs by reducing the number of active physical servers being operated through optimal placement of containers. Therefore, an optimal container deployment method is required to reduce the number of active physical servers and, consequently, the operating costs of data centers.

Common tools for container deployment include Docker Swarm and Kubernetes. Docker Swarm offers container deployment capabilities integrated directly within Docker, allowing users already employing Docker to utilize Swarm without separate installation. Kubernetes, an open-source container orchestration tool developed by Google, is designed to effectively manage large-scale container deployments, leveraging its high scalability and flexibility. These orchestration tools typically support both manual deployments to specified physical servers and automatic server selection and deployment when no specific target is selected. Docker Swarm distributes containers across available resources using a round-robin approach [5]. Kubernetes places containers based on a combination of filtering and preference criteria [16]. These methods assess whether a container can be accommodated and determine the most suitable physical server for deployment.

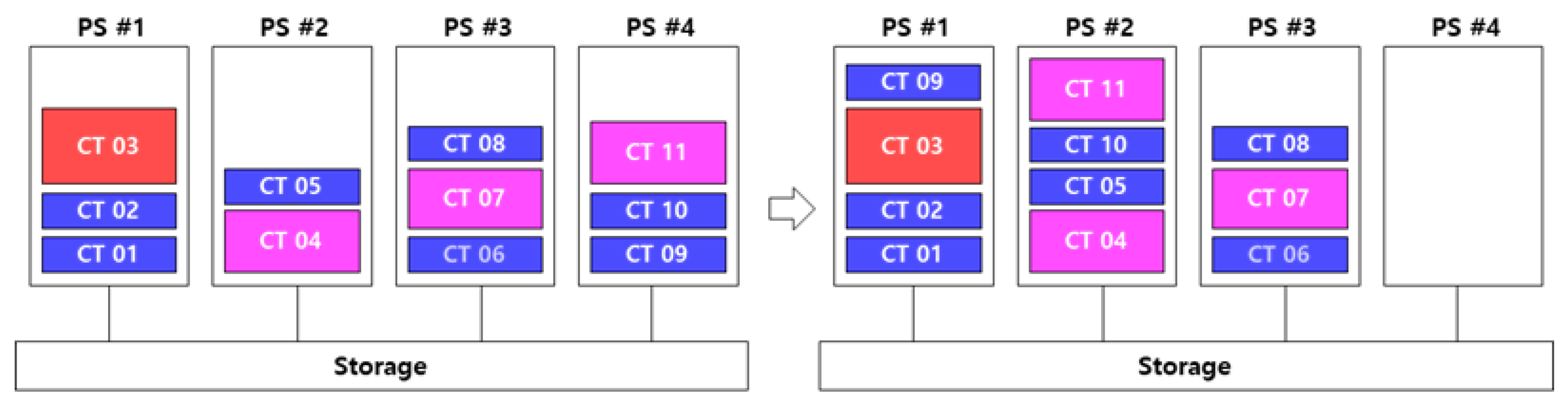
In contrast, optimal container placement seeks to minimize the number of active physical servers (PSs) by strategically distributing containers (CTs), as shown in Figure 1. This approach allows idle servers to be powered off, leading to significant reductions in server resource consumption, electricity usage, cooling requirements, and overall operational costs.

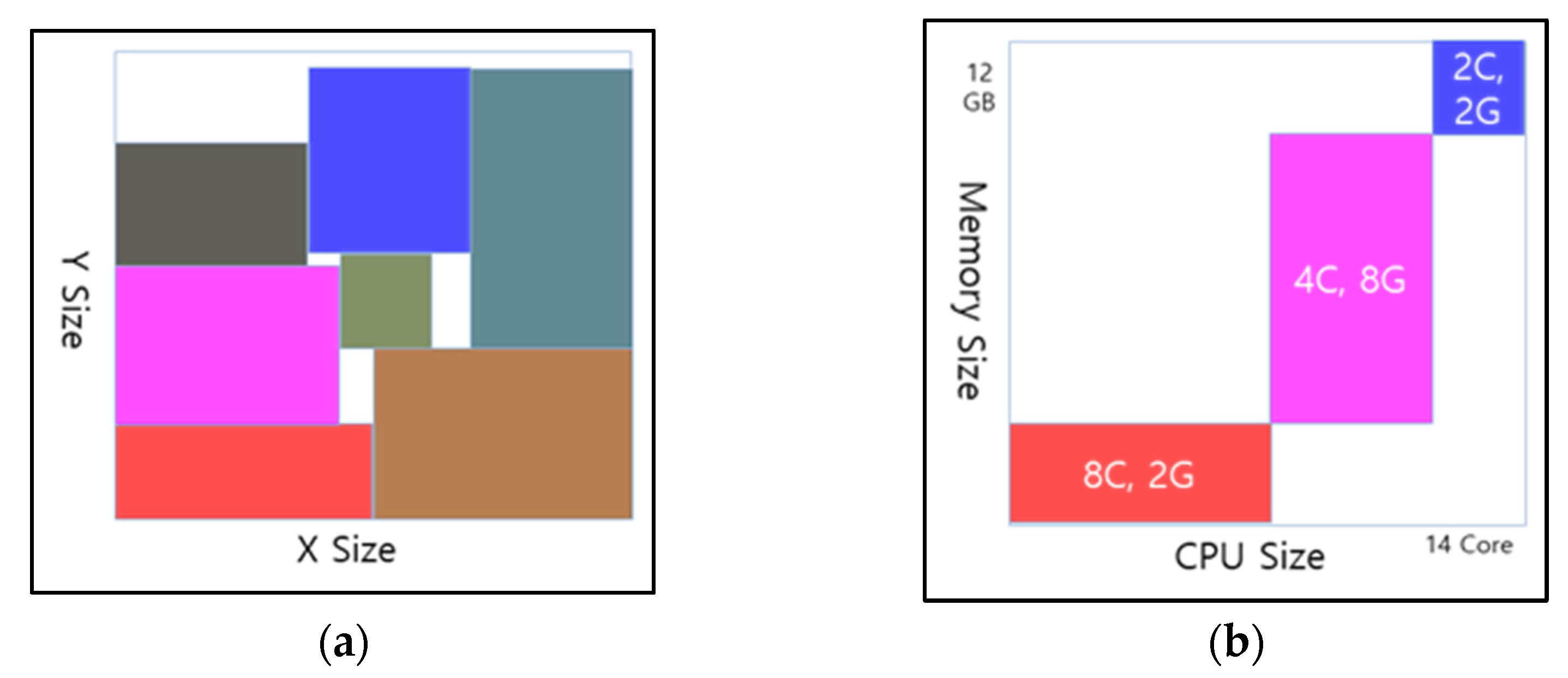
When placing containers, CPU and memory capacity must be considered, while storage is managed separately by dedicated software and does not factor into placement decisions. Therefore, CPU and memory should be allocated as a single unit to PSs. Figure 2 shows the concepts of bin packing and container placement [7].

Based on this approach, container CPU and memory resources must fit within the CPU and memory capacity of the physical server. While CPU overcommitment is possible, it is not used in this allocation strategy because overcommitment can cause containers to be terminated (“killed”), meaning only the physical CPU capacity is assigned. Similarly, memory is not overcommitted, as doing so can lead to significant performance degradation. Typically, 60% of the total memory capacity is considered the maximum allocation limit to ensure system stability. By setting predefined limits for CPU and memory usage, this method ensures stable and efficient resource allocation.

4. Container Placement Optimization

4.1. Container Placement Optimization Using DRL

The symbols used in this algorithm are described in

Table 1. Symbols and descriptions.

Symbol	Description	Symbol	Description
$N_{ps}$	Number of PSs	$N_{batch}$	Number of a batch
$N_{{ps}_{unused}}$	Number of unused physical servers	B	Buffer to store a batch
		${CPU}_{{ps}_i}$	CPU size of physical server i
${ps}_i$	Physical server i	${MEM}_{{ps}_i}$	Memory size of physical server i
$N_{ct}$	Number of containers	${CPU}_{{ct}_j}$	CPU size of container j
${ct}_j$	Container j	${MEM}_{{ct}_j}$	Memory size of container j
${ID}_{{ct}_j}$	Identification of container j	${NSC}_{{ps}_i}$	Number of stacked containers on physical server i
$s_t$	State s of time t
$a_t$	Action a of time t
$r_t$	Reward r of time t	${CPU}_{{SC}_{i,j}}$	CPU size of stacked container j on physical server i
Done	Whether to terminate
$\mathsf{\gamma }$	$\mathrm{Discount}\mathrm{rate}\mathsf{\gamma }\in [0,1]$	${MEM}_{{SC}_{i,j}}$	Memory size of stacked container j on physical server i
$\mathrm{\pi }(\mathrm{s},\mathrm{a})$	Probability of actions
$\mathrm{V}(s_t)$	$\mathrm{Value}\mathrm{of}\mathrm{state}{s}_t$	${TPS}_k$	Type of PSs k

.

Container placement optimization focuses on placing containers on the minimum number of PSs to maximize the number of unused servers.

The objective function is defined as follows: max($N_{{ps}_{unused}}$), $0\le N_{{ps}_{unused}} \le N_{ps}$.

To achieve this optimal arrangement, the actor-critic method is employed. Actor-critic is a prominent reinforcement-learning algorithm where an agent learns to select optimal actions within a given environment. This powerful method can solve complex problems across various environments and enables learning at each step. This agent consists of two key components: an actor, which learns policies, and a critic, which learns a value function. The actor is responsible for learning the policy function that determines the agent’s actions. The policy function generates a probability distribution over possible actions in a given state and selects an action accordingly. The critic learns the value function, which estimates the expected value or average reward for a given state. It evaluates the action chosen by the agent and updates its value accordingly, ensuring improved decision-making over time [17,18].

The state at time t, denoted as $s_t$, represents information about the container currently being considered for placement. It is defined as a vector comprising four parameters: total number of containers ($N_{ct}$), identifier of container j to be placed (${ID}_{{ct}_i}$), its CPU size, and its memory size of container j:

$$s_t=[N_{ct}, { ID}_{{ct}_i}, \mathrm{C}\mathrm{P}\mathrm{U} \mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e} \mathrm{o}\mathrm{f} {ct}_i, \mathrm{M}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y} \mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e} \mathrm{o}\mathrm{f} {ct}_i].$$

This state vector value is fed to a neural network with a linear network with fixed-size input values. The rectified linear unit (ReLU) activation function is employed, and the Adam optimizer is used, with a learning rate of 0.01. The output of the actor network passes through a Softmax function to produce a probability distribution over the available PSs. The critic network outputs an estimate of the state value.

Algorithm 1 illustrates the proposed algorithm, which is implemented as follows: First, the state value is fed into the actor network to generate the probability distribution ($\mathrm{\pi }(s_t,a_t)$) corresponding to the number of available PSs. An action ($a_t$) is probabilistically selected from this distribution (line 7 in Algorithm 1). After executing the state value and action within the environment, the reward ($r_t$), next state ($s_{t+1}$), and termination (done) are obtained (line 8). The transitions, such as the state value, action, reward, next state, and termination status, are stored in memory (line 9). The state value is then updated to the next state (line 10), and this process repeats for the number of batch iterations (line 6). The Temporal Difference (TD) target is then computed by extracting stored transitions (line 14). Because TD learning is used, the TD target enables stepwise learning [10]. The TD error is obtained by subtracting the current state value ($\mathrm{V}(s_t)$) from the TD target (line 15). Using the TD error, the critic loss is calculated (line 16), and loss optimization is performed (line 18) using Huber loss. Huber loss is a hybrid of L1 loss (absolute difference) and L2 loss (square difference), making it robust to outliers and differentiable at all points. Next, the action probability distribution ($\mathrm{\pi }(s_t,a_t)$) is updated using the policy gradient method. The log of the probability distribution ($\mathrm{\pi }(s_t,a_t)$) for a specific action is multiplied by the TD error to compute the actor loss (line 17), which is then optimized (line 19). These steps continue until the termination condition is met (line 11). Upon termination, the number of unused servers is calculated, and the final reward is assigned. By repeating this process over multiple episodes (line 2), the algorithm gradually converges toward an optimal solution.

Algorithm 1: Optimization algorithm based on DRL.

1: $\mathrm{Initialize} \mathrm{neural} \mathrm{network} {\pi }_{\theta }$$, V_w$ 2: For episode = 1, …, M 3: $\mathrm{Initialize} s_t$ 4: done = false 5: while not done 6:$\mathrm{for} \mathrm{t}=0, \dots , N_{batch}$ 7:$\mathrm{sample} a_t$~$\mathrm{\pi }(s_t, a_t$) 8:$\mathrm{execute} \mathrm{action} a_t$$\mathrm{in} \mathrm{emulator} \mathrm{and} \mathrm{observe} \mathrm{reward} r_t$$, s_{t+1}$ and done 9:$\mathrm{store} \mathrm{transitions} (s_t$$, a_t$$, r_t$$, s_{t+1}$, done) in B 10: $s_t$ ← $s_{t+1}$ 11: if done 12: break 13: $\mathrm{extract} \mathrm{a} \mathrm{batch} \mathrm{of} \mathrm{transitions} (s_t$$, a_t$$, r_t$$, s_{t+1}$, done) in B 14: $\mathrm{TD} \mathrm{Target}=r_t+\mathsf{\gamma }\ast \mathrm{V}\left(s_{t+1}\right)\ast (1-done)$ 15: $\mathrm{TD} \mathrm{Error}=\mathrm{TD} \mathrm{Target}-\mathrm{V}\left(s_t\right)$ 16: $\mathrm{Critic} \mathrm{loss}=\mathrm{huber}\_\mathrm{loss} (\mathrm{V}(s_t)$, TD error) 17: $\mathrm{Actor} \mathrm{loss}=-\mathit{log}\pi \left(s_t, a_t\right)\ast$ TD error 18: Critic loss optimization 19: Actor loss optimization

4.2. Reward Design

A reward system plays a crucial role in training a DRL agent. For reinforcement learning agents, frequent rewards are needed. However, in most cases, the environment provides only sparse rewards [19]. The primary reward is to maximize the number of idle servers, which aligns with the goal of the objective function. Therefore, rewards should be assigned according to the number of servers left unused at the end of the process. However, providing rewards only at the final stage is insufficient for effective learning. Instead, intermediate rewards must be incorporated to facilitate continuous learning and optimization [20].

To achieve this, the minimum number of PSs required for container placement is first determined, and rewards are assigned to encourage placement on the fewest possible PSs. If multiple types of PSs are available, they must also be considered. To maximize the number of unused servers, containers should be placed starting from larger PSs, ensuring that more servers remain unused later. Therefore, rewards are assigned according to physical server size to promote this placement strategy. Since container placement aims to fit the maximum number of containers onto the fewest PSs, stacking containers efficiently is encouraged by awarding positive rewards when successful stacking occurs. However, if placement exceeds resource limits, a negative reward is given to prevent further stacking beyond capacity. These intermediate rewards must be carefully balanced to not interfere with the ultimate objective—maximizing the number of unused PSs. If intermediate rewards outweigh final rewards, the agent may optimize for them instead, preventing the objective function from being maximized. Therefore, a clear difference must exist between intermediate and final reward values.

Based on these principles, the reward system was designed as follows. First, the ideal minimum number of PSs required to accommodate a given container set was calculated. This was determined by calculating the total CPU cores and memory size of all containers and identifying the minimum number of PSs needed. If a container is successfully deployed on a physical server within this ideal minimum range, a reward of 0.2 points is granted.

$$r_t=0.2,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n} N_{ideal},$$

$$N_{ideal}=\mathrm{m}\mathrm{a}\mathrm{x}[\mathrm{t}1,\mathrm{t}2],$$

$$\mathrm{t}1=\mathrm{m}\mathrm{i}\mathrm{n}[{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^{N_{ct}}}{CPU}_{{ct}_j}}{{\displaystyle {\sum }_{i=1}^{t1}}{CPU}_{{ps}_i}}}<1,(1\le \mathrm{t}1\le N_{ps})],$$

$$\mathrm{t}2=\mathrm{m}\mathrm{i}\mathrm{n}[{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^{N_{ct}}}{MEM}_{{ct}_j}}{{\displaystyle {\sum }_{i=1}^{t2}}{MEM}_{{ps}_i}}},(1\le \mathrm{t}2\le N_{ps})].$$

In other cases, the reward value is adjusted based on the type of physical server used. A higher reward is assigned for larger servers, while smaller rewards are given for smaller servers, with reward values ranging between 0 and −0.05.

$$r_t=\left\{\begin{array}{c}0, { TPS}_3\\ -0.01, {TPS}_2\\ -0.03, {TPS}_1\\ -0.05, {TPS}_0\end{array}\right.,{TPS}_3>{TPS}_2>{TPS}_1>{TPS}_0$$

Because maximizing container stacking on a single physical server is the key objective, exponential rewards are granted when containers are placed on an already occupied server. First, the number of container stacks on a physical server is determined, and the reward increases exponentially based on this stacking count.

$$r_t=0.2\ast \left({1.1}^{{NSC}_{{ps}_i}}\right),$$

$${NSC}_{{ps}_i}=| A \cap B |, A=\left\{a_1, a_2, \dots , a_{t-1}\right\}, B=\left\{a_t\right\}.$$

To further incentivize efficient packing, a distinct, larger reward is granted when a container placement results in a physical server becoming completely full. This condition is met if the sum of the CPU or memory of all containers allocated to the server equals the server’s capacity for that resource. This “server full” reward is greater than the standard reward given for merely stacking containers on a partially filled server.

$$r_t=\left\{\begin{array}{c}0.7, { TPS}_3, {TPS}_2\\ 0.6, { TPS}_1 \\ 0.5, { TPS}_0 \end{array}, {\displaystyle \sum _{j=1}^m}{CPU}_{{SC}_{i, j}}={CPU}_{{ps}_i} or {\displaystyle \sum _{j=1}^m}{MEM}_{{SC}_{i,j}}={MEM}_{{ps}_i}\right.$$

However, if excessive stacking exceeds resource limits and results in placement failure, a negative reward of −0.09 points is applied. This discourages the agent from attempting placements beyond capacity.

$$r_t=-0.09.$$

(1)

Because the number of unused PSs at the final step serves as the primary objective function, the final reward is calculated by multiplying the number of unused servers by 4.2. This ensures a clear distinction between intermediate and final rewards.

$$r_t=N_{{ps}_{unused}}\ast 4.2$$

(2)

The constant values used in this reward system were determined through sensitivity analysis, selecting those that yielded the best results when the DRL agent was executed. The intermediate reward value of 0.2 serves as the central reference point, with the stacking and final rewards scaled relative to this base value. Consequently, any adjustments to this central reward value would necessitate corresponding adjustments to the dependent stacking and final rewards to maintain their intended relationship.

5. Experiments and Results

The dataset consists of a set of PSs and containers, which are assigned to PSs based on their resource requirements. Both PSs and containers are expressed as pairs of CPU and memory sizes.

The CPU and memory sizes for containers and PSs in the dataset reflect configurations the author observed while working in an actual data center environment. The container dataset includes 10 types of containers with the following CPU and memory configurations: [(4, 120), (4, 16), (8, 24), (8, 32), (10, 32), (10, 36), (12, 36), (12, 48), (16, 48), and (16, 64)]. The number of containers in each type was adjusted to reflect real-world scenarios where container operations range from 300 to 1000 instances. The physical server dataset includes four types of servers with the following CPU and memory configurations: [(28, 84), (36, 120), (54, 180), and (72, 240)]. The number of PSs was adjusted to simulate an environment with 80 to 248 servers in operation. The container and physical server datasets, structured based on these types, are detailed in

Table 2. Container and physical server datasets.

Type		Data1	Data2	Data3	Data4	Data5	Data6	Data7	Data8
CT	Total	300	400	500	600	700	800	900	1000
	(4, 12)	30	40	50	60	70	80	90	100
	(4, 16)	30	40	50	60	70	80	90	100
	(8, 24)	30	40	50	60	70	80	90	100
	(8, 32)	30	40	50	60	70	80	90	100
	(10, 32)	30	40	50	60	70	80	90	100
	(10, 36)	30	40	50	60	70	80	90	100
	(12, 36)	30	40	50	60	70	80	90	100
	(12, 48)	30	40	50	60	70	80	90	100
	(16, 48)	30	40	50	60	70	80	90	100
	(16, 64)	30	40	50	60	70	80	90	100
PS	Total	80	104	128	152	176	200	224	248
	(28, 84)	20	26	32	38	44	50	56	62
	(36, 120)	20	26	32	38	44	50	56	62
	(54, 180)	20	26	32	38	44	50	56	62
	(72, 240)	20	26	32	38	44	50	56	62

.

To evaluate the performance of optimal container placement using DRL agents, we compared it against traditional bin-packing algorithms. Among these, first fit is widely recognized for its superior performance in many cases, particularly when items are placed in descending order from largest to smallest. This ordering tends to improve placement efficiency. For comparison, we selected four bin-packing algorithms: next fit (NF), first fit (FF), declining next fit (DNF), and declining first fit (DFF).

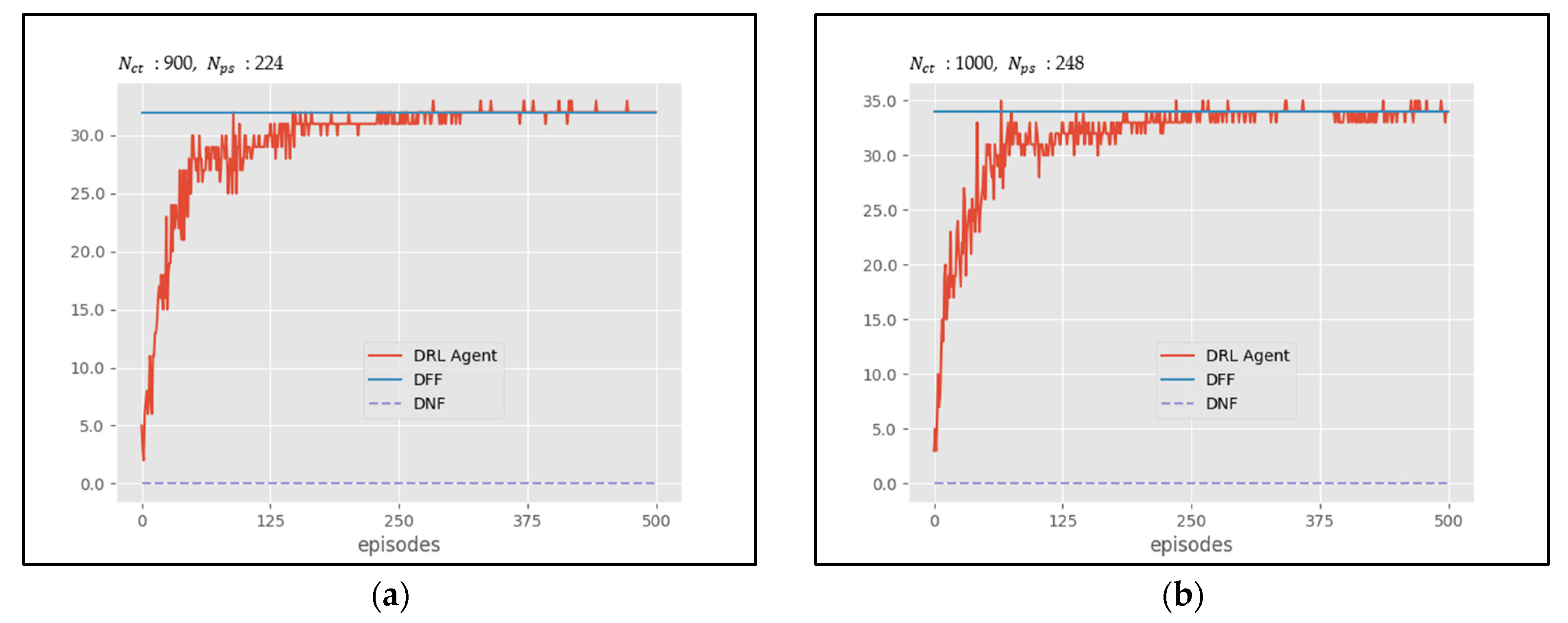
Figure 3 presents the learning curve for the DRL agent, showing the improvements in the maximum number of unused PSs achieved as training progresses over episodes for the Data7 and Data8 cases. Additionally, the final performance levels achieved by the DFF and DNF algorithms are also displayed as horizontal lines. The results indicate that the DRL agent typically reaches peak performance after 200 episodes.

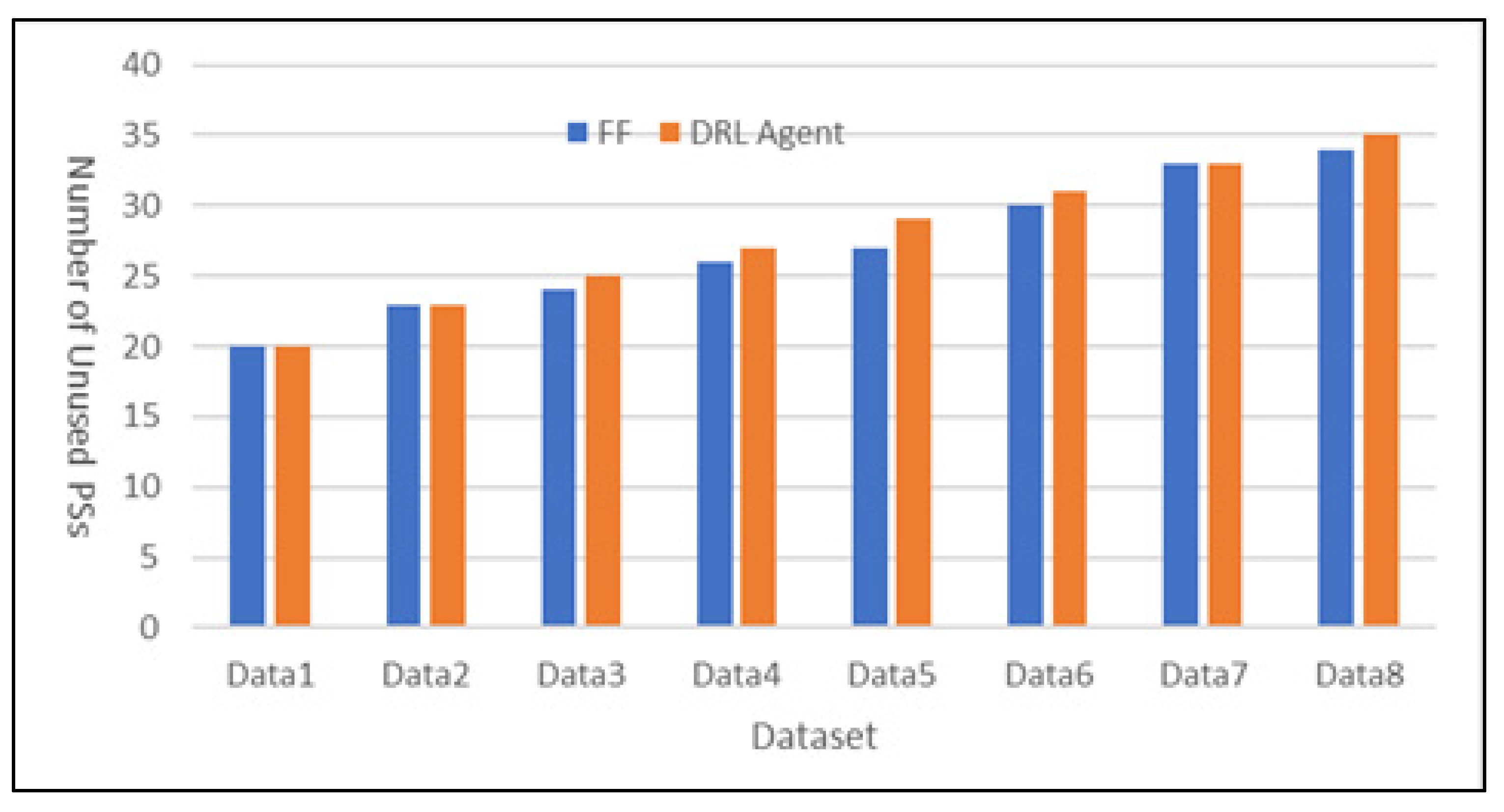
The results for the number of unused PSs using traditional bin-packing algorithms and the DRL agent for each of the eight datasets are presented in

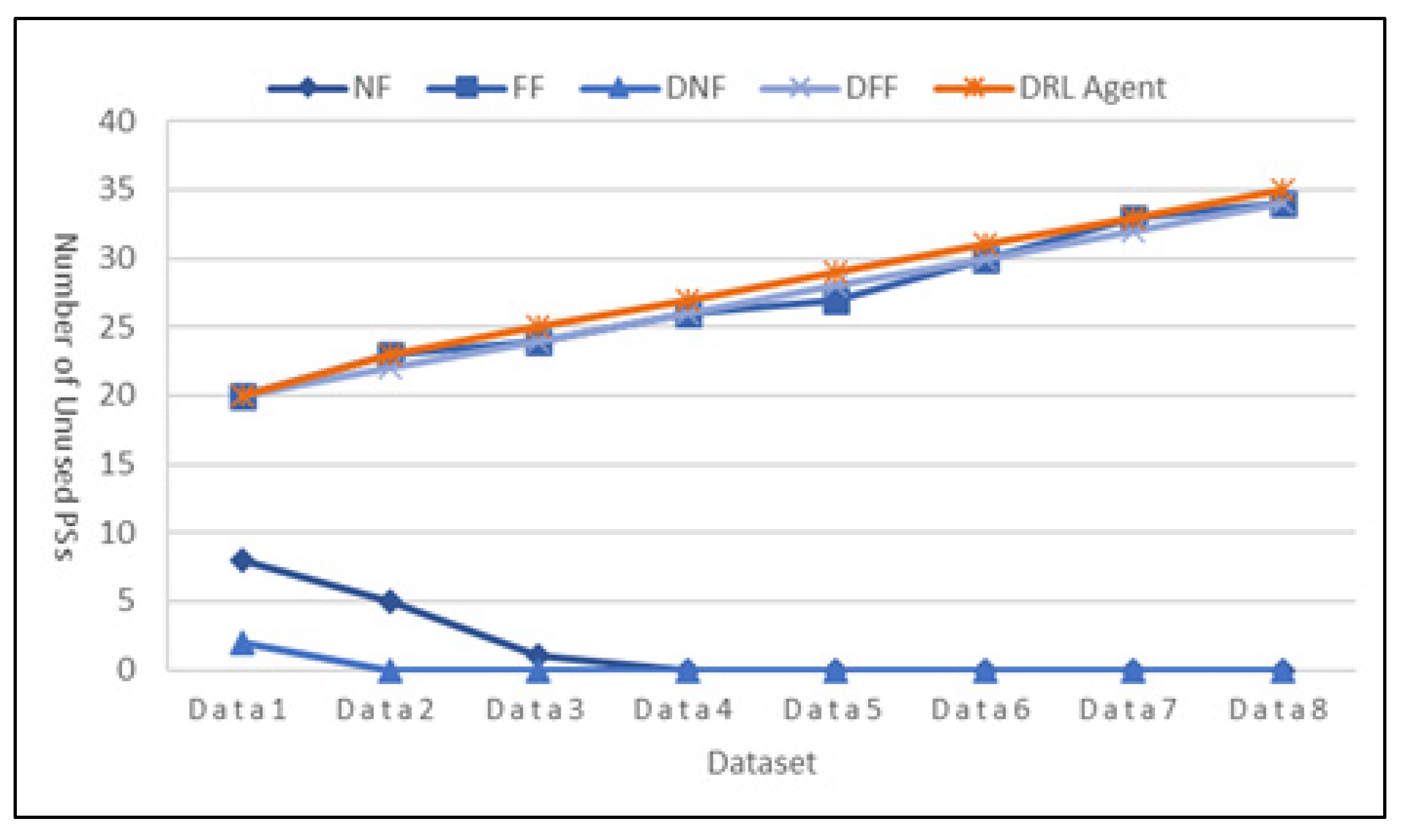
Table 3. Traditional algorithm and DRL agent results.

Type	Data1	Data2	Data3	Data4	Data5	Data6	Data7	Data8
NF	8	5	1	0	0	0	0	0
FF	20	23	24	26	27	30	33	34
DNF	2	0	0	0	0	0	0	0
DFF	20	22	24	26	28	30	32	34
DRL	20	23	25	27	29	31	33	35

.

The DRL agent showed equivalent performance to traditional algorithms on three datasets (Data1, Data2, Data7) and outperformed them on the remaining five datasets. On the remaining five datasets (Data3, Data4, Data5, Data6, Data8), the DRL agent outperformed the best traditional methods, resulting in one additional unused physical server in each case. This indicates that the DRL-based optimization algorithm is generally more effective than traditional bin-packing approaches. Figure 4 shows the performance variations across different algorithms. Figure 5 compares the performance of First Fit and DRL Agent, which show high performance.

The experimental results clearly show that FF performed well, while the DRL-based optimization algorithm achieved the best overall performance. Notably, the NF method performed significantly worse, highlighting the inefficiency of non-optimized container placement, which can lead to excessive server usage. These findings confirm that without proper optimization, many servers may be wasted, resulting in higher operational costs. The results also reinforce that the DRL-based optimization algorithm consistently outperforms existing heuristic algorithms, making it a superior approach for efficient container placement in data centers.

6. Discussion and Conclusions

The container placement problem in data centers is an important issue because it directly affects operating costs. This paper proposes an optimization algorithm for container placement that allows unused servers to transition to idle mode, reducing resource consumption. This algorithm demonstrated better performance than the benchmark heuristic methods, successfully minimizing active PSs and enhancing resource efficiency. Additionally, although many optimization approaches focus on container placement based on VMs, this study considered the container form directly along with stable operation methods typically employed in actual data center environments, offering advantages in operational stability and adaptability. This excellent performance was achieved using the actor-critic method, which, combined with the use of fixed-length state values and a structured reward system, also provided flexibility for application to various environments and suggests possibilities for future improvements. In the future, integrating container orchestration and DRL is expected to stimulate further research and discussion, contributing to broader goals such as IT operation automation and automatic optimization of cloud environments.

Although the experimental results confirmed that DRL is an effective approach for optimizing container placement in data centers, it is impossible to determine whether the current optimization represents the absolute best solution, as evaluating all possible placements is infeasible. Therefore, better algorithms may emerge over time. The DRL agent proposed in this paper performed comparably to existing methods in some cases, and even when it performed better, the difference was not substantial, indicating room for further improvement.

Several potential enhancements can be explored. First, this study used linear networks and Softmax for learning [19]. However, implementing long short-term memory networks could improve performance by remembering past states and actions to decide on future actions. In addition, instead of using a single network, employing multiple independent networks that exchange learning results could yield better performance.

Further research is also needed to develop an optimal placement model for containers operating across multiple zones. Currently, the proposed method assumes that containers can be placed freely within a single zone. Future studies should explore container placement methods that distribute workloads across multiple zones, ensuring greater stability in the event of a failure in an entire zone or individual PSs. In addition, as traffic loads fluctuate, containers must be dynamically scaled. Thus, an optimal placement method that accounts for sudden traffic surges is essential. Finally, simultaneously optimizing all virtual servers and containers within a data center could further reduce costs, making ongoing research in this area crucial.