Abstract
Artificial intelligence-based biomedical image processing has become an important area of research in recent decades. In this context, one of the most important problems encountered is the close contrast values between the pixels to be segmented in the image and the remaining pixels. Among the crucial advantages provided by metaheuristic algorithms, they are generally able to provide better performances in the segmentation of biomedical images due to their randomized and gradient-free global search abilities. Math-inspired metaheuristic algorithms can be considered to be one of the most robust groups of algorithms, while also generally presenting non-complex structures. In this work, the recently proposed Circle Search Algorithm (CSA), Tangent Search Algorithm (TSA), Arithmetic Optimization Algorithm (AOA), Generalized Normal Distribution Optimization (GNDO), Global Optimization Method based on Clustering and Parabolic Approximation (GOBC-PA), and Sine Cosine Algorithm (SCA) were implemented for clustering and then applied to the retinal vessel segmentation task on retinal images from the DRIVE and STARE databases. Firstly, the segmentation results of each algorithm were obtained and compared with each other. Then, to compare the statistical performances of the algorithms, analyses were carried out in terms of sensitivity (Se), specificity (Sp), accuracy (Acc), standard deviation, and the Wilcoxon rank-sum test results. Finally, detailed convergence analyses were also carried out in terms of the convergence speed, mean squared error (MSE), CPU time, and number of function evaluations (NFEs) metrics.
1. Introduction
In recent years, optimization problems—especially those in the area of image processing—have become increasingly complex, leading to the requirement for more effective methods for their solution. New directions of theoretical research have appeared in the literature in accordance with this requirement, involving the improvement of existing conventional or metaheuristic algorithms, hybridizing different algorithms, and proposing new metaheuristic algorithms [1]. The results presented in the literature have also proved that, due to their non-random search characteristics, conventional gradient-based approaches cannot produce results as effective as metaheuristic algorithms.
Metaheuristic algorithms are usually classified into four main groups: evolutionary-based, swarm intelligence-based, physics-based, and human-inspired algorithms. Furthermore, inspired by the search strategies utilized, these algorithms can also be alternatively classified into two main groups. Simple local search and global search algorithms [2]: these search algorithms have the important disadvantages of becoming stuck inside local minima and dependence on the initial solutions. In contrast, population-based algorithms may provide higher optimization performance as a result of their global search ability, which is achieved through improving the population iteratively. In the literature, the majority of population-based algorithms have been improved in a manner inspired by swarm intelligence, physical laws, evolutionary strategies, and human behaviors. In addition to these well-established and frequently used algorithms, some novel population-based metaheuristic algorithms inspired by mathematical laws have also been proposed in recent years [1,2,3,4,5,6]. The most recently proposed math-inspired algorithms include the Circle Search Algorithm (CSA), Tangent Search Algorithm (TSA), Arithmetic Optimization Algorithm (AOA), Generalized Normal Distribution Optimization (GNDO) Algorithm, Global Optimization Method based on Clustering and Parabolic Approximation (GOBC-PA), and Sine Cosine Algorithm (SCA).
The SCA has been applied to several engineering problems in the existing literature, including the optimization of the cross-section of an aircraft wing [1], optimizing the combined economic and emission dispatch problem in power systems [7], optimizing the size and location of energy resources in radial distribution networks [8], optimizing the parameters of fractional order PID (FOPID) controller for load frequency control systems [9], designing an effective PID controller for power systems [10], designing a hybrid power generation system with minimized total annual cost and emissions [11], solving the unit commitment problem of an electric power system [12], solving the bend photonic crystal waveguides design problem [13], solving the short-term hydrothermal scheduling problem in power systems [14], tuning the FOPID/PID controller parameters for an automatic voltage regulator system [15], determining the optimal PID controller parameters for an automatic voltage regulator system [16], designing a PD-PID controller for the frequency control of a hybrid power system [17], implementation of a novel future selection approach for text categorization [18], solving the economic power-generation scheduling (EcGS) problem for thermal units [19], implementation of a parallel SCA for three communication strategies [20], implementation of an enhanced sine cosine algorithm (ESCA) to determine the threshold for use in the segmentation of color images [21], development of an optimum photovoltaic pumping system based on monitoring the maximum power point under certain meteorological conditions [22], achievement of an optimal thermal stress distribution in symmetric composite plates with non-circular holes under a uniform heat flux [23], and the implementation of an SCA-based intelligent approach for effective underwater visible light communication [24].
The AOA has also been applied to several engineering problems in the existing literature, including the implementation of the AOA for optimization in mechanical engineering design problems [4,25,26], designing skeletal structures (e.g., 72 bar space truss, 384 bar double-layer barrel vault, and a 3 bay, 15 story steel frame) [27], the implementation of a dynamic AOA for truss optimization under natural frequency constraints [28], optimizing the shapes of vehicle components using metaheuristic algorithms to minimize fuel emissions [29], applying enhanced hybrid AOAs to real-world engineering problems (e.g., welded beam, gear train, 3 bar truss, speed reducer, multiple disk clutch brake, step-cone pulley, 25 bar truss, and 4-stage gearbox design problems) [30], the enhancement of a hybrid AOA for DC motor regulation and fluid-level sequential tank system design [31], the implementation of an AOA-based efficient text document clustering approach [32], the implementation of a deep convolutional spiking neural network optimized using the AOA for lung disease detection from chest X-ray images [33], and the design of an electric vehicle fast-charging station connected with a renewable energy source and battery energy storage system [34].
The TSA only has a restricted number of real-world applications in the existing literature, including the adjustment of the optimal forecasting interval and enhancement of the interval forecasting performance in ensemble carbon emissions forecasting systems [35], the implementation of a hybrid method (named the Aquila optimizer–tangent search algorithm; AO-TSA) for global optimization problems [36], and the implementation of a basic TSA which integrates the fitness-weighted search strategy (FWSS) and opposition-based learning (OBL) concepts for the solution of complex optimization problems [37].
The GNDO algorithm has several real-world applications in the existing literature, including parameter extraction for photovoltaic models for energy conversion [5], estimating the parameters of the triple-diode model of a photovoltaic system [38], the design of truss structures with optimal weight [39], and enabling voltage and current control in an energy storage system and adjusting the optimum gain settings of the PI controller [40].
The GOBC-PA algorithm has been applied to engineering problems such as the optimization of the parameters of an osmotic dehydration process for enhanced performance in the drying of mushroom products [41], as well as the implementation of a novel search method consisting of deterministic and stochastic approaches and testing its performance over benchmark functions in addition to one- and two-dimensional optimization problems [42].
Finally, the CSA has also been applied to several engineering problems, including tracking global maxima power under partial shading conditions in solar photovoltaic systems [43] and the implementation of a maximum-power point-tracking control system to increase the efficiency of grid-connected photovoltaic systems [44].
In the recent literature, there are also studies that have detailed the application of approaches other than metaheuristic algorithms for retinal vessel segmentation. In [45], Saeed et al. propose a preprocessing module including four stages to assess the impact of retinal vessel coherence on retinal vessel segmentation and then applied the proposed method to retinal images from the DRIVE and STARE databases. In [46], Xian et al. propose a novel hybrid algorithm to segment dual-wavelength retinal images with high accuracy and enlarge the measurement range of hemoglobin oxygen saturation in retinal vessels. Wang and Li propose a novel approach based on gray relational analysis for the segmentation of retinal images under the constraint of a limited sample size and the resulting associated uncertainties [47]. Jiang et al. propose a deep-learning-based network model, called feature selection-UNet (FS-UNet), with the aim of optimizing attention mechanisms and task-specific adaptations when analyzing complex retinal images [48], and proved the efficiency of the model using images from the DRIVE, STARE, and CHASE databases. In [49], a novel deep-learning-based network model, called plenary attention mechanism-UNet (PAM-UNet), is proposed by Wang et al. to enhance the feature extraction capabilities of existing algorithms. The performance of the model was analyzed using retinal images from the DRIVE and CHASE DB1 databases. In [50], Ramesh and Sathiamoorthy propose a hybrid model which combines metaheuristic and deep learning approaches to detect diabetic retinopathy with high accuracy. Similarly, Sau et al. propose a deep learning architecture based on a metaheuristic algorithm for retinal vessel segmentation [51].
As can be seen from this literature review, math-inspired metaheuristic algorithms have only been utilized for applications within a restricted number of research areas. Retinal image segmentation has become one of the most common application areas in the field of image processing in recent years. In this context, the segmentation of retinal images with high accuracy is extremely important for the detection of eye diseases.
The highlights of this work can be expressed as follows:
- The math-inspired metaheuristic algorithms of CSA, TSA, AOA, GNDO, GOBC-PA, and SCA are implemented for clustering and retinal vessel segmentation.
- The segmentation results demonstrate that the considered math-inspired metaheuristic approaches are able to produce similar or better results when compared to evolutionary-based, swarm-intelligence-based, physics-based, and human-inspired algorithms [52,53].
- The statistical analyses indicate that the considered math-inspired algorithms are able to produce effective results despite their simple algorithmic structures.
2. Materials and Methods
In retinal image segmentation, the images should first be enhanced in terms of their contrast by applying pre-processing operations. The most commonly used pre-processing operations in the relevant literature are band selection, bottom-hat transformation, and brightness correction. Retinal images consist of Red (R), Green (G), and Blue (B) layers, and the most effective layer (i.e., that which will provide the highest clustering performance) can be determined using band selection. After the most appropriate layer is determined, the contrast of the relevant layer is further increased via bottom-hat transformation and brightness correction pre-processing. The retinal images obtained as a result of these pre-processing operations, with higher contrast, are then subjected to clustering-based segmentation through the use of metaheuristic algorithms.
Figure 1a and Figure 1b shows healthy and diseased retinal images, respectively, taken from the Digital Retinal Images for Vessel Extraction (DRIVE) database [54]. Similarly, healthy and diseased retinal images taken from the Structured Analysis of the Retina (STARE) database [55] are shown in Figure 2a and Figure 2b, respectively.
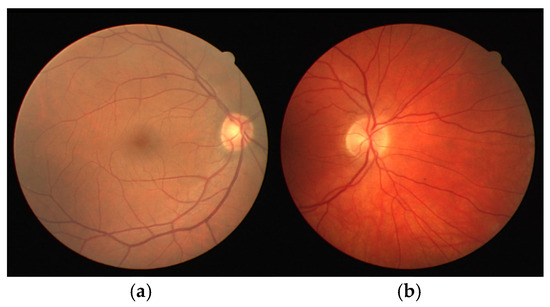
Figure 1.
Retinal images from the DRIVE database: (a) healthy retinal image; (b) diseased retinal image.
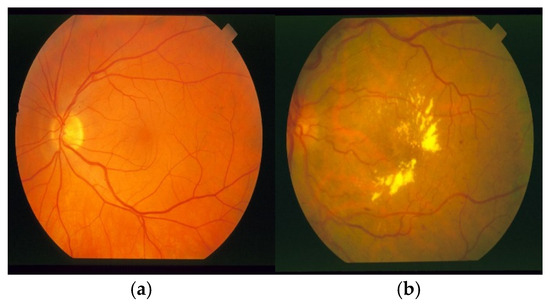
Figure 2.
Retinal images from the STARE database: (a) healthy retinal image; (b) diseased retinal image.
The green layer of RGB retinal images is frequently able to produce better clustering performance due to its higher illuminance, contrast, and brightness levels. After applying band selection, the G layers of the DRIVE and STARE retinal images were obtained, as shown in Figure 3a and Figure 3c and Figure 4a and Figure 4c, respectively. Afterward, bottom-hat transformation and brightness correction were applied consecutively to increase the contrast of the retinal images. The enhanced retinal images are shown in Figure 3b,d for DRIVE images and in Figure 4b,d for STARE images.
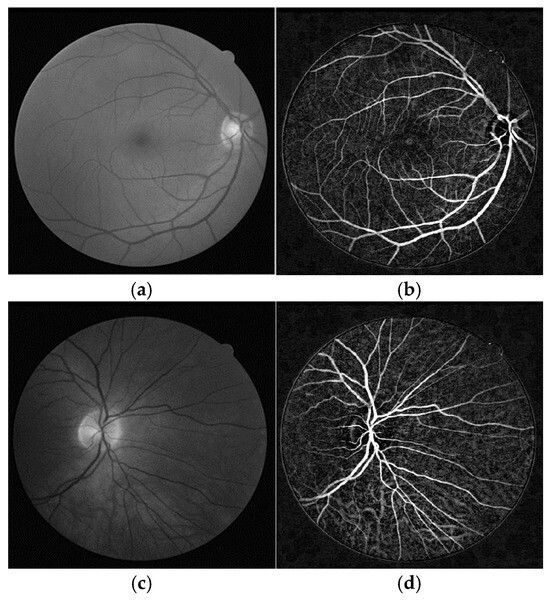
Figure 3.
Enhanced retinal images from the DRIVE database: (a,c) are the G layers obtained as a result of band selection; (b,d) are the corresponding retinal images obtained as a result of the bottom-hat filtering and brightness correction.
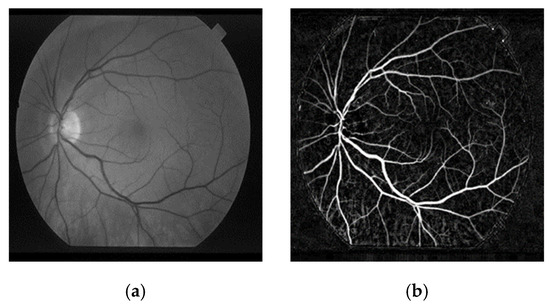
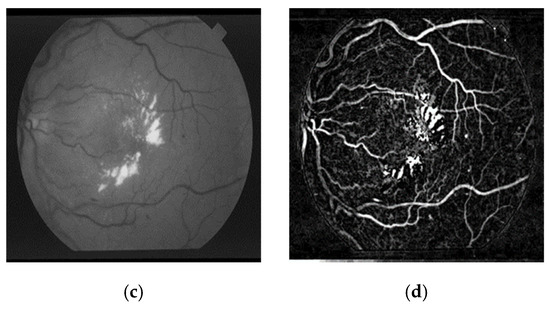
Figure 4.
Enhanced retinal images from the STARE database: (a,c) are the G layers obtained as a result of band selection; (b,d) are the corresponding retinal images obtained as a result of the bottom-hat filtering and brightness correction.
In this study, field of view (FOV) mask images were also used to analyze the performance of the algorithms in detail. The FOV mask images include only the vessel pixels; namely, all other pixels except the vessel pixels were removed from the image. For both the DRIVE and STARE databases, pixel-based comparisons were carried out between the segmented images and the relevant mask images to analyze the performance of the algorithms.
Math-inspired metaheuristic algorithms provide robust approaches for optimization problems, reflecting the effectiveness of basic mathematical laws. These algorithms especially stand out due to their lower computational costs and simple algorithmic structures. In this work, the most recent math-inspired metaheuristic algorithms in the literature were applied for retinal vessel segmentation, after which their performances were compared in detail. The math-inspired metaheuristic algorithms were improved using MATLAB R2019a software. Furthermore, the mathematical and statistical analyses were also carried out using the same software.
2.1. Circle Search Algorithm
The CSA, which was proposed by Qais et al. in 2022, is an effective metaheuristic approach inspired by the unique characteristics of circles, such as their diameter, perimeter, center point, and tangent line. It may provide significantly improved performance, in terms of the exploration and exploitation phases, due to the integration of the geometric features of circles into the algorithm [3].
The detailed pseudo-code for the CSA is given as follows:
| Randomly create an initial population by, |
| Determine the parameter |
| Cycle = 1 |
| WHILE |
| Calculate the values of the variables , and |
| Calculate the value of |
| Update by using, |
| If Updated solutions are out of the boundaries |
| Set the solutions equal to the boundaries |
| Calculate the fitness value of |
| End |
| Evaluate with the current best solution |
| Update and |
| Cycle = Cycle + 1 |
| END |
In the CSA, and represent the lower and upper limit values of the search space, respectively; the operator constitutes a random vector including randomly produced values within the interval of [0, 1]; and the parameter is a constant ranging between [0, 1] that represents the percentage of maximum cycles. Furthermore, , , and are variables set within the intervals of [, 0], [−, 0] and [1, 0], respectively. These variables can be calculated as
Furthermore, represents an angle that can be used while updating , which is calculated using the following equation:
2.2. Tangent Search Algorithm
The TSA, which was proposed by Layeb in 2021, is a novel math-inspired metaheuristic algorithm inspired by the two important features of the tangent function [2]. The variation interval of the tangent function provides the algorithm with an effective exploration ability in searching the solution space. Additionally, the inherently periodic structure of the tangent function provides a balance between the exploration and exploitation processes during optimization.
The detailed pseudo-code for the TSA is given as follows:
| Randomly create uniformly distributed initial population, |
| Cycle = 1 |
| WHILE |
| Apply Switch procedure for each according to Pswitch |
| If : Intensification phase |
| Produce a random local walk by, |
| Exchange some variables of the obtained solution with the related variables of the |
| current optimal solution by to produce new possible solutions |
| Check the boundaries of the recently produced solutions |
| Repair the overflowed solutions |
| Else : Exploration phase |
| Apply to each variable with a probability equal to 1/D |
| in order to expand the research capacity |
| End |
| Apply Escape Local Minima procedure according a given probability value called Pesc |
| If : Escape local minima phase |
| Randomly select one of the current solutions and apply selection procedures of |
| End |
| Replace with a randomly selected solution having lower fitness value |
| Cycle = Cycle + 1 |
| END |
In the TSA, and denote the lower and upper bounds of the problem to be optimized, respectively; the operator produces uniformly distributed numbers in the interval of [0, 1]; and D is the dimension of the problem. represents a probability value, which is used to control the phase of the algorithm, and is a global step value, which directs the existing solutions toward the optimal solution. In order to check the boundaries and repair the overflowed solutions in the intensification phase, the following expressions can be used:
In the escape from local minima phase, one of the following two procedures (which produce the optimal fitness value) can be applied to select the optimal solutions:
2.3. Arithmetic Optimization Algorithm
The AOA, which was proposed by Abualigah et al. in 2021, simulates the distribution behavior of the arithmetic operators of multiplication, division, subtraction, and addition [4]. The simple algorithm structure of the AOA includes only two control parameters, providing the ability to maintain effective optimization performance in a wide range of engineering problems. In the AOA, a population consisting of possible solutions is evaluated according to some predetermined mathematical criteria in order to reach the global solution.
The detailed pseudo-code for the AOA is given as follows:
| Randomly create an initial population consisting of positions of the solutions, |
| Cycle = 1 |
| WHILE |
| Calculate the fitness value of each solution in the population |
| Determine the best solution so far |
| Update the Math Optimizer Accelerated (MOA) value |
| Update Math Optimizer probability (MOP) value |
| For |
| For |
| Produce a random values between [0, 1] for the conditions of r1, r2 and r3 |
| If : Exploration phase |
| If |
| Apply Division math operator (D “”) and update the position of |
| solution i |
| Else |
| Apply Multiplication math operator (M “”) and update the position of |
| solution i |
| End if |
| Else |
| If : Exploitation phase |
| Apply Substraction math operator (S “”) and update the position of |
| solution i |
| Else |
| Apply Addition math operator (A “”) and update the position of |
| solution i |
| End if |
| End if |
| End |
| End |
| Cycle = Cycle + 1 |
| END |
In the AOA, represents the math optimizer accelerated function, which can be calculated as follows:
where Min and Max denote the minimum and maximum values of the accelerated function, respectively, and and denote the current cycle and maximum number of cycles, respectively. On the other hand, the value can be calculated as
where is a sensitive parameter affecting the exploitation accuracy over the cycles. In the exploration phase, the (D “”) and (M “”) operators update the positions according to the following expressions:
where is a small integer, is a control parameter to adjust the search process, and, finally, and represent the upper and lower bounds of solution j, respectively. On the other hand, in the exploitation phase, the update of each position can be performed by the (S “”) and (A “”) operators, as detailed below:
2.4. Generalized Normal Distribution Optimization Algorithm
The basic philosophy of the GNDO algorithm is to optimize the position of each individual in the population based on the generalized normal distribution curve. The GNDO algorithm has a very simple structure, consisting of only two control parameters. The GNDO algorithm performs local exploitation and global exploration phases according to the current and the mean positions of the individuals on a constructed generalized normal distribution model. This algorithm was proposed by Zhang et al. in 2020 as an effective math-inspired metaheuristic algorithm, in terms of its efficiency and accuracy [5].
Detailed pseudo-code of the GNDO algorithm is given as follows:
| Randomly create an initial population by, and |
| Calculate the fitness value of each solution and determine the best solution as |
| Cycle = 1 |
| WHILE |
| For |
| Produce a random number () in the interval of [0, 1] |
| If : Local exploitation strategy |
| Select the current optimal solution and calculate the mean position M |
| Compute the generalized mean position , generalized standard variances |
| and penalty factor |
| Apply the local exploitation strategy to calculate and |
| Else: Global exploration strategy |
| Apply the global exploration strategy |
| End if |
| End for |
| Cycle = Cycle + 1 |
| END |
In the GNDO algorithm, and are the lower and upper boundaries of the design problem, respectively; the operator produces random numbers in the interval of [0, 1]; and D represents the dimension of the problem.
In the local exploitation strategy, the mean position (M) can be calculated as
In addition, the values of , and can be calculated as
In order to apply the local exploitation strategy, and can be calculated as
Finally, the global exploration strategy can be applied according to the following expressions:
where , , and () are random integers taken in the interval of [1, N]; represents a random number taken from a standard normal distribution; and is an adjustment parameter with value between 0 and 1.
2.5. Global Optimization Method Based on Clustering and Parabolic Approximation
The GOBC-PA approach, which was proposed by Pençe et al. in 2016, simulates the clustering and function approximation processes in order to reach the global minimum [6]. The GOBC-PA algorithm differs from the other metaheuristic approaches primarily in terms of its crossover and mutation processes; in particular, the evaluation of each solution is followed by means of second-order polynomials and clustering instead of crossover and mutation. The updating of cluster centers via curve fitting and the usage of clustering mechanisms based on the fitness values strengthen this method, especially in terms of its convergence speed.
The detailed pseudo-code of the GOBC-PA algorithm is given as follows:
| Randomly create an initial population |
| Set the number of cluster size as and maximum epoch size as |
| Calculate the fitness value produced by the objective function |
| For |
| Determine the cluster centers |
| Determine the membership matrix of via clustering |
| Sort the cluster centers with ascending order in accordance with the fitness values |
| Select the first ceil cluster centers as () |
| For |
| Determine the H set which represent the members of taken from depending |
| on |
| If |
| Determine the parabola coefficient matrix () |
| Find the coefficients of approximated parabola () |
| End if |
| End for |
| For |
| Determine the vertex of parabola |
| If , the parabola can be assumed as concave and keep |
| Else if , the parabola can be assumed as convex, and if is better |
| than then replace with |
| Else if is not a number or infinite then keep |
| End if |
| End for |
| Randomly create a new population around the |
| Randomly create new population around the current best two solutions |
| Randomly create a new population |
| Determine as |
| Calculate the fitness value of the objective function by using the new population |
| Determine as the best solution of |
| If , can be defined as the global minimum |
| End if |
| End for |
In the GOBC-PA algorithm, and represent the population size and the number of variables, respectively. The parabola coefficient matrix () and the coefficients of the approximated parabola () can be calculated as
On the other hand, the vertex of the parabola can be calculated as
The new population can be created around the using the following expression:
where represents the standard deviation of . Furthermore, can be calculated as follows:
where and represent the lower and upper bounds of the solution space, respectively.
Finally, can be obtained as follows:
2.6. Sine Cosine Algorithm
The SCA is a population-based metaheuristic algorithm inspired by the fluctuating behaviors and cyclic patterns of the sine and cosine trigonometric functions, which was proposed by Mirjalili in 2016 [1]. In the SCA, while the exploration of the search space is controlled by changing the range of the sine and cosine functions, the repositioning of a solution around another solution can also be realized according to its cyclic pattern property.
The detailed pseudo-code for the SCA is given as follows:
| Randomly create an initial population consisting a set of search agents, |
| Cycle = 1 |
| WHILE |
| Calculate the fitness value of each search agent in the population |
| Determine the best search agent so far and store it in a variable as destination agent |
| Update the random parameters and |
| Update the position of each search agent in the current population |
| Store the current destination point as the best search agent obtained so far |
| Cycle = Cycle + 1 |
| END |
In the SCA, the random parameter decides whether a solution updates its position towards the best solution ( < 1) or away from it ( > 1). It can be updated using the following equation:
where a is a constant and t is the current cycle. Meanwhile, varies randomly in the interval of , which determines the required distance towards or away from the destination. Furthermore, varies randomly in the interval of and represents a random weight for the destination, either emphasizing () or de-emphasizing () the effect of the destination in defining the distance. Finally, varies randomly in the interval of and acts as a switch to choose between the sine and cosine functions. The position of each search agent in the current population can be updated using the following equation:
where represents the current search agent in cycle and denotes the position of the best search agent in cycle .
The values of the Population Size and Maximum Cycle Number parameters were determined as 10 and 100, respectively, for each algorithm. Furthermore, the maximum and minimum pixel values were defined as and , respectively. The remaining control parameter values used in the simulations for each algorithm are provided in Table 1. The optimal control parameter values for the CSA, TSA, AOA, GNDO, GOBC-PA, and SCA algorithms were taken from [1,2,3,4,5,6], respectively. On the other hand, for the control parameters that can take values within a certain range, simulations were carried out for different values within the relevant range and the value at which the optimum segmentation results were obtained was defined as the optimal value. In particular, the parameter values that produced the highest segmentation performance (i.e., in terms of Se, Sp, and Acc) and also produced the lowest MSE values were determined as the optimal parameter values.

Table 1.
The control parameter values for each algorithm.
In this work, the metaheuristic algorithms were used to obtain the optimal cluster centers corresponding to optimal pixel values. While investigating the optimal cluster center values, the quality of each possible clustering center was calculated depending on the mean squared error (MSE) function:
where is the number of total pixels, represents the closest clustering center value to the pixel, and, finally, is determined as the pixel value of the pixel . According to this, the fitness value of any solution k can be calculated as follows:
where represents the error value produced by solution k.
In order to present a fair performance comparison, analyses were carried out for both healthy and diseased retinal images taken from the DRIVE and STARE databases. The DRIVE database was established by Alonso-Montes et al., and the images in this database were captured using a Canon CR5 3CCD camera under a 45° FOV with a resolution of 565 × 584 pixels. The STARE database was constructed by Hoover et al. using a Topcon TRV-50 fundus camera under a 35° FOV with a resolution of 700 × 605 pixels. Each of the DRIVE and STARE databases contain 20 raw retinal images and their mask images separately. In both databases, half of the retinal images are healthy images, while the others present pathologies.
3. Results
In this work, recently proposed math-inspired algorithms—including the CSA, TSA, AOA, GNDO, GOBC-PA, and SCA—were implemented for clustering in order to classify the vessels from the background pixels of retinal images with high accuracy. The obtained results are presented in three groups below: segmentation performance, statistical analysis, and convergence analysis.
3.1. Segmentation Performance
The resulting retinal images from the DRIVE database after applying the CSA-, TSA-, AOA-, GNDO-, GOBC-PA-, and SCA-based segmentation processes are shown in Figure 5. It can be seen that some of the background pixels were incorrectly classified as vessel pixels. Similarly, Figure 6 shows the segmentation results for the retinal images taken from the STARE database. The results obtained for the STARE images indicate that the segmentation performance of the algorithms was similar, but slightly worse, when compared to the DRIVE images. When the results obtained for both databases are analyzed, it can be concluded that, although there were a certain number of misclassified pixels, the algorithms generally provide highly accurate segmentation results.
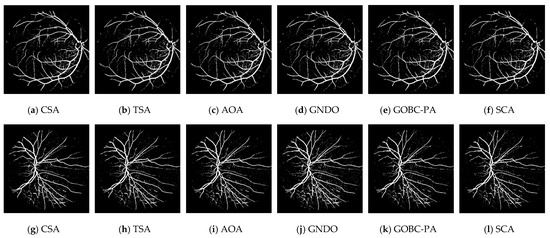
Figure 5.
Results after applying CSA-, TSA-, AOA-, GNDO-, GOBC-PA-, and SCA-based segmentation to the images in Figure 1a,b.
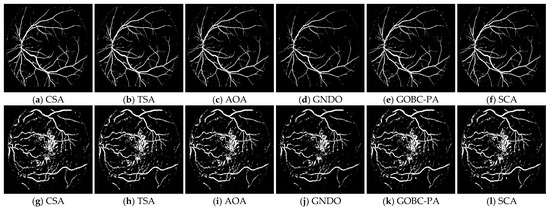
Figure 6.
Results after applying CSA-, TSA-, AOA-, GNDO-, GOBC-PA-, and SCA-based segmentation to the images in Figure 2a,b.
3.2. Statistical Analysis
The results produced by the metaheuristic algorithms were tested and verified in terms of the Se, Sp, Acc and standard deviation metrics due to their non-deterministic nature. Furthermore, the Wilcoxon rank-sum test was applied to statistically validate the obtained numerical results and investigate the significant differences among the algorithms [56].
The Se, Sp, and Acc metrics can be defined according to the following expressions:
where true positives (TP) are the correctly classified vessel pixels, false negatives (FN) are the incorrectly classified vessel pixels, true negatives (TN) are the correctly classified background pixels, and, finally, false positives (FP) are the incorrectly classified background pixels [55].
Performance measures and statistical analyses were applied separately to all 40 images in the DRIVE and STARE databases in order to perform a more comprehensive and global analysis. The performances of the algorithms in terms of Se, Sp, and Acc on the DRIVE and STARE databases are given in Table 2 and Table 3, respectively, where higher Se, Sp, and Acc values correspond to better segmentation performance. From the tables, it can be seen that all of the algorithms converged to similar values in terms of Se, Sp, and Acc for almost all retinal images in the DRIVE and STARE databases.

Table 2.
Se, Sp, and Acc values obtained for 20 retinal images from the DRIVE database.

Table 3.
Se, Sp, and Acc values obtained for 20 retinal images from the STARE database.
When the mean values obtained for the DRIVE images are examined, the performance of the TSA in terms of correctly classified TP pixels seems better than that of the other algorithms due to its highest mean Se value. On the other hand, the highest mean Sp value produced by the GOBC-PA algorithm demonstrates that it is able to produce better performance in terms of correctly classified TN pixels when compared to other algorithms. Finally, the highest mean Acc value obtained for the TSA proves its superior performance in terms of the total number of image pixels that are correctly classified.
From the mean values obtained for the STARE images, it can be seen that the CSA produced the highest performance in terms of the mean Se value, which corresponds to the correctly classified TP pixels. Moreover, the highest mean Sp value obtained for the SCA shows that it produced the best results in terms of correctly classified TN pixels. Finally, the performance of the TSA in terms of correctly classified total image pixels seems better than that of the other algorithms due to its highest mean Acc value.
Another important statistical performance metric for metaheuristic algorithms is the standard deviation, which indicates the ability of an algorithm to reach similar results in each run. In particular, smaller standard deviation values prove the stability and robustness of an algorithm. The standard deviation values of each algorithm obtained for 20 random runs are shown in Figure 7. It can be seen that the GOBC-PA algorithm reached the lowest standard deviation values on both the DRIVE and STARE images. It can be concluded that the GOBC-PA algorithm exhibits somewhat stabler and more robust behavior when compared to other algorithms, although the results were generally similar. It can also be seen that the performance of the TSA and AOA seems to be slightly worse than that of the other algorithms in terms of the standard deviation.
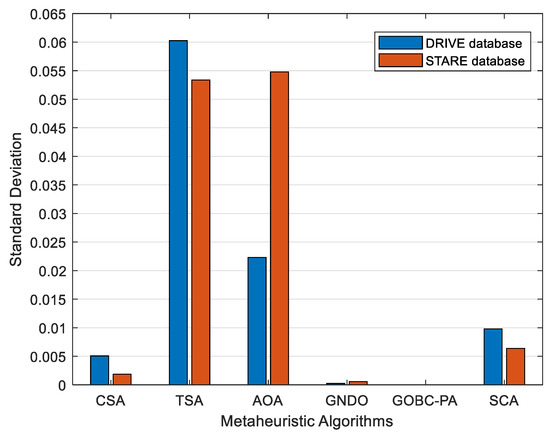
Figure 7.
Standard deviation values obtained for the algorithms.
In order to prove the validity of the numerical results and to establish statistical relationships among the algorithms, the Wilcoxon rank-sum test was applied. In the statistical analyses carried out, the desired accuracy rate was defined as 95%, which corresponds to a significance level of p < 0.05. Table 4 shows the statistically significant differences (p < 0.05) observed between the algorithms. It can be expressed, for both the DRIVE and STARE databases, that the CSA, GNDO, and GOBC-PA algorithms presented significantly better performances than the other algorithms. On the other hand, it can also be expressed that the TSA for the DRIVE database and the TSA and AOA for the STARE database did not produce statistically significant results when compared to the other algorithms.

Table 4.
Wilcoxon rank-sum test results obtained for the algorithms (p < 0.05).
3.3. Convergence Analysis
Convergence speed is one of the most important metrics reflecting the performance of metaheuristic algorithms, indicating the number of cycles at which the algorithm reaches the global solution. Figure 8 demonstrates the convergence speeds obtained in terms of the mean MSE values for 20 random runs. As can be seen from the figure, the performances of the TSA and AOA in terms of convergence speed and mean squared error seem slightly worse than those of the other algorithms. On both databases, the TSA reached its global optimum at approximately cycle 40, while the AOA reaches it at approximately cycle 95. In contrast, the other algorithms reached similar MSE values at close convergence rates on both the DRIVE and STARE images.
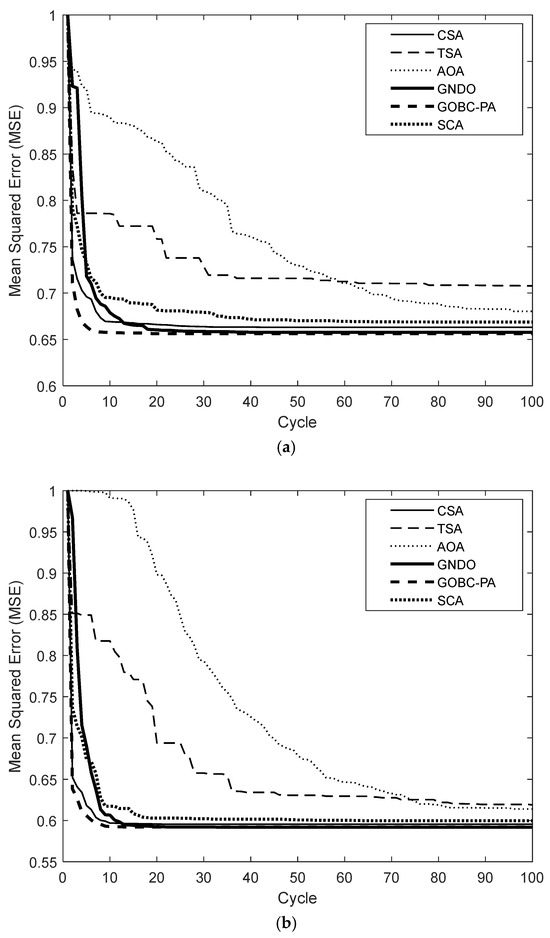
In addition to the convergence speed, the CPU time required for each algorithm to reach the global solution is another important parameter. Analyses were carried out using a computer with a 3.4 GHz Intel i7-6700 CPU, 16 GB RAM, and 64 bit Windows 10 Pro. The minimum MSE values reached by the algorithms and the related CPU times are given in Table 5 for both databases. Evaluating Figure 8 and Table 5 simultaneously, it can be seen that, although they presented a slower rate of convergence, the TSA and AOA produced better results in terms of the CPU time for both databases. Meanwhile, the GNDO and GOBC-PA algorithms produced worse results in terms of the CPU time despite their higher convergence rates.

Table 5.
Performance comparison of the CSA, TSA, AOA, GNDO, GOBC-PA, and SCA implementations on the DRIVE and STARE databases.
Due to the structural differences between the metaheuristic algorithms, the computational complexity of each algorithm was also analyzed in detail. In particular, in order to compare their computational complexities, the algorithms were analyzed in terms of the Number of Function Evaluations (NFEs) metric, which indicates the number of times the objective function is evaluated during the optimization process. In addition to the NFEs for each algorithm, the Elapsed CPU time for NFEs and the Percentage of this time in the total CPU time were also calculated. The results obtained using the NFEs analyses are given in Table 6. As can be seen from the table, the relationship between the NFEs and CPU time values can be defined as linear. However, by analyzing Figure 8 and Table 6 simultaneously, it can be concluded that the NFEs value does not cause an important variation in the minimum MSE values reached.

Table 6.
Performance comparison in terms of the NFEs convergence analysis.
The analysis results can be summarized as follows: for both the DRIVE and STARE databases, all of the algorithms produced similar results in terms of correctly classified and misclassified pixels. The CSA stands out, with its simple algorithm structure, when compared to the other algorithms. Furthermore, the GNDO algorithm stands out, as it does not contain any control parameters, while the GOBC-PA algorithm stands ou as it contains only one control parameter. In general, it can be expressed that all of the considered algorithms provide high performance in terms of segmentation. On the other hand, the Se, Sp, and Acc values obtained for the CSA, TSA, AOA, GNDO, GOBC-PA, and SCA implementations indicate that each algorithm is able to produce effective results in terms of correctly and incorrectly classified vessel and background pixels. However, the performances of the algorithms in terms of Se seem a bit worse when compared to the Sp- and Acc-based performances. The lowest standard deviation values produced by the GOBC-PA algorithm for both the DRIVE and STARE databases prove that this algorithm is stabler and more robust when compared to the other algorithms. On the other hand, the TSA and AOA produced the highest standard deviation values for the DRIVE and STARE databases, respectively. On the DRIVE database, the GOBC-PA algorithm reached the minimum MSE value with the highest convergence speed. However, on the STARE database, the GNDO algorithm reached the lowest error value while the GOBC-PA algorithm exhibited the best performance in terms of convergence speed. Furthermore, for both databases, the worst MSE value was obtained for the TSA, while the worst convergence speed performance was observed for the AOA. Finally, although it produced relatively worse results in terms of other performance metrics, it was found that the TSA had the most effective performance in terms of CPU time.
4. Discussion
In this work, math-inspired metaheuristic algorithms—including the CSA, TSA, AOA, GNDO, GOBC-PA, and SCA—were implemented as clustering approaches for high-accuracy retinal vessel segmentation. Analyses were carried out on both healthy and diseased retinal images from the DRIVE and STARE databases. From the obtained segmentation results, it can be seen that each of the algorithms successfully distinguished the vessel and background pixels of the retinal images. The close and high Se, Sp, and Acc values produced by the algorithms prove the robustness of each algorithm in terms of their statistical performance. In addition, due to the lower standard deviation values of the CSA, GNDO, and GOBC-PA algorithms, it can be concluded that these algorithms are slightly more stable in the context of clustering-based retinal vessel segmentation. Furthermore, according to the results of the Wilcoxon rank-sum test carried out among the algorithms, it can be expressed that the CSA, GNDO, and GOBC-PA algorithms produced statistically better results compared to the TSA, AOA, and SCA. Finally, when the convergence performances of the algorithms were evaluated as a whole, it was found that, despite their higher convergence rates, the GNDO and GOBC-PA algorithms present slightly worse performance in terms of CPU time. It can additionally be expressed that the TSA presented the lowest NFEs rates in both databases compared to the other algorithms. It can consequently be expressed that the considered math-inspired metaheuristic algorithms can successfully be used in the context of biomedical image processing.
When the efficiency of math-inspired metaheuristic algorithms is compared to that of evolutionary-based, swarm-intelligence-based, and physics-based metaheuristic algorithms [52,53], it can be seen that these algorithms are able to produce similar results in terms of retinal vessel segmentation. The MSE, CPU time, and NFEs values obtained using the considered math-inspired metaheuristic algorithms reveal that these algorithms perform well in terms of convergence speed. On the other hand, the Se, Sp, Acc, standard deviation, and Wilcoxon rank-sum test results obtained demonstrate the good statistical performance and robustness of these algorithms. Consequently, it can be expressed that math-inspired metaheuristic algorithms are capable of producing similar performances to other algorithms in the considered context, despite their simpler algorithm structures and lower number of control parameters.
Author Contributions
Conceptualization, M.B.Ç.; methodology, M.B.Ç. and S.A.; software, M.B.Ç.; validation, M.B.Ç. and S.A.; formal analysis, M.B.Ç. and S.A.; investigation, M.B.Ç. and S.A.; writing—original draft preparation, M.B.Ç.; writing—review and editing, M.B.Ç. and S.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors have no relevant financial or non-financial interests to disclose. The authors declare that they have no conflict of interests.
References
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Layeb, A. Tangent search algorithm for solving optimization problems. Neural Comput. Appl. 2022, 34, 8853–8884. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Turky, R.A.; Alghuwainem, S.; Tostado-Véliz, M.; Jurado, F. Circle search algorithm: A geometry-based metaheuristic optimization algorithm. Mathematics 2022, 10, 1626. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Mirjalili, S. Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 224, 113301. [Google Scholar] [CrossRef]
- Pence, I.; Cesmeli, M.S.; Senel, F.A.; Cetisli, B. A new unconstrained global optimization method based on clustering and parabolic approximation. Expert Syst. Appl. 2016, 55, 493–507. [Google Scholar] [CrossRef]
- Gonidakis, D.; Vlachos, A. A new sine cosine algorithm for economic and emission dispatch problems with price penalty factors. J. Inf. Optim. Sci. 2019, 40, 679–697. [Google Scholar] [CrossRef]
- Abdelsalam, A.A. Optimal distributed energy resources allocation for enriching reliability and economic benefits using sine–cosine algorithm. Technol. Econ. Smart Grids Sustain. Energy 2020, 5, 8. [Google Scholar] [CrossRef]
- Babaei, F.; Safari, A. SCA based fractional-order PID controller considering delayed EV aggregators. J. Oper. Autom. Power Eng. 2020, 8, 75–85. [Google Scholar] [CrossRef]
- Mishra, S.; Gupta, S.; Yadav, A. Design and application of controller based on sine–cosine algorithm for load frequency control of power system. In Intelligent Systems Design and Applications; Springer: Cham, Switzerland, 2020; pp. 301–311. [Google Scholar] [CrossRef]
- Algabalawy, M.A.; Abdelaziz, A.Y.; Mekhamer, S.F.; Aleem, S.H.A. Considerations on optimal design of hybrid power generation systems using whale and sine cosine optimization algorithms. J. Electr. Syst. Inf. Technol. 2018, 5, 312–325. [Google Scholar] [CrossRef]
- Bhadoria, A.; Marwaha, S.; Kamboj, V.K. An optimum forceful generation scheduling and unit commitment of thermal power system using sine cosine algorithm. Neural Comput. Appl. 2019, 32, 2785–2814. [Google Scholar] [CrossRef]
- Mirjalili, S.M.; Mirjalili, S.Z.; Saremi, S.; Mirjalili, S. Sine Cosine Algorithm: Theory, Literature Review, and Application in Designing Bend Photonic Crystal Waveguides. In Nature-Inspired Optimizers; Springer: Cham, Switzerland, 2020; pp. 201–217. [Google Scholar]
- Das, S.; Bhattacharya, A.; Chakraborty, A.K. Solution of short-term hydrothermal scheduling using sine cosine algorithm. Soft Comput. 2018, 22, 6409–6427. [Google Scholar] [CrossRef]
- Bhookya, J.; Jatoth, R.K. Optimal FOPID/PID controller parameters tuning for the AVR system based on sine-cosine-algorithm. Evol. Intell. 2019, 12, 725–733. [Google Scholar] [CrossRef]
- Hekimoğlu, B. Sine–cosine algorithm-based optimization for automatic voltage regulator system. Trans. Inst. Meas. Control 2019, 41, 1761–1771. [Google Scholar] [CrossRef]
- Gorripotu, T.S.; Ramana, P.; Sahu, R.K.; Panda, S. Sine cosine optimization based proportional derivative-proportional integral derivative controller for frequency control of hybrid power system. In Computational Intelligence in Data Mining; Springer: Singapore, 2020; pp. 789–797. [Google Scholar] [CrossRef]
- Belazzoug, M.; Touahria, M.; Nouioua, F.; Brahimi, M. An improved sine cosine algorithm to select features for text categorization. J. King Saud Univ. Comput. Inf. Sci. 2020, 32, 454–464. [Google Scholar] [CrossRef]
- Kaur, G.; Dhillon, J.S. Economic power generation scheduling exploiting hill-climbed sine–cosine algorithm. Appl. Soft Comput. 2021, 111, 107690. [Google Scholar] [CrossRef]
- Fan, F.; Chu, S.C.; Pan, J.S.; Yang, Q.; Zhao, H. Parallel sine cosine algorithm for the dynamic deployment in wireless sensor networks. J. Internet Technol. 2021, 22, 499–512. [Google Scholar] [CrossRef]
- Mookiah, S.; Parasuraman, K.; Chandar, S.K. Color image segmentation based on improved sine cosine optimization algorithm. Soft Comput. 2022, 26, 13193–13203. [Google Scholar] [CrossRef]
- Karmouni, H.; Chouiekh, M.; Motahhir, S.; Qjidaa, H.; Jamil, M.O.; Sayyouri, M. Optimization and implementation of a photovoltaic pumping system using the sine–cosine algorithm. Eng. Appl. Artif. Intell. 2022, 114, 105104. [Google Scholar] [CrossRef]
- Jafari, M.; Chaleshtari, M.H.B.; Khoramishad, H.; Altenbach, H. Minimization of thermal stress in perforated composite plate using metaheuristic algorithms WOA, SCA and GA. Compos. Struct. 2023, 304, 116403. [Google Scholar] [CrossRef]
- Chen, D.; Fan, K.; Wang, J.; Lu, H.; Jin, J.; Liu, C. Two-dimensional power allocation scheme for NOMA-based underwater visible light communication systems. Appl. Opt. 2023, 62, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Agushaka, J.O.; Ezugwu, A.E. Advanced arithmetic optimization algorithm for solving mechanical engineering design problems. PLoS ONE 2021, 16, e0255703. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. Improved multi-core arithmetic optimization algorithm-based ensemble mutation for multidisciplinary applications. Intell. Manuf. 2022, 34, 1833–1874. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B. Improved arithmetic optimization algorithm and its application to discrete structural optimization. Structures 2022, 35, 748–764. [Google Scholar] [CrossRef]
- Khodadadi, N.; Snasel, V.; Mirjalili, S. Dynamic arithmetic optimization algorithm for truss optimization under natural frequency constraints. IEEE Access 2022, 10, 16188–16208. [Google Scholar] [CrossRef]
- Gürses, D.; Bureerat, S.; Sait, S.M.; Yıldız, A.R. Comparison of the arithmetic optimization algorithm, the slime mold optimization algorithm, the marine predators algorithm, the salp swarm algorithm for real-world engineering applications. Mater. Test. 2021, 63, 448–452. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Du, B.; Wei, G. An enhanced hybrid arithmetic optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 394, 114901. [Google Scholar] [CrossRef]
- Issa, M. Enhanced arithmetic optimization algorithm for parameter estimation of PID controller. Arab. J. Sci. Eng. 2023, 48, 2191–2205. [Google Scholar] [CrossRef]
- Abualigah, L.; Almotairi, K.H.; Al-qaness, M.A.; Ewees, A.A.; Yousri, D.; Abd Elaziz, M.; Nadimi-Shahraki, M.H. Efficient text document clustering approach using multi-search Arithmetic Optimization Algorithm. Knowl.-Based Syst. 2022, 248, 108833. [Google Scholar] [CrossRef]
- Rajagopal, R.; Karthick, R.; Meenalochini, P.; Kalaichelvi, T. Deep Convolutional Spiking Neural Network optimized with Arithmetic optimization algorithm for lung disease detection using chest X-ray images. Biomed. Signal Process. Control 2023, 79, 104197. [Google Scholar] [CrossRef]
- Antarasee, P.; Premrudeepreechacharn, S.; Siritaratiwat, A.; Khunkitti, S. Optimal Design of Electric Vehicle Fast-Charging Station’s Structure Using Metaheuristic Algorithms. Sustainability 2022, 15, 771. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, P.; Wang, J.; Zhang, L. Ensemble system for short term carbon dioxide emissions forecasting based on multi-objective tangent search algorithm. J. Environ. Manag. 2022, 302, 113951. [Google Scholar] [CrossRef]
- Akyol, S. A new hybrid method based on Aquila optimizer and tangent search algorithm for global optimization. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 8045–8065. [Google Scholar] [CrossRef] [PubMed]
- Pachung, P.; Bansal, J.C. An improved tangent search algorithm. MethodsX 2022, 9, 101839. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Basset, M.; Mohamed, R.; El-Fergany, A.; Abouhawwash, M.; Askar, S.S. Parameters identification of PV triple-diode model using improved generalized normal distribution algorithm. Mathematics 2021, 9, 995. [Google Scholar] [CrossRef]
- Khodadadi, N.; Mirjalili, S. Truss optimization with natural frequency constraints using generalized normal distribution optimization. Appl. Intell. 2022, 52, 10384–10397. [Google Scholar] [CrossRef]
- Chankaya, M.; Hussain, I.; Ahmad, A.; Malik, H.; García Márquez, F.P. Generalized normal distribution algorithm-based control of 3-phase 4-wire grid-tied PV-hybrid energy storage system. Energies 2021, 14, 4355. [Google Scholar] [CrossRef]
- Pençe, İ.; Çeşmeli, M.Ş.; Kovacı, R. Determination of the Osmotic Dehydration Parameters of Mushrooms using Constrained Optimization. Sci. J. Mehmet Akif Ersoy Univ. 2019, 2, 77–83. [Google Scholar]
- Pençe, İ.; Çeşmeli, M.Ş.; Kovacı, R. A New Stochastic Search Method for Filled Function. El-Cezeri J. Sci. Eng. 2020, 7, 111–123. [Google Scholar] [CrossRef]
- Kishore, D.J.K.; Mohamed, M.R.; Sudhakar, K.; Peddakapu, K. Application of circle search algorithm for solar PV maximum power point tracking under complex partial shading conditions. Appl. Soft Comput. 2024, 165, 112030. [Google Scholar] [CrossRef]
- Ghazi, G.A.; Ammar Hasanien, H.M.; Ko, W.; Lee, S.M.; Turky, R.; Veliz, M.T.; Jurado, F. Circle search algorithm-based super twisting sliding mode control for MPPT of different commercial PV modules. IEEE Access 2024, 12, 33109–33128. [Google Scholar] [CrossRef]
- Saeed, A.; Soomro, T.A.; Jandan, N.A.; Ali, A.; Irfan, M.; Rahman, S.; Aldhabaan, W.A.; Khairallah, A.S.; Abuallut, I. Impact of retinal vessel image coherence on retinal blood vessel segmentation. Electronics 2023, 12, 396. [Google Scholar] [CrossRef]
- Xian, Y.; Zhao, G.; Wang, C.; Chen, X.; Dai, Y. A novel hybrid retinal blood vessel segmentation algorithm for enlarging the measuring range of dual-wavelength retinal oximetry. Photonics 2023, 10, 722. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H. A novel single-sample retinal vessel segmentation method based on grey relational analysis. Sensors 2024, 24, 4326. [Google Scholar] [CrossRef]
- Jiang, L.; Li, W.; Xiong, Z.; Yuan, G.; Huang, C.; Xu, W.; Zhou, L.; Qu, C.; Wang, Z.; Tong, Y. Retinal vessel segmentation based on self-attention feature selection. Electronics 2024, 13, 3514. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, S.; Jia, J. PAM-UNet: Enhanced retinal vessel segmentation using a novel plenary attention mechanism. Appl. Sci. 2024, 14, 5382. [Google Scholar] [CrossRef]
- Ramesh, R.; Sathiamoorthy, S. Diabetic retinopathy classification using improved metaheuristics with deep residual network on fundus imaging. Multimed. Tools Appl. 2024, 1–27. [Google Scholar] [CrossRef]
- Sau, P.C.; Gupta, M.; Bansal, A. Optimized ResUNet++-enabled blood vessel segmentation for retinal fundus image based on hybrid meta-heuristic improvement. Int. J. Image Graph. 2024, 24, 2450033. [Google Scholar] [CrossRef]
- Çetinkaya, M.B.; Duran, H. Performance comparison of most recently proposed evolutionary, swarm intelligence, and physics-based metaheuristic algorithms for retinal vessel segmentation. Math. Probl. Eng. 2022, 2022, 4639208. [Google Scholar] [CrossRef]
- Çetinkaya, M.B.; Duran, H. A detailed and comparative work for retinal vessel segmentation based on the most effective heuristic approaches. Biomed. Eng. Biomed. Tech. 2021, 66, 181–200. [Google Scholar] [CrossRef]
- Alonso-Montes, C.; Vilariño, D.L.; Dudek, P.; Penedo, M.G. Fast retinal vessel tree extraction: A pixel parallel approach. Int. J. Circuit Theory Appl. 2008, 36, 641–651. [Google Scholar] [CrossRef]
- Hoover, A.D.; Kouznetsova, V.; Goldbaum, M. Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response. IEEE Trans. Med. Imaging 2000, 19, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Arcuri, A.; Briand, L. A hitchhiker’s guide to statistical tests for assessing randomized algorithms in software engineering. Softw. Test. Verif. Reliab. 2014, 24, 219–250. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).