A Supernet-Only Framework for Federated Learning in Computationally Heterogeneous Scenarios
Abstract
1. Introduction
2. Background and Related Work
2.1. Federated Learning
2.2. Neural Architecture Search
2.3. Federated Neural Architecture Search (Fed-NAS)
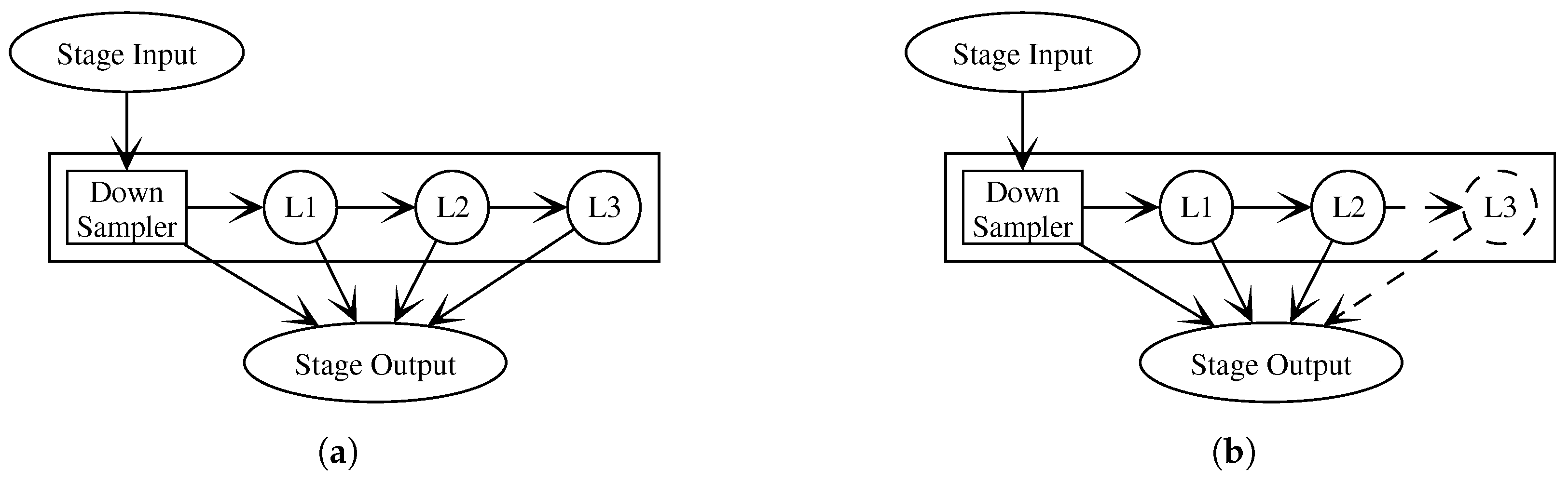
3. Method
3.1. Reinterpret Approach
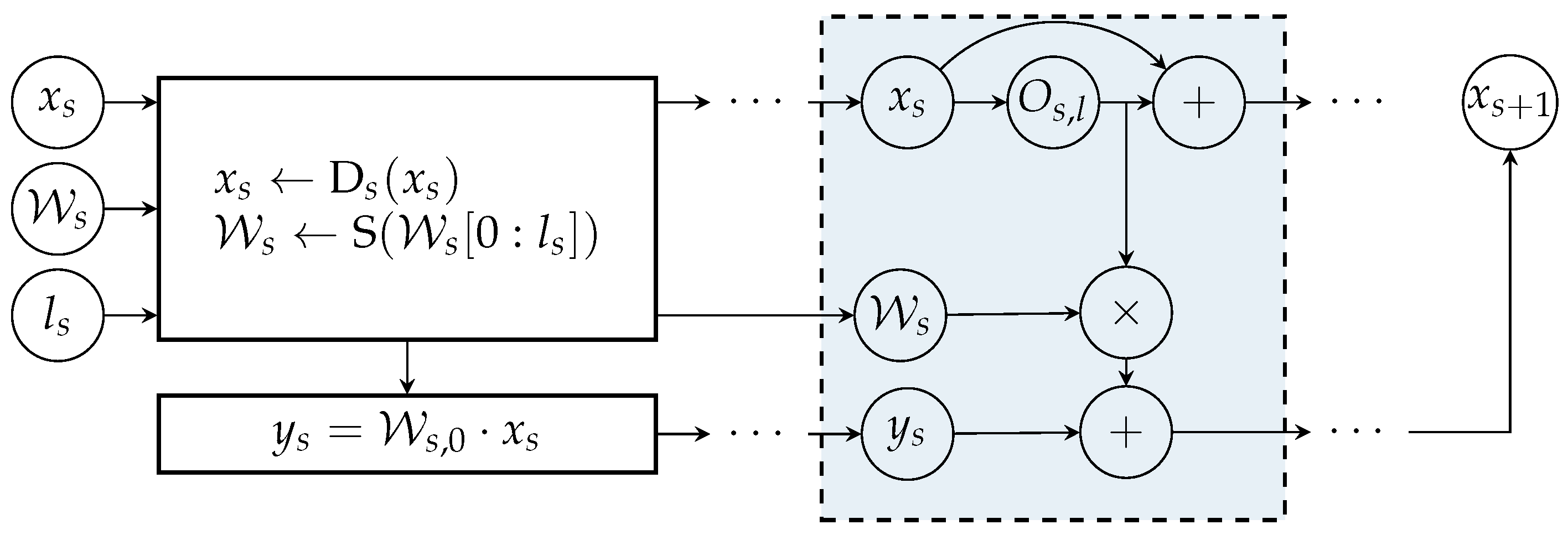
| Algorithm 1 Supernet forward algorithm |
| Require: Input: x, Truncation lengthes: L, Network: Each stage contains: - - Weight parameters - Nonlinear transformations Ensure: y
|
3.2. Training Pipeline
4. Experiments
4.1. Evaluation of Supernet-Only Framework
- Max Trainable: The largest sub-network that all clients can train is used as the federated model, equivalent to traditional FL.
- Max Runnable: The smallest sub-network that all clients can use for inference is selected as the federated model. Clients unable to train only perform inference, while capable clients participate in training.
- No Federated: Each client uses the strongest sub-network it can support without FL.
- Grouped: Clients are divided into three different scale categories, with each group using the largest sub-network it can support for federated learning.
- Peaches: The cells of sub-network are separated into private cells and public ones. Only public cells are shared among the federal model.
4.1.1. Evaluation of the Supernet-Only Framework Under Ring-Based Federated Learning
4.1.2. Evaluation of the Supernet-Only Framework Under Federated Averaging (FedAvg)
4.1.3. Evaluation of the Supernet-Only Framework Under FedAvg with Small Backbone
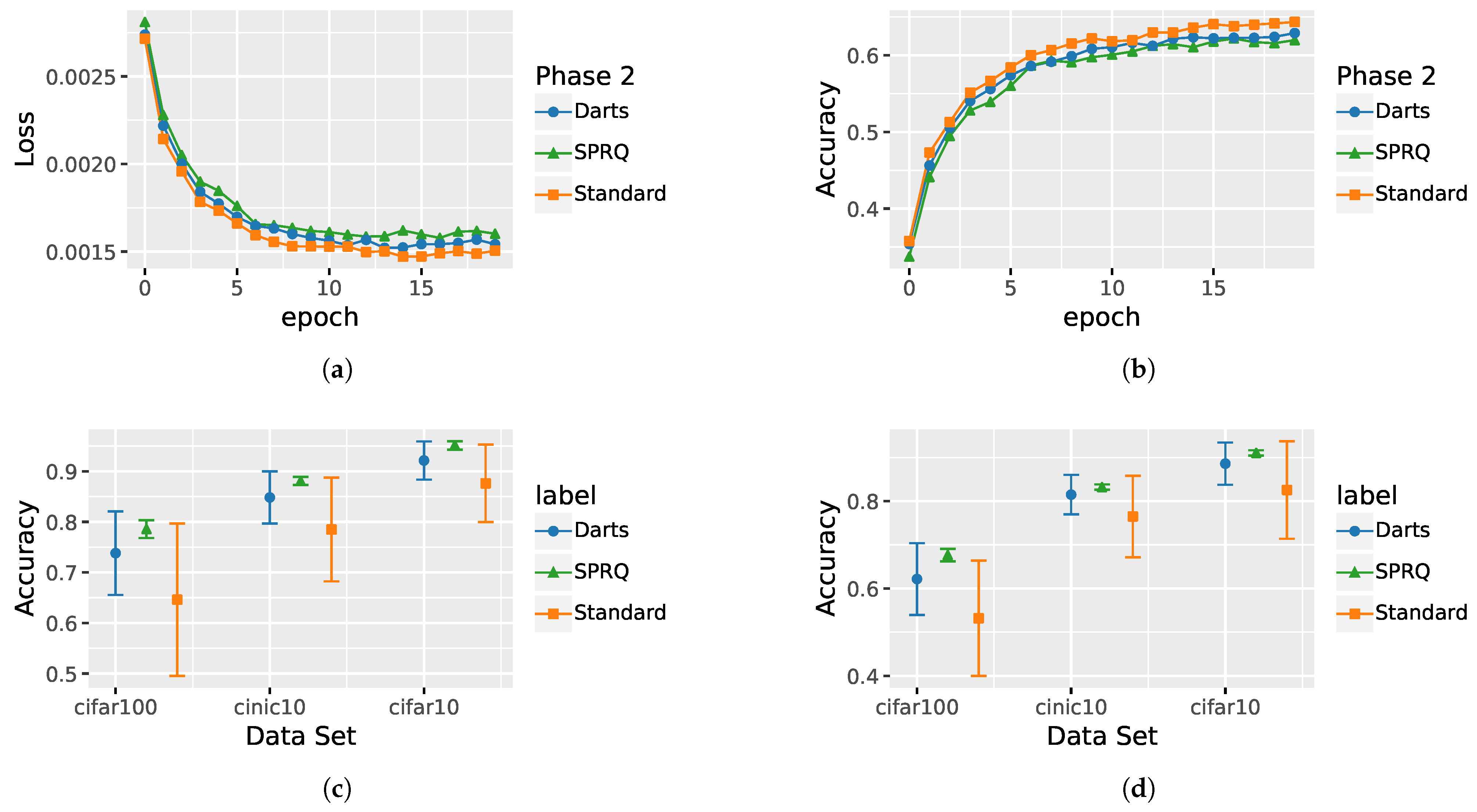
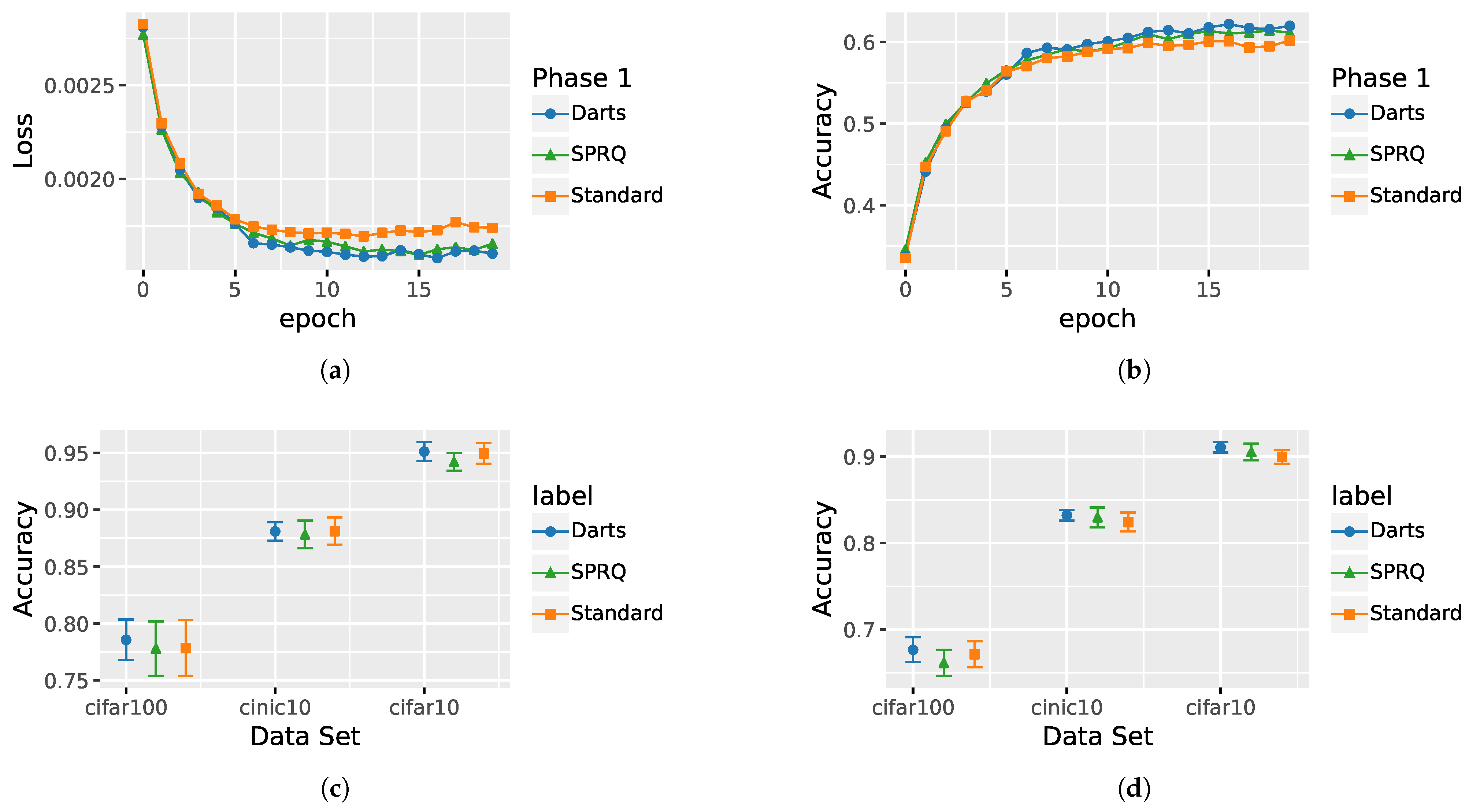
4.2. Evaluation of the Training Pipeline
- Normal: In this set, we pretrain the supernet using conventional network training methods and common optimizers, treating architecture parameters as regular network parameters.
- DARTS: In this set, we use the two-step optimization method from DARTS [7], alternately training weights and architecture parameters on training and validation datasets.
- SPRQ: In this set, we generate sub-networks by randomly skipping layers during pretraining to simulate client diversity and computational constraints (detailed in Section 3.2).
4.2.1. Evaluation of the Main Pretraining Phase
4.2.2. Evaluation of Warm-Up Phase
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IoT | Internet of Things |
| IID | Independent and Identically Distributed |
| FL | Federated Learning |
| non-IID | non-Independent and Identically Distributed |
| NAS | Neural Architecture Search |
| Fed-NAS | Federated Neural Architecture Search |
| SPRQ | Single-Path Random Quit |
| DARTS | Differentiable ARchiTecture Search |
References
- Aouedi, O.; Vu, T.H.; Sacco, A.; Nguyen, D.C.; Piamrat, K.; Marchetto, G.; Pham, Q.V. A survey on intelligent Internet of Things: Applications, security, privacy, and future directions. IEEE Commun. Surv. Tutor. 2024, 27, 1238–1292. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, Z.; Lan, Y.; Cui, Z.; Cai, J.; Zhang, W. A survey on federated learning: Challenges and applications. Int. J. Mach. Learn. Cybern. 2023, 14, 513–535. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.I.; Galindo, M.; Xie, H.; Wong, L.K.; Shuai, H.H.; Li, Y.H.; Cheng, W.H. Lightweight Deep Learning for Resource-Constrained Environments: A Survey. ACM Comput. Surv. 2024, 56, 267. [Google Scholar] [CrossRef]
- Heuillet, A.; Nasser, A.; Arioui, H.; Tabia, H. Efficient automation of neural network design: A survey on differentiable neural architecture search. ACM Comput. Surv. 2024, 56, 1–36. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, H.; Jin, Y. From federated learning to federated neural architecture search: A survey. Complex Intell. Syst. 2021, 7, 639–657. [Google Scholar] [CrossRef]
- Xu, G.; Wang, X.; Wu, X.; Leng, X.; Xu, Y. Development of residual learning in deep neural networks for computer vision: A survey. Eng. Appl. Artif. Intell. 2025, 142, 109890. [Google Scholar] [CrossRef]
- Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable architecture search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning multiple layers of features from tiny images. In Handbook of Systemic Autoimmune Diseases; Technical Report; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Darlow, L.N.; Crowley, E.J.; Antoniou, A.; Storkey, A.J. Cinic-10 is not imagenet or cifar-10. arXiv 2018, arXiv:1810.03505. [Google Scholar]
- Jia, C.; Hu, M.; Chen, Z.; Yang, Y.; Xie, X.; Liu, Y.; Chen, M. AdaptiveFL: Adaptive heterogeneous federated learning for resource-constrained AIoT systems. In Proceedings of the 61st ACM/IEEE Design Automation Conference, Francisco, CA, USA, 23–27 June 2024; pp. 1–6. [Google Scholar]
- Lee, J.W.; Oh, J.; Lim, S.; Yun, S.Y.; Lee, J.G. Tornadoaggregate: Accurate and scalable federated learning via the ring-based architecture. arXiv 2020, arXiv:2012.03214. [Google Scholar]
- Konečnỳ, J.; McMahan, H.B.; Ramage, D.; Richtárik, P. Federated optimization: Distributed machine learning for on-device intelligence. arXiv 2016, arXiv:1610.02527. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Diao, E.; Ding, J.; Tarokh, V. Heterofl: Computation and communication efficient federated learning for heterogeneous clients. arXiv 2020, arXiv:2010.01264. [Google Scholar]
- Kim, M.; Yu, S.; Kim, S.; Moon, S.M. Depthfl: Depthwise federated learning for heterogeneous clients. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Ilhan, F.; Su, G.; Liu, L. Scalefl: Resource-adaptive federated learning with heterogeneous clients. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 24532–24541. [Google Scholar]
- Han, Y.; Huang, G.; Song, S.; Yang, L.; Wang, H.; Wang, Y. Dynamic Neural Networks: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7436–7456. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Howard, A.G. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Wu, B.; Dai, X.; Zhang, P.; Wang, Y.; Sun, F.; Wu, Y.; Tian, Y.; Vajda, P.; Jia, Y.; Keutzer, K. Fbnet: Hardware-aware efficient convnet design via differentiable neural architecture search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10734–10742. [Google Scholar]
- Guo, Z.; Zhang, X.; Mu, H.; Heng, W.; Liu, Z.; Wei, Y.; Sun, J. Single path one-shot neural architecture search with uniform sampling. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 544–560. [Google Scholar]
- Khan, S.; Rizwan, A.; Khan, A.N.; Ali, M.; Ahmed, R.; Kim, D.H. A multi-perspective revisit to the optimization methods of Neural Architecture Search and Hyper-parameter optimization for non-federated and federated learning environments. Comput. Electr. Eng. 2023, 110, 108867. [Google Scholar] [CrossRef]
- Pan, Z.; Hu, L.; Tang, W.; Li, J.; He, Y.; Liu, Z. Privacy-Preserving Multi-Granular Federated Neural Architecture Search—A General Framework. IEEE Trans. Knowl. Data Eng. 2021, 35, 2975–2986. [Google Scholar] [CrossRef]
- Yuan, J.; Xu, M.; Zhao, Y.; Bian, K.; Huang, G.; Liu, X.; Wang, S. Federated neural architecture search. arXiv 2020, arXiv:2002.06352. [Google Scholar]
- Laskaridis, S.; Fernandez-Marques, J.; Dudziak, Ł. Cross-device Federated Architecture Search. In Proceedings of the Workshop on Federated Learning: Recent Advances and New Challenges (in Conjunction with NeurIPS 2022), New Orleans, LA, USA, 2 December 2022. [Google Scholar]
- Liu, J.; Yan, J.; Xu, H.; Wang, Z.; Huang, J.; Xu, Y. Finch: Enhancing federated learning with hierarchical neural architecture search. IEEE Trans. Mob. Comput. 2023, 23, 6012–6026. [Google Scholar] [CrossRef]
- Yu, S.; Muñoz, J.P.; Jannesari, A. Resource-Aware Heterogeneous Federated Learning with Specialized Local Models. In Proceedings of the European Conference on Parallel Processing, Madrid, Spain, 26–30 August 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 389–403. [Google Scholar]
- Khare, A.; Agrawal, A.; Annavajjala, A.; Behnam, P.; Lee, M.; Latapie, H.; Tumanov, A. SuperFedNAS: Cost-Efficient Federated Neural Architecture Search for On-device Inference. In Proceedings of the European Conference on Computer Vision, Shanghai, China, 1–2 January 2025; Springer: Berlin/Heidelberg, Germany, 2025; pp. 161–179. [Google Scholar]
- Hoang, M.; Kingsford, C. Personalized neural architecture search for federated learning. In Proceedings of the 1st NeurIPS Workshop on New Frontiers in Federated Learning (NFFL 2021), Virtual, 13 December 2021. [Google Scholar]
- Yan, J.; Liu, J.; Xu, H.; Wang, Z.; Qiao, C. Peaches: Personalized federated learning with neural architecture search in edge computing. IEEE Trans. Mob. Comput. 2024, 23, 10296–10312. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]
- Lin, H.; Jegelka, S. Resnet with one-neuron hidden layers is a universal approximator. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; Volume 31. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Laskaridis, S.; Kouris, A.; Lane, N.D. Adaptive Inference through Early-Exit Networks: Design, Challenges and Directions. In Proceedings of the 5th International Workshop on Embedded and Mobile Deep Learning, EMDL’21, New York, NY, USA, 25 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A stochastic approximation method. In The Annals of Mathematical Statistics; Institute of Mathematical Statistics: Hayward, CA, USA, 1951; pp. 400–407. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the Convergence of Adam and Beyond. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Rattray, M.; Saad, D.; Amari, S.i. Natural gradient descent for on-line learning. Phys. Rev. Lett. 1998, 81, 5461. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Loizou, N.; Vaswani, S.; Hadj Laradji, I.; Lacoste-Julien, S. Stochastic Polyak Step-Size for SGD: An Adaptive Learning Rate for Fast Convergence. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics, Virtual, 13–15 April 2021; Volume 130, pp. 1306–1314. [Google Scholar]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.u.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Yang, J.; Shi, R.; Ni, B. MedMNIST Classification Decathlon: A Lightweight AutoML Benchmark for Medical Image Analysis. In Proceedings of the IEEE 18th International Symposium on Biomedical Imaging (ISBI), Nice, France, 13–16 April 2021; pp. 191–195. [Google Scholar]
- Foley, P.; Sheller, M.J.; Edwards, B.; Pati, S.; Riviera, W.; Sharma, M.; Moorthy, P.N.; Wang, S.H.; Martin, J.; Mirhaji, P.; et al. OpenFL: The open federated learning library. Phys. Med. Biol. 2022, 67, 214001. [Google Scholar] [CrossRef] [PubMed]
- Caldas, S.; Duddu, S.M.K.; Wu, P.; Li, T.; Konečnỳ, J.; McMahan, H.B.; Smith, V.; Talwalkar, A. Leaf: A benchmark for federated settings. arXiv 2018, arXiv:1812.01097. [Google Scholar]

| Dataset | CIFAR-100 | CIFAR-10 | CINIC-10 |
|---|---|---|---|
| Supernet-Only | |||
| Max Trainable | |||
| Max Runnable | |||
| No Federated | |||
| Grouped | |||
| Peaches |
| Dataset | CIFAR-100 | CIFAR-10 | CINIC-10 |
|---|---|---|---|
| Supernet-Only | |||
| Max Trainable | |||
| Max Runnable | |||
| No Federated | |||
| Grouped | |||
| Peaches |
| Dataset | CIFAR-100 | CIFAR-10 | CINIC-10 |
|---|---|---|---|
| Supernet-Only | |||
| Max Trainable | |||
| Max Runnable | |||
| No Federated | |||
| Grouped | |||
| Peaches |
| Dataset | Compared to | W | Z | Raw p | Corr. p | r |
|---|---|---|---|---|---|---|
| CIFAR-10 | Max Runnable | 30 | −7.57 | 1.08 × | 2.17 × | 0.85 |
| Max Trainable | 1986 | −5.09 | 9.43 × | 1.89 × | 0.45 | |
| CIFAR-100 | Max Runnable | 159 | −6.94 | 1.41 × | 2.82 × | 0.78 |
| Max Trainable | 959 | −7.54 | 9.35 × | 1.87 × | 0.67 | |
| CINIC-10 | Max Runnable | 8 | −7.68 | 3.30 × | 6.61 × | 0.86 |
| Max Trainable | 920 | −7.63 | 2.54 × | 5.08 × | 0.67 |
| Dataset | CIFAR-100 | CIFAR-10 | CINIC-10 |
|---|---|---|---|
| Supernet-Only (pretrained) | |||
| Supernet-Only (not pretrained) | |||
| AdaptiveFL |
| Dataset | AdaptiveFL | Supernet Only | ||
|---|---|---|---|---|
| Best | Full | Best | Max | |
| CIFAR-100 | ||||
| CIFAR-10 | ||||
| CINIC-10 | ||||
| DARTS | Standard | SPRQ | |
|---|---|---|---|
| Time Spent (h) | 25.40 | 25.66 | 19.34 |
| Method | Maximize Federation | Maximize Computation | Full Sharing |
|---|---|---|---|
| Supernet-Only | ✔ | ✔ | ✔ |
| Max Trainable | ✔ | ✔ | |
| Max Runnable | ✔ | ||
| No Federated | ✔ | ||
| Grouped | ✔ | ||
| Peaches | ✔ | ✔ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Chen, D.; Zhong, C. A Supernet-Only Framework for Federated Learning in Computationally Heterogeneous Scenarios. Appl. Sci. 2025, 15, 5666. https://doi.org/10.3390/app15105666
Chen Y, Chen D, Zhong C. A Supernet-Only Framework for Federated Learning in Computationally Heterogeneous Scenarios. Applied Sciences. 2025; 15(10):5666. https://doi.org/10.3390/app15105666
Chicago/Turabian StyleChen, Yu, Danyang Chen, and Cheng Zhong. 2025. "A Supernet-Only Framework for Federated Learning in Computationally Heterogeneous Scenarios" Applied Sciences 15, no. 10: 5666. https://doi.org/10.3390/app15105666
APA StyleChen, Y., Chen, D., & Zhong, C. (2025). A Supernet-Only Framework for Federated Learning in Computationally Heterogeneous Scenarios. Applied Sciences, 15(10), 5666. https://doi.org/10.3390/app15105666






