An Investigation of the Promotion of the Aerodynamic Performance of a Supersonic Compressor Cascade Using a Local Negative-Curvature Ramp
Abstract
1. Introduction
2. Geometric Model
2.1. Baseline Supersonic Compressor Cascade
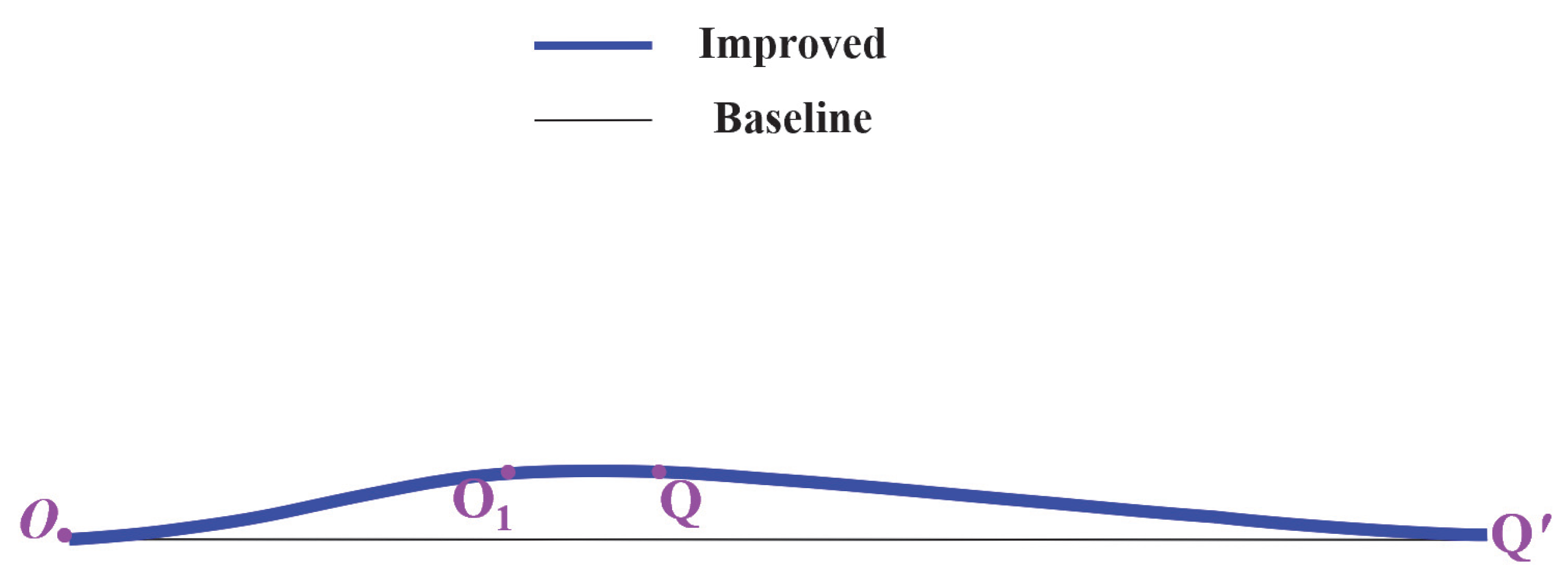
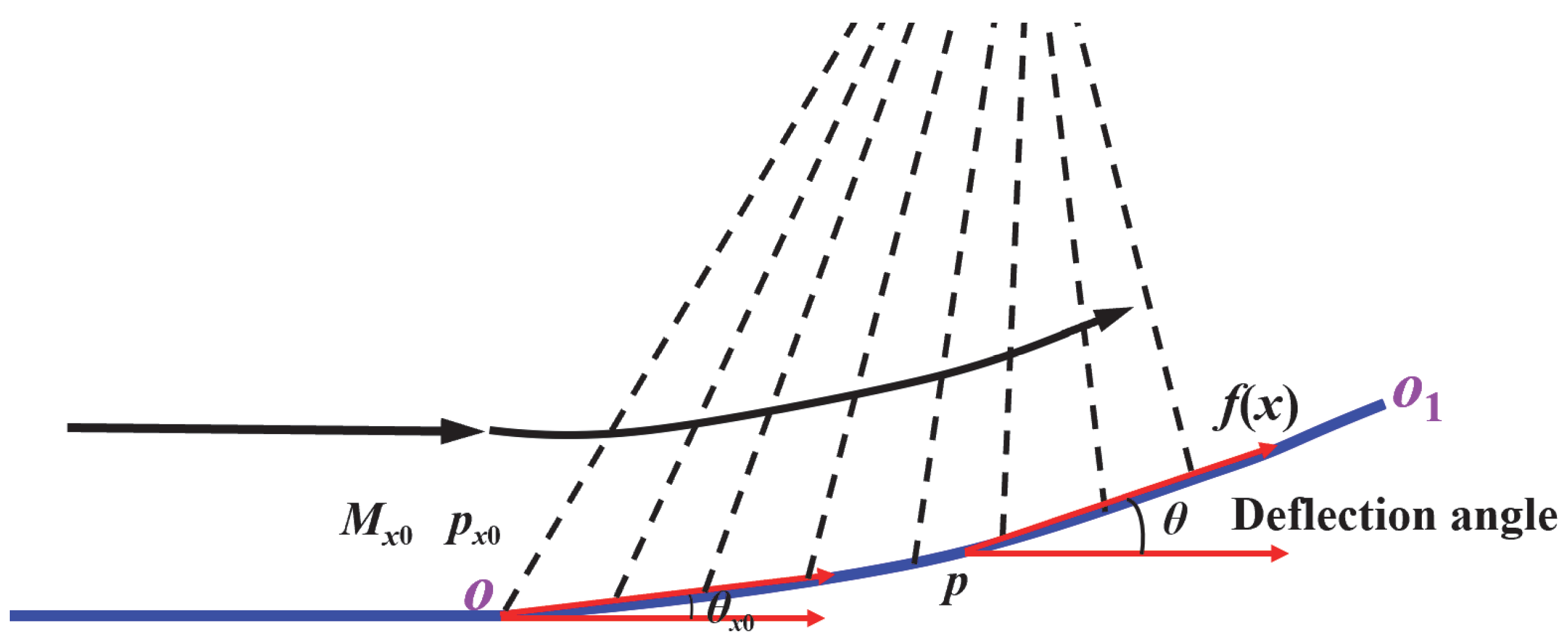
2.2. Modified Supersonic Compressor Cascade
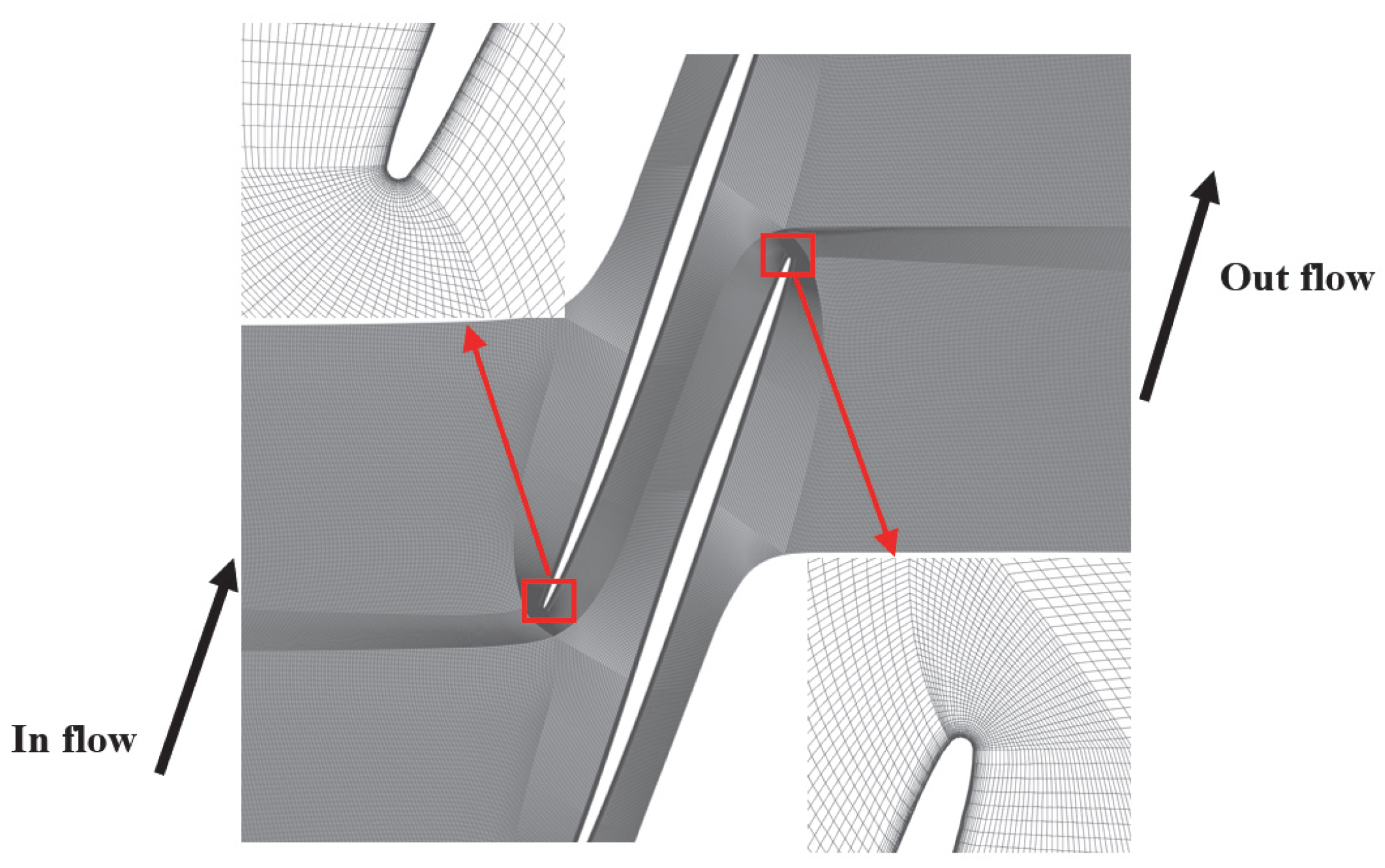
3. Experimental Facility and Numerical Validation
3.1. Experimental Facility
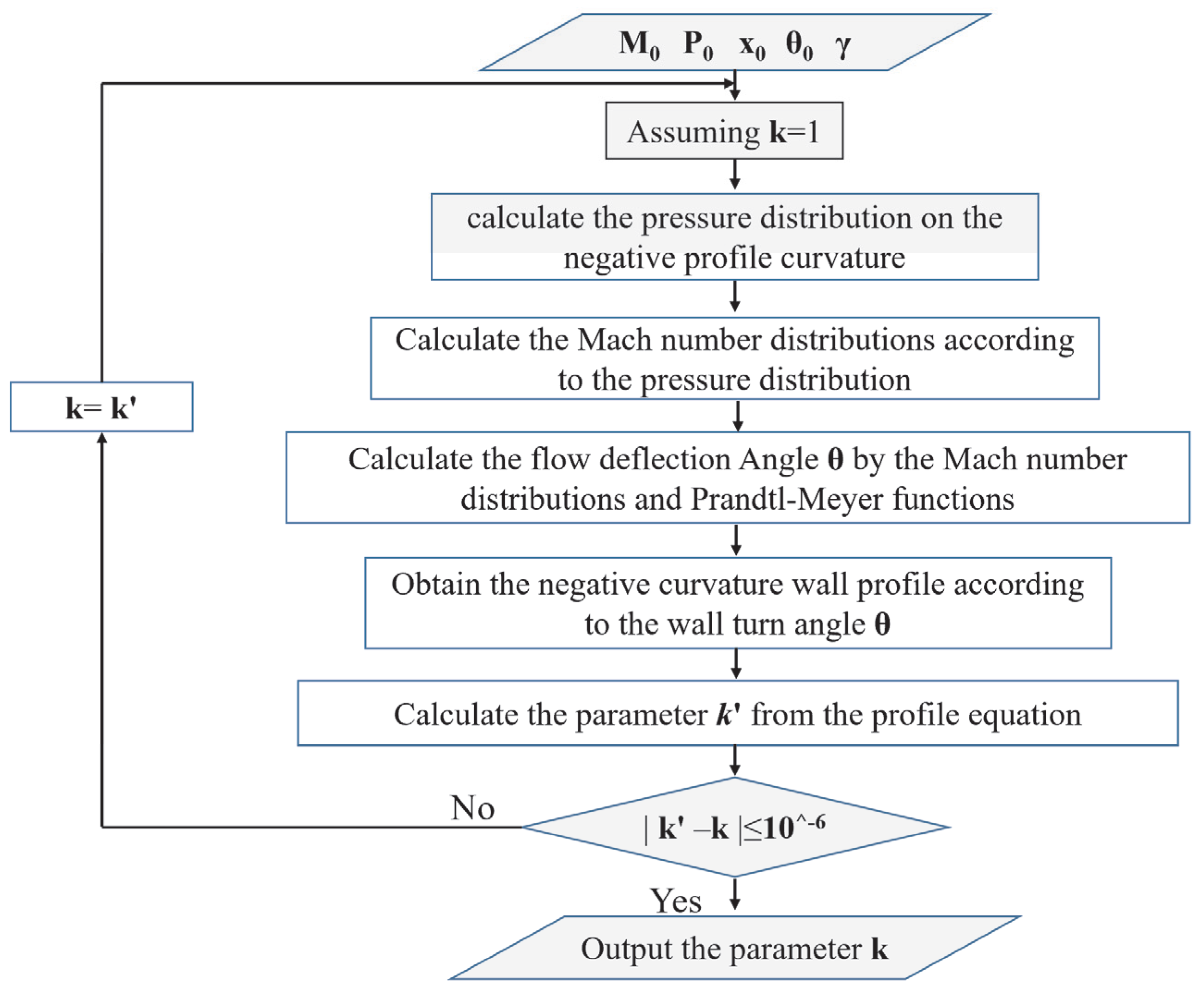
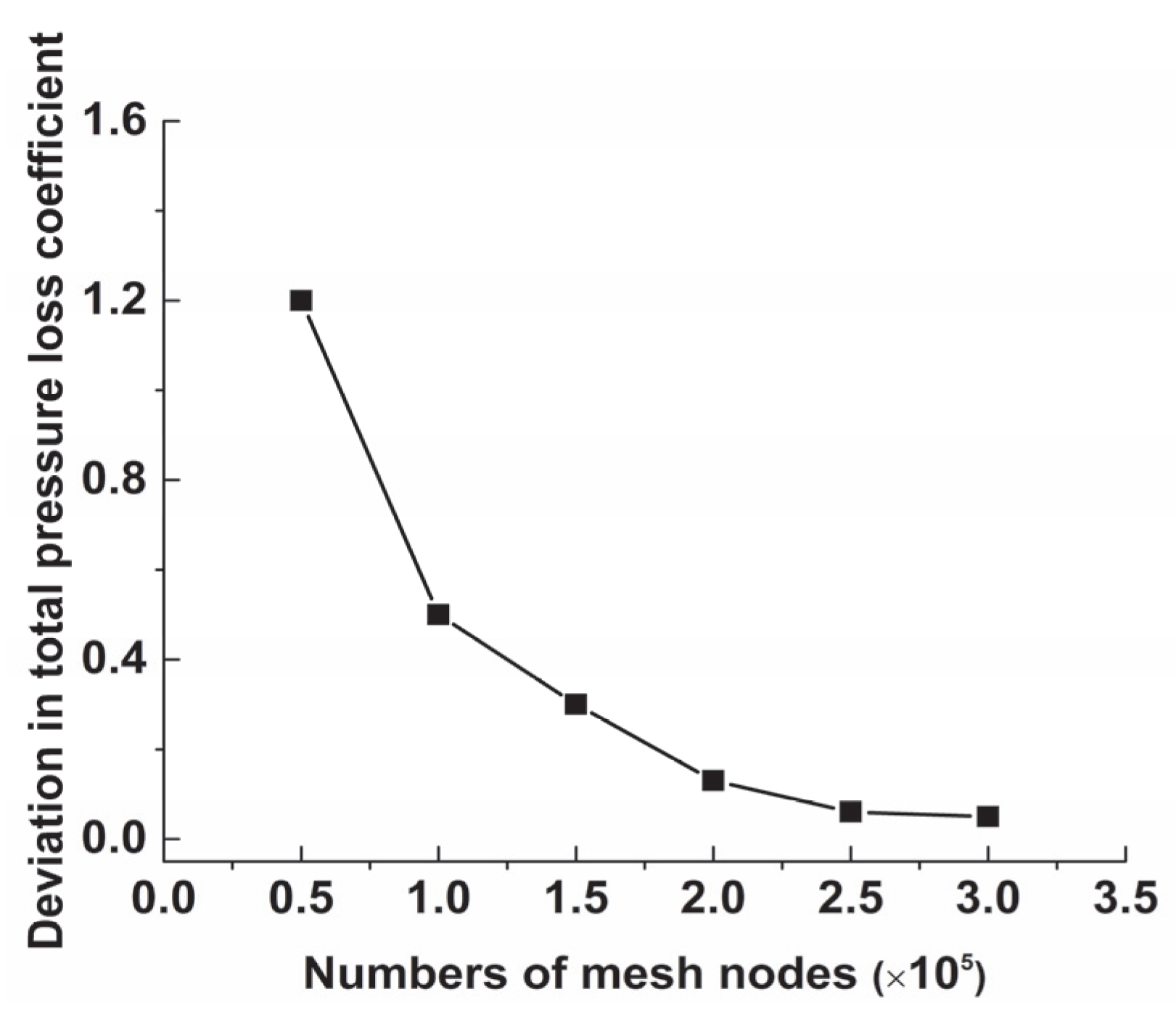
3.2. Numerical Calculation Method
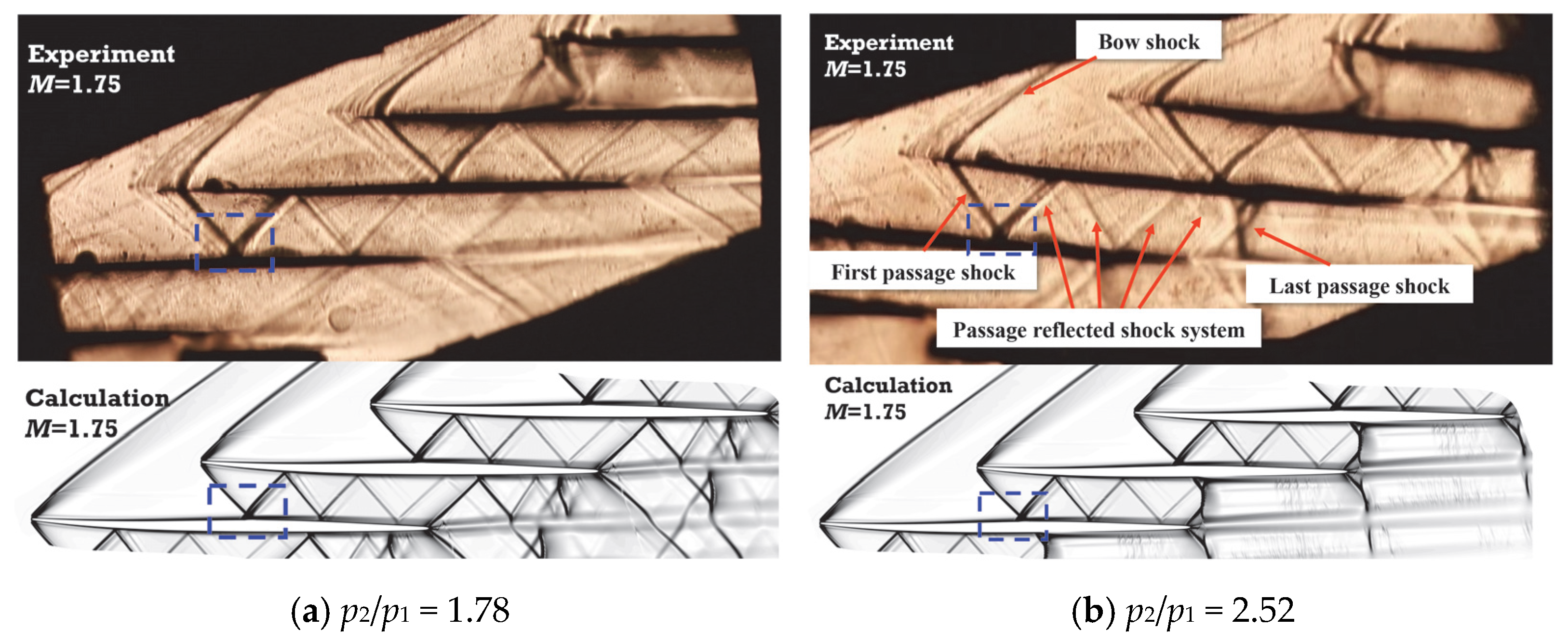
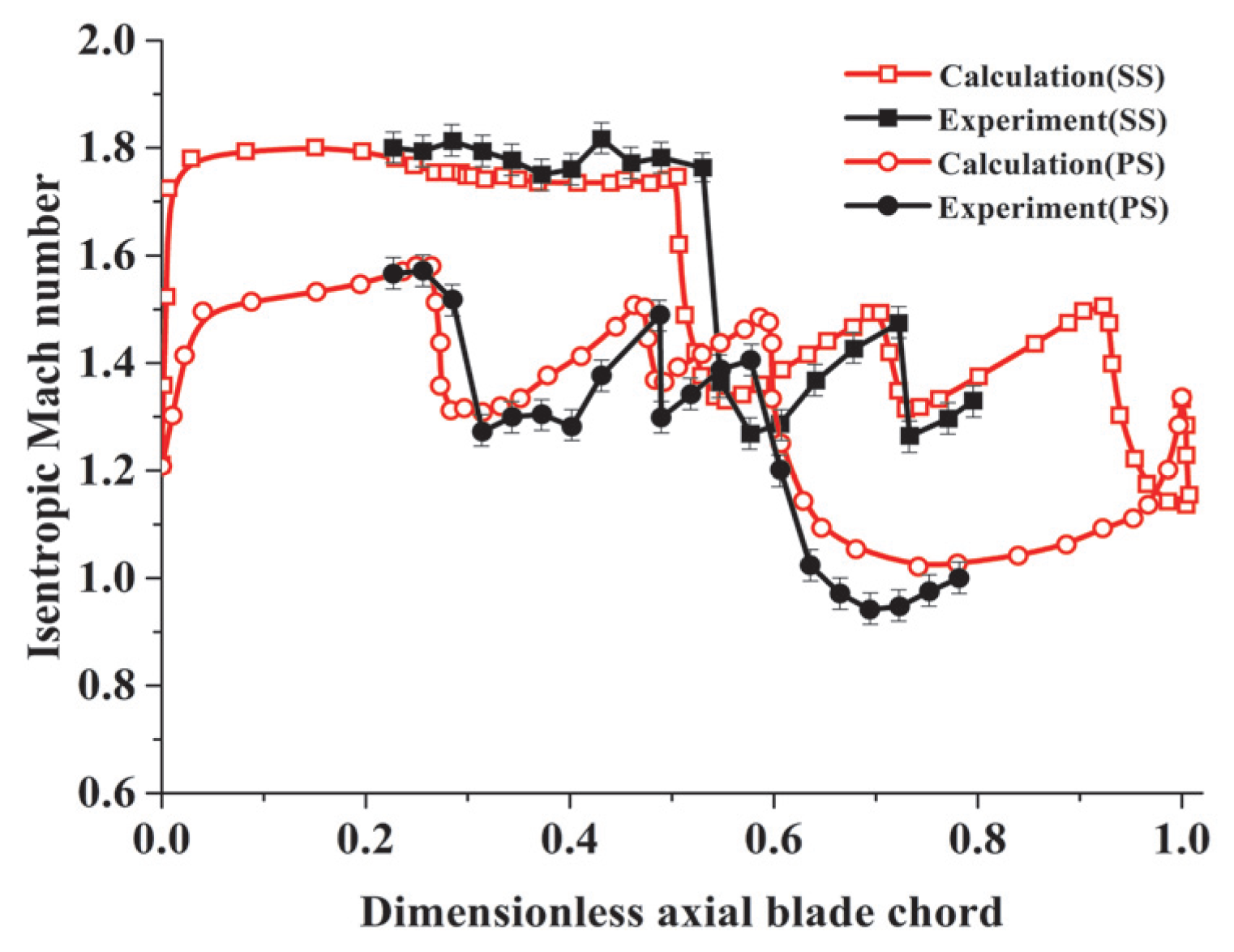
3.3. General Flow Characteristics and Numerical Validation
4. Analyses of Numerical Simulation Results
4.1. Flow Physics on Aerodynamic Performance Under Design Conditions
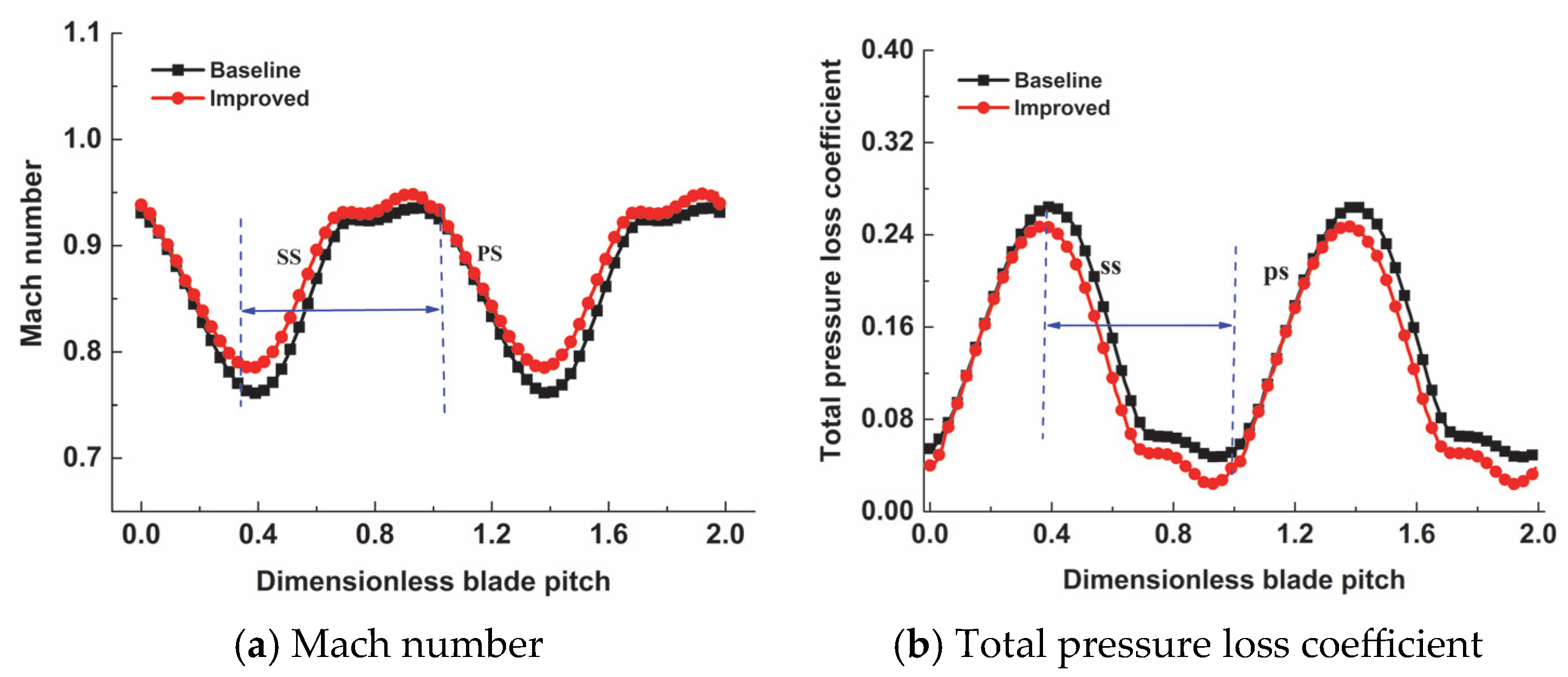
4.1.1. Aerodynamic Performance
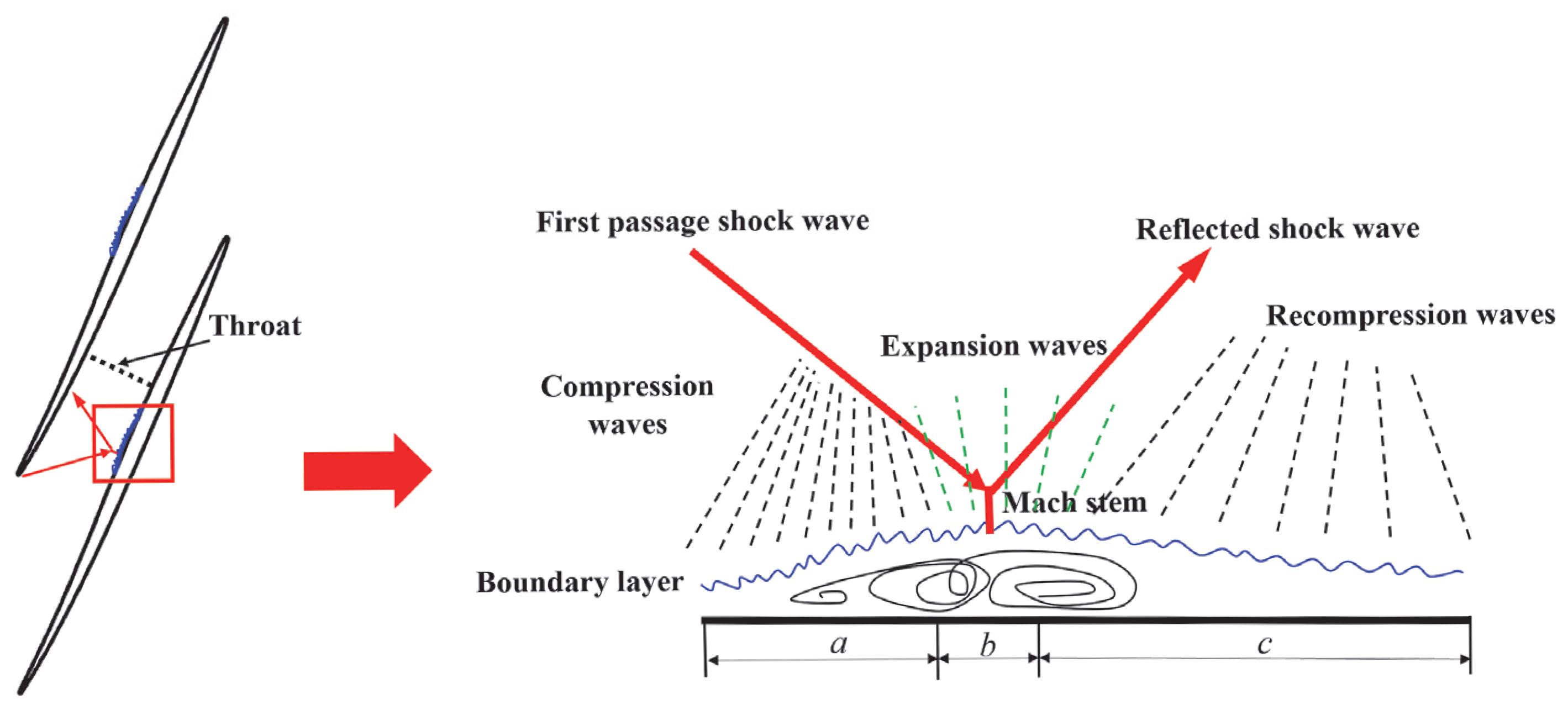
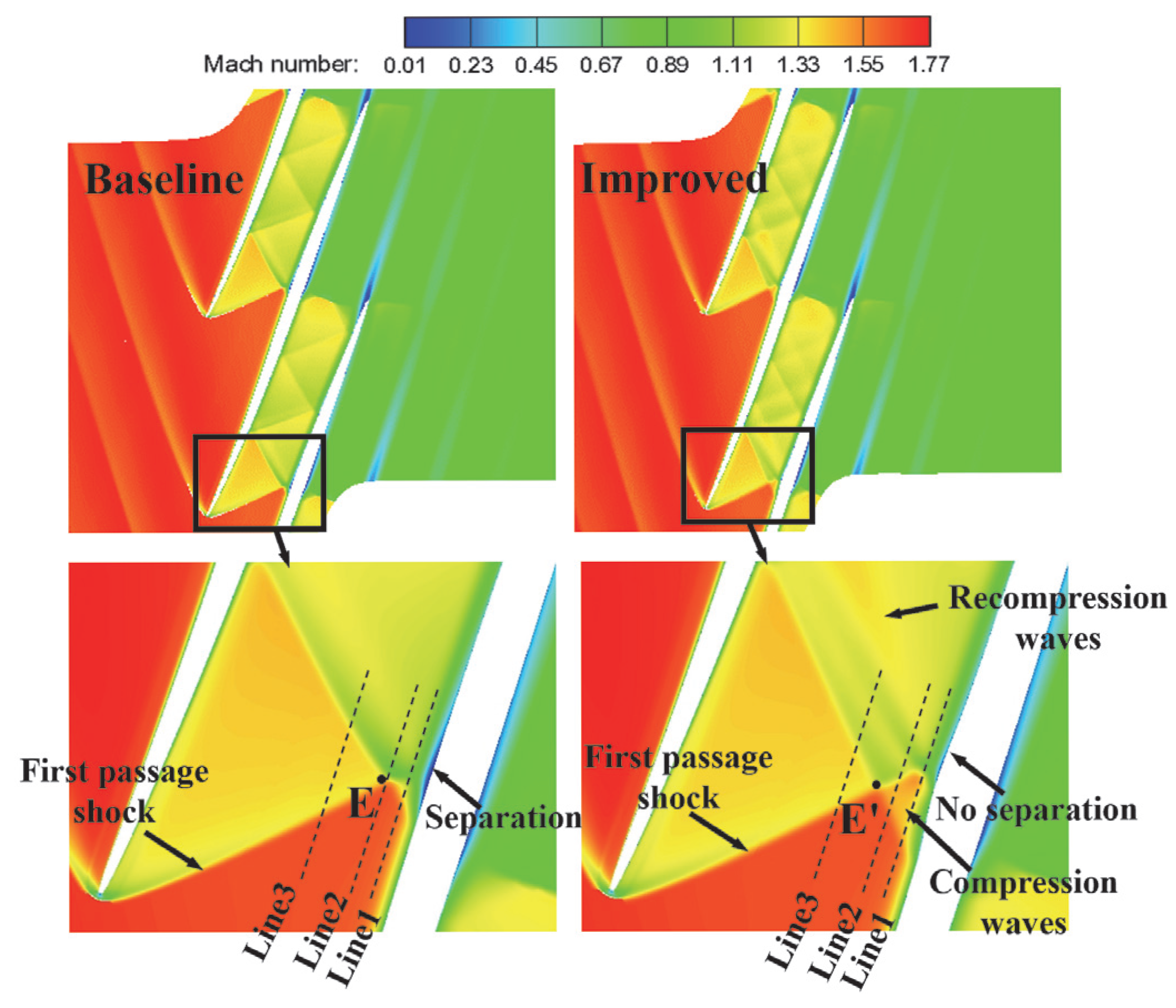
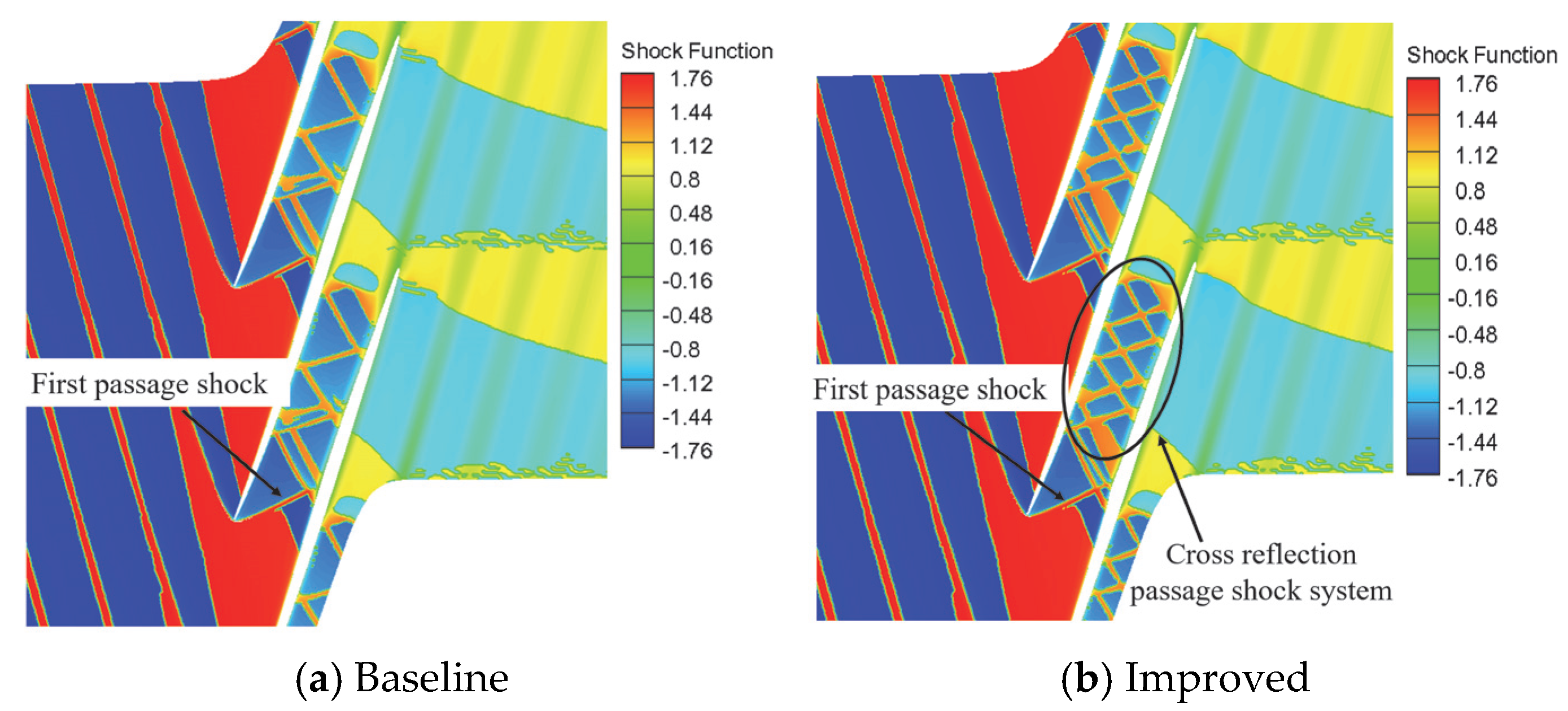
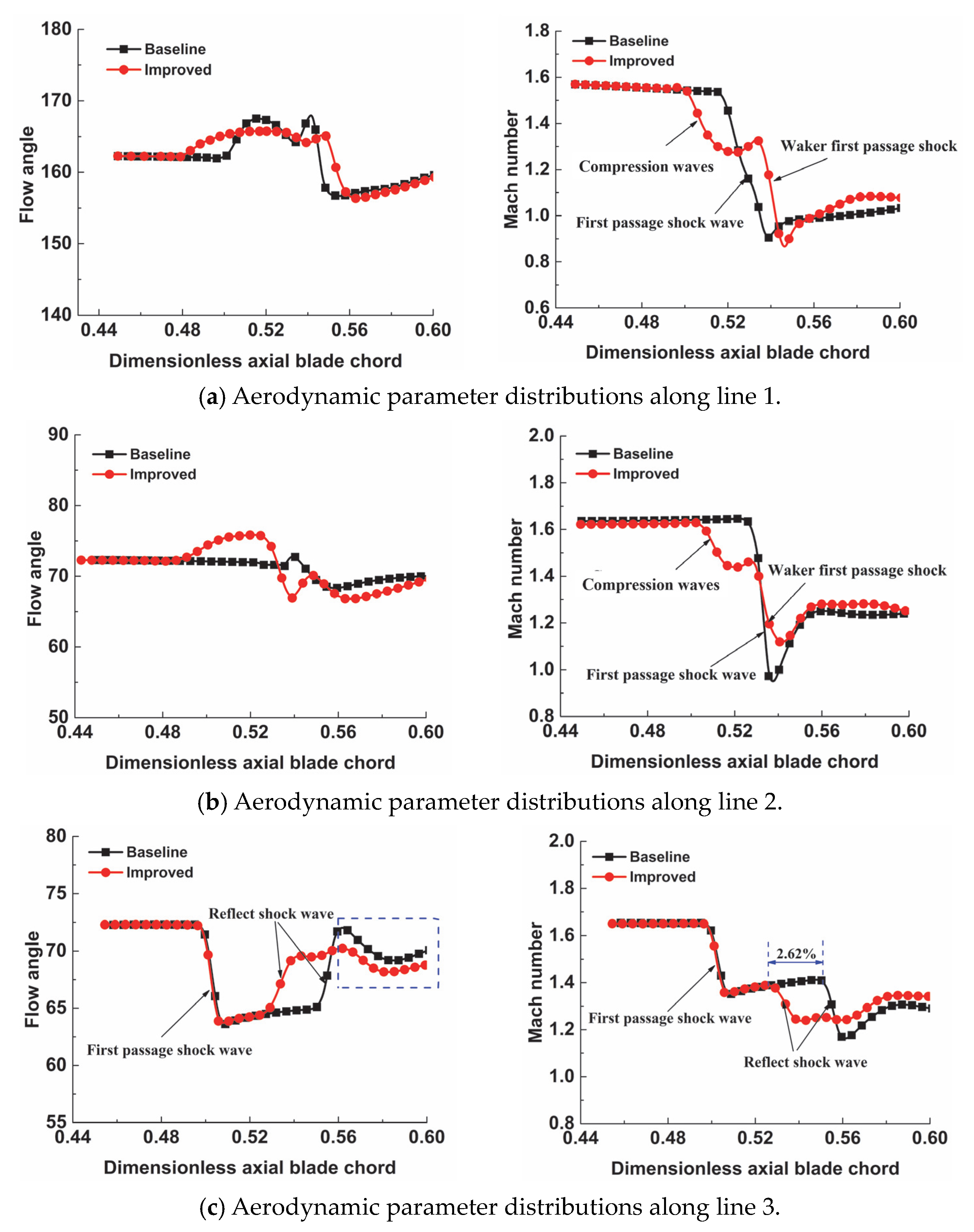
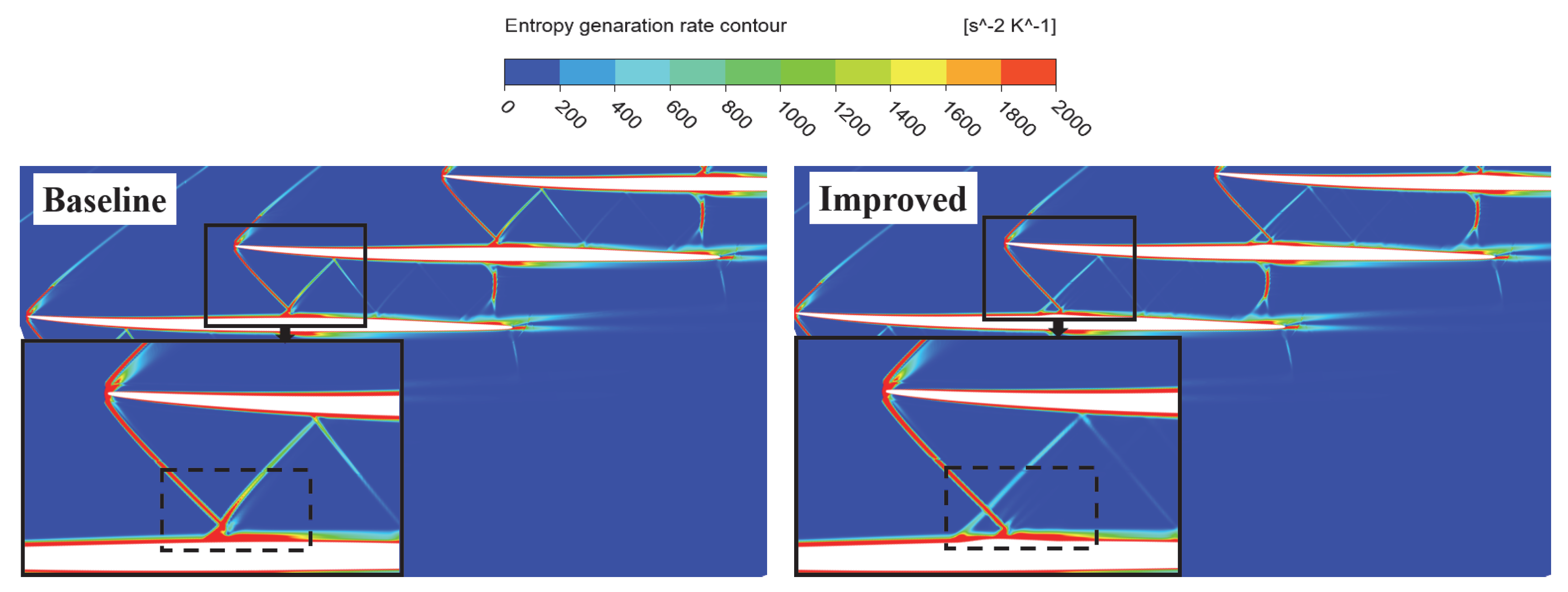
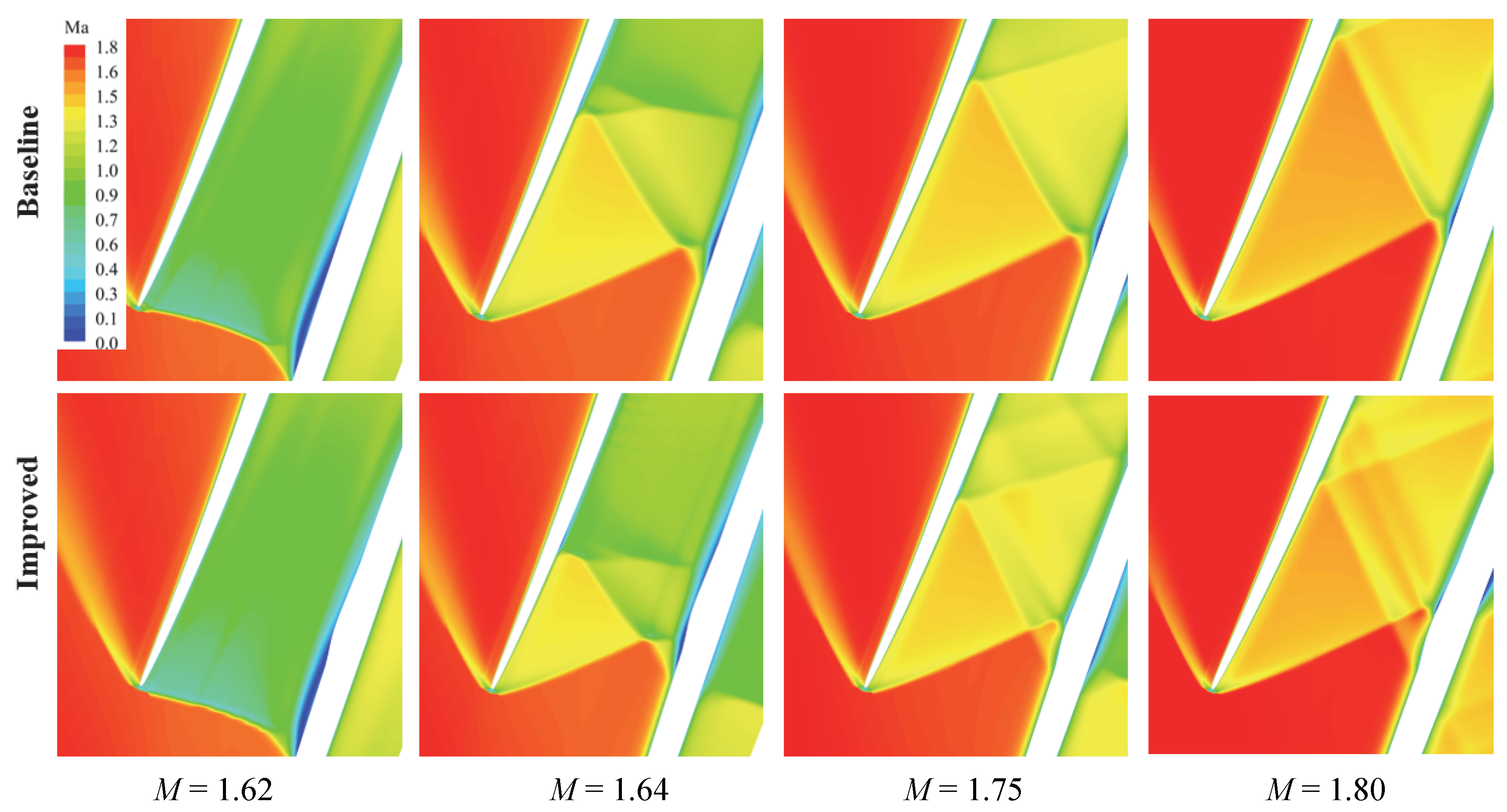
4.1.2. Flow Field Analysis
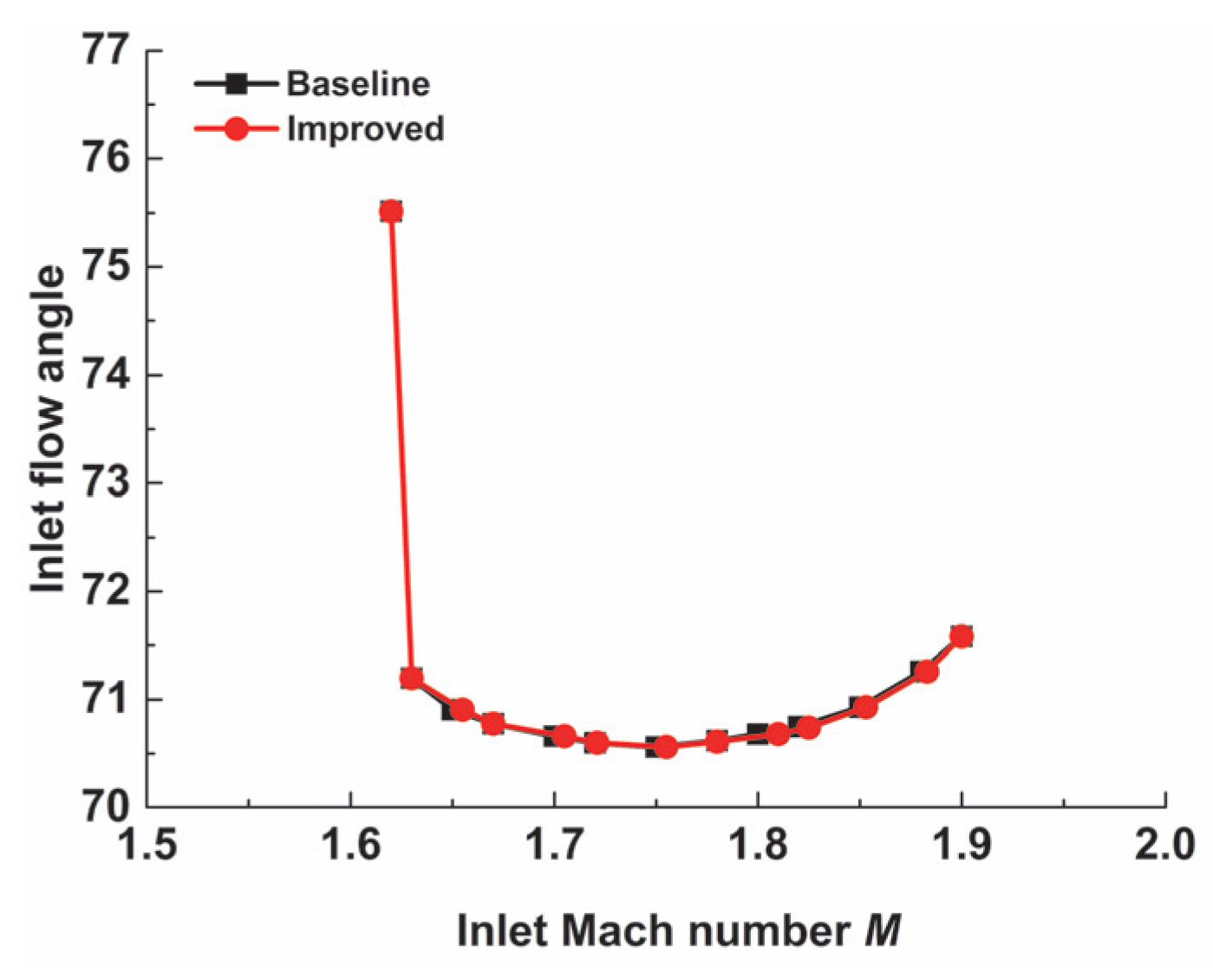
4.2. Compatibility of Negative-Curvature Ramp Under Off-Design Conditions
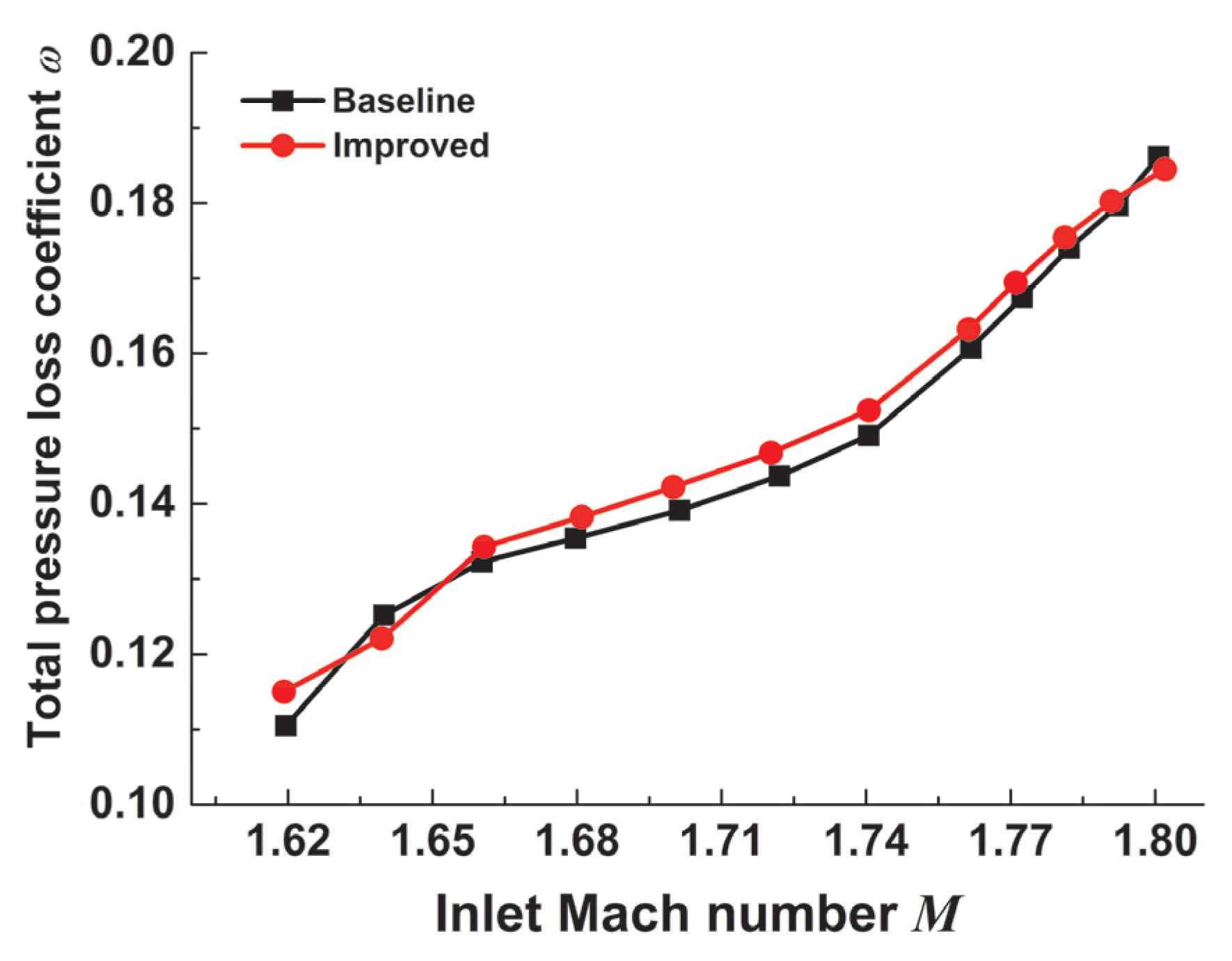
4.2.1. Variation in Inlet Mach Number
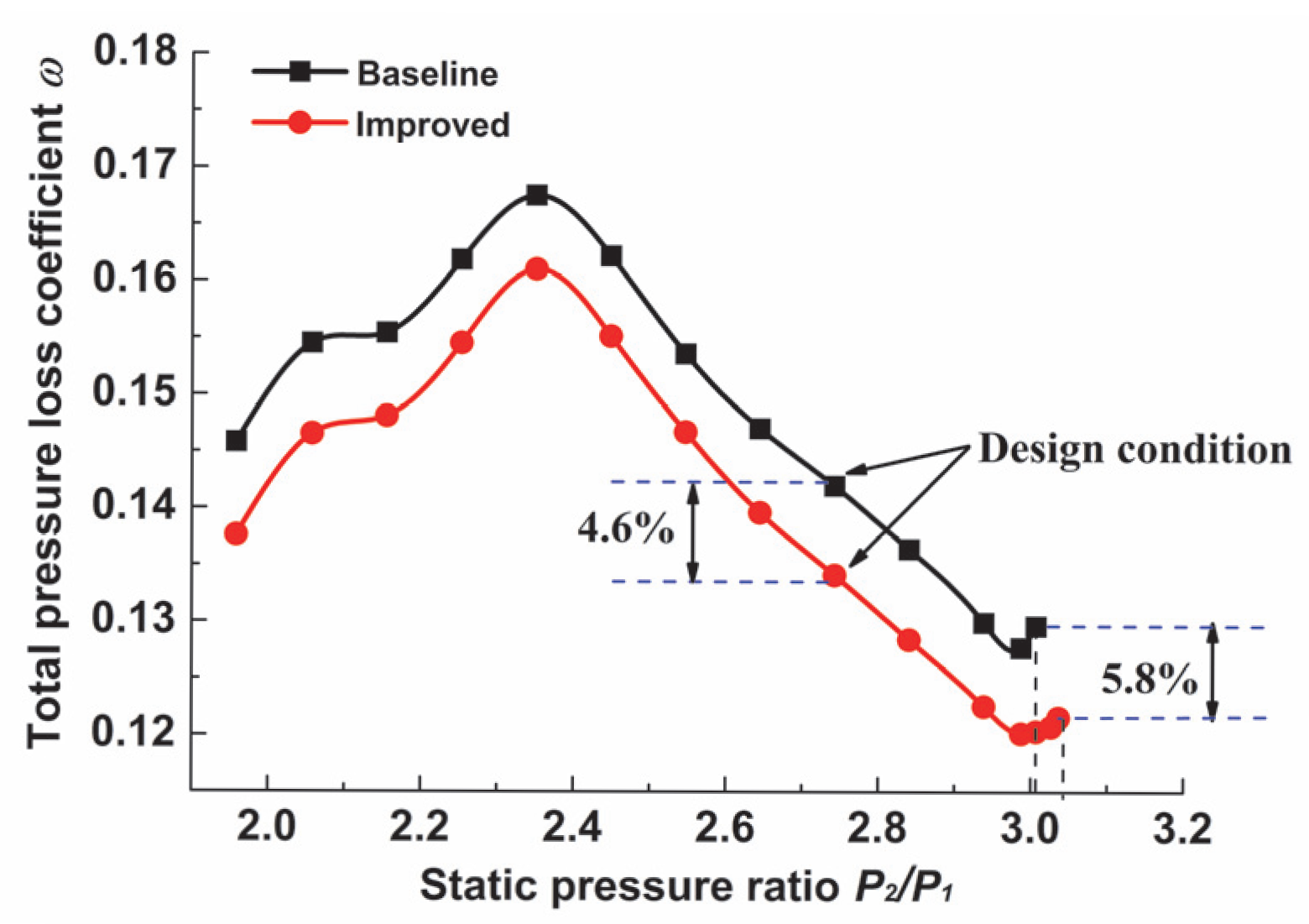
4.2.2. Variation in Outlet Pressure
5. Conclusions
- (1)
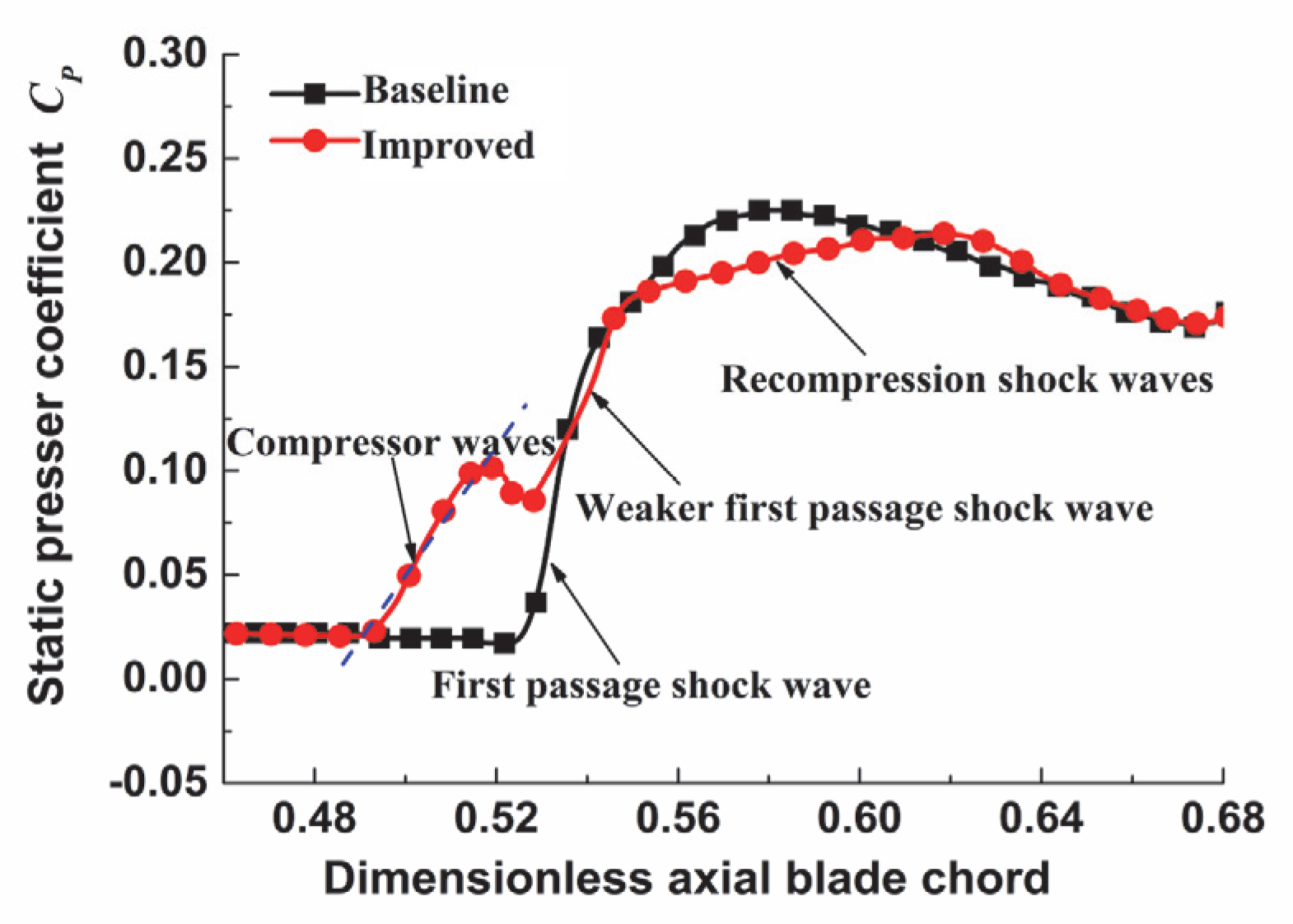
- Under design conditions, the negative-curvature ramp splits the first-passage shock foot into a series of compression waves and a weaker-passage shock foot, which reduces the strong adverse-pressure gradient generated by the shock. The shock-induced flow separation is significantly suppressed, resulting in less loss from the interaction between the shockwave and the boundary layer;
- (2)
- The heavy adverse-pressure gradient induced by the first-passage shock of the improved cascade is divided into three sections with a moderate pressure rise. There is an increasing tendency with a constant pressure gradient on the negative-curvature profile, which demonstrates the feasibility of the initial design method;
- (3)
- Under off-design conditions, the overall aerodynamic performance of the improved supersonic compressor cascade is superior to that of the baseline cascade at various inlet Mach numbers and exit pressure conditions, and the negative-curvature smooth ramp is compatible to some extent.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Speed of sound |
| Cp | Static pressure coefficient |
| H | Boundary layer shape factor |
| l | Vane chord length, mm |
| M | Mach number |
| P | Pressure, Pa |
| P* | Total pressure, Pa |
| RLE | Leading-edge radius, mm |
| RTE | Trailing-edge radius, mm |
| s | Solidity, l/t |
| Entropy generation rate | |
| t | Vane spacing, mm |
| T | Temperature, K |
| u | Velocity, m/s |
| β | Flow angle, deg |
| βs | Stagger angle, deg |
| γ | Ratio of specific heats |
| θ | Camber angle, deg |
| ω | Total pressure loss coefficient |
| Subscripts | |
| 0 | Position at point “O” |
| 1 | Inlet plane |
| 2 | Outlet plane |
References
- Wennerstrom, A.J. Highly loaded axial flow compressors: History and current developments. J. Turbomach. 1990, 112, 567–578. [Google Scholar] [CrossRef]
- Biollo, R.; Benini, E. Recent advances in transonic axial compressor aerodynamics. Prog. Aerosp. Sci. 2013, 56, 1–18. [Google Scholar] [CrossRef]
- Denton, J.D. Loss mechanisms in turbomachines. J. Turbomach. 1993, 115, 621–656. [Google Scholar] [CrossRef]
- Saito, S.; Furukawa, M.; Yamada, K.; Watanabe, K.; Matsuoka, A.; Niwa, N. Mechanisms and Quantitative Evaluation of Flow Loss Generation in a Multi-Stage Transonic Axial Compressor. In Proceedings of the ASME Turbo Expo 2019, Phoenix, AZ, USA, 17–21 June 2019. ASME Paper GT2019-90439. [Google Scholar] [CrossRef]
- Burguburu, S.P.; Toussaint, C.; Bonhomme, C.; Leroy, G. Numerical optimization of turbomachinery bladings. J. Turbomach. 2004, 126, 91–100. [Google Scholar] [CrossRef]
- Xu, W.; Du, X.; Tao, C.; Wang, S.; Wang, Z. Correlation of solidity, aspect ratio and compound lean vane in compressor cascade design. Appl. Therm. Eng. 2019, 150, 175–192. [Google Scholar] [CrossRef]
- Green, J.E. Interactions between shock waves and turbulent boundary layers. Prog. Aerosp. Sci. 1970, 11, 235–340. [Google Scholar] [CrossRef]
- Inger, G.R. Transonic shock/turbulent boundary-layer interaction on curved surfaces. J. Aircr. 1983, 20, 571–574. [Google Scholar] [CrossRef]
- Brouwer, K.R.; Gogulapati, A.; McNamara, J.J. Interplay of Surface Deformation and Shock-Induced Separation in Shock/Boundary-Layer Interactions. AIAA J. 2017, 55, 4258–4273. [Google Scholar] [CrossRef]
- Hoffmann, P.H.; Muck, K.C.; Bradshaw, P. The effect of concave surface curvature on turbulent boundary layers. J. Fluid Mech. 1985, 161, 371–403. [Google Scholar] [CrossRef]
- Swearingen, J.D.; Blackwelder, R.F. The growth and breakdown of streamwise vortices in the presence of a wall. J. Fluid Mech. 1987, 182, 255–290. [Google Scholar] [CrossRef]
- Tandiono; Winoto, S.H.; Shah, D.A. On the linear and nonlinear development of Görtler vortices. Phys. Fluids 2008, 20, 094103. [Google Scholar] [CrossRef]
- Wang, Q.C.; Wang, Z.G. Structural characteristics of the supersonic turbulent boundary layer subjected to concave curvature. Appl. Phys. Lett. 2016, 108, 114102. [Google Scholar] [CrossRef]
- Sun, M.; Sandham, N.D.; Hu, Z. Turbulence structures and statistics of a supersonic turbulent boundary layer subjected to concave surface curvature. J. Fluid Mech. 2019, 865, 60–99. [Google Scholar] [CrossRef]
- Tai, T.C. Theoretical Aspects of Dromedaryfoil, Report 77-0104; Technical report; David, W., Ed.; Taylor Naval Ship Research and Development Center: Bethesda, MD, USA, 1997. [Google Scholar]
- Bruce, P.J.K.; Colliss, S.P. Review of research into shock control bumps. Shock Waves 2015, 25, 451–471. [Google Scholar] [CrossRef]
- Bruce, P.J.K.; Babinsky, H. Experimental study into the flow physics of three-dimensional shock control bumps. J. Aircr. 2012, 49, 1222–1233. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, P.Q.; Feng, P.H. Shock control bumps parametric research on supercritical airfoil. Technol. Sci. 2011, 54, 2935–2944. [Google Scholar] [CrossRef]
- Mazaheri, K.; Nejati, A.; Kiani, K.C.; Taheri, R. The application of the gradient-based adjoint multi-point optimization of single and double shock control bumps for transonic airfoils. Shock Waves 2016, 26, 491–511. [Google Scholar] [CrossRef]
- Mazaheri, K.; Kiani, K.C.; Nejati, A.; Zeinalpour, M.; Taheri, R. Optimization and analysis of shock wave/boundary-layer interaction for drag reduction by Shock control bumps. Aerosp. Sci. Technol. 2015, 42, 196–208. [Google Scholar] [CrossRef]
- Pätzold, M.; Lutz, T.; Krämar, E.; Wagner, S. Numerical Optimization of Finite Shock Control Bumps. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; AIAA: Reston, VA, USA, 2006; p. 1054. [Google Scholar]
- König, B.; Pätzold, M.; Lutz, T.; Krämer, E.; Rosemann, H.; Richter, K.; Uhlemann, H. Numerical and experimental validation of three-dimensional shock control bumps. J. Aircr. 2009, 46, 675–682. [Google Scholar] [CrossRef]
- Ogawa, H.; Babinsky, H. Shock-Wave/Boundary-Layer Interaction Control Using Three-Dimensional Bumps for Transonic Wings. AIAA J. 2008, 46, 1442–1452. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, H.J.; Tian, F.C. Control of incident shock/boundary-layer interaction by a two-dimensional bump. AIAA J. 2014, 52, 767–776. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, H.J.; Sun, S.; Rao, C.Y. Control of cowl shock/boundary-layer interaction in hypersonic inlets by bump. AIAA J. 2015, 53, 3492–3496. [Google Scholar] [CrossRef]
- Mazaheri, K.; Khatibirad, S. Using a Shock control bumps to Improve the Performance of an Axial Compressor vane Section. Shock Waves 2017, 27, 299–312. [Google Scholar] [CrossRef]
- Mazaheri, K.; Khatibirad, S. Optimization of bump and blowing to control the flow through a transonic compressor vane cascade. Shock Waves 2018, 8, 285–297. [Google Scholar] [CrossRef]
- John, A.; Shahpar, S.; Qin, N. Alleviation of shock-wave effects on a highly loaded axial compressor through novel vane shaping. In Proceedings of the ASME Turbo Expo 2016, Seoul, Republic of Korea, 13–17 June 2016. ASME Paper GT2016-57550. [Google Scholar] [CrossRef]
- John, A.; Qin, N.; Shahpar, S. Using shock control bumps to improve transonic fan/compressor vane performance. J. Turbomach. 2019, 141, 081003. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Zhao, W.; Zhao, Q.J.; Zhou, Q.; Xu, J.Z. Passage shock wave/boundary layer interaction control for transonic compressors using bumps. Chin. J. Aeronaut. 2022, 35, 82–97. [Google Scholar] [CrossRef]
- Babinsky, H.; Harvey, J.K. Shock Wave-Boundary-Layer Interactions; Cambridge University Press: Cambridge, UK, 2011; Available online: https://www.cambridge.org/9780521848527 (accessed on 10 May 2025).
- Drayna, T.; Nompelis, I.; Candler, G. Hypersonic Inward Turning Inlets: Design and Optimization. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; AIAA: Reston, VA, USA, 2006; p. 297. [Google Scholar]
- Venturelli, G.; Benini, E. Kriging-assisted design optimization of S-shape supersonic compressor cascades. Aerosp. Sci. Technol. 2016, 58, 275–297. [Google Scholar] [CrossRef]
- Casoni, M.; Magrini, A.; Benini, E. Supersonic Compressor Cascade Shape Optimization under Multiple Inlet Mach Operating Conditions. Aerospace 2019, 6, 64. [Google Scholar] [CrossRef]
- Mowatt, S.; Skews, B. Three-dimensional shock wave/boundary layer interactions. Shock Waves 2011, 21, 467. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modelling for CFD; DCW Industries: La Canada, CA, USA, 2004. [Google Scholar] [CrossRef]
- Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Acquaye, F.; Li, J.; Wray, T.; Agarwal, R.K. Validation of the Wray-Agarwal Turbulence Model for Shock-Wave Boundary Layer Interaction Flows. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; AIAA: Reston, VA, USA, 2016; p. 3477. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Betelin, V.B.; Nikitin, V.F.; Stamov, L.I.; Altoukhov, D.I. Accumulation of errors in numerical simulations of chemically reacting gas dynamics. Acta Astronaut. 2015, 117, 338–355. [Google Scholar] [CrossRef]
- Greizer, E.M.; Tan, C.S.; Graf, M.B. Internal Flow: Concepts and Applications; Cambridge University Press: New York, NY, USA, 2004; Available online: https://www.cambridge.org/9780521343930 (accessed on 10 May 2025).
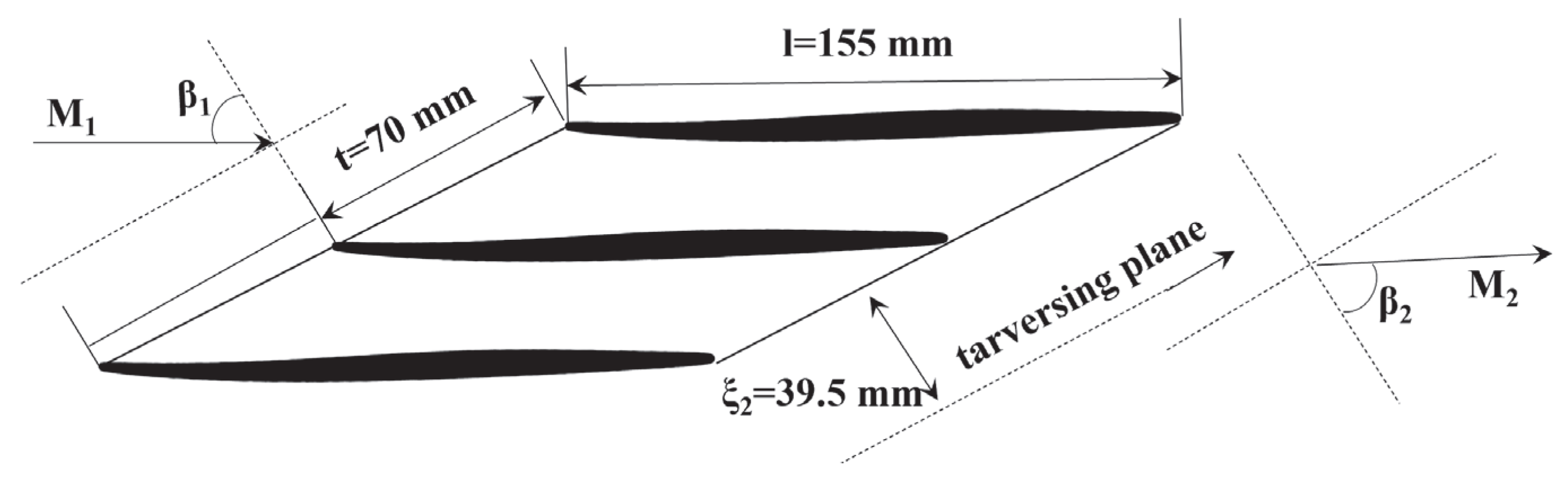




| Upstream Mach number | M1 | 1.75 |
| Solidity | s = l/t | 2.21 |
| Upstream flow angle, deg | β1 | 70.5 |
| Camber angle, deg | θ | −2.5 |
| Stagger angle, deg | βs | 69.5 |
| Vane chord length, mm | l | 155 |
| Vane spacing, mm | t | 70 |
| Leading-edge radius, mm | RLE | 0.2 |
| Trailing-edge radius, mm | RTE | 0.2 |
| Initiation Position (Chord) | Length (mm) | Flow Deflection Angle (deg) | Adverse Pressure Gradient k (Pa/m) |
|---|---|---|---|
| 0.49 | 5.1 | 8.2 | 1.39 × 107 |
| Boundary Conditions | Setting |
|---|---|
| Inlet | Total temperature, total pressure, and velocity |
| Outlet | Static pressure |
| Wall | Nonslip and adiabatic wall |
| Turbulence model | SST(k–ω) |
| Fluid | Ideal gas |
| Periodicity | Translational periodicity |
| Initialization | Inlet parameters |
| Baseline Cascade | Improved Cascade | Differences (%) | |
|---|---|---|---|
| M2 | 0.86 | 0.87 | 1.16% |
| β2 | 73.75 | 73.69 | −0.03% |
| ω | 0.142 | 0.1354 | −4.6% |
| Baseline | Improved | Deviation | ||
|---|---|---|---|---|
| Relative | Absolute | |||
| Boundary layer loss | 0.966 | 0.908 | −6.0% | −5.8% |
| First-passage shock foot loss | 0.022 | 0.020 | −9.1% | −0.2% |
| Reflected shock loss | 0.012 | 0.008 | −33.3% | −0.4% |
| Total loss | 1 | 0.936 | −6.4% | −6.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Fan, Z.; Cui, W.; Zhou, Q.; Xu, J. An Investigation of the Promotion of the Aerodynamic Performance of a Supersonic Compressor Cascade Using a Local Negative-Curvature Ramp. Appl. Sci. 2025, 15, 5664. https://doi.org/10.3390/app15105664
Liu Y, Fan Z, Cui W, Zhou Q, Xu J. An Investigation of the Promotion of the Aerodynamic Performance of a Supersonic Compressor Cascade Using a Local Negative-Curvature Ramp. Applied Sciences. 2025; 15(10):5664. https://doi.org/10.3390/app15105664
Chicago/Turabian StyleLiu, Yongzhen, Zhen Fan, Weiwei Cui, Qiang Zhou, and Jianzhong Xu. 2025. "An Investigation of the Promotion of the Aerodynamic Performance of a Supersonic Compressor Cascade Using a Local Negative-Curvature Ramp" Applied Sciences 15, no. 10: 5664. https://doi.org/10.3390/app15105664
APA StyleLiu, Y., Fan, Z., Cui, W., Zhou, Q., & Xu, J. (2025). An Investigation of the Promotion of the Aerodynamic Performance of a Supersonic Compressor Cascade Using a Local Negative-Curvature Ramp. Applied Sciences, 15(10), 5664. https://doi.org/10.3390/app15105664






