An Improved Integral Response Deformation Method for Seismic Response Analysis of Underground Structures Considering Far-Field Effects

Abstract

In the seismic analysis of underground structures, the traditional integral response displacement method may misestimate far-field constraint effects because of the empirical placement of cutoff boundaries, leading to inaccuracies and a significant increase in computational costs. This study proposes a cutoff boundary distance criterion of three times the structural size, effectively eliminating boundary reflection errors. Furthermore, by introducing artificial boundary conditions that simulate the static resistance of a semi-infinite foundation and the far-field constraint effects, an improved integral response deformation method considering the far-field effect is developed. Verification based on the dynamic time history method (implemented with the Abaqus/Explicit solver) confirms that the computational error of the proposed method is essentially controlled within 5%, and compared with that of the traditional method, the number of mesh elements and nodes is reduced by 80%~90%. This advancement provides a computationally efficient and highly accurate solution for the seismic analysis of large-scale underground structures, making it highly valuable for practical engineering applications.

1. Introduction

With the accelerated urbanization process, underground engineering structures, such as metro systems, utility tunnels, and deeply buried tunnels, serve as critical components of national infrastructure, drawing significant attention to their seismic performance. Under seismic loading, underground structures are prone to severe damage or even progressive collapse due to the complexity of the soil–structure interaction (SSI). Historical seismic events such as the 1995 Great Hanshin earthquake in Japan [1] and the 2008 Wenchuan earthquake in China [2] revealed the substantial seismic risk associated with underground infrastructure. Consequently, the development of efficient and accurate analytical methods for evaluating the seismic responses of underground structures has become an urgent requirement for enhancing engineering safety and advancing disaster prevention and mitigation strategies.

Current seismic analysis methods for underground structures can be divided into two main categories: the dynamic time history method and simplified practical methods. The dynamic time history method, which directly solves dynamic differential equations to obtain structural seismic responses [3,4], is highly accurate in simulating the time-dependent dynamic behavior of underground structures. As a result, it has become the most predominant approach for evaluating the seismic performance of underground structures. However, its computational complexity and inefficiency often limit its applicability in the analysis of large-scale engineering projects. Recent advancements have introduced incremental dynamic analysis (IDA) as an extension of dynamic methodologies. By gradually modulating the amplitude of earthquake motion intensity [5], IDA can be used to systematically evaluate the seismic performance margin of structures, making it particularly suitable for probabilistic risk assessment. Nevertheless, the resource-intensive nature of such approaches remains a barrier for routine engineering applications. To address these limitations, researchers have developed various quasistatic simplified methods. Among these methods, the response displacement method (RDM) has gained widespread adoption in practical engineering because of its theoretical clarity and computational efficiency. Notably, this method has been codified in the Standard for Seismic Design of Underground Structures (GB/T 51336-2018) [6], further solidifying its role as a standard approach for underground structural analysis.

The accuracy of the traditional RDM is highly dependent on the rational determination of the equivalent foundation spring stiffness. Focusing on this critical aspect, Li et al. [7] developed an improved algorithm for calculating foundation spring stiffness tailored to underground structures with rectangular cross-sections, significantly enhancing computational efficiency. Bin et al. [8,9] systematically evaluated the precision of six distinct approaches for deriving foundation spring coefficients by modifying load application modes. Their findings demonstrated that methods that independently solve for horizontal and vertical spring coefficients yield optimal accuracy. Ding et al. [10,11] conducted a comparative analysis of foundation spring stiffness coefficients determined through the test method, Li’s method, the MIDAS method, and the finite element method. Their study recommended prioritizing experimental methods and proposed applying a safety correction factor of 1.10 to structural internal force calculations to enhance structural integrity. Furthermore, Wang et al. [12] derived an analytical solution for the foundation modulus incorporating radial–tangential modulus interactions and deformation effects, allowing for a precise and explicit consideration of soil deformation patterns.

To overcome the inherent limitations of traditional methods that rely on foundation spring calculations, researchers have developed multiple enhanced methodologies. Liu et al. [13,14,15] systematically addressed the error sources of the classical RDM and then advanced the Integral Response Deformation Method (IRDM), which integrates the explicit physical concepts and rigorous theoretical framework of the original approach while eliminating traditional foundation spring models. Instead, it employs an integrated soil–structure mechanical model that directly characterizes continuum interactions, thereby eliminating errors associated with spring stiffness calibration and localized spring approximations. Xu et al. [16] proposed a generalized response displacement method (GRDM) based on a “spring–stratum–structure” framework. This approach effectively mitigates errors caused by inappropriate spring stiffness assignments, particularly for underground structures with complex cross-sectional geometries. An et al. [17] introduced an improved RDM that accounts for the influence of overlying frame structures on the seismic responses of metro stations. Bao et al. [18] theoretically demonstrated that equivalent seismic loads induced by peripheral soil stresses in the IRDM can be obtained through a single static analysis of substructure models containing only one soil layer, with minimal influence from soil inertial forces. Building on this foundation, they developed an improved IRDM implementation that eliminates the computation and application of free-field soil inertial forces while maintaining accuracy, thereby streamlining the workflow [19]. Akira [20], Zhang et al. [21], and Yan et al. [22] proposed the forced response displacement method (FRDM) using a stratum-structure model. This method simplifies seismic action application by treating stratum relative displacements at model boundaries as static inputs for finite element analysis. Expanding on this concept, Chen et al. [23,24] proposed the Integral Forced Response Displacement Method (IFRDM), which mitigates load attenuation effects by imposing stratum deformations across entire soil domains.

However, existing methods typically employ fixed or free-field displacement assumptions at the cutoff boundaries, overlooking the radiation effects induced by far-field media on seismic wave propagation. This omission results in discrepancies between computational models and actual seismic environments. Insufficient boundary distances cause computational inaccuracies arising from spurious wave reflections from the far field. Furthermore, current codes lack explicit guidelines for boundary configuration in the IRDM, leading to widespread reliance on empirical estimations in practice. Although expanding the model domain can mitigate boundary effects, it disproportionately increases computational costs.

In response to these challenges, this study systematically investigates the influence of the truncation distance on computational accuracy, establishing quantitative criteria for boundary configuration. By incorporating artificial boundary conditions that simulate the static resistance of semi-infinite foundations and the constraint effects of far-field media, an improved IRDM considering far-field effects is developed. Comparative analyses of representative underground structures demonstrate that the proposed method maintains precision while significantly reducing the computational scale. This methodology provides an innovative solution that balances accuracy and efficiency for the seismic design of underground infrastructure, offering substantial practical implications for advancing safety assessment and disaster mitigation in large-scale underground engineering projects.

2. Introduction to the Integral Response Deformation Method

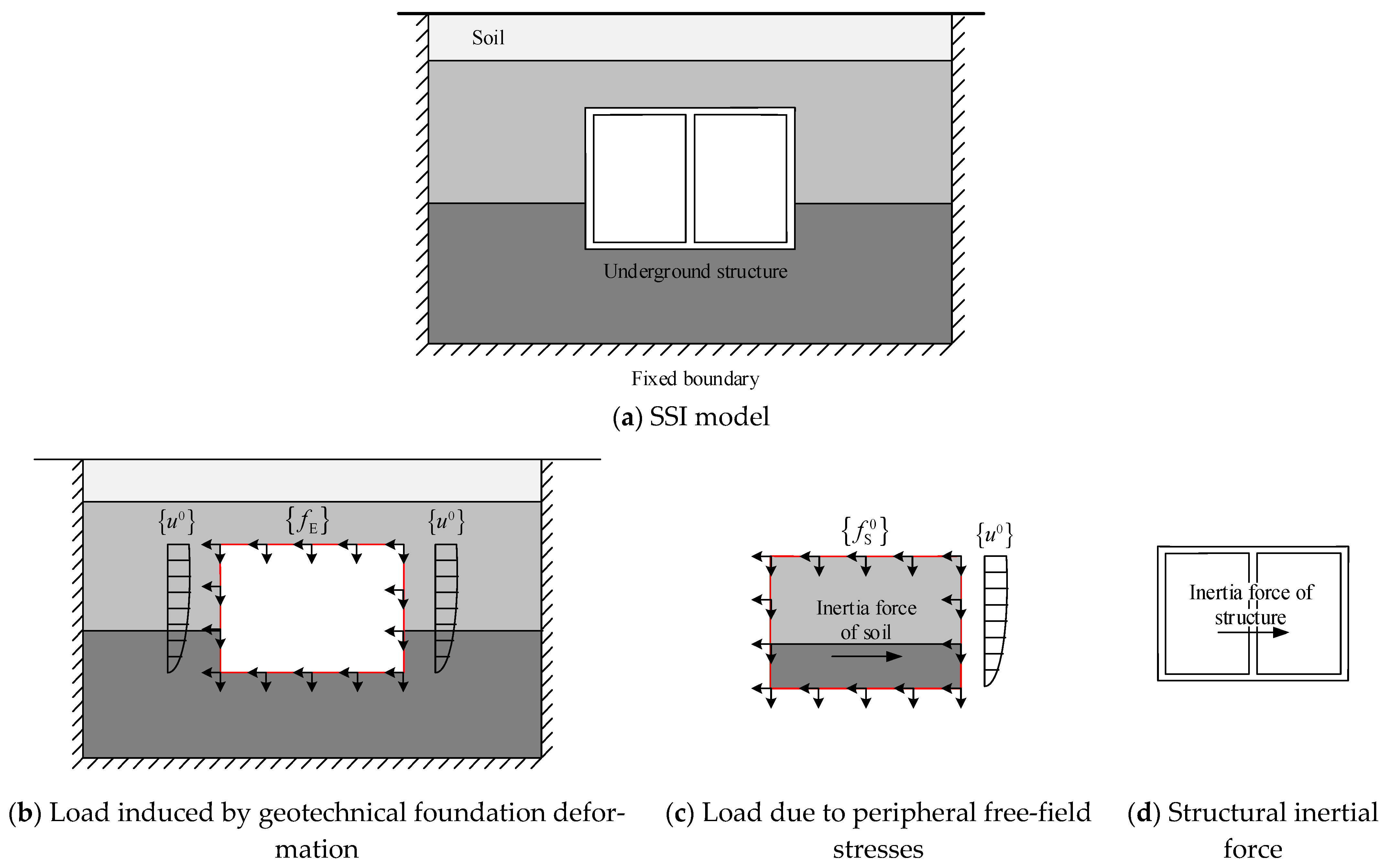
The computational model of the IRDM for underground structures is illustrated in Figure 1a. On the basis of the fundamental theory of this method, the seismic-induced loads acting on underground structures can be decomposed into three constituent components:

(1)

Load induced by geotechnical foundation deformation f_E:

This component corresponds to the forces required to enforce free-field deformation at all the soil–structure interface nodes in a soil stratum finite element model with the structure removed, as illustrated in Figure 1b.

(2)

Load induced by free-field stresses fs0:

This component originates from the stresses in the soil medium surrounding the structure. Specifically, free-field displacements are applied at the boundaries of the free-field model, whereas free-field inertial forces are imposed internally. The resultant nodal reaction forces at the interface S f_s⁰ can be obtained through static analysis, as shown in Figure 1c.

(3)

Structural inertial force:

This load represents the product of the structural mass and seismic acceleration (Figure 1d).

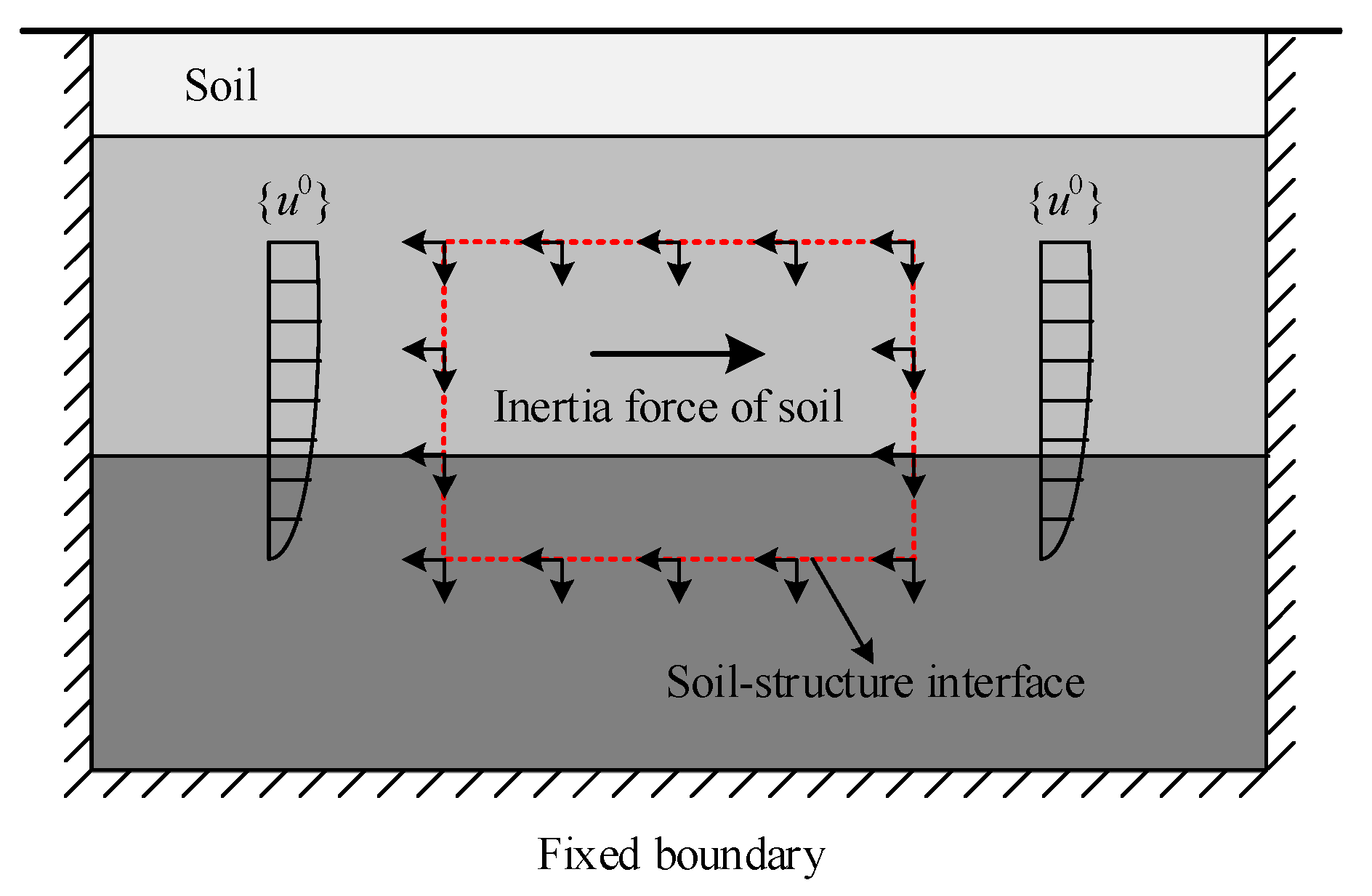
In practical applications of the IRDM for determining the peak seismic responses of underground structures, the first two load components can be combined for calculation. This process is facilitated by the auxiliary free-field model illustrated in Figure 2, where the structural zone is replaced with free-field geological media. The implementation workflow is as follows:

(1)

Impose the free-field relative displacements at the critical moment on the soil–structure interface of the free-field model;

(2)

Apply the free-field inertial forces at the critical moment to the geological media within the interface domain;

(3)

Perform a static analysis to obtain the nodal reaction forces at the soil–structure interface;

(4)

The interface reaction forces are combined with the structural inertial forces to formulate the equivalent seismic loads, and these loads are applied to the corresponding nodes in the SSI model;

(5)

Conduct a static analysis on the SSI model to derive peak seismic responses.

3. Influence of Boundary Distance in the Integral Response Deformation Method

In the traditional IRDM, exterior fixed boundaries are used to simulate the influence of semi-infinite medium domains. Consequently, these boundaries must be positioned sufficiently distantly to ensure that non-free-field displacements at interface S, induced by the uncoordinated movement of the soil structure, undergo adequate attenuation. However, current design codes lack explicit guidance on boundary setting. In practice, empirical approaches are commonly adopted, typically setting the bottom boundary at the bedrock surface and lateral boundaries at approximately three times the structural span. While this method generally ensures acceptable accuracy, its universal validity remains unverified. In specific scenarios, such as when structures are located far from bedrock or those with large transverse dimensions, this boundary configuration may result in excessively large models, significantly increasing computational complexity and resource demands. To address these limitations, this study investigates the impact of boundary distance on the computational accuracy of the IRDM, aiming to optimize boundary placement strategies and achieve a balance between precision and efficiency.

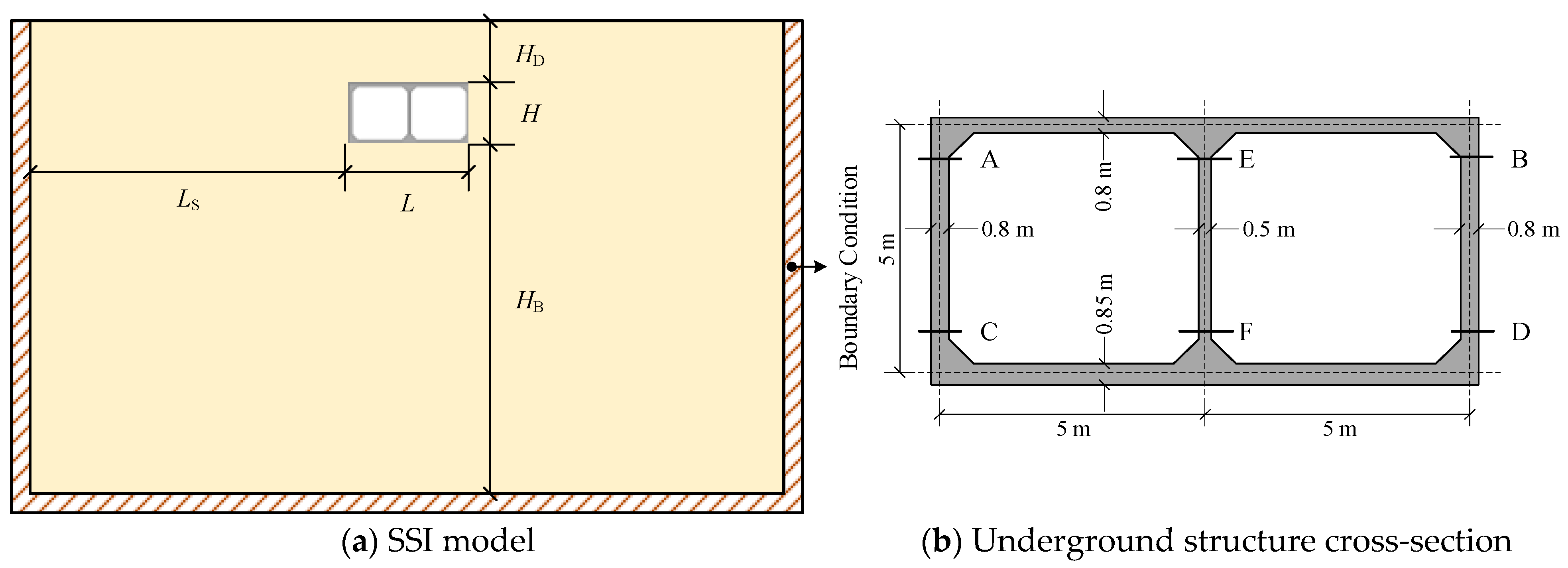
An SSI model is established as depicted in Figure 3. The lateral boundary distance L_S denotes the horizontal distance from the outer wall of the structure to the lateral boundary, whereas the bottom boundary distance H_B denotes the vertical distance from the structural floor to the lower boundary. A single-story, double-span structure is adopted for modeling, featuring a span of L = 10 m and height of H = 5 m, as illustrated in Figure 3b. The burial depth of the underground structure remains fixed at H_D = 5 m. The soil domain is discretized using plane strain elements 0.5 m × 0.5 m in size, characterized by a mass density of 2000  kg/m³, a shear wave velocity of 300 m/s, and a Poisson’s ratio of 0.3. 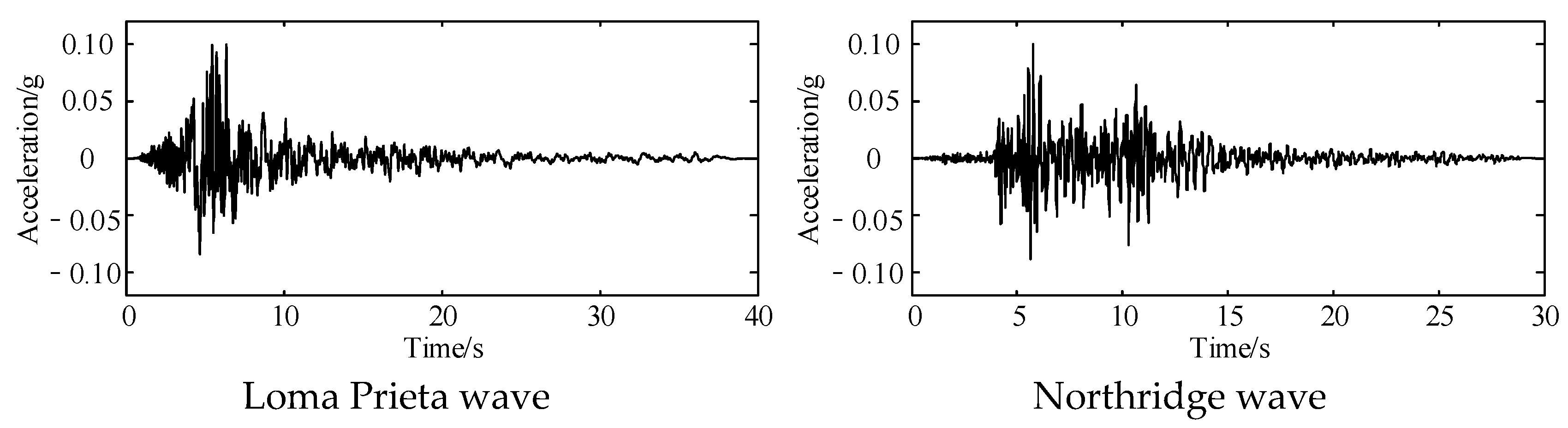The reinforced concrete structure, which is composed of C30-grade concrete, is modeled with a mass density of 2500  kg/m³, an elastic modulus of 30  GPa, and a Poisson’s ratio of 0.15. Shear-deformable beam elements with a mesh size of 0.5 m are used for structural discretization. The Kobe earthquake record (Figure 4) is selected as the seismic input, with a total duration of 40.95  s.

To evaluate the computational accuracy of the IRDM, the dynamic time history method is employed as the benchmark in this study. For dynamic time history analysis, viscoelastic artificial boundaries are applied to simulate wave radiation effects in semi-infinite media, and seismic motions are introduced via the seismic wave input method, which is based on the substructure of the artificial boundary.

3.1. Influence of the Lateral Boundary Distance

This study first investigates the impact of the lateral boundary distance on the computational accuracy of the IRDM. A dimensionless lateral boundary distance ratio R_S = L_S/L is introduced and is set to 0.5, 1.0, 2.0, 3.0, 4.0, and 5.0 for parametric analysis via the IRDM. The bottom boundary of the numerical model is fixed at the bedrock surface.

3.1.1. Internal Forces and Deformations

The errors in the internal forces and deformation results computed by the IRDM are defined as follows: $\mathsf{\gamma }={\displaystyle \frac{\mathrm{S}-{\mathrm{S}}_{\mathrm{D}}}{{\mathrm{S}}_{\mathrm{D}}}}\ast 100\%$ where S denotes the internal forces (including the axial force N, shear force Q, and bending moment M) or deformation results obtained from the IRDM, and S_D represents the corresponding results derived from the dynamic time history method. 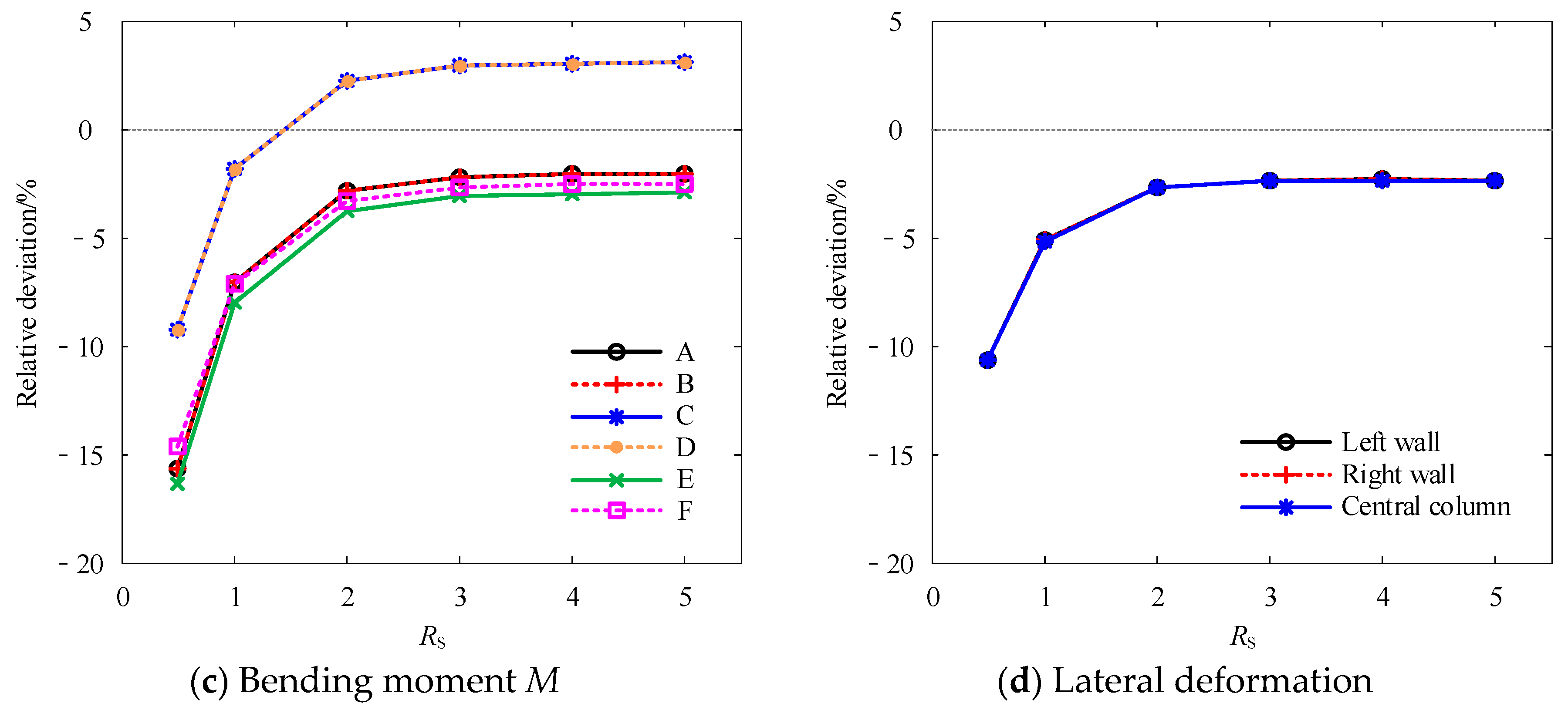Figure 5 illustrates the relationship between the relative errors of the internal forces and lateral deformations of the vertical structural members and the dimensionless lateral boundary distance ratio R_S.

The results demonstrate that the errors in the internal forces across all sections of the underground structure, as well as the lateral deformations of the vertical members, decrease significantly as the R_S increases. Specifically, as the R_S increases from 0.5 to 5, the axial force error decreases from −17.11% to −1.63%, the shear force error decreases from −17.35% to −1.64%, the bending moment error decreases from −16.35% to −2.09%, and the lateral deformation error of the vertical members decreases from −10.63% to −2.35%.

Further analysis reveals that the errors in the internal forces and lateral deformations decrease significantly as the R_S increases from 0.5 to 2.0, and then stabilize and remain under 5% for R_S > 2.0. Although minor increases in shear and moment errors occur at specific sections (e.g., Sections C and D) when R_S > 2.0, these deviations remain below 5%. As the calculated values slightly exceed the dynamic time history results, they provide conservative estimates from a safety perspective.

3.1.2. Soil Stress

Under seismic loading, the deformation of underground structures is primarily controlled by the surrounding geotechnical medium. Accordingly, the internal forces and deformations of a structure are closely related to the stress and deformation distributions within the surrounding soil or rock. Studies have demonstrated that the maximum shear stress in a geotechnical medium can, to some degree, reflect the constraints exerted on underground structures. 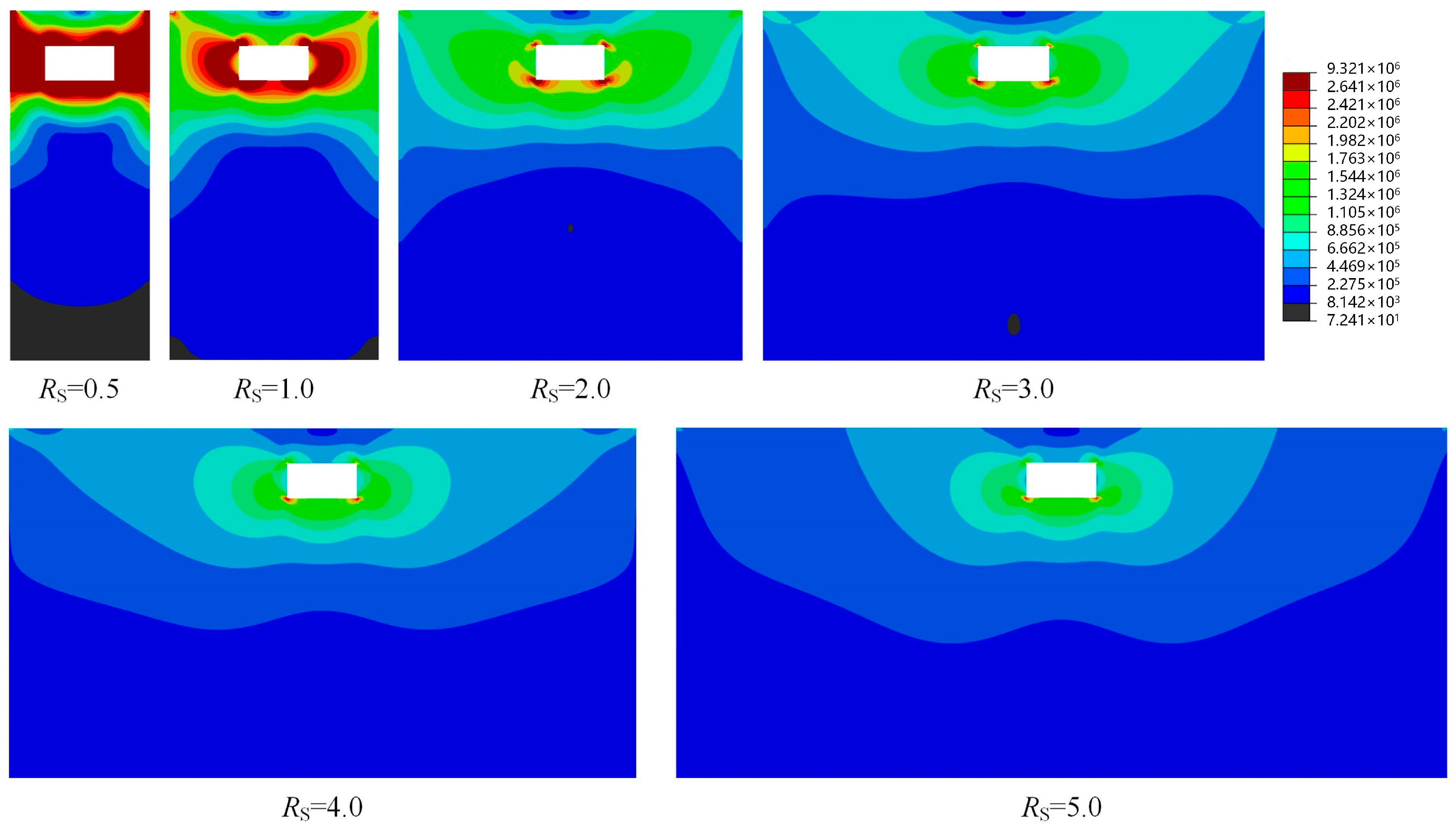Figure 6 shows the maximum shear stress contours in the geotechnical medium computed by the IRDM under varying lateral boundary distances.

As the R_S increases, the shear stress in the geotechnical medium surrounding the structure gradually decreases. When R_S ≤ 1.0, the lateral boundaries are too close to the structure, imposing excessive constraints and causing elevated stress levels in the surrounding area. For R_S = 2.0, the boundary influence on the surrounding region weakens significantly, although localized horizontal shear stress concentrations persist near the intersections of the sidewalls and floors. When R_S ≥ 3.0, boundary effects on adjacent regions become negligible.

Therefore, when the IRDM is applied for seismic analysis of underground structures, lateral boundaries should be placed far enough to minimize boundary effects on computational accuracy. These findings suggest that setting the lateral boundary distance to three times the structural width effectively controls the boundary effect while maintaining high precision.

3.2. Influence of the Bottom Artificial Boundary Distance

For underground structures located far above bedrock, positioning the bottom boundary at the bedrock surface can lead to an excessively large computational domain, substantially increasing computational complexity and resource demands. To balance efficiency and accuracy, this study examines the influence of the bottom boundary distance on the computational precision of the IRDM. A dimensionless bottom boundary distance ratio, R_B = H_B/H, is introduced for parametric analyses with R_B set to 0.5, 1.0, 2.0, 3.0, 4.0 and 5.0. Moreover, the lateral boundaries are fixed at three times the structural width, following the findings from Section 3.1.

3.2.1. Internal Forces and Deformations

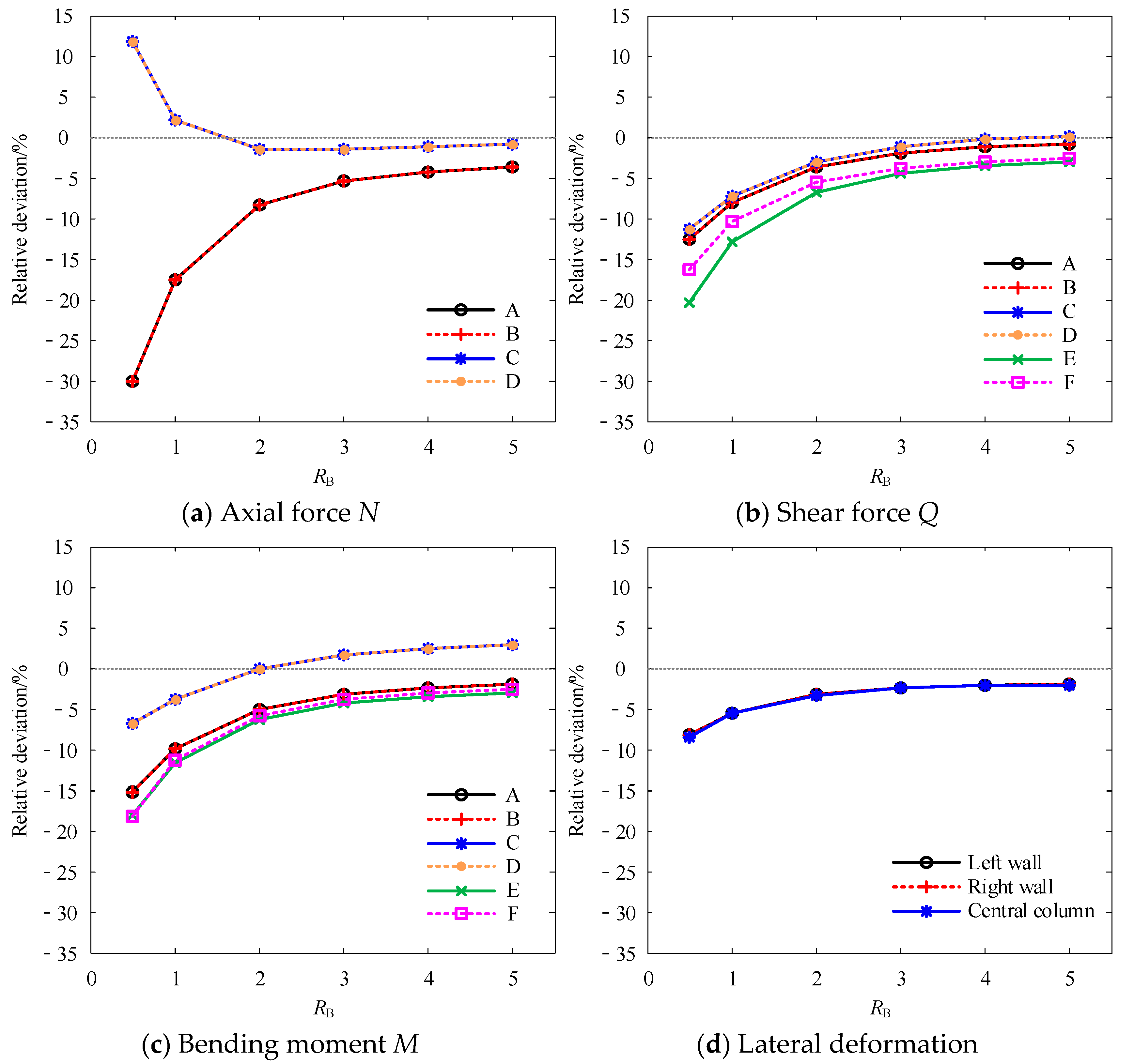
Figure 7 presents the variation in the relative errors of the internal forces and lateral deformations of the underground structure with the R_B. Overall, the errors significantly increase with increasing R_B. Specifically, as R_B increases from 0.5 to 5.0, the axial force errors at Sections A and B decrease from −30.02% to −3.70%; the shear force error at Section E decreases from −20.38% to −3.06%; the bending moment error at Section F decreases from −18.19% to −2.63%; and the lateral deformation error of the central column decreases from −8.49% to −2.04%.

Further analysis reveals that for R_B between 0.5 and 3.0, errors in internal forces and lateral deformations decrease markedly with increasing R_B. However, when R_B ≥ 3.0, the error variations stabilize and remain consistently below 5%.

3.2.2. Soil Stress

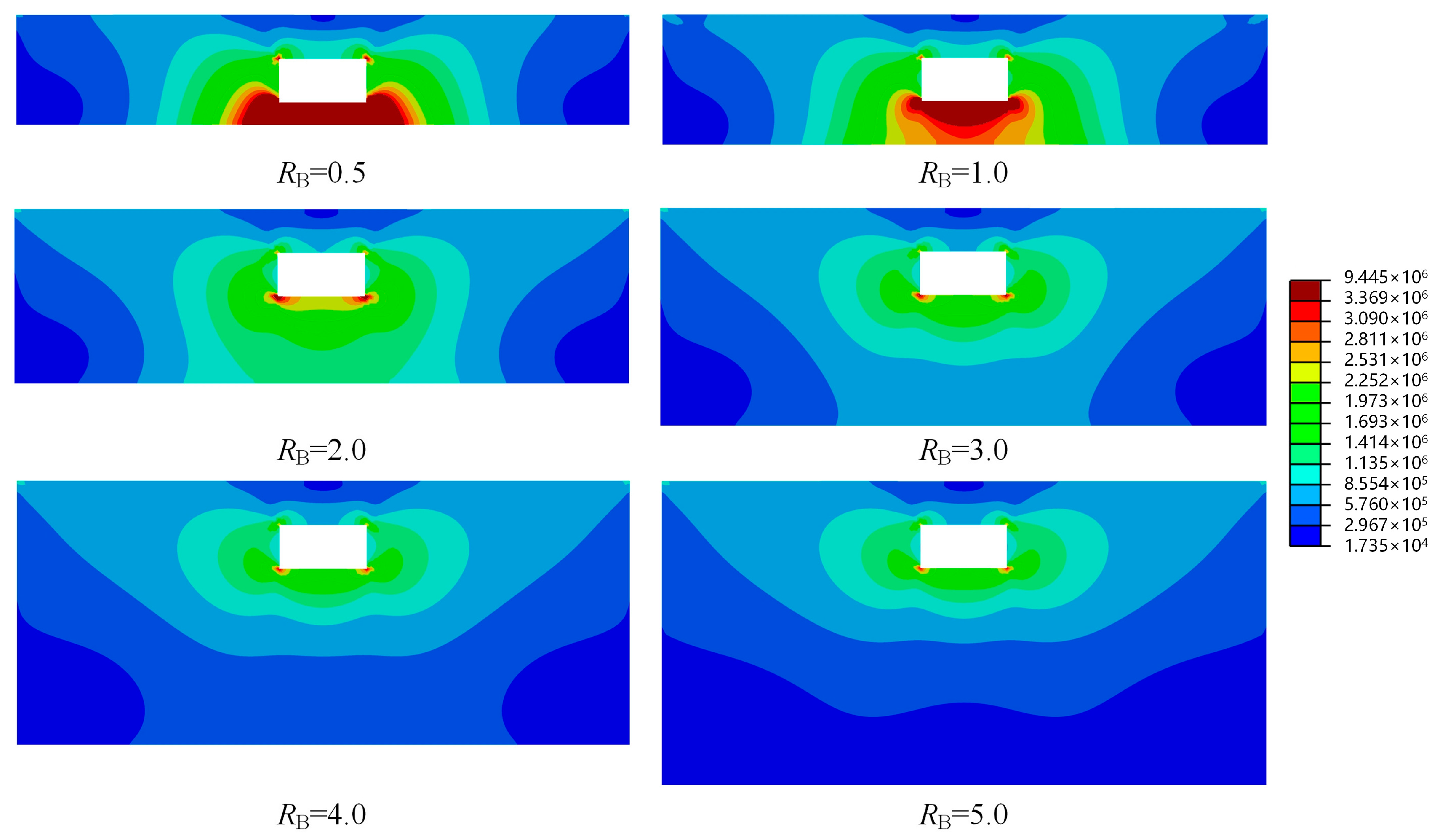
Figure 8 presents the shear stress distributions in the geotechnical medium under varying R_B. As R_B increases, the shear stress levels in the soil surrounding the structure gradually decrease, indicating a weakening of the constraints imposed by the bottom boundary. Specifically, when R_B ≤ 1.0, the bottom boundaries are too close to the structure, imposing excessive constraints and causing elevated stress levels in the surrounding area, especially near the floor. As R_B increases to the range of 2.0–3.0, the shear stress levels around the structure decrease significantly, although residual boundary effects remain observable. When R_B ≥ 3.0, the influence of the bottom boundary on the soil stresses becomes negligible, and the shear stress distribution stabilizes to a converged state.

A comprehensive analysis reveals that the bottom boundary distance plays a crucial role in the computational accuracy of the IRDM. When the bottom boundary is too close to the structure, the intensified constraints imposed by fixed boundaries distort the stress distributions in the surrounding soil, thereby undermining computational accuracy and resulting in reliability. To ensure the validity of the IRDM, the vertical distance from the structural floor to the bottom boundary should be set to at least three times the vertical height of the underground structure while also adhering to prescribed lateral boundary distance requirements.

3.3. Theoretical Basis and Engineering Specification Consensus

According to the classical theory of body wave (P- and S-wave) propagation in elastic media [25], the displacement amplitude of a wave field radiating from a point source obeys a geometric spreading law:

u(r)∝1/r

(1)

where r is the radial distance from the source. Consequently, the kinetic energy density decays proportionally to ${\displaystyle \frac{1}{r^2}}$.

If the lateral boundary distance is taken as r = 3 L, the total round–trip distance for a reflected wave becomes 2r = 6 L, and the reflected energy density is ${\left({\displaystyle \frac{1}{2r}}\right)}^2$ = ${\displaystyle \frac{1}{36}}$ ≈ 2.78%. This implies that less than 3% of the original wave energy returns to the structure, meeting the noninterference threshold proposed by Lysmer’s radiation damping theory [26], which stipulates that reflected energy below 5% has negligible influence. Solving the energy decay inequality ${\left({\displaystyle \frac{1}{2r}}\right)}^2\le 0.05$ yields r ≥ 2.24 L, and adopting r = 3 L as a conservative integer multiple ensures safe truncation.

The proposed criterion aligns with the Standard for Seismic Design of Underground Structures [6]: “The boundary distance in time history analysis should not be less than three times the characteristic dimension of the structure to ensure full attenuation of far-field wave effects”.

Japan’s Tunnel Seismic Design Guide [27] and ASCE standards in the U.S. [28] also adopt similar guidelines.

This consistency demonstrates the broad professional consensus supporting the 3 L guideline as a practical, validated approach in seismic modeling.

4. An Improved Integral Response Deformation Method Considering Far-Field Effects

In the IRDM, ideal boundary conditions should ensure that non-free-field displacements resulting from uncoordinated motion between the soil and structure undergo sufficient attenuation, thereby accurately capturing the confinement effects of the external infinite medium. On the basis of the preceding analysis, the lateral boundary distance (L_S) and vertical bottom boundary distance (H_B) must each reach three times the structural width (3 L) and height (3H), respectively, to ensure the accuracy of the IRDM. However, for large-scale three-dimensional seismic analyses of underground structures, such boundary configurations lead to excessively large computational models, significantly increasing modeling complexity and computational costs.

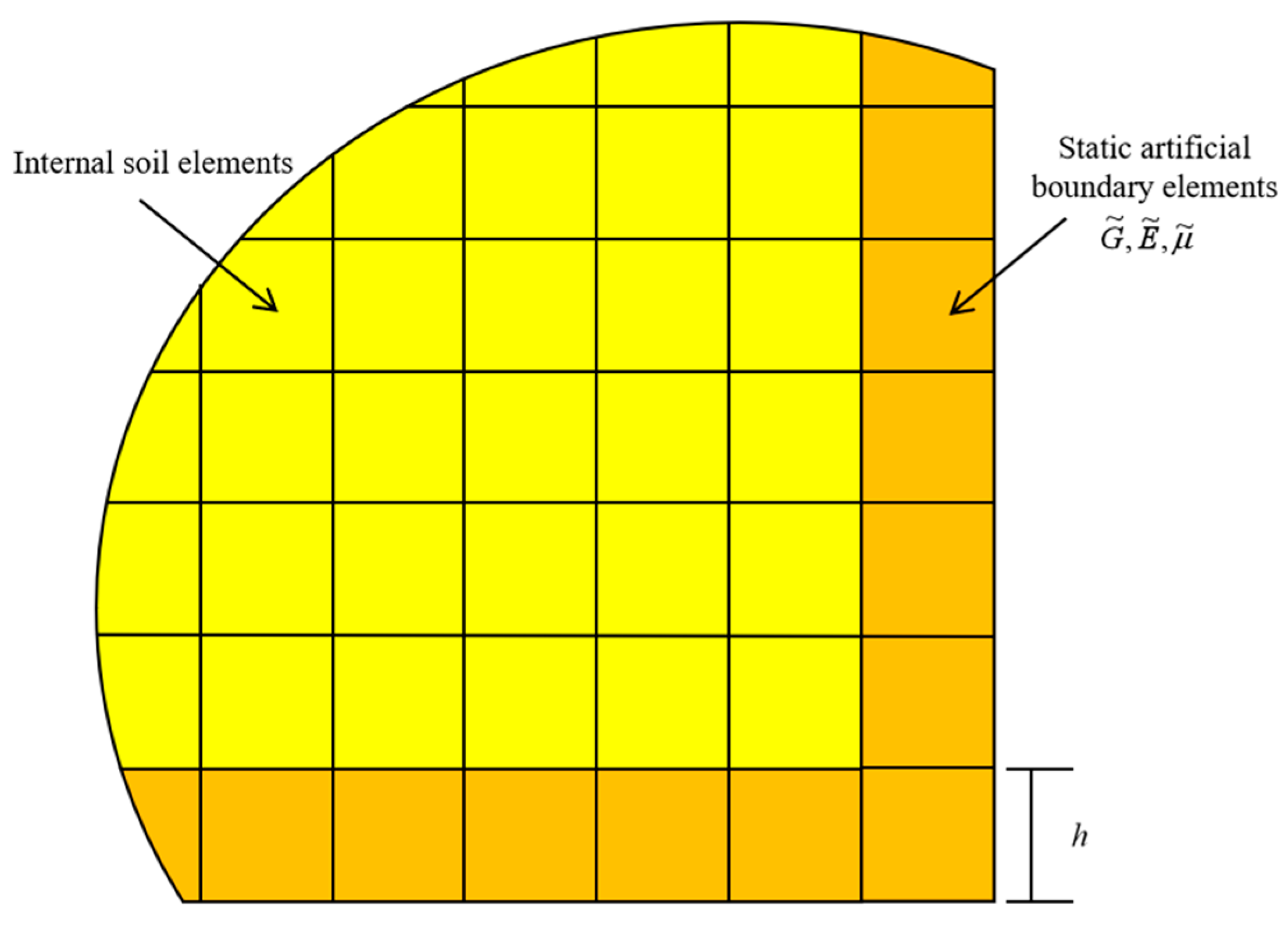
To address these challenges, boundary conditions that simulate the static resistance of semi-infinite foundations and far-field constraint effects, namely, static artificial boundaries, can be introduced into computational models, thereby reducing the required analysis domain. For dynamic problems, researchers have developed a variety of artificial boundary methods to consider the wave radiation in an infinite domain. Our research team has conducted extensive research and proposed several artificial boundary techniques, including viscoelastic artificial boundaries and viscoelastic artificial boundary elements. By degenerating the viscoelastic artificial boundary into static conditions, a static artificial boundary element suitable for the IRDM can be derived, as shown in Figure 9, with its shear modulus ($\tilde{G}$), Young’s modulus ($\tilde{E}$), and Poisson’s ratio ($\tilde{\mu }$) determined as follows:

$$\tilde{\mathrm{G}}={\mathsf{\alpha }}_{\mathrm{T}} \mathrm{h}{\displaystyle \frac{\mathrm{G}}{\mathrm{R}}},\tilde{\mathrm{E}}={\mathsf{\alpha }}_{\mathrm{N}} \mathrm{h}{\displaystyle \frac{\mathrm{G}}{\mathrm{R}}}\times {\displaystyle \frac{(1+\tilde{\mathsf{\mu }})(1-2\tilde{\mathsf{\mu }})}{1-\tilde{\mathsf{\mu }}}},\tilde{\mathsf{\mu }}={\displaystyle \frac{\mathsf{\alpha }-2}{2(\mathsf{\alpha }-1)}}$$

(2)

Here, h denotes the thickness of the equivalent element, R represents the distance from the structure to the boundary node, G represents the shear modulus of the geological medium, and $\mathsf{\alpha }={\mathsf{\alpha }}_{\mathrm{N}}/{\mathsf{\alpha }}_{\mathrm{T}}$, ${\mathsf{\alpha }}_{\mathrm{T}}$, and ${\mathsf{\alpha }}_{\mathrm{N}}$ represent the tangential and normal artificial boundary parameters, respectively.

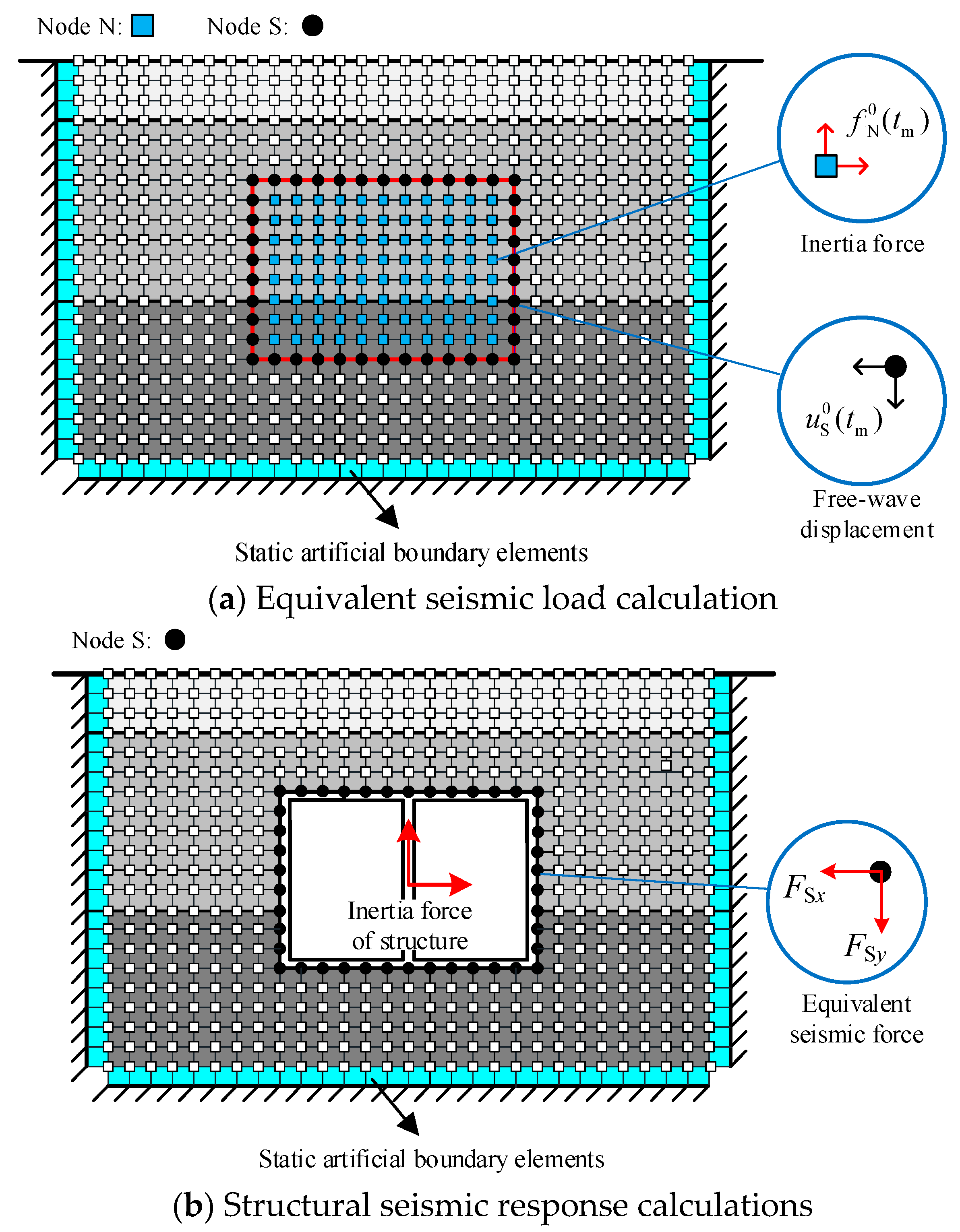
By incorporating static artificial boundary elements into the IRDM, an improved IRDM considering far-field effects is proposed. The implementation processes are as follows:

(1)

Free-Field Seismic Response Analysis

Free-field seismic analysis is performed via standard finite element solvers (e.g., ANSYS 2022R1, ABAQUS 2022(64bit), Plaxis 3D 2024, or FLAC 3D 3.0-261) to obtain free-field displacements and accelerations at the structural location under vertically propagating seismic waves. The critical time instants corresponding to peak seismic responses are extracted.

(2)

Equivalent seismic load calculation

A free-field soil finite element model with an outer layer of static artificial boundary elements (material properties defined by Equation (2)) and fixed exterior nodes is constructed. The free-field displacements from Step 1 at the soil–structure interface nodes are applied, and free-field inertial forces are imposed on the internal nodes (Figure 10a). Then, the nodal reaction forces at the interface are computed as the equivalent seismic loads.

(3)

Structural inertial force calculation

Determine the structural inertial forces at critical time instants via the free-field accelerations obtained in Step 1.

(4)

Integrated Static Analysis

An SSI model with an outer layer of static artificial boundary elements (material properties defined by Equation (2)) and fixed exterior nodes is developed. The equivalent seismic loads and structural inertial forces at designated positions (Figure 10b) are applied to derive the seismic responses through static computation.

Key adaptability notes for engineers:

(1)

Static artificial boundary elements: these can be implemented as equivalent solid elements with adjusted material properties (Equation (2)) in any software supporting user-defined material models.

(2)

Load application: free-field displacements and inertial forces are applied via standard nodal displacement/force boundary conditions.

(3)

Static analysis workflow: this method avoids dynamic solvers and relies solely on static analysis modules available in all commercial FE software such as ANSYS 2022R1.

5. Analysis of the Effects of Artificial Boundary Parameters on Computational Accuracy

To investigate the optimal static artificial boundary parameter values, a computational model of the IRDM accounting for far-field medium effects is established. The lateral and bottom boundaries are set at 0.5 times the structural width and height (R_S = R_B = 0.5), respectively. The artificial boundary parameter α_T is assigned values of 0.35, 0.5, 0.75, and 1.0, with the parameter α_N set to twice α_T on the basis of Liu et al.’s study. 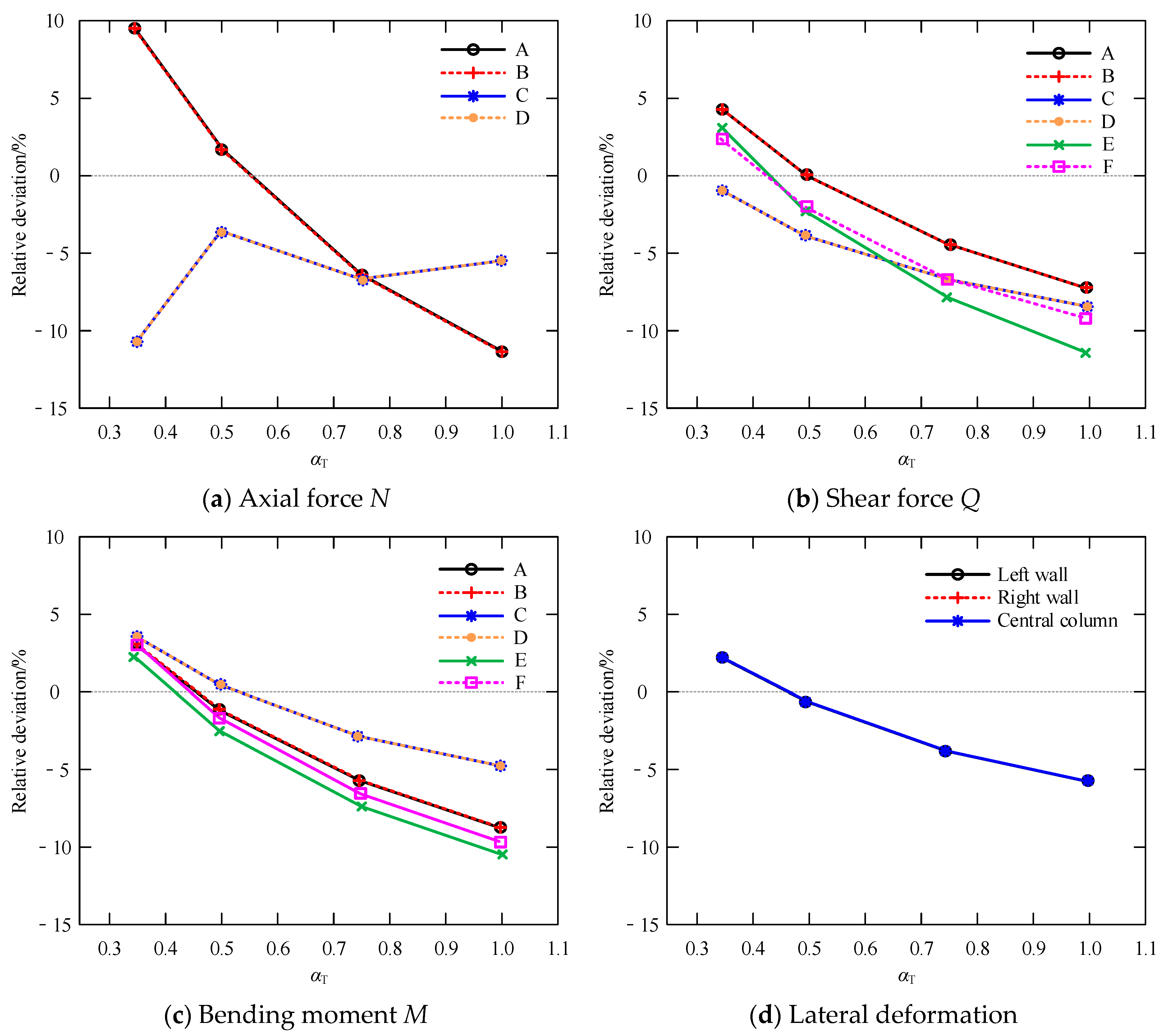By calculating the internal forces (axial force N, shear force Q, and bending moment M) and lateral deformations of vertical structural members and comparing these results with those of dynamic time history analyses, the relative errors under different α_T conditions are systematically evaluated, as shown in Figure 11.

The analysis results indicate that as α_T increases from 0.35 to 1.0, the computational errors of the proposed method initially decrease and subsequently increase. When α_T increases from 0.35 to 0.5, the errors transition from positive to negative. This phenomenon arises because insufficient artificial boundary stiffness at lower α_T values prevents static foundation reactions from adequately balancing non-free-field displacements caused by soil–structure kinematic incompatibility. The unbalanced residual displacements are superimposed onto free-field displacements and are converted into equivalent seismic loads, leading to overestimation of internal forces and deformations. As α_T further increases from 0.5 to 1.0, non-free-field displacements are effectively balanced; however, excessive boundary stiffness introduces overconstraint effects on the SSI model, gradually amplifying errors. A comprehensive evaluation demonstrates that the optimal parameters α_T = 0.5 and α_N = 1.0 minimize computational errors while achieving an ideal balance between accuracy and model complexity, which is a recommended configuration.

6. Case Study Validation

To validate the effectiveness of the proposed IRDM and the rationality of its parameter configuration, the underground structure model described in Section 3.1 is adopted. Six SSI models are established with dimensionless boundary distance ratios R = R_S = R_B set to 0.5, 1.0, 2.0, 3.0, 4.0, and 5.0. Seismic responses under the Kobe, Loma Prieta, and Northridge earthquake records are computed via three approaches: the dynamic time history method, the conventional IRDM, and the proposed improved IRDM (with artificial boundary parameters of α_T = 0.5 and α_N = 1.0). The ground surface acceleration time histories of the three seismic motions are shown in Figure 4 and Figure 12, with the peak ground acceleration (PGA) normalized to 0.1 g and a time step of 0.01 s.

6.1. Computational Accuracy Analysis

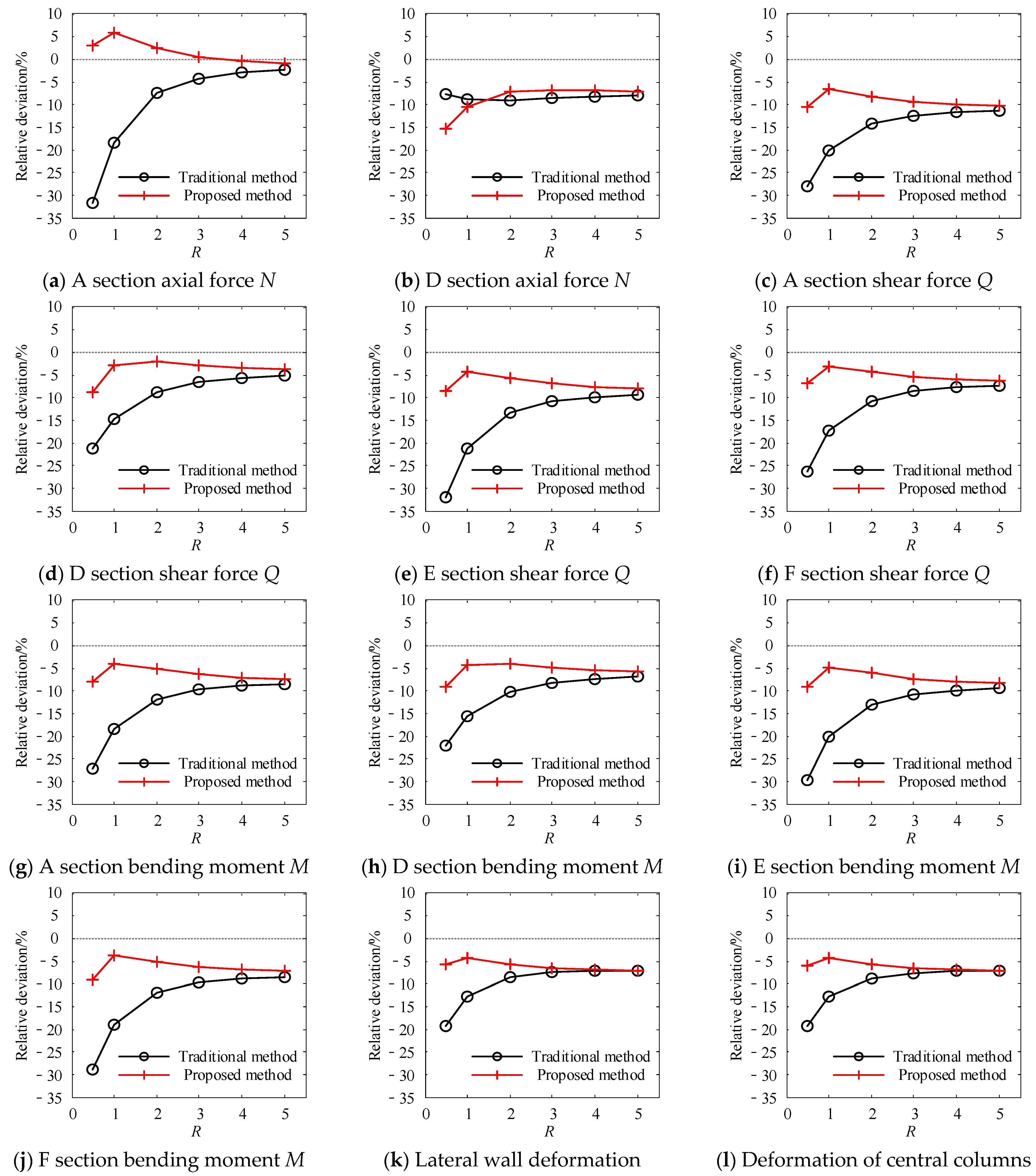
Figure 13, Figure 14 and Figure 15 illustrate the error variation trends of the internal forces at critical cross-sections and lateral deformations of vertical structural members calculated via the proposed method and conventional methods relative to the dynamic time history results, plotted against the dimensionless boundary distance ratio R, under three real earthquake records. Owing to the consistent internal forces between Sections A and B, as well as between Sections C and D, and the identical deformation patterns of the left and right sidewalls, the graphical representations are simplified. For each seismic scenario, only the internal force results for Section A and Section D, along with the deformation results for the left sidewall, are displayed.

Table 1. Internal forces at selected sections and deformation of the central columns under different loading cases.

RT	Seismic Wave	Method	A section Axial Force N (kN)	E Section Shear Force Q (kN)	F Section Bending Moment M (kN·m)	Deformation of Central Columns (mm)
0.5	Loma Prieta	Dynamic time history method	−31.54	−11.51	−32.91	−0.6801
		Traditional IRDM	−21.52 (−31.78%)	−7.82 (−32.07%)	−23.42 (−28.82%)	−0.5482 (−19.39%)
		New method	−32.48 (2.96%)	−10.51 (−8.66%)	−30.44 (−7.50%)	−0.6403 (−5.85%)
	Kobe	Dynamic time history method	−32.54	−10.85	−31.87	−0.6587
		Traditional IRDM	−21.92 (−32.64%)	−7.88 (−27.35%)	−24.24 (−23.93%)	−0.5616 (−14.74%)
		New method	−33.09 (1.71%)	−10.62 (−2.12%)	−31.38 (−1.54%)	−0.6542 (−0.69%)
	Northridge	Dynamic time history method	−31.88	−11.32	−32.66	−0.6703
		Traditional IRDM	−21.96 (−31.11%)	−8.06 (−28.84%)	−23.94 (−26.70%)	−0.5603 (−16.40%)
		New method	−33.19 (4.11%)	−10.82 (−4.41%)	−31.14 (−4.64%)	−0.6555 (−2.20%)
1.0	Loma Prieta	Dynamic time history method	−31.54	−11.51	−32.91	−0.6801
		Traditional IRDM	−25.77 (−18.31%)	−9.06 (−21.27%)	−26.64 (−19.03%)	−0.5923 (−12.91%)
		New method	−33.37 (5.80%)	−11.02 (−4.23%)	−31.68 (−3.72%)	−0.6512 (−4.25%)
	Kobe	Dynamic time history method	−32.54	−10.85	−31.87	−0.6587
		Traditional IRDM	−26.26 (−19.30%)	−9.15 (−15.73%)	−27.51 (−13.67%)	−0.6058 (−8.03%)
		New method	−34.01 (4.52%)	−11.14 (2.64%)	−32.64 (2.41%)	−0.6651 (0.97%)
	Northridge	Dynamic time history method	−31.88	−11.32	−32.66	−0.6703
		Traditional IRDM	−26.29 (−17.52%)	−9.33 (−17.57%)	−27.24 (−16.57%)	−0.6057 (−9.63%)
		New method	−34.11 (7.00%)	−11.35 (0.24%)	−32.43 (−0.70%)	−0.6671 (−0.46%)
5.0	Loma Prieta	Dynamic time history method	−31.54	−11.51	−32.91	−0.6801
		Traditional IRDM	−30.79 (−2.40%)	−10.43 (−9.38%)	−30.14 (−8.40%)	−0.6319 (−7.09%)
		New method	−31.26 (−0.89%)	−10.58 (−8.02%)	−30.54 (−7.20%)	−0.6320 (−7.07%)
	Kobe	Dynamic time history method	−32.54	−10.85	−31.87	−0.6587
		Traditional IRDM	−31.37 (−3.57%)	−10.54 (−2.90%)	−31.08 (−2.50%)	−0.6458 (−1.96%)
		New method	−31.86 (−2.08%)	−10.70 (−1.43%)	−31.48 (−1.23%)	−0.6457 (−1.98%)
	Northridge	Dynamic time history method	−31.88	−11.32	−32.66	−0.6703
		Traditional IRDM	−31.43 (−1.41%)	−10.74 (−5.17%)	−30.84 (−5.57%)	−0.6467 (−3.51%)
		New method	−31.91 (0.10%)	−10.90 (−3.77%)	−31.23 (−4.35%)	−0.6473 (−3.43%)

systematically summarizes the internal forces and deformation results for key sections obtained via different computational methods from the three earthquake records.

The proposed method has significant advantages in terms of computational accuracy over the conventional IRDM. Under various seismic excitations, the errors of the new method are generally controlled within 5%, with a maximum error not exceeding 10%, which is markedly superior to the conventional method’s maximum error of −32.64%. As the boundary distance ratio R varies, the errors of the new method initially decrease but then increase, ultimately converging with the conventional method’s error curves toward the same asymptote. This behavior arises because at smaller R values, the artificial boundaries not only balance non-free-field displacements induced by soil–structure kinematic incompatibility, but also provide sufficient constraints to the computational model, whereas as R increases, the constraining effects of artificial boundaries gradually diminish. When R becomes sufficiently large, the boundary type exerts a negligible influence on the results, leading to convergence between different boundary configurations. Furthermore, the proposed method demonstrates enhanced computational accuracy under boundary distance ratios of R = 0.5 and 1.0, exhibiting significantly lower errors than conventional methods while effectively reducing the computational scale. This dual advantage of precision and efficiency renders the method particularly suitable for seismic response analysis of large-scale, complex underground structures, aligning with the stringent requirements of modern seismic design standards.

6.2. Computational Efficiency Comparison

Table 2. Computational efficiency comparison of different analysis methods.

Computational Efficiency Index	New Method			Traditional IRDM (R = 4.0)
	R = 0.5	R = 1.0	R = 2.0
Elements	1836 (91.36%)	3496 (83.55%)	8016 (62.29%)	21,256
Node	2028 (90.69%)	3738 (82.85%)	8358 (61.65%)	21,792

compares the differences in the number of elements and nodes between the proposed method and the conventional method, with the reduction percentages relative to those of the conventional method indicated in parentheses. The results demonstrate that the proposed method significantly reduces both element and node counts. When the dimensionless boundary distance ratio R is set to 0.5, the element and node quantities are reduced by more than 90%, confirming that the new method substantially lowers the computational complexity and resource demands while maintaining accuracy. This advancement provides a more efficient and economical solution for the seismic design and analysis of underground structures.

6.3. Applicability Analysis

The applicability of the proposed method is further examined under varying medium stiffness and structural stiffness conditions.

First, the applicability of the proposed method under varying medium stiffnesses is assessed while keeping all other model parameters consistent with those outlined in Section 3. The dimensionless boundary distance ratio is set to R = 0.5, and the artificial boundary parameters are specified as α_T = 0.5 and α_N = 1.0.

In this analysis, only the shear wave velocity of the surrounding soil medium is varied. The internal force and deformation responses of the underground structure, which are calculated via the proposed method under Kobe wave excitation, are compared with those obtained via the dynamic time history method for soil shear wave velocities of 140 m/s, 200 m/s, 300 m/s, and 600 m/s. The corresponding comparison results are summarized in

Table 3. Internal forces at selected sections and deformation of the central columns under different soil shear velocities.

Soil Shear Velocity/(m/s)	Method	A section Axial Force N (kN)	E section Shear Force Q (kN)	F section Bending Moment M (kN·m)	Deformation of Central Columns (mm)
140	Dynamic time history method	−34.80	−22.64	−63.02	−1.6181
	Proposed method	−34.44 (−1.03%)	−22.34 (−1.33%)	−62.22 (−1.27%)	−1.5987 (−1.20%)
200	Dynamic time history method	−35.41	−17.68	−49.90	−1.1003
	Proposed method	−35.02 (−1.10%)	−17.10 (−3.28%)	−48.50 (−2.81%)	−1.0801 (−1.84%)
300	Dynamic time history method	−32.54	−10.85	−31.87	−0.6587
	Proposed method	−33.09 (1.71%)	−10.62 (−2.12%)	−31.38 (−1.54%)	−0.6542 (−0.69%)
600	Dynamic time history method	−29.14	−2.78	−11.65	−0.2342
	Proposed method	−27.57 (−5.39%)	−2.65 (−4.68%)	−11.32 (−2.83%)	−0.2277 (−2.78%)

.

As shown in Table 3, the errors in the axial force, shear force, bending moment, and deformation calculated via the proposed method under varying medium stiffnesses are all within 6%. Moreover, as the shear wave velocity of the surrounding soil medium decreases, the errors tend to diminish.

The applicability of the proposed method is further examined under varying structural stiffness conditions. Let the elastic modulus of the structural material in Section 3 be denoted as E*. In this analysis, the elastic modulus E_s is set to 0.5E*, 1.5E*, and 2.0E*, while all other parameters remain consistent with those in Section 3. The dimensionless boundary distance ratio is fixed at R = 0.5, and the artificial boundary parameters are set to α_T = 0.5 and α_N = 1.0.

Seismic response analyses of the underground structure under Kobe wave excitation are performed via both the proposed method and the dynamic time history method. A comparative study is conducted, and the results are presented in

Table 4. Internal forces at selected sections and deformation of the central columns under different structural stiffnesses.

Es/E*	Method	A Section Axial Force N (kN)	E Section Shear Force Q (kN)	F Section Bending Moment M (kN·m)	Deformation of Central Columns (mm)
0.5	Dynamic time history method	−32.07	−6.02	−19.75	−0.8016
	Proposed method	−32.87 (2.49%)	−5.83 (−3.16%)	−19.11 (−3.24%)	−0.7798 (−2.72%)
1	Dynamic time history method	−32.54	−10.85	−31.87	−0.6587
	Proposed method	−33.09 (1.71%)	−10.62 (−2.12%)	−31.38 (−1.54%)	−0.6542 (−0.69%)
1.5	Dynamic time history method	−34.11	−14.27	−40.49	−0.5718
	Proposed method	−32.75 (−3.99%)	−13.24 (−7.22%)	−39.04 (−3.58%)	−0.5539 (−3.13%)
2	Dynamic time history method	−34.63	−16.83	−46.92	−0.5114
	Proposed method	32.98(−4.76%)	−16.00 (−4.93%)	−44.91 (−4.28%)	−0.5011 (−2.01%)

.

The results indicate that the errors in the internal force and deformation calculated via the proposed method remain within 8% across all structural stiffness scenarios. Furthermore, as the structural stiffness increases, the calculation errors of the proposed method show minimal variation. This demonstrates that the proposed method offers high computational accuracy and robust applicability, with the influence of structural stiffness on the method’s accuracy being relatively insignificant.

6.4. Applicable Boundaries and Limitations of the Method

While the proposed method has demonstrated robust performance in simulating the seismic responses of underground structures, its current applicability is bounded by the following conditions:

(1)

Geological Complexity

The method is theoretically applicable to deep underground structures and heterogeneous or layered geological media. However, the current validation cases focus on homogeneous soils. Additional verification for stratified or spatially variable soil profiles will strengthen its generalizability.

(2)

Earthquake Type:

The present verification is based solely on horizontal ground motions. The influences of vertical earthquake components and their coupling effects have not yet been considered. To fully capture three-dimensional seismic behavior, the method must be extended to three-dimensional analyses.

(3)

Soil Constitutive Model:

The current framework assumes elastic soil behavior. Thus, it does not account for soil nonlinearity or liquefaction phenomena, which may occur under strong seismic excitation. The incorporation of nonlinear constitutive models is necessary for applications involving severe ground motions or soft soils.

(4)

Structural Type:

The validation is currently limited to single-story underground structures. Structures with complex cross-sectional configurations, such as multicell tunnels or irregular geometries, have not yet been validated and require further verification to confirm the generalizability of the method.

(5)

Boundary Representation Fidelity

Current boundary conditions are based on static artificial boundaries without the incorporation of specialized infinite elements. In future work, the proposed method will be integrated with infinite elements to synergistically enhance both computational efficiency and accuracy.

In addition, a comparative summary table is summarized to enhance clarity and allow better evaluation of the advantages and limitations of each method. The results are presented in

Table 5. Comparison of different methods.

Criteria	Dynamic Time History Method	Conventional IRDM	Improved IRDM
Accuracy	High (benchmark)	Moderate (errors up to 30% for small R)	High (errors < 5% for R = 0.5)
Computational Demands	Very high (full dynamic model)	High (large domain, R ≥ 3.0)	Low (80–90% reduction vs. conventional)
Boundary Treatment	Requires artificial boundaries (e.g., viscoelastic boundary)	Fixed boundaries at R ≥ 3.0	Static artificial boundaries (R ≥ 0.5)
Applicability	Complex 3D/nonlinear analyses	Homogeneous/layered soils	Homogeneous/layered soils
Ease of Use	Complex (time-step integration)	Moderate (empirical boundary placement)	High (small model)

.

7. Conclusions

This study systematically investigates the influence of boundary truncation distances on the computational accuracy of the conventional IRDM. By introducing static artificial boundary conditions simulating semi-infinite medium constraints, an improved IRDM considering the far-field effect is developed. The key findings are as follows:

(1)

The boundary distance in the IRDM significantly affects the computational accuracy. When boundaries are positioned close to the structure, excessive constraining effects degrade precision. To ensure reliable results, the lateral boundary distance must be at least three times the structural span, and the vertical bottom boundary distance must be at least three times the structural height.

(2)

By degenerating viscoelastic dynamic artificial boundaries to static conditions, static artificial boundary conditions are derived to simulate both static foundation reactions and far-field constraint effects. These boundaries are integrated into the IRDM, resulting in an improved methodology that accounts for far-field medium interactions.

(3)

The computational accuracy of the IRDM considering far-field effects is influenced by the static artificial boundary parameters αT and αN and the dimensionless boundary distance ratio R. Through comprehensive numerical analyses, the following optimal parameters are recommended: αT = 0.5, αN =1.0, and R = 0.5 or 1.0. Compared with conventional approaches, the proposed method achieves significantly greater accuracy in terms of these parameters. This advancement provides an efficient and precise solution for seismic response analysis of large-scale underground structures.

(4)

The proposed method facilitates rapid evaluation of multiple structural design schemes—such as variations in cross-sectional geometry or reinforcement layout—during early-stage design. For example, designers can now assess and compare the seismic performance of a three-cell metro station with that of a five-cell metro station within 2–3 h, a significant reduction from the 2–3 days typically required for full dynamic finite element simulations. This acceleration in decision-making efficiency is achieved without compromising compliance with the safety margins stipulated in codes.