Frequency Regulation Provided by Doubly Fed Induction Generator Based Variable-Speed Wind Turbines Using Inertial Emulation and Droop Control in Hybrid Wind–Diesel Power Systems
Abstract
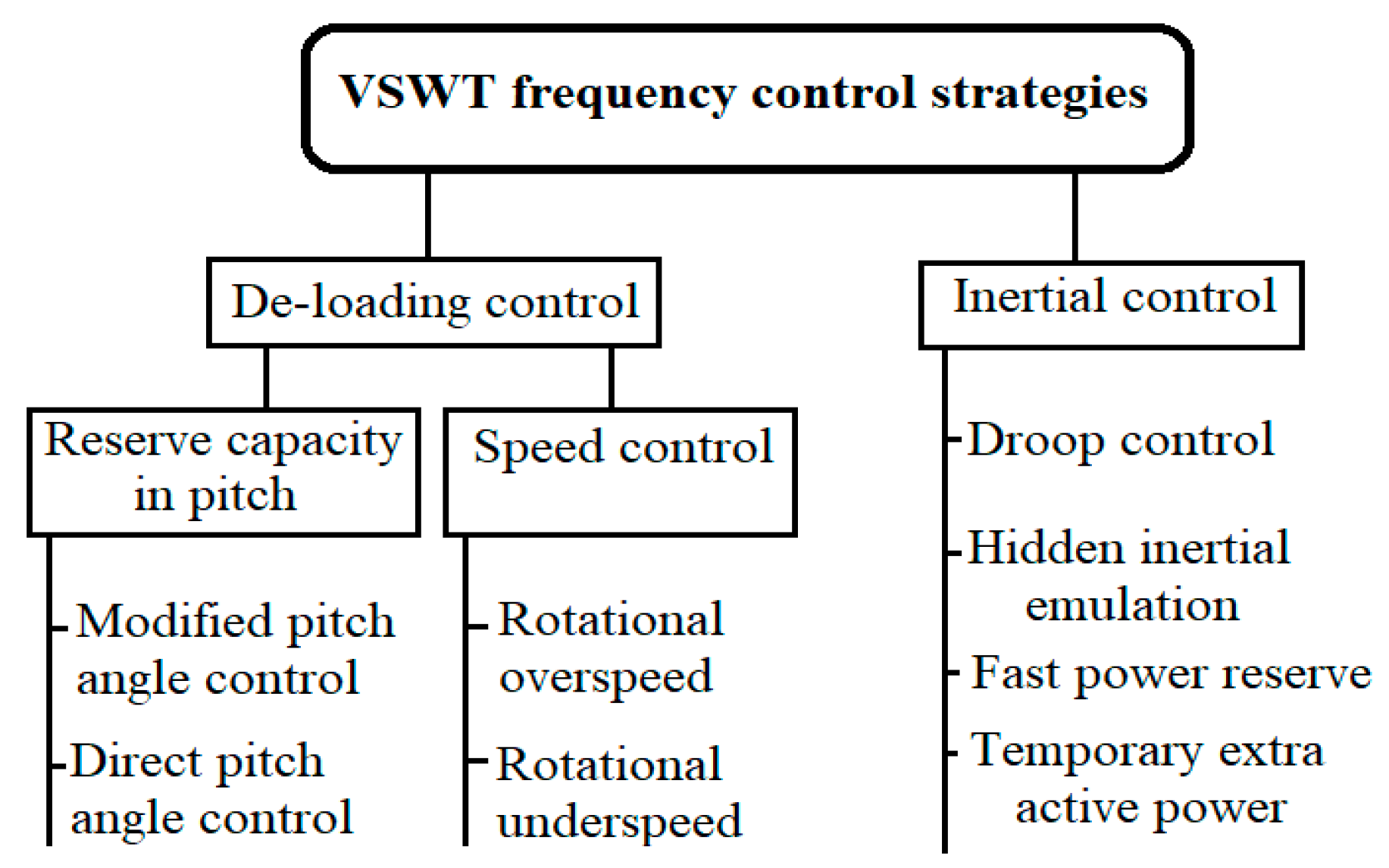
1. Introduction
2. Materials and Methods
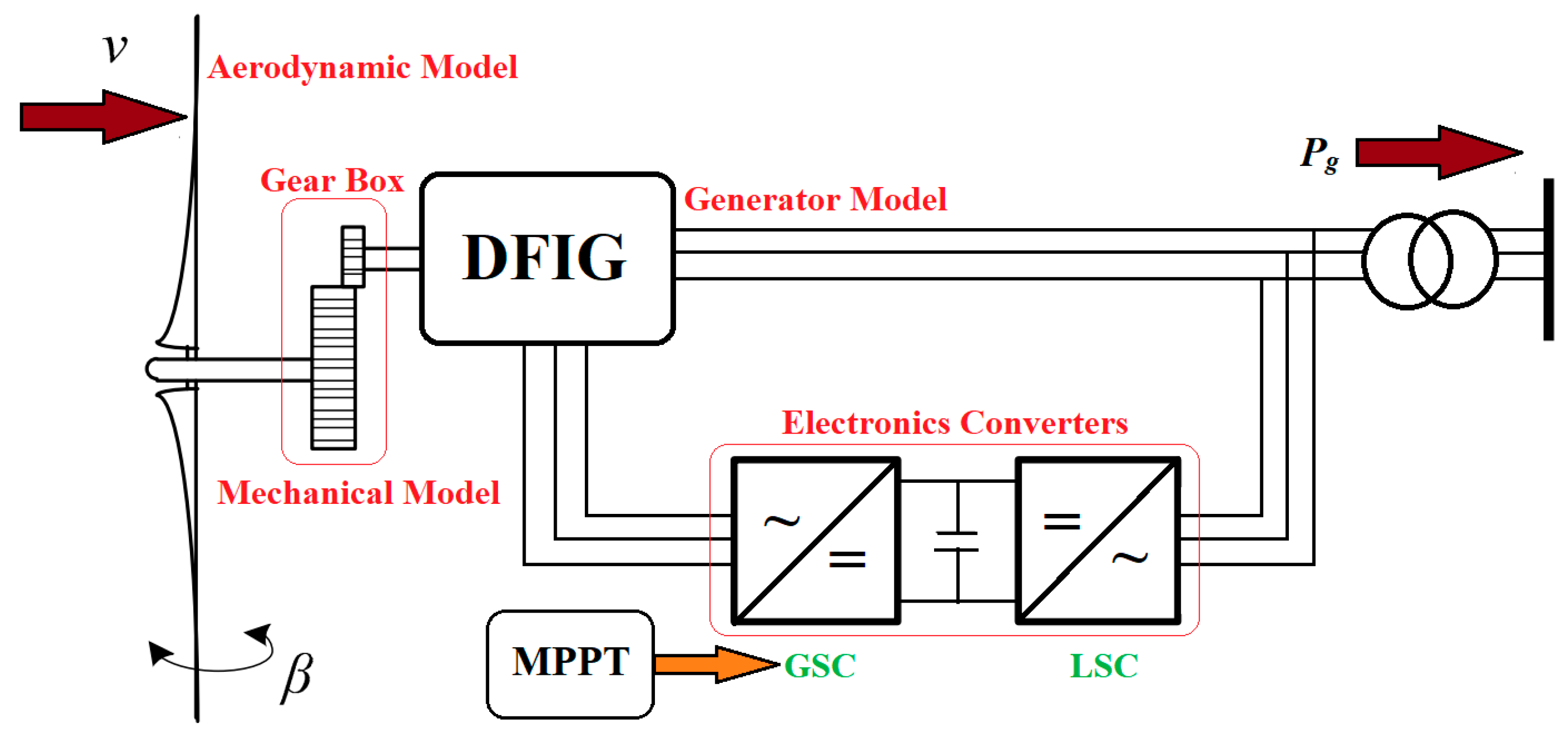
2.1. Wind Turbine (WT) Modeling
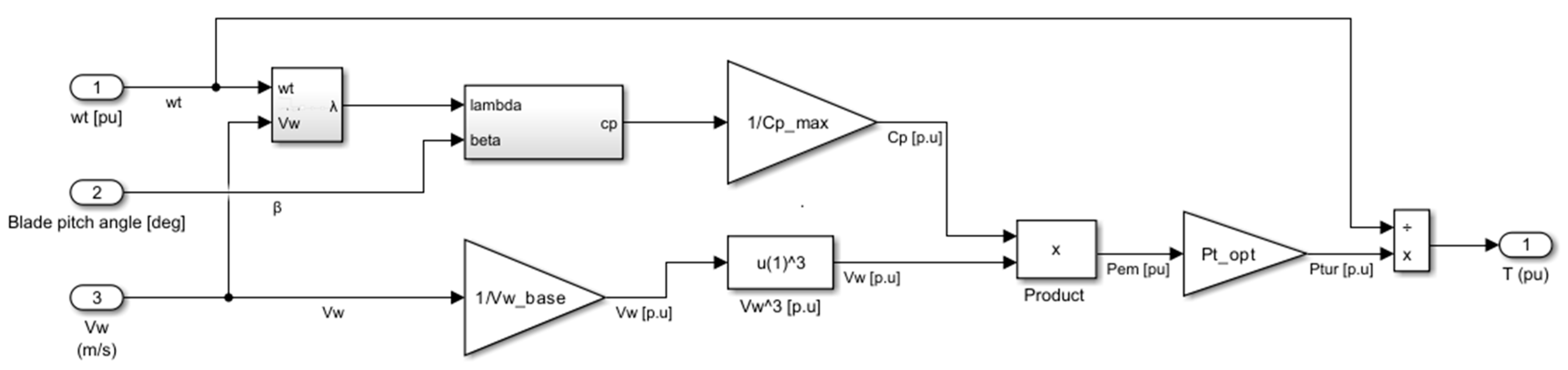
2.1.1. Aerodynamic Model
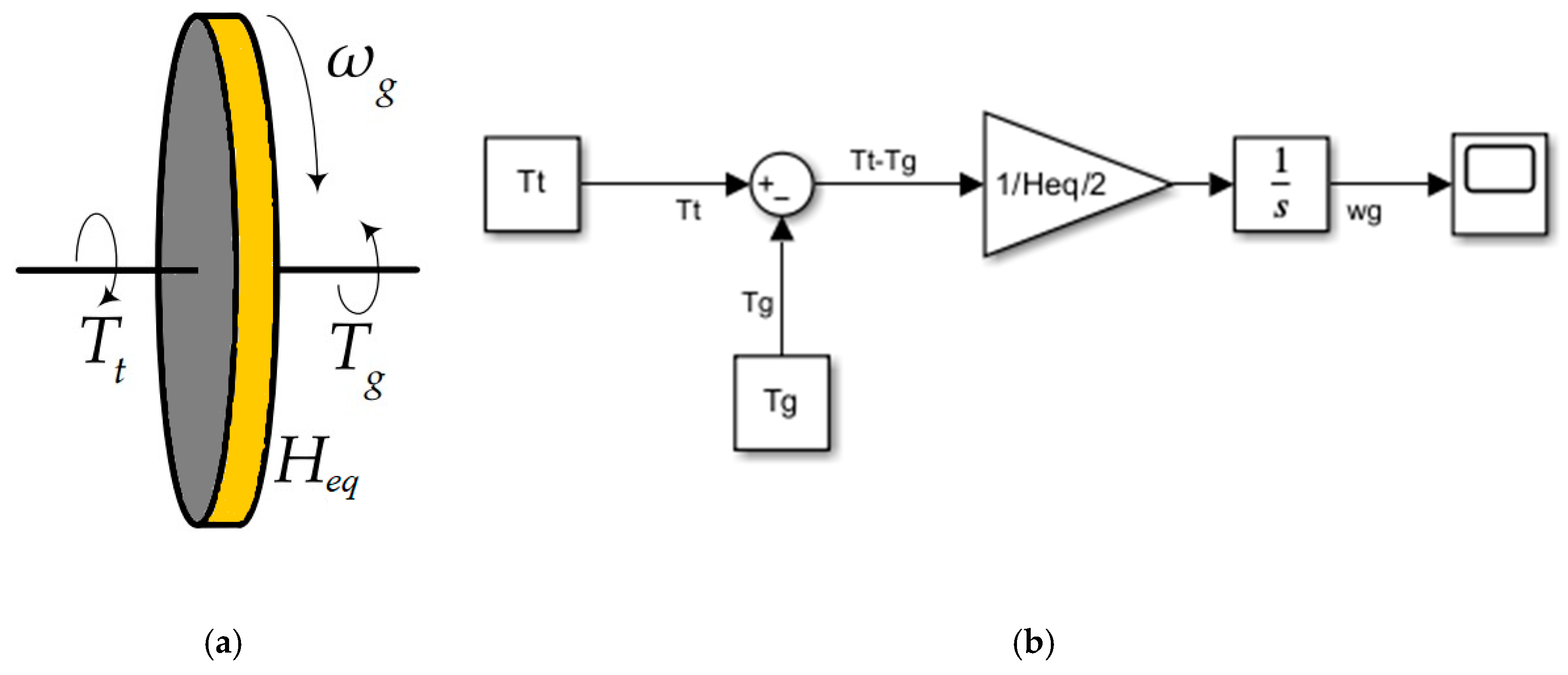
2.1.2. Mechanical Model
2.1.3. DFIG and Converters
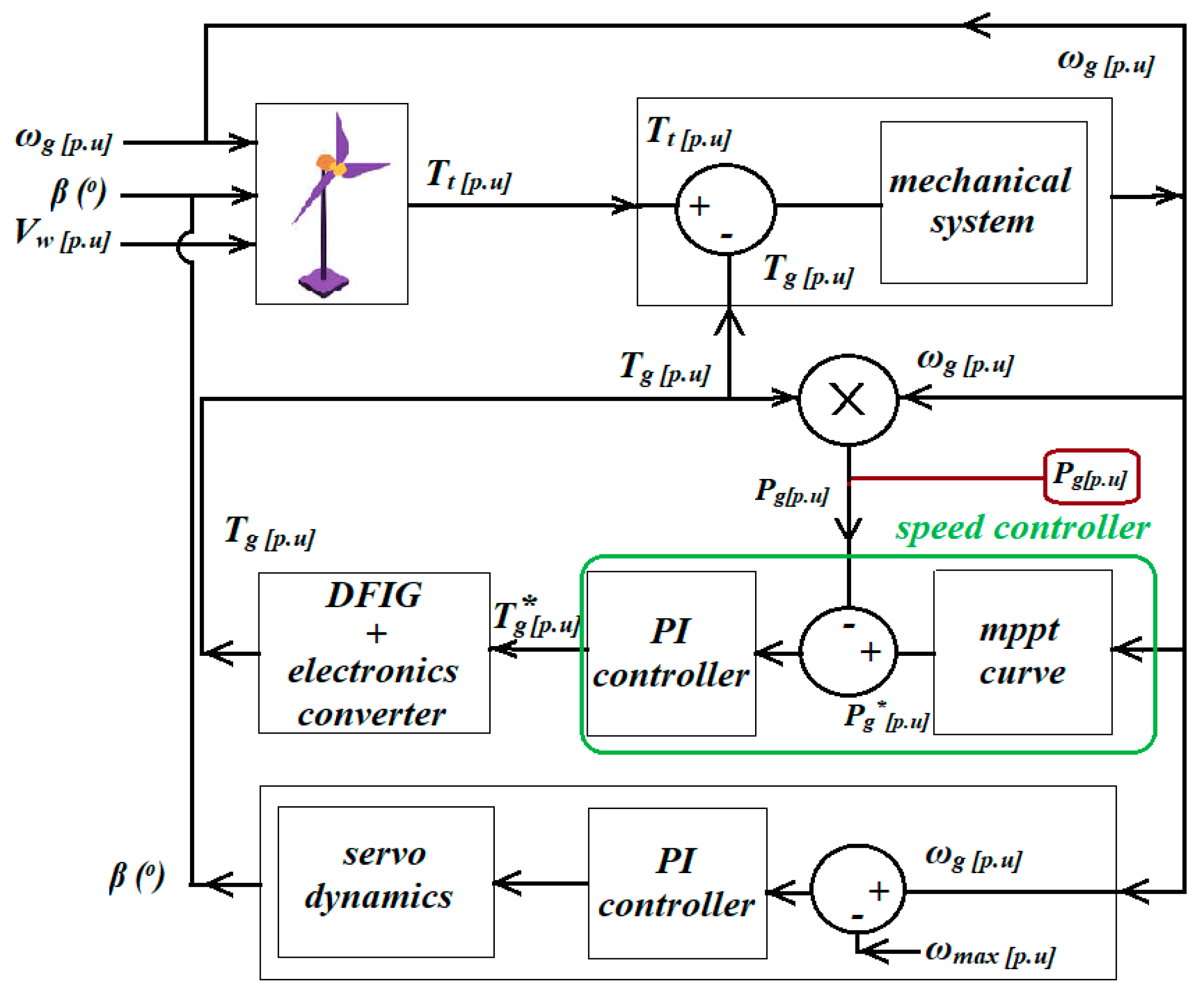
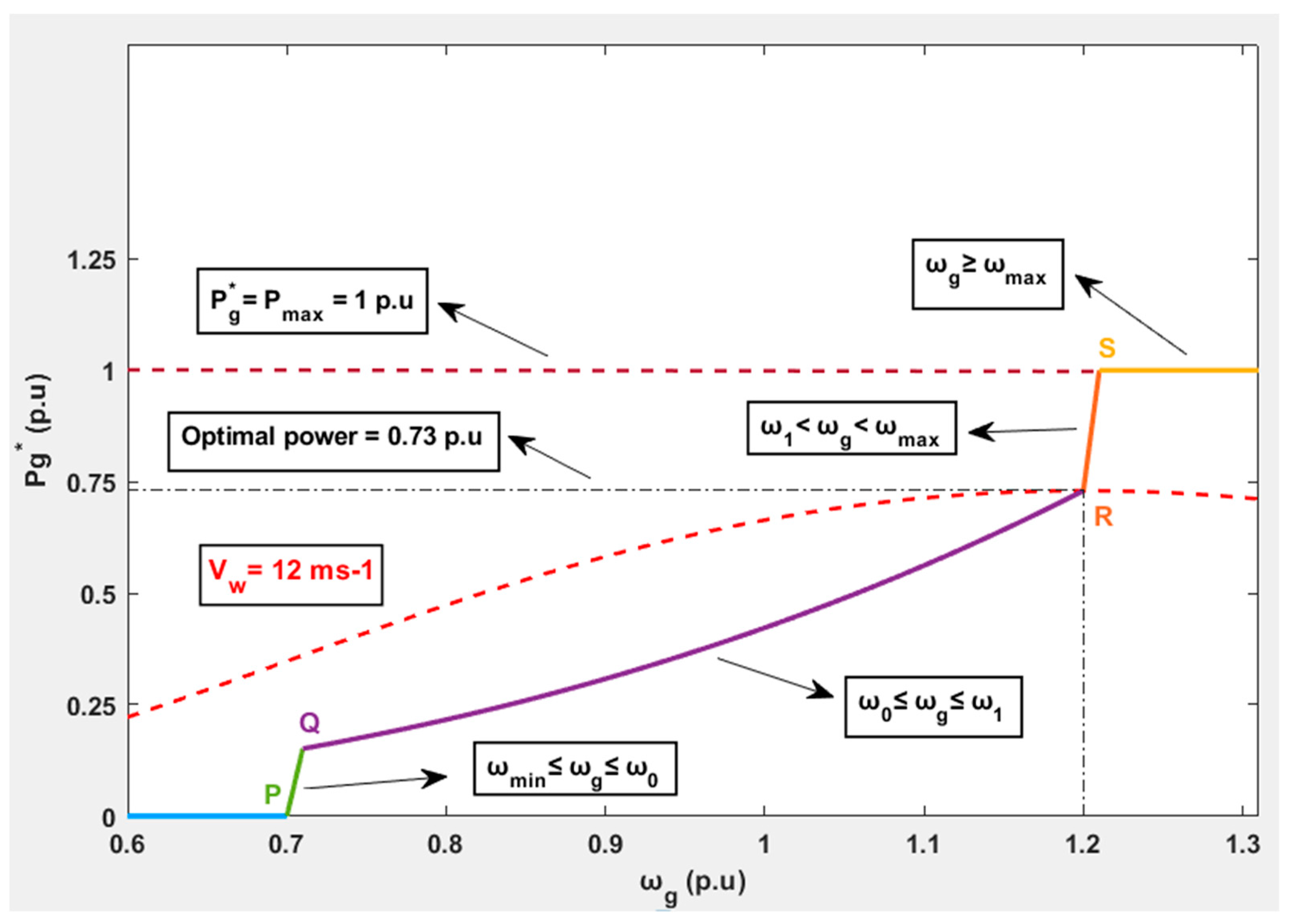
2.1.4. Maximum Power Point Tracking
2.1.5. Blade Pitch Angle Control (BPAC)
2.2. Modeling of Diesel Power Plant (DPP)
3. Proposed Hybrid Wind–Diesel Contribution to Frequency Regulation
3.1. BPAC with Pitch Compensation
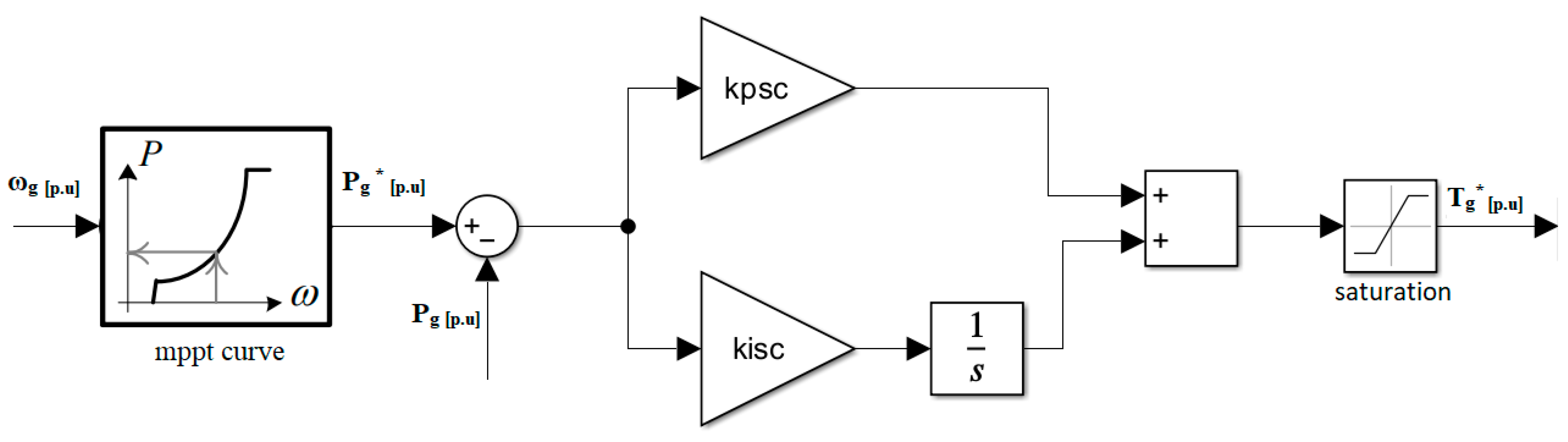
3.2. VSWT Inertial and Proportional (I&P) Control Loops
4. Controller Tuning Methodology
4.1. Base Case: FR Provided by Diesel Governor
4.2. Case A: VSWT Contribution to FR Using Proposed Control Without Tuning Diesel Governor Gain Parameters
4.3. Case B: VSWT Contributes to FR by Tuning the Proposed Controls and Diesel Governor Gain Parameters in Combination
5. Results and Discussion
5.1. VSWT Hybrid WDPS Performance Under Normal Conditions
5.1.1. Ramp Response
5.1.2. Random Response
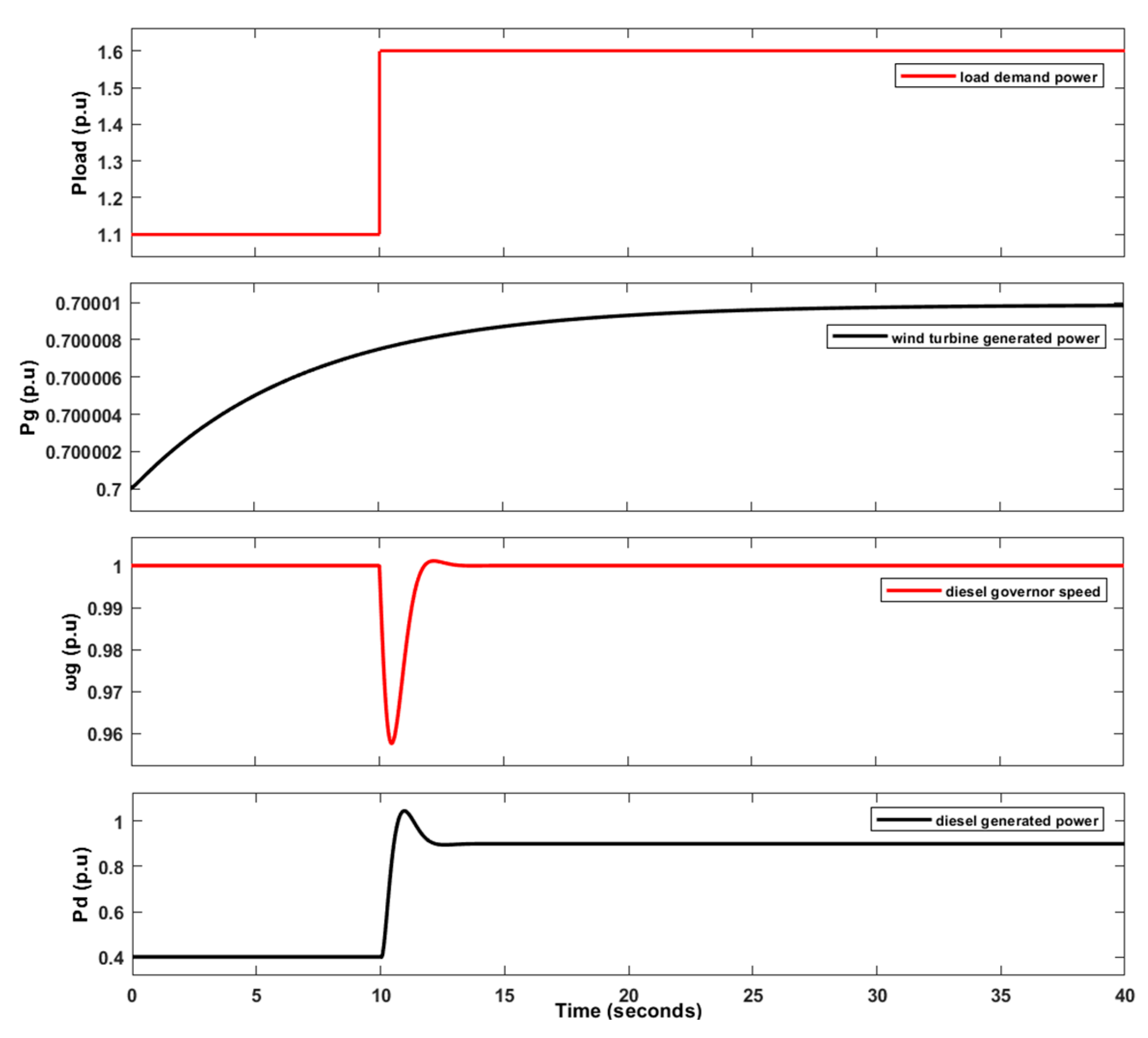
5.2. VSWT Hybrid WDPS Performance Under Abnormal Conditions
5.3. VSWT Hybrid WDPS Performance During Simultaneous Fluctuations in Wind Speed and Load Demand
5.4. Summarized Discussion
6. Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters | Values and Units |
|---|---|
| Model of diesel engine | CAT-3512 DITA |
| Capacity | 813 kVA |
| Rated power | 650 kW |
| Rated frequency | 60 Hz |
| Synchronous speed | 1200 rpm |
| Constant of inertia (HT) | 0.4208 s |
| Torque min/max (Tmin/Tmax) | 0/1.1 pu |
| Time constants: t1, t2, t3 | 0.024 s, 0.1 s, 0.01 s |
| Output voltage | 480 V ± 5% |
| Parameters | Values and Units |
|---|---|
| Base power (Pbase) | 1.5 MW |
| Generator min/max power (Pg,min/Pg,max) | 0.04/1 pu |
| Generator base speed (ωg,base) | 157.08 rad/s |
| Air density | 1.225 kg∙m−3 |
| Speed constant (Kλ) | 63.29 ms−1 |
| Rotor diameter (D) | 77 m |
| Nominal frequency | 50 Hz |
| Nominal wind speed (at Pg = 0.73 p.u) | 12 ms−1 |
| Generator min/max torque | 0.057/0.826 p.u |
| Turbine base speed (ωt,base) | 1.644 rad/s |
| Blade pitch angle min/max | 0/450° |
| Inertial constant (Heq) | 5.29 s |
| Gain parameters of speed controller (Kisc/Kpsc) | 8/0.3 |
| Time constant of blade pitch servo motor (tp) | 0 s |
| Gain parameters of blade pitch controller (Kppc/Kipc) | 0/500 |
| Blade pitch angle rate min/max (dβ/dt) | ±2°/s |
| MPPT optimization constant (Kopt) | 0.4225 |
| MPPT constants c1, c2, c3, c4, c5, c6 | 0.5176, 116, 0.4, 5, 21, 0.0068 |
| MPPT curve speed limits ωmin, ω0, ω1, ωmax | 0.7 p.u, 0.71 p.u, 1.2 p.u, 1.21 p.u |
| Parameters | Values |
|---|---|
| Gain parameter of DG (Kp_d/Ki_d) | 21.01/14.89 |
| VSWT I&P control gain parameters (Kpn/Kdn) | 9/0.47 |
| Pitch compensation gains parameters (Kpc/Kic) | 0/80 |
| BPAC gain parameters (Kppc/Kipc) | 6000/1400 |
References
- Asad, M. Improving Power Flow Using Static Synchronous Series Compensator. Egypt. J. Eng. Sci. Technol. 2021, 33, 69–74. [Google Scholar] [CrossRef]
- Hoseinzadeh, S.; Nastasi, B.; Groppi, D.; Astiaso Garcia, D. Exploring the Penetration of Renewable Energy at Increasing the Boundaries of the Urban Energy System—The PRISMI plus Toolkit Application to Monachil, Spain. Sustain. Energy Technol. Assess. 2022, 54, 102908. [Google Scholar] [CrossRef]
- Dalala, Z.; Al-Omari, M.; Al-Addous, M.; Bdour, M.; Al-Khasawneh, Y.; Alkasrawi, M. Increased Renewable Energy Penetration in National Electrical Grids Constraints and Solutions. Energy 2022, 246, 123361. [Google Scholar] [CrossRef]
- Terlouw, T.; Savvakis, N.; Bauer, C.; McKenna, R.; Arampatzis, G. Designing Multi-Energy Systems in Mediterranean Regions towards Energy Autonomy. Appl. Energy 2025, 377, 124458. [Google Scholar] [CrossRef]
- Deng, X.; Lv, T. Power System Planning with Increasing Variable Renewable Energy: A Review of Optimization Models. J. Clean. Prod. 2020, 246, 118962. [Google Scholar] [CrossRef]
- Impram, S.; Varbak Nese, S.; Oral, B. Challenges of Renewable Energy Penetration on Power System Flexibility: A Survey. Energy Strategy Rev. 2020, 31, 100539. [Google Scholar] [CrossRef]
- Matsumoto, K.; Matsumura, Y. Challenges and Economic Effects of Introducing Renewable Energy in a Remote Island: A Case Study of Tsushima Island, Japan. Renew. Sustain. Energy Rev. 2022, 162, 112456. [Google Scholar] [CrossRef]
- Zhang, Z.-S.; Sun, Y.-Z.; Lin, J.; Li, G.-J. Coordinated Frequency Regulation by Doubly Fed Induction Generator-Based Wind Power Plants. IET Renew. Power Gener. 2012, 6, 38. [Google Scholar] [CrossRef]
- Kies, A.; Schyska, B.; von Bremen, L. Curtailment in a Highly Renewable Power System and Its Effect on Capacity Factors. Energies 2016, 9, 510. [Google Scholar] [CrossRef]
- Asad, M.; Sanchez-Fernandez, J.A. Enhancing Frequency Regulation Support through Several Synthetic Inertial Approaches for WDPS. Electronics 2024, 13, 852. [Google Scholar] [CrossRef]
- Samala, N.; Bethi, C. Harnessing Synergy: A Holistic Review of Hybrid Renewable Energy Systems and Unified Power Quality Conditioner Integration. J. Electr. Syst. Inf. Technol. 2025, 12, 4. [Google Scholar] [CrossRef]
- Rahman, A.; Farrok, O.; Haque, M.M. Environmental Impact of Renewable Energy Source Based Electrical Power Plants: Solar, Wind, Hydroelectric, Biomass, Geothermal, Tidal, Ocean, and Osmotic. Renew. Sustain. Energy Rev. 2022, 161, 112279. [Google Scholar] [CrossRef]
- Guerra, O.J.; Zhang, J.; Eichman, J.; Denholm, P.; Kurtz, J.; Hodge, B.-M. The Value of Seasonal Energy Storage Technologies for the Integration of Wind and Solar Power. Energy Environ. Sci. 2020, 13, 1909–1922. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, D.; Wang, X.; Jia, H.; Pu, T.; Chen, N.; Liu, K. Frequency Control Ancillary Service Provided by Efficient Power Plants Integrated in Queuing-Controlled Domestic Water Heaters. Energies 2017, 10, 559. [Google Scholar] [CrossRef]
- Prabhakar, K.; Jain, S.K.; Padhy, P.K. Inertia Estimation in Modern Power System: A Comprehensive Review. Electr. Power Syst. Res. 2022, 211, 108222. [Google Scholar] [CrossRef]
- Andersson, G.; Donalek, P.; Farmer, R.; Hatziargyriou, N.; Kamwa, I.; Kundur, P.; Martins, N.; Paserba, J.; Pourbeik, P.; Sanchez-Gasca, J.; et al. Causes of the 2003 Major Grid Blackouts in North America and Europe, and Recommended Means to Improve System Dynamic Performance. IEEE Trans. Power Syst. 2005, 20, 1922–1928. [Google Scholar] [CrossRef]
- Martins, A.C.B.; Gomes, P.; Guarini, A.; Alves, F.; Martins, N.; Djalma, F.; Taranto, G.N.; Ribeiro, C. Lessons Learned in Restoration from Recent Blackout Incidents in Brazilian Power System. In Proceedings of the 44th International Conference on Large High Voltage Electric Systems 2012, Paris, France, 26–31 August 2012. [Google Scholar]
- Rampurkar, V.; Pentayya, P.; Mangalvedekar, H.A.; Kazi, F. Cascading Failure Analysis for Indian Power Grid. IEEE Trans. Smart Grid 2016, 7, 1951–1960. [Google Scholar] [CrossRef]
- Ochoa, D.; Martinez, S. Proposals for Enhancing Frequency Control in Weak and Isolated Power Systems: Application to the Wind-Diesel Power System of San Cristobal Island-Ecuador. Energies 2018, 11, 910. [Google Scholar] [CrossRef]
- Report on Blackout in Turkey on 31 St March 2015-Final Version 1.0-Project Group Turkey. 2015. Available online: https://eepublicdownloads.entsoe.eu/clean-documents/SOC%20documents/Regional_Groups_Continental_Europe/20150921_Black_Out_Report_v10_w.pdf (accessed on 3 March 2025).
- Yan, R.; Masood, N.-A.; Kumar Saha, T.; Bai, F.; Gu, H. The Anatomy of the 2016 South Australia Blackout: A Catastrophic Event in a High Renewable Network. IEEE Trans. Power Syst. 2018, 33, 5374–5388. [Google Scholar] [CrossRef]
- Schmelter, A.; Mohd, A.; Ortjohann, E.; Hamsic, N.; Mohd, A.; Ortjohann, E.; Schultze, E.; Tuckey, A.; Zimmermann, J. Stabilising the Grid Voltage and Frequency in Isolated Power Systems Using a Flywheel Energy Storage System; The Great Wall World Renewable Energy Forum: Beijing, China, 2006. [Google Scholar]
- Delille, G.; Francois, B.; Malarange, G. Dynamic Frequency Control Support by Energy Storage to Reduce the Impact of Wind and Solar Generation on Isolated Power System’s Inertia. IEEE Trans. Sustain. Energy 2012, 3, 931–939. [Google Scholar] [CrossRef]
- Mi, Y.; Xu, Y.; Lang, Z.; Yang, X.; Ge, X.; Fu, Y.; Jin, C. The Frequency-Voltage Stability Control for Isolated Wind-Diesel Hybrid Power System. Electr. Power Syst. Res. 2021, 192, 106984. [Google Scholar] [CrossRef]
- Shezan, S.K.A. Feasibility Analysis of an Islanded Hybrid Wind-Diesel-Battery Microgrid with Voltage and Power Response for Offshore Islands. J. Clean. Prod. 2021, 288, 125568. [Google Scholar] [CrossRef]
- Kumar, N.K.; Gopi, R.S.; Kuppusamy, R.; Nikolovski, S.; Teekaraman, Y.; Vairavasundaram, I.; Venkateswarulu, S. Fuzzy Logic-Based Load Frequency Control in an Island Hybrid Power System Model Using Artificial Bee Colony Optimization. Energies 2022, 15, 2199. [Google Scholar] [CrossRef]
- Nguyen Hong, N.; Nakanishi, Y. Optimal Scheduling of an Isolated Wind-Diesel-Energy Storage System Considering Fast Frequency Response and Forecast Error. Energies 2019, 12, 843. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasúa, J.; Sánchez-Fernández, J. Frequency Regulation of a Hybrid Wind–Hydro Power Plant in an Isolated Power System. Energies 2018, 11, 239. [Google Scholar] [CrossRef]
- Ejuh Che, E.; Roland Abeng, K.; Iweh, C.D.; Tsekouras, G.J.; Fopah-Lele, A. The Impact of Integrating Variable Renewable Energy Sources into Grid-Connected Power Systems: Challenges, Mitigation Strategies, and Prospects. Energies 2025, 18, 689. [Google Scholar] [CrossRef]
- Asad, M.; Martinez, S.; Sanchez-Fernandez, J.A. Diesel Governor Tuning for Isolated Hybrid Power Systems. Electronics 2023, 12, 2487. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. Overview of Wind Power Intermittency Impacts on Power Systems. Electr. Power Syst. Res. 2010, 80, 627–632. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Vigueras-Rodríguez, A.; Molina-García, Á. Analysis of Power System Inertia Estimation in High Wind Power Plant Integration Scenarios. IET Renew. Power Gener. 2019, 13, 2807–2816. [Google Scholar] [CrossRef]
- Lei, M.; Meng, K.; Feng, H.; Bai, J.; Jiang, H.; Zhang, Z. Flywheel Energy Storage Controlled by Model Predictive Control to Achieve Smooth Short-Term High-Frequency Wind Power. J. Energy Storage 2023, 63, 106949. [Google Scholar] [CrossRef]
- Bebars, A.D.; Eladl, A.A.; Abdulsalam, G.M.; Badran, E.A. Internal Electrical Fault Detection Techniques in DFIG-Based Wind Turbines: A Review. Prot. Control Mod. Power Syst. 2022, 7, 18. [Google Scholar] [CrossRef]
- Boyle, J.; Littler, T.; Foley, A.M. Coordination of Synthetic Inertia from Wind Turbines and Battery Energy Storage Systems to Mitigate the Impact of the Synthetic Inertia Speed-Recovery Period. Renew. Energy 2024, 223, 120037. [Google Scholar] [CrossRef]
- Quan, Y.; Hang, L.; He, Y.; Zhang, Y. Multi-Resonant-Based Sliding Mode Control of DFIG-Based Wind System under Unbalanced and Harmonic Network Conditions. Appl. Sci. 2019, 9, 1124. [Google Scholar] [CrossRef]
- Shen, Y.-W.; Ke, D.-P.; Sun, Y.-Z.; Kirschen, D.S.; Qiao, W.; Deng, X.-T. Advanced Auxiliary Control of an Energy Storage Device for Transient Voltage Support of a Doubly Fed Induction Generator. IEEE Trans. Sustain. Energy 2016, 7, 63–76. [Google Scholar] [CrossRef]
- Papadaki, A.; Savvakis, N.; Sifakis, N.; Arampatzis, G. Analysis of Hybrid Renewable Energy Systems for European Islands: Market Dynamics, Opportunities and Challenges. Sustain. Futures 2025, 9, 100601. [Google Scholar] [CrossRef]
- Alsharafi, A.; Besheer, A.; Emara, H. Primary Frequency Response Enhancement for Future Low Inertia Power Systems Using Hybrid Control Technique. Energies 2018, 11, 699. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Vigueras-Rodríguez, A.; Gómez-Lázaro, E.; Molina-García, Á. Fast Power Reserve Emulation Strategy for VSWT Supporting Frequency Control in Multi-Area Power Systems. Energies 2018, 11, 2775. [Google Scholar] [CrossRef]
- Fang, X.; Krishnan, V.; Hodge, B.-M. Strategic Offering for Wind Power Producers Considering Energy and Flexible Ramping Products. Energies 2018, 11, 1239. [Google Scholar] [CrossRef]
- Renuka, T.K.; Reji, P. Frequency Control of Wind Penetrated Hydro-Dominated Power System. In Proceedings of the 2015 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 24–26 June 2015; pp. 316–321. [Google Scholar]
- Kasera, R.A.; Moses, P.M.; Wekesa, C. Frequency Stability of a Smart Grid with Solar Power Integration Using STATCOM. In Proceedings of the 2023 IEEE AFRICON, Nairobi, Kenya, 20–22 September 2023; pp. 1–6. [Google Scholar]
- Chen, K.; Miao, L.; Chen, D.; Qin, Y.; Jian, W.; Duan, K. Optimal Primary Frequency Regulation Control Strategy for Wind Farms to Prevent Secondary Frequency Drop. Adv. Comput. Mater. Sci. Res. 2025, 2, 133. [Google Scholar] [CrossRef]
- Abdeen, M.; Sayyed, M.; Dominguez-Garcia, J.L.; Kamel, S. Supplemental Control for System Frequency Support of DFIG-Based Wind Turbines. IEEE Access 2022, 10, 69364–69372. [Google Scholar] [CrossRef]
- Ekanayake, J.; Jenkins, N. Comparison of the Response of Doubly Fed and Fixed-Speed Induction Generator Wind Turbines to Changes in Network Frequency. IEEE Trans. Energy Convers. 2004, 19, 800–802. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Invernizzi, M.; Labella, A.; Procopio, R. Design and Implementation of a Variable Synthetic Inertia Controller for Wind Turbine Generators. IEEE Trans. Power Syst. 2019, 34, 754–764. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Marano, A.; Gomez-Exposito, A.; Martinez Ramos, J.L. Frequency Regulation Contribution Through Variable-Speed Wind Energy Conversion Systems. IEEE Trans. Power Syst. 2009, 24, 173–180. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H.; Kling, W.L.; Ferreira, J.A. Wind Turbines Emulating Inertia and Supporting Primary Frequency Control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Singarao, V.Y.; Rao, V.S. Frequency Responsive Services by Wind Generation Resources in United States. Renew. Sustain. Energy Rev. 2016, 55, 1097–1108. [Google Scholar] [CrossRef]
- Shankar, G.; Mukherjee, V. Load Frequency Control of an Autonomous Hybrid Power System by Quasi-Oppositional Harmony Search Algorithm. Int. J. Electr. Power Energy Syst. 2016, 78, 715–734. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Frequency Control of a Wind-Diesel-Generator Hybrid System with Squirrel Search Algorithm Tuned Robust Cascade Fractional Order Controller Having Disturbance Observer Integrated. Electr. Power Compon. Syst. 2022, 50, 814–839. [Google Scholar] [CrossRef]
- Kumar, A.; Suhag, S. Whale Optimization Algorithm Optimized Fuzzy-PID Plus PID Hybrid Controller for Frequency Regulation in Hybrid Power System. J. Inst. Eng. Ser. B 2022, 103, 633–648. [Google Scholar] [CrossRef]
- Panwar, A.; Sharma, G.; Bansal, R.C. Optimal AGC Design for a Hybrid Power System Using Hybrid Bacteria Foraging Optimization Algorithm. Electr. Power Compon. Syst. 2019, 47, 955–965. [Google Scholar] [CrossRef]
- Monroy-Morales, J.L.; Peña-Alzola, R.; Sebastián-Fernández, R.; Campos-Gaona, D.; Castellano, J.Q.; Guardado, J.L. Frequency Control in an Isolated Wind-diesel Hybrid System with Energy Storage and an Irrigation Water Supply System. IET Renew. Power Gener. 2024, 18, 1040–1054. [Google Scholar] [CrossRef]
- Wu, L.; Infield, D. Power System Frequency Management Challenges—A New Approach to Assessing the Potential of Wind Capacity to Aid System Frequency Stability. IET Renew. Power Gener. 2014, 8, 733–739. [Google Scholar] [CrossRef]
- Wu, L.; Infield, D.G. Towards an Assessment of Power System Frequency Support From Wind Plant—Modeling Aggregate Inertial Response. IEEE Trans. Power Syst. 2013, 28, 2283–2291. [Google Scholar] [CrossRef]
- Gampa, S.R.; Das, D. Real Power and Frequency Control of a Small Isolated Power System. Int. J. Electr. Power Energy Syst. 2015, 64, 221–232. [Google Scholar] [CrossRef]
- Jazaeri, M.; Chitsaz, H. A New Efficient Scheme for Frequency Control in an Isolated Power System with a Wind Generator. Electr. Power Compon. Syst. 2011, 40, 21–40. [Google Scholar] [CrossRef]
- Ding, X.; Lin, W.; Xu, J.; Sun, Y.; Yao, L.; Mao, B. Coordinated Frequency Control for Isolated Power Systems with High Penetration of DFIG-Based Wind Power. CSEE J. Power Energy Syst. 2022, 10, 1399–1414. [Google Scholar] [CrossRef]
- Van de Vyver, J.; De Kooning, J.D.M.; Meersman, B.; Vandevelde, L.; Vandoorn, T.L. Droop Control as an Alternative Inertial Response Strategy for the Synthetic Inertia on Wind Turbines. IEEE Trans. Power Syst. 2016, 31, 1129–1138. [Google Scholar] [CrossRef]
- Vidyanandan, K.V.; Senroy, N. Primary Frequency Regulation by Deloaded Wind Turbines Using Variable Droop. IEEE Trans. Power Syst. 2013, 28, 837–846. [Google Scholar] [CrossRef]
- Xu, L.; Yao, L.; Sasse, C. Grid Integration of Large DFIG-Based Wind Farms Using VSC Transmission. IEEE Trans. Power Syst. 2007, 22, 976–984. [Google Scholar] [CrossRef]
- Muller, S.; Deicke, M.; De Doncker, R.W. Doubly Fed Induction Generator Systems for Wind Turbines. IEEE Ind. Appl. Mag. 2002, 8, 26–33. [Google Scholar] [CrossRef]
- Ochoa, D.; Martinez, S. Fast-Frequency Response Provided by DFIG-Wind Turbines and Its Impact on the Grid. IEEE Trans. Power Syst. 2017, 32, 4002–4011. [Google Scholar] [CrossRef]
- Hau, E.; Renouard, H. Physical Principles of Wind Energy Conversion. In Wind Turbines; Springer: Berlin/Heidelberg, Germany, 2006; pp. 81–89. [Google Scholar] [CrossRef]
- Munteanu, I.; Cutululis, N.-A.; Bratcu, I.A.; CeangĂ, E. Optimal Control of Wind Energy Systems; Springer: London, UK, 2008; ISBN 978-1-84800-079-7. [Google Scholar]
- Reyes, V.; Rodriguez, J.J.; Carranza, O.; Ortega, R. Review of Mathematical Models of Both the Power Coefficient and the Torque Coefficient in Wind Turbines. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Rio de Janeiro, Brazil, 3–5 June 2015; pp. 1458–1463. [Google Scholar]
- Schmidlin, C.R.; Lima, F.K.A. Wind Turbine and PMSG Dynamic Modelling in PSIM. IEEE Lat. Am. Trans. 2016, 14, 4115–4120. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W.; Saidur, R. A Review of Maximum Power Point Tracking Algorithms for Wind Energy Systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Wilkie, J.; Leithead, W.E.; Anderson, C. Modelling of Wind Turbines by Simple Models. Wind. Eng. 1990, 14, 247–274. [Google Scholar]
- Perdana, A. Dynamic Models of Wind Turbines: A Contribution Towards the Establishment of Standardized Models of Wind Turbines for Power System Stability Studies; Department of Energy and Environment, Division of Electric Power Engineering, Chalmers University of Technology: Gothenburg, Sweden, 2008; ISBN 9789173852265. [Google Scholar]
- Bektache, A.; Boukhezzar, B. Nonlinear Predictive Control of a DFIG-Based Wind Turbine for Power Capture Optimization. Int. J. Electr. Power Energy Syst. 2018, 101, 92–102. [Google Scholar] [CrossRef]
- Mohapatra, S.P.; Dash, P.K.; Bisoi, R.; Sarangi, S.; Anjaiah, K. Fractional-Order Sliding Mode Control Based MPPT of a DFIG Connected to a Variable Speed Wind Turbine. In Proceedings of the 2022 2nd Odisha International Conference on Electrical Power Engineering, Communication and Computing Technology (ODICON), Bhubaneswar, India, 11–12 November 2022; pp. 1–5. [Google Scholar]
- Nanou, S.; Tsourakis, G.; Vournas, C.D. Full-Converter Wind Generator Modelling for Transient Stability Studies. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–7. [Google Scholar]
- Miller, N.W.; Sanchez-Gasca, J.J.; Price, W.W.; Delmerico, R.W. Dynamic Modeling of GE 1.5 and 3.6 MW Wind Turbine-Generators for Stability Simulations. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Online, 13–17 July 2003; pp. 1977–1983. [Google Scholar]
- Dharmawardena, H.; Uhlen, K.; Gjerde, S.S. Modelling Wind Farm with Synthetic Inertia for Power System Dynamic Studies. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar]
- Ullah, N.R.; Thiringer, T.; Karlsson, D. Temporary Primary Frequency Control Support by Variable Speed Wind Turbines— Potential and Applications. IEEE Trans. Power Syst. 2008, 23, 601–612. [Google Scholar] [CrossRef]
- Hussain, J.; Mishra, M.K. Adaptive Maximum Power Point Tracking Control Algorithm for Wind Energy Conversion Systems. IEEE Trans. Energy Convers. 2016, 31, 697–705. [Google Scholar] [CrossRef]
- Bhowon, A.; Abo-Al-Ez, K.M.; Adonis, M. Variable-Speed Wind Turbines for Grid Frequency Support: A Systematic Literature Review. Mathematics 2022, 10, 3586. [Google Scholar] [CrossRef]
- Ochoa, D.; Martinez, S. A Simplified Electro-Mechanical Model of a DFIG-Based Wind Turbine for Primary Frequency Control Studies. IEEE Lat. Am. Trans. 2016, 14, 3614–3620. [Google Scholar] [CrossRef]
- Chinchilla, M.; Arnaltes, S.; Burgos, J.C. Control of Permanent-Magnet Generators Applied to Variable-Speed Wind-Energy Systems Connected to the Grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef]
- Zhao, M.; Yuan, X.; Hu, J. Modeling of DFIG Wind Turbine Based on Internal Voltage Motion Equation in Power Systems Phase-Amplitude Dynamics Analysis. IEEE Trans. Power Syst. 2018, 33, 1484–1495. [Google Scholar] [CrossRef]
- Clark, K.; Nicholas, W.M.; Juan, J.S.-G. Modeling of GE Wind Turbine-Generators for Grid Studies. GE Energy 2010, 4, 0885-8950. [Google Scholar]
- Attya, A.B.; Hartkopf, T. Wind Turbine Contribution in Frequency Drop Mitigation—Modified Operation and Estimating Released Supportive Energy. IET Gener. Transm. Distrib. 2014, 8, 862–872. [Google Scholar] [CrossRef]
- Arnaltes, S.; Rodriguez-Amenedo, J.; Montilla-DJesus, M. Control of Variable Speed Wind Turbines with Doubly Fed Asynchronous Generators for Stand-Alone Applications. Energies 2017, 11, 26. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Z.; Li, G.; Lin, J. Review on Frequency Control of Power Systems with Wind Power Penetration. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010; pp. 1–8. [Google Scholar]
- Aziz, A.; Than Oo, A.; Stojcevski, A. Frequency Regulation Capabilities in Wind Power Plant. Sustain. Energy Technol. Assess. 2018, 26, 47–76. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasúa, J.I.; Sánchez-Fernández, J.Á. Eigen Analysis of Wind–Hydro Joint Frequency Regulation in an Isolated Power System. Int. J. Electr. Power Energy Syst. 2018, 103, 511–524. [Google Scholar] [CrossRef]
- Ahmadyar, A.S.; Verbic, G. Control Strategy for Optimal Participation of Wind Farms in Primary Frequency Control. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Eriksson, R.; Modig, N.; Elkington, K. Synthetic Inertia versus Fast Frequency Response: A Definition. IET Renew. Power Gener. 2018, 12, 507–514. [Google Scholar] [CrossRef]
- Yang, X.S. Bat Algorithm for Multi-Objective Optimisation. Int. J. Bio-Inspired Comput. 2011, 3, 267. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Akhtar, T.; Haider, N.G.; Khan, S.M. A Comparative Study of the Application of Glowworm Swarm Optimization Algorithm with Other Nature-Inspired Algorithms in the Network Load Balancing Problem. Eng. Technol. Appl. Sci. Res. 2022, 12, 8777–8784. [Google Scholar] [CrossRef]
- Kao, Y.-T.; Zahara, E. A Hybrid Genetic Algorithm and Particle Swarm Optimization for Multimodal Functions. Appl. Soft Comput. 2008, 8, 849–857. [Google Scholar] [CrossRef]
- Paruchuri, T.; Kancharla, G.R.; Dara, S.; Yadav, R.K.; Jadav, S.S.; Dhamercherla, S.; Vidyarthi, A. Nature Inspired Algorithms for Solving Multiple Sequence Alignment Problem: A Review. Arch. Comput. Methods Eng. 2022, 29, 5237–5258. [Google Scholar] [CrossRef]
- Hsiao, Y.-T.; Chen, C.-H.; Chien, C.-C. Optimal Capacitor Placement in Distribution Systems Using a Combination Fuzzy-GA Method. Int. J. Electr. Power Energy Syst. 2004, 26, 501–508. [Google Scholar] [CrossRef]
- Jones, D.I.; Mansoor, S.P.; Aris, F.C.; Jones, G.R.; Bradley, D.A.; King, D.J. A Standard Method for Specifying the Response of Hydroelectric Plant in Frequency-Control Mode. Electr. Power Syst. Res. 2004, 68, 19–32. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasúa, J.I.; Sánchez-Fernández, J.Á.; Wilhelmi, J.R. Frequency Control Support of a Wind-Solar Isolated System by a Hydropower Plant with Long Tail-Race Tunnel. Renew. Energy 2016, 90, 362–376. [Google Scholar] [CrossRef]
- GE Energy 1.5MW Wind Turbine. Available online: https://geosci.uchicago.edu/~moyer/GEOS24705/Readings/GEA14954C15-MW-Broch.pdf (accessed on 3 March 2025).
- Wada, K.; Yokoyama, A. Load Frequency Control Using Distributed Batteries on the Demand Side with Communication Characteristics. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar]
- Wang, C.; Li, J.; Hu, Y. Frequency Control of Isolated Wind-Diesel Microgrid Power System by Double Equivalent-Input-Disturbance Controllers. IEEE Access 2019, 7, 105617–105626. [Google Scholar] [CrossRef]











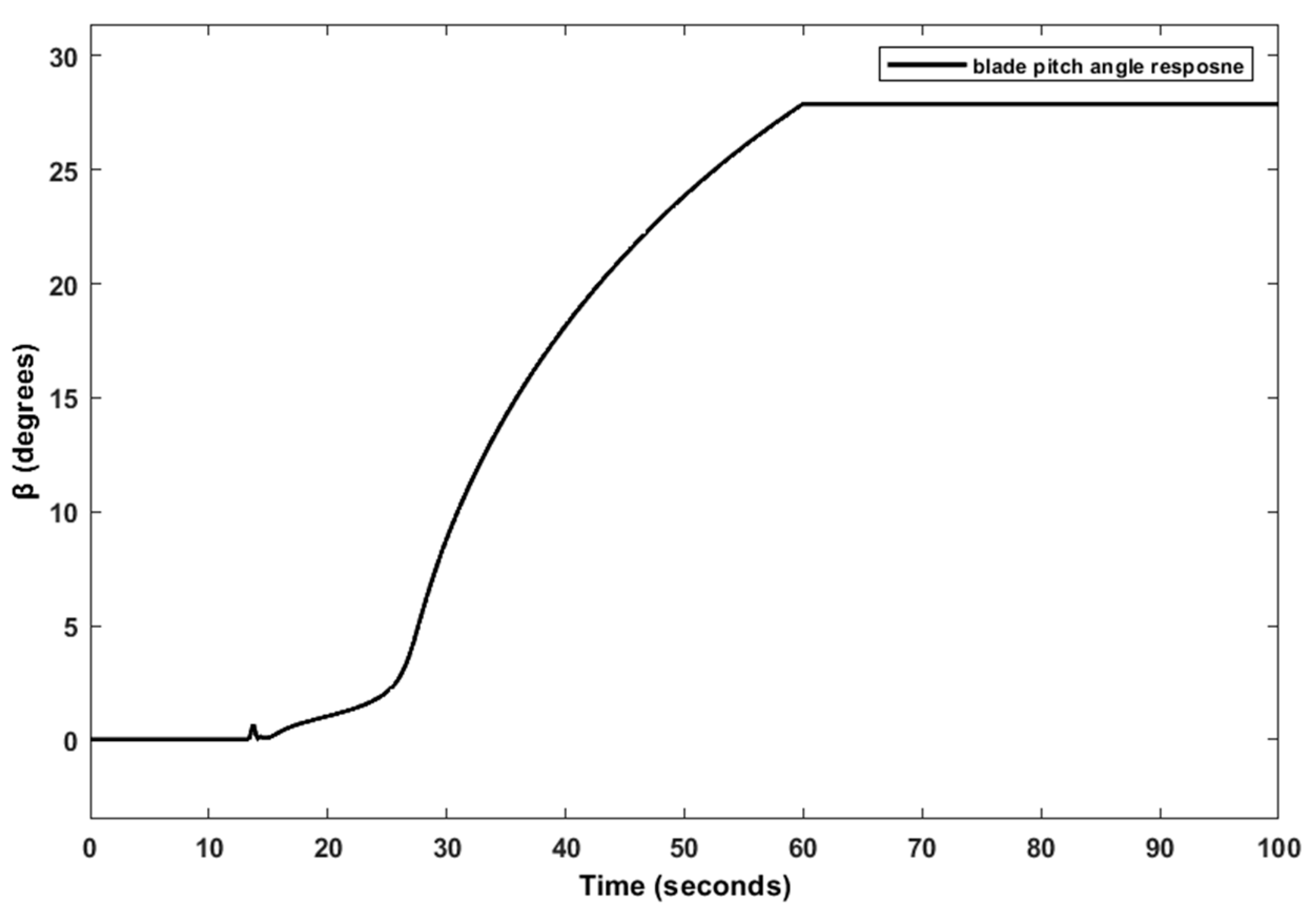

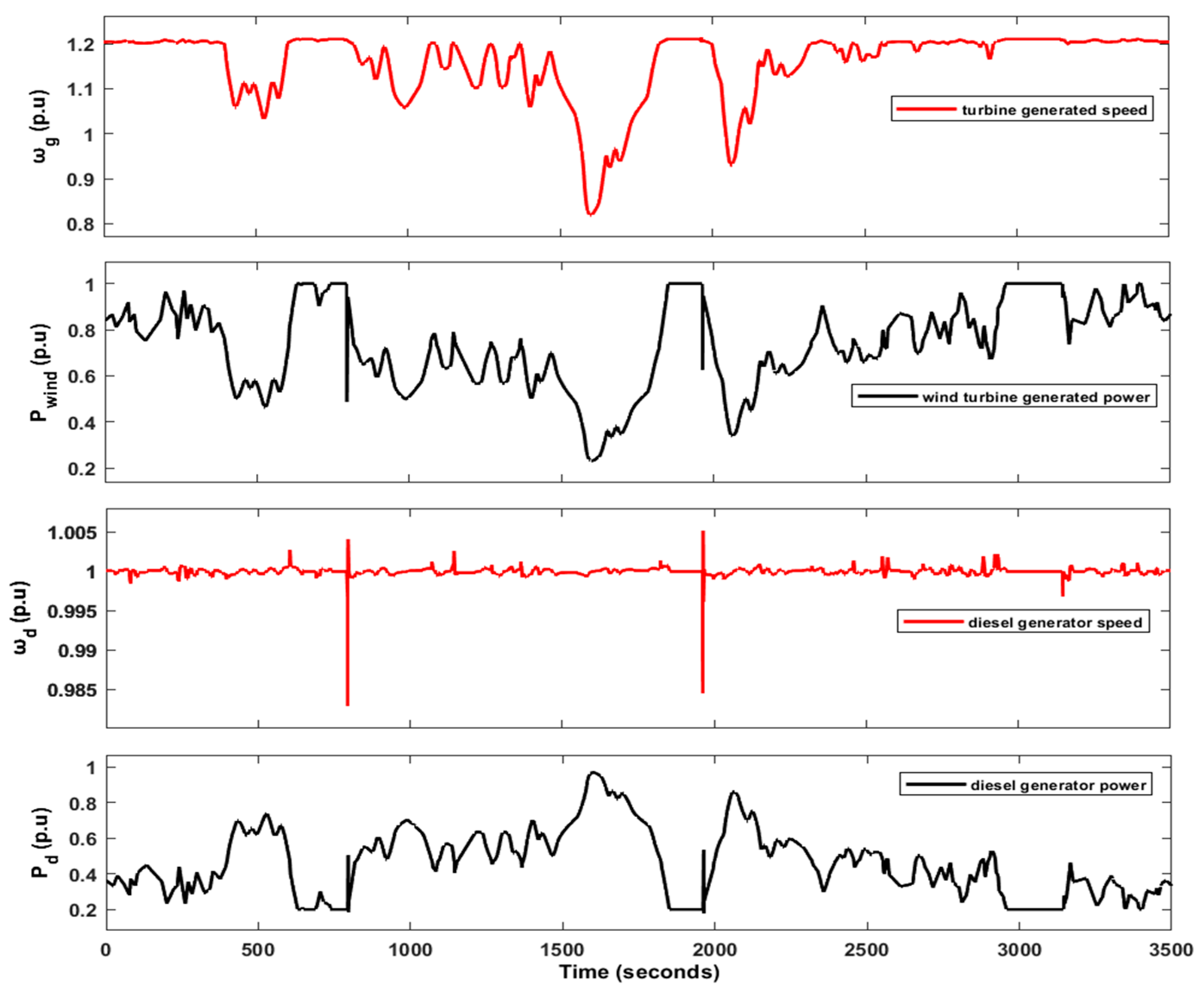
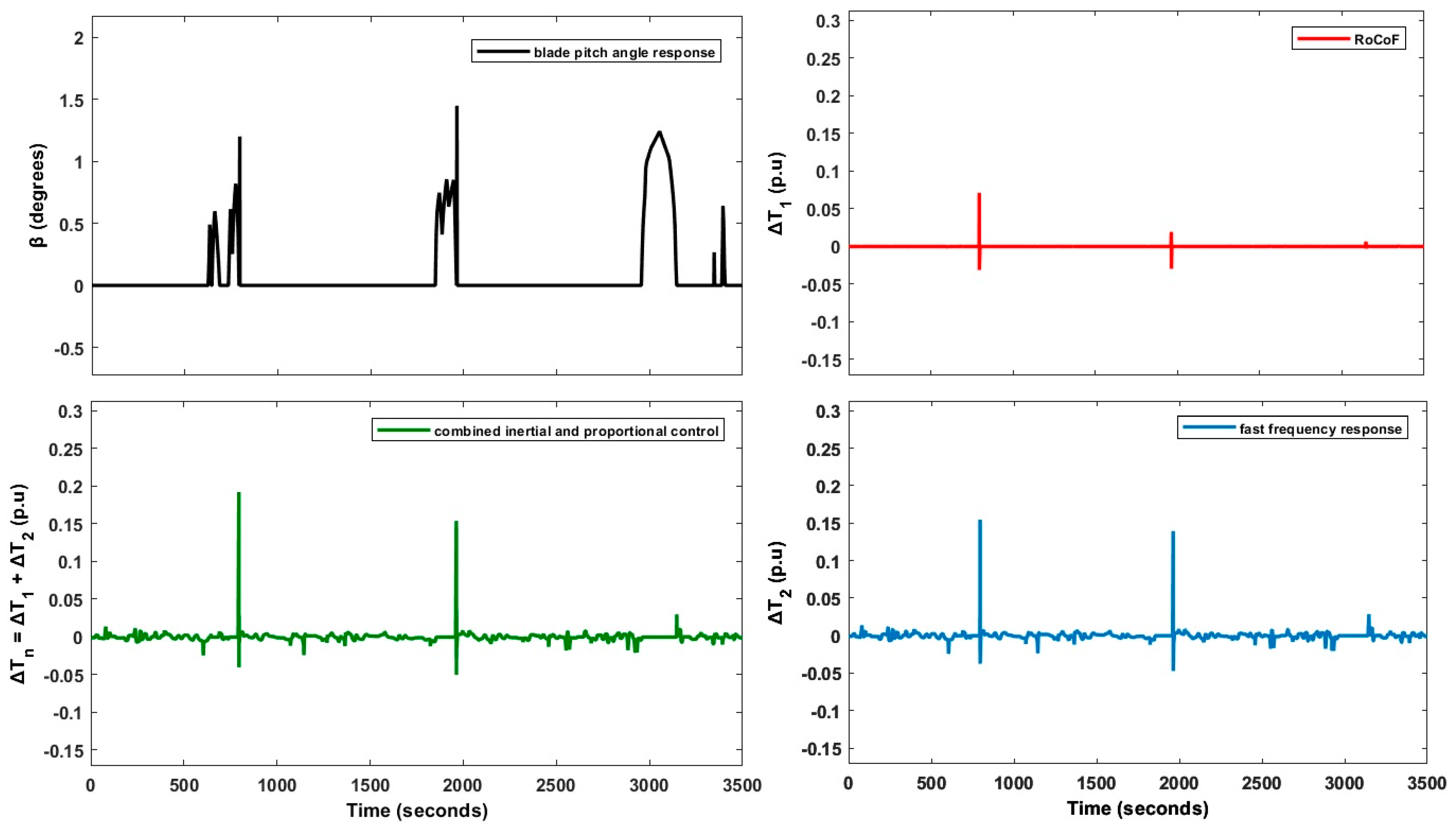



| Reference | Type of WT/Power System | Methodology | Limitations/Drawbacks/Future Directions |
|---|---|---|---|
| [55] | Isolated WDPS | This study provides FR (isochronous) using the proposed PI controller but is limited to wind-only (WO) mode. Moreover, the ES and irrigation water supply system are used for FR. The main goal is to provide FR and save fuel consumption. | Shutting down the diesel generator is not a viable solution, because diesel must have minimum operation limits, either under load or no-load conditions. |
| [56] | VSWT—Great Britain (GB) power system | In this study, the authors propose a new probabilistic approach by modifying the demanded torque in response to the RoCoF to assess the inertial response in the GB power system (both summer and winter days). | The lack of a WT response against the ramp response and the effects of blade pitch angle control are missing. Future work should focus on spatiotemporal wind field models. |
| [57] | Wind power plant | In this study, the WT inertial response is estimated using the Gaussian probabilistic approach. A fixed df/dt and WT power tracking constant, Koptω3, is used to explore synthetic inertia in WT. | There is a lack of WT integration with conventional power systems and their effects. It is still unclear in this study whether grid frequency restoration in the case of high wind can still be provided by using these services. |
| [42] | Hydro–wind power system | FR is provided using an inertial emulation control loop against the variation in frequency, and it is added to the electrical power of the turbine. A fuzzy logic scheme is used for blade pitch angle control during high winds; however, the MPPT is adopted during low and medium wind speeds. | Irrespective of robustness, fuzzy logic schemes have various concerns when they are used for large systems, such as limited accuracy, computational complexity, and interpretability. |
| [58] | Isolated WDPS | A dynamic analysis of a small isolated WDPS is carried out in the time domain, considering simplified models of the WT pitch controller and the diesel engine speed governor. Two controllers (PI and PID) for the BPAC are proposed to provide frequency control and examine power flow. The optimal solution of both control loops is found using GA and PSO (partial swarm optimization). | There is a lack of information about inertial support, i.e., the release of K.E in rotating masses. GA is computationally less efficient than PSO. |
| [59] | Isolated hybrid WDPS | Frequency control in an isolated hybrid WDPS is provided using various methods, i.e., dump load, BPAC regulator, and ES (flywheel). | There is a lack of inertial response discussion and optimal solutions. |
| [60] | Isolated WDPS | In this study, FR is provided by nonlinear regulator theory. FD and power imbalances are used to design nonlinear feedback controllers that achieve the reserve power distribution between DFIGs and generators. | Frequency fluctuations still exist in this study against random wind speed. Therefore, nonlinear regulator theory should be extended to coordinate between both generation and demand-side control. |
| [46] | DFIG and FSIG WTs | In this study, frequency regulation is provided by releasing synthetic inertia using a one-loop inertial control (∆p ∝ RoCoF). Moreover, the DIFG WT response is compared with the inertial control loop and FSIG WT to highlight the inertial significance. | Future work will be extended to improve inertial control or highlight the inertial response in the hybrid generation mix. |
| [47] | PMSG WT | In this study, a new control loop, virtual hidden inertial emulation (HIE), is proposed to provide frequency stability. As in HIE, with a reduction in rotor speed recovery during NADIR, the secondary frequency drop persists. Therefore, VHIE is more effective. | The proposed approach can be modified by introducing a droop control or ES to achieve the same characteristics of traditional power plants. However, it can enhance the complexity of the systems and make it difficult to globally optimize the system. |
| [61] | VSWT | In this study, droop control is used as an alternative inertial emulation control (IEM) strategy to release synthetic inertia in VSWTs. The main benefit of such a strategy is to enhance robustness by eliminating the differentiation of the frequency in IEM. | There is a lack of BPAC adoption in this study, with the assumption that the pitch controller for the synthetic inertia strategy is too slow in tracking the variations in fast power set-points. Global optimum tuning is necessary to achieve inertia using droop control. |
| [62] | VSWT | A de-loading strategy is adopted in this study to provide an inertial response with the aim of providing relief to the grid during depressed frequency conditions. | De-loading control strategies are not economically viable [41]. |
| Parameters | With Kpn, Kdn, Kpc, and Kic = 0 |
|---|---|
| NADIR (p.u) | 0.957609 |
| IAE | 0.039205 |
| ISE | 0.001197 |
| C | 2 |
| Frequency (Hz) | 57.45654 |
| Z | 10,202.87614 |
| Parameters | With Kdn = 0.47, Kpn = 9, Ki_d = 14.89, and Kp_d = 21.01 |
|---|---|
| NADIR (p.u) | 0.975204 |
| IAE | 0.033579 |
| ISE | 0.000461 |
| C | 1 |
| Frequency (Hz) | 58.51224 |
| Z | 62,998.00405 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asad, M.; Sánchez-Fernández, J.Á. Frequency Regulation Provided by Doubly Fed Induction Generator Based Variable-Speed Wind Turbines Using Inertial Emulation and Droop Control in Hybrid Wind–Diesel Power Systems. Appl. Sci. 2025, 15, 5633. https://doi.org/10.3390/app15105633
Asad M, Sánchez-Fernández JÁ. Frequency Regulation Provided by Doubly Fed Induction Generator Based Variable-Speed Wind Turbines Using Inertial Emulation and Droop Control in Hybrid Wind–Diesel Power Systems. Applied Sciences. 2025; 15(10):5633. https://doi.org/10.3390/app15105633
Chicago/Turabian StyleAsad, Muhammad, and José Ángel Sánchez-Fernández. 2025. "Frequency Regulation Provided by Doubly Fed Induction Generator Based Variable-Speed Wind Turbines Using Inertial Emulation and Droop Control in Hybrid Wind–Diesel Power Systems" Applied Sciences 15, no. 10: 5633. https://doi.org/10.3390/app15105633
APA StyleAsad, M., & Sánchez-Fernández, J. Á. (2025). Frequency Regulation Provided by Doubly Fed Induction Generator Based Variable-Speed Wind Turbines Using Inertial Emulation and Droop Control in Hybrid Wind–Diesel Power Systems. Applied Sciences, 15(10), 5633. https://doi.org/10.3390/app15105633







