Abstract
The Logical Range is a mission-oriented, reconfigurable environment that integrates testing, training, and simulation by virtually connecting distributed systems. In such environments, task-processing devices often experience highly dynamic workloads due to varying task demands, leading to scheduling inefficiencies and increased latency. To address this, we propose GCSG, a hybrid load forecasting model tailored for Logical Range operations. GCSG transforms time-series device load data into image representations using Gramian Angular Field (GAF) encoding, extracts spatial features via a Convolutional Neural Network (CNN) enhanced with a Squeeze-and-Excitation network (SENet), and captures temporal dependencies using a Gated Recurrent Unit (GRU). Through the integration of spatial–temporal features, GCSG enables accurate load forecasting, supporting more efficient resource scheduling. Experiments show that GCSG achieves an of 0.86, MAE of 4.5, and MSE of 34, outperforming baseline models in terms of both accuracy and generalization.
1. Introduction
In recent years, enhancing the capability of test and training operations under integrated land, sea, air, space, and electromagnetic warfare environments has become a focal point in military competition. To support such complex missions, the concept of the Logical Range has emerged. A Logical Range is a mission-oriented, reconfigurable range system that integrates testing, training, and simulation resources through distributed networking and high-performance computing technologies [1,2]. Unlike traditional test ranges, Logical Ranges can dynamically reorganize functional elements across geographically dispersed platforms to meet the demands of new tasks that a single range cannot fulfill alone.
This flexible architecture enables cross-domain resource integration and real-time mission composition, but it also presents new technical challenges. During joint operations, such as cross-regional flight testing or collaborative weapon system evaluation, Logical Range platforms often suffer from uneven workload distribution, high concurrency, and complex system heterogeneity. These factors can cause delays in task scheduling and execution, leading to reduced responsiveness and efficiency. Consequently, accurate load forecasting becomes crucial for optimizing task allocation and maintaining system stability under fluctuating conditions.
Although traditional statistical approaches [3,4,5,6] have been applied for time-series load prediction, they typically rely on strict assumptions (e.g., Poisson distribution) and fail to handle the stochastic, nonlinear nature of real-world Logical Range workloads [7]. To overcome these limitations, more adaptable, learning-based forecasting frameworks are needed to support intelligent resource scheduling in such dynamic environments.
To capture temporal patterns in such data, autoregressive models and probabilistic statistical approaches [8,9,10,11] have been employed with some success. However, in dynamically evolving Logical Range environments, their predictive performance often deteriorates due to their limited adaptability to abrupt changes and temporal nonstationarity [12].
Recently, deep learning-based prediction models—notably those based on recurrent neural networks (RNNs)—have demonstrated strong capabilities in learning nonlinear temporal dependencies directly from historical data [13,14,15,16,17,18]. Nevertheless, many of these approaches fail to account for spatial correlations that may exist across subsystems or geographically distributed nodes. Recent studies have highlighted the importance of jointly modeling both spatial and temporal features, which can significantly improve the accuracy of forecasting in nonstationary and highly volatile load environments [19].
To address the aforementioned challenges, we propose GCSG: a novel hybrid deep learning model that integrates Gramian Angular Field (GAF) encoding, a Convolutional Neural Network with Squeeze and Excitation (CNN-SENet), and a Gated Recurrent Unit (GRU). This model is specifically designed to handle the complexity of load forecasting in Logical Range environments, offering several key innovations:
First, we employ the GAF approach to transform 1D nonstationary load sequences into 2D images, enabling CNNs to effectively capture spatial correlations. Second, we develop a CNN-SENet module that adaptively recalibrates channel-wise feature responses, enhancing the model’s ability to focus on informative features while suppressing noise, which is crucial for robust feature extraction in complex environments. Finally, we introduce an attention-based spatiotemporal fusion mechanism that dynamically combines spatial features (from CNN-SENet) with temporal dependencies (from GRU), significantly improving the prediction accuracy under highly dynamic workloads by capturing both transient patterns and long-term trends in the data.
The main contributions of this study are as follows:
- (1)
- We propose a domain-specific hybrid forecasting model tailored to the Logical Range context. Combining spatial and temporal representation learning through a GAF–CNN-SENet–GRU architecture, our approach effectively addresses the unique challenges of dynamic load behavior and distributed task execution observed in modern test and training infrastructures.
- (2)
- We design an innovative spatiotemporal attention fusion module that adaptively learns the significance of both spatial and temporal components in the data. This fusion mechanism enhances the model’s ability to generalize across diverse scenarios and operational conditions typically observed in Logical Range settings.
- (3)
- We conduct comprehensive experiments on real-world Logical Range datasets. The results demonstrate that our model outperforms state-of-the-art baselines in terms of accuracy, generalization, and robustness. Specifically, GCSG achieves an of 0.86, a mean absolute error (MAE) of 4.5, and a mean squared error (MSE) of 34, underscoring its practical utility in supporting more efficient and responsive resource scheduling across complex range systems.
2. Materials and Methods
2.1. Architecture for Logical Range
As introduced in Section 1, the Logical Range comprises a variety of networked task-processing devices, including theodolites, cameras, radar systems, and Time–Space–Position Information (TSPI) units. These devices are interconnected through a high-speed network to support real-time data processing, task coordination, and multimedia information flow (e.g., image/video display).
Figure 1 illustrates the overall structure of the Logical Range, where heterogeneous devices collaborate to execute computationally intensive tasks. These devices are responsible for data computation, command distribution, real-time acquisition, and visualization, resulting in dynamic and unpredictable workloads.
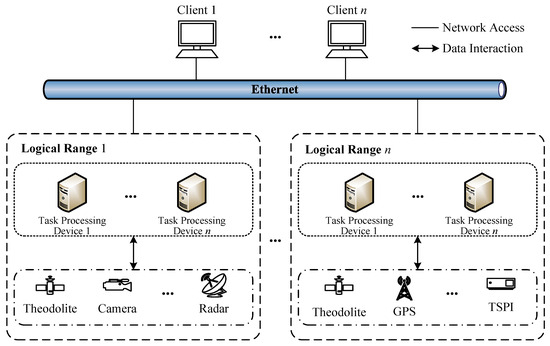
Figure 1.
Architecture of Logical Range Environment.
The resource usage of these devices is highly complex and variable, typically involving metrics such as CPU usage, memory consumption, network I/O (uplink/downlink), and disk activity. Among them, CPU usage is particularly critical, as most operations in Logical Range scenarios are computationally intensive and latency-sensitive. Therefore, this study focuses on CPU usage as the primary time-series signal for load forecasting and task scheduling optimization.
As illustrated in Figure 2, the CPU usage data from all task-processing devices are recorded over time to form a multivariate time series, denoted as
where represents the aggregated CPU usage at time step i. The sequence exhibits strong temporal dependencies, and accurate forecasting of its future values is essential for reducing latency, avoiding resource bottlenecks, and improving experimental throughput in Logical Range systems.
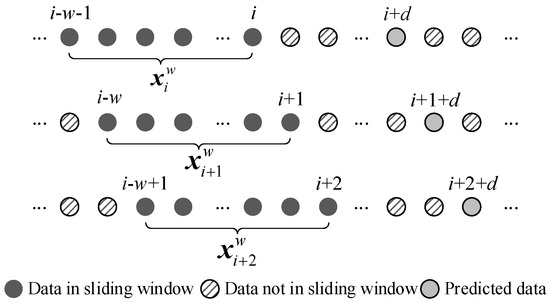
Figure 2.
Sliding window-based processing of device load data in Logical Range.
To construct an effective forecasting dataset, we normalize and apply a sliding time window strategy. At each time step i, a subsequence of length w,
is extracted as the input sample, and the forecasting target is set as the value at a future time step d ahead. The forecasting function is defined as
where f is the deep learning model proposed in this study and d is the forecasting step, with . The complete dataset can be constructed as
and we denote each sample as . This sliding window mechanism enables continuous load forecasting and dynamic resource allocation. The processing of S is depicted in Figure 2.
2.2. Proposed Load Forecasting Methodology
The proposed forecasting model integrates the GAF, CNN, SENet, and GRU methods and is thus abbreviated as GCSG (GAF–CNN-SENet–GRU). The overall architecture of the GCSG load forecasting model for the Logical Range is shown in Figure 3.
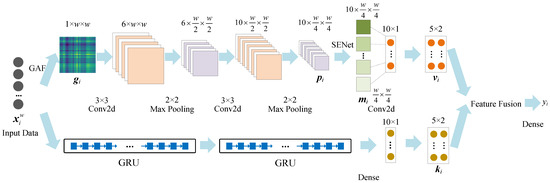
Figure 3.
Processing pipeline of the GCSG model.
The processing pipeline of the GCSG model comprises three stages: (1) spatial feature extraction via GAF and CNN-SENet; (2) temporal feature extraction using GRU; (3) attention-based feature fusion.
2.2.1. Spatial Feature Extraction
Spatial feature extraction involves transforming the dataset from time-series data into image data via GAF encoding.
Subsequently, a CNN extracts features from the resulting images, with feature optimization through channel attention mechanisms such as SENet [20].
- Image conversion.
GAF encoding is a visualization and feature extraction technique for time-series analysis and signal processing. It converts one-dimensional time-series data into two-dimensional images while preserving their temporal characteristics. In this study, the GAF approach is used to transform the input data within each dataset of Logical Range load data into two-dimensional images, expanding the data dimensionality. Figure 4 illustrates the conversion process.
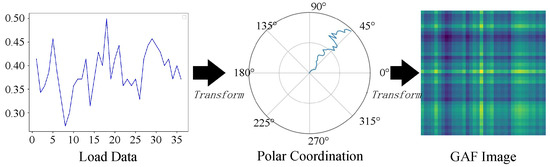
Figure 4.
Gramian Angular Field (GAF) -based conversion of Logical Range load data.
The main steps of the GAF conversion process for Logical Range load data are as follows:
- (1)
- Extract the input data from the dataset , where w is the length of and ;
- (2)
- Convert to polar coordinates using Equation (5):where is the polar radius, is the timestamp of , T is the total timestamp length, and is the polar angle. Here, preserves the temporal characteristics of the time-series data, while retains the numerical variations.
- (3)
- Construct the GAF matrix using the cosine function (Equation (6)), with dimensions :
Compared to , enhances the correlations between load data values across different timestamps in the Logical Range.
- 2.
- Feature extraction.
The CNN is a deep learning architecture that is primarily used for tasks involving structured data, such as image recognition, classification, and object detection. A CNN operates by applying convolutional operations to extract features from images, followed by pooling operations to reduce the dimensionality of the extracted features. CNNs can automatically learn and capture local features within images and exhibit certain invariance to translations, scaling, and other transformations, making them highly effective for image data processing [21].
The channel attention mechanism enhances the interaction of information between channels in CNN feature maps, helping to learn the importance of different channels [22]. SENet, as one type of channel attention mechanism, adaptively adjusts the weights of individual channels to improve the network’s focus on essential features, thereby enhancing the CNN’s feature representation capability [23].
The GCSG model employs a CNN to extract features from and integrates SENet to adjust feature weights, thus improving the CNN’s perception of important features. The specific process is as follows:
- (1)
- Conduct successive convolution, activation, and pooling operations on to obtain feature maps , where the size of is and c is the number of channels, with each channel containing a two-dimensional feature.
- (2)
- Compute the global statistics for each channel feature in , where , using Equation (7):The global pooling operation aggregates the values of across its spatial dimensions to derive .
- (3)
- Compute the weight for each channel feature in to obtain the weight vector , where , using Equation (8):where denotes the sigmoid function, represents the ReLU function, and and are full layer matrices.
- (4)
- Compute the weighted feature map using Equation (9):
- (5)
- Apply convolutional and transformation operations on to obtain the spatial feature output vector for .
2.2.2. Temporal Feature Extraction
The GRU is a recurrent neural network architecture that incorporates gating mechanisms to address the problems of vanishing and exploding gradients faced when using traditional RNNs [24].
When processing time-series load data in the Logical Range, the GRU preserves temporal features through its hidden states. The GCSG model employs a two-layer stacked GRU to extract temporal features from :
- (1)
- Input vector from dataset (where ) with initialized zero hidden state into the first GRU layer.
- (2)
- Compute reset gate, update gate, candidate hidden state, and hidden state updates using to obtain the hidden state vector .
- (3)
- Process and through the second GRU layer to generate the hidden state vector .
- (4)
- Transform via a fully connected layer to derive the temporal features output vector .
2.3. Feature Fusion
An attention-based fusion method enhances the model’s focus on critical spatial and temporal features. The method weights the spatial feature and temporal feature of according to their contributions to load forecasting accuracy in the Logical Range. The weight computation follows Equation (10):
where is the dimension weight for , and is the attention-fused feature vector.
A fully connected layer transforms ’s dimensions as shown in Equation (11):
where is the weight matrix and is the final forecasting result.
3. Results
3.1. Experimental Setup
To evaluate the effectiveness of the GCSG model, the experimental data used in this study were collected from the multi-region joint simulation test system of the Digital Twin Logical Range, jointly developed by the Chinese Flight Test Establishment and Xi’an University of Technology. This system primarily processes aircraft flight status data obtained from devices such as GPS, theodolites, cameras, and radars during flight tests. It integrates six high-performance servers to form a central processing node cluster that is responsible for data processing, digital twin model rendering, and command forwarding.
Scripts were developed to collect and store various load metrics from each node in the central processing cluster. The data collection spanned 144 h, with a sampling interval of 90 s, resulting in 5760 records per node (Logical Range task processing device). The dataset contains timestamps, Logical Range IDs, device IDs, and CPU load measurements (0–100%).
To ensure consistency in model training and convergence, all input features were normalized using standardization (i.e., zero mean and unit variance) based on the statistics of the training set. This preprocessing step improves the numerical stability of the model and ensures fair comparison across different methods.
To ensure the accuracy and reproducibility of the experimental results, all experiments were conducted under consistent software and hardware conditions. The detailed hardware and software configurations are summarized in Table 1.

Table 1.
Experimental setup.
3.2. Performance Evaluation Metrics
To ensure a comprehensive and reliable evaluation of the GCSG model’s performance, we adopt a multi-metric strategy comprising the coefficient of determination (, see Equation (12)), mean absolute error (MAE, see Equation (13)), and mean squared error (MSE, see Equation (14)). Specifically, measures the proportion of variance explained by the model, while the MAE and MSE quantify the prediction errors from absolute and squared perspectives, respectively. This combination of metrics enables a more holistic assessment of the model’s accuracy and robustness, avoiding overreliance on any single evaluation indicator.
- The coefficient of determination () measures the proportion of variance in the predicted Logical Range load data explained by the model. Higher values indicate better performance:
- The mean absolute error (MAE) is computed as the average absolute difference between predicted and actual load forecasting values:
- The mean squared error (MSE) quantifies average squared prediction errors, penalizing larger deviations:
In the above formulas, denotes the predicted value, denotes the true (actual) value, and is the mean of the true values.
These metrics were used to assess the model’s accuracy for time-series load forecasting in the Logical Range.
3.3. Performance Analysis
To evaluate the performance of the proposed GCSG model in the Logical Range scenario, we conducted comparative experiments with several widely used deep learning models, including CNN, LSTM, GRU, LSTM-ED [25], BiLSTM [26], LSTM-GRU [27], and ConvLSTM [28] models. For a fair comparison, each baseline model was individually fine-tuned to achieve its best performance through grid search. All models were trained and evaluated using the same dataset splits and experimental conditions.
The specific hyperparameter settings for each model, including hidden size, learning rate, number of training epochs, batch size, dropout rate, number of layers, and optimizer, are summarized in Table 2.

Table 2.
Model parameter configurations.
- (1)
- Input window size analysis.
Figure 5 displays the performance metrics of different models under varying input window sizes w using the prediction step in the Logical Range. As shown in Figure 5a, the GCSG model achieved the highest values, consistently above 0.85 for w values between 16 and 40. The BiLSTM, ConvLSTM, LSTM-ED, and LSTM-GRU models (all LSTM variants) followed, with scores of 0.83–0.85. The GRU and LSTM models demonstrated comparable performance () due to their single-model architectures. The CNN showed the lowest values (0.75–0.77), potentially due to its parameters and structural configuration.
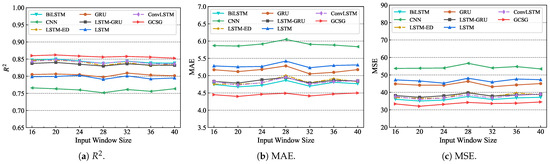
Figure 5.
Comparison of models under different input window sizes.
In particular, Figure 5a demonstrates the fluctuation degree of scores across different w values for each model in the Logical Range, with the GCSG model exhibiting the most stable performance. This indicates the GCSG model’s superior robustness when adapting to varying w values.
Figure 5b,c present the MAE and MSE metrics of each model, respectively. The error trends consistently align with the results in Figure 5a. The GCSG model achieves the lowest errors, followed by the BiLSTM, ConvLSTM, LSTM-ED, and LSTM-GRU models, with marginally higher error rates. The GRU and LSTM models showed intermediate error levels, while the CNN yielded the highest number of errors.
In summary, Figure 5 confirms that the GCSG model delivers optimal load forecasting accuracy across different input window sizes w in the Logical Range, outperforming both combined models (BiLSTM, ConvLSTM, LSTM-ED, LSTM-GRU) and traditional single models (LSTM, GRU, CNN).
- (2)
- Prediction step analysis.
According to the results presented in Figure 5, an input window size w of 36 was chosen based on the average , MAE, and MSE values, and the prediction step d was varied from 1 to 29 in order to compare the prediction accuracy of the various models, as shown in Figure 6.
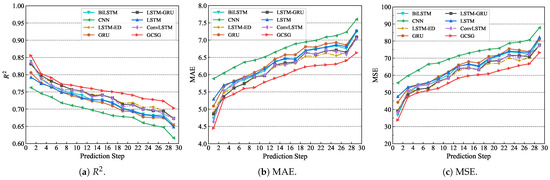
Figure 6.
Comparison of models under different prediction steps.
Figure 6 demonstrates that the GCSG model consistently achieved superior load forecasting accuracy across different prediction steps d in the Logical Range compared to the other models. As shown in Figure 6a, the combined models (ConvLSTM, LSTM-ED, and LSTM-GRU) exhibited higher values than single models (LSTM, GRU, and CNN). Among all combined models, the GCSG model maintained the highest values.
According to Figure 6b, the CNN exhibited the highest MAE values, while the LSTM and GRU models demonstrated lower MAE than the CNN but higher values than ConvLSTM, LSTM-ED, LSTM-GRU, and GCSG. When , BiLSTM’s MAE was lower than those of the LSTM and GRU. However, when , its MAE became comparable to that of the LSTM. Additionally, the combined models (ConvLSTM, LSTM-ED, and LSTM-GRU) maintained similar MAE values across different d values, with LSTM-ED exhibiting marginally lower MAE than LSTM-GRU and ConvLSTM. The GCSG model consistently achieved the lowest MAE values across all prediction steps d.
Figure 6c reveals that the MSE of the GCSG model follows a nearly linear growth trend with increasing prediction step d, reflecting the expected accumulation of error. In contrast, the LSTM, GRU, LSTM-ED, ConvLSTM, BiLSTM, and LSTM-GRU models exhibited fluctuating MSE growth patterns. This demonstrates the GCSG model’s stable linear relationship in load forecasting applications.
3.3.1. Ablation Experiment
To rigorously evaluate the contribution of each component in the GCSG model for Logical Range load forecasting, we conducted systematic ablation studies using the following model variants:
- GCSG: Full model (GAF+CNN+SENet+GRU).
- GCG: Ablated SENet (GAF+CNN+GRU).
- CSG: Ablated GAF (CNN+SENet+GRU).
- CG: Baseline (CNN+GRU).
The experimental parameters maintained strict consistency across all model variants, with the detailed configuration provided in Table 3.

Table 3.
Experimental configuration for ablation study.
Table 4 and Table 5 present the load forecasting performance metrics (, MAE, and MSE) for each model in the Logical Range, evaluated across varying input window sizes w and prediction step lengths d.

Table 4.
Comparison of , MAE, and MSE for different input window sizes (w).

Table 5.
Comparison of , MAE, and MSE for different prediction steps (d).
Table 4 demonstrates the experimental results for the four models with fixed and different values of w. The four models (GCSG, GCG, CSG, and CG) exhibited stable performance across varying w values, with no significant fluctuations observed. Notably, when , the , MSE, and MAE values most closely approximated the average metrics across all tested values of w.
Table 5 demonstrates that, as the prediction step d increases, the capability of the models for temporal dependency feature extraction in the Logical Range presents a decreasing trend. While all models exhibited declining values, the GCSG model consistently maintained superior load forecasting accuracy compared to the other models. The model performance ranking was GCSG > GCG > CSG > CG, with MAE and MSE metrics confirming this trend. These results validate that the combined GAF–CNN-SENet–GRU architecture in GCSG achieves optimal prediction performance.
The MAE and MSE values indicate that GCG outperforms CSG while approaching GCSG’s accuracy, underscoring the GAF’s greater impact on load forecasting accuracy compared to the SENet channel attention mechanism. GAF encoding effectively preserves temporal correlations while enhancing the relevance of inter-temporal values, enabling more comprehensive feature extraction. The GCSG model synergistically combines the GAF’s temporal preservation effect with SENet’s channel importance weighting.
These experimental results conclusively demonstrate the GCSG model’s superior accuracy across all prediction steps, proving that the simultaneous integration of SENet and GAF significantly enhances the resulting model’s load forecasting performance.
3.3.2. Generalization Performance
To evaluate the generalization capability of the GCSG model across different Logical Range training datasets, we conducted experiments using ten distinct data partitioning schemes with varying random seeds. Each scheme maintained an input window size of and prediction steps d ranging from 1 to 29 with an interval of 2. The experimental results are presented in Figure 7.
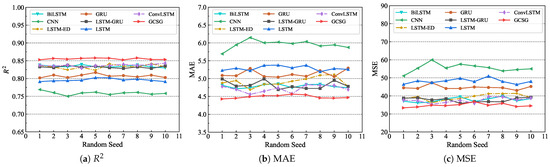
Figure 7.
Comparison of models under different datasets.
Analysis of the datasets partitioned with different random seeds in the Logical Range revealed that the GCSG model can maintain consistent load forecasting performance. Figure 7a demonstrates stable values around 0.85, while Figure 7b shows MAE values consistently near 4.4. Similarly, Figure 7c confirms the stabilization of the MSE at around 35. Compared to other models, GCSG exhibited superior stability across all three metrics without significant fluctuations, demonstrating its robust generalization capability across different data partitions.
4. Discussion
The results demonstrate that the GCSG model consistently outperformed other models in predicting time-series load data, achieving higher R-squared values and lower MAE and MSE across different window sizes and prediction steps. This suggests that the integration of GAF, CNN, SENet, and GRU in the GCSG model contributes significantly to its predictive accuracy. These findings align with prior studies emphasizing the importance of incorporating attention mechanisms and sequential learning in time-series forecasting tasks.
A comparison with the existing literature reveals both similarities and differences. While our study corroborated previous findings regarding the effectiveness of LSTM-based models in time-series prediction, the novel combination of GAF and SENet in the GCSG model provides additional improvements in capturing temporal dependencies and feature extraction.
We acknowledge several limitations in our study. The choice of hyperparameters and model configurations could have influenced the results, and the generalizability of the GCSG model to other domains requires further investigation.
In future research, exploring the application of the GCSG model in different domains and incorporating domain-specific features could enhance its robustness and applicability. Further investigations focused on the optimization of hyperparameters and evaluating model interpretability will be valuable for advancing the understanding of deep learning techniques in time-series analysis.
5. Conclusions
This study presented GCSG, an innovative hybrid deep learning model designed for precise load forecasting in Logical Range environments. The integration of Gramian Angular Field transformation with CNN-SENet spatial feature extraction and GRU-based temporal modeling was shown to be particularly effective in handling the complex, uneven workload distributions that are characteristic of Logical Range testing scenarios. Experimental validation demonstrated that GCSG achieves superior performance, with an of 0.86, MAE of 4.5, and MSE of 34.5, representing significant improvements of 2.2%, 25.7%, and 40.4%, respectively, over conventional approaches (including BiLSTM, LSTM-ED, and other baselines).
The model exhibited remarkable stability across varying operational conditions, maintaining consistent accuracy with input window sizes ranging from 16 to 40 and prediction steps spanning 1 to 29. This robustness was further verified through testing on multiple data partitioning schemes using different random seeds, confirming GCSG’s reliable generalization capability.
Looking ahead, two promising research directions emerge: extension to multi-device collaborative forecasting scenarios and optimization for edge computing deployment in order to enhance computational efficiency. These developments would further strengthen the model’s applicability in large-scale Logical Range implementations while addressing potential latency constraints in time-sensitive applications.
Author Contributions
Conceptualization, H.C.; methodology, H.C.; writing—original draft preparation, H.C.; formal analysis, Z.D.; data curation, Z.D.; supervision, H.C. and Z.D. H.C. and Z.D. reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All materials and data used are available from Xi’an University of Technology, China. The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, H.; Dang, Z.; Hei, X.; Wang, K. Design and application of logical range framework based on digital twin. Appl. Sci. 2023, 13, 6589. [Google Scholar] [CrossRef]
- Huan, M. Development of Logical Range Planning Furthermore, Verification Tool for Joint Test Platform. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Li, D.; Li, L.; Jin, L.; Huang, G.; Wu, Q. Research of load forecasting and elastic resources scheduling of openstack platform based on time series. J. Chongqing Univ. Posts Telecommun. Nat. Sci. Ed. 2016, 28, 560–566. [Google Scholar]
- Khan, A.; Yan, X.; Tao, S.; Anerousis, N. Workload characterization and prediction in the cloud: A multiple time series approach. In Proceedings of the 2012 IEEE Network Operations and Management Symposium, Maui, HI, USA, 16–20 April 2012; pp. 1287–1294. [Google Scholar]
- He, J.; Hong, S.; Zhang, C.; Liu, Y.; Deng, F.; Yu, J. A method to cloud computing resources requirement prediction on saas application. In Proceedings of the 2021 International Conference on Machine Learning and Intelligent Systems Engineering (MLISE), Chongqing, China, 9–11 July 2021; pp. 107–116. [Google Scholar]
- Shyam, G.K.; Manvi, S.S. Virtual resource prediction in cloud environment: A bayesian approach. J. Netw. Comput. Appl. 2016, 65, 144–154. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, H.; Palazoglu, A.; Singh, A.; Zhang, W.; Liu, S. Prediction of 24-hour-average PM2.5 concentrations using a hidden markov model with different emission distributions in northern california. Sci. Total Environ. 2013, 443, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Dinda, P.A.; O’Hallaron, D.R. Host load prediction using linear models. Clust. Comput. 2000, 3, 265–280. [Google Scholar] [CrossRef]
- Liu, X.; Xie, X.; Guo, Q. Research on cloud computing load forecasting based on lstm-arima combined model. In Proceedings of the 2022 Tenth International Conference on Advanced Cloud and Big Data (CBD), Guilin, China, 4–5 November 2022; pp. 19–23. [Google Scholar]
- Mehdi, H.; Pooranian, Z.; Vinueza Naranjo, P.G. Cloud traffic prediction based on fuzzy arima model with low dependence on historical data. Trans. Emerg. Telecommun. Technol. 2022, 33, e3731. [Google Scholar] [CrossRef]
- Xie, Y.; Jin, M.; Zou, Z.; Xu, G.; Feng, D.; Liu, W.; Long, D. Real-time prediction of docker container resource load based on a hybrid model of arima and triple exponential smoothing. IEEE Trans. Cloud Comput. 2020, 10, 1386–1401. [Google Scholar] [CrossRef]
- Sharma, A.K.; Punj, P.; Kumar, N.; Das, A.K.; Kumar, A. Lifetime prediction of a hydraulic pump using arima model. Arab. J. Sci. Eng. 2024, 49, 1713–1725. [Google Scholar] [CrossRef]
- Prevost, J.J.; Nagothu, K.; Kelley, B.; Jamshidi, M. Prediction of cloud data center networks loads using stochastic and neural models. In Proceedings of the 2011 6th International Conference on System of Systems Engineering, Albuquerque, NM, USA, 27–30 June 2011; pp. 276–281. [Google Scholar]
- Karim, M.E.; Maswood, M.M.S.; Das, S.; Alharbi, A.G. Bhyprec: A novel bi-lstm based hybrid recurrent neural network model to predict the cpu workload of cloud virtual machine. IEEE Access 2021, 9, 131476–131495. [Google Scholar] [CrossRef]
- Shu, W.; Zeng, F.; Ling, Z.; Liu, J.; Lu, T.; Chen, G. Resource demand prediction of cloud workloads using an attention-based gru model. In Proceedings of the 2021 17th International Conference on Mobility, Sensing and Networking (MSN), Exeter, UK, 13–15 December 2021; pp. 428–437. [Google Scholar]
- Bi, J.; Ma, H.; Yuan, H.; Zhang, J. Accurate prediction of workloads and resources with multi-head attention and hybrid lstm for cloud data centers. IEEE Trans. Sustain. Comput. 2023, 8, 375–384. [Google Scholar] [CrossRef]
- Patel, E.; Kushwaha, D.S. A hybrid cnn-lstm model for predicting server load in cloud computing. J. Supercomput. 2022, 78, 1–30. [Google Scholar] [CrossRef]
- Kumar, J.; Goomer, R.; Singh, A.K. Long short term memory recurrent neural network (lstm-rnn) based workload forecasting model for cloud datacenters. Procedia Comput. Sci. 2018, 125, 676–682. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.; Lee, H.-J. A review on deep learning models for forecasting time series data of solar irradiance and photovoltaic power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Ilesanmi, A.E.; Ilesanmi, T.O. Methods for image denoising using convolutional neural network: A review. Complex Intell. Syst. 2021, 7, 2179–2198. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Huang, J.; Ren, L.; Zhou, X.; Yan, K. An improved neural network based on senet for sleep stage classification. IEEE J. Biomed. Health Inform. 2022, 26, 4948–4956. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using rnn encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Nguyen, H.M.; Kalra, G.; Kim, D. Host load prediction in cloud computing using long short-term memory encoder–decoder. J. Supercomput. 2019, 75, 7592–7605. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, D.; Xue, R. Hourly prediction of PM2.5 concentration in beijing based on bi-lstm neural network. Multimed. Tools Appl. 2021, 80, 24455–24468. [Google Scholar] [CrossRef]
- Cho, M.; Kim, C.; Jung, K.; Jung, H. Water level prediction model applying a long short-term memory (lstm)–gated recurrent unit (gru) method for flood prediction. Water 2022, 14, 2221. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y. Convolutional lstm network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).