A Forecasting Approach for Wholesale Market Agricultural Product Prices Based on Combined Residual Correction
Abstract
1. Introduction
2. Literature Review
2.1. Single Prediction Models
2.2. Combined Prediction Models
3. Model Construction
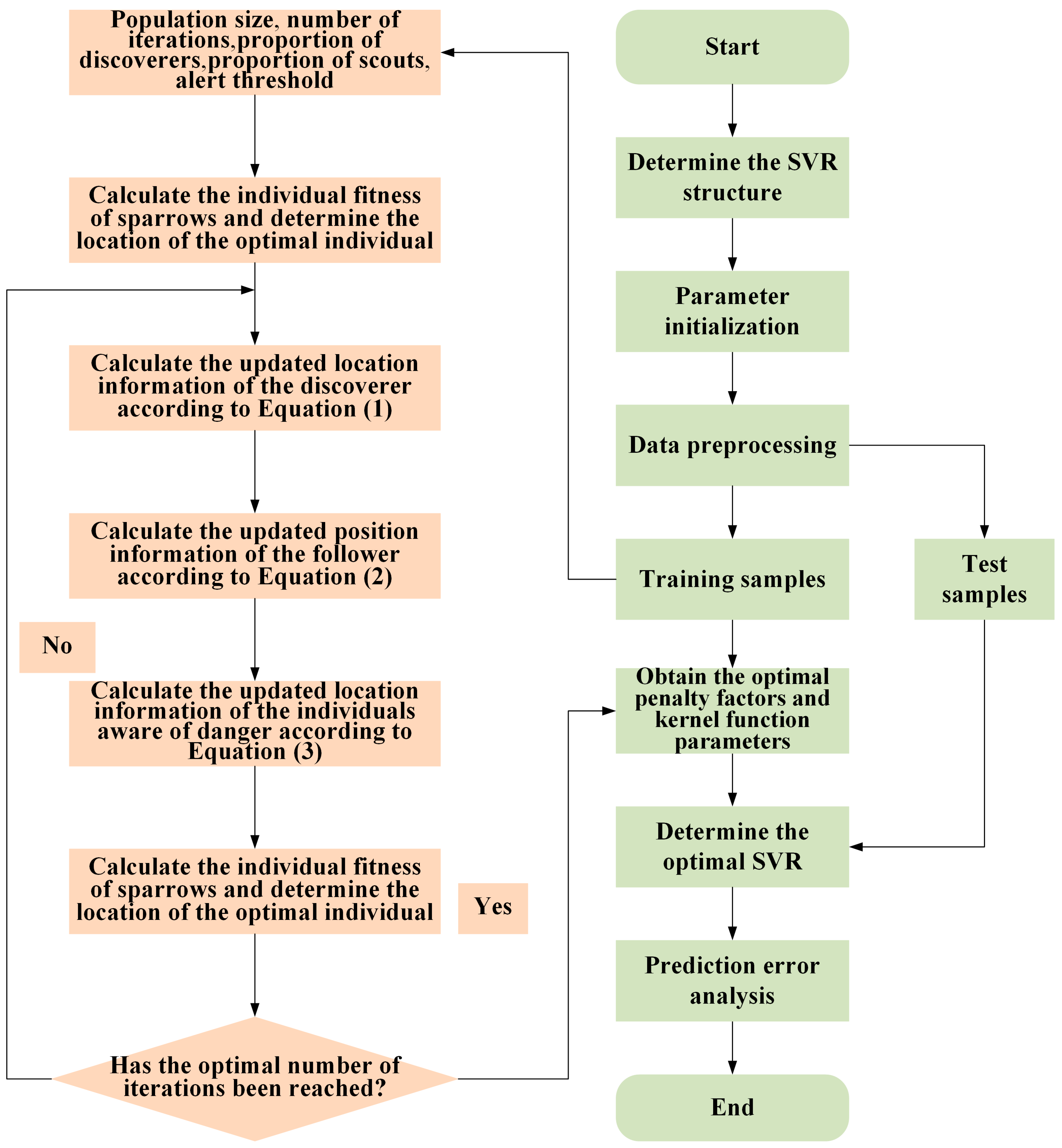
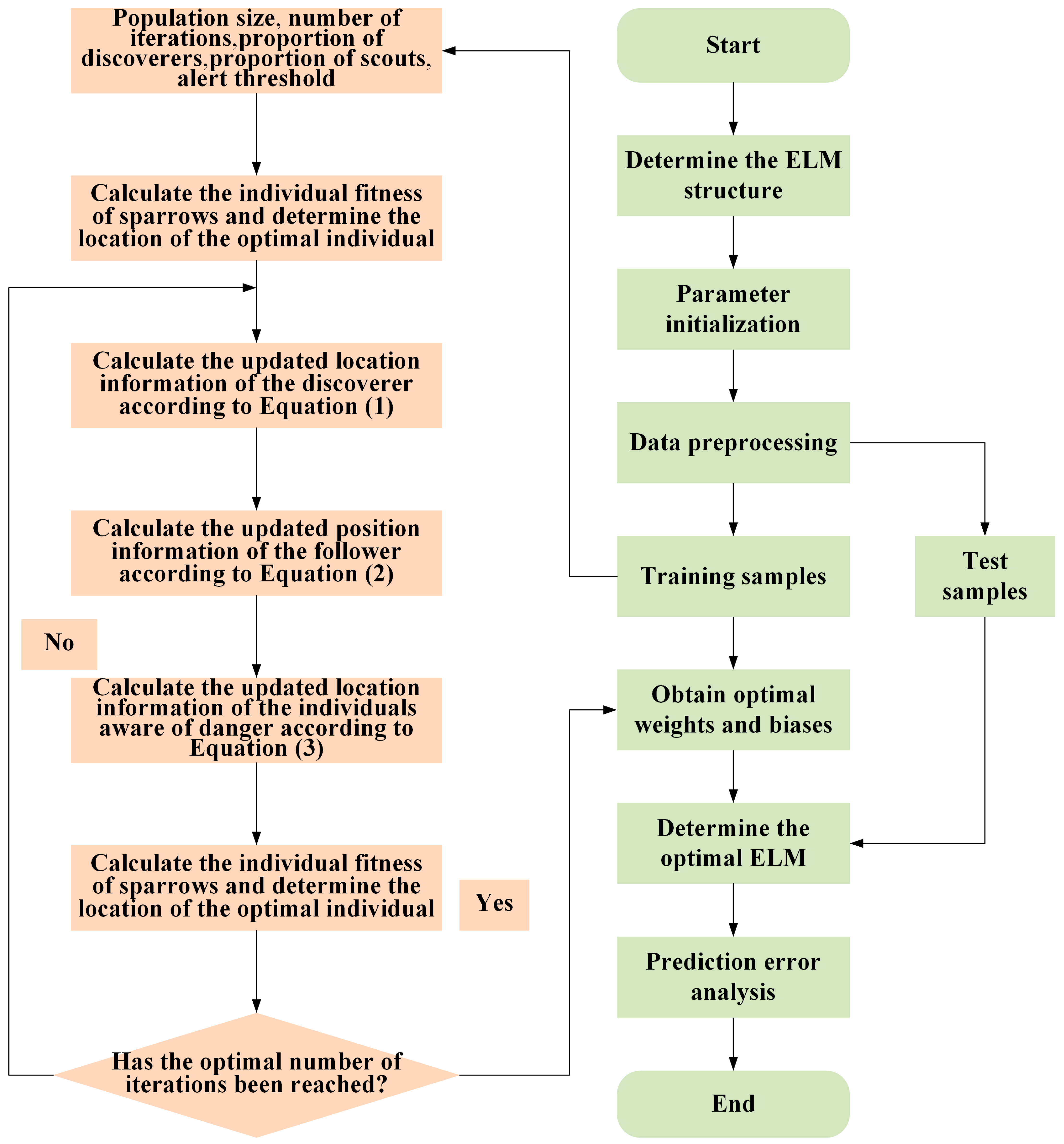
3.1. Optimized Prediction Model Construction
3.2. Construction of Combined Prediction Models
3.2.1. IOWA Operator
3.2.2. A Combined Residual Correction Prediction Model of Optimal Machine Learning Based on the IOWA Operator
3.3. Residual Correction Forecast for Future Intervals
4. Results and Discussion
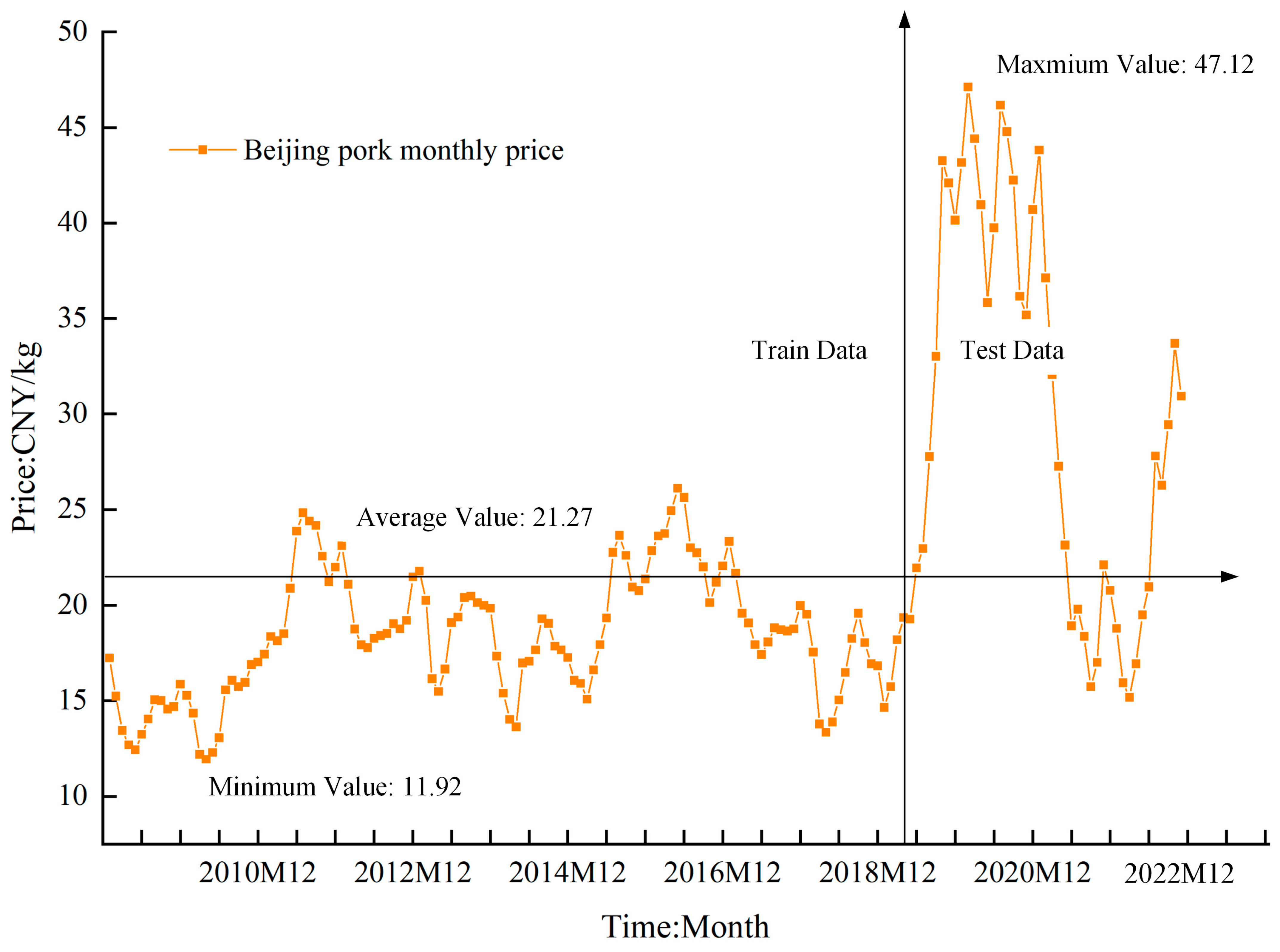
4.1. Data Source
4.2. Evaluation Metrics
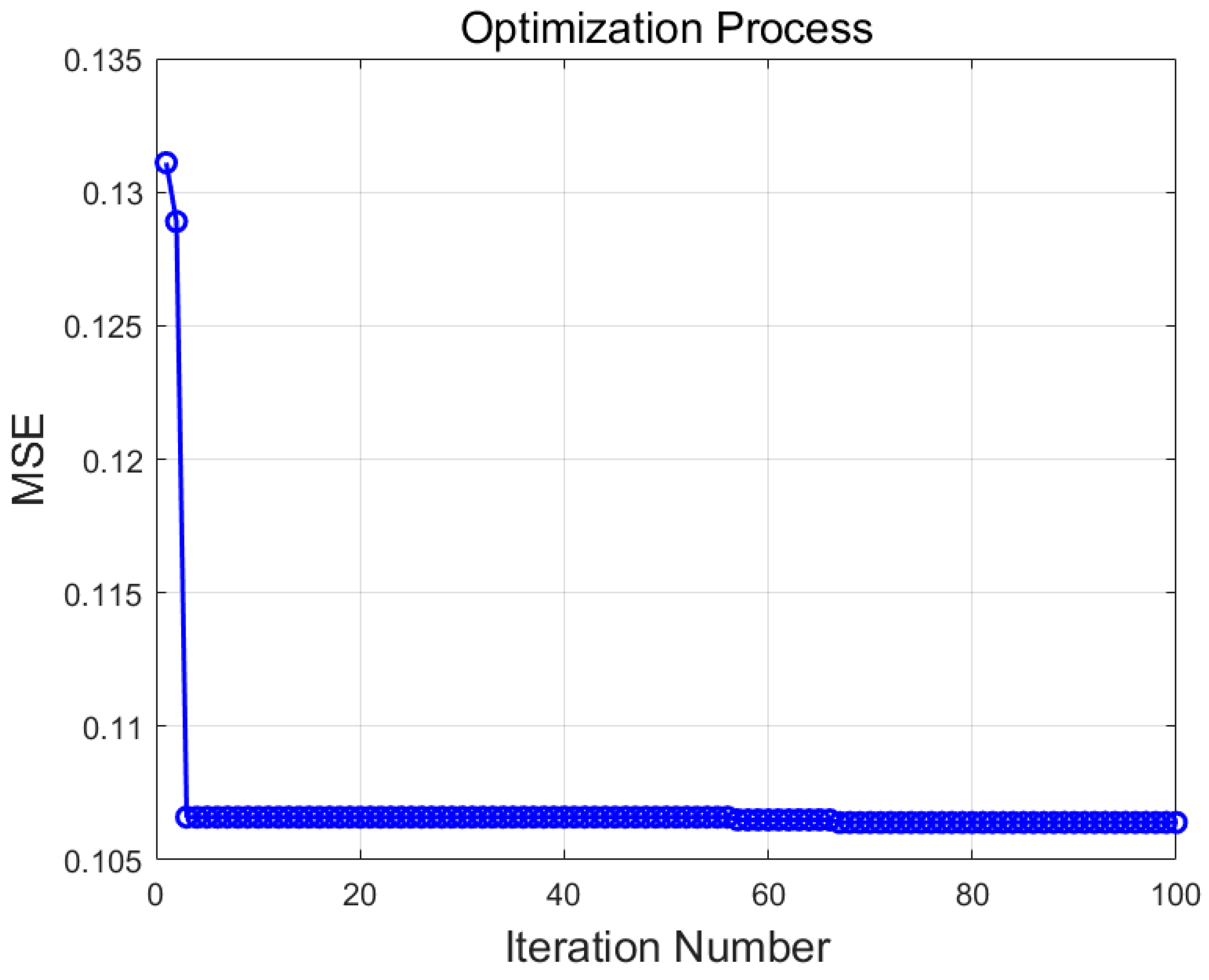
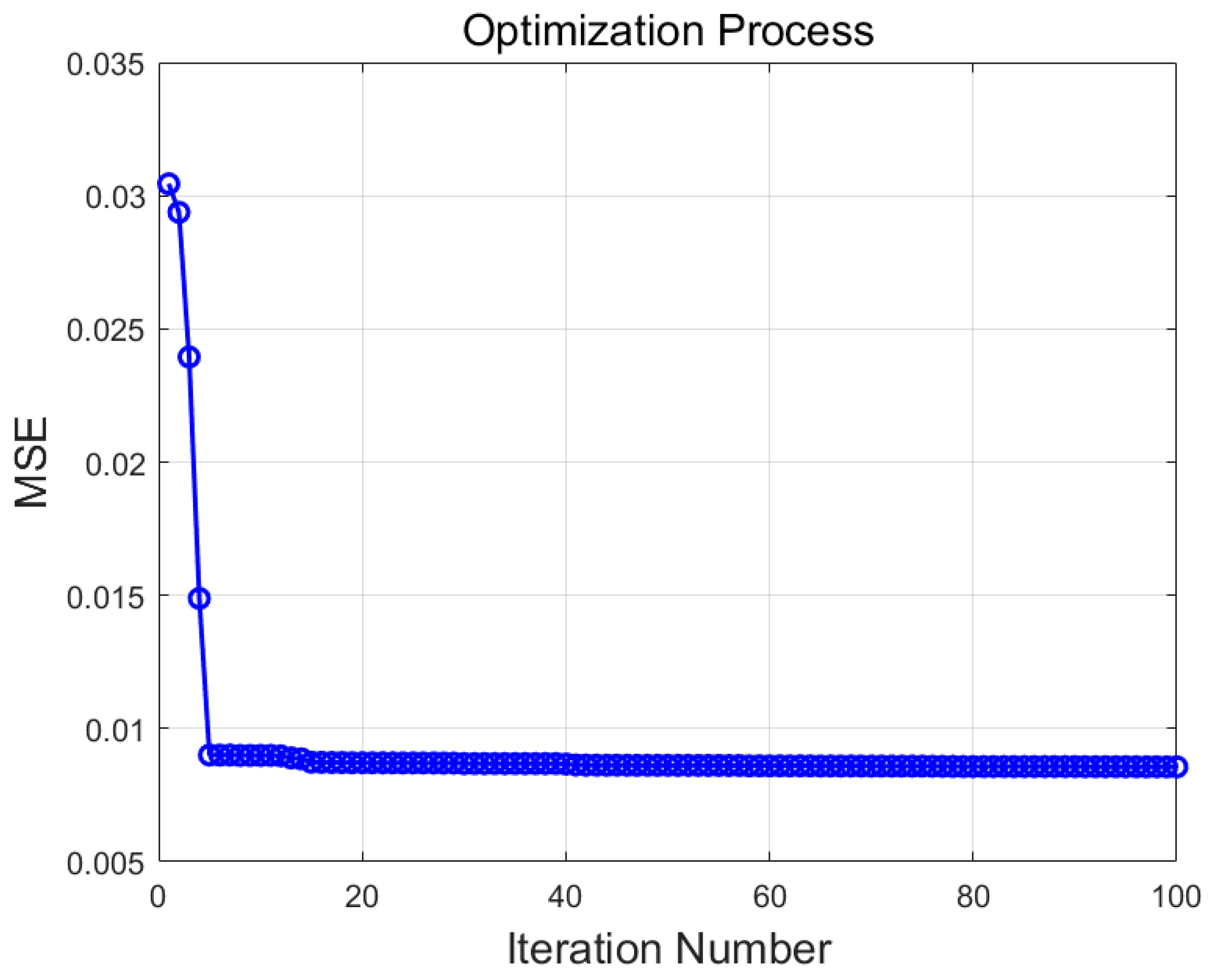
4.3. SSA Optimization Process for the SVR and ELM
4.4. Combined Prediction Model Weighting Vector Determination
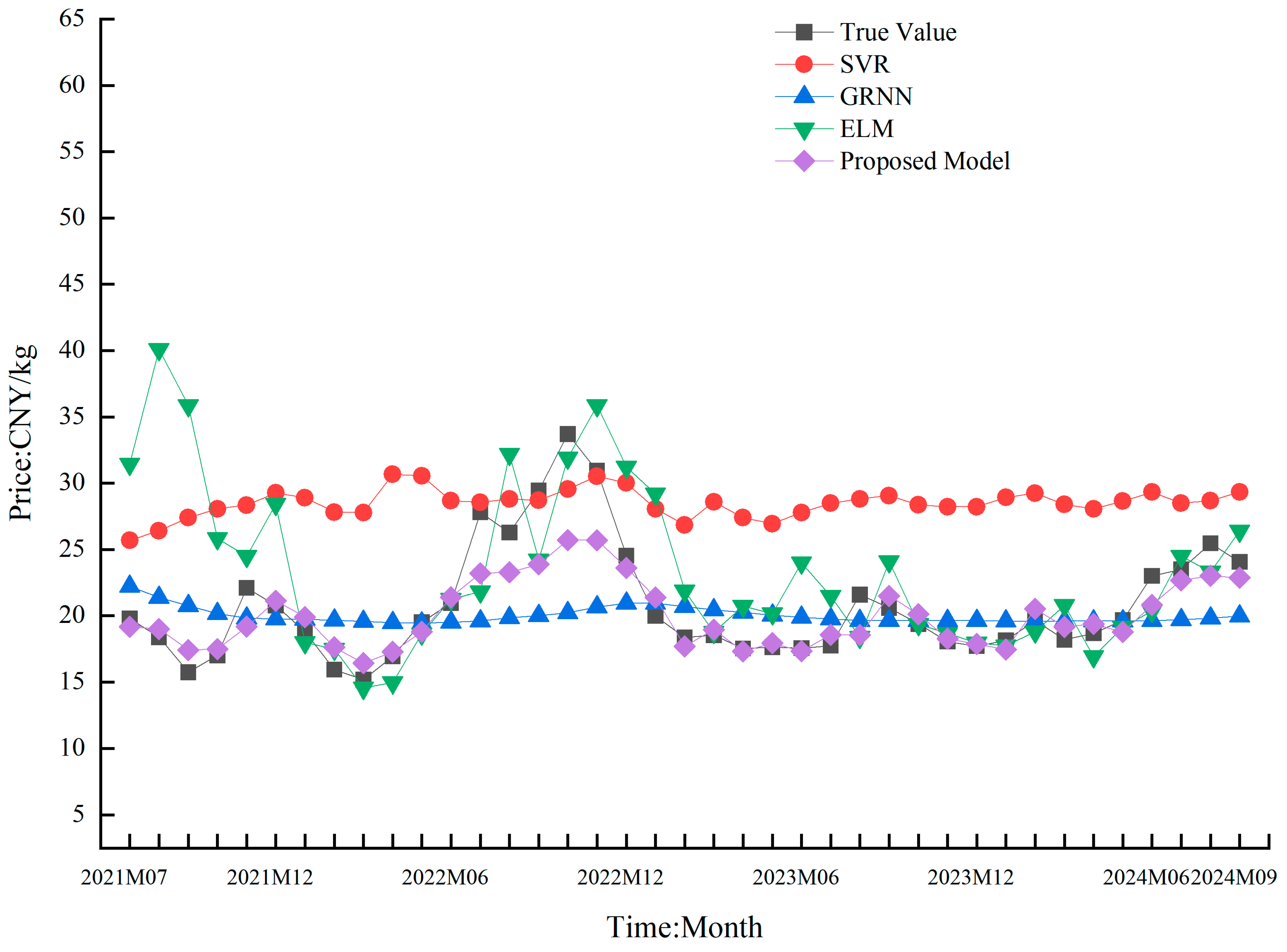
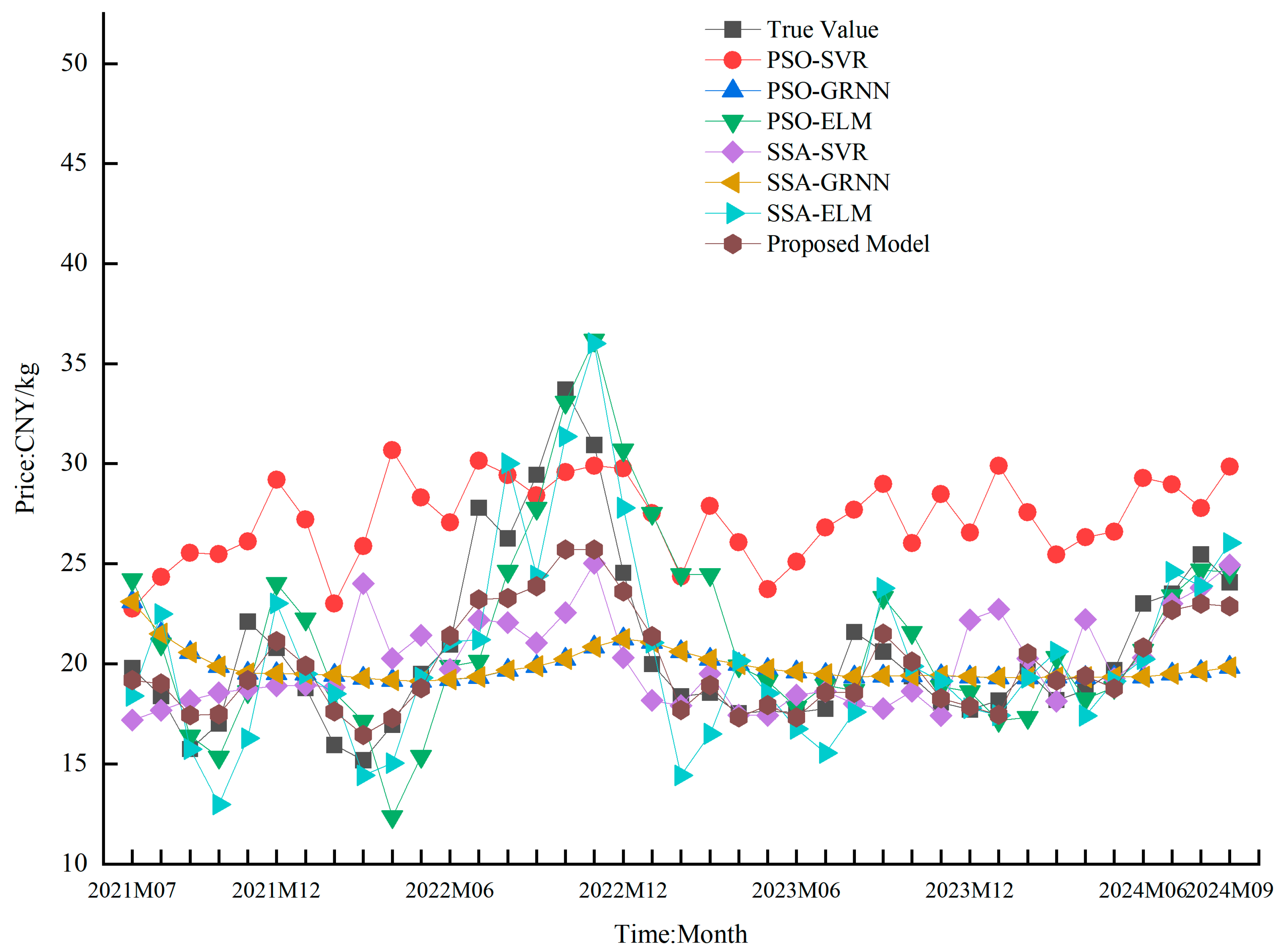
4.5. Comparison of the Results of Different Prediction Models
4.6. Forecast of Agricultural Product Prices in the Coming Period
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, Y.; Li, W.; Gil, J.M. Forecasting fish prices with an artificial neural network model during the tuna fraud. J. Agric. Food Res. 2024, 18, 101340. [Google Scholar] [CrossRef]
- Zhang, D.; Zang, G.; Li, J.; Ma, K.; Liu, H. Prediction of soybean price in China using QR-RBF neural network model. Comput. Electron. Agric. 2018, 154, 10–17. [Google Scholar] [CrossRef]
- Xiong, T.; Li, C.; Bao, Y. Seasonal forecasting of agricultural commodity price using a hybrid STL and ELM method: Evidence from the vegetable market in China. Neurocomputing 2018, 275, 2831–2844. [Google Scholar] [CrossRef]
- Li, B.; Ding, J.; Yin, Z.; Li, K.; Zhao, X.; Zhang, L. Optimized neural network combined model based on the induced ordered weighted averaging operator for vegetable price forecasting. Expert Syst. Appl. 2021, 168, 114232. [Google Scholar] [CrossRef]
- Shukur, O.B.; Lee, M.H. Daily wind speed forecasting through hybrid KF-ANN model based on ARIMA. Renew. Energy 2015, 76, 637–647. [Google Scholar] [CrossRef]
- Tealab, A. Time series forecasting using artificial neural networks methodologies: A systematic review. Future Comput. Inform. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Fallah Tehrani, A.; Ahrens, D. Enhanced predictive models for purchasing in the fashion field by using kernel machine regression equipped with ordinal logistic regression. J. Retail. Consum. Serv. 2016, 32, 131–138. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, R.; Deng, H. A novel STL-based hybrid model for forecasting hog price in China. Comput. Electron. Agric. 2022, 198, 107068. [Google Scholar] [CrossRef]
- Esen, H.; Ozgen, F.; Esen, M.; Sengur, A. Artificial neural network and wavelet neural network approaches for modelling of a solar air heater. Expert Syst. Appl. 2009, 36, 11240–11248. [Google Scholar] [CrossRef]
- Jha, G.K.; Sinha, K. Time-delay neural networks for time series prediction: An application to the monthly wholesale price of oilseeds in India. Neural Comput. Appl. 2012, 24, 563–571. [Google Scholar] [CrossRef]
- Liu, Y.; Duan, Q.; Wang, D.; Zhang, Z.; Liu, C. Prediction for hog prices based on similar sub-series search and support vector regression. Comput. Electron. Agric. 2019, 157, 581–588. [Google Scholar] [CrossRef]
- Yao, X.; Wang, Z.; Zhang, H. Prediction and identification of discrete-time dynamic nonlinear systems based on adaptive echo state network. Neural Netw. 2019, 113, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Zaghloul, M.; Barakat, S.; Rezk, A. Predicting E-commerce customer satisfaction: Traditional machine learning vs. deep learning approaches. J. Retail. Consum. Serv. 2024, 79, 103865. [Google Scholar] [CrossRef]
- Bates, J.M.; Granger, C.W.J. The Combination of Forecasts. J. Oper. Res. Soc. 1969, 20, 451–468. [Google Scholar] [CrossRef]
- Nowotarski, J.; Liu, B.; Weron, R.; Hong, T. Improving short term load forecast accuracy via combining sister forecasts. Energy 2016, 98, 40–49. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, Z.; Wei, Y. An adaptive hybrid model for short term electricity price forecasting. Appl. Energy 2020, 258, 114087. [Google Scholar] [CrossRef]
- Song, C.; Fu, X. Research on different weight combination in air quality forecasting models. J. Clean. Prod. 2020, 261, 121169. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Li, X.; Zhou, H. Artificial bee colony-based combination approach to forecasting agricultural commodity prices. Int. J. Forecast. 2019, 38, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Y.; Wei, G. A feature-enhanced long short-term memory network combined with residual-driven ν support vector regression for financial market prediction. Eng. Appl. Artif. Intell. 2023, 118, 105663. [Google Scholar] [CrossRef]
- Hu, R.; Wen, S.; Zeng, Z.; Huang, T. A short-term power load forecasting model based on the generalized regression neural network with decreasing step fruit fly optimization algorithm. Neurocomputing 2017, 221, 24–31. [Google Scholar] [CrossRef]
- Wu, W.; Chen, K.; Tsotsas, E. Prediction of particle mixing in rotary drums by a DEM data-driven PSO-SVR model. Powder Technol. 2024, 434, 119365. [Google Scholar] [CrossRef]
- Du, H.; Song, D.; Chen, Z.; Shu, H.; Guo, Z. Prediction model oriented for landslide displacement with step-like curve by applying ensemble empirical mode decomposition and the PSO-ELM method. J. Clean. Prod. 2020, 270, 122248. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.; Kisi, O.; Yaseen, Z.M.; Shahid, S.; Zounemat-Kermani, M. Improving streamflow prediction using a new hybrid ELM model combined with hybrid particle swarm optimization and grey wolf optimization. Knowl. Based Syst. 2021, 230, 107379. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. Open Access J. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, S. A stochastic configuration network based on chaotic sparrow search algorithm. Knowl. Based Syst. 2021, 220, 106924. [Google Scholar] [CrossRef]
- Colino, E.V.; Irwin, S.H.; Garcia, P. Improving the accuracy of outlook price forecasts. Agric. Econ. 2011, 42, 357–371. [Google Scholar] [CrossRef]
- Mohammadi, H.; Su, L. International evidence on crude oil price dynamics: Applications of ARIMA-GARCH models. Energy Econ. 2010, 32, 1001–1008. [Google Scholar] [CrossRef]
- Teste, F.; Makowski, D.; Bazzi, H.; Ciais, P. Early forecasting of corn yield and price variations using satellite vegetation products. Comput. Electron. Agric. 2024, 221, 108962. [Google Scholar] [CrossRef]
- Elavarasan, D.; Vincent, D.R.; Sharma, V.; Zomaya, A.Y.; Srinivasan, K. Forecasting yield by integrating agrarian factors and machine learning models: A survey. Comput. Electron. Agric. 2018, 155, 257–282. [Google Scholar] [CrossRef]
- Avinash, G.; Ramasubramanian, V.; Ray, M.; Paul, R.K.; Godara, S.; Nayak, G.H.H.; Kumar, R.R.; Manjunatha, B.; Dahiya, S.; Iquebal, M.A. Hidden Markov guided Deep Learning models for forecasting highly volatile agricultural commodity prices. Appl. Soft Comput. 2024, 158, 111557. [Google Scholar] [CrossRef]
- Jin, C.; Jin, S.; Qin, L. Attribute selection method based on a hybrid BPNN and PSO algorithms. Appl. Soft Comput. 2012, 12, 2147–2155. [Google Scholar] [CrossRef]
- Cui, L.; Tao, Y.; Deng, J.; Liu, X.; Xu, D.; Tang, G. BBO-BPNN and AMPSO-BPNN for multiple-criteria inventory classification. Expert Syst. Appl. 2021, 175, 114842. [Google Scholar] [CrossRef]
- Ghritlahre, H.K.; Prasad, R.K. Exergetic performance prediction of solar air heater using MLP, GRNN and RBF models of artificial neural network technique. J. Environ. Manag. 2018, 223, 566–575. [Google Scholar] [CrossRef] [PubMed]
- Ni, Y.Q.; Li, M. Wind pressure data reconstruction using neural network techniques: A comparison between BPNN and GRNN. Measurement 2016, 88, 468–476. [Google Scholar] [CrossRef]
- Blanc, S.M.; Setzer, T. When to choose the simple average in forecast combination. J. Bus. Res. 2016, 69, 3951–3962. [Google Scholar] [CrossRef]
- Wu, R.; Huang, H.; Wei, J.; Ma, C.; Zhu, Y.; Chen, Y.; Fan, Q. An improved sparrow search algorithm based on quantum computations and multi-strategy enhancement. Expert Syst. Appl. 2023, 215, 119421. [Google Scholar] [CrossRef]
- Zamfirache, I.A.; Precup, R.E.; Roman, R.C.; Petriu, E.M. Reinforcement Learning-based control using Q-learning and gravitational search algorithm with experimental validation on a nonlinear servo system. Inf. Sci. 2022, 583, 99–120. [Google Scholar] [CrossRef]
- Yang, W.D.; Wang, J.Z.; Niu, T.; Du, P. A novel system for multi-step electricity price forecasting for electricity market management. Appl. Soft Comput. 2020, 88, 106029. [Google Scholar] [CrossRef]
- Bi, J.; Zhao, M.; Yao, G.; Cao, H.; Feng, Y.; Jiang, H.; Chai, D. PSOSVRPos: WiFi indoor positioning using SVR optimized by PSO. Expert Syst. Appl. 2023, 222, 119778. [Google Scholar] [CrossRef]
- Xie, K.; Yi, H.; Hu, G.; Li, L.; Fan, Z. Short-term power load forecasting based on Elman neural network with particle swarm optimization. Neurocomputing 2020, 416, 136–142. [Google Scholar] [CrossRef]
- Liang, H.; Zou, J.; Li, Z.; Khan, M.J.; Lu, Y. Dynamic evaluation of drilling leakage risk based on fuzzy theory and PSO-SVR algorithm. Future Gener. Comput. Syst. 2019, 95, 454–466. [Google Scholar] [CrossRef]
- Jia, Y.; Su, Y.; Zhang, R.; Zhang, Z.; Lu, Y.; Shi, D.; Xu, C.; Huang, D. Optimization of an extreme learning machine model with the sparrow search algorithm to estimate spring maize evapotranspiration with film mulching in the semiarid regions of China. Comput. Electron. Agric. 2022, 201, 107298. [Google Scholar] [CrossRef]
| Month | Residual Actual Value Pork Price (CNY /kg) | Residual Prediction Value | Prediction Accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Pork Price (CNY/kg) | |||||||||
| SVR | ELM | SSA-SVR | SSA-ELM | SVR | ELM | SSA-SVR | SSA-ELM | ||
| 2021M07 | −2.44 | 0.14 | −2.08 | −2.45 | −3.31 | 0.00 | 0.85 | 0.99 | 0.64 |
| 2021M08 | −3.01 | 0.11 | −2.53 | −2.23 | −2.72 | 0.00 | 0.84 | 0.74 | 0.91 |
| 2021M09 | −5.03 | 0.00 | −2.09 | −2.38 | −5.54 | 0.00 | 0.42 | 0.47 | 0.90 |
| 2021M10 | −3.16 | 0.13 | −2.15 | −2.57 | −2.96 | 0.00 | 0.68 | 0.81 | 0.94 |
| 2021M11 | 2.28 | 0.28 | 0.50 | −1.82 | 2.01 | 0.12 | 0.22 | 0.00 | 0.88 |
| 2021M12 | 1.01 | 0.33 | −0.25 | 1.20 | 1.44 | 0.32 | 0.00 | 0.81 | 0.58 |
| 2022M01 | −0.94 | 0.22 | 1.19 | 0.74 | −1.11 | 0.00 | 0.00 | 0.00 | 0.82 |
| 2022M02 | −3.73 | 0.07 | −1.42 | −1.36 | −3.62 | 0.00 | 0.38 | 0.36 | 0.97 |
| 2022M03 | −4.39 | 0.04 | −5.39 | −2.47 | −4.62 | 0.00 | 0.77 | 0.56 | 0.95 |
| 2022M04 | −2.54 | 0.14 | −2.38 | −2.35 | −2.14 | 0.00 | 0.94 | 0.92 | 0.84 |
| 2022M05 | 0.04 | 0.27 | −1.63 | −0.14 | −0.91 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2022M06 | 1.46 | 0.35 | 0.30 | 1.28 | 2.18 | 0.24 | 0.20 | 0.88 | 0.51 |
| 2022M07 | 8.21 | 0.72 | 2.55 | 2.13 | 6.97 | 0.09 | 0.31 | 0.26 | 0.85 |
| 2022M08 | 6.43 | 0.62 | 8.07 | 2.28 | 6.09 | 0.10 | 0.74 | 0.35 | 0.95 |
| 2022M09 | 9.44 | 0.69 | 6.26 | 1.43 | 9.42 | 0.07 | 0.66 | 0.15 | 1.00 |
| 2022M10 | 13.46 | 0.87 | 11.43 | 2.08 | 13.09 | 0.06 | 0.85 | 0.15 | 0.97 |
| 2022M11 | 10.28 | 0.83 | 12.49 | 3.07 | 9.50 | 0.08 | 0.78 | 0.30 | 0.92 |
| 2022M12 | 3.59 | 0.47 | 4.09 | 2.11 | 3.91 | 0.13 | 0.86 | 0.59 | 0.91 |
| 2023M01 | −0.95 | 0.22 | −2.00 | −0.77 | 1.00 | 0.00 | 0.00 | 0.81 | 0.00 |
| 2023M02 | −2.34 | 0.15 | −3.13 | −2.53 | −3.23 | 0.00 | 0.66 | 0.92 | 0.62 |
| 2023M03 | −1.91 | 0.17 | −1.13 | −2.11 | −1.26 | 0.00 | 0.59 | 0.90 | 0.66 |
| 2023M04 | −2.73 | 0.13 | −3.64 | −2.53 | −3.11 | 0.00 | 0.67 | 0.93 | 0.86 |
| 2023M05 | −2.40 | 0.14 | −2.94 | −2.61 | −1.86 | 0.00 | 0.77 | 0.91 | 0.78 |
| 2023M06 | −2.32 | 0.10 | −3.37 | −2.50 | −2.58 | 0.00 | 0.55 | 0.92 | 0.89 |
| 2023M07 | −2.00 | 0.16 | −2.16 | −2.06 | −0.79 | 0.00 | 0.92 | 0.97 | 0.40 |
| 2023M08 | 1.97 | 0.36 | −0.08 | −1.72 | 0.42 | 0.18 | 0.00 | 0.00 | 0.21 |
| 2023M09 | 0.96 | 0.32 | 2.31 | 0.78 | 2.34 | 0.34 | 0.00 | 0.81 | 0.00 |
| 2023M10 | −0.27 | 0.26 | 0.25 | 0.73 | −0.16 | 0.00 | 0.00 | 0.00 | 0.60 |
| 2023M11 | −1.59 | 0.19 | 0.82 | −1.35 | −1.45 | 0.00 | 0.00 | 0.85 | 0.91 |
| 2023M12 | −1.91 | 0.17 | −0.85 | −2.05 | −1.62 | 0.00 | 0.45 | 0.93 | 0.85 |
| 2024M01 | −1.44 | 0.19 | −0.88 | −1.48 | −2.43 | 0.00 | 0.61 | 0.97 | 0.31 |
| 2024M02 | 0.04 | 0.28 | 0.79 | −0.15 | 1.41 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2024M03 | −1.42 | 0.20 | 0.53 | 0.40 | −2.36 | 0.00 | 0.00 | 0.00 | 0.33 |
| 2024M04 | −0.93 | 0.22 | 0.29 | −1.12 | 0.19 | 0.00 | 0.00 | 0.80 | 0.00 |
| 2024M05 | 0.06 | −0.47 | 0.71 | −1.86 | −0.38 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2024M06 | 3.39 | 3.53 | 0.56 | 0.57 | 2.60 | 0.96 | 0.17 | 0.17 | 0.77 |
| 2024M07 | 3.80 | 4.28 | 3.31 | 2.43 | 4.18 | 0.87 | 0.87 | 0.64 | 0.90 |
| 2024M08 | 5.64 | 3.98 | 4.85 | 2.34 | 5.11 | 0.71 | 0.86 | 0.41 | 0.91 |
| 2024M09 | 4.10 | 7.08 | 6.04 | 2.23 | 4.43 | 0.28 | 0.53 | 0.54 | 0.92 |
| Mean | 0.12 | 0.44 | 0.53 | 0.65 | |||||
| Prediction Model | MAE | MAPE | MSE | RMSE | TIC |
|---|---|---|---|---|---|
| SVR | 2.82 | 1.38 | 15.16 | 3.89 | 0.66 |
| ELM | 1.42 | 2.31 | 3.10 | 1.76 | 0.21 |
| SSA-SVR | 1.88 | 1.53 | 9.87 | 3.14 | 0.51 |
| SSA-ELM | 0.63 | 1.93 | 0.60 | 0.77 | 0.09 |
| Prediction Model | MAE | MAPE | MSE | RMSE | TIC |
|---|---|---|---|---|---|
| SVR | 8.04 | 0.43 | 75.43 | 8.69 | 0.17 |
| GRNN | 3.17 | 0.14 | 18.45 | 4.30 | 0.10 |
| ELM | 4.09 | 0.21 | 39.82 | 6.31 | 0.14 |
| PSO-SVR | 6.85 | 0.36 | 54.76 | 7.40 | 0.15 |
| PSO-GRNN | 2.93 | 0.13 | 16.47 | 4.06 | 0.10 |
| PSO-ELM | 2.60 | 0.13 | 10.82 | 3.29 | 0.08 |
| SSA-SVR | 2.64 | 0.12 | 13.42 | 3.66 | 0.09 |
| SSA-GRNN | 2.88 | 0.13 | 15.82 | 3.98 | 0.10 |
| SSA-ELM | 2.18 | 0.10 | 7.57 | 2.75 | 0.07 |
| Proposed model | 1.52 | 0.07 | 5.20 | 2.28 | 0.06 |
| Month | Forecasted Value (CNY/kg) | Month | Forecasted Value (CNY/kg) |
|---|---|---|---|
| 2024M10 | 21.37 | 2025M06 | 17.95 |
| 2024M11 | 21.49 | 2025M07 | 17.39 |
| 2024M12 | 22.07 | 2025M08 | 18.55 |
| 2025M01 | 19.81 | 2025M09 | 20.04 |
| 2025M02 | 18.13 | 2025M10 | 17.37 |
| 2025M03 | 19.39 | 2025M11 | 17.11 |
| 2025M04 | 18.20 | 2025M12 | 16.84 |
| 2025M05 | 17.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Lian, Y. A Forecasting Approach for Wholesale Market Agricultural Product Prices Based on Combined Residual Correction. Appl. Sci. 2025, 15, 5575. https://doi.org/10.3390/app15105575
Li B, Lian Y. A Forecasting Approach for Wholesale Market Agricultural Product Prices Based on Combined Residual Correction. Applied Sciences. 2025; 15(10):5575. https://doi.org/10.3390/app15105575
Chicago/Turabian StyleLi, Bo, and Yuanqiang Lian. 2025. "A Forecasting Approach for Wholesale Market Agricultural Product Prices Based on Combined Residual Correction" Applied Sciences 15, no. 10: 5575. https://doi.org/10.3390/app15105575
APA StyleLi, B., & Lian, Y. (2025). A Forecasting Approach for Wholesale Market Agricultural Product Prices Based on Combined Residual Correction. Applied Sciences, 15(10), 5575. https://doi.org/10.3390/app15105575






