Machine Learning for the Prediction of Thermodynamic Properties in Amorphous Silicon
Abstract
1. Introduction
2. Materials and Methods
2.1. MD Simulations
2.2. Dataset Preparation
2.3. Predictive Models
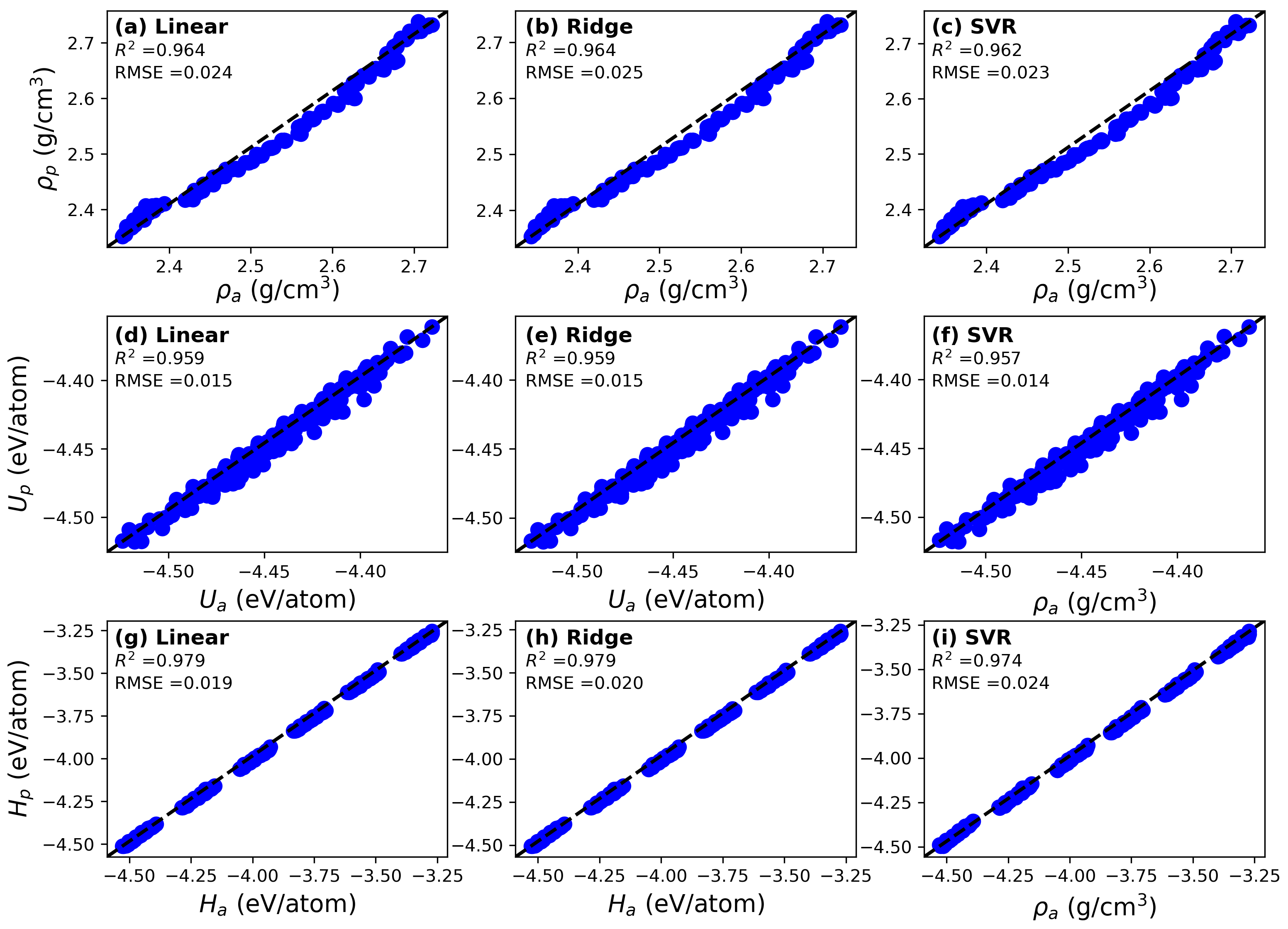
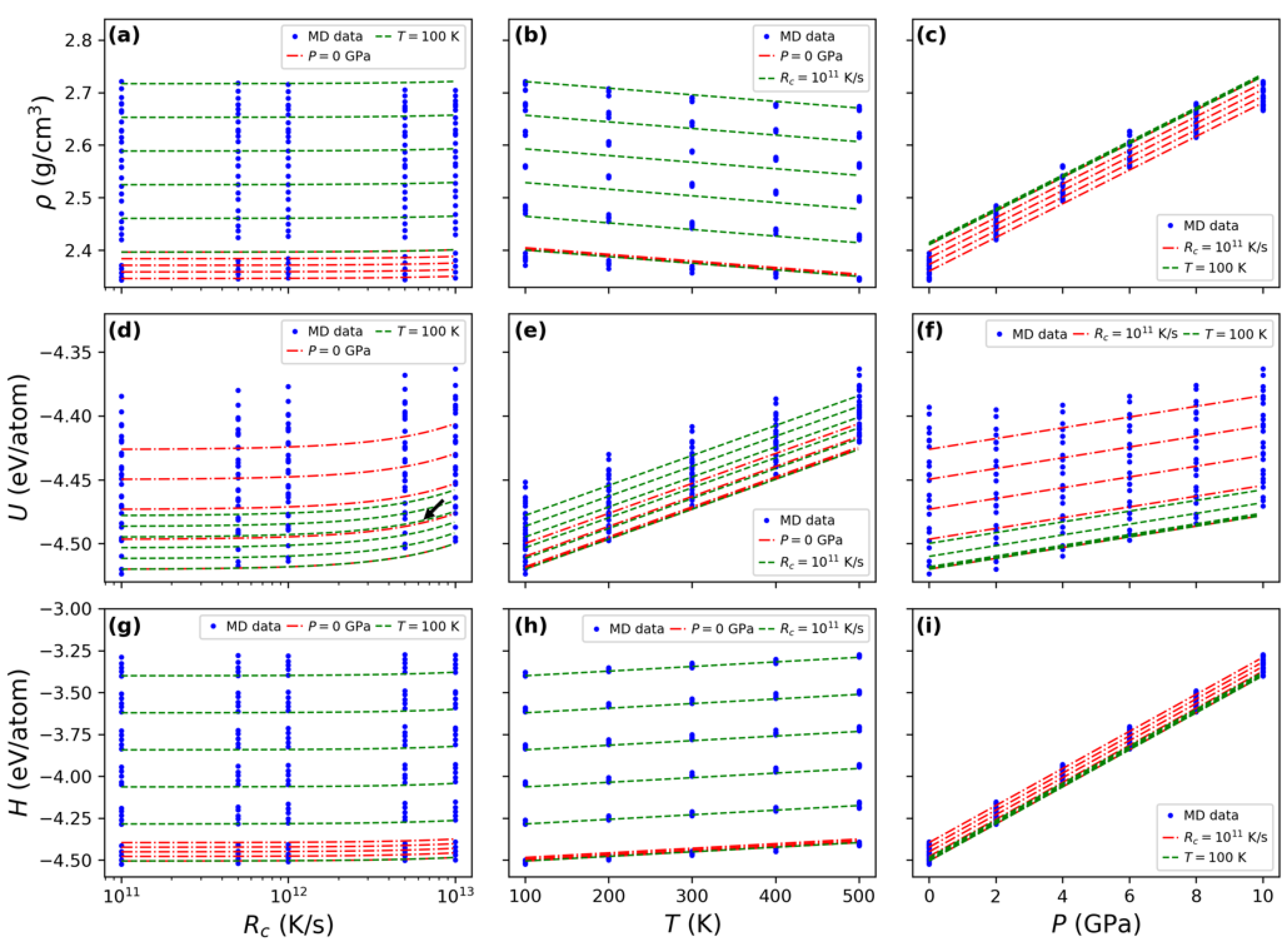
3. Results
3.1. Statistical Exploration
3.2. Predictive Models
4. Discussions
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Le Comber, P. Present and future applications of amorphous silicon and its alloys. J. -Non-Cryst. Solids 1989, 115, 1–13. [Google Scholar] [CrossRef]
- Shen, D.; Kowel, S.T.; Eldering, C.A. Amorphous silicon thin-film photodetectors for optical interconnection. Opt. Eng. 1995, 34, 881–886. [Google Scholar] [CrossRef]
- Crawford, G.P. Flexible flat panel display technology. In Flexible Flat Panel Displays; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 1–9. [Google Scholar]
- Bose, S.K.; Winer, K.; Andersen, O.K. Electronic properties of a realistic model of amorphous silicon. Phys. Rev. B 1988, 37, 6262–6277. [Google Scholar] [CrossRef] [PubMed]
- Car, R.; Parrinello, M. Structural, Dymanical, and Electronic Properties of Amorphous Silicon: An ab initio Molecular-Dynamics Study. Phys. Rev. Lett. 1988, 60, 204–207. [Google Scholar] [CrossRef]
- Larkin, J.M.; McGaughey, A.J.H. Thermal conductivity accumulation in amorphous silica and amorphous silicon. Phys. Rev. B 2014, 89, 144303. [Google Scholar] [CrossRef]
- Yan, X.; Gouissem, A.; Sharma, P. Atomistic insights into Li-ion diffusion in amorphous silicon. Mech. Mater. 2015, 91, 306–312. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, Y.; Dai, X.; Li, T.; Xia, Y.; Zheng, P.; Li, H.; Jiang, Y. Atomistic origin of amorphous-structure-promoted oxidation of silicon. Appl. Surf. Sci. 2020, 504, 144437. [Google Scholar] [CrossRef]
- Chen, S.; Du, A.; Yan, C. Molecular dynamic investigation of the structure and stress in crystalline and amorphous silicon during lithiation. Comput. Mater. Sci. 2020, 183, 109811. [Google Scholar] [CrossRef]
- Shargh, A.K.; Madejski, G.R.; McGrath, J.L.; Abdolrahim, N. Mechanical properties and deformation mechanisms of amorphous nanoporous silicon nitride membranes via combined atomistic simulations and experiments. Acta Mater. 2022, 222, 117451. [Google Scholar] [CrossRef]
- Liu, Z.; Panja, D.; Barkema, G.T. Structural dynamics of a model of amorphous silicon. Phys. Stat. Mech. Its Appl. 2024, 650, 129978. [Google Scholar] [CrossRef]
- Ding, B.; Hu, L.; Gao, Y.; Chen, Y.; Li, X. Anomalous tension–compression asymmetry in amorphous silicon: Insights from atomistic simulations and elastoplastic constitutive modeling. J. Mech. Phys. Solids 2024, 186, 105575. [Google Scholar] [CrossRef]
- Santonen, M.; Lahti, A.; Jahanshah Rad, Z.; Miettinen, M.; Ebrahimzadeh, M.; Lehtiö, J.P.; Laukkanen, P.; Punkkinen, M.; Paturi, P.; Kokko, K.; et al. Polycrystalline silicon, a molecular dynamics study: I. Deposition and growth modes. Model. Simul. Mater. Sci. Eng. 2024, 32, 065025. [Google Scholar] [CrossRef]
- Kim, G.; Yang, M.J.; Lee, S.; Shim, J.H. Comparison Between Crystalline and Amorphous Silicon as Anodes for Lithium Ion Batteries: Electrochemical Performance from Practical Cells and Lithiation Behavior from Molecular Dynamics Simulations. Materials 2025, 18, 515. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Qian, K.; Huang, J.; Liu, M.; Shibuta, Y. Molecular dynamics simulation and machine learning of mechanical response in non-equiatomic FeCrNiCoMn high-entropy alloy. J. Mater. Res. Technol. 2021, 13, 2043–2054. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Zhang, Y.; Kitipornchai, S.; Yang, J. Machine learning assisted prediction of mechanical properties of graphene/aluminium nanocomposite based on molecular dynamics simulation. Mater. Des. 2022, 213, 110334. [Google Scholar] [CrossRef]
- Amigo, N.; Palominos, S.; Valencia, F.J. Machine learning modeling for the prediction of plastic properties in metallic glasses. Sci. Rep. 2023, 13, 348. [Google Scholar] [CrossRef]
- Williamson, F.; Naciff, N.; Catania, C.; dos Santos, G.; Amigo, N.; Bringa, E.M. Machine learning-based prediction of FeNi nanoparticle magnetization. J. Mater. Res. Technol. 2024, 33, 5263–5276. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Hu, H.; Qi, L.; Chao, X. Physics-informed Neural Networks (PINN) for computational solid mechanics: Numerical frameworks and applications. Thin-Walled Struct. 2024, 205, 112495. [Google Scholar] [CrossRef]
- Ge, G.; Rovaris, F.; Lanzoni, D.; Barbisan, L.; Tang, X.; Miglio, L.; Marzegalli, A.; Scalise, E.; Montalenti, F. Silicon phase transitions in nanoindentation: Advanced molecular dynamics simulations with machine learning phase recognition. Acta Mater. 2024, 263, 119465. [Google Scholar] [CrossRef]
- Zongo, K.; Sun, H.; Ouellet-Plamondon, C.; Béland, L.K. A unified moment tensor potential for silicon, oxygen, and silica. Npj Comput. Mater. 2024, 10, 218. [Google Scholar] [CrossRef] [PubMed]
- Rosset, L.A.M.; Drabold, D.A.; Deringer, V.L. Signatures of paracrystallinity in amorphous silicon from machine-learning-driven molecular dynamics. Nat. Commun. 2025, 16, 2360. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991–7000. [Google Scholar] [CrossRef]
- Albaret, T.; Tanguy, A.; Boioli, F.; Rodney, D. Mapping between atomistic simulations and Eshelby inclusions in the shear deformation of an amorphous silicon model. Phys. Rev. E 2016, 93, 053002. [Google Scholar] [CrossRef]
- Urata, S.; Li, S. A multiscale model for amorphous materials. Comput. Mater. Sci. 2017, 135, 64–77. [Google Scholar] [CrossRef]
- Gu, H.; Wang, H. Effect of strain on thermal conductivity of amorphous silicon dioxide thin films: A molecular dynamics study. Comput. Mater. Sci. 2018, 144, 133–138. [Google Scholar] [CrossRef]
- Dmitriev, A.I.; Nikonov, A.Y.; Österle, W. Molecular Dynamics Modeling of the Sliding Performance of an Amorphous Silica Nano-Layer—The Impact of Chosen Interatomic Potentials. Lubricants 2018, 6, 43. [Google Scholar] [CrossRef]
- Lévesque, C.; Roorda, S.; Schiettekatte, F.m.c.; Mousseau, N. Internal mechanical dissipation mechanisms in amorphous silicon. Phys. Rev. Mater. 2022, 6, 123604. [Google Scholar] [CrossRef]
- García-Vidable, G.; Amigo, N.; Palay, F.E.; González, R.I.; Aquistapace, F.; Bringa, E.M. Simulation of the mechanical properties of crystalline diamond nanoparticles with an amorphous carbon shell. Diam. Relat. Mater. 2025, 154, 112188. [Google Scholar] [CrossRef]
- Fan, Z.; Tanaka, H. Microscopic mechanisms of pressure-induced amorphous-amorphous transitions and crystallisation in silicon. Nat. Commun. 2024, 15, 368. [Google Scholar] [CrossRef] [PubMed]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; van der Walt, S., Millman, J., Eds.; ACM: New York, NY, USA, 2010; pp. 56–61. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. In Proceedings of the 10th International Conference on Neural Information Processing Systems, Cambridge, MA, USA, 3–5 December 1996; NIPS’96. pp. 155–161. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Valladares, A.; Valladares, R.; Alvarez-Ramírez, F.; Valladares, A.A. Studies of the phonon density of states in ab initio generated amorphous structures of pure silicon. J. -Non-Cryst. Solids 2006, 352, 1032–1036. [Google Scholar] [CrossRef]
- Popov, Z.I.; Fedorov, A.S.; Kuzubov, A.A.; Kozhevnikova, T.A. A theoretical study of lithium absorption in amorphous and crystalline silicon. J. Struct. Chem. 2011, 52, 861–869. [Google Scholar] [CrossRef]
- Amigo, N. Role of high pressure treatments on the atomic structure of cuzr metallic glasses. J. -Non-Cryst. Solids 2022, 576, 121262. [Google Scholar] [CrossRef]
- Amigo, N.; Careglio, C.A.; Ardiani, F.; Manelli, A.; Tramontina, D.R.; Bringa, E.M. Thermal effects on the mechanical behavior of CuZr metallic glasses. Appl. Phys. A 2024, 130, 616. [Google Scholar] [CrossRef]
- Dewapriya, M.; Gillespie, J.; Deitzel, J. Exploring the effects of temperature, transverse pressure, and strain rate on axial tensile behavior of perfect UHMWPE crystals using molecular dynamics. Compos. Part B Eng. 2025, 294, 112160. [Google Scholar] [CrossRef]
- Yue, X.; Liu, C.; Pan, S.; Inoue, A.; Liaw, P.; Fan, C. Effect of cooling rate on structures and mechanical behavior of Cu50Zr50 metallic glass: A molecular-dynamics study. Phys. B Condens. Matter 2018, 547, 48–54. [Google Scholar] [CrossRef]
- Amigo, N.; Valencia, F.J. Structural, mechanical and rheological characterization of ZrNb metallic glasses using atomistic simulations. J. -Non-Cryst. Solids 2024, 641, 123147. [Google Scholar] [CrossRef]
- Wang, M.; Liu, H.; Li, J.; Jiang, Q.; Yang, W.; Tang, C. Thermal-pressure treatment for tuning the atomic structure of metallic glass Cu-Zr. J. -Non-Cryst. Solids 2020, 535, 119963. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lim, K.R.; Lee, D.W.; Choi, Y.S.; Na, Y.S. Quenching Temperature and Cooling Rate Effects on Thermal Rejuvenation of Metallic Glasses. Met. Mater. Int. 2021, 27, 5108–5113. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amigo, N. Machine Learning for the Prediction of Thermodynamic Properties in Amorphous Silicon. Appl. Sci. 2025, 15, 5574. https://doi.org/10.3390/app15105574
Amigo N. Machine Learning for the Prediction of Thermodynamic Properties in Amorphous Silicon. Applied Sciences. 2025; 15(10):5574. https://doi.org/10.3390/app15105574
Chicago/Turabian StyleAmigo, Nicolás. 2025. "Machine Learning for the Prediction of Thermodynamic Properties in Amorphous Silicon" Applied Sciences 15, no. 10: 5574. https://doi.org/10.3390/app15105574
APA StyleAmigo, N. (2025). Machine Learning for the Prediction of Thermodynamic Properties in Amorphous Silicon. Applied Sciences, 15(10), 5574. https://doi.org/10.3390/app15105574





