Abstract
Currently, in countries with warm climatic conditions, the average height of corn stalks during silage harvesting reaches 2.5 m. However, trailed forage harvesters are designed for mowing stalks not more than 1.5 m. That is why there is a demand to develop a compact forage harvester that can mow and shred tall stalks. This research proposes a two-level mowing method for tall stalks. According to the obtained analytical expressions, the technological distance between the vertical axes of the mowing rotors is determined to be 700 mm. A forage harvester is developed, equipped with a device that orientates itself by the length of stalks at the entrance to the shredding chamber and two mowing rotors designed for mowing tall stalks. Analytical expressions are obtained, which determine the required power for the mass transportation processes by the screw working device and the mass supply by the orienting drum into the chamber of the radial-knife blade shredding rotor. The required powers of the screw conveyor and the orienting drum are determined based on the obtained expressions; they are, respectively, equal to 0.42 kW and 0.11 kW. As a result of the conducted laboratory field tests, the required powers for mowing and for the general processes of mowing, shredding, and transporting the mass through the deflector are determined. The power balance of the harvester units is compiled. It is established that 75% of the consumed power is used for effective work, while 25% is for used for idling the harvester. During the mowing and shredding of corn stalks with a height of 2.9 m, the harvester’s productivity reaches 16.3 tons per hour, with a required power of 12.5 kW. During the tests, the harvester functioned without losses and without any violation of the technological process. The test proves the performance of the design and technological scheme and the accuracy of the obtained analytical expression determining the technological distance between the vertical axes of mowing rotors.
1. Introduction and Analysis of the Scientific and Technical Literature
In modern agriculture, the preparation of high-quality stalk forage is a priority task for increasing livestock production efficiency. On farms, the harvesting of stalk forage (shredded hay, haylage, and corn silage) is carried out by forage harvesters.
There is a growing global interest in improving forage harvesting machinery, particularly for use in small- and medium-sized farming operations. On such farms, compact machines that can operate efficiently under limited resources, complex terrain, and high crop density are of particular value.
Research conducted at German universities, notably at the University of Hohenheim, focuses on the implementation of intelligent guiding systems integrated into harvesting units. Technologies such as machine vision and adaptive control enable the precise capture of forage material even on uneven fields with variable crop heights [1]. These systems contribute to reducing losses and improving forage quality.
American companies, such as John Deere and New Holland, have introduced GPS-based navigation and automated plant guidance systems to optimize harvester movement trajectories. These technologies, also applied in trailed models, demonstrate high accuracy in delivering biomass to the chopping mechanism [2].
In China and India, significant efforts are being made to develop cost-effective compact forage harvesters. For example, Chinese engineers have proposed a small harvester with an adjustable guiding device that sets the intake angle and delivers stalks in an optimal position to the chopping drum. Field experiments showed a 12–15% reduction in corn harvesting losses [3].
In addition, Japanese researchers focus on precise chopping mechanisms to enhance forage digestibility. Rotor systems with a dynamic adjustment of cutting length are being developed to adapt to crop density and moisture content [4].
Despite these achievements, most of these systems are designed for large-scale farming and require substantial financial investment. For small farms, it remains essential to adapt such technologies while maintaining reliability and minimizing costs.
Against this background, research into the development of guiding devices for trailed or compact forage harvesters is especially relevant. These devices aim to solve the problem of capturing tall stalks, particularly corn over 2 m in height, which is a known source of losses in existing machines.
Thus, international experience confirms the feasibility of developing compact and functional guiding systems tailored to the conditions of small farms. This concept underpins the technical solution proposed in the present study.
Modern self-propelled forage harvesters are highly productive and ensure the harvesting of stalk forage regardless of height and yield. However, they are designed for use on large farms, while their trailed versions are used on small farms.
Among trailed forage harvesters, the Sterh and KSD-2.0 models are highly versatile. They are equipped with a mowing rotor with L-shaped knives. The rotor with L-shaped knives permits the mowing of stalk forage and picking up hay from a windrow, i.e., these machines ensure the harvesting of shredded hay, haylage, and corn silage on small farms.
However, the main disadvantage of these machines is that they do not permit the mowing of tall corn stalks more than 1.5 m.
In certain climatic regions, the height of corn stalks can reach 2.5 m.
When tall stalks are mowed, they are cut by L-shaped knives, rotate upwards relative to the front bar, and due to centrifugal forces are directed into the mowing rotor chamber, where they are cut again by the knives at the level of the front bar. However, when the stalk height exceeds 2 m, after the second cut, the outer part of the stalk has a length of about 1.5 m and considerable mass. In this case, a significant part of the stalks falls to the ground and is not picked up, leading to considerable losses during harvesting. Consequently, these harvesters are inefficient for cutting stalks taller than 1.5 m.
Self-propelled forage harvesters manufactured by Krone and Claas, equipped with roller pre-shredding devices, are used for the efficient shredding of high-yield corn mass with cobs [5].
Trailed forage harvesters are equipped with a mowing rotor, L-shaped knives, and a radial shredding device, which are their advantages. It is noted that the machine can operate on different row spacings and has multiple options for loading mowed mass while ensuring economical fuel consumption [6].
One article notes that radial-disk shredding devices have some disadvantages: uneven load on the shaft caused by changes in the angle of inclination in the cutting pair, as well as the large dimensions of the shredding device itself [7].
As a result of theoretical studies, formulas for determining the speed and thickness of the lifted mass, as well as the diameter of the shredding drum, have been obtained [8].
Modern forage harvesters are equipped with a high-capacity shredding drum, a three-stage compressor system for leaf–stem mass, and a three-row mass discharge accelerator [9].
The authors of [10] developed a mathematical model of the forage mass movement process in the deflector. High-speed filming revealed that in the initial section of the deflector, the particles move discretely, and further on in the crank section of the pipe, the forage mass particles move in a dense flow.
Article [11] defines the optimal composition of harvesting and transport complexes, considering the design features of forage harvesters. It also provides recommendations for the use of harvesters, depending on the volume of harvested forage.
One paper presents the results of tests conducted on the RSMF-2650 forage harvester. The types of damage to the bearings of the harvester’s pre-shredder and the actual operating time of the unit until failure are determined. The main causes of pre-shredder damage are identified: misalignment of the pre-shredder shaft; inefficient lubrication; and bearing sealing issues [12].
Another study presents the results of tests conducted on the new shredding drum of the KPI-2.4 harvester. It is also noted that the major disadvantage of many forage harvesters is the lack of a device to adjust the size of shredded particles [13].
Observation of the forage harvester’s operation revealed that the machine, equipped with a disc mower, cuts tall maize stalks and, by rotating them, directs them toward the cutting drum. Owing to the induced rotational motion and centrifugal forces, the stalks are guided to the shredding drum [14]. However, such machines are associated with very high costs.
According to the technical specifications of the KSD-2.0 forage harvester, the use of this machine is not recommended for harvesting tall-stemmed crops exceeding 1.5 m in height [15].
For operation in hilly and mountainous regions, a single-disc harvester for maize silage harvesting has been developed. The optimal combination of operational parameters was determined: the working speed of the unit is 1.0 m/s, the rotational speed of the cutter head is 1035.89 rpm, and the drum speed is 30 m/s [16].
The study presented in [17] describes the development of a forage harvester capable of simultaneously harvesting both the grain and the stalk portion of maize. However, this method is not employed for maize silage harvesting.
Currently, a single-disc forage harvester has been designed specifically for use on small farms. This machine is primarily intended for harvesting forage crops such as lucerne and other green fodder [18].
Experimental studies have established the following optimal parameters: the cutting rotor speed should be 1000 rpm, and the feed rate of biomass into the shredding chamber should be 3.5 m/s [19].
In [20], the influence of the cutting drum’s inclination angle on the energy consumption of the shredding process was analyzed. It was found that at the optimal angle of inclination, the energy consumption during the shredding of stalk forage decreased by 11.35%.
In recent years, as a result of theoretical and experimental studies, a compact forage harvester equipped with an orientation device that ensures oriented supply along the length of the stalks into the chamber of the shredding rotor blade has been developed. An analytical expression was also derived to determine the average size of particles shredded by the mowing and shredding rotors of a forage harvester [21].
As a result of theoretical studies, analytical expressions have been obtained to determine the mass flow velocity at the exit of a rectilinear deflector of a forage harvester [22].
The above literature review shows that co-modern combines equipped with a cutter bar with disc cutters provide mowing and feeding of high-growing stem forage to the cutting drum.
Combines equipped with a mowing rotor with an L-shaped knife grab the stalks and direct them into the feed auger chamber. In this case, the mass is captured by the knife on the fly, and therefore, the capture of stalks taller than 1.5 m may result in significant losses.
Analyses of the operation of existing self-propelled forage harvesters show that they provide highly productive mowing of high-growing and high-yielding stalks of cultivated plants. In recent years, researchers have been engaged in the substantiation of the parameters of corn stalk grain shredders.
Among trailed forage harvesters, it is noted that harvesters with L-shaped mowing knives, radial discs, and blade chopping devices have high versatility, and can make shredded hay, haylage, and corn silage. However, they do not mow tall stalks with a height of more than 2 m.
Researchers have proposed equipping the harvester with a device that ensures supply along the length of the stalks into the shredding rotor chamber in order to improve the quality of shredded stalk forages. Additionally, analytical expressions have been obtained to determine the average size of shredded forages.
Significant studies aim to justify the movement nature of forage mass through the deflector pipe. Analytical expressions have been derived to determine the forage mass velocity movement at the deflector exit.
The results of the review of existing forage harvester designs and theoretical studies show that universal trailed forage harvesters currently do not ensure effective mowing of tall stalks. Therefore, further research is required to clarify the nature of the mowing process of tall forage stalks.
2. Aims and Objectives of the Research
Aim of the research: The development a forage harvester that ensures two-level mowing of tall stalk forage and an analysis of the required power of the forage harvester units.
Objectives of the research:
- -
- To justify the design and technological scheme of the harvester equipped with two mowing rotors, ensuring two-level mowing of tall stalk forage, as well as to determine the technological distance between the vertical axes of the mowing rotors;
- -
- To determine the required power of the feeding screw and the orienting drum;
- -
- To conduct laboratory field tests to determine the required power for the mowing and shredding processes of stalk forage, as well as to determine the required power of the forage harvester units.
3. Materials and Methods of Research
For the development of the forage harvester, the object of the research is to determine the technological processes of two-level mowing for tall forage stalks and oriented feeding along the length of stalks into the chamber of the shredding rotor of the harvester.
To justify the design and technological scheme, a hypothesis is proposed: to facilitate the work of the lower mowing rotor, a second upper rotor is installed at the level of half the height of the stalks. At the beginning, the upper rotor cuts the upper half of the stalk. Then, the lower rotor cuts the lower half of the stalk, i.e., each rotor cuts a part of the stalk that is less than 1.5 m. This should ensure loss-free harvester performance. A crucial aspect of this process is determining the technological distance between the vertical axes of the mowing rotors.
If the vertical axes of the rotors are too close, the stalk mass is cut by the lower rotor, whereas too large spacing increases the mass and dimensions of the harvester. The minimum value of this distance is determined by the condition in which, at a certain inclination of the stalk by the front bar of the upper rotor, simultaneous contact with the rotation circle of both rotors may occur. Consequently, the rational technological distance should be more by than the minimum 3–5%.
The performance of harvesters with an orientation device and the nature of oriented stalk feeding are presented in ref. [21].
It is impossible to experimentally determine the required power for the screws and orienting drums separately. Therefore, the theoretical determination of the required power for these harvester units is conducted. In this case, the mown mass enters the screw chamber from above and is initially engaged by the screw blades, causing significant friction as the layer moves along the bottom surface of the screw chamber.
After being engaged by the screw blades, the stalk mass reaches a certain velocity, leading to a change in the kinetic energy of the moving mass. This change in kinetic energy is equal to the work of external forces.
Considering the change in kinetic energy during the movement of the forage mass in the screw chamber and under the orienting drum, the required power of these units is determined.
The determination of the required power for the idling of harvester working devices, for overall performance and for mowing lucerne, is carried out through laboratory field tests and experimental research.
The determination of required powers is carried out using a TRK-50 load cell (ZETLAB, Moscow, Russia) and an ATSD-1P-0.5 electric dynamometer (Saint Petersburg, Russia).
The determination of the required power for individual mowing and for the overall performance of mowing, shredding, and mass discharge into the vehicle body is carried out in the same field, at the same machine speed and productivity.
The determination of agrotechnical indicators is carried out according to GOST 28722-2018 Agricultural Machinery, Mowers and Mower-Conditioners. Test Methods: Electronic scales F-1976 were used for weighing the mowed and shredded mass. To determine the quality indicators of shredded forage and the mass fraction of shredded particles, MW-II electric scales from CAS Company (Seoul, Republic of Korea) were used.
4. Research Results on the Development of a Forage Harvester Ensuring Two-Level Mowing of Tall Stalk Forage
4.1. Justification of the Design and Technological Scheme of a Harvester Equipped with Two Mowing Rotors to Ensure Two-Level Mowing of Tall Stalk Forage, and Determination of the Technological Distance Between the Vertical Axes of Mowing Rotors
In countries located in northern parts of Europe and Asia, during silage harvesting, corn is typically not more than 1.5 m, so most forage harvesters are not designed to harvest tall corn stalks.
In countries with warmer climatic conditions, the height of corn stalks reaches 2.5 m.
For instance, in the Southern region of the Republic of Kazakhstan during corn silage harvesting, the average height of corn reaches 2.43 m [22].
Currently, forage harvesters are equipped with rotary headers for harvesting tall stalks. The use of such headers in the design of trailed harvesters, therefore, complicates the design and increases the cost of the machines.
In recent years, trailed harvesters have been equipped with mowing rotors with L-shaped knives and a radial-blade shredding unit. The main advantage of these machines is that the mowing rotor ensures both grass mowing and windrow pickup. Nevertheless, they are unable to facilitate mowing of corn stalks with a height of more than 2.0 m, leading to significant losses. Therefore, such machines are not recommended for harvesting tall stalks.
For example, the technical specifications of the KSD-2 forage harvester indicate that its use is not recommended for mowing tall-stemmed plants exceeding 1.5 m in height [15].
To clarify the rationale behind this recommendation, a conceptual model illustrating the mowing process of plants with varying stem heights by a single-rotor forage harvester is presented (Figure 1).
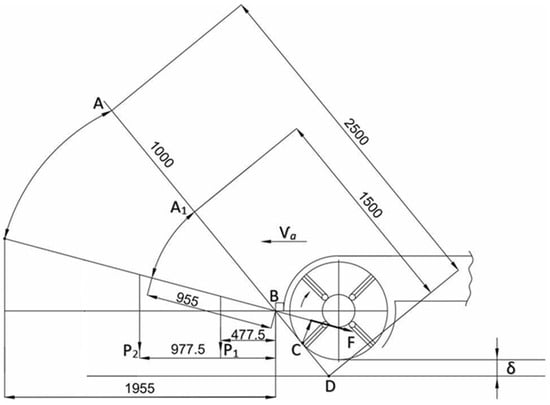
Figure 1.
Diagram demonstrating mowing of stalks with heights of 1.5 m and 2.5 m.
The figure illustrates the process of mowing stalks with heights of 1.5 m and 2.5 m. Line A1D represents the mowing trajectory of a 1.5 m tall stalk as it encounters the cutting blades. Initially, the stalk is cut at point C and captured by the L-shaped blade, then rotated upward relative to the front bar, i.e., around point B. Under the influence of centrifugal force (F), the stalk is directed into the mowing rotor chamber. After rotating around point B, the stalk is cut a second time. These technological processes of stalk fragmentation have been described in previous studies [21]. The resulting stalk particle lengths were measured as follows: BC = 0.208 m; CD = 0.337 m; BD = 0.545 m. This shows that the lower part of the stalk with a length of 0.545 m is initially cut.
When mowing 1.5 m tall stalks (as indicated by line A1D in the diagram), the outer portion of the stalk extending beyond the mowing rotor chamber is 0.955 m long, and its center of gravity is located 0.477 m from the front bar. Before the next cut of the lower portion, the stalk continues to move toward the mowing rotor chamber due to the centrifugal force (F). The formula used to determine this velocity is provided in [21].
In addition, the forward motion of the unit increases the stalk’s entry speed into the mowing rotor chamber. Therefore, it can be assumed that the outer portion of the stalk, measuring 0.955 m, can enter the rotor chamber freely before falling to the ground.
The figure also shows the position of the outer portion of a stalk with a height of 2.5 m. When the lower part of the stalk is mowed, the remaining outer portion is 0.1955 m, with its center of gravity located 0.977 m from the front bar. In this case, it is unlikely that a stalk nearly 2.0 m long can fully enter the mowing rotor chamber. Thus, mowing stalks taller than 1.5 m may result in significant losses.
To address this issue, we initiated the design of a compact dual-rotor forage harvester capable of performing two-level mowing of tall-stemmed crops.
Upon analyzing existing forage harvester designs and reviewing published studies, we found no existing design of a dual-rotor harvester capable of two-level mowing of tall stalks.
The design process began by ensuring that each rotor, operating independently, could mow and chop stalks shorter than 1.5 m. Based on this requirement, the installation height of the upper rotor’s horizontal axis was determined.
The upper rotor mows and chops the upper portion of the stalks located at heights above approximately 1.2–1.3 m. Assuming the average height of maize stalks is 2.5 m, each rotor is designed to mow and process a 1.25 m section of the stalk.
An important design factor is the distance between the vertical axes of the mowing rotors. An optimal distance must be maintained to ensure the upper portion of tall stalks is reliably mowed by the upper rotor. If the distance between rotor axes is too small, the stalks may miss the upper rotor, resulting in substantial harvesting losses.
Conversely, an excessively large distance between the vertical axes increases the overall mass and cost of the machine.
Therefore, theoretical studies were planned to determine the optimal value of this distance.
Following this, a structural and technological schematic, along with detailed engineering drawings, was developed for the manufacture of the forage harvester. This provided a graphical explanation of the proposed two-level mowing model and initiated the design process of a dual-rotor forage harvester intended to perform two-level mowing of tall-stemmed crop plants.
The validity of the proposed design model will be verified through laboratory and field tests assessing the mowing of tall-stemmed plants.
Moreover, the aforementioned distance ensures the optimal implementation of the two-level mowing process. Hence, we propose the term “technological distance” for the distance between the vertical axes of the two mowing rotors.
Another disadvantage of these trailed harvesters is that their average length of shredded particles does not meet zootechnical requirements.
To improve the quality of shredded forages, we propose orienting stalks to be fed into the shredding chamber.
The results of theoretical and experimental studies have shown the efficiency of the orienting device [21].
Mowing tall stalks with trailed combines is a challenging task. For this reason, we propose a design and technological scheme of a harvester that ensures the two-level mowing of tall stalks (Figure 2).
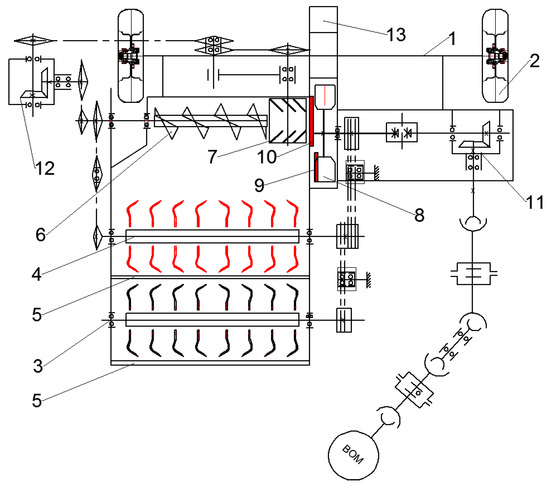
Figure 2.
Design and technological scheme of forage harvester that ensures two-level mowing of tall stalks. 1—frame; 2—wheel; 3—upper mowing rotor; 4—lower mowing rotor; 5—front bar; 6—auger; 7—orienting drum; 8—blades; 9—cutting blade; 10—contra-cutting blade; 11, 12—gear train; 13—deflector.
The harvester is attached to a tractor, the drive gear train (11) is connected by a universal joint to the PTO of the tractor, and a cart is attached behind the harvester to load the shredded mass.
When the harvester is working, the front bar of the upper mowing rotor inclines the corn stalks, and at a certain inclination the stalks are shredded by the rotating knives of the upper mowing rotor. The upper part of the stalks is mowed, and the mowed upper part of the stalks is engaged by the knives, partially shredded, and fed through the upper channel to the screw chamber.
As the machine moves, the lower part of the stalks is mowed by the lower rotor and also fed into the screw chamber. Further, the mowed and pre-shredded mass is fed by the screw to the orienting drum. The blades of the orienting drum move the mass to the center and the drum compresses it, i.e., the fed mass is oriented along its length in the horizontal and vertical planes. The length-oriented stalks are cut, falling between the rotor knives and the contra-cutting plate. The shredded mass is then discharged by the shredding rotor blades into the deflector and then into the vehicle body.
Grant funding was provided by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan, No. 286/23-25, dated 3 August 2023 (Grant No. AP19676816 Development of Compact Forage Harvester Equipped with a Device Orienting on The Length of Stalks). The first prototype of the forage harvester equipped with two mowing rotors and an orienting device was developed and manufactured according to the developed design and technological scheme (Figure 3).

Figure 3.
General view of a forage harvester, providing two-level mowing of high-growing stalks.
The technological distance between the vertical axes of the rotors is determined. The location of the upper mowing rotor is determined by two parameters. The first is the location of the horizontal axis relative to the ground surface. In this case, the height should be determined taking into account that the upper mowing rotor cuts half of the stem height, and the installation height of the horizontal axis h0 is determined by the following formula:
where
- Lc—the average value of stalk height during maize silage harvesting, m;
- R—the mowing rotor radius at the ends of the blades, m.
When determining the technological distance between the vertical axes of the mowing rotors, a potential critical position of the stalk was taken into account, in which a stalk may simultaneously come into contact with two mowing rotors (Figure 4).
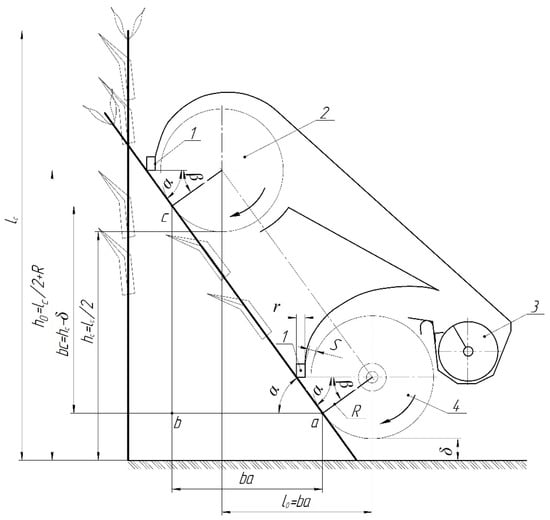
Figure 4.
Stem position when simultaneously encountering two mowing rotors. 1—front bar; 2—upper mowing rotor; 3—auger; 4—lower mowing rotor.
Figure 4 shows the simultaneous meeting of the stem with the blades of two rotors. This process can occur when the stem takes a position tangential to the circle of rotation of the two rotors. Here, the angle between the stem and the horizontal axes of the rotors is determined by the following formula:
where
- R—the mowing rotor radius, m;
- S—the gap between mowing rotor circles and rotor bodies, m;
- r—the thickness of the front bar, m.
The peculiarity of this stalk position lies in the fact that at a smaller angle α, the stalk always comes under the impact of the upper rotor, increasing the length of side ab in triangle abc. As seen from the diagram, side ab is equal to the distance between the vertical axes of the rotors l0 (ab = l0).
Thus, with a greater distance of ab or l0 and a smaller angle α than indicated in the diagram, the stalks will always come under the impact of the upper blade. Conversely, with a larger angle α and a smaller length of side ab or l0, the stalk will come under the impact of the lower rotor. In this case, the upper rotor will not actually work, highlighting the importance of accurately determining the distance between the vertical axes of the two rotors.
Based on the above-mentioned, considering the triangle abc, we can determine the value of the length of the side of the triangle ab or the distance between the vertical axes of the two rotors. In this case, the distance between the vertical axes of the two rotors is calculated using a formula.
Therefore, to determine the technological distance between the vertical axes of the mowing rotors, the following expression was derived:
where
- h—the stalk height cut by the upper rotor, m;
- Lc—the average stalk height, m;
- δ—the stalk height cut by the lower rotor, m.
In this case, to determine the technological distance, there is a need to determine the average height of corn stalks during their harvesting for silage. Therefore, we conducted special measurements to determine the physical and mechanical characteristics of corn stalks during their milk–wax ripeness [14]. The results of the measurements revealed that the average height of corn stalks was equal to 2.4 m.
Taking into account the average height of corn stalks and using formula (3), the following parameters of the forage harvester were determined: δ = 0.15 m; R = 0.285 m; S = 0.015 m; r = 0.04 m. In addition, the technological distance between the vertical axes of rotors l0 ≥ 0.6818 m was calculated.
Therefore, the following expression is obtained to determine the technological distance between the vertical axes of the mowing rotors:
Using this formula, the actual value is defined: l0 = 0.7 m.
Consequently, to determine the optimal value of the distance between the vertical axes of the two rotors, i.e., the technological distance, an analytical expression was obtained that takes into account the parameters of the forage harvester and stalks.
4.2. Determination of the Required Power of the Feeding Screw and the Orienting Drum
When developing a new forage harvester that provides two-level mowing of tall stalks, equipped with a device orienting the length of stalks at the entrance to the shredding rotor chamber, at the initial stage it is necessary to conduct laboratory field tests to determine the performance and required power of the harvester units, i.e., to identify the energy assessment of the main units of the forage harvester.
When conducting laboratory field tests, it is possible to individually determine the required power for idling the machine and for mowing stalks, as well as for the total required power of the harvester when mowing grasses and tall corn stalks. In this case, it is extremely difficult to experimentally determine the required power for the operation of the screw and the orienting drum separately. Therefore, for the general energy assessment of harvester performance, we carried out a theoretical determination of the required powers for the working processes of mass feed by the screw conveyor and the orienting drum into the shredding rotor chamber.
The existing analytical expressions are intended to define the required power for the performance of the screw working device when moving bulk materials, i.e., the application of these expressions is associated with the determination of many coefficients. In addition, the work of the screw working device relates to the work of the mowing rotor. For this reason, we carried out a theoretical determination of the required power for the performance of the screw when feeding the mass to the orienting drum.
Only the lower mowing rotor works during mowing grass and picking up hay from the windrow. The upper mowing rotor only works when mowing tall stalks of crop plants (Figure 4).
In this case, the harvester productivity during grass mowing is calculated by the following formula:
where
- m—the mass of grass per 1 m2, kg/m2;
- B—the cutting width of the mowing rotor, m;
- υa—the machine velocity, m/s.
As illustrated in Figure 4, the mown mass enters the screw chamber from above and is engaged by the screw blades. At the same time, the mass gains a velocity equal to the linear velocity of the screw blade. Then, the mass moves along the screw body. In this case, the velocity of mass movement in the screw chamber υm is calculated by the following formula:
where
- Sm—the screw blade pitch, m;
- t1—the time for one screw rotation, s;
- n—the screw speed, rpm.
Now, we define how long it takes to release the screw chamber from the incoming mass:
where
- lm—screw length, m.
In the harvesting process, the mass continuously enters the screw chamber and is released during the time t0. The value of the mass entering the screw chamber at time t0 is calculated according to the following formula:
Now, the mass distribution along the length of the screw (linear mass) is determined:
According to the design, it is known that half of the screw blade will be on one side of the screw rotation circle. The mass coming from above is engaged by the screw blades, and at the initial stage the screw blades do not encounter great resistance. At the moment of moving the mass along the horizontal section of the bottom of the screw body, the blades experience great resistance. This is due to the fact that the mass moves at a speed equal to the peripheral speed of the screw blades.
In this case, the value of the mass to be engaged by one half of the screw blade is calculated by the following formula:
In the horizontal section of the bottom of the screw body, force F is applied on the mass to be engaged on the side of the blade, and the blades encounter a great resistance on the side of the mass equal to the friction force (Figure 5).
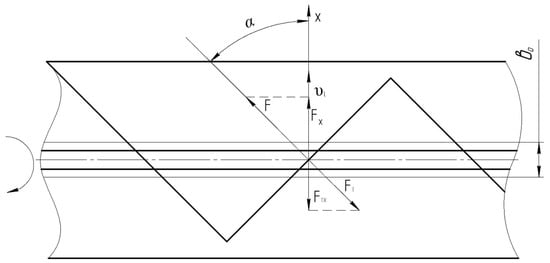
Figure 5.
Diagram of engaged mass movement at the bottom section of screw chamber.
The screw blades encounter great resistance when moving the mass over a distance of . This is due to the fact that when the mass is lifted along the side wall of the screw chamber, the mass starts moving along the chamber, and in this case the resistance of the mass is reduced, so we can consider that the screw blades experience a great resistance in the section of mass movement at a distance of .
It should be noted that the mown mass flows along the entire length of the screw and along the outer side wall. The screw blades pick up the mass and guide it down the wall from the top to the bottom of the screw.
In this case, in the course of the circular movement of the mass in the first half of the screw blade bottom, it can be considered that the screw blades do not experience great resistance. This is confirmed by the fact that if the direction of shaft rotation is clockwise, the movement of the transported mass is carried out in the third quarter of the screw blade rotation circle.
From the course of physics, it is known that when a body moves, if external forces act on it, then the following condition must be met [23]:
where
- —the final and initial kinetic energies of a body, N·m;
- A1 and A2—the work performed by external forces, N·m.
Herein,
It should be noted that the initial kinetic energy is equal to zero. This is due to the fact that when the mass is engaged by the screw blade, it first loses its velocity and instantly gains a velocity equal to the peripheral velocity of the screw blade υl.
That is why the equality of the change in kinetic energy considering the work performed by external forces can be given in the following form:
From here, we determine the value of the force acting on the screw blades:
In this case, formula (13) determines the value of force per blade, and taking into account the simultaneously working blades, the analogous expression has the following form:
The required power for the working process of the screw is calculated by the following formula:
Substituting the values and into formula (15), we obtain
where
- —the radius of the screw blade at the end of the blade, m.
In this way, taking into account the output of the machine and the kinematic modes of the screw, an analytical expression for determining the required power for the process of moving the mass by the screw working device is obtained.
4.3. Determination of Required Power for the Process of Stalk Orientation upon Entrance to the Chamber of the Shredding Rotor
The mass is moved in the screw body, fed to the orienting drum, and engaged by its blades. The stalk mass is oriented along its length and fed to the shredding rotor.
It is known that each row of blades engages a separate portion of the moved mass. Depending on the drum speed, it takes time for each row of blades to engage the mass:
where
- —the speed of the orienting drum, rpm;
- K—the number of blade rows along the drum periphery, pcs.
Within the defined time, the screw moves the mass over the distance :
Depending on the linear mass distributed along the length of the screw, we determine the value of the fed mass located at section , i.e., we define the value of the mass to be engaged by one row of drum blades.
As the mass is engaged by the blades of the drum, it experiences great resistance as it moves the mass along the bottom of the screw body.
Our laboratory experiments demonstrated that at the initial stage, the drum blades rotate the mass relative to the center of the fed mass, i.e., relative to the OS radius (Figure 6).
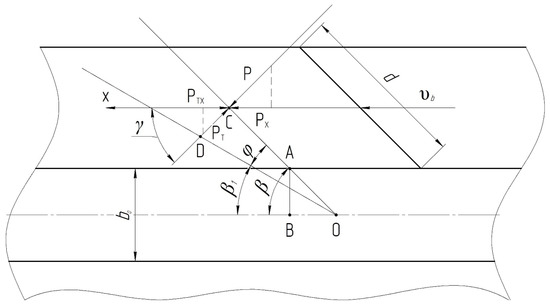
Figure 6.
Scheme of mass movement by the blades of the orienting drum.
In order to define the required power for the orienting drum, we will also consider the change in kinetic energy of the discarded mass by the drum blades.
When the mass engaged by the drum blade, the screw-driven mass losses its velocity, and when the blade rotates in the third quarter of the drum periphery, it experiences great resistance from the moving mass.
This resistance will continue until the radius of the mass center of gravity rotates by an angle β1 equal to 38°. It is known that when the steel plate is inclined by 38°, the stalk mass starts moving downward regardless of its moisture content.
At this angle of mass rotation, the blades will move through the mass without experiencing significant resistance, ensuring the further rotation of the mass’s center of gravity. This is related to the fact that, as the angle β decreases, the tangential component of the force increases, promoting the sliding of the mass along the drum blade.
That is why we will assume that the drum blades undertake the maximum work when the center of gravity of the mass moves to the distance DC.
It is necessary to determine the value of this distance Se.
The radius of rotation of the center of gravity of the mass is calculated by the following formula:
where
- b0—the width of the horizontal section of the screw body, m;
- d—the drum blade length, m;
- β—the angle of inclination of the orienting drum screw blade from the horizontal axis of the screw.
At a small angle of rotation of radius R by the angle φ, the value of the length of the path of movement of the center of gravity of the mass can be calculated by the following formula:
During the working process, the blade motion takes place along the horizontal axis X. That is why we will project the force acting on the mass from the blade side P, as well as the friction force PT on the X axis.
According to the design of the orienting drum, the angle β = 45°, and as noted earlier, β = 38°, i.e., the angle = 7°. Also, due to the small value of change in angles β and β1, the direction of line CD is taken as perpendicular to the radius of rotation of the mass at its angle of inclination equal to . For this reason, the value γ is calculated by the following formula:
Taking into account the change in kinetic energy of the mass supplied by the drum blades and the projections of forces P and Pт on the X axis, it is possible to write the equation of equality of kinetic energy with regard to the work of forces P and Pт:
Hence, we determine the mass resistance force on the drum blades:
By expressing the value through the productivity of the machine, we obtain
where
- —the drum blade peripheral velocity, m/s.
In fact, each blade actually catches the mass . Substituting the full value into formula (24), we consider the simultaneous performance of two blades and express the linear velocity of the drum through its speed. So, the total required power of the orienting drum is calculated by the following formula:
where
- —the radius of the orienting drum at the blade ends, m.
An analytical expression for determining the required power for the process of stalk orientation at the entrance to the shredding chamber has been obtained.
4.4. Conducting Laboratory Field Tests to Determine the Required Power for Mowing and Stalk Forage Shredding Processes, and Defining the Required Power of the Forage Harvester Units
Laboratory field tests were carried out to determine the power balance by units of the forage harvester, as well as its performance in mowing tall corn stalks. The registration of required powers was carried out with a load cell TRK-50 and an electronic dynamometer ATSD-1R-0.5 (Figure 7).

Figure 7.
General view of the load cell connected to the tractor’s power take-off shaft and the harvester’s drive shaft.
In order to determine the required power of the combine harvester, tests on mowing lucerne were conducted.
At first, we conducted experiments to determine the mass of lucerne from one square meter of lucerne field area. The average value of lucerne mass from 1 m2 was 1.006 kg/m2 ≈ 1.0 kg/m2.
The velocity of machine movement of υa = 0.83 m/s was chosen for the experiments. In this case, the power measurement was carried out while the machine was moving at a distance of 50 m. The experiments were repeated three times.
The value of required power for the idle running of the working devices of the harvester at the PTO speed of the tractor of 850 min−1 was determined, and all the experiments were carried out at this operating mode of the harvester. This is due to the fact that all forage harvesting field work is carried out at medium engine speed. In this case, the idle power was equal to Nxx = 2.45 kW (Figure 8).

Figure 8.
Value in an experiment determining the idle torque of the forage harvester.
The required power of the harvester for mowing lucerne was determined using the developed program (Figure 9).

Figure 9.
Process of mowing and shredding lucerne by forage harvester.
The productivity of the harvester while mowing lucerne was equal to Q = 1.12 kg/s = 4.03 t/h. The total power input was equal to NO = 9.78 kW.
It should be noted that during the harvesting of grass and low-growing plants, only the lower rotor is in operation. This is because, at the time of forage grass harvesting within the agrotechnical window, the plant stem height typically ranges from 0.6 to 0.65 m. In such cases, the front bar of the lower mowing rotor is positioned at a height of approximately 0.4 to 0.45 m.
As the unit moves forward, the front bar merely bends the upper leafy portion of the grass, which then immediately enters the mowing rotor chamber and is captured by the cutting blades.
Field observations of the harvester’s operation during mowing confirmed that the machine functioned without disrupting the technological process and without incurring losses. This confirms the validity of the stated assumption.
Further, experiments were conducted to determine the required power for the process of mowing lucerne only.
For mowing lucerne only, the screw cover was opened, and an additional cover was placed on top of the screw body. This ensured discharge of the mowed mass directly to the swath. Therefore, the required power for grass mowing only was determined (Figure 10).

Figure 10.
Process of mowing lucerne by forage harvester.
In these experiments, the average required power for mowing lucerne was NK = 3.7 kW, and the average required power for the mowing process without idling was NK = 1.25 kW.
In order to determine the total power balance, the required power for the processes of mass transportation by the screw working device and the orienting drum into the chamber of the shredding rotor was determined by the obtained analytical expressions.
At the pitch of the blade screw of Sm = 0.28 m and a speed of n = 306 rpm, the speed of mass movement along the length of the screw was equal to = 1.428 m/s. Here, the screw length = 0.817 m, and at the speed of mass movement along the screw, its body is released in the time tO = 0.572 s.
At the harvester productivity Q = 1.12 kg/s (Q = 4.03 t/h), 0.64 kg of mowed mass enters the screw chamber during the time tO. This mass will be distributed along the length of the screw and the linear mass my = 0.7834 kg/m.
At the beginning, we determined the resistance encountered by one half of the screw blade on the side of the engaged mass = 0.11 kg, i.e., one pitch of the screw blade engages 0.11 kg of mowed mass.
The distance at which the screw blades encounter maximum resistance when the mass is moving is also important for the calculation. It is known that screw blades encounter great resistance at the bottom of the screw body. In this case, the length of the horizontal section at the bottom of the screw is 0.1 m.
Considering that the mass enters from above along the outer side wall of the screw, it may be considered that the screw blades encounter resistance in the second half of the screw bottom, so m.
At a screw radius of 0.14 m, the peripheral velocity at the ends of the screw blades was = 4.484 m/s and the angle of inclination from the horizontal axis at the ends of the blades was 45°; consequently, cos 45° = 0.7071.
Special experiments revealed that stalk forage at the angle of the steel plate of 38° began to roll down; consequently, f = 0.78.
The experiments were conducted on chopped lucerne with a moisture content of 72.58% and on chopped maize stalks with a moisture content of 72.38%.
This high moisture content was chosen because the forage harvester is mainly designed for harvesting green mass, haylage, and corn silage.
In this case, the lucerne and maize stalks used for the experiment were chopped by the forage harvester.
During the experiments, these chopped stalks of lucerne and maize were rolled down at an angle of inclination of the steel plate of 37–39°; i.e., the average value of the angle of inclination of the stalks was 38°. From here, it is known that tan38° = 0.78; i.e., the friction coefficient of pre-shredded lucerne and corn stalks f = 0.78.
With the values of the parameters mentioned above, the calculation of formula (26) showed that = 0.42 kW.
The following parameters included in formula (26) were also established and were equal to Q = 1.12 kg/s; = 0.16 m; = 170 rpm; K = 4; and f = 0.78.
Taking into account the known values of the parameters included in formula (26), the value of the required power for the process of the orientation of the stalks at the entrance to the chamber of the shredding radial cutting and bladed rotor was determined: Nδ = 0.11 kW.
These calculated values of screw and drum required power were determined at average values of productivity of Q = 4.03 t/h. In addition, for more productive horizontal screw conveyors, drive motors should be installed with a capacity of 1.1–1.5 kW. That is why the obtained theoretical values of power can be considered close to a reliable result.
On this basis, it was possible to identify the distribution of the required power by units of the forage harvester (Table 1).

Table 1.
Balance of required powers of forage harvester while mowing lucerne with productivity of 4.03 t/h.
The balance of the forage harvester required power shows that 75% of the power is used for the full performance of the harvester. As the productivity of the machine increases, the share of power for full performance should increase. All this indicates that the harvester has a high efficiency in carrying out technological processes.
The technological distance between the vertical axes of the mowing rotors was determined during the development of the drawing documentation for the harvester.
Using the average stalk height and the analytical expressions obtained, the technological distance of l0 = 676 mm was defined. That is why the value of l0 = 700 mm was accepted in the drawing documentation.
Laboratory field tests of the harvester were conducted on the corn field at “Aydarbayev E” farm, where the average height of corn stalks was 2.9 m.
To validate the performance of the top mowing rotor, experiments were carried out in a corn field. The moisture content of the mass amounted to 72.38%. It should be noted that the lower part of the corn stalks was dry, with a humidity of 16–18%, and corn cobs were harvested earlier. Experiments were carried out at different speeds and the required power was measured. For this purpose, the speed of the machine during each experiment and the mass of shredded corn stalks were determined (Figure 11).

Figure 11.
Harvester performance during mowing and shredding of corn stalks.
The results of the harvester’s performance are presented in Table 2.

Table 2.
Harvester performance results during mowing and shredding of corn stalks.
The results given in the table demonstrate that, at all the above-mentioned speeds, the combine harvester performed the mowing and shredding of tall corn stalks without violating the technological process. In this case, at a machine speed of 0.91 m/s, corn stalk losses amounted to 3.0%, which is acceptable for forage harvesters.
The results of the third experiment demonstrate that the specified mode of the work is higher than the optimum productivity of the harvester. It should be noted that the harvester performed without violation of the technological process.
The results of the experimental studies also confirm the reliability of the proposed graphical model for single-rotor mowing and for theoretical investigations related to the two-level mowing of tall-stemmed crops.
In this case, experiments on mowing tall maize stalks were conducted at various forward speeds of the machine, ranging from 0.67 to 0.91 m/s. At the beginning of the field trials, different travel speeds were selected to assess the harvester’s operational feasibility. For instance, in [16], a speed of 1.0 m/s was identified as the optimal forward speed for a trailed forage harvester.
In reality, the speed of the machine is selected depending on the type of plants to be mown and their yield.
There are recommendations in the literature for selecting machine speeds for trailed combines:
- -
- When working with high-yielding and wet forage (e.g., maize for silage)—0.42–0.83 m/s (1.5–3.0 km/h);
- -
- When harvesting hay or less dense mass—0.83–1.39 m/s (3.0–5.0 km/h);
- -
- When working in light conditions (dry mass, flat terrain, low grass)—up to 1.67 m/s (up to 6.0 km/h) [24,25].
Hence, it can be seen that the selected speeds of the machine correspond to the recommendations for mowing high-yielding maize stalks.
For the field experiments, the circumferential speeds of the mowing and chopping rotors were selected in accordance with the circumferential speeds of the cutting drums, as well as the mowing and chopping rotors of existing forage harvesters.
For example, the following forage harvesters have cutting drums with circumferential speed as detailed: Jaguar-830 Claas—39.56 m/s; FX 307 New Holland—39.23 m/s; BiGXV12, Krone—37.99 m/s. Hence, it can be seen that in existing forage harvesters, the circumferential speeds of cutting drums are within 37.99–39.56 [13]. In addition, the circumferential speeds of mowing and chopping rotors of trailed forage harvesters are within 35–40 m/s [15].
Thus, the above-mentioned circumferential speeds of chopping and mowing working bodies provide mowing and chopping of all types of grasses and plants, including high-growing and wet crops, at permissible energy consumption and minimum losses.
Therefore, the same tractor engine speed was set in all field trials, regardless of the speed of the machine. In this case, the tractor PTO speed and the rotational speed of the blade chopping rotor were equal to 850 rpm (linear speed of radial knives—35.6 m/s), and the rotational speed of the mowing rotors was 1250 rpm (linear speed of knives—36.9 m/s).
Therefore, in the field experiments, the cutting speeds of the mowing and chopping rotors were set at the same level and were equal to the circumferential speeds of the chopping drums and rotors of existing machines.
The speed of mass feeding by the orienting drum into the chamber of the shredding rotor also had a constant value.
At the speed of rotation of the orienting drum of 170 rpm, with a diameter at the ends of the feeding fingers of 0.32 m, the speed of mass feeding was equal to 2.85 m/s.
This speed of mass feeding into the chamber of the chopping rotor provided the calculated cutting length of 34.9 mm, and the actual value of the cutting length when mowing and chopping lucerne was 33.79 mm [21], which corresponds to the expected cutting length of stem forage for feeding sheep and cattle.
Therefore, the selected operating mode of the forage harvester in terms of cutting speed and mass feeding into the chamber of the chopping rotor provided the expected cutting length and ensured the quality of chopped fodder corresponding to zootechnical requirements (the average cutting length of chopped particles for sheep and cattle should be within 30–50 mm).
Regarding the cutting length of maize stalks given in Table 2, it can be noted that the lower part of the stalks had low moisture, and the stalks were chopped by breaking, so these stalks had a larger cutting length.
It is clear that when making silage, the moisture content of maize stalks along their length has the same value, and they are well cut by the knives of mowing and chopping rotors. Therefore, the average length of the chopped particles should be close to the calculated cutting length of the stalks.
Moreover, the mowing rotor demonstrates effective performance in cutting grass regardless of lodging conditions. This is evident from the harvester’s loss-free operation while mowing maize stalks up to 2.9 m in height.
It is also necessary to note that tall corn stalks are not suitable for harvesting corn silage. According to the requirements, silage harvesting should be carried out at milk–wax ripeness, when the moisture content of the mass is more than 80%. Under these conditions, corn stalks are much easier to mow and shred. The shredding quality has to be much better than that presented in the table.
It is significant that these experiments established the performance of the harvester under harsh conditions.
In summary, the results of the above-mentioned experimental studies prove the reliability of theoretical research on the technological distance between the vertical axes of mowing rotors and the design and technological scheme of the harvester, as well as the performance of the orienting drum and other units of the harvester.
5. Discussion of Research Results
From the mentioned research results, the main difference of the machine is that the elaborated forage harvester is equipped with a device orienting the length of stalks at the entrance to the shredding chamber, and the upper mowing rotor is designed for mowing tall stalk forage.
The results of harvester performance with the orienting device are given in article [21]. Analytical expressions for determining the average size of shredded particles are obtained, and the reliability of the expressions is proven with experimental research. In this article, for the first time, we propose a method of two-level mowing of tall stalks and determine the technological distance between the vertical axes of mowing rotors.
The results of research on the justification of the distance between the vertical axes of rotors and the height of installation of the upper rotor are not revealed in previously conducted studies. For this reason, a design, a technological scheme, drawing documentation, and an experimental prototype for a new forage harvester were developed.
The review of forage harvester devices showed that there were no harvesters with an orienting device and with two mowing rotors, ensuring the mowing of tall stalks.
To support theoretical and experimental studies, we took on the fulfillment of this task. The required power of the combine harvester units for the mowing and shredding of stalk forage were determined, i.e., the balance of power of the combine harvester units was obtained.
In the process of harvester performance, there is no possibility of experimentally determining the required power for the conveying screw and the orienting drum. It should be noted that analytical expressions for determining the required power for screw conveyors are present. However, the screw operation is connected to the mowing rotor and the process of stalk orientation is being considered for the first time, so specific theoretical research was carried out to determine the required power of the above-mentioned units of the harvester. In addition, the obtained analytical expressions have significant value for theoretical studies of other similar processes.
Another important point in the conducted research is the experimental verification of the upper mowing rotor performance and the reliability of determining the technological distance between the vertical axes of the mowing rotors. In this case, the highly productive performance of the harvester was almost loss-free, demonstrating the reliability of all machine units in difficult conditions and the validity of the theoretical research.
A certain limitation in using the harvester is that the article does not provide a way to turn off the upper rotor during mowing short grasses, or harvesting haylage and shredded hay.
In addition, the obtained analytical expressions can be used for the consideration of similar processes in other machines.
6. Conclusions
1. For mowing tall stalk forage, we proposed using a two-level mowing method. In this case, in the beginning, the stalks should be cut by the upper rotor; therefore, as a result of theoretical research, the technological distance between the two vertical axes of the mowing rotors is defined. Taking into account the average height of corn stalks, the required technological distance was determined by the obtained analytical expression: l0 = 700 mm.
The design and technological scheme of a compact forage harvester equipped with a device orienting the length of stalks and two mowing rotors providing two-level mowing of tall stalks were developed. Drawing documentation was developed and an experimental prototype of the harvester was manufactured.
2. Theoretical research and analytical expressions for determining the required powers of the conveying screw and orienting drum were obtained. Laboratory field tests were conducted in which lucerne was mown at 4.03 t/h to determine the power balance. The idle power was determined as 2.45 kW. The required power for mowing lucerne is 3.7 kW, and the total power required for mowing, shredding, and transporting the mass is 9.78 kW. At the specified productivity of the harvester, the theoretical power requirements for the processes of mass movement by the screw working device and for the process of mass supply to the chamber of the shredding rotor by the orienting drum were determined, and they are, respectively, equal to 0.42 kW and 0.11 kW. According to the obtained results, the balance of power for the harvester units is compiled. It can be observed that even at lower output of the machine, the power consumption for technological processes is 75%, which indicates the efficiency of all units of the harvester.
3. During the mowing of corn stalks with a height of 2.9 m, the harvester productivity was equal to 16.3 t/h and the required power was 13.5 kW. The specified operating mode of the harvester ensured mowing and shredding of tall corn stalks without losses and without violating the technological process. This demonstrates the performance of the developed design and technological scheme and the reliability of the analytical expression determining the technological distances between the vertical axes of the mowing rotors.
Author Contributions
Conceptualization, T.A. and D.A.; methodology, T.A. and N.K.; software, D.A.; validation, D.K. (Dimitar Karaivanov) and N.K.; formal analysis, D.A., N.K., and D.K. (Dimitar Karaivanov); investigation, D.A. and O.S.; resources, T.A. and D.A.; data curation, O.S., D.K. (Dimitar Karaivanov) and D.K. (Dauren Kosherbay); writing—original draft preparation, T.A. and D.K. (Dauren Kosherbay); writing—review and editing, T.A. and D.K. (Dauren Kosherbay); visualization, D.K. (Dauren Kosherbay); supervision, T.A.; project administration, T.A.; funding acquisition, T.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan, grant number AP19676816.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are contained in this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Müller, J.; Scholz, A.; Wendorff, M. Precision forage harvesting: Automatic guidance and sensor-based crop detection. Biosyst. Eng. 2019, 184, 112–121. [Google Scholar]
- Smith, R.; Patel, D. Intelligent Harvesting in Small-Scale Farms Using GPS-Aided Forage Systems. Agric. Technol. Rev. 2020, 35, 44–51. [Google Scholar]
- Li, X.; Wang, Y.; Chen, J. Development of Small-Scale Corn Harvester with Adjustable Guiding Frame. J. Chin. Agric. Eng. 2021, 39, 75–81. [Google Scholar]
- Tanaka, H.; Sato, K. Optimization of cutting length and energy efficiency in forage harvesters. Jpn. J. Farm Mach. 2020, 58, 202–209. [Google Scholar]
- Gribok, K.A.; Kopchik, D.I. Overview of Modern Grain Crushers Used in Self-Propelled Forage Harvesters. In Proceedings of the Materials of Scientific and Practical Conferences of Students and Graduate Students, Techservice-2020, Minsk, Belarus, 20–22 May 2020; Belarusian National Technical University (BNTU): Minsk, Belarus, 2020; pp. 287–291. [Google Scholar]
- Forage Harvesters. In Proceedings of the 29th International Exhibition for Equipment, Technologies, Raw Materials and Ingredients for the Food Processing Industry, Moscow, Russia, 7–11 October 2024; Available online: https://www.agroprodmash-expo.ru/ru/ui/17128/ (accessed on 10 February 2025).
- Kokunova, I.V.; Shpenkov, D.R. Radial-Disc Crushing Units of Forage Harvesters: Design Features and Improvement Directions. In Modern Trends in the Development of the Agro-Industrial Complex: Technologies, Quality, Safety, Proceedings of the International Scientific and Practical Conference, Velikiye Luki State Agricultural Academy, Velikiye Luki, Russia, 20–21 May 2021; Velikiye Luki State Agricultural Academy: Pskov Oblast, Russia, 2021; pp. 113–116. [Google Scholar]
- Pleskachevsky, Y.M.; Mikhailov, M.I.; Mikhailov, K.M. About the mathematical model of the cutting drum of the device for shredding plant matter of forage harvester. Actual Issues Mach. Sci. 2020, 9, 181–185. [Google Scholar]
- Productivity, Versatility, Comfort: Gomselmash Advantages of Combines of New Generation. Available online: https://gomselmash.by/produktsiya/kormouborochnye-kombainy (accessed on 5 March 2025).
- Lisowski, A.; Świątek, K.; Klonowski, J.; Sypuła, M.; Chlebowski, J.; Nowakowski, T.; Kostyra, K.; Strużyk, A. Movement of chopped material in the discharge nozzle of a forage harvester with flywheel chopper: Measurements on corn and numerical modeling. Biosyst. Eng. 2012, 111, 381–391. [Google Scholar] [CrossRef]
- Grigory Iovlev, G.A.; Goldina, I.I.; Staheeva, L.M. Influence of the design of the chopping device on the productivity of vehicles. Vestn. Kurgan State Agric. Acad. 2023, 4, 56–64. [Google Scholar]
- Bannikova, D.A.; Zaitseva, M.I.; Kalinin, A.A. Analysis of the Design, Working Conditions and Causes of Failure of the Forage Harvester Dosimshredder; Technologies, Machines and Equipment for Agroindustrial Complex; Bulletin of Bryansk State Agricultural Academy: Bryansk, Russia, 2024; Volume 3, pp. 48–53. [Google Scholar]
- Ermolaev, V.I.; Otroshko, S.A.; Shevtsov, A.V. New shredding working organ for forage harvesters. Tech. Equip. Rural. Areas 2010, 11, 14–15. [Google Scholar]
- New Claas Jaguar 850 in the Farm. Available online: https://yandex.kz/video/preview/4787838393203677100 (accessed on 6 March 2025).
- Klever Ltd. Operation Manual and Spare Parts Catalog for the KSD-2.0 “Sterh” Trailed Forage Harvester. Klever Ltd., Rostov-on-Don, Russian Federation, 50-letiya Rostselmasha St. 2-6/22. Available online: https://www.kleverltd.ru/upload/iblock/b30/qlvd16mrg9f70k4ak7frpgac9jj49fbl/Rukovodstvo-po-ekspluatatsii-KSD-_10-versiya_.pdf (accessed on 12 March 2025).
- Wang, W.; Sun, W.; Li, H.; Li, X.; Yuan, Y. Design and Experiment of a Single-Disk Silage Corn Harvester. Agriculture 2025, 15, 751. [Google Scholar] [CrossRef]
- Hemmelgarn, A.B.; Shinners, K.J.; Timm, A.J.; Digman, M.F. Single-Pass, Single-Stream Harvest of Corn Grain and Stover: A Comparison of Two Harvest Methods. Bioenergy Res. 2024, 17, 2158–2163. [Google Scholar] [CrossRef]
- Pathaka, A.; Prabhu, T.; Chaudhari, H.; Rajhans, N.R. Development in Small Scale Multipurpose Fodder Harvester—A Review. Available online: https://www.researchgate.net/publication/312159446_Development_In_Small_Scale_Multipurpose_Fodder_Harvestor_-_A_review (accessed on 15 March 2025).
- Xue, Z.; Fu, J.; Chen, Z.; Wang, F.-D.; Han, S.-P.; Ren, L.-Q. Optimization experiment on parameters of chopping device of forage maize harvester. J. Jilin Univ. (Eng. Technol. Ed.) 2020, 50, 739–748. [Google Scholar]
- Wang, Z.; Song, Z.; Liu, P.; Ren, L.; Song, Y. Development and Experiment of Crop Feeding Angle Parameter Model in Chopping Roll of Hay Cutter. Trans. Chin. Soc. Agric. Mach. 2024, 55, 200–211. [Google Scholar]
- Abilzhanuly, T.; Iskakov, R.; Nurgozhayev, S.; Abilzhanov, D.; Seipataliyev, O.; Kosherbay, D. Mathematical Modeling of the Processes of Mowing, Oriented Feeding, and Chopping of Stalk Forage by a Forage Harvester. Agric. Eng. 2024, 6, 4766–4785. [Google Scholar] [CrossRef]
- Abilzhanuly, T.; Abilzhanov, D.; Khamitov, N.; Iskakov, R.; Orazakhyn, D.; Naydenko, E. Justification of Blade and Paddle Velocity Based on the Throwing Distance of the Mass through the Forage Harvester Deflector. Izdenister Natigeler 2023, 3, 345–355. (In Russian) [Google Scholar]
- Myasnikov, S.P.; Osanova, T.N. Physics Manual: A Study Guide for University Preparatory Departments; Vysshaya Shkola: Moscow, Russia, 1981; p. 391. (In Russian) [Google Scholar]
- Trailed Forage Harvester KSD-2.0 “Sterh”. Available online: https://orelagro.ru/tehnika/kormozagotovitelnaya-tehnika/pricepnye-kormouborochnye-kombainy/ksd-20.html (accessed on 1 May 2025).
- Corn Harvesters of the Pottinger Mex Series. Available online: https://agrovesti.net/lib/tech/machinery-and-equipment/kombajny-dlya-kukuruzy-serii-pottinger-mex.html (accessed on 1 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).