Abstract
The study presents the first application of the Connected Linear Network (CLN) package implemented in MODFLOW-USG to an existing Ground-Source Heat Pump (GSHP) system. The numerical element was specifically adapted by the authors in a previous study to simulate vertical Borehole Heat Exchangers (BHEs) and is here applied for the first time to evaluate the heat transfer in Milano subsurface induced by a GSHP system. The evaluation of interference between geothermal systems and wells is an important topic, especially in densely populated areas, which has scarcely been explored in the literature. Specifically, the aim is to evaluate the thermal perturbation and the possible interference between BHE systems and the drinkable water wells of the Armi pumping station managed by MM S.p.A. The simulation results show moderate groundwater thermal perturbation: approximately 3 °C at 100 m downgradient of the borefield and, furthermore, a limited impact (maximum 1 °C) in just two wells of the Armi pumping station. After 3 years of GSHP system operation, the thermal perturbation can extend for kilometers, but with limited variation in groundwater temperature (lower than 1 °C). Although the predicted groundwater temperature variation is not critical, the real-time monitoring of temperatures coupled with numerical modeling is essential to prevent thermal interference and optimize GSHP system performance.
1. Introduction
In recent decades, the growing focus on renewable energy has led to an increasing interest in low-temperature geothermal energy (i.e., geo-exchange resource) as a sustainable source of energy for air-climatization of buildings. The coupling of ground heat exchangers (such as borehole heat exchangers (BHEs) or pumping/injection wells) with Ground-Source Heat Pump (GSHP) systems, used for heating and cooling of buildings, represents a valid and modern technology that exploits the constant heat source of the subsoil [1]. By exploiting the temperature of the ground surrounding the ground exchanger at shallow depths (usually 100–150 m), the installation of geo-exchange systems can cause significant thermal disturbances in the subsurface, affecting not only the efficiency of the system itself but also local ecosystems and groundwater resources [2,3,4]. Thermal perturbations generated by ground exchangers can result in long-term effects on subsoil temperature, altering natural thermal gradients and potentially affecting biodiversity and habitat stability [5,6,7,8]. Understanding the dynamics of these perturbations is essential to assess the environmental impact of geothermal installations and optimize energy management practices [9,10,11].
The most common geo-exchange systems include Groundwater Heat Pump (GWHP) and Ground-Source Heat Pump (GSHP) systems, each with its unique operational mechanisms, benefits, and challenges. Both systems exploit the yearly constant temperature of the subsurface to provide energy-efficient heating and cooling systems for buildings, but they differ significantly in terms of heat transfer mechanisms, system configuration, and environmental conditions.
GWHP systems are open-loop systems, which directly use groundwater as a heat source or sink and consist of one or more wells (for extraction and injection). Water is pumped from an aquifer, passed through a heat exchanger, and then returned to the aquifer through the injection well or to a surface water body [12,13]; they can effectively operate in areas with abundant groundwater resources, offering high efficiency due to the thermal properties of groundwater [14], which typically maintains a more consistent temperature throughout the year compared to soil or rock [15,16]. GSHP systems are closed-loop systems, which operate by circulating heat transfer fluid (usually water or an antifreeze solution) through a network of single, double U-shape, or coaxial plastic pipes (i.e., BHE) buried in the subsurface. In general, BHE systems can be installed in various configurations (vertical, horizontal, or coaxial), making them suitable for a wide range of site conditions, including those with limited access to groundwater or where space for groundwater wells is restricted [4,17,18,19,20]. These systems are generally more durable and require less maintenance than open-loop ones, as they operate in a closed environment, reducing the risks of contamination of the heat exchange fluid. They can be optimized in terms of number and layout by means of analytical or numerical tools [21,22,23]. Closed-loop systems can also be installed in decommissioned wells and sometimes coupled with existing air conditioning systems [24].
Geo-exchange systems have high thermal interaction with the surrounding environment, in terms of thermal perturbation and groundwater thermal effects. If in some regions of Italy, GWHP systems are subject to specific regulation on thermal perturbation [25], for GSHP systems, no specific issue has been defined so far [26]. Indeed, continuous extraction of groundwater can lead to issues such as groundwater depletion and localized thermal pollution, which can affect aquatic ecosystems or neighboring users [27,28,29]. In densely populated urban areas, where the demand for energy-efficient solutions is high, the deployment of GSHP systems offers an opportunity to lower both carbon emissions and the environmental footprint of buildings [30,31]. However, as the number of these systems increases, concerns about their impact become more significant. A more comprehensive assessment of thermal plume migration is essential for the design and management of GSHPs in urban areas, particularly in locations with high system densities or where aquifer resources are in close proximity [32,33]. The effect of geo-exchange systems adds to other important anthropic systems in the urban environment, such as subway tunnels, industrial plants, and underground tanks. The resulting rise in temperature contributes to the urban heat island (UHI) effect. This was widely studied by many authors for different urban areas: Worsa-Kozak and Arsen [34] demonstrated the existence of a UHI in the city of Breslava (Polonia); Menberg et al. [35] studied the impact of anthropic activities on groundwater temperatures in different cities of Germany (Berlin, Munich, Cologne, and Karlsruhe); Zhu et al. [5] showed an increase in groundwater temperature equal to 5 °C in the industrial area of the city of Cologne. The effects of UHI have important implications for human health, increasing the risk of mortality during summer heat waves and also negatively impacting ecosystems and water bodies [36,37].
Numerical models are common tools used to quantitatively evaluate the effects of external stresses in the subsoil. There are many examples of their use in different fields, from groundwater resource extraction and management in complex geological settings [38,39,40] to groundwater pollution remediation [41,42,43], groundwater subsidence study [44,45], or interaction between deep and shallow water [46] and their consequences on shallow sediment transport [47,48]. Furthermore, numerical models can also be applied to evaluate the extension of the thermal interference in the subsurface [49]. Previati et al. [50] presented an analysis of the anthropogenic and natural factors responsible for the thermal balance of the subsoil in Milan. Alaie et al. [9] developed a semi-analytical model to study the outlet fluid temperature of a BHE according to different hydrogeological settings. To evaluate the extent of thermal perturbation in different aquifers, Tolooiyan and Hemmingway [51] proposed different simulations, considering groundwater flow velocities. An interesting analysis was conducted by Dehkordi and Schincariol [52], which developed a finite numerical model to show the main parameters influencing the heat exchange between BHE and subsoil. Di Pierdomenico et al. [53] reproduced finite elements numerical models simulating annual heating and cooling cycles to verify the sustainability of geothermal resources and the thermal impact induced by the BHEs during a long-term (20 years) operation. Predictive models of thermal plume behavior and groundwater temperature distribution, considering factors such as aquifer permeability, groundwater flow rates, and system configuration, are also essential to optimize the placement and operation of GSHPs [16]. Updating the thermal conditions of the ground with continuous temperature measurements can increase the optimization of the geo-exchange system: Soltan Mohammadi et al. [54] demonstrated the performance of a sequential optimization applied to two borefields with 5 and 26 BHEs over 15 years of operation. By incorporating these models, it will be possible to minimize the risks associated with thermal interference and ensure that the deployment of BHEs and GSHPs remains a sustainable and environmentally responsible solution.
When a GSHP system is installed close to other operating wells, the induced thermal perturbation should be carefully evaluated to prevent negative effects on other uses of the groundwater resource. However, the evaluation of more than one BHE is unfeasible with classical techniques, making this task hard to accomplish. To overcome this issue, this study is the first case in the literature of the application of a new tool in MODFLOW-USG [55], named Connected Linear Network (CLN) package, specifically adapted to simulate BHE operation in aquifers [49,56]. Through the adaptation of the CLN package, the implementation of several BHEs in one numerical model is now possible. The goal of the present work is to explore the effects of thermal interference caused by a real GSHP system (60 BHEs) located in the city of Milan, whose purpose is to provide air-climatization of a multi-house building (named “MIA—La Casa Italiana”). By means of a transient state numerical model built in MODFLOW-USG, the thermal plume migration and its impact on the Armi pumping station wells (managed by MM S.p.A. for drinking purposes) were evaluated. Simulating three operation years of the geo-exchange system, a provision of thermal perturbation was carried out, and the effect of the thermal interference between BHE and Armi station wells was evaluated.
The study area is initially presented to define the geographical and hydrogeological context where the GSHP system is installed. Subsequently, the system characteristics are detailed in Section 3, including the implementation of the numerical models developed in MODFLOW-USG, with particular emphasis on the CLN component. Finally, the simulation results are presented, accompanied by a discussion of each outcome to demonstrate the capabilities of this tool.
2. The Study Area
The study area lies within the city of Milan and is part of a larger project named “MODEL-MI”, founded by MM S.p.A. (water manager of the city of Milan, Italy). The MODEL-MI project’s aim (presented in [40]) was to renovate the stratigraphy of the city of Milano according to the new information and to develop a groundwater flow model of the city, useful for the development of the Water Safety Plan for the Milan Functional Urban Area, in collaboration with the service manager and other actors involved in the water management system (i.e., the ISS—Italian National Institute of Health; the ARPA—Lombardy Regional Agency for Environmental Protection; and the Municipality of Milan). Starting from the basis of the previous project, the study area of this work was more detailed at a lower scale than the study area shown in [40] and is reported in Figure 1a. The target of the new study focuses on the evaluation of the thermal interference induced in Milan aquifers by closed-loop GSHP systems. According to MM S.p.A., the area in proximity to the drinkable wells of the Armi pumping station (NW sector of Milan) was chosen as the pilot investigation area. Close to the Armi station, a residential building named “MIA—La Casa Italiana” presents a geo-exchange system consisting of 60 vertical borehole heat exchangers 140 m deep (Figure 1b) and depicts a perfect case for the study of the thermal interference in the aquifer caused by geothermal systems.
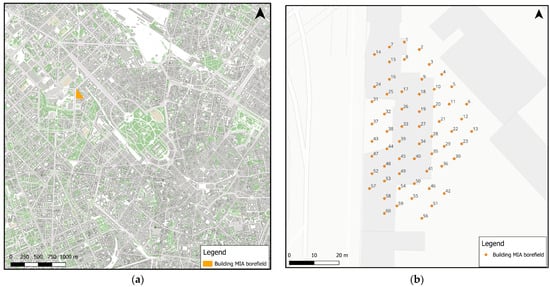
Figure 1.
(a) A view of the study area inside the city of Milan and (b) BHE layout.
The analysis of the hydrogeological setting of the study area is essential to better evaluate the heat exchanged and the thermal interference in the Milan aquifers. Based on the fluvioglacial Plio-Pleistocenic depositional cycles, the deposits in Milan can be divided into four hydrogeological units denoted as Aquifer Groups A, B, C, and D (from youngest to oldest) (Figure 2). These units host aquifers separated by clayey deposits. In detail, Aquifer Group A is mainly composed of gravels with sandy layers and represents the shallow unconfined aquifer. It is characterized by high values of transmissivity (often higher than 10−2 m2/s). Aquifer Group B is constituted by sands with silty–clayey lenses, presenting a transmissivity ranging between 10−3 and 10−2 m2/s. Aquifer Group C is mainly composed of alternating sandy silts and clays with subordinate intercalations of medium to fine sands and gravels, and the average transmissivity in the shallowest part is 1.1 × 10−2 m2/s versus the average of 8 × 10−3 m2/s found in the basal part [40].
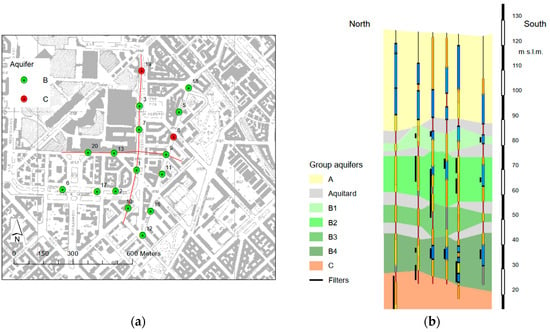
Figure 2.
(a) A study area and trace of hydrogeological section; (b) hydrogeological section with stratigraphic logs, where A is the phreatic shallow aquifer named as Aquifer Group A; B1, B2, B3 and B4 are 4 different confined aquifers belonging to Aquifer Group B; C is the confined Aquifer Group C.
In the proximity of the MIA building, 18 extraction wells belonging to the MM Armi pumping station are present. The study focuses on the thermal perturbation occurring in Aquifer B, since most of the Armi pumping station wells are screened within that aquifer. In detail, the Armi pumping wells (Figure 3) have depths ranging from 39 m to 102 m: 8 of them are screened only in Aquifer Group B (wells n. 5, 9, 11, 12, 13, 16, 17, 18), 8 are screened in both Aquifer Group A and B (wells n. 1, 2, 3, 4, 6, 7, 10, 20), and 2 in both Aquifer Groups B and C (wells n. 8 and 19). Some wells are located straight along the hypothetical preferential direction of the thermal plume generated by MIA’s GSHP system, accordingly to the groundwater flow direction, and thus present the risk of capturing water for drinking purposes at a temperature different from the undisturbed groundwater temperature. For instance, an increase in temperature could cause the development of microorganisms potentially problematic for human health.
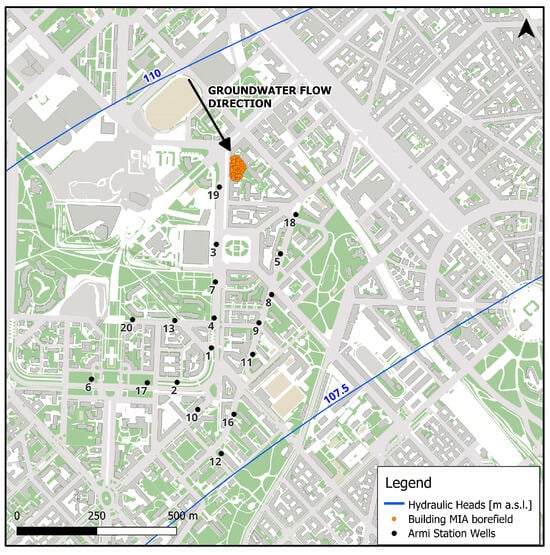
Figure 3.
A view of the Armi pumping wells station, the MIA building’s BHE, and the hydraulic heads of the shallow aquifer from public regional data (2014).
3. Materials and Methods
3.1. Building “MIA—La Casa Italiana”
The building “MIA—La casa Italina” has a surface of about 4600 m2 and 10 floors, for a total of 94 apartments. The building is climatized all year round thanks to two heat pumps. Each heat pump covers a heat rate peak equal to 200 kW during the winter season and a cold rate peak equal to 187 kW during the summer season. The performance indexes usually considered are the Coefficient of Performance (COP) during the winter season and Energy Efficiency Ratio (EER) during the summer season. These indexes are a measure of efficiency, specifically the amount of thermal energy provided for the amount of electrical energy consumed by the heat pump; in general, values range from 3.5 to 7. The heat pump COP is equal to 4.9 (production of 4.9 kW of thermal power produced using 1 kW of electric power), whereas the EER is equal to 4.9. Considering the instantaneous thermal peak values, corresponding to the period of maximum heating or cooling, the amount of heat rate extracted (during winter) or injected (during summer) is specifically equal to 318 kW and 451 kW. The BHEs are composed of 140 m deep, 32 mm diameter, and double U-shaped HDPE (High-Density Polyethylene) pipes.
3.2. Numerical Model Implementation
The numerical model was implemented starting from the regional-scale model developed within the MODEL-MI project, presented in the study by Alberti et al. (2025) [40]. The model presented in this work was developed using the Telescopic Mesh Refinement (TMR) technique, which allows the extraction of a new model from a subregion of a larger-scale numerical model. The TMR is characterized by a rectangular domain with an extent of 4 km2 (2.3 km × 1.7 km, Figure 4), a sufficiently wide area that allows for the representation of the thermal perturbation with negligible boundary effects. Although the original model was developed in MODFLOW-2005 [57], the TMR was developed using MODFLOW-USG due to its more robust formulation, which allows the use of the CLN package and the unstructured grids (Control Volume Finite Difference formulation, CVFD). Furthermore, MODFLOW-USG allows coupled groundwater flow and heat transport simulations in the same code.
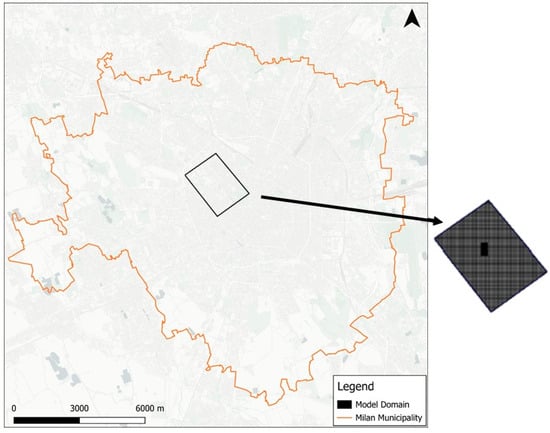
Figure 4.
A view of the numerical model domain.
The Quadtree refinement (a methodology for progressively decreasing the size of adjacent cells available for the CVFD formulation) was used in proximity to the GSHP system by defining 6 zones, starting from a maximum cell size of 16 m until a minimum cell size of 50 cm (Figure 5), defined in the area covered by the MIA building extent. The influence of the grid discretization was further analyzed by the authors in a previous study [49], showing a temperature difference lower than 0.25 °C 5 m downstream of the BHEs for the implemented grids. Given this result, a minimum cell size of 50 cm was assumed to be small enough for the scale and the aim of the study. The maximum grid refinement is not at the center of the quadtree rectangle because the thermal perturbation produced by BHE is expected to be downgradient of the GSHP system; therefore, being the groundwater flow directed from North to South, the need to create more refined cells towards South is essential. This technique resulted in the generation of specific refinement just in the area of interest, avoiding an unnecessary increase in the cells’ number, which generally increases the computational burden.

Figure 5.
A view of the numerical horizontal grid discretization in the study area.
As for the horizontal discretization, a vertical spatial discretization was developed on the basis of the regional-scale model [40] (details are shown in Figure 2b). The highly detailed subsurface representation is an important advantage of this numerical model compared to those present in the literature for the Milan area (Table 1).

Table 1.
Vertical discretization of the numerical model.
The implementation of 60 BHEs in MODFLOW-USG represents the first application on a real case of the adaptation of the Connected Linear Network (CLN) package, which was presented and validated in comparison with analytical solutions (Infinite Line Source and Moving Line Source) in these studies [49,56]. The BHE is implemented as two vertical pipes (using Wells elements) and one horizontal pipe (Polyline element) to reproduce the real U-shape pipe. For the sake of simplification, the BHEs were represented as a single U, calculating the equivalent area from the actual area of the double-U BHE. The fluid inlet temperature to the BHE depends on the GSHP system operation. Here, it was assumed to be equal to 1 °C during the winter season and to 28 °C during the summer season, as reported in Table 2.

Table 2.
Time discretization of the numerical model simulation.
The temporal discretization of the numerical simulations was set into 4 stress periods (SPs) to reproduce the typical annual operation of a GSHP system (according to the Italian regulation [58]), for a total of three years of simulation (12 SPs). Each stress period reproduced the heating operation (during the winter season, 180 days), the cooling operation (during the summer season, 90 days), and the two intermediate seasons (spring and autumn, respectively, 50 and 40 days), as shown in Table 2. During spring and autumn, the GSHP system is not supposed to be in operation, and consequently, no flow is simulated within the BHEs in these periods. Inside each SP, the numerical solver implemented in the code is able to automatically choose the best time step size to avoid numerical dispersion into the cells where the heat transfer equation is solved.
A type I boundary condition (Dirichlet condition), i.e., constant hydraulic head, was assigned along the entire perimeter of the TMR domain by imposing the hydraulic head values achieved in the last SP of the transient simulation of the calibrated regional-scale model [40]. The simulated head in the same regional model SP was used as the initial condition for the TMR. Concerning initial and boundary groundwater temperature conditions, it is generally the case within the Milan aquifers that the distribution of groundwater temperatures varies with depth. Within the Aquifer Group A (layers 1 to 4), a value of 15.2 °C was assigned, based on field data measured 360 m North-East of the 60 geothermal BHEs as part of a monitoring campaign performed by Politecnico di Milano. This value was imposed as a constant temperature (Dirichlet condition) at all the boundaries. As for the Aquifer Group B, a value of 14.5 °C was imposed, based on temperatures detected by a data logger placed inside well n. 19 of the Armi station, screened in both Aquifer Groups B and C.
The hydrogeological properties implemented into the model were derived from the regional-scale model [40]. The hydraulic conductivity and porosity values of the aquifer implemented in the model are shown in Table 3. The specific storage value is constant in all layers and equal to 10−4 m−1, and the specific yield value was set equal to the porosity value. The recharge (reproducing the water infiltration on the top of the model) was assigned to the 1st layer with values ranging between 5 × 10−9 and 4.18 × 10−8 m/s (derived from [40]) and a constant temperature value of 15.2 °C (assumed equal to the unperturbed temperature assumed for Aquifer A).

Table 3.
Hydrogeological parameter values implemented into the heat transport numerical model.
The subsurface thermal properties were deduced by a Thermal Response Test (TRT) executed during the GSHP system design. The TRT is an in situ test performed on a single BHE aimed at evaluating the borehole thermal resistance, the ground temperature, and subsoil thermal conductivity by injecting a constant heat source into the subsurface. The thermal conductivity value estimated was equal to 2.07 W/m/K. Moreover, the maximum thermal capacity and the thermal diffusion were reported in the TRT results as 2.4 MJ/m3 and 8.6 × 10−7 m2/s. The thermal dispersivity was set to zero, due to the difficulties in estimating this parameter for real cases. However, a value of zero allows for performing safety-oriented simulations, as the simulated groundwater temperatures may be slightly higher than the actual temperatures.
4. Results and Discussion
In accordance with the hydrogeological and operational parameters discussed before, a numerical simulation was implemented to assess the thermal perturbation evolution during the yearly operation of the GSHP system and to verify the thermal interference in the Armi station wells. The outputs of the simulations are the hydraulic head distribution and the groundwater temperature distribution over time and space.
The hydraulic heads distribution and the groundwater flow directions relative to Aquifer B are reported in Figure 6.
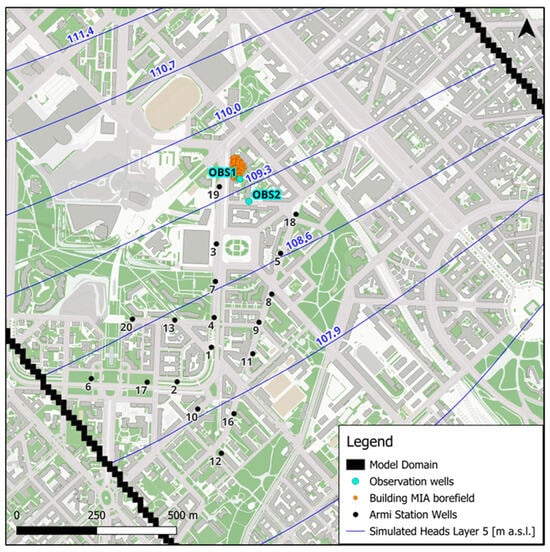
Figure 6.
Simulated hydraulic head distribution in Aquifer B.
The simulated piezometry was in accordance with the real one [40], with groundwater flow directed NW-SE. No important groundwater flow variations are expected during the duration of the heat transport simulations.
The simulated groundwater temperature could not be validated due to the impossibility of performing temperature measurements in the MM wells invested by the thermal plume. The groundwater temperature was monitored for the whole simulation period at 2 different observation points (OBS 1 and OBS 2) located 5 and 80 m downgradient of the borefield, respectively. Such monitoring points are not physically present but were introduced in the model just to analyze the groundwater temperature variation over the Aquifer Groups A and B (Figure 7).
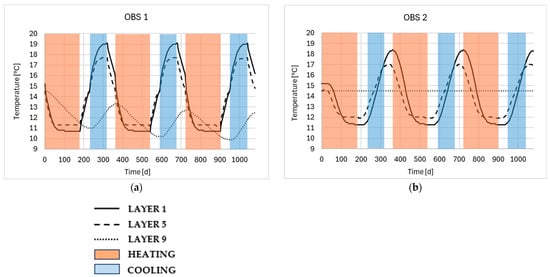
Figure 7.
Groundwater temperature distribution inside (a) observation point 1 (OBS 1) and (b) observation point 2 (OBS 2).
At the OBS 1 location (Figure 7a), the groundwater temperature in Aquifer A (Layer 1) decreases during the heating period (winter season), moving from the aquifer’s unperturbed value (15.2 °C) to a minimum value of 10.8 °C. Instead, during the summer period, the temperature increases from 10.8 °C to a maximum value of 19.0 °C. Concerning Aquifer B (layer 5), the temperature decreases during the heating period (winter season), going from the aquifer unperturbed value (14.5 °C) to a minimum value of 11.1 °C; on the contrary, during the summer period the temperature increases from 11.1 °C to a maximum value of 17.8 °C. In Aquifer C (layer 9), the groundwater temperature has more inertial behavior due to the lower hydraulic conductivity of the aquifer material, ranging from 14.5 °C to 10.0 °C. At the OBS 2 location (Figure 7b), similar behavior of groundwater temperature was detected, but reduced groundwater temperature oscillations around the unperturbed value were observed. This is because OBS2 is located 80 m downgradient of the borefield, and therefore, the temperature is affected by the thermal gradient and advection phenomenon. At OBS 2, the groundwater temperature increases by a maximum of 3.5 °C and decreases by a maximum of 4 °C compared to the unperturbed value (Aquifer A), demonstrating that a thermal interference is still present. For the aforementioned reasons, if a new GSHP system were installed in this area, a problem related to the energy performance of the new system would be present. Specifically, the new GSHP system would work in a thermal-altered environment (not in an unperturbed condition), reducing the COP value during winter and the EER value during summer of about 10%, considering a COP reduction equal to 2.5% for 1 °C of groundwater temperature gain or loss, calculated from technical schemes of different heat pumps present in the market.
To better evaluate the extent of the thermal perturbation downgradient of the borefield at fixed time (the latter heating period of the 3rd year simulation), 90 monitoring wells were placed along the preferential groundwater flow direction (Figure 8).
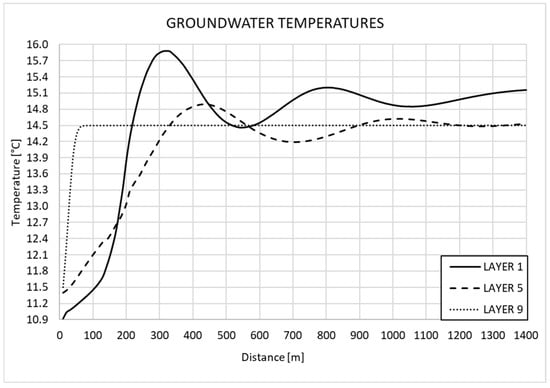
Figure 8.
Groundwater temperature distribution inside 90 observation points in Aquifer Groups A, B, and C after the last heating period of the 3rd year simulation.
Figure 8 is a picture of the aquifer temperature downgradient of the BHE on the last simulated day. The temperature in the proximity of the BHE (10 m downgradient) is around 11 °C because the aquifer has been cooled by the thermal plumes of the previous seasons (to be noted that the heating period, i.e., extraction of heat from subsurface, is greater than the cooling one). Over the distance, a trace of the succession of all the plumes of the previous seasons is present. For instance, the warm plume induced by the cooling period can be seen in layer 1 at 320, 750, and 1400 m; similarly, the warm plumes can be seen in layer 5 at 420, 1000 m. After 3 years, the warm and cold peaks of each year decrease in intensity, so the maximum groundwater temperature value can be measured at a specific distance from the borefield for each aquifer. The temperature distribution in Aquifer A (continuous line in Figure 8) shows an important variation (greater than 1 °C compared to the unperturbed value) up to 250 m. From 210 m onward, the groundwater temperature variation around the unperturbed value is lower than 1 °C. In Aquifer B (similarly to Aquifer A), the greatest groundwater temperature variation is found within 230 m from the borefield, and then it shows values lower than 1 °C. In Aquifer C, because of the lower hydraulic conductivity values, the biggest effects on temperature variation are recorded within 60 m, showing a more radial thermal perturbation around the borefield. This result shows how any future GSHP systems installed in a radius area of 200 m around the building MIA will need to take this temperature variation into account for their design.
To account for the thermal perturbation at the Armi pumping well locations, which is the main focus of this study, the temperatures at wells number 3, 5, 8, 18, and 19 were monitored through the numerical model. This was not possible in the real wells because of their continuous operation or the impossibility of placing measuring instruments in the wells. Wells n. 8 and n. 19 are screened in Aquifer Groups B and C but are not currently in operation. Wells n. 5 and n. 19 are screened in Aquifer Group B (model layers from 5 to 7), while well n. 3 is screened in Aquifer Groups A and B (i.e., from layer 2 to layer 7). Figure 9 shows the groundwater temperature variation for each aquifer (Aquifer A—layer 1, Aquifer B—layer 5, Aquifer C—layer 9) over 3 years of GHSP system operation.
Figure 9.
Groundwater temperature distribution inside Armi station wells: (a) well n.3, (b) well n.5, (c) well n. 8, (d) well n. 18, and (e) well n. 19.
In wells n. 3, 18, and 19 (Figure 9), no groundwater temperature variation is observed, since these wells fall outside the thermal perturbation area induced by the GSHP system. Indeed, the groundwater temperature values observed are equal to the unperturbed value of the aquifer. In wells n. 5 and n. 8 (Figure 9), the groundwater temperature oscillates around the unperturbed value according to the operational season. After the heating period, the temperature increases, whereas after the cooling period, a decreasing groundwater temperature is observed. However, the thermal variation is always less than 1.2 °C in both Aquifer Groups A and B, while no thermal effect was predicted for Aquifer Group C. Table 4 and Table 5 show the computed thermal variation from the undisturbed aquifer values (15.2 °C in layer 1 and 14.5 °C in layer 5) at the maximum and minimum peaks of the curves presented in Figure 9.

Table 4.
Groundwater temperature difference in well n. 5 between the maximum or minimum temperature value and the unperturbed temperature value for every year of simulation.

Table 5.
Groundwater temperature difference in well n. 8 between the maximum or minimum temperature value and the unperturbed temperature value for every year of simulation.
A maximum decrease of −1.17 °C (day 328) and −0.78 °C (day 744) and a maximum increase of +0.96 °C (day 504) and +0.35 °C (day 557) were predicted in well n. 5 and well n. 8, respectively. In other periods, a similar increase or decrease was achieved. Generally, the observed thermal interference is negligible for well with drinking water purposes, and such temperature fluctuations are too limited to contribute to bacterial growth that could harm human health.
The last result analyzed is the groundwater temperature distribution of the area of interest, studying the evolution of the thermal perturbation according to seasonal operations of the GSHP system across the Aquifer Group B, where most of the Armi pumping wells are screened. Figure 10 shows the groundwater temperature distribution at the end of the simulation, while the results at the end of the heating and cooling operation are shown in Supplementary Material Figures S1–S6.
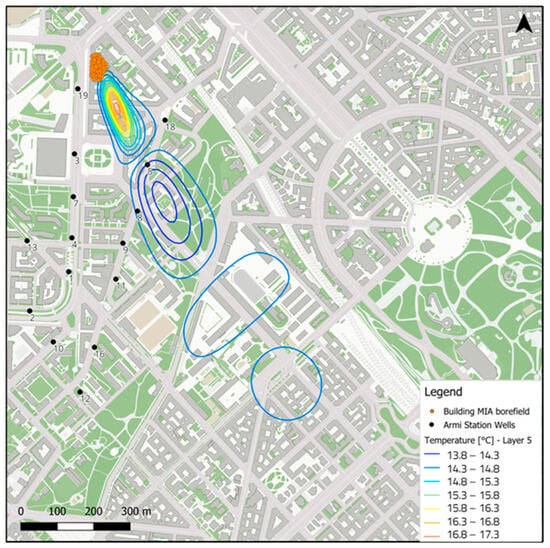
Figure 10.
Thermal perturbation (plumes) induced by the GSHP system in Aquifer B at the end of the simulation.
The groundwater temperature profiles shown in Figure 9 are verified by the analysis of the thermal plume (Figure 10), which reaches only wells n. 5 and n. 8. Well n. 5, located 270 m downgradient of the last BHE, appeared to be most affected due to its proximity to the GSHP system and its location along the groundwater flow direction. Well n. 8 instead is placed more laterally to the main flow direction and at a larger distance from the GSHP system (300 m), showing much smaller oscillations, particularly in Aquifer Group B. In both wells, no thermal perturbation is detected in Aquifer Group C, due to the low groundwater flow velocity of this aquifer (Table 3). No thermal perturbation was observed in any of the other Armi pumping wells.
The representation of the thermal perturbation extension at the 3rd year of simulation (Figure 10) showed how warm and cold plumes alternate in their movement toward S-SE. However, due to the shorter period of operation of the system in cooling mode, the warm plume is visible only immediately downstream of the plant and almost disappears beyond about 500 m. In contrast, two cold plumes are clearly visible, which follow each other spatially, taking on a gradually larger shape and with less pronounced temperature variations than the average as they move away from the GSHP system. At a distance of about 1 km from the system, no temperature increase is expected after 3 years of operation, but a periodic decrease that reaches a maximum value of −0.4 °C and −0.1 °C is observed in Aquifer Groups A and B, respectively. Thus, the presence of the GSHP system in the MIA building, even adopting pro-safety simulation conditions, generates a thermal perturbation in the examined aquifers that only slightly affects the temperatures of two wells of the Armi station (n. 5 and n. 8) and is negligible after 400 m.
As shown by the results, the presence of the GSHP system does not result in any environmental or quality issues associated with the increased groundwater temperature extracted by the wells serving the MM Armi pumping station. Furthermore, implementing more similar operational conditions to the real GSHP system (i.e., probably lower and diversified BHE circulating flow rate and temperature for summer and winter periods), the thermal effect induced by BHE may be even lower on the wells of the Armi pumping station. The change in the thermal dispersivity coefficient of the aquifer could also cause a lateral spread of the thermal plumes, reducing their longitudinal extension. This could cause thermal perturbation to reach other wells of the Armi station (such as wells n. 3 and n. 18), but the perturbation is expected to be lower than 1 °C, thus avoiding any environmental or quality issue.
Nonetheless, when considering the overall thermal disturbance induced in the subsurface by this GSHP system, it becomes evident how crucial it is to design new installations with the support of numerical or analytical simulations, considering the number of existing systems present in the area. In urban environments, the overlapping of thermal effects from multiple installations is increasingly frequent, making a more sustainable approach to resource management essential to prevent a shift from responsible use to overexploitation. Another key point in GSHP systems’ numerical modeling is the groundwater flow velocity, which is frequently neglected due to the nature of the software used or lack of information. Ignoring or miscalculating the value of this hydrogeological factor could lead to biased results, even more than mistaking thermal parameters when advection governs heat transport phenomena [27,59].
In accordance with the findings reported in these two studies [28,60], the present work serves as a preliminary investigation of the thermal impact on the subsurface generated by a typical residential building in a northern Italian city.
5. Conclusions
The study demonstrates for the first time in the literature the application of the MODFLOW-USG CLN package, adapted to allow the representation in numerical models of multiple BHEs behavior in aquifers. Through the development of a 3D transient state numerical model, the subsurface thermal interference induced by a real GSHP system consisting of 60 BHEs (MIA building) was simulated and evaluated. The purpose of the study was to evaluate how the GSHP system thermal perturbation could affect the water extracted by the wells of the Armi pumping station, property of MM S.p.A., located in the city of Milan.
The results of the numerical simulations highlighted that the presence of 60 BHEs belonging to the GSHP system causes moderate thermal interference in one observation point placed 80 m downgradient of the borefield (maximum 4 °C). Therefore, possible interferences must be considered if new GSHP systems were designed in this area, accounting for a potential GSHP system energy performance reduction.
Groundwater temperature variations were more pronounced in terms of cooling the aquifer than in terms of heating, since the systems usually operate for a longer period and with greater temperature changes during the winter season. The cold thermal plume extended 2 km downstream, but with induced temperature variations lower than 1 °C compared to unperturbed groundwater temperature.
Concerning the Armi pumping station, only limited thermal interferences (maximum of about 1.2 °C) were observed at the pumping well locations. Currently, such variations are expected to affect only 2 (wells n. 5 and n. 8) of the 18 wells present in the area. Therefore, no environmental or quality issues related to the influence of the GSHP system were detected for the Armi pumping station.
In general, concerning the potential of shallow geothermal resources in the city of Milan, the numerical simulations highlighted some important issues related to the management of groundwater resources. Large GSHP systems such as that of MIA could determine moderate temperature variations in Aquifer Groups A, B, and C (greater than 1 °C), no more than 200 m along the preferential direction of groundwater flow. This distance could be taken as the first reference to protect groundwater and shallow geothermal resources.
Furthermore, the presence of existing water supply infrastructures should be carefully addressed, even considering superimposition effects with existing geo-exchange systems. Therefore, in urban areas such as the city of Milan, it is becoming essential to evaluate aquifer thermal perturbations generated by geo-exchange systems using appropriate local-scale numerical models, aimed at optimizing the energy performance of GWHP or GSHP systems, avoiding thermal short-circuit effects and interactions with existing infrastructures.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/app15105522/s1, Figure S1: Thermal perturbation (plumes) induced by GSHP system in Aquifer B at the end of heating period of 1st year simulation; Figure S2: Thermal perturbation (plumes) induced by GSHP system in Aquifer B at the end of cooling period of 1st year simulation; Figure S3: Thermal perturbation (plumes) induced by GSHP system in Aquifer B at the end of heating period of 2nd year simulation; Figure S4: Thermal perturbation (plumes) induced by GSHP system in Aquifer B at the end of cooling period of 2nd year simulation; Figure S5: Thermal perturbation (plumes) induced by GSHP system in Aquifer B at the end of heating period of 3rd year simulation; Figure S6: Thermal perturbation (plumes) induced by GSHP system in Aquifer B at the end of cooling period of 3rd year simulation.
Author Contributions
Conceptualization, M.A., L.A., and S.B.; methodology, M.A. and S.B.; software, M.A.; P.M., and S.B.; validation, M.A. and S.B.; resources, L.A. and S.R.; data curation, M.A. and S.B.; writing—original draft preparation, M.A. and S.B.; writing—review and editing, M.A.; P.M. and L.A.; supervision, M.A. and L.A.; funding acquisition, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MM S.p.A., grant number 42/2017 CIG-7188325970.
Data Availability Statement
The original contributions presented in this study are included in the article and Supplementary Materials. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. Fabio Marelli, along with Sara Rizzo on behalf of MM S.p.A., was responsible for the MODEL-MI project together playing an important coordination role between the Politecnico di Milano and the institutions for the collection of all data useful for numerical modeling. He had no role in the analysis and interpretation of data. Sara Barbieri from the company Tethys s.r.l. declares no conflicts of interest.
Abbreviations
| CLN | Connected linear network |
| BHEs | Borehole heat exchangers |
| GSHP | Ground-source heat pump |
| GWHP | Groundwater heat pump |
| UHI | Urban heat island |
| TMR | Telescopic mesh refinement |
| CVFD | Control volume finite difference |
| TRT | Thermal response test |
References
- Lund, J.W.; Boyd, T.L. Direct Utilization of Geothermal Energy 2015 Worldwide Review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Alberti, L.; Angelotti, A.; Antelmi, M.; La Licata, I. A Numerical Study on the Impact of Grouting Material on Borehole Heat Exchangers Performance in Aquifers. Energies 2017, 10, 703. [Google Scholar] [CrossRef]
- Alberti, L.; Angelotti, A.; Antelmi, M.; La Licata, I. Borehole Heat Exchangers in Aquifers: Simulation of the Grout Material Impact. Rend. Online Soc. Geol. Ital. 2016, 41, 268–271. [Google Scholar] [CrossRef]
- Angelotti, A.; Alberti, L.; La Licata, I.; Antelmi, M. Borehole Heat Exchangers: Heat Transfer Simulation in the Presence of a Groundwater Flow. J. Phys. Conf. Ser. 2014, 501, 012033. [Google Scholar] [CrossRef]
- Zhu, K.; Bayer, P.; Grathwohl, P.; Blum, P. Groundwater Temperature Evolution in the Subsurface Urban Heat Island of Cologne, Germany. Hydrol. Process. 2015, 29, 965–978. [Google Scholar] [CrossRef]
- Previati, A.; Crosta, G. Impact of Groundwater Flow on Thermal Response Tests in Heterogeneous Geological Settings. Geothermics 2025, 127, 103266. [Google Scholar] [CrossRef]
- Mao, R.; Chen, Y.; Zhang, Z.; Chen, J.; Zhou, J.; Wu, H. Study on Performance and Layout Optimization of Buried Heat Exchangers Array in Karst Landform. Appl. Therm. Eng. 2025, 271, 126307. [Google Scholar] [CrossRef]
- Champagne-Péladeau, L.; Pasquier, P.; Millette, D.; Dupuis, J.C. Delineation of the Thermal Plume Associated with a Standing Column Well System in a Fractured Aquifer Using Numerical Modeling. Geothermics 2025, 127, 103260. [Google Scholar] [CrossRef]
- Alaie, O.; Maddahian, R.; Heidarinejad, G. Investigation of Thermal Interaction between Shallow Boreholes in a GSHE Using the FLS-STRCM Model. Renew. Energy 2021, 175, 1137–1150. [Google Scholar] [CrossRef]
- Piga, B.; Casasso, A.; Pace, F.; Godio, A.; Sethi, R. Thermal Impact Assessment of Groundwater Heat Pumps (GWHPs): Rigorous vs. Simplified Models. Energies 2017, 10, 1385. [Google Scholar] [CrossRef]
- Perego, R.; Dalla Santa, G.; Galgaro, A.; Pera, S. Intensive Thermal Exploitation from Closed and Open Shallow Geothermal Systems at Urban Scale: Unmanaged Conflicts and Potential Synergies. Geothermics 2022, 103, 102417. [Google Scholar] [CrossRef]
- Halilovic, S.; Böttcher, F.; Zosseder, K.; Hamacher, T. Optimization Approaches for the Design and Operation of Open-Loop Shallow Geothermal Systems. Adv. Geosci. 2023, 62, 57–66. [Google Scholar] [CrossRef]
- Cappellari, D.; Piccinini, L.; Pontin, A.; Fabbri, P. Sustainability of an Open-Loop GWHP System in an Italian Alpine Valley. Sustain. 2023, 15, 270. [Google Scholar] [CrossRef]
- Di Dato, M.; D’Angelo, C.; Casasso, A.; Zarlenga, A. The Impact of Porous Medium Heterogeneity on the Thermal Feedback of Open-Loop Shallow Geothermal Systems. J. Hydrol. 2022, 604, 127205. [Google Scholar] [CrossRef]
- Böttcher, F.; Halilovic, S.; Günther, M.; Hamacher, T.; Zosseder, K. Integration of Thermal Groundwater Use in Heat Planning. Grundwasser 2025, 30, 19–35. [Google Scholar] [CrossRef]
- Casasso, A. The Role of Numerical Modelling in the Design of Open-Loop Shallow Geothermal Systems. Rend. Online Soc. Geol. Ital. 2024, 64, 20–25. [Google Scholar] [CrossRef]
- Casasso, A.; Sethi, R. Efficiency of Closed Loop Geothermal Heat Pumps: A Sensitivity Analysis. Renew. Energy 2014, 62, 737–746. [Google Scholar] [CrossRef]
- Criollo, R.; Vilarrasa, V.; Orfila, A.; Marbà, N.; Fernández-Mora, A. Borehole Heat Exchangers in Coastal Areas May Reduce Heatwave Seagrass Loss. Geosci. Lett. 2025, 12, 2. [Google Scholar] [CrossRef]
- Brown, C.S.; Falcone, G. Investigating the Impact of Groundwater Flow on Multi-Lateral, U-Type, Advanced Geothermal Systems. Appl. Therm. Eng. 2025, 271, 126269. [Google Scholar] [CrossRef]
- Ahmadfard, M.; Bernier, M. Simulation of Borehole Thermal Energy Storage (BTES) Systems Using Simplified Methods. J. Energy Storage 2023, 73, 109240. [Google Scholar] [CrossRef]
- Katsifarakis, K.L.; Kontos, Y.N. Analytical Optimization of Vertical Closed-Loop Ground Source Heat Pump Systems. Energies 2025, 18, 163. [Google Scholar] [CrossRef]
- Lund, A.E.D. Performance Analysis of Deep Borehole Heat Exchangers for Decarbonization of Heating Systems. Deep Undergr. Sci. Eng. 2024, 3, 349–357. [Google Scholar] [CrossRef]
- Kahwaji, G.Y.; Capuano, D.; Boudekji, G.; Samaha, M.A. Design and Optimization of Ground-Coupled Refrigeration Heat Exchanger in Dubai: Numerical Approach. Heat Transf. 2024, 53, 1474–1500. [Google Scholar] [CrossRef]
- Gizzi, M.; Hosseinpour, F. Evaluating Outlet Working Fluid’s Temperature by Implementing Closed-Loop Geothermal Systems in Decommissioned Hydrocarbon Wells: The Case Studies of San Benigno and Cinzano Wells. Geoing. Ambient. E Mineraria 2024, 171, 44–50. [Google Scholar] [CrossRef]
- Regione Lombardia. Regolamento Regionale n. 2. In Bollettino Ufficiale Della Regione Lombardia; Comune di Milano: Milan, Italy, 2006. [Google Scholar]
- Berta, A.; Gizzi, M.; Taddia, G.; Lo Russo, S. The Role of Standards and Regulations in the Open-Loop GWHPs Development in Italy: The Case Study of the Lombardy and Piedmont Regions. Renew. Energy 2024, 223, 120016. [Google Scholar] [CrossRef]
- Pandey, U.; Basu, D. Effect of Groundwater Flow on Thermal Performance of SBTES Systems. J. Energy Storage 2023, 74, 109375. [Google Scholar] [CrossRef]
- Krcmar, D.; Kovacs, T.; Molnar, M.; Hodasova, K.; Zatlakovic, M. Estimating Thermal Impact on Groundwater Systems from Heat Pump Technologies: A Simplified Method for High Flow Rates. Hydrology 2023, 10, 225. [Google Scholar] [CrossRef]
- Dong, L.; Luo, Z.; Guo, H.; Cheng, L.; Wang, X.; Zhao, Q. The Impact of Developing a Regional Multiwell Groundwater Heat Pump System on the Geological Environment: A Case Study in Haimen, China. Hydrogeol. J. 2024, 33, 257–277. [Google Scholar] [CrossRef]
- Lund, J.W. Direct Utilization of Geothermal Energy. Energies 2010, 3, 1443–1471. [Google Scholar] [CrossRef]
- Bayer, P.; Attard, G.; Blum, P.; Menberg, K. The Geothermal Potential of Cities. Renew. Sustain. Energy Rev. 2019, 106, 17–30. [Google Scholar] [CrossRef]
- Makasis, N.; Kreitmair, M.J.; Bidarmaghz, A.; Farr, G.J.; Scheidegger, J.M.; Choudhary, R. Impact of Simplifications on Numerical Modelling of the Shallow Subsurface at City-Scale and Implications for Shallow Geothermal Potential. Sci. Total Environ. 2021, 791, 148236. [Google Scholar] [CrossRef]
- Ngarambe, J.; Raj, S.; Yun, G.Y. Subsurface Urban Heat Islands: From Prevalence and Drivers to Implications for Geothermal Energy and a Proposed New Framework Based on Machine Learning. Sustain. Cities Soc. 2025, 120, 106153. [Google Scholar] [CrossRef]
- Worsa-Kozak, M.; Arsen, A. Groundwater Urban Heat Island in Wrocław, Poland. Land 2023, 12, 658. [Google Scholar] [CrossRef]
- Menberg, K.; Bayer, P.; Zosseder, K.; Rumohr, S.; Blum, P. Subsurface Urban Heat Islands in German Cities. Sci. Total Environ. 2013, 442, 123–133. [Google Scholar] [CrossRef] [PubMed]
- Hancock, P.J.; Hunt, R.J.; Boulton, A.J. Preface: Hydrogeoecology, the Interdisciplinary Study of Groundwater Dependent Ecosystems. Hydrogeol. J. 2009, 17, 1–3. [Google Scholar] [CrossRef]
- Hähnlein, S.; Bayer, P.; Ferguson, G.; Blum, P. Sustainability and Policy for the Thermal Use of Shallow Geothermal Energy. Energy Policy 2013, 59, 914–925. [Google Scholar] [CrossRef]
- Alberti, L.; Antelmi, M.; Oberto, G.; La Licata, I.; Mazzon, P. Evaluation of Fresh Groundwater Lens Volume and Its Possible Use in Nauru Island. Water 2022, 14, 3201. [Google Scholar] [CrossRef]
- Lepore, D.; Bucchignani, E.; Montesarchio, M.; Allocca, V.; Coda, S.; Cusano, D.; De Vita, P. Impact Scenarios on Groundwater Availability of Southern Italy by Joint Application of Regional Climate Models (RCMs) and Meteorological Time Series. Sci. Rep. 2024, 14, 20337. [Google Scholar] [CrossRef]
- Alberti, L.; Mazzon, P.; Colombo, L.; Cantone, M.; Antelmi, M.; Marelli, F.; Gattinoni, P. Enhancing Groundwater Resource Management in the Milan Urban Area Through a Robust Stratigraphic Framework and Numerical Modeling. Water 2025, 17, 165. [Google Scholar] [CrossRef]
- Casiraghi, G.; Pedretti, D.; Beretta, G.P.; Cavalca, L.; Varisco, S.; Masetti, M. A Multispecies Reactive Transport Model of Sequential Bioremediation and Pump-and-Treat in a Chloroethenes-Polluted Aquifer. Water. Air. Soil Pollut. 2025, 236, 54. [Google Scholar] [CrossRef]
- Pedretti, D.; Masetti, M.; Beretta, G. Pietro Stochastic Analysis of the Efficiency of Coupled Hydraulic-Physical Barriers to Contain Solute Plumes in Highly Heterogeneous Aquifers. J. Hydrol. 2017, 553, 805–815. [Google Scholar] [CrossRef]
- Antelmi, M.; Mazzon, P.; Höhener, P.; Marchesi, M.; Alberti, L. Evaluation of Mna in a Chlorinated Solvents-Contaminated Aquifer Using Reactive Transport Modeling Coupled with Isotopic Fractionation Analysis. Water 2021, 13, 2945. [Google Scholar] [CrossRef]
- Cusano, D.; Coda, S.; De Vita, P.; Fabbrocino, S.; Fusco, F.; Lepore, D.; Nicodemo, F.; Pizzolante, A.; Tufano, R.; Allocca, V. A Comparison of Methods for Assessing Groundwater Vulnerability in Karst Aquifers: The Case Study of Terminio Mt. Aquifer (Southern Italy). Sustain. Environ. Res. 2023, 33, 42. [Google Scholar] [CrossRef]
- Coda, S.; Tufano, R.; Calcaterra, D.; Colantuono, P.; De Vita, P.; Di Napoli, M.; Guerriero, L.; Allocca, V. Groundwater Flooding Hazard Assessment in a Semi-Urban Aquifer through Probability Modelling of Surrogate Data. J. Hydrol. 2023, 621, 129659. [Google Scholar] [CrossRef]
- Muffels, C.; Panday, S.; Andrews, C.; Tonkin, M.; Spiliotopoulos, A. Simulating Groundwater Interaction with a Surface Water Network Using Connected Linear Networks. Groundwater 2022, 60, 801–807. [Google Scholar] [CrossRef]
- Corti, M.; Ghirlanda, E.; Mainetti, M.; Abbate, A.; De Vita, P.; Calcaterra, D.; Papini, M.; Longoni, L. Evaluation of the Applicability of Sediment Transport Models To Dam Filling Prediction in Different Italian Geological Contexts. Ital. J. Eng. Geol. Environ. 2023, 1, 27–32. [Google Scholar] [CrossRef]
- Gatti, F.; Bonaventura, L.; Menafoglio, A.; Papini, M.; Longoni, L. A Fully Coupled Superficial Runoff and Soil Erosion Basin Scale Model with Efficient Time Stepping. Comput. Geosci. 2023, 177, 105362. [Google Scholar] [CrossRef]
- Antelmi, M.; Alberti, L.; Barbieri, S.; Panday, S. Simulation of Thermal Perturbation in Groundwater Caused by Borehole Heat Exchangers Using an Adapted CLN Package of MODFLOW-USG. J. Hydrol. 2021, 596, 126106. [Google Scholar] [CrossRef]
- Previati, A.; Epting, J.; Crosta, G.B. The Subsurface Urban Heat Island in Milan (Italy)—A Modeling Approach Covering Present and Future Thermal Effects on Groundwater Regimes. Sci. Total Environ. 2022, 810, 152119. [Google Scholar] [CrossRef]
- Tolooiyan, A.; Hemmingway, P. A Preliminary Study of the Effect of Groundwater Flow on the Thermal Front Created by Borehole Heat Exchangers. Int. J. Low-Carbon Technol. 2014, 9, 284–295. [Google Scholar] [CrossRef]
- Dehkordi, S.E.; Schincariol, R.A. Effect of Thermal-Hydrogeological and Borehole Heat Exchanger Properties on Performance and Impact of Vertical Closed-Loop Geothermal Heat Pump Systems. Hydrogeol. J. 2014, 22, 189–203. [Google Scholar] [CrossRef]
- Di Pierdomenico, M.; Taussi, M.; Galgaro, A.; Dalla Santa, G.; Maggini, M.; Renzulli, A. Shallow Geothermal Potential and Numerical Modelling of the Geo-Exchange for a Sustainable Post-Earthquake Building Reconstruction (Potenza River Valley, Marche Region, Central Italy). Geothermics 2024, 119, 102954. [Google Scholar] [CrossRef]
- Soltan Mohammadi, H.; Ringel, L.M.; de Paly, M.; Bayer, P. Sequential Long-Term Optimization of Shallow Geothermal Systems under Descriptive Uncertainty and Dynamic Variation of Heating Demand. Geothermics 2024, 121, 103021. [Google Scholar] [CrossRef]
- Panday, S. USG-Transport Version 1.5.0: The Block-Centered Transport (BCT) Process for MODFLOW-USG; GSI Environment: Irvine, CA, USA, 2020. [Google Scholar]
- Barbieri, S.; Antelmi, M.; Panday, S.; Baratto, M.; Angelotti, A.; Alberti, L. Innovative Numerical Procedure for Simulating Borehole Heat Exchangers Operation and Interpreting Thermal Response Test through MODFLOW-USG Code. J. Hydrol. 2022, 614, 128556. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, The U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process; Geological Survey Techniques and Methods 6-A16; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005. [Google Scholar]
- Regione Lombardia. Deliberazione n. XI/3502. In Bollettino Ufficiale Della Regione Lombardia; Comune di Milano: Milan, Italy, 2020; p. 44. [Google Scholar]
- Wagner, V.; Blum, P.; Kübert, M.; Bayer, P. Analytical Approach to Groundwater-Influenced Thermal Response Tests of Grouted Borehole Heat Exchangers. Geothermics 2013, 46, 22–31. [Google Scholar] [CrossRef]
- FascÌ, M.L.; Lazzarotto, A.; Acuna, J.; Claesson, J. Analysis of the Thermal Interference between Ground Source Heat Pump Systems in Dense Neighborhoods. Sci. Technol. Built Environ. 2019, 25, 1069–1080. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).