A Hybrid Deep Learning Model Based on FFT-STL Decomposition for Ocean Wave Height Prediction

Abstract

Accurate prediction of the height of ocean waves is critical to ensuring maritime safety, optimizing offshore operations, and mitigating coastal hazards. To improve the accuracy of ocean wave height prediction, we developed a hybrid model that integrates decomposition and deep learning. The approach combines Fourier transform, seasonal and trend decomposition using Loess, and various deep learning models, which can more accurately capture the periodicity, trends, and random fluctuations. The trend, seasonality, and residual components are predicted using the LSTM model, SARIMAX, and 1D-CNN, respectively. The mean square error of the model prediction was calculated to be 0.0087 and the root mean square error was 0.0935. The results show that the hybrid model outperforms the other methods compared in our experiments. This model can accurately predict ocean wave heights and provides a reference for predicting time-series data with seasonal fluctuations.

1. Introduction

Wave height is closely related to various human activities [1]. On the one hand, wave height plays a vital role in marine operations, directly affecting the safety and efficiency of ship navigation and marine operations [2,3]. Accurate prediction of wave height is essential to ensure navigation safety and optimize marine operations [4]. Therefore, in-depth research on wave height dynamics and improving forecast accuracy is of great significance to improving the safety and efficiency of marine activities. On the other hand, waves are a promising renewable energy source that helps alleviate energy shortages [5]. Reliable wave height forecasting is essential to optimize wave energy conversion and ensure the stability and efficiency of wave energy utilization. Therefore, based on the two pressing issues of protecting human activities and promoting renewable energy, the study of wave height prediction is urgent.

Over the years, various methodologies have been developed to enhance the accuracy and reliability of wave height forecasting. Traditional approaches, such as numerical wave models and hydrodynamic models, have been widely used for their ability to simulate wave dynamics based on meteorological and oceanographic data. Wei and Hu (2024) developed a numerical wave model, experimentally verified the collinear wave–current interaction, and extended it to the non-collinear scenario through theoretical verification, while studying the orthogonal interaction observation region [6]. Zhang et al. (2025) systematically verified and validated the numerical wave pool based on momentum source and quantified the numerical modeling errors under 13 sea states [7]. To investigate the hydrodynamics of the main channel, Khenifiss lagoon, Vashist and Singh (2024) integrated hydrodynamic models with existing hydrological data and utilized them as a comprehensive tool in the flood modeling process [8]. Although these models can effectively simulate complex fluid dynamics to predict ocean wave height variations, their accuracy in capturing local wave behavior is often limited by the quality of input data and computational limitations.

To overcome the limitations of traditional numerical wave models, which depend on high-quality input data, researchers have increasingly adopted data-driven approaches for wave height prediction. In particular, autoregressive models, neural networks, and ensemble learning methods have emerged as prominent techniques in this field.

Autoregressive (AR) models, which employ linear combinations of historical observations to predict future values, have served as fundamental tools in wave height forecasting due to their mathematical transparency and computational efficiency [9,10]. Many scholars have applied the SARIMA model to make long-term predictions of significant wave height and achieved good prediction performance [11,12]. However, these methods are fundamentally affected by the strict assumption of stationarity and linear parameterization, which in turn limits their ability to effectively capture the nonlinear dynamics and nonstationary properties inherent in complex ocean processes.

Neural networks have the ability to learn and extract complex patterns from large amounts of data. Through training, neural networks can identify the inherent laws and associations in data, provide model-free solutions for data prediction, and improve tolerance to data errors [13]. This understanding has promoted the application and development of neural networks, among which recurrent neural networks (RNNs) are similar to autoregressive (AR) models in time-series modeling in terms of recursive characteristics, but have stronger nonlinear expression capabilities. Many scholars have used RNN models to predict changes in ocean wave height. Studies have found that wave prediction using RNNs produces better results than previous neural network methods [14]. However, the practical effectiveness of RNNs is constrained by gradient pathology issues during backpropagation through time, which manifests itself as vanishing gradients suppressing long-range memory or explosion gradients destabilizing training [15]. These critical limitations were systematically addressed by long short-term memory (LSTM) networks through innovative gated cell architectures, which explicitly regulate information flow via forget/input/output gates to preserve multi-scale temporal dependencies essential for wave evolution modeling. da Silva et al. (2025) predicted wave height by establishing an LSTM model [16]. Hu et al. (2021) applied an LSTM-based hybrid model to predict wave height and period under near-ideal wave growth conditions in Lake Erie [17]. In ocean data modeling, the traditional unidirectional long short-term memory network can capture the lagged effects of historical wave heights, but has limitations in explaining the delayed effects of future meteorological changes on current wave conditions [18]. To overcome this limitation, this study uses the BiLSTM model for trend component forecasting, which can capture the forward and backward temporal dependencies in the time series.

In order to improve the accuracy of the calculation, two independent LSTMs are combined. One model processes the sequence forwards in chronological order, and the other model processes the sequence in reverse chronological order to form a new model BiLSTM. Wu et al. (2024) [19] proposed an innovative ocean wave height prediction model, RIME-CNN-BiLSTM. The model combines the RIME algorithm, CNN and BiLSTM. Compared with traditional models, the model can more accurately grasp the complex nonlinear characteristics between these factors and wave height, and it shows stronger generalization performance in different sea areas. Nawin Raj and Reema Prakash (2024) used a bidirectional long short-term memory network to process forward and reverse time-series data, in order to more comprehensively extract the temporal dynamic characteristics of wave height [20]. This bidirectional architecture breaks through the limitation that the traditional unidirectional long short-term memory model can only capture the temporal dependency in a single direction, thus helping to more accurately understand the change of wave height over time.

Although traditional methods for the prediction of wave height have achieved certain results, recent research has achieved significant breakthroughs in model accuracy and applicability by adopting innovative technical means. Numerous studies have shown that hybrid modeling methods that incorporate prior knowledge, such as fluid dynamics equations, into a machine learning framework exhibit powerful wave height prediction capabilities [21,22]. However, due to the inherent multi-scale characteristics of complex ocean systems, these models still face significant limitations in capturing high-frequency fluctuations and long-range temporal dependencies.

In addition, some other methods, such as the design of new neural network architecture, feature enhancement technology based on integrated signal processing and so on. Some scholars have proposed a new deep learning model. This model uses the variable importance measure of random forests and the ability of graph neural networks to extract long-term temporal features to construct an adaptive weight matrix to capture potential spatial dependencies and long-term temporal patterns in input data [23]. Tan et al. (2023) applied empirical mode decomposition to wave signals and merged the resulting intrinsic mode functions into the original dataset, using a feature extraction module combined with a self-attention network to improve the prediction of significant wave height [24]. However, the prediction performance of this model on small-scale datasets may not be well generalized to large-scale scenarios. Its scalability and effectiveness in capturing complex spatiotemporal dependencies under large-scale data conditions still need to be verified.

Most existing methods, both traditional and data-driven, rely heavily on external variables such as meteorological and oceanographic data. When these data are incomplete, as is often the case at some measurement-constrained stations, the accuracy of wave height predictions is severely affected.

This study addresses the limitations of existing wave height prediction methods by effectively capturing the seasonal characteristics of wave height data. The model can independently learn the underlying patterns of wave height data without the need for external variables, thus reducing the risk of forecast bias due to missing information. Its ability to capture seasonal characteristics improves forecast performance, especially when ocean observations are sparse or limited. The hybrid model integrates seasonal–trend decomposition using Loess (STL) with component-specific prediction submodels. The proposed method leverages STL decomposition to partition the wave height time series into seasonal, trend, and remainder components, enabling targeted predictions for each. The Seasonal Autoregressive Integrated Moving Average (SARIMAX) model is used for the prediction of the seasonal component, a bidirectional long short-term memory (BiLSTM) model for trend prediction, and a one-dimensional convolutional neural network (1D-CNN) model to capture the remainder.

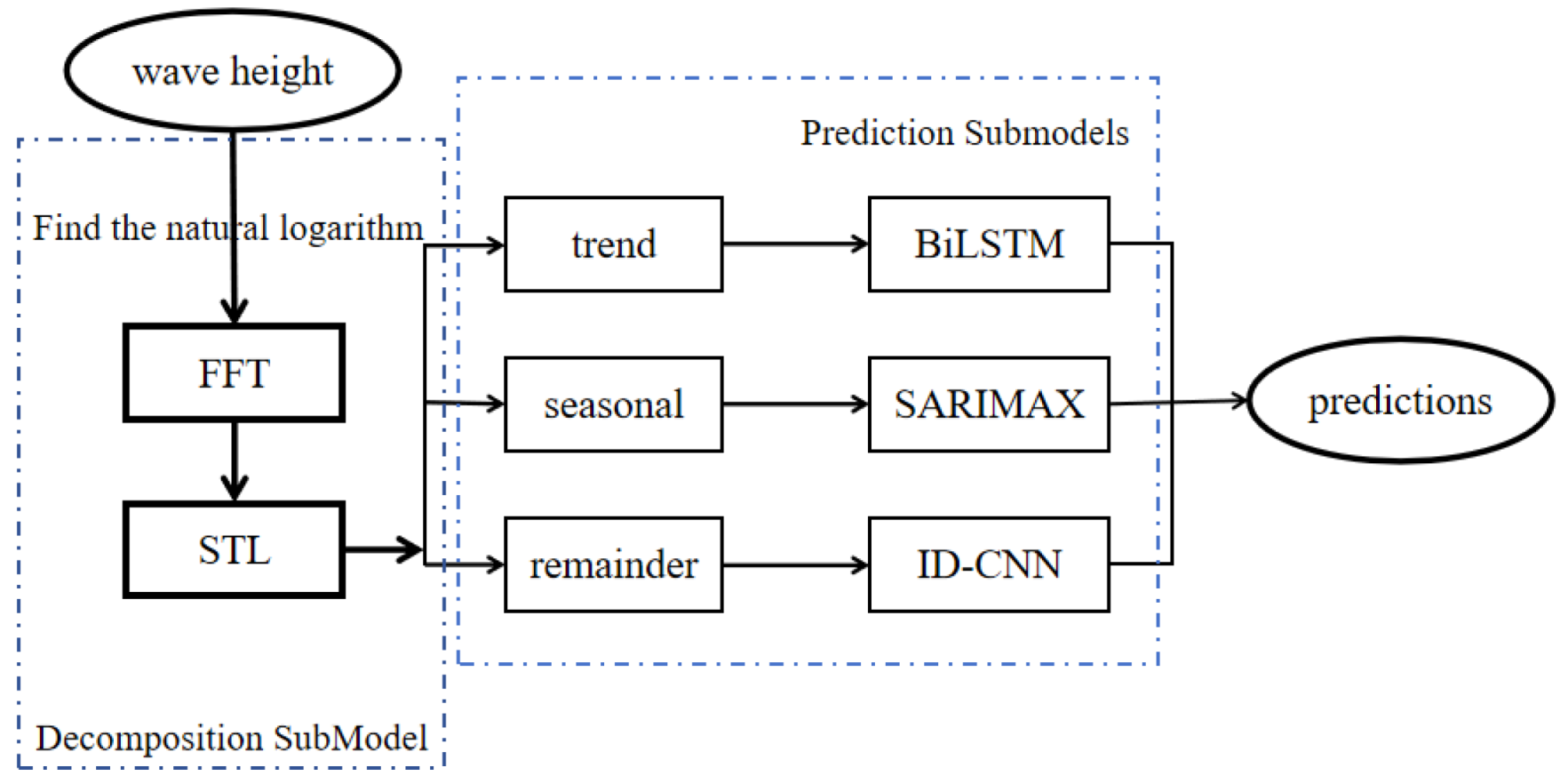
2. Model Design

Due to the inherent complexity and variability of the physical mechanisms involved in wave generation, propagation, and interaction, traditional physical models often struggle to accurately capture the highly uncertain and dynamic nature of these environments. Consequently, identifying efficient methods to model and represent these complex relationships has emerged as a significant challenge in the field. To overcome this challenge, this study introduced a multimodal hybrid model that used deep learning techniques. This model was able to effectively capture the characteristics of the underlying data and provide accurate wave height predictions by separately modeling the seasonality, trend, and remainder components of the data. The general design of the model and the comprehensive analysis of its components are described and discussed below.

The model adopts multilevel data decomposition and multi-model fusion methods to make class-specific predictions based on the seasonality, trend, and remainder components of wave data. According to the classification results, the most appropriate model is selected for each type of feature data for prediction. The BiLSTM model can effectively capture long-term dependencies and nonlinear trends, and has strong noise resistance, making it very suitable for trend prediction. The SARIMAX model can capture well the periodicity of the remaining data and is very suitable for the prediction of seasonal data. The 1D-CNN model can effectively identify multidimensional anomalies in the remainder, providing strong support for the prediction of the remainder. As shown in Figure 1, the process includes multiple steps such as data division, model selection, and application.

2.1. Decomposition Submodel

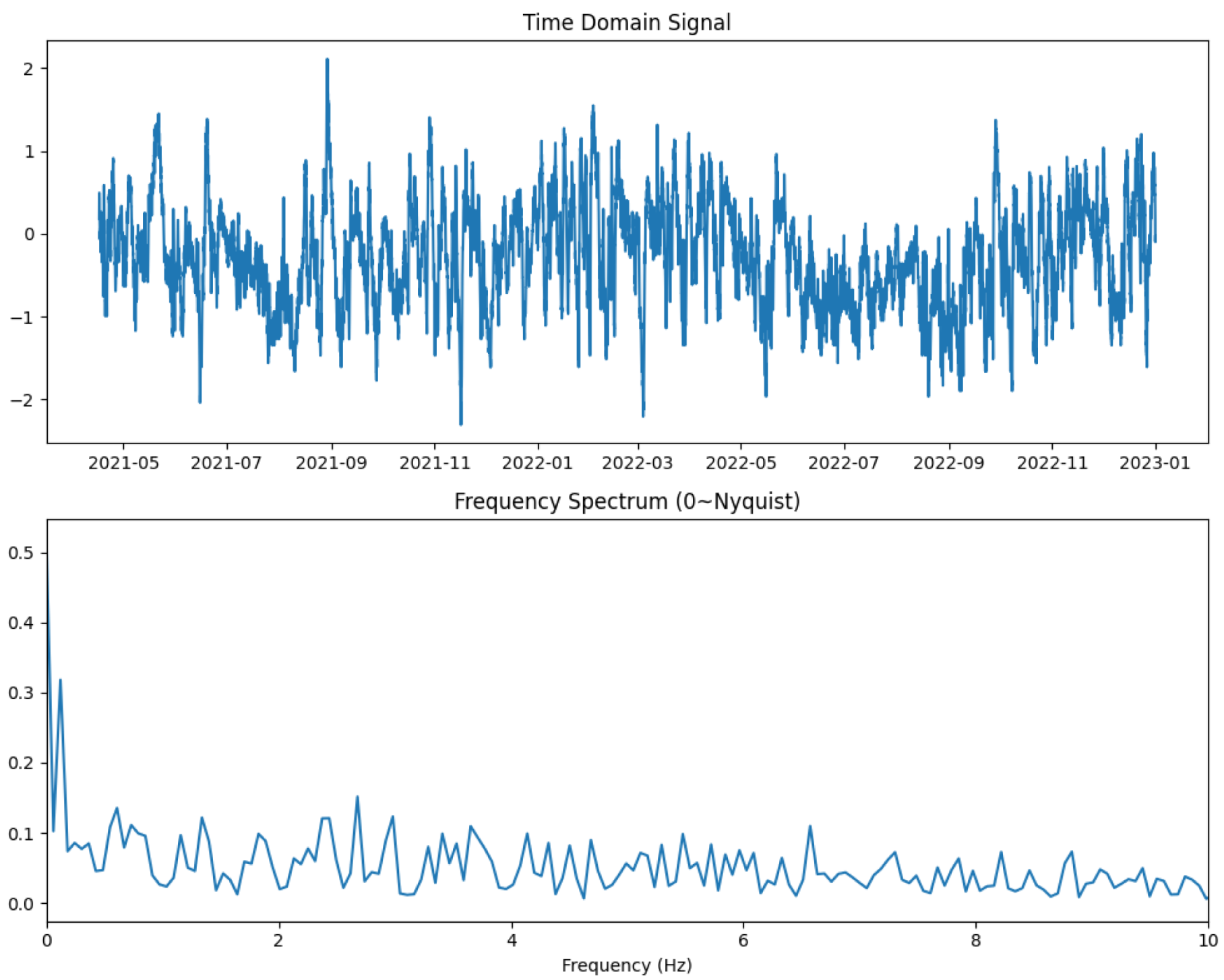
2.1.1. Fast Fourier Transform for Dominant Frequency Extraction

Before decomposing the wave height data, accurately extracting the dominant frequency of the signal is crucial to identify and analyze the periodic characteristics of the fluctuations, thus providing an important basis for subsequent signal modeling and trend prediction. Fast Fourier Transform (FFT) is a widely used and effective tool in spectrum analysis, which converts a time-domain signal into a frequency-domain representation [25]. It effectively decomposes the frequency components of a signal, revealing the dominant frequency and other key frequency characteristics. This can effectively distinguish periodic fluctuations from random noise and enhance the extraction of fluctuation patterns.

The raw wave height time series were subjected to Fourier transform analysis to extract T and dominant frequency components. For a discrete time series, $x\left(n\right)$ (with n = 0, 1, …, $N-1$) is defined by

$$X\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j{\displaystyle \frac{2\pi }{N}}kn},k=0,1,\dots ,N-1$$

(1)

Once the Fourier coefficients $X\left(k\right)$ are calculated, we can obtain the power spectral density ($PSD$) by taking the square of these coefficients:

$$PSD\left(k\right)={\left|X\left(k\right)\right|}^2$$

(2)

Through power spectral density analysis, a quantitative framework is obtained to characterize the frequency-domain energy distribution of the wave height time series, thereby identifying the main periodicities governing the oscillatory behavior of the signal.

By systematically sorting the values $PSD$, the most prominent frequency components are identified as dominant frequencies, corresponding to the highest energy contribution within the spectrum. The inverse of the dominant frequency defines the characteristic periodicity, which is then used to dynamically parameterize the seasonal window in the seasonal and trend decomposition using STL.

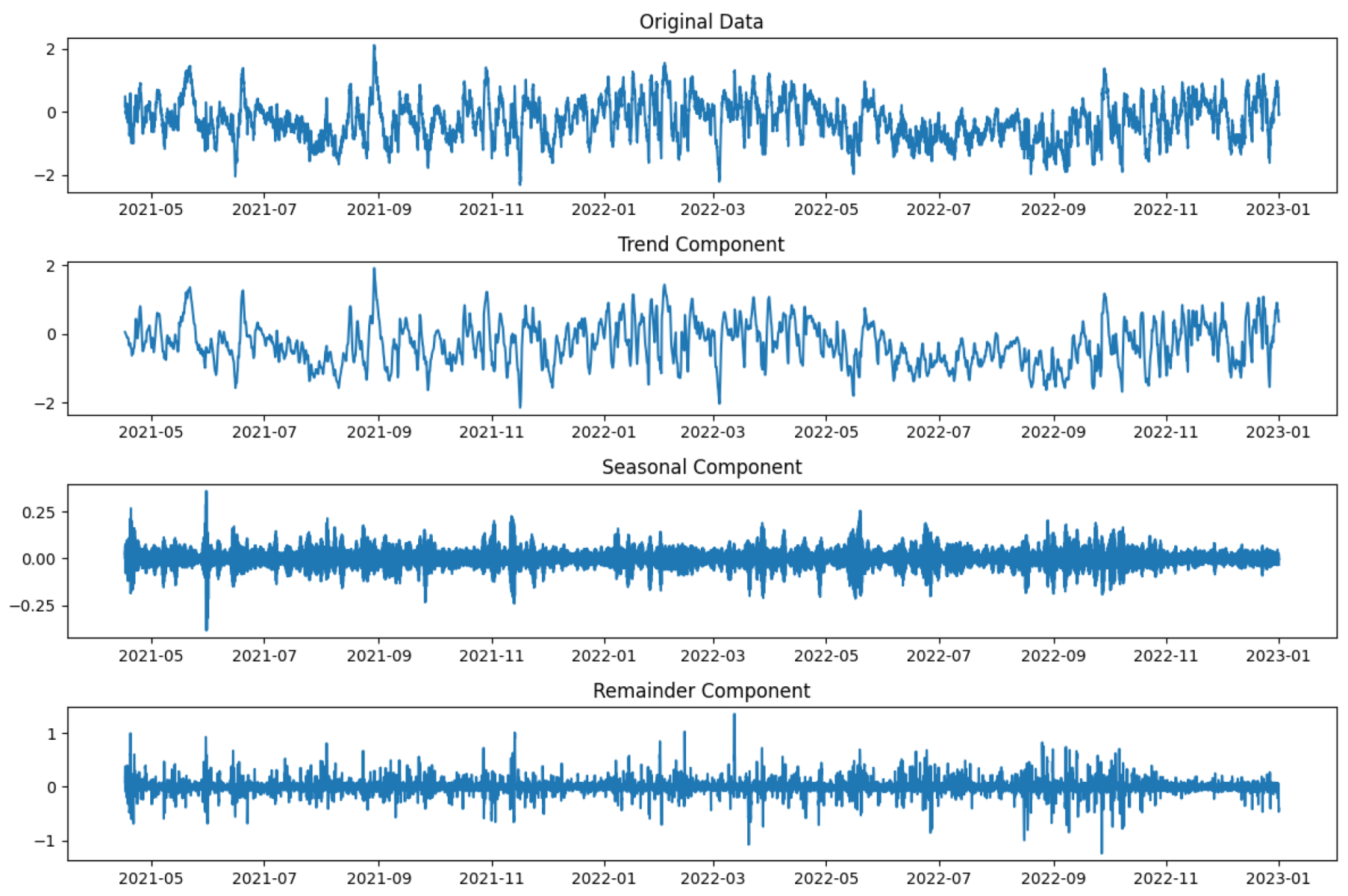
2.1.2. STL for Decomposition

Traditional time-series decomposition methods usually assume that seasonality and trend are static. However, in real data, both seasonality and trend may change dynamically, so more flexible and adaptive methods are needed. The STL method, as a nonparametric technique, can dynamically decompose the time-series signal, so that the trend and seasonal components can be flexibly extracted without relying on a fixed seasonal window [26,27]. Therefore, the STL method can be used to analyze wave height data for decomposition.

For a given wave height time series $X\left(t\right)$, it can be expressed as

$$X\left(t\right)=T\left(t\right)S\left(t\right)R\left(t\right)$$

(3)

$T\left(t\right)$ represents the trend component, reflecting the long-term changes of the time series; $S\left(t\right)$ represents the seasonal component, describing periodic fluctuations; $R\left(t\right)$ represents the remainder component, including irregular changes and noise. For the convenience of decomposition, we take the natural logarithm of both sides of the equation and convert the multiplication relationship into an additive form:

$$lnX\left(t\right)=lnT\left(t\right)+lnS\left(t\right)+lnR\left(t\right)$$

(4)

In this way, the trend, seasonality, and remainder parts of the wave height data can be decomposed by the STL method to improve the stability and interpretability of the decomposition. The algorithmic implementation of STL decomposition is structured as (Algorithm 1):

Algorithm 1: Optimized STL decomposition algorithm.

2.2. Component-Specific Prediction Submodels

The component-specific prediction submodels are classified as follows: the BiLSTM model for trend component prediction, the SARIMAX model for seasonal component prediction, and the 1D-CNN model for remainder component prediction. A detailed explanation of each model is provided below.

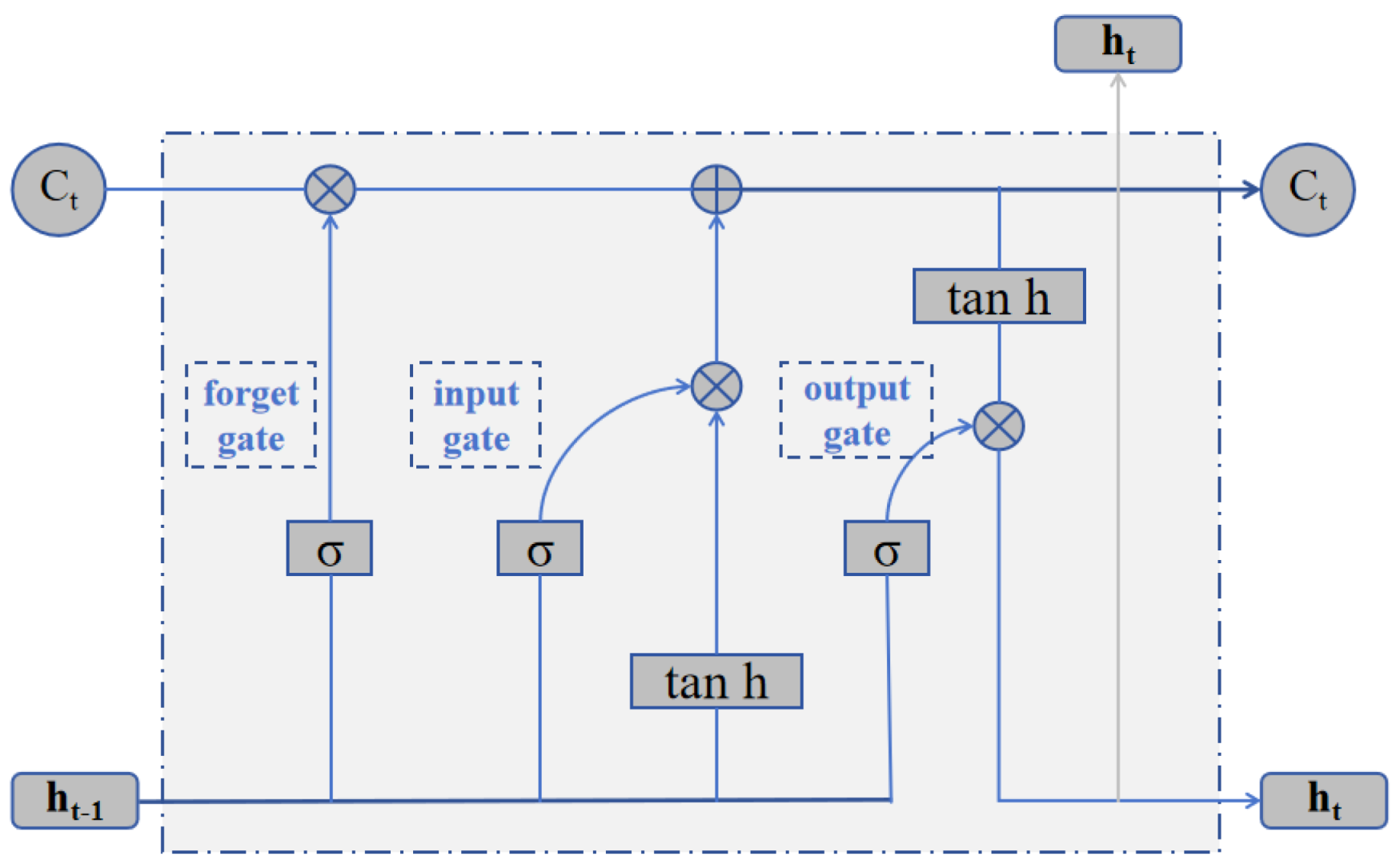
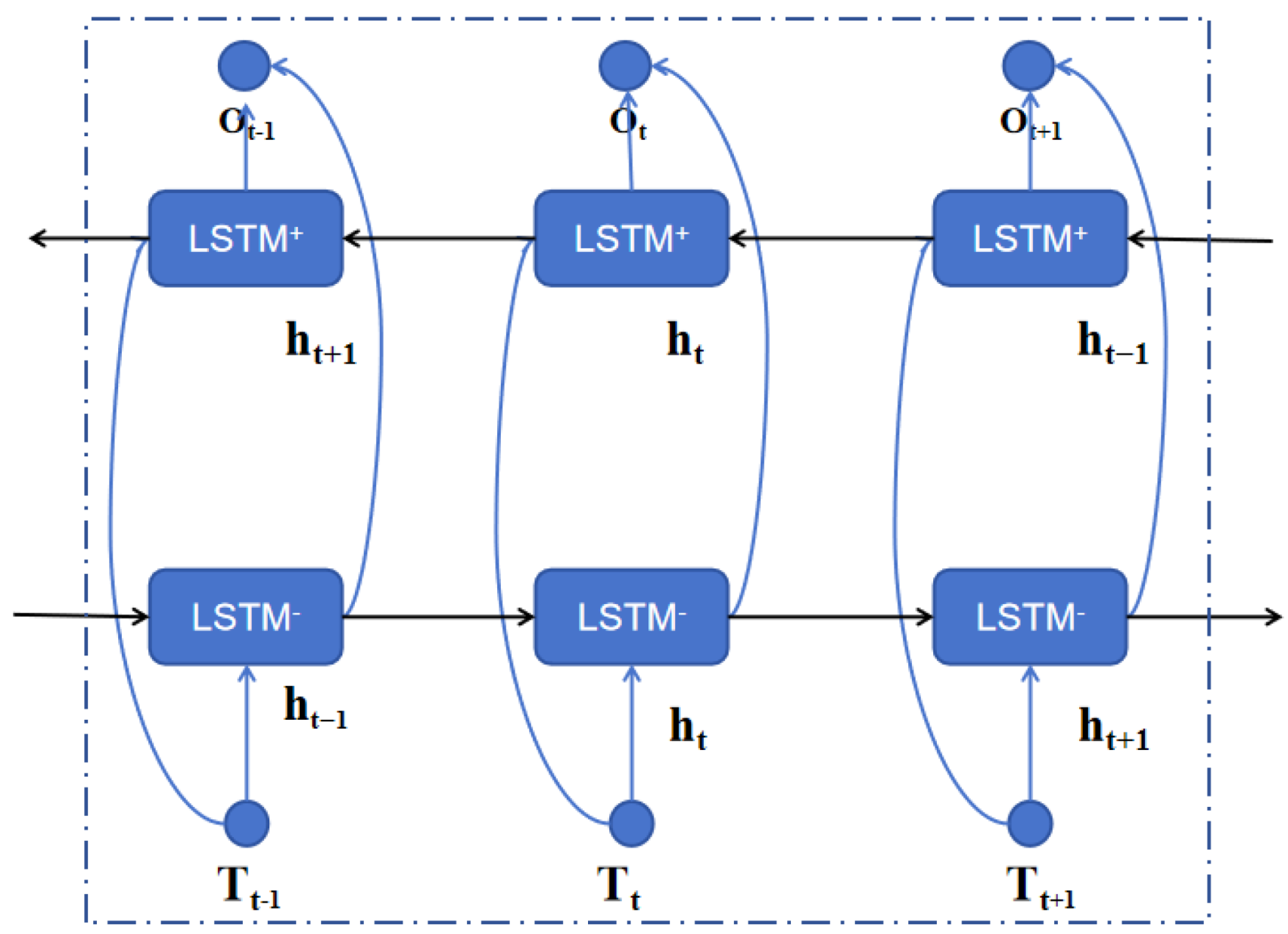
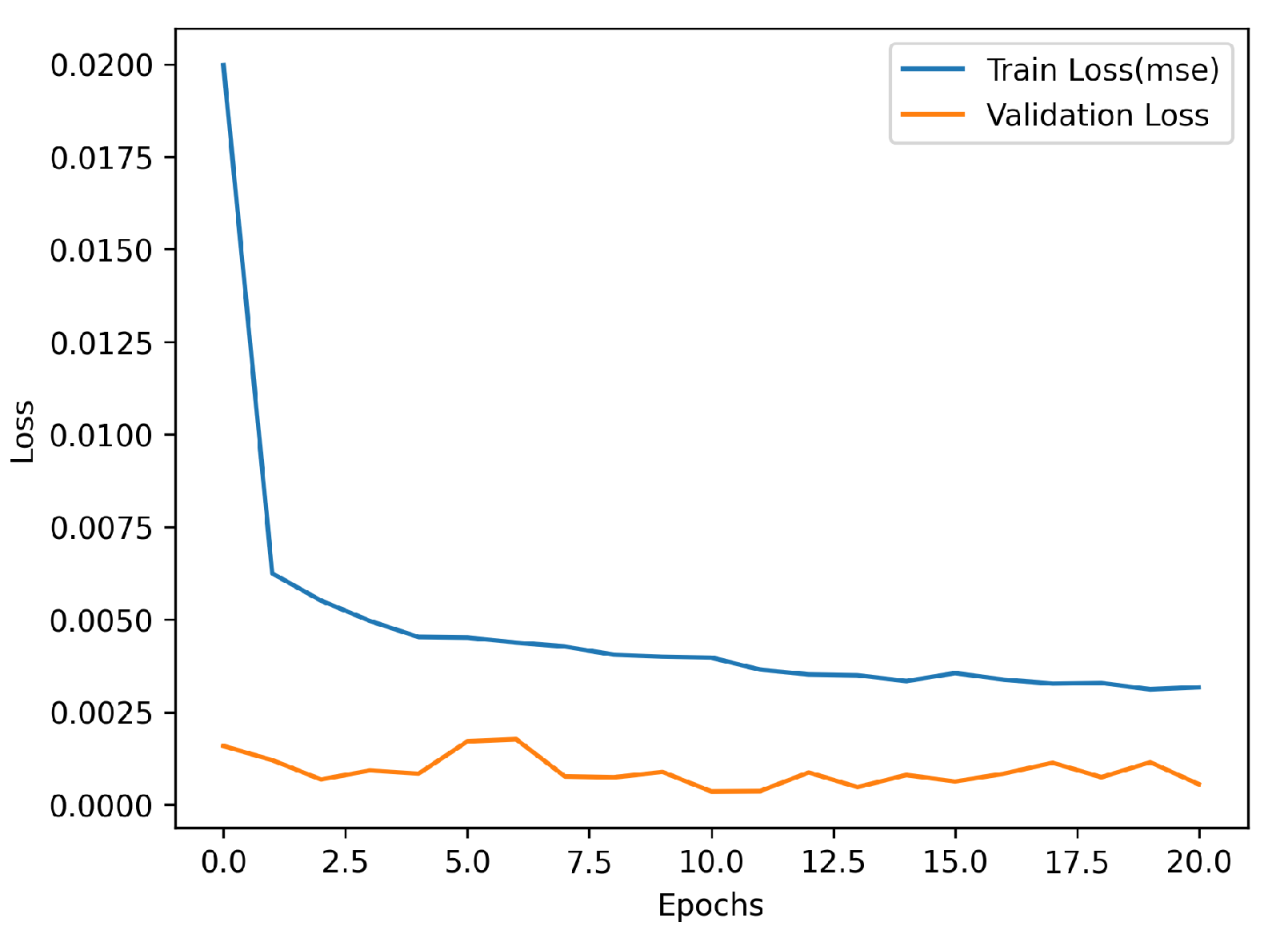
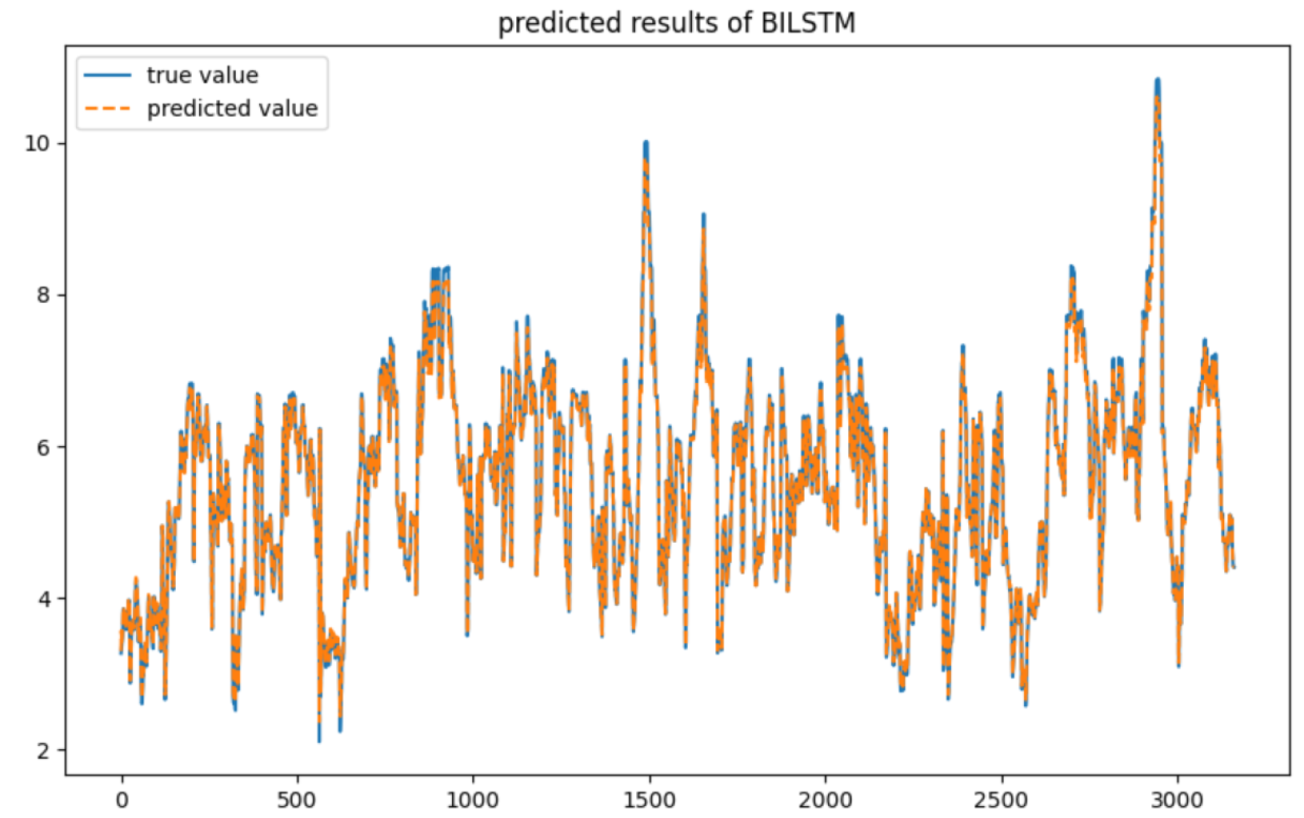
2.2.1. BiLSTM Model for Trend Component Prediction

In trend probability prediction, trend components often exhibit complex and long-term evolutionary characteristics. Traditional methods, such as moving average, linear regression, and ARIMA, have limitations in capturing nonlinearity and high-order dependencies, making it challenging to accurately model trend variations. These limitations become particularly evident in long-term predictions, where error accumulation is a common issue. In contrast, BiLSTM model excels at capturing long-term temporal dependencies in nonstationary signals and effectively predicting changes in wave height trend components, offering a more robust solution to the challenges of trend probability prediction. The BiLSTM model has strong learning ability, which stems from its unique data processing method. It evaluates data in both forward and backward directions by training two LSTM networks, one of which processes the input sequence forward and the other processes the reverse copy of the input in reverse. This bidirectional processing mechanism enables BiLSTM to capture data features more comprehensively, greatly improving the performance and prediction accuracy of the model [28].

LSTM is a special type of recurrent neural network that consists mainly of an input gate, a forget gate, an output gate, and a memory unit. Its mathematical expression is as follows:

$$\begin{array}{cc}\hfill i_t& =\sigma (W_i[h_{t-1},T_t]+b_i)\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill f_t& =\sigma (W_f[h_{t-1},T_t]+b_f)\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill o_t& =\sigma (W_o[h_{t-1},T_t]+b_o)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\tilde{C}}_t& =tanh(W_c·[h_{t-1},T_t]+b_c)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill C_t& =f_t·C_{t-1}+i_t·{\tilde{C}}_t\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill h_t& =O_t·tanh·C_t\hfill \end{array}$$

(10)

Here, $i_t$ represents the input gate, $f_t$ represents the forget gate, and $o_t$ represents the output gate. $C_t$ and $C_{t-1}$ denote the cell state at the current and previous time steps, respectively. W refers to the weight matrix assigned to each layer, $T_t$ is the input at the current time step, and b represents the bias term. $\sigma$ denotes the sigmoid activation function, while · represents the Hadamard product.

The internal mechanism of the LSTM regulates the flow of information through these gates. The input gate regulates the extent to which the current input information is stored in the memory unit. The forget gate controls the degree to which past information is discarded from the memory unit, preventing the model from losing long-term dependencies. The output gate determines the information to be emitted based on both the memory unit’s content and the current input. The memory unit, which can retain and update information over extended periods, effectively captures long-term dependencies within input sequences. The specific structure of the internal hidden layer is shown in Figure 2.

The BiLSTM neural network model can be regarded as a composite of two LSTM networks that process data in opposite directions. Its structure is shown in Figure 3.

Given the wave height data decomposition trend sequence, it is expressed as

$${T\left(t\right)}_{t=1}^N$$

(11)

The forward LSTM layer computes a series of hidden states $\overrightarrow{h_t}$ by iterating from $t=1$ to $t=N$. Meanwhile, the backward LSTM layer processes the sequence in reverse, producing the hidden state $\overleftarrow{h_t}ht$ by iterating from $t=N$ downward to $t=1$. The outputs from these two layers are then combined by concatenation to form a comprehensive latent representation:

$$H_t={[\overleftarrow{h_t},\overrightarrow{h_t}]}^T$$

(12)

2.2.2. SARIMAX for Seasonality Component Prediction

In order to accurately capture the characteristics of seasonal components, the SARIMAX model is used to effectively model and predict seasonal data components with periodic patterns [29].

$$\phi \left(B\right)\varphi \left(B^S\right){(1-B)}^d{(1-B^S)}^{D}S\left(t\right)=\theta \left(B\right)\mathsf{\Theta }\left(B^S\right){\epsilon }_t+c$$

(13)

${(1-B)}^d$ and ${(1-B^S)}^D$ denote the non-seasonal and seasonal differencing operations, respectively, to remove the trend and seasonal effects. B denotes the backshift operator, while $S\left(t\right)$ corresponds to the seasonal component of the data. $\phi \left(B\right)$ and $\theta \left(B\right)$ are the polynomials of the non-seasonal autoregressive (AR) and moving average (MA) components, respectively. $\varphi \left(B^S\right)$ and $\mathsf{\Theta }\left(B^S\right)$ denote the seasonal autoregressive and seasonal moving average polynomials, where S denotes the seasonal period. ${\epsilon }_t$ is a term of white noise to account for random errors, and c is a constant term to capture the effects of exogenous variables on seasonal data.

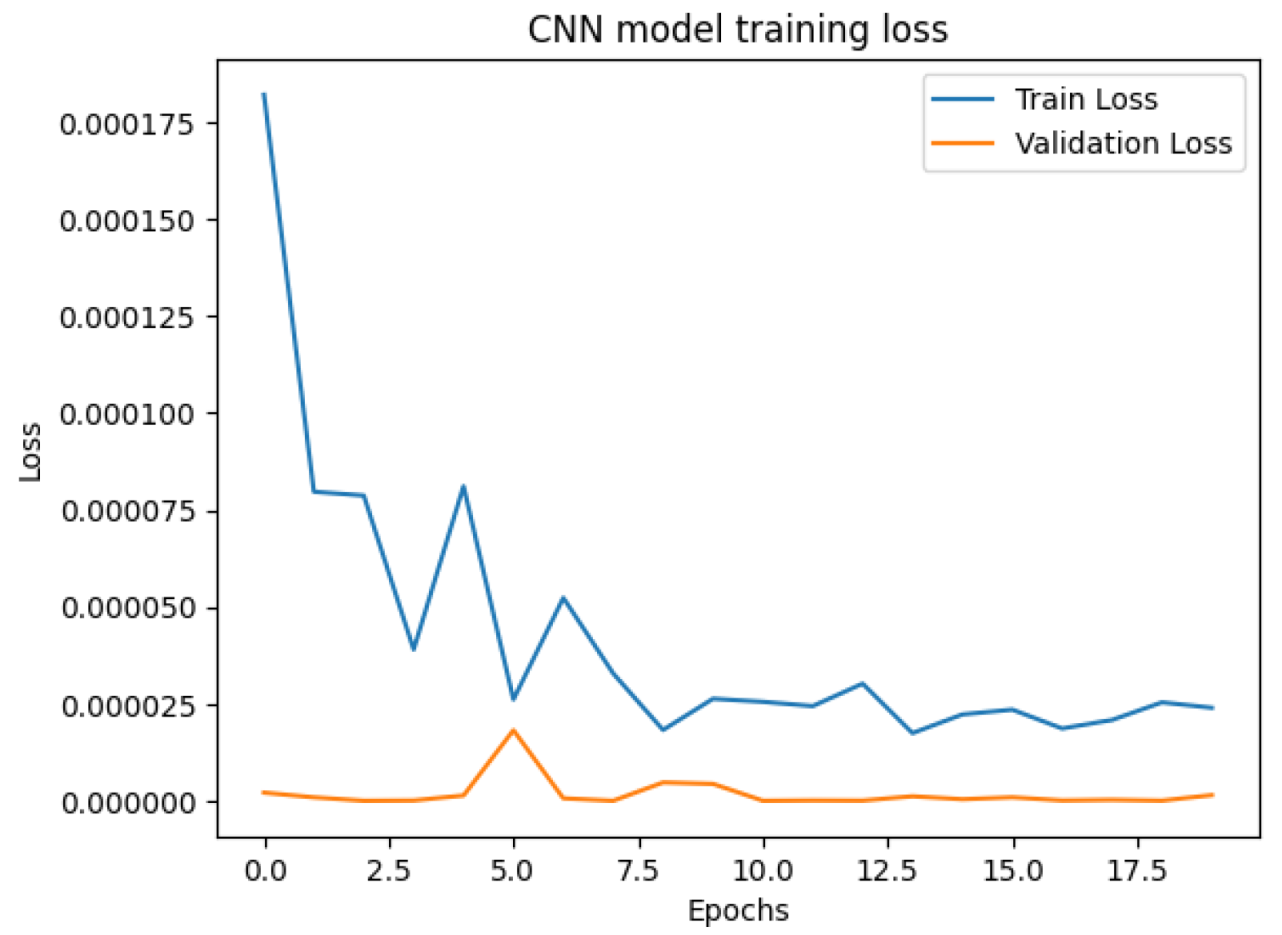
2.2.3. 1D-CNN for Remainder Component Prediction

The remainder part contains information that traditional models cannot capture in the original dataset. Effectively modeling and predicting this part can significantly improve the accuracy of the overall prediction. The one-dimensional convolutional neural network is a powerful deep learning model that excels at processing time-series data. This section explains in detail the principle of using the 1D-CNN model for remainder prediction.

1D-CNN mainly consists of convolution layers, pooling layers and fully connected layers. The convolution layer is the core part of the 1D-CNN model. Through the convolution operation, local features can be automatically extracted from the remainder. Different convolution kernels can learn various types of features, such as trend patterns, periodic features, etc. By using multiple convolution kernels in parallel, the convolution layer can effectively capture diverse feature representations, thereby enhancing the model’s ability to represent complex residual patterns. The pooling layer is usually placed after the convolutional layer and is responsible for downsampling the output of the convolution operation. This process reduces the dimension of the data and computational complexity, while enhancing the robustness of the model. In addition, the pooling layer provides a certain invariance to small changes in the input, thereby improving the generalization ability of the model. The function of the fully connected layer is to integrate the features extracted by the previous convolution layer and pooling layer. Each neuron in this layer is fully connected to all neurons in the previous layer, thus achieving a comprehensive aggregation of feature. After a series of convolution and pooling operations, the output of the fully connected layer is used for the remainder prediction.

3. Experimental Results and Analysis

To verify the effectiveness of the multi-model decomposition deep learning hybrid model, experiments were performed using ocean hydrological data, and its effectiveness and prediction accuracy were evaluated using different indicators.

3.1. Datasets

The dataset used in this study comes from the National Data Buoy Center and consists of observations recorded at Station 42040 (LLNR 245)—LUKE OFFSHORE TEST PLATFORM, located 63 nautical miles south of Dauphin Island, Alabama (29.207° N, 88.237° W). This particular station was chosen because it has well-documented instrumentation that provides high-resolution measurements of ocean dynamics under pressure. The key variables extracted from the dataset are the significant wave height (column 9: the 9th column of the data is the wave height data measured at this station).

In this study, 16,427 wave height observation data points were converted into natural logarithms to construct a logarithmic wave height dataset. The distribution of wave height data is shown in Figure 4.

The data distribution span is calculated by the difference between the maximum value of 2.1126 and the minimum value of −2.3026, which is as high as 4.415 logarithmic units, which directly shows the breadth of the data value range. From the perspective of central tendency, the mean is −0.2608, slightly higher than the median of −0.2744, which initially suggests that the data distribution has a right-skewed tendency. Dispersion is a key indicator for assessing data stability. The standard deviation was calculated to be 0.6288, reflecting the degree to which the data points deviate from the mean. In addition, the interquartile range (IQR) was derived from the first quartile ($Q1=-0.7340$) and the third quartile (Q3 = 0.1906), which was 0.9246. Compared with the theoretical IQR under the normal distribution, the observed IQR is significantly larger. This significant deviation indicates a higher dispersion and suggests that the data distribution has a fat tail phenomenon, that is, the probability of extreme values appearing is greater than that of the normal distribution.

3.2. Evaluation Metrics

To assess model performance, various quantitative evaluation metrics are used. The mean absolute error (MAE) and root mean square error (RMSE) quantify the average magnitude of the prediction error in the same units as the target variable, intuitively measuring the deviation between the predicted value and the actual value. The coefficient of determination $R^2$ represents the proportion of the variance of the observed data explained by the model, reflecting the goodness of fit of the model.

The $R^2$ is $0\sim 1$. The closer it is to 1, the stronger its explanatory capacity. In the prediction of wave height, $R^2$ is used to evaluate the degree to which the model captures the actual changes in wave height, reflecting the degree of fit and prediction accuracy of the model. The mean absolute percentage error (MAPE) measures the relative error between the predicted value and the actual value. The lower the MAPE value, the smaller the difference between the predicted value and the observed value. The specific calculation formula is as follows:

$$MAPE={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|\begin{array}{c}{\displaystyle \frac{\widehat{x_i}-x_i}{x_i}}\end{array}\right|$$

(14)

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^N{(x_i-\widehat{x_i})}^2}{{\sum }_{i=1}^N{(x_i-\overline{x_i})}^2}}$$

(15)

where $x_t$ refers to the true value (actual observation) at time t. $\widehat{x_t}$ is the value predicted at time t. $\overline{x}$ refers to the mean of the true values.

3.3. Data Preprocessing

In the data preprocessing and cleaning stage, the first step is to integrate the original wave height records collected in different years to build a unified and comprehensive dataset. In the process of processing the wave height data, invalid or abnormal records with a wave height equal to 99 are strictly identified and eliminated to ensure the reliability and consistency of the data and lay a solid foundation for subsequent analysis.

The first four columns of the data are the measurement times that correspond to the data. For the data in the first four columns (the four columns of the dataset represent the specific timestamps associated with each corresponding observation), each data point is assigned an accurate timestamp to accurately index. To solve the inevitable missing value problem, we use linear interpolation to fill in the gaps to maintain the continuity of the time series.

Given that the original wave height data presents a skewed distribution, which may affect the effectiveness of subsequent decomposition and modeling, we perform a natural logarithmic transformation on the processed values. This transformation effectively reduces the skewed distribution, making the distribution more symmetric and more conducive to statistical analysis. In addition, in order to reduce the impact of high-frequency noise and improve signal clarity, we also use a smoothing filter. As shown in Figure 5, the original wave height data shows violent fluctuations, and high-frequency peaks and troughs appear frequently, indicating that there may be noise or transient disturbances. After filtering, the amplitude of these fluctuations is significantly reduced, the high-frequency components are attenuated, and the overall trend of the data is smoother and easier to interpret. This improvement helps to decompose more accurately and efficiently in the subsequent modeling steps.

3.4. Data Analysis and Modeling

Observational data for 2021 and 2022 were selected as a training dataset. Initially, a Fast Fourier Transform (FFT) was applied to the raw time series to extract both the underlying time-domain signal and its corresponding frequency spectrum. The FFT analysis revealed a dominant frequency of approximately 0.12175 Hz, as shown in Figure 6. Given the inverse relationship between frequency and period, this dominant frequency corresponds to a fundamental cycle of approximately 8 days, a value that is both reasonable and physically meaningful for subsequent analysis.

Based on the derived period, the STL model was refined by setting the seasonal window parameter to reflect an 8-day cycle specifically, as shown in Figure 7. This adjustment enabled the significant wave height time series to be decomposed into three distinct components: a long-term trend capturing the underlying wave behavior over extended periods, seasonal fluctuations representing the recurring periodic patterns, and the remainder embodying the irregular or noise-like variations.

To further verify the effectiveness of STL decomposition, the Dickey–Fuller enhanced test was performed on the remaining component $R\left(t\right)$, and the p-value obtained by the test was 0.00, which was significantly lower than the conventional significance level. Based on this, the null hypothesis that the remaining sequence contains a unit root was rejected, and it was clearly confirmed that the remainder is stationary. The stationarity of the residual is a key indicator in STL decomposition. This feature shows that STL decomposition successfully separates the system trend component and the seasonal component, and the final residual contains only random component noise, which strongly proves the effectiveness of STL decomposition in this data processing.

To model the decomposed trend component, we use a bidirectional long short-term memory network. The network contains 132,737 trainable parameters, corresponding to a memory footprint of about 518.5 KB. We use a two-layer bidirectional architecture to enhance the extraction of temporal features by capturing forward and backward dependencies in the sequence. The first BiLSTM layer consists of 128 units (64 units in each direction) with a total of 33,792 parameters, designed to capture local temporal patterns within a 24-step input window. The second BiLSTM layer is a fully connected structure with 128 units, resulting in a total of 98,816 parameters. This layer performs spatiotemporal feature compression, thereby achieving a high-level abstraction from sequence input to latent representation. The output layer uses a fully connected neuron to generate the final prediction. To mitigate overfitting and enhance generalization, we use a two-layer dropout regularization scheme with a dropout rate of 0.1. The resulting network maintains a sparse connectivity rate of about 0.3%. The bidirectional design of the BiLSTM network helps to comprehensively model both past and future temporal dependencies, thus enhancing its ability to capture the long-term patterns inherent in the trend component of the wave height time series.

Before building the model, the dataset was reasonably divided. All observations were divided into training subsets and test subsets at a ratio of 80% and 20%, respectively. Among them, the training subset is used for model calibration, and the model performs parameter learning and optimization on this part of the data, while the test subset is reserved and is specifically used to evaluate the performance of the model on unknown data to ensure that the generalization ability of the model is effectively tested. The model training process lasts for 100 training cycles. In the initial stage (0 to 5 iterations), the training loss reflected by the mean square error (MSE) shows a rapid downward trend, rapidly decreasing from approximately 0.035 to approximately 0.010. At this stage, the model quickly learns the main features of the data. As training progresses, the training loss continues to decrease at a relatively slow rate and eventually stabilizes at about 0.005. This shows that the model constantly optimizes the parameters and gradually converges to a relatively stable state, as shown in Figure 8. From the trend of changes in training loss and validation loss, both are on a downward trend throughout the training process. This phenomenon intuitively shows that the model is effectively learning the characteristics of the data. It should be noted that the validation loss is lower than the training loss in most iterations. This result strongly shows that the model shows good performance in the validation set, there is no obvious overfitting problem, and it has strong generalization ability.

During model training, the loss curves in Figure 8 show a special pattern. For most of the training time, the validation set loss is always lower than the training set loss. This phenomenon is due to the use of dropout, a regularization technique used to alleviate overfitting. Dropout encourages the model to learn more generalizable features by randomly deactivating some neurons during training. As a result, the model may perform better on the validation set, resulting in a lower loss in the validation set than loss in the training set. The training results are shown in the Figure 9.

In this study, the SARIMAX model is used to predict the seasonal component of the decomposed significant wave height data. The model is based on 16,427 observation samples and is targeted at seasonal difference series. The parameter estimation results show that the non-seasonal autoregressive coefficient is −0.3845 and the non-seasonal moving average coefficient is −0.9578; the seasonal autoregressive coefficient and moving average coefficient are 0.2010 and 0.5145, respectively. The variance of the disturbance term is estimated to be ${\sigma }^2$ = 0.0002. All parameter estimates are statistically significant at the 0.1% level.

The model evaluation indicators show that the model has a high goodness of fit, with a log-likelihood value of 47,580.405, and information criterion values of AIC = −95,150.81, BIC = −95,112.28, and HQIC = −95,138.08, indicating that the model has a high degree of fit. The residual diagnostics rejected the null hypothesis of residual independence at the 5% significance level, indicating the presence of autocorrelation. The Jarque–Bera test statistic reaches 965,897.14 (p < 0.001), the skewness is −0.13, and the kurtosis is 40.58, indicating that the residuals have obvious characteristic of a peak and a thick tail. The heteroskedasticity White test yields a p-value < 0.001 and the heteroskedasticity coefficient H = 0.87, indicating the existence of conditional heteroskedasticity.

In order to further improve the impact of residual autocorrelation, the weighted least squares method is used to assign lower weights to observations with larger residual variances, thereby improving the robustness of parameter estimation. The SARIMAX model effectively captures the seasonal pattern and short-term dynamics of the wave height series.

For the remainder, we used an improved deep convolutional neural network model to predict the data. The convolution model consists of five sequentially connected modules. At the front end of the network, the first-layer module performs preliminary feature extraction on the input signal through a trainable one-dimensional convolution kernel. This layer effectively captures the basic features based on the local pattern and time dependency of the data, and outputs a standardized feature map, laying the foundation for subsequent processing. The second-layer module constructs a deep convolution operation unit based on 10,304 trainable parameters. Through the stacking and nonlinear transformation of multiple layers of convolution kernels, it completes the abstraction and extraction of high-order features, and finally outputs a 64-channel feature tensor, which greatly enhances the richness and hierarchy of data feature expression. The third layer innovatively introduces the gated activation unit architecture, which integrates 8320 parameters to construct a dynamic gating mechanism. Through adaptive weight adjustment, intelligent screening of interdisciplinary features and nonlinear fusion of cross-channel information are achieved, which effectively suppresses the risk of overfitting while improving the model’s expression ability. To adapt to the input requirements of the fully connected layer, the fourth layer adopts a flattening operation module. This module compresses the three-dimensional feature tensor into a two-dimensional feature matrix, eliminates spatial dimension redundancy and optimizes computational efficiency while retaining the core features of the data. The fully connected layer is configured as the output module at the end of the network. The nonlinear mapping relationship is constructed through 65 parameters to accurately map the abstract feature space with the prediction target, and finally output the prediction result. The modules are connected through feature dimension matching and calculation logic to form a complete end-to-end data prediction system, taking into account the depth of feature extraction and the efficiency of prediction tasks.

During the training process, the loss function showed a steady downward trend, as shown in Figure 10. The training loss dropped from about 0.02% to below 0.0050%. At the same time, the validation loss always fluctuated below the 0.0025% threshold. Figure 11 shows that the model’s predictions on the test data are almost exactly the same as the actual observations, indicating a high accuracy in capturing the remainder.

The final prediction is obtained by summing the three predicted components and applying an exponential transformation. A comparison between the predicted and actual values is illustrated in Figure 12. The evaluation metrics indicate that the model achieves an MSE of 0.0087, RMSE of 0.0935, and MAE of 0.0783, demonstrating its predictive accuracy.

3.5. Model Comparison

This study develops a hybrid forecasting model based on the seasonal trend using Loess, which decomposes the time series into trend, seasonal and remainder components. These components are modeled using BiLSTM, SARIMAX, and 1D-CNN, respectively. To evaluate the effectiveness of the Hybrid-STL model, we use independent BiLSTM, and 1D-CNN models as benchmarks and conduct a comparative analysis in terms of computational efficiency and forecast precision.

After calculation, the results are shown in

Table 1. Prediction of each model based on the site 42040 dataset.

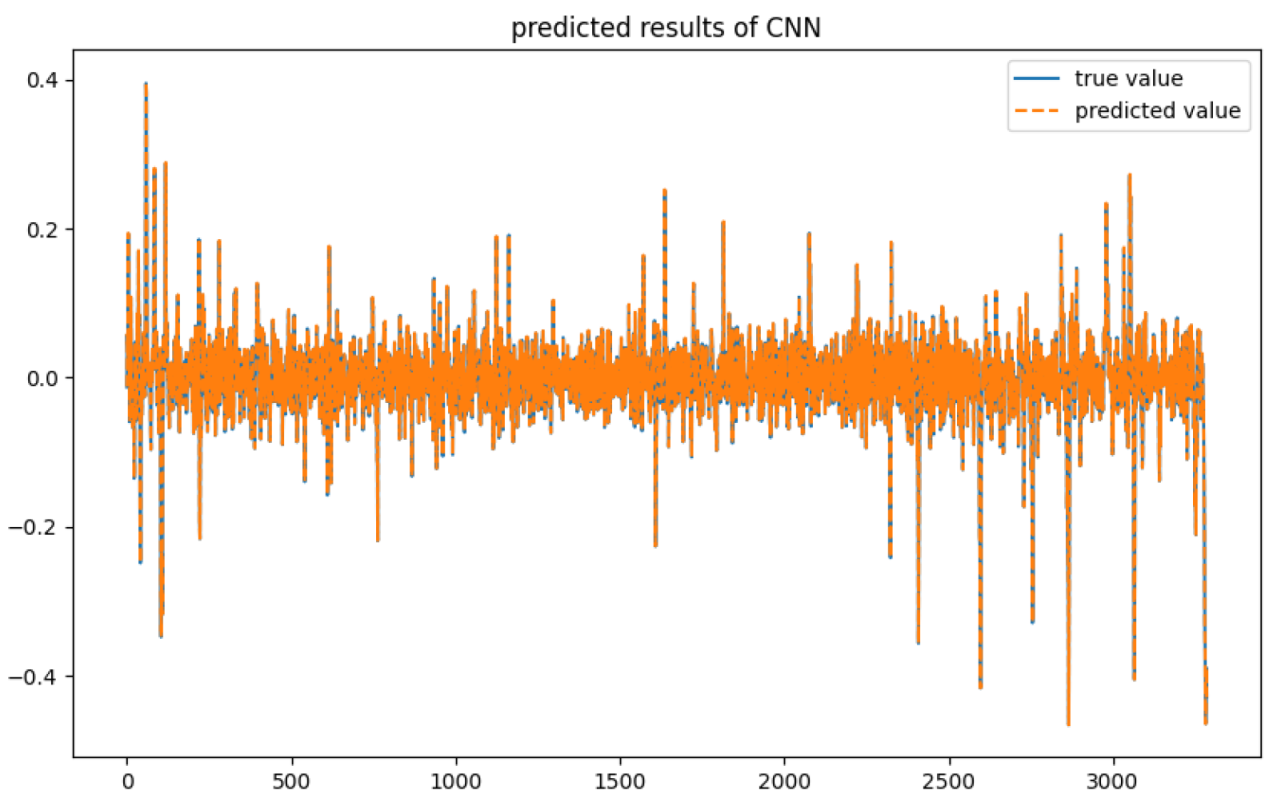
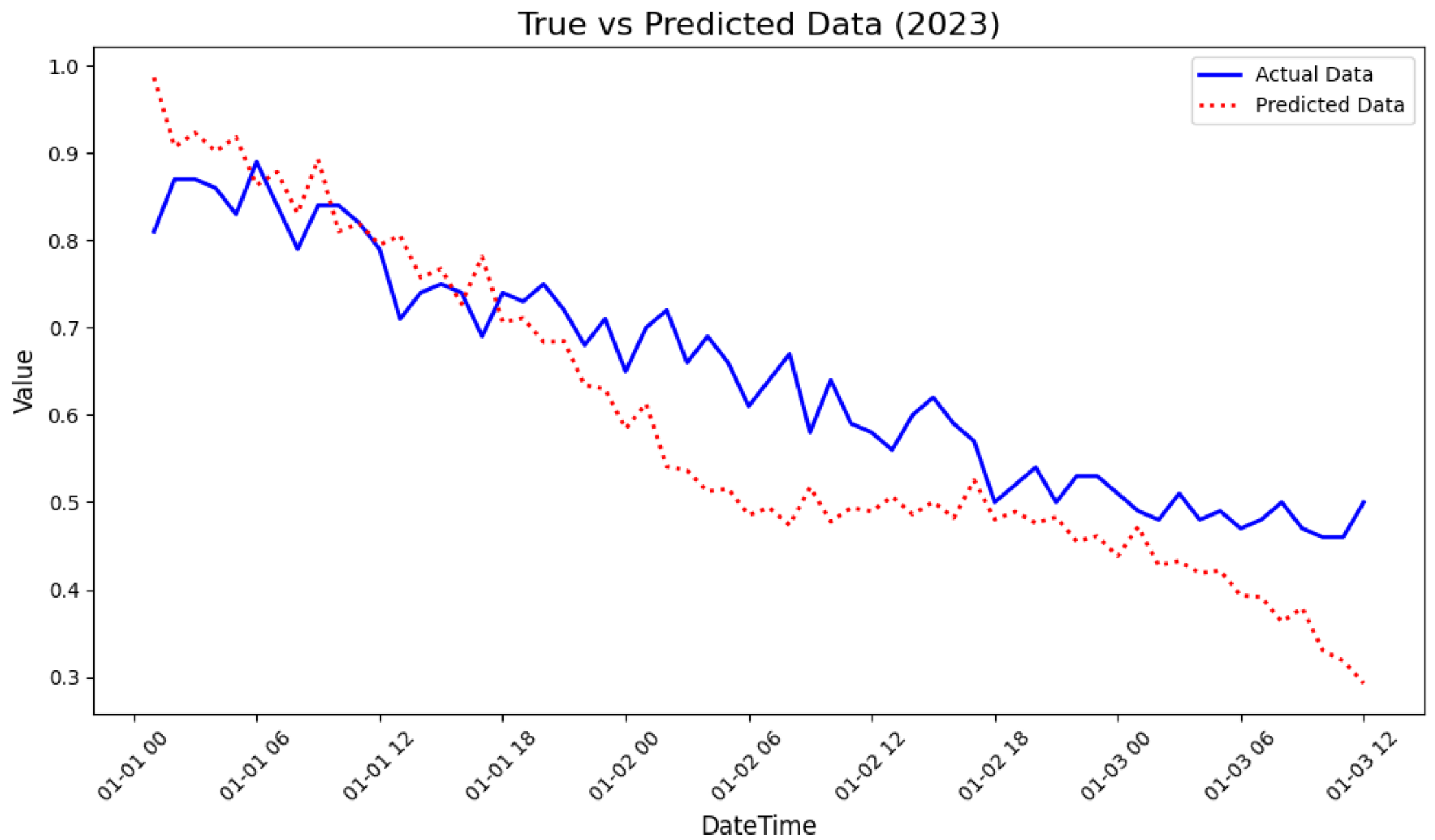
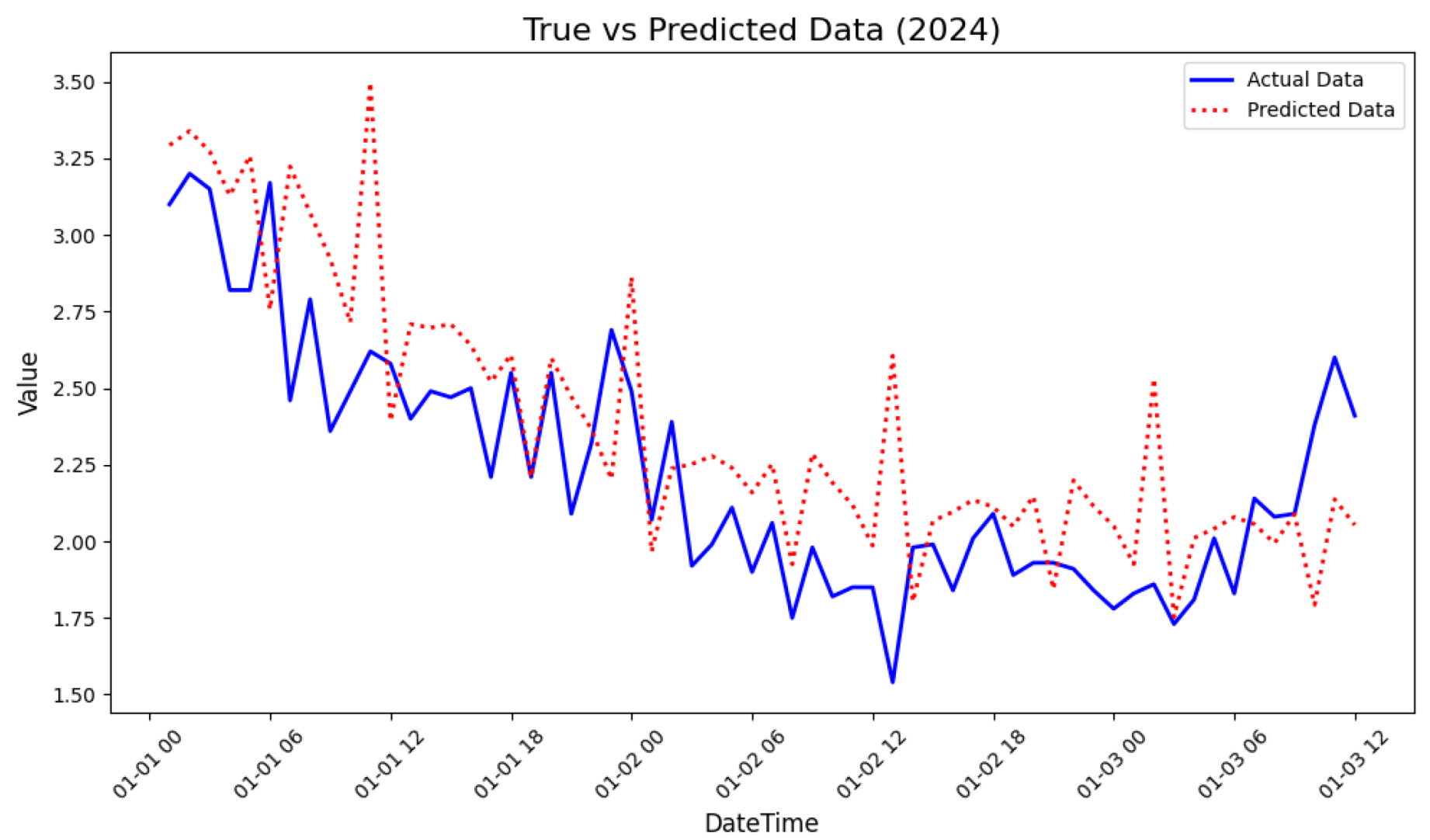
Model	MSE	RMSE	MAE	Runtime (/epoch)
Hybrid-STL model	0.0087	0.0935	0.0783	24 s
BiLSTM	0.0554	0.2353	0.1478	16.1 s
1D-CNN	0.0292	0.1709	0.1534	4.2 s

. In terms of mean square error, the Hybrid-STL model performs best, only 0.0087, indicating that the average square of the error between its predicted value and the true value is extremely small, and it can accurately fit the data characteristics. The MSE of the BiLSTM model is 0.0554, which is nearly 6 times higher than that of the Hybrid-STL model, indicating that its prediction error is relatively large. The MSE of the 1D-CNN model is 0.02992, which is between the first two. The fitting effect is inferior to the Hybrid-STL model, but better than the BiLSTM model. The mean absolute error measures the average of the absolute values of the errors between the predicted value and the true value. The MAE of the Hybrid-STL model is 0.0783, which once again proves its advantage in prediction accuracy. The MAE of the BiLSTM model is 0.1478, and the MAE of the 1D-CNN model is 0.1534. The MAE values of the latter two are higher than that of the Hybrid-STL model, and the MAE value of the 1D-CNN model is even slightly higher than that of the BiLSTM model, which shows that the 1D-CNN model performs relatively worse in terms of direct measurement of absolute error.

Based on the three prediction accuracy indicators, the Hybrid-STL model is significantly better than the BiLSTM and 1D-CNN models in capturing data features and accurately predicting wave heights, while the BiLSTM and 1D-CNN models have certain limitations in prediction accuracy. Although the 1D-CNN model performs slightly better than the BiLSTM model in MSE and RMSE, it performs poorly in the MAE indicator.

From the perspective of runtime, the 1D-CNN model has the highest training efficiency, taking only 4.2 s per epoch, thanks to the high efficiency of its convolutional structure in feature extraction, which can process data quickly; the BiLSTM model takes 16.1 s per epoch, because its recurrent neural network structure needs to process sequence information, the computational complexity is high, resulting in a longer runtime; the Hybrid-STL model takes 24 s per epoch, which is the longest among the three models, which may be due to its integration of multiple analysis methods and model structures, requiring more computing resources and time for data decomposition, feature extraction and prediction.

The Hybrid-STL model, with its absolute advantage in prediction accuracy, can provide more reliable and accurate results for wave height prediction, especially for fields such as marine engineering and disaster warning that require extremely high prediction accuracy. Although its operating efficiency is relatively low, it can be compensated by optimizing algorithms and improving hardware performance in the pursuit of high-precision prediction scenarios. The BiLSTM model is at an intermediate level in both prediction accuracy and operating efficiency, and is suitable for general prediction tasks that require a relatively balanced balance between accuracy and efficiency. Although the 1D-CNN model has excellent operating efficiency, its prediction accuracy is average and has certain application value in scenarios that require high prediction speed and relatively low accuracy. In general, the Hybrid-STL model shows unique comprehensive advantages in wave height prediction tasks, providing a better model selection direction for subsequent research and practical applications.

3.6. Prediction About Data

Wave conditions for January 2024 are predicted using observational data from 46047 station in 2022 and 2023. FFT was applied to the dataset to identify the dominant frequency components. Subsequently, the data underwent STL, resulting in the separation of the time series into trend, seasonal, and residual components, as illustrated in Figure 13. The data were forecasted using the proposed predictive model, and the resulting predictions are illustrated in Figure 14.

Pearson correlation coefficient and dynamic time warping distance quantitatively show a highly significant positive correlation, which effectively verifies the model’s ability to capture the overall trend of wave height changes. In the period of stable fluctuations, taking January 1 from 16:00 to 19:00 as an example, the correlation coefficient between the predicted curve and the actual data reaches 0.89, indicating that the model has a high accuracy in trend fitting during this period. From the perspective of error evaluation, the MSE of the model is 0.1123, and RMSE is 0.3351. According to the established error evaluation criteria, the error level is within an acceptable range, indicating that the prediction results of the model are reasonable and reliable.

4. Conclusions

In response to the multi-scale dynamic challenges of ocean wave height prediction, this study proposes a hybrid prediction framework that integrates signal processing and machine learning. The characteristics of the wave height series were extracted by Fourier spectrum analysis and STL decomposition, and BiLSTM, SARIMA and 1D-CNN were used to model the trend, seasonality and remainder, respectively. In the training site scenario, the model showed high prediction accuracy. The mean square error (MSE) of the model prediction was calculated to be 0.0087 and the root mean square error (RMSE) was 0.0935, which verified the effectiveness of the collaboration between multi-scale decomposition and heterogeneous models. The model has limited generalization ability across locations. When applied to different sites, the MSE increases to 0.1123, indicating that the model is sensitive to local environmental characteristics and needs to be combined with physical prior knowledge to enhance spatial adaptability.

The contributions of this paper are threefold. First, it introduces a novel hybrid model that combines STL decomposition and an LSTM network, which provides a balanced approach for wave height prediction and improves interpretability and prediction accuracy. Second, the proposed framework has practical significance for marine engineering, offshore safety, and renewable energy development, as accurate wave height forecasting is essential. Finally, this study bridges the gap between data-driven methods and traditional physics-based models, establishing a framework that combines machine learning with oceanographic research. Future research will prioritize the integration of multi-site heterogeneous datasets and physical constraints based on spectral wave propagation models to alleviate domain adaptability limitations in spatially heterogeneous marine environments.