Abstract
The flexural buckling failure is a relatively common instability phenomenon in rock slopes both at the small and large scale. It poses a serious threat to the normal operation and maintenance of nearby infrastructure and the life and property safety of surrounding residents. A profound understanding of the deformation and failure mechanism of flexural buckling, as well as the development of quantitative approaches for buckling stability analyses, are of great significance for the risk identification and control of buckling landslides. This study combines the literature relevant to flexural buckling of rock slopes by systematically reviewing the research progress and trends from 1970 to 2023, following the research path of “triggering mechanism → analysis methods”. Based on this proposition, the intrinsic and triggering factors that influence the deformation process of flexural buckling failure in dip rock slopes are detailed and clarified. Then, the main progress achieved in physical, analytical, and numerical modelling regarding the stability and run-out analysis of buckling landslides is comprehensively introduced. Finally, this study provides some outlooks for future research and practice in the field of buckling landslides.
1. Introduction
Under internal and external forces, layered rock masses in the upper portion of a dip slope may slide along weak structural planes, thus compressing the stratified rock masses in the lower portion and causing them to bend and bulge. When bending proceeds, the breaking of rock layers due to shearing or tension may occur at the slope toe, resulting successive failure [1,2,3,4,5]. The deformation and failure mechanism of flexural buckling is quite complex, involving the action of interlayer sliding in the active zone and bending uplift in the passive zone, as well as the dynamic adjustment of the boundary between the active and passive zones. Although such landslides usually experience a long period of time-dependent deformation before failure, they may cause significant casualties and economic damage if timely countermeasures are not adopted [2,6,7,8,9,10]. For example, the Athytos highway landslide in the Central Macedonia region of Greece cut off the main road connecting the Chalkidiki peninsula with the mainland [6]. The Yokawatashi landslide in Niigata, Japan, resulted in three people missing and severe damage to several railway lines [11,12]. The Shiaolin ancient landslide in southern Taiwan led to 397 fatalities and hundreds of millions in economic losses [4]. The largest Dhampu–Chhoya landslide occurred along a 20 km stretch of the Kali Gandaki River (one of the largest rivers traversing southward from Tibet to India through the High Himalayas), temporarily damming the river and causing dramatic morphological changes [13]. With an estimated debris volume of 4.9 × 107 m3, the Xiaguiwa landslide impacted the Jinsha River, SE Tibetan Plateau, forming a dam over 60 m high that temporarily blocked the river [14,15,16]. Thus, the research on the deformation and failure mechanism of buckling landslides under the coupled action of internal and external forces, as well as the corresponding methods for stability evaluation and run-out analysis, holds significant scientific and practical value. This is particularly true for the identification, monitoring, early warning, and risk prevention and control of such landslides.
However, the refinement and advancement of theoretical knowledge on the flexural buckling failure of dip rock slopes are often constrained by existing analysis methods. For flexural buckling failure, since the potential sliding surface does not daylight on the slope face but dips into the slope toe, the formation of a rupture surface involves complex geological and mechanical processes. Assessing the stability condition and changing trend of such a landslide is intricate and challenging. Consequently, existing quantitative methods for the stability analysis of buckling landslides need to simplify this aforementioned complex process equivalently, which leads to the applicability and consistency of a variety of approaches that usually cannot achieve satisfactory results and are worth further discussion.
For this purpose, this study comprehensively reviews the current research achievements related to buckling landslides, following the research path of “triggering mechanism → analysis methods”. This study re-examines the intrinsic and triggering factors influencing the deformation process of flexural buckling failure, as well as the existing physical, analytical, and numerical methods. Finally, this study summarizes the primary deficiencies in the research field of buckling failure and outlines the future research directions.
2. Analysis of Previous Studies on Flexural Buckling of Dip Slopes
2.1. Bibliometric Analysis
A bibliometric analysis was conducted on the core literature database of the Web of Science related to buckling failure of rock slopes using the visualization analysis tool Citespace 6.1.R6. The search terms “buckling landslide” and “buckling failure & slope” were used to retrieve literature, with a time span from 1 January 1970 to 31 December 2023. A collection of documents that included the aforementioned search terms in their titles, abstracts, or keywords were obtained, resulting in a total of 133 valid documents.
From Figure 1, it can be seen that the number of papers related to buckling failure in the past 15 years is more than five times that of the previous period, and the number of papers has shown a significant increasing trend since 2015. The reason may lie in the fact that during this period, disaster cases captured the attention of both the academic and engineering communities, thereby effectively promoting the development of research on buckling landslides. For instance, the Xinmo landslide, which occurred in Xinmo Village, Maoxian County, Aba Prefecture, Sichuan Province, blocked a 2 km stretch of the river and resulted in over 100 casualties, causing significant loss of life and property [3]. In terms of document types, there are a total of 131 research papers (accounting for 98.5%), which make up the vast majority; there are only two review papers (accounting for 1.5%), which mainly focus on the research methods for the buckling of engineering components, and there is no systematic review on the research on buckling landslides.
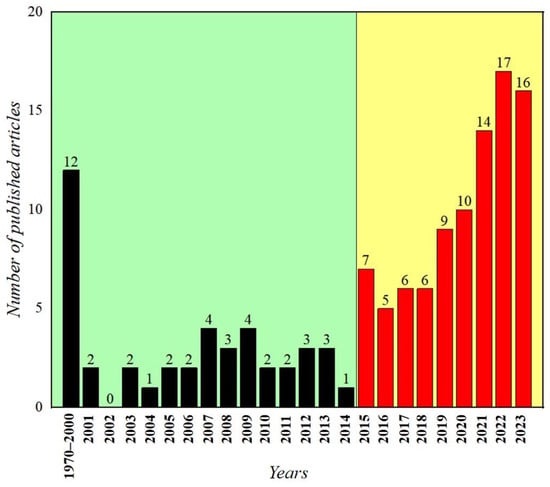
Figure 1.
Number of articles related to buckling failure from the year 1970 to 2023 in the Web of Science database.
By analyzing the keywords of the obtained literature related to buckling landslides, a total of 316 keywords were identified, with the top 100 high-frequency keywords retained for co-occurrence analysis. The analysis results are shown in Figure 2, where the larger the node size, the higher the frequency of the keyword appearing in different papers. The node connection lines represent the correlation between different keywords appearing in the same paper, and the color of the connection lines represents the temporal relevance of this correlation. It can be found that the keywords with higher frequency include “deformations”, “gravitational slope deformation”, “landslide”, “failure”, “behavior”, and “strength”, indicating that there is relatively more research around the topics of deformation and failure mechanisms of buckling landslides, as well as their evolution laws from deformation to instability. In addition, high-frequency keywords related to modelling methods such as “finite-element analysis”, “distinct element method”, and “physical modelling” also appear, indicating that the above methods are commonly used in the research on buckling landslides. Regarding the connections between keywords, some keywords, such as “landslide” and “gravitational slope deformation”, “failure”, and “refined analytical model”, are often mentioned together, indicating that the trends and progress of buckling landslide research mainly follow the path of “triggering mechanism → analysis methods”. In short, the results of bibliometric analysis show that instability mechanisms, evolution laws, and quantitative evaluation methods are hot topics in the research field of buckling landslides.
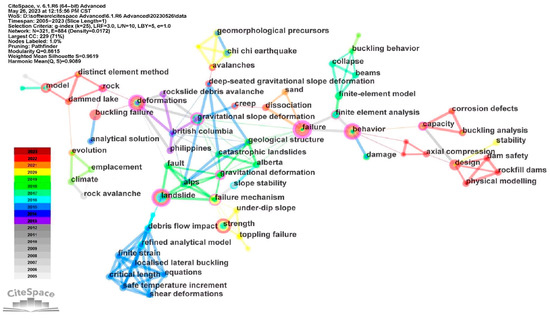
Figure 2.
Keyword co-occurrence analysis of buckling failure.
2.2. Brief Historical Retrospect of the Buckling Failure Phenomenon in the Literature
In terms of buckling failure, Kutter [17] introduced this phenomenon that occurred in British open pit coal mines and discussed the underlying mechanism and the corresponding recognition criterion. Later, Cavers [18] summarized three modes of buckling failure for stratified rock slopes (flexural buckling of plane slopes, three hinge buckling of plane slopes, and three hinge buckling of curved slopes) and proposed corresponding quantitative evaluation methods for buckling stability. The aforementioned study laid the foundation for the subsequent development of analytical approaches for buckling stability assessment in the twentieth century [19,20,21,22,23]. After that, with the progress and innovation of monitoring and modelling technologies [24,25,26,27,28,29,30,31,32,33,34], the academic and engineering communities have conducted in-depth studies on buckling failure through in situ investigations and modelling (analytical, numerical, and physical), mainly focusing on the deformation and failure mechanisms, as well as the stability analyses of buckling landslides.
3. Deformation Process of Flexural Buckling Failure and Its Influencing Factors
3.1. Deformation Process of Flexural Buckling Failure
According to previous studies [2,35,36,37,38], the deformation process of flexural buckling failure in rock slopes can be divided into three stages, as shown in Figure 3. In the slight bending stage (Figure 3a), under the downslope driving force, the middle and rear portions of a rock slope slide along the non-daylighting basal sliding surface and the rock layers at the front edge of the slope show slight bending due to compression. In addition, tension cracks, local crushing, and loosening can be observed in the bending segment. During the intense bending and uplift stage (Figure 3b), enhanced bending of rock layers leads to strong dilatancy of rock mass within the bending segment, with a significantly uplifted slope surface, and intense loosening and fracturing of rock mass can be found in the front edge of the rock slope. In the shearing failure and landslide stage (Figure 3c), a through-going sliding surface is formed due to the shearing failure of rock mass within the bending segment, and then a landslide is initiated. It is notable that Yan et al. [39] believed that there is a fracturing and disintegration stage between the intense bending and uplift stage and the shearing failure and landslide stage, but from the perspective of deformation and failure characteristics, this intermediate stage can be regarded as one part of the intense bending and uplift stage.
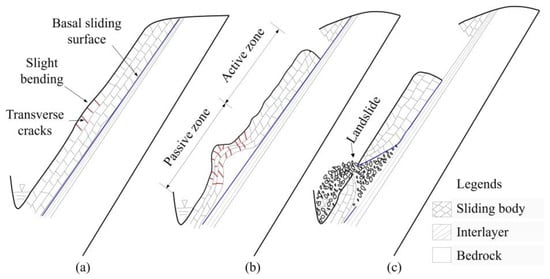
Figure 3.
Deformation process of flexural buckling failure: (a) slight bending stage; (b) intense bending and uplift stage; (c) shearing failure and landslide stage.
3.2. Factors Affecting the Deformation Process of Flexural Buckling
The deformation process of flexural buckling failure of dip rock slopes is typically affected by the coupled actions of intrinsic and triggering factors. The intrinsic factors mainly refer to the structural and geomechanical features of a dip rock slope, including the thickness of the rock layer, the dip angle of the rock layer, the shear strength parameters of the basal sliding surface (cohesion and internal friction angle), the deformation parameters of the rock mass, and others. Conversely, the triggering factors include natural factors such as earthquakes and rainfall, as well as human engineering activities such as reservoir water level fluctuations, blasting vibrations, excavation of slopes, and loading at the slope crest. The aforementioned factors from both aspects jointly influence each stage of flexural buckling of rock slopes, such as the buckling depth, and, in the case of failure, the location of the tension cracks at the rear edge of the rock slope, the location of the rupture surface near the slope toe, and the degree of fragmentation and disintegration of rock mass after the landslide.
3.2.1. Intrinsic Factors
(1) Thickness of rock layer
From the perspective of material mechanics, the thin-layer rock mass with lower cross-sectional bending stiffness is prone to buckling instability. Tang et al. [29] believed that the influence of rock layer thickness on the buckling stability is mainly reflected in the buckling depth (buckling depth equals the number of bending rock layers multiplied by the single-layer thickness of rock); the thicker the single rock layer, the more pronounced its decisive role in the overall bending stiffness and the final buckling state. Through the experimental investigation of the deformation and failure features in cataclinal slopes, Lo and Weng [30] indicated a negative relationship between the buckling stability and the single-layer thickness. Later, the aforementioned negative relationship, in other words, the positive relationship between the critical slope length/height and the single-layer thickness, has also been demonstrated through sensitivity analyses using various analytical approaches [36,40,41].
Table 1 presents data on the geometry (including layer thickness) of typical events of flexural buckling failure [3,14,31,40,42,43,44,45,46,47]. According to the Chinese Code for Investigation of Geotechnical Engineering (GB50021-2001, 2009), the thickness of a single rock layer can be classified into four categories: very thick (>1.0 m), thick (0.5 m ~ 1.0 m), medium-thick (0.1 m ~ 0.5 m), and thin (<0.1 m). The data indicate that the majority of flexural buckling failures occurred in the thin and medium-thick rock layers, with occurrences also noted in very thick rock layers. The reason for that feature is that the ratio of singe-layer thickness to slope length or height remains relatively small, leading to buckling deformation of the rock layer with high flexibility.

Table 1.
Historical events of flexural buckling failure and their associated information.
(2) Strength parameters of basal sliding surface
Based on the deformation process of flexural buckling failure, the shear strength parameters of basal sliding surface (cohesion and internal friction angle) directly affect the residual sliding force of rock masses in the active zone, which finally induces the bending of layered rock masses in the passive zone, altering the buckling stability of rock slope accordingly. At present, the effect of shear strength parameters of basal sliding surface on the flexural buckling stability is mainly investigated using analytical approaches. Referring to the Zhu et al. [48] and Jin et al. [40], the relationship curves between the buckling stability indicators and the shear strength parameters of basal sliding surface generally follow the same pattern of change, as shown in Figure 4. From the figure, it can be seen that as the cohesion or internal friction angle of basal sliding surface increases, the critical slope length for buckling failure first shows a linear and gentle growth trend in the bending-dominated stage. However, when the cohesion or internal friction angle of basal sliding surface exceeds a certain critical value, the critical slope length for buckling failure increases sharply and abruptly during the sliding-dominated stage. The reason lies in the fact that when the shear strength parameters of basal sliding surface increase to a certain extent, the anti-sliding force acting on the upper-middle part of the slope is greater than the sliding force, then the interlayer sliding in the upper-middle part of the slope will cease and the compression effect exerting on the layered rock mass of the lower portion will disappear, hence the critical slope length for buckling instability increases sharply.
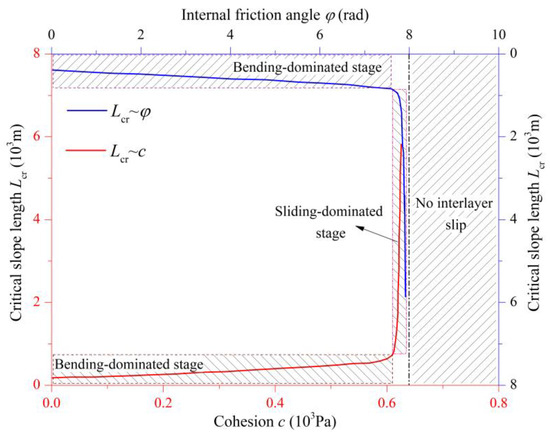
Figure 4.
Relationship between shear strength parameters of basal sliding surface and critical slope length (data from Zhu et al. [48]).
According to above analyses, it is theoretically feasible to increase the slope stability against flexural buckling by enhancing the shear strength of basal sliding surface. In engineering practices, reinforcements such as anchor rods, anchor cables, and anti-sliding piles can be selected according to specific situations, as well as preventions of water-induced softening of basal sliding surface.
(3) Dip angle of rock layer
In general, the slope stability against flexural buckling gradually decreases with the increase of the dip angle of rock layer [23,29,36,40,48,49]. The main reason is that an increased dip angle leads to high bending moments and shear forces in the stratified rock mass, and the self-weight component parallel to basal sliding surface also increases, intensifying the risk of flexural buckling failure. For dip rock slopes consisting of medium-soft rocks, such as marl, slate, phyllite, shale, Tang et al. [29] conducted a systematic and in-depth study on the influence of dip angle combing model testing and numerical simulation. By monitoring the deformation of slope model, it was found that when the dip angle of the rock layer was 20°, the slope model only underwent slight deformation; with the increase of the dip angle, the rock layers exhibited creeping deformation, and the rock layers of the lower part of the slope model showed bending phenomena; when the dip angle of the rock layer was less than or equal to 20°, the front edge of the slope model was usually relatively stable and did not uplift. Based on the above phenomena, Tang et al. [29] believed that a dip angle of rock layer greater than 20° is an important geological condition for the buckling instability of dip slopes with medium-soft rocks. Recently, Chen et al. [50] statistically investigated the relationship between the instability deformation of buckling landslides and the dip angle of the strata, pointing out that the dip angles of rock layers with buckling deformation are mostly distributed between 20° and 50°. The main reason is that rock layers with a gentler dip angle generally undergo bedding sliding–tension cracking, while rock layers with a steeper dip angle are mostly dominated by toppling deformation. It should be noted that buckling failure can also occur in very steep rock layers when the boundary condition of the layer toe is pinned, owing to the fracturing and loosening [1].
Table 1 also lists the dip angle information of nine typical buckling landslides. As can be seen from the table, the dip angles of the above buckling landslide cases generally vary between 20° and 50°, fully corroborating the research conclusions of Chen et al. [50]. Therefore, extra caution should be exercised when encountering this dip angle range in the site.
(4) Deformation parameters of rock mass
At present, there is relatively little research on how deformation parameters of rock mass influence the buckling stability of rock slopes. In this respect, most studies use theoretical analysis to explore these relationships [36,41,49,51]. The relationship between critical length and the deformation modulus is often nonlinear positive, as shown in Figure 5. The reason is that intact rock with high elastic moduli has strong sectional bending performance and is not prone to plastic deformation, thus exhibiting better buckling stability. From the perspective of lithology, the elastic modulus of intact rock can indirectly reflect the strength of the rock. Soft rocks with lower elastic moduli are more prone to buckling failure due to their poor bending and shear resistance. For instance, in the field investigation of the deformation and failure modes of rock slopes in soft rocks, Sun [21] found that buckling dominates when the boundary conditions of the rock layer are fixed.
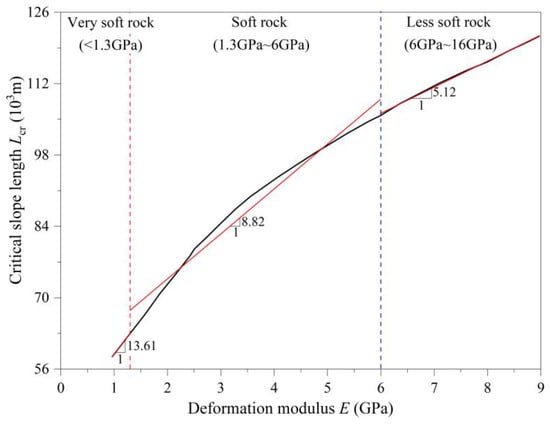
Figure 5.
Variation of critical slope length with deformation modulus (data from Zhu et al. [48]).
3.2.2. Triggering Factors
(1) Rainfall
Rainfall, especially continuous heavy rainfall, could trigger buckling landslides. For example, in 2017, continuous rainfall in Xinmo, Sichuan, for as long as two months, resulted in the reactivation of old landslides in the Xinmo area, blocking the river for 2 km and burying more than 100 people [3]. The mechanism of rainfall affecting the stability of buckling landslides is mainly manifested in the following aspects. First, the rainfall-induced softening weakens the strength of the basal sliding surface, which significantly affects the buckling stability adversely. Second, the seepage field formed by rainfall infiltration generates static water pressure within the slope body, exerting a buoyant force and reducing the resisting force along the base of the sliding mass, thereby reducing the buckling stability. Finally, the rainfall infiltration will gradually reduce the matrix suction in unsaturated soil-like infillings or interbeds between layers, along which sliding occurs, which also leads to a reduction in buckling stability. The instability and failure of buckling landslides induced by rainfall is usually a relatively slow process, and current research mainly focuses on the impact of long-term heavy rainfall on buckling landslides investigated by using numerical methods, or the impact of static and dynamic water pressure formed by rainfall on buckling landslides through theoretical calculations. Due to the complicated mechanism of rainfall-induced buckling landslides, it remains a key and challenging issue in this research field.
(2) Earthquakes
Seismic landslides undergo the process of initiation, run-out, and accumulation in an extremely short period of time, releasing tremendous energy that often causes incalculable losses to the surrounding ecological environment and the safety of lives and property. The Tangjiashan coseismic landslide triggered by the Wenchuan earthquake in 2008 resulted in 84 deaths, and at the same time blocked the Jianjiang River to form a barrier lake, causing huge economic losses [47]. Under normal circumstances, the structural loosening of the slope body, the formation of internal fracture surfaces, and the sharp rise in pore water pressure within the slope body caused by earthquakes can create favorable conditions for the rapid initiation of buckling landslides.
At present, the stability assessment of buckling landslides under earthquakes still poses a great challenge, and there is a relative scarcity of relevant research literature, which mainly focuses on theoretical analysis. Based on the principle of energy balance, Qi et al. [47] proposed an analytical approach for evaluating the stability of buckling landslides considering the action of earthquakes and pore water pressure and verified the effectiveness of the developed analytical method with the Tangjiashan landslide case. By simplifying the seismic action as horizontal or vertical inertial forces using the pseudo-static method, Liao et al. [52] derived analytical expressions for the stability assessment of dip slopes against flexural buckling and three hinge buckling under earthquakes and pointed out that the buckling instability of dip slopes is closely related to the direction of the horizontal seismic force. Utilizing the parameter sensitivity analysis method, Yang et al. [53] investigated the impact of the horizontal seismic coefficient on the buckling stability of dip slopes, and the study showed that as the horizontal seismic coefficient increased, the critical buckling length decreased, and the buckling stability decreased. Recently, Pei et al. [54] adopted a shaking table test to analyze the response of buckling landslides under continuous seismic loads, pointing out that the stress amplification of the bedding structure under earthquakes is an important reason for triggering buckling instability.
(3) Human engineering activities
Among human engineering activities, reservoir water level fluctuation is a special factor influencing the buckling stability of bank slopes of reservoirs, such as the Three Gorges, Lijiaxia on the Yellow River, Yalong River, and Chihaxia [31,45,55]. The direct effect of reservoir water level fluctuations on buckling stability is mainly manifested in the changes in static and dynamic water pressure, buoyancy, and seepage field within the bank slope, as well as the water–rock interaction in the drawdown zone. By analyzing the monitoring data of the Muyubao landslide, Feng et al. [56] believed that its deformation is mainly affected by buoyancy and dynamic water pressure, and when the rate of reservoir water level fluctuation is small, buoyancy controls the deformation of the landslide; when the rate of reservoir water level fluctuation increases, dynamic water pressure becomes the main controlling factor of landslide deformation. Through field investigations, Yan et al. [57] found that the deterioration and damage of rock mass near the front edge of dip slopes induced by long-term water–rock interaction is an important factor triggering buckling failure of reservoir bank, and they proposed an approach for evaluating the buckling stability of bank slopes considering the effect of rock mass deterioration. In addition, excavations of dip slopes in road and mining projects can cause changes in the original stress state and boundary conditions of dip slopes, triggering the buckling deformation and failure of rock layers [1,22,43].
4. Analysis Methods for Flexural Buckling Failure
4.1. Physical Model Tests
By comprehensively and realistically reproducing the complex geological conditions of a landslide, physical model tests can intuitively simulate the entire process of landslide deformation, instability, run-out, and accumulation, revealing the effects of key parameters on the whole landslide process, and further provide a scientific basis for the construction of new theoretical and numerical models.
At present, common physical model tests of buckling landslides include conventional indoor model tests, base friction tests, centrifugal model tests, and shaking table tests. Utilizing resin-bonded spherical artificial rock particles to assembly rock slabs and small-scale indoor models of stratified rock slopes, Weng et al. [58] and Lo and Weng [30] reproduced the evolution process of flexural buckling and systematically studied the effects of slope angle, dip angle, layer thickness, and material deterioration caused by rainfall on the buckling deformation and failure of dip slopes. By experimentally modelling the dynamic excavation processes in a model of open pit mines, Wen et al. [59] found that rocks on the upper part of the slope slipped along the bedding planes, while slip-buckling failure occurred near the foot of the slope. Taking the generalized model of the Qingshi bank slope in the Three Gorges Reservoir area as an example, Yan et al. [57] studied the effect of rock mass deterioration in the hydro-fluctuation belt on the buckling stability of bank slopes, and they found that the thrusting of the rear edge is the premise of buckling failure of the bank slope, and that the continuous deterioration of rock mass in the hydro-fluctuation belt is the leading factor of buckling failure. Specifically, the rock mass deterioration in the hydro-fluctuation belt involves the weakening of the mechanical parameters, the separation of interlayers, and the increasing fragmentation of the rock mass [55,60,61,62]. As to the base friction tests for the modelling of the buckling landslide evolution process, Du et al. [27] discussed and analyzed the main influencing factors of critical slope length and the uplift height. Subsequently, Tang et al. [29] also explored the relationship between the buckling mechanism and controlling factors. Based on centrifugal model tests, Weng et al. [35] reproduced the entire process of buckling instability of stratified rock slopes and revealed the impact of scale effects on the buckling instability and failure mechanism of stratified rock slopes. The scale effect refers to the phenomenon where the size of a slope influences its deformation and failure [63,64]. Recently, based on shaking table tests, Li et al. [65] physically modeled the failure process and acceleration responses of two interbedded dip slopes under different seismic intensities, and they found that buckling failure tends to occur when the dip of rock layer is less than 65°. Combining shaking table tests with a digital image correlation technique, Pei et al. [54] analyzed the dynamic response and deformation characteristics of the Xinmo landslide under accumulated seismic actions, revealing the contribution of stress amplification on the discontinuities to the buckling failure. Using the Xiaguiwa landslide as a case study, Wang et al. [66] experimentally investigated the dynamic damage mechanism of dip slopes under multiple earthquakes and found that damage in the bedding rock slope first appeared at one-quarter of the elevation due to buckling. Based on the large-scale centrifugal shaking table test platform, Li [67] observed that the seismic failure pattern in layered rock slopes with steep strata is significantly influenced by lithological assemblies. Specifically, a slope with an interbedded rock stratum is prone to seismic buckling failure.
In the physical model tests of buckling failure, the preparation of similar materials for the geological body and the set-up of the reduced-scale landslide models are costly and complicated, coupled with the fact that the deformation, instability, and failure process of buckling landslides generally span a longer time, leading to high resource investment, long time consumption, and limited parameter acquisition in model tests. The number of existing physical modelling studies on the buckling failure is still relatively small. In the future, it is necessary to develop more rational and reliable equipment for modelling internal and external forces, as well as more refined monitoring instruments for stress, kinematic parameters, and water pressure, to further promote the development and application of physical model tests in the research field of buckling landslides.
4.2. Analytical Methods
At present, analytical methods for evaluating flexural buckling stability of dip slopes mainly adopt three theoretical mechanical schemes, namely, the single beam (column) model, the multi-layer beam model, and the elastic (plastic) slab model, as illustrated in Figure 6. By simplifying the flexural buckling failure of dip slopes under various loads into the instability problems of the previous mechanical models, the deflection equations of the column, beam, or slab models are assumed according to the boundary constraint conditions, and then the explicit or implicit solutions to the critical slope length or critical load are determined based on methods such as the Euler buckling theory, the energy balance principle, the catastrophe theory, or the force balance conditions. Subsequently, the critical slope length or critical load can be adopted to evaluate the flexural buckling stability of dip rock slopes, that is, when the longitudinal load at the slope crest is greater than the critical buckling load (Pcr) or the actual slope length is greater than the critical slope length (Lcr), the slope will undergo buckling.
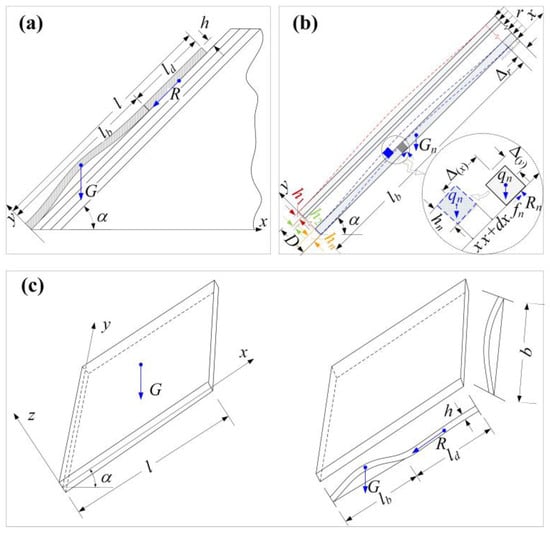
Figure 6.
Simplified mechanical model. (a) Single beam (column) model (modified from Yang et al. [53]). (b) Multi-layer beam model (modified from Zhang et al. [36]). (c) Elastic (plastic) slab model (modified from Feng et al. [68]).
(1) Single beam (column) model
The instability and evolution process of the flexural buckling of dip slopes may involve a single rock layer or multiple rock layers. The single beam (column) model simplifies the single buckled rock layer or the pack of buckled rock layers as a single beam (column) with assumed end conditions, and the beam (column) stability theory is capable of analyzing the flexural buckling of the dip slope. Adopting the model of column with pinned ends, Cavers [18] derived the critical slope length against flexural buckling based on the Euler buckling theory. Then, by solving the eigenvalue of the basic differential equation of beam deflection under the combined action of transverse load, axial concentrated load, and distributed load, Sun and Zhang [19] proposed the analytical solution to critical buckling load considering the self-weight of rock layer and the hydrostatic pressure. Based on the cusp catastrophe theory, Qin et al. [42] determined the necessary and sufficient conditions for the flexural buckling failure of stratified rock slopes. By considering the effects of earthquakes and hydrostatic pressure along the basal sliding surface, Qi et al. [47] developed an analytical approach in the frame of energy equilibrium theory and analyzed the typical buckling failure of the Tangjiashan landslide. In order to investigate the flexural buckling failure of stratified rock slopes under top loading, Liu et al. [49] presented an explicit analytical approach by combining Euler’s method and the superposition principle. Under equilibrium conditions, Garzon [69] evaluated the flexural buckling stability of stratified rock slopes using the tangent-modulus theory and classified the buckling failure modes into three types: brittle, elastic, and inelastic failure. Recently, accounting for the longitudinal and transverse bending of layered rock mass under the combined action of the self-weight of rock layer, the hydrostatic pressure, and the seismic load, Yang et al. [53] presented the conditional equation for the length of the buckling segment based on the elastic column stability theory and energy principles. Representative analytical approaches for the stability evaluation of flexural buckling based on the single beam (column) model are shown in Table 2.

Table 2.
Typical analytical approaches based on the single beam (column) model.
(2) Multi-layer beam model
This model regards the pack of buckled rock layers as a multi-layer beam with fixed ends, assuming that multiple rock layers bend in the same way under the combined action of self-weight and external loads, and no relative slip occurs in the buckled rock layers. Based on the multi-layer beam model, Li et al. [23] derived the analytical solutions for the critical buckling load and the critical buckling length of dip slopes using the energy equilibrium principle. Considering the effects of water pressure and earthquakes, Zhu et al. [48] proposed theoretical buckling curves for each rock layer based on special function theory and deeply discussed the buckling failure characteristics of stratified rock slopes. Zhang et al. [36] derived analytical solutions for the critical buckling length and critical buckling depth of stratified rock slopes using the energy equilibrium principle and introduced the generalized Hoek–Brown criterion to account for the impact of scale effect on buckling stability. Similarly, utilizing the energy equilibrium principle, Wang et al. [32] provided a calculation formula for the critical buckling length of dip slopes, and they verified it in combination with numerical simulation and field data. Later, Wang et al. [70] suggested that critical sliding displacement is more suitable for quantitatively analyzing the progressive evolution process of buckling landslides. They proposed a calculation method for determining critical sliding displacement and established corresponding criterion for assessing flexural buckling stability, taking into account both the tensile and compressive strengths of rock. Based on the mechanical analysis, Jin et al. [40] established the buckling curve equation of multi-layered rock masses under the action of earthquake and top loading and presented the analytical formula of critical slope length for buckling failure using the energy method, as well as the method for determining the position of failure surface according to the maximum deflection point. Then, this approach was successfully applied to typical landslide cases. Typical methods for the stability evaluation of flexural buckling based on the multi-layer beam model are given in Table 3.

Table 3.
Typical analytical approaches based on the multi-layer beam model.
(3) Elastic (plastic) slab model
Considering the presence of joints, fissures, and fractures in dip rock slopes, the longitudinal and transverse lengths of the buckled rock layers are usually limited. Therefore, simplifying the flexural buckling of dip slopes as thin plate instability problems is more in line with the actual situation. This model regards the rock layer as a plate with a hinged bottom, peripheral roller supports, and finite length, and it can be analyzed according to the stability theory of elastic (plastic) compressed plates. In combination with the elastic plate model and the energy equilibrium principle, Liu and Zhou [71] systematically investigated the effect of the self-weight component of the rock layer in the direction parallel to the strata, interlayer friction, and cohesion on the buckling stability of stratified rock slopes. Considering that the rock mass will exhibit plastic deformation when the compressive stress exceeds its elastic limit, Feng et al. [68] regarded the rock layer as an elastic-plastic plate in the analysis of flexural buckling. Recently, in response to the buckling deformation caused by the rock mass deterioration in the hydro-fluctuation belt of the Wuxia Gorge, Yan et al. [41] proposed a formula for the critical length of buckling segment considering the dynamic deterioration effect of the rock mass based on the elastic–plastic plate model. According to the energy equilibrium of the elastic–plastic plate model, Wu et al. [72] and Zhang et al. [73] presented a criterion to judge whether the dip slope is sliding or structurally unstable under the combined effects of self-weight, hydrostatic pressure, and earthquakes, and they subsequently applied this method to analyze three practical buckling cases. Some typical methods for the stability evaluation of flexural buckling developed on the elastic (plastic) slab model are shown in Table 4.

Table 4.
Typical analytical approaches based on the elastic (plastic) slab model.
4.3. Numerical Simulations
Currently, numerical research on the flexural buckling of dip rock slopes can be mainly classified into the stability analysis and the run-out analysis. The stability analysis generally accounts for the small deformation of slope, such as the formation of sliding surface and the local bending of rock layers. In terms of run-out analysis, more attention is paid to large deformation and complex motions, such as the fracturing of rock layers and the run-out and accumulation of landslides. Accordingly, there are various numerical methods that are suitable for analyzing the different phases of flexural buckling of dip rock slopes.
Mostly, the finite difference method (FDM) and the finite element method (FEM) are capable of modelling the instability process of the flexural buckling of dip slopes. For instance, combining the FDM with the Cosserat continuum model, Pant and Adhikary [74] deeply investigated the buckling deformation process and failure mechanism of a stratified rock slope, and they found that the explicit joint model would overestimate the critical buckling coefficient of the rock masses with fewer layers. Subsequently, Adhikary et al. [24] introduced the large deformation Cosserat continuum model into the AFENA code and numerically recreated the entire process of buckling instability of a stratified rock slope. Pereira and Lana [26], and Silva and Lana [28] used the finite element software Phase2 to simulate the buckling deformation process of phyllite rock layers, focusing on the influences of the shear and normal stiffness of discontinuities, cohesion, and in situ stress on the buckling failure process of a stratified slope. Recently, Ridl et al. [75] regarded the inherent anisotropic characteristics of the rock mass as a discrete crack network, and they implemented numerical analysis of the buckling deformation of the stratified rock mass using the FEM.
In terms of numerical modelling of the entire evolution of flexural buckling failure, the Universal Distinct Element Code (UDEC), Particle Flow Code (PFC), Discontinuous Deformation Analysis (DDA), and Numerical Manifold Method (NMM) are more suitable. For example, by using the UDEC program, the buckling instability and failure process of the slope at the Westfield open-pit coal mine was detailed analyzed [76,77]. Alzo’ubi et al. [78] investigated the effect of long-term weathering on buckling deformation and found that changes in the in situ stress state of a slope and the tensile strength of rock significantly affect the flexural buckling stability of the slope. According to the UDEC simulation results, Tang et al. [29] proposed some insightful views on the geological and mechanical conditions, the determination of critical failure state, and early signs for the buckling instability of a stratified rock slope. Later, taking the Xiaguiwa landslide in the upper Jinsha River, southeastern Tibetan Plateau, as an example, Li et al. [15] simulated the entire process from buckling deformation and failure to the formation of a landslide dam using the UDEC. Through discrete element modeling that accounted for the rheological properties of anisotropic gneissic rocks, Huber et al. [79] identified the critical orientation configuration between isotropy planes and slope faces that leads to buckling failure. Based on the PFC simulations of the buckling instability process of the Xinglangpo landslide, Miao et al. [33] conducted an in-depth study of the micro-mechanical mechanism of the landslide. Wu [80] employed the DDA method to simulate buckling deformation and ground subsidence phenomena in the lower slope area of the Chu-fen-er-shan landslide. By combining DEM and DDA, Tommasi et al. [25,44] conducted a back-analysis of the buckling phenomenon of the Lavini di Marco area of Trento, Italy, and deeply investigated the effect of rock mass properties, slope geometry, and hydrological conditions on the buckling deformation behavior of stratified rock slopes. Zhang [81] proposed a stiffness reduction method to evaluate the flexural buckling stability of a stratified rock slope and simulated the entire process of buckling deformation and instability of a single rock layer using the DDA. Recently, by simulating the instability and evolution process of Malvern Hills in New Zealand using the NMM, Wang et al. [32,69] explored the effect of soft interlayers and staggered joints on the buckling deformation and failure process of the stratified rock slope, confirming that NMM simulation can well reproduce the entire process from the progressive instability and failure to the run-out and accumulation of buckling landslides.
5. Concluding Remarks and Future Prospects
To fully understand the behavior of buckling failure of dip rock slopes, a bibliometric analysis was conducted to synthesize relevant literature and systematically review research hotspots and development trends in this field. Although significant advancements have been made in studying the deformation process, influencing factors and analysis methods related to the flexural buckling failure of dip slopes, challenges remain in both theoretical research and engineering practice.
Existing theoretical studies on instability mechanisms and stability evaluation of flexural buckling in dip rock slopes have primarily focused on exploring the influence of either intrinsic or triggering factors through numerical and analytical modelling, while rarely considering the coupled effects of multiple factors. The application of physical model tests, particularly centrifugal modeling which can reproduce prototype stress states while accounting for time-dependent effects, remains at an early stage. In future research, refined numerical methods should be combined with novel physical modelling techniques to systematically investigate the influence mechanisms of multi-factor coupling on buckling failures of dip slopes.
Based on case reviews, flexural buckling failures predominantly develop in soft–hard interbedded dip rock slopes with layer inclination of 20–50° and thin-to-medium thickness characteristics. For rapid assessment of dip slope buckling, analytical approaches and corresponding assessment indicators must be carefully selected. Regarding stiff and fragile rock layers, force-equilibrium or energy-based analytical methods at precise limit states are preferable. The assessment index of the elastic critical load is particularly useful here, as rock mass strength drops sharply once this threshold is reached, leading to destructive landslides. For soft rock layers, critical-displacement-based methods are more appropriate, although their application across different scenarios remains challenging. Civil engineering applications require strict displacement limits to protect structures and maintain serviceability. In contrast, mining engineering often permits larger displacements and operates with marginal safety conditions when short-term bench stability is prioritized.
Author Contributions
Conceptualization and methodology, Y.Z., N.F. and J.S.; investigation, Y.Z., N.F., J.S., L.P., J.T. and R.Y.; resources, Y.Z., N.F. and J.T.; writing—original draft preparation, Y.Z., N.F. and J.S.; writing—review and editing, Y.Z., N.F., J.S. and L.L.; visualization, Y.Z., N.F., J.S. and L.P.; funding acquisition, Y.Z., N.F., R.Y. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Hubei Provincial Natural Science Foundation of China (no. 2021CFB280); the Follow-up of the Geological Disaster Prevention and Control Project in the Three Gorges area (no. 000121 2024C C60 002); the National Natural Science Foundation of China (nos. 52108337, 41702383); the “Qianlong Plan” Youth Talent Project of Wuhan Center, China Geological Survey (no. QL2022-10); and the Project of China Geological Survey (no. DD20221740).
Data Availability Statement
All data, models, and code generated or used during this study appear in the submitted article.
Acknowledgments
The authors thank all the scholars responsible for the referenced work and professional websites for providing figures.
Conflicts of Interest
All the authors of this manuscript have approved the submission of this article for publication, and there are no conflicts of interest to declare. This paper has not been published elsewhere and is not under consideration by another journal.
List of Symbols
The following symbols are used in this manuscript:
| l | Slope length |
| lcr | Critical slope length |
| lb | Length of buckling segment |
| lbcr | Critical buckling length |
| ld | Length of driving segment |
| lw | Slope length subjected to hydrostatic pressure |
| Dcr | Critical buckling depth |
| Pcr | Critical buckling load |
| Ucr | Critical sliding displacement |
| n | Number of rock layers (slabs) |
| h | Thickness of rock layer (slab) |
| hi | Thickness of the i-th rock layer (slab) |
| b | Width of rock slab |
| γ | Unit weight of rock layer (slab) |
| γi | Unit weight of the i-th rock layer (slab) |
| γw | Unit weight of water |
| α | Dip angle of rock layer (slab) |
| ϕ | Internal friction angle of basal sliding surface |
| c | Cohesion of basal sliding surface |
| ϕn | Internal friction angle between the n-th and the underlying stable rock slab |
| cn | Cohesion between the n-th and the underlying stable rock slab |
| E | Elastic modulus of intact rock |
| Ei | Elastic modulus of intact rock in the i-th layer |
| Et | Tangent modulus of intact rock |
| E(t) | Deformation modulus of rock mass at time t |
| μ | Poisson’s ratio |
| ψt | Modulus reduction coefficient |
| D | Bending stiffness of rock slab of unit width |
| βs | Dynamic amplification coefficient |
| Ks | Horizontal seismic coefficient |
| r | Intensity of residual driving force along the axial direction of rock layer |
| q | Intensity of top loading along the axial direction of rock layer |
| Q | Top loading along the axial direction of rock layer |
| y | Deflection curve equation of rock layer |
| y′ | Derivative of deflection curve equation |
| I | Moment of inertia |
| N | Normal force |
| M | Bending moment |
| R | Residual driving force |
References
- Hu, X.Q.; Cruden, D.M. Buckling deformation in the high wood pass, Alberta, Canada. Can. Geotech. J. 1993, 30, 276–286. [Google Scholar] [CrossRef]
- Huang, R.Q. Large-Scale Landslides and Their Sliding Mechanisms in China since the 20th Century. Chin. J. Rock Mech. Eng. 2007, 26, 433–454. [Google Scholar]
- Zhao, S.Y.; Chigira, M.; Wu, X.Y. Buckling deformations at the 2017 Xinmo landslide site and nearby slopes, Maoxian, Sichuan, China. Eng. Geol. 2018, 246, 187–197. [Google Scholar] [CrossRef]
- Yang, C.M.; Kang, K.H.; Yang, S.H.; Li, K.W.; Wang, H.J.; Lee, Y.T.; Lin, K.K.; Pan, Y.W.; Liao, J.J. Large paleo-rockslide induced by buckling failure at Jiasian in Southern Taiwan. Landslides 2020, 17, 1319–1335. [Google Scholar] [CrossRef]
- Ghasemi, M.; Corkum, A.G.; Gorrell, G.A. Ground surface rock buckling: Analysis of collected cases and failure mechanisms. Bull. Eng. Geol. Environ. 2021, 80, 4255–4276. [Google Scholar] [CrossRef]
- Makedon, T.; Chatzigogos, N. Failure mechanism of overhanging slopes in sedimentary rocks with dissimilar mechanical properties. Bull. Eng. Geol. Environ. 2012, 71, 703–708. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, J.; Du, Y.L.; Gao, Y.; Li, J.Z. A laboratory and field-monitoring experiment on the ability of anti-slide piles to prevent buckling failures in bedding slopes. Environ. Earth Sci. 2021, 80, 44. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, J.; Gao, H.S.S. Analysis of the buckling failure of bedding slope based on monitoring data—A model test study. Geomech. Eng. 2022, 28, 335–346. [Google Scholar] [CrossRef]
- Pei, Z.W.; Zhang, Y.J.; Nian, T.K.; Song, X.L.; Zhao, W. Performance investigation of micropile groups in stabilizing unstable talus slopes via centrifuge model tests. Can. Geotech. J. 2023, 60, 351–365. [Google Scholar] [CrossRef]
- Pei, Z.W.; Zhang, Y.J.; Nian, T.K.; Xiao, S.G.; Liu, H.S. Cross-Scale Analysis on the Working Performance of Micropile Group and Talus Slope System. Sustainability 2023, 15, 8154. [Google Scholar] [CrossRef]
- Onoue, A.; Wakai, A.; Ugai, K.; Higuchi, K.H.; Fukutake, K.Y.; Hotta, H.Y.; Kuroda, S.C.; Nagai, H. Slope failures at Yokowatashi and Nagaoka College of technology due to the 2004 Niigata-ken Chuetsu earthquake and their analytical considerations. Soils Found. 2006, 46, 751–764. [Google Scholar] [CrossRef][Green Version]
- Numada, M.; Konagai, K. Proposal of evaluation approach of slide surface friction coefficient of landslide that uses buckling theory. Seisan Kenkyu 2010, 61, 1021–1024. [Google Scholar] [CrossRef]
- Chigira, M.; Tsou, C.Y.; Higaki, D.; Amatya, S.C. A series of rockslides and gravitational slope deformations aligned along the Kali Gandaki across the Nepal Himalaya. Geomorphology 2022, 400, 108098. [Google Scholar] [CrossRef]
- Li, Y.Y.; Feng, X.Y.; Yao, A.J.; Lin, S.; Wang, R.; Guo, M.Z. A massive ancient river-damming landslide triggered by buckling failure in the upper Jinsha River, SE Tibetan Plateau. Bull. Eng. Geol. Environ. 2021, 80, 5391–5403. [Google Scholar] [CrossRef]
- Li, Y.Y.; Feng, X.Y.; Yao, A.J.; Zhang, Z.H.; Li, K.; Wang, Q.S.; Song, S.Y. Progressive evolution and failure behavior of a Holocene river-damming landslide in the SE Tibetan plateau, China. Landslides 2022, 19, 1069–1086. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Guo, Y.C.; Dai, F.C.; Zhao, S.Y.; Yao, A.J. Analysis of buckling failure process for the Xiaguiwa landslide in southeastern Tibetan Plateau. Q. J. Eng. Geol. Hydrogeol. 2022, 55, 3. [Google Scholar] [CrossRef]
- Kuttėr, H.K. Mechanisms of Slope Failure Other Than Pure Sliding. In Rock Mechanics; Müller, L., Ed.; Springer: Vienna, AT, USA, 1972; pp. 213–220. [Google Scholar] [CrossRef]
- Cavers, D.S. Simple methods to analyze bulking of rock slops. Rock Mech. 1981, 14, 87–104. [Google Scholar] [CrossRef]
- Sun, G.Z.; Zhang, W.B. A Commonly-Sighted Rock Mass Structure—Slab-Rent Structure and Its Mechanical Model. Chin. J. Geol. 1985, 20, 275–282. [Google Scholar]
- Ni, G.R.; Ye, M.X. Mechanicai Analysis of Rock Mass with the “Plate Fracture” Structure. Chin. J. Geotech. Eng. 1987, 9, 99–108. [Google Scholar]
- Sun, G.Z. Rock Mass Structure Mechanics; Science Press: Beijing, China, 1988; pp. 355–362. [Google Scholar]
- Choquet, P.; Hadjigeorgiou, J.; Manini, P.; Mathieu, E.; Soukatchoff, V.; Paquette, Y. Analysis of the strata buckling mechanism at the Grand-Baume coal mine, France. Int. J. Surf. Min. Reclam. Environ. 1993, 7, 29–35. [Google Scholar] [CrossRef]
- Li, S.S.; Ren, G.M.; Zou, S.S. Mechanical analysis of instability mechanism of dip slope in bedded rock mass. J. Geol. Hazards Environ. Preserv. 1995, 6, 24–29. [Google Scholar]
- Adhikary, D.P.; Mühlhaus, H.B.; Dyskin, A.V. A numerical study of flexural buckling of foliated rock slopes. Int. J. Numer. Anal. Met. 2001, 25, 871–884. [Google Scholar] [CrossRef]
- Tommasi, P.; Campedel, P.; Consorti, C.; Ribacchi, R. A discontinuous approach to the numerical modelling of rock avalanches. Rock Mech. Rock Eng. 2008, 41, 37–58. [Google Scholar] [CrossRef]
- Pereira, L.C.; Lana, M.S. Stress–strain analysis of buckling failure in phyllite slopes. Geotech. Geol. Eng. 2013, 31, 297–314. [Google Scholar] [CrossRef]
- Du, Y.Q.; Ren, G.M.; Du, F.; Zhu, S.S.; Yu, T.B. Physical Simulation of Dip slope Bulking Deformation and Its Influencing Factor Sensitivity Analysis. J. Sichuan Univ. Sci. Eng. 2014, 27, 68–71. [Google Scholar]
- Silva, C.; Lana, M.S. Numerical modeling of buckling failure in a mine slope. Rev. Esc. Minas. 2014, 67, 81–86. [Google Scholar] [CrossRef]
- Tang, M.G.; Ma, X.; Zhang, T.T.; Huang, R.Q.; Li, J.Q. Early Recognition and Mechanism of Creep-Buckling of Bedding Slope. J. Eng. Geol. 2016, 24, 442–450. [Google Scholar] [CrossRef]
- Lo, C.M.; Weng, M.C. Identification of deformation and failure characteristics in cataclinal slopes using physical modeling. Landslides 2017, 14, 499–515. [Google Scholar] [CrossRef]
- Zhou, C.; Cao, Y.; Yin, K.L.; Wang, Y.; Shi, X.G.; Catani, F.; Ahmed, B. Landslide Characterization Applying Sentinel-1 Images and InSAR Technique: The Muyubao Landslide in the Three Gorges Reservoir Area, China. Remote Sens. 2020, 12, 3385. [Google Scholar] [CrossRef]
- Wang, Q.S.; Zhang, R.T.; Zheng, H. Buckling failure analysis and numerical manifold method simulation for Malvern Hills slope. Rock Soil Mech. 2022, 43, 1951–1960. [Google Scholar] [CrossRef]
- Miao, C.; Zhang, Y.; Li, Q.K.; Yi, J.S. The deformation mechanism analysis of gently inclined and consequent sliding-buckling rock landslides based on PFC2D. Drilling Eng. 2023, 50, 11–17. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Zhang, Y.J.; Lian, Z.P.; Pei, L.Z.; Liu, Y.L. GIS and cellular automata based slope rainwater movement process model and its application. Sci. Rep. 2024, 14, 9750. [Google Scholar] [CrossRef] [PubMed]
- Weng, M.C.; Chen, T.C.; Tsai, S.J. Modeling scale effects on dip slope deformation by centrifuge model tests and the discrete element method. Landslides 2017, 14, 981–993. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Nian, T.K.; Guo, X.S.; Chen, G.Q.; Zheng, L. Modelling the flexural buckling failure of stratified rock slopes based on the multilayer beam model. J. Mt. Sci. 2019, 16, 1170–1183. [Google Scholar] [CrossRef]
- Shi, J.L.; Zhang, Y.J.; Fan, N.; Tan, J.M.; Pei, L.Z.; Ye, R.Q.; Liu, L. Research Progress on the Instability Mechanisms and Stability Evaluation Method of Buckling Landslides. South China Geol. 2025, 41, 38–50. [Google Scholar]
- Lo, C.M.; Feng, Z.Y. Deformation characteristics of slate slopes associated with morphology and creep. Eng. Geol. 2014, 178, 132–154. [Google Scholar] [CrossRef]
- Yan, M.; Chen, J.P.; Huang, R.Q.; Zhang, Z.Y.; Wang, S.T. Engineering geological analysis on intermediate state before slide-bending failure for rock slope. Water Resour. Hydropower Eng. 2005, 36, 41–44. [Google Scholar]
- Jin, L.L.; Ju, G.H.; Chen, Z.F.; Xiao, Q.F.; Fu, W.X.; Ye, F.; Wei, Y.F. An analytical solution to predict slip-buckling failure of bedding rock slopes under the influence of top loading and earthquakes: Case studies of Hejia landslide and Tangjiashan landslide. Landslides 2024, 21, 152–169. [Google Scholar] [CrossRef]
- Yan, G.Q.; Huang, B.L.; Wang, X.; Dai, Z.W.; Zhang, P.; Qin, Z. Sliding-bending failure mechanism and evaluation of bedding limestone bank slope based on rock mass deterioration in Three Gorges Reservoir area. J. Eng. Geol. 2021, 29, 668–679. [Google Scholar] [CrossRef]
- Qin, S.; Jiao, J.J.; Wang, S. A cusp catastrophe model of instability of slip-buckling slope. Rock Mech. Rock Eng. 2001, 34, 119–134. [Google Scholar] [CrossRef]
- Seale, J. An Engineering Geological Investigation of Footwall Toe-Buckle Instability at the Malvern Hills Opencast Coal Mine. Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 2006. [Google Scholar]
- Tommasi, P.; Verrucci, L.; Campedel, P.; Veronese, L.; Pettinelli, E.; Ribacchi, R. Buckling of high natural slopes: The case of lavini di marco (trento-Italy). Eng. Geol. 2009, 109, 93–108. [Google Scholar] [CrossRef]
- Dai, Z.W.; Yin, Y.P.; Wei, Y.J.; Lu, T.; Luo, J.H.; Yao, W. Deformation and Failure Mechanism of Outang Landslide in Three Gorges Reservoir Area. J. Eng. Geol. 2016, 24, 44–55. [Google Scholar] [CrossRef]
- Huang, D.; He, J.; Song, Y.X.; Guo, Z.Z.; Huang, X.C.; Guo, Y.Q. Displacement Prediction of the Muyubao Landslide Based on a GPS Time-Series Analysis and Temporal Convolutional Network Model. Remote Sens. 2022, 14, 2656. [Google Scholar] [CrossRef]
- Qi, S.W.; Lan, H.X.; Dong, J.Y. An analytical solution to slip buckling slope failure triggered by earthquake. Eng. Geol. 2015, 194, 4–11. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Ma, M.L.; Shang, Y.Q. Analysis of buckling failure of consequent rock slope. J. Zhejiang Univ. Eng. Sci. 2004, 38, 1144–1149. [Google Scholar]
- Liu, H.Y.; Wang, G.H.; Huang, F. Methods to analyze flexural buckling of the consequent slabbed rock slope under top loading. Math. Probl. Eng. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Q.; Zheng, G.; Wang, Z.; Jiang, J.J.; Liu, J.Q. Study on the formation condition of buckling deformation along the bedding slope and the contribution rate of the bevel angle. Sci. Technol. Eng. 2021, 21, 2616–2625. [Google Scholar]
- Zou, Z.X.; Mu, R.; Luo, Y.F.; Guo, B.; Tan, L.; Su, A.J.; Tang, C.Y. Progressive evaluation of buckling landslide stability considering strain softening behavior of the slip zone. Int. J. Numer. Anal. Methods Géoméch. 2022, 46, 2680–2697. [Google Scholar] [CrossRef]
- Liao, L.P.; Zhu, Y.Y.; Yang, Z.Q.; Zou, D.H.; Muhammad, W. Analysis on Rock Bedded Slope of Karakoram Highway, Pakistan. Chin. J. Undergr. Space Eng. 2016, 12, 243–249. [Google Scholar]
- Yang, M.Y.; Zou, Z.S.; Wang, G.B.; Zhang, G.X.; Liu, H.Y. Mechanical Analysis of Slip-Buckling Failure of the Consequent Bedded Rock Slope. Henan Sci. 2023, 41, 1036–1045. [Google Scholar]
- Pei, X.J.; Cui, S.H.; Liang, Y.F.; Wang, H. The multiple earthquakes induced progressive failure of the Xinmo landslide, China: Based on shaking table tests. Environ. Earth Sci. 2023, 82, 465. [Google Scholar] [CrossRef]
- Dai, Z.W.; Zhang, Y.J.; Zhang, C.Y.; Fu, X.L.; Zhang, P.; Ye, R.Q. A photographic method to identify reservoir geohazards induced by rock mass deterioration of hydro-fluctuation belt. Front. Earth Sci. 2024, 12, 1365272. [Google Scholar] [CrossRef]
- Feng, W.K.; Yi, X.Y.; Meng, R.; Xiao, R.H.; Su, Y.C.; Zhu, Q.W. Study on deformation response of Muyubao landslide in Three Gorges region under different water fluctuation rates by centrifugal model test. J. Hydrol. Eng. 2021, 52, 578–588. [Google Scholar] [CrossRef]
- Yan, G.Q.; Yin, Y.P.; Huang, B.L.; Hu, L. Deterioration-buckling failure mechanism of consequent bedding limestone bank slope in Three Gorges Reservoir area. Rock Soil Mech. 2022, 43, 2568–2580. [Google Scholar] [CrossRef]
- Weng, M.C.; Lo, C.M.; Wu, C.H.; Chuang, T.F. Gravitational deformation mechanisms of slate slopes revealed by model tests and discrete element analysis. Eng. Geol. 2015, 189, 116–132. [Google Scholar] [CrossRef]
- Wen, Y.M.; Cheng, Y.; Liang, W.; Chen, C.; Zeng, X.Y.; Sun, W.; Lin, Y. Similitude model experiments for studying slipbuckling failures in high and steep side slopes set along the bedding plane of layered rocks. J. Mines Met. Fuels 2017, 65, 515–520. [Google Scholar]
- Cui, L.; Yang, W.Y.; Sheng, Q.; Zheng, J.J.; Ali, N. Deformation behaviour of strain-softening rock mass in tunnels considering deterioration model of elastic modulus. Géoméch. Geophys. Geo-Energy Geo-Resour. 2024, 10, 171. [Google Scholar] [CrossRef]
- Cui, L.; Yang, W.Y.; Sheng, Q.; Zheng, J.J.; Zhang, W.G.; Guan, K.; Song, F. An enhanced numerical model for considering coupled strain-softening and seepage effects on rock masses surrounding a submarine tunnel. J. Rock Mech. Geotech. Eng. 2025, 17, 1445–1458. [Google Scholar] [CrossRef]
- Cui, L.; Sheng, Q.; Zheng, J.J.; Luo, S. Strain-softening constitutive model of granite and sandstone based on experiments and discrete element method. Sci. Rep. 2024, 14, 24308. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the mechanics of jointed rock. J. Soil. Mech. Found. Div. ASCE 1968, 94, 637–659. [Google Scholar] [CrossRef]
- Bandis, S.C.; Lumsden, A.C.; Barton, N.R. Fundamentals of rock joint deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
- Li, L.Q.; Ju, N.P.; Sheng, D.C. Seismic performance and failure mechanism of interbedded slopes with steep rock layers. Eng. Geol. 2023, 326, 107312. [Google Scholar] [CrossRef]
- Wang, C.; Guo, M.Z.; Chen, X.L.; Gu, K.S.; Gong, Y.F.; Qi, Y.P.; Yuan, D.D.; Zhu, C.; Chen, B.B. Damage evolution of the bedding rock landslide and debris landslide under earthquakes in the Three-rivers Basin. Eng. Geol. 2024, 339, 107631. [Google Scholar] [CrossRef]
- Li, L.Q. Seismic stability of steep consequent rockslides with different lithology assemblies: A comparative Study. Bull. Eng. Geol. Environ. 2024, 83, 353. [Google Scholar] [CrossRef]
- Feng, J.; Zhou, D.P.; Yang, T. Stability analysis of consequent rock slopes using elastic-plastic plate theory. Chin. J. Geotech. Eng. 2010, 32, 1184–1188. [Google Scholar]
- Garzon, S.E.R. Analytical solution for assessing continuum buckling in sedimentary rock slopes based on the tangent-modulus theory. Int. J. Rock Mech. Min. Sci. 2016, 90, 53–61. [Google Scholar] [CrossRef]
- Wang, Q.S.; Zhang, R.T.; Zheng, H.; Zhou, P.Z. An analytical solution of critical sliding displacement for the flexural buckling failure of layered rock slopes. Int. J. Rock Mech. Min. Sci. 2023, 169, 105450. [Google Scholar] [CrossRef]
- Liu, X.L.; Zhou, D.P. Stability analysis of layered dip rocky slopes with elastic plane theory. Rock Soil Mech. 2002, 23, 162–165. [Google Scholar] [CrossRef]
- Wu, P.Y.; Zhang, Z.H.; Dai, F.C.; Yao, A.J. Buckling Deformation Mechanism and Instability Judgment Method of Bedding Rock Slope. J. Jilin Univ. Earth Sci. Ed. 2022, 52, 517–525. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Wu, P.Y.; Dai, F.C.; Li, R.J.; Zhao, X.M.; Jiang, S. An analytical solution for buckling failure of rock slopes based on elastoplastic slab theory. Geomech. Eng. 2024, 37, 1–8. [Google Scholar] [CrossRef]
- Pant, S.R.; Adhikary, D.P. Implicit and explicit modelling of flexural buckling of foliated rock slopes. Rock Mech. Rock Eng. 1999, 32, 157–164. [Google Scholar] [CrossRef]
- Ridl, R.N.; Bell, D.H.; Villenueve, M.C.; Macfarlane, D.F. A Simple Method to Model Buckling Slope Instability Using Continuum Numerical Models. In The Evolution of Geotech-25 Years of Innovation, 1st ed.; Hammah, R., Yacoub, T., McQuillan, A., Curran, J., Eds.; CRC Press: London, UK, 2021; pp. 443–449. [Google Scholar]
- Stead, D.; Eberhardt, E. Developments in the analysis of footwall slopes in surface coal mining. Eng. Geol. 1997, 46, 41–61. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D. Mechanisms of Slope Instability in Thinly Bedded Surface Mine Slopes. In Engineering Geology: A global view from the Pacific Rim, Proceedings of 8th International Congress, International Association for Engineering Geology and the Environment, Vancouver, BC, Canada, 21 September 1998; Morre, D., Hungr, O., Morre, D., Hungr, O., Eds.; Eds.; A.A. Balkema: Rotterdam, Netherlands, 1998; pp. 3011–3018. [Google Scholar]
- Alzo’ubi, A.K.; Martin, C.D.; Mughieda, O.S. Numerical modeling of buckling rock movement. In Proceedings of the Continuum and Distinct Element Numerical Modeling in Geomechanics—2011, Melbourne, Australia, 14–16 January 2011. [Google Scholar]
- Huber, M.; Scholtès, L.; Lavé, J. Stability and failure modes of slopes with anisotropic strength: Insights from discrete element models. Geomorphology 2024, 444, 108946. [Google Scholar] [CrossRef]
- Wu, J.H. Applying discontinuous deformation analysis to assess the constrained area of the unstable Chiu-fen-erh-shan landslide slope. Int. J. Numer. Anal. Methods Geomech. 2006, 31, 649–666. [Google Scholar] [CrossRef]
- Zhang, Y.J. Methods for Seismic Stability of Consequent Bedding Rock Slope and DDA Simulation of Landslide Process. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).