Nationwide Adjustment of Unified Geodetic Control Points for the Modernization of South Korea’s Spatial Reference Frame
Abstract
1. Introduction
2. Materials and Methods
2.1. GNSS Quality Management
- I.
- Total observation time (h),
- II.
- Data acquisition intervals (dt),
- III.
- Estimated vs. actual number of observations,
- IV.
- Multipath effect estimates for L1 and L2 signals (MP1, MP2),
- V.
- Cycle-slip ratios (slps, non_slps, o/slps).
2.2. GNSS Double-Differenced
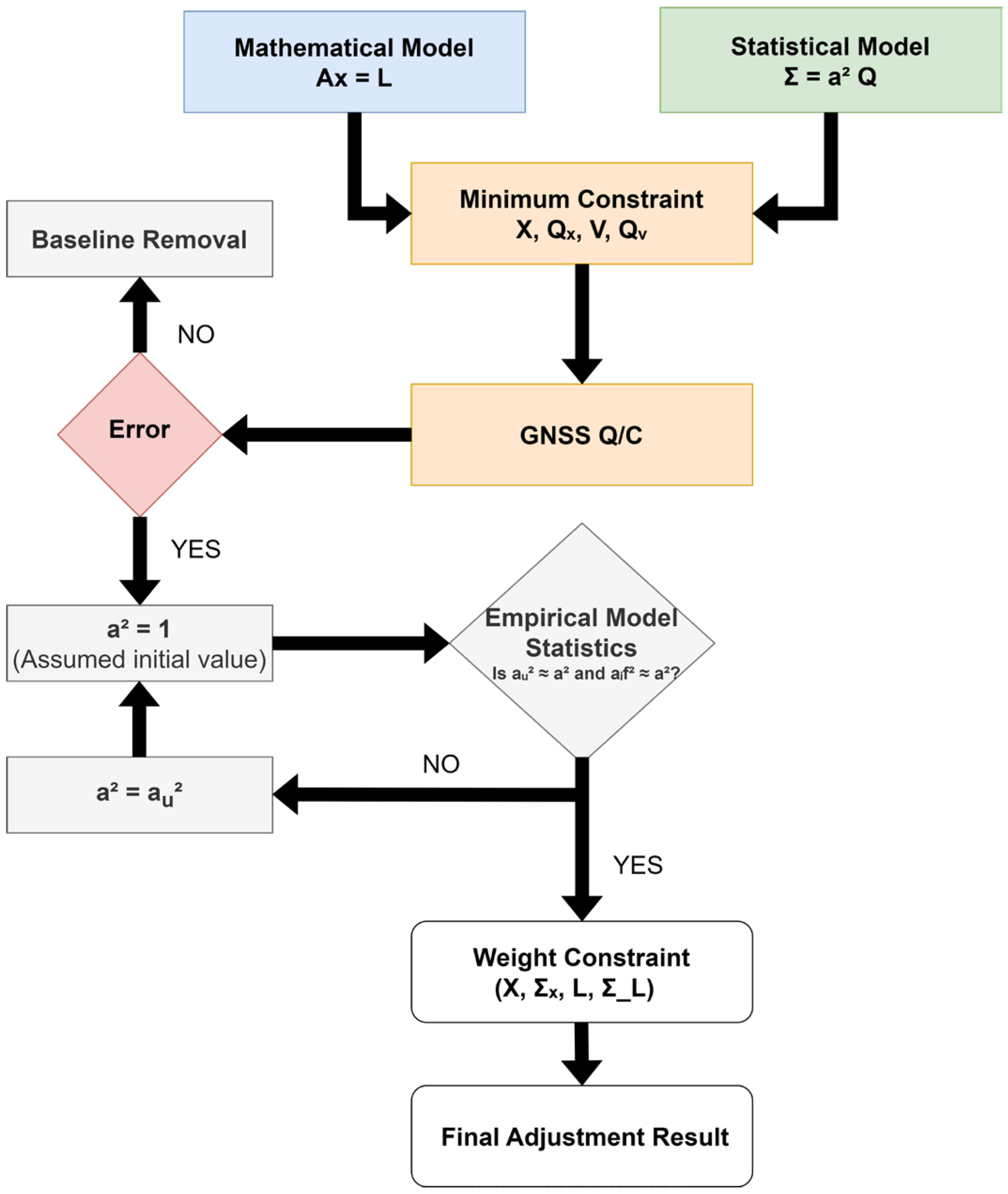
2.3. Network Adjustment Process
2.4. Using GNSS Software
3. Results
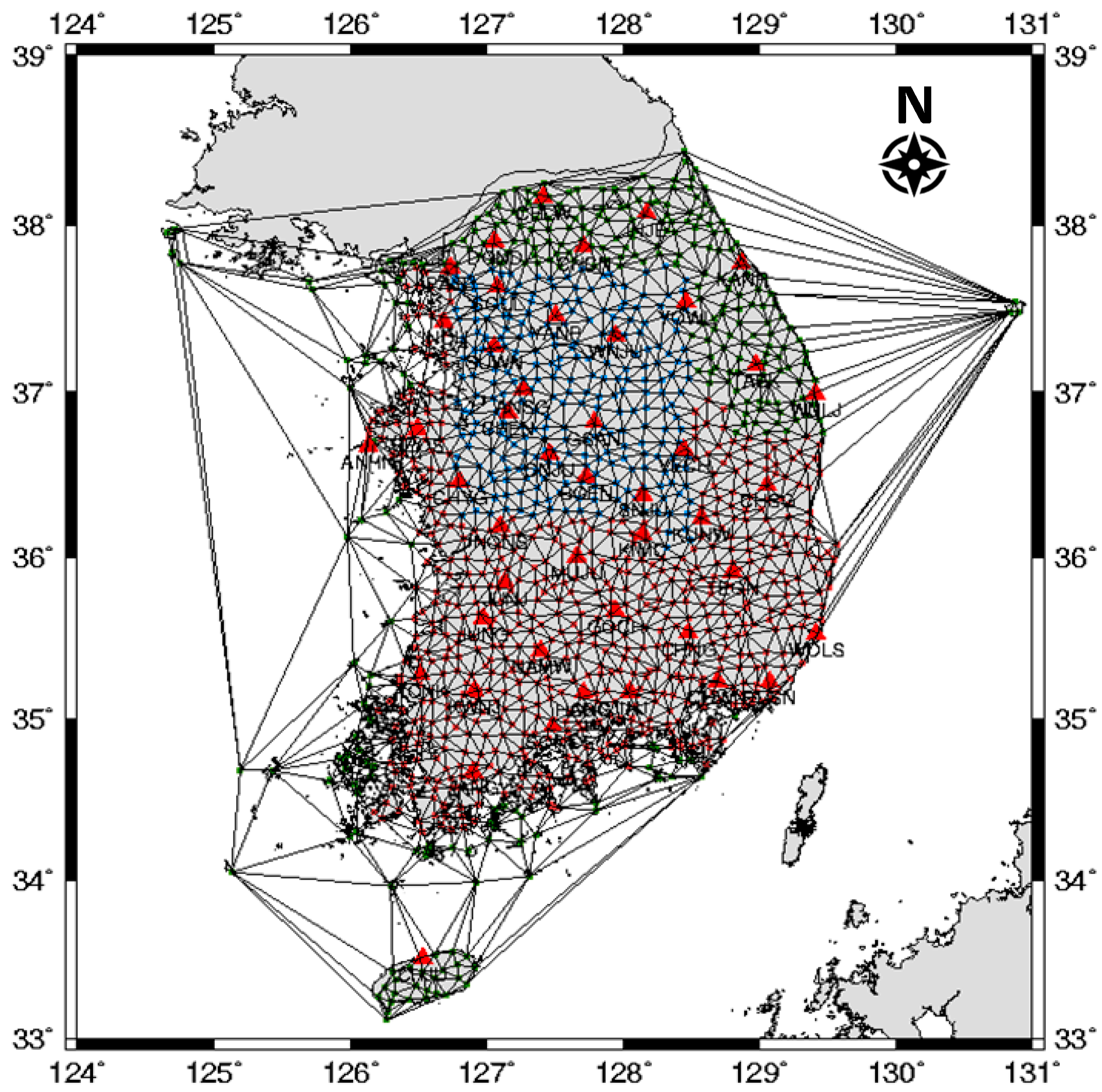
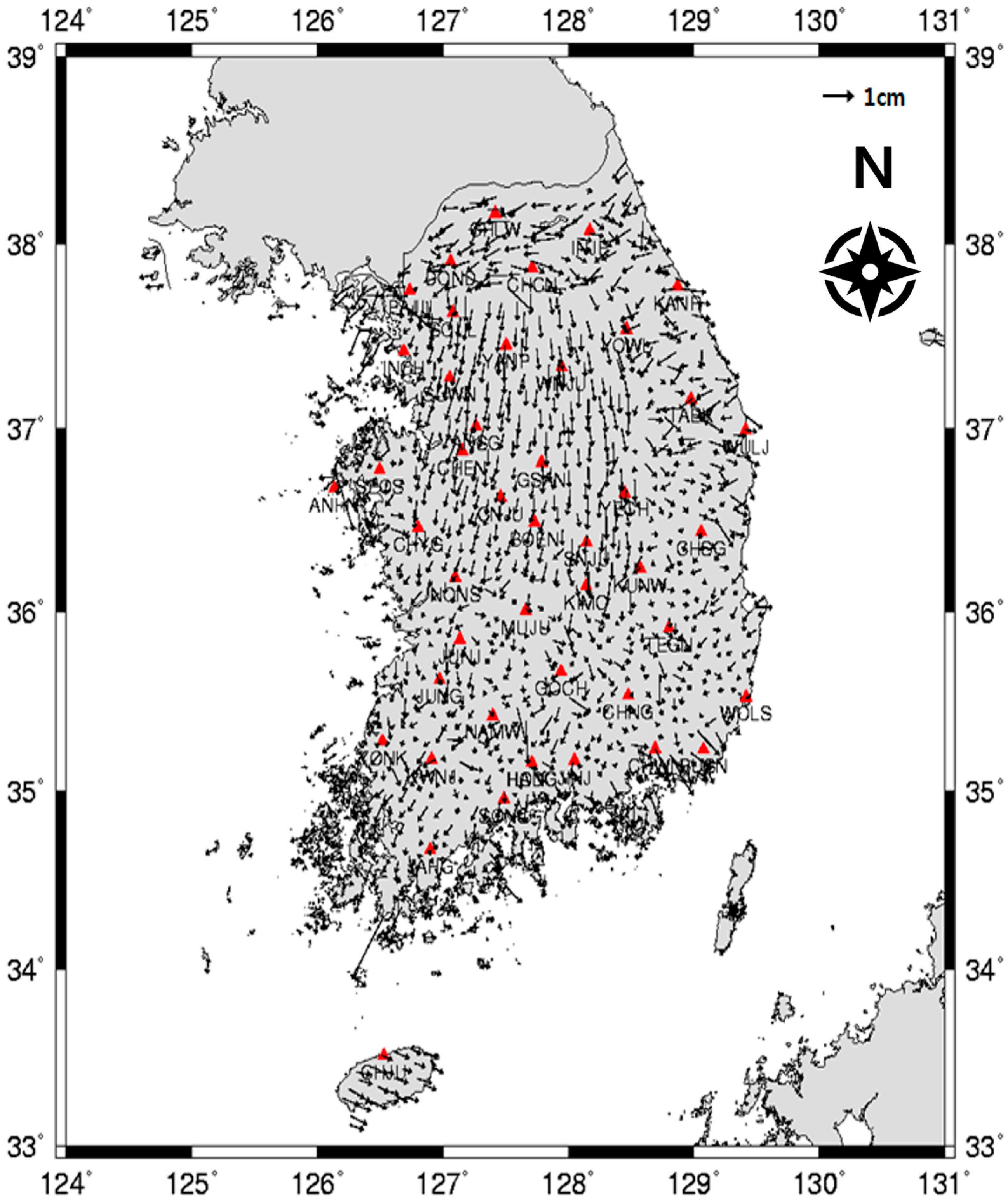
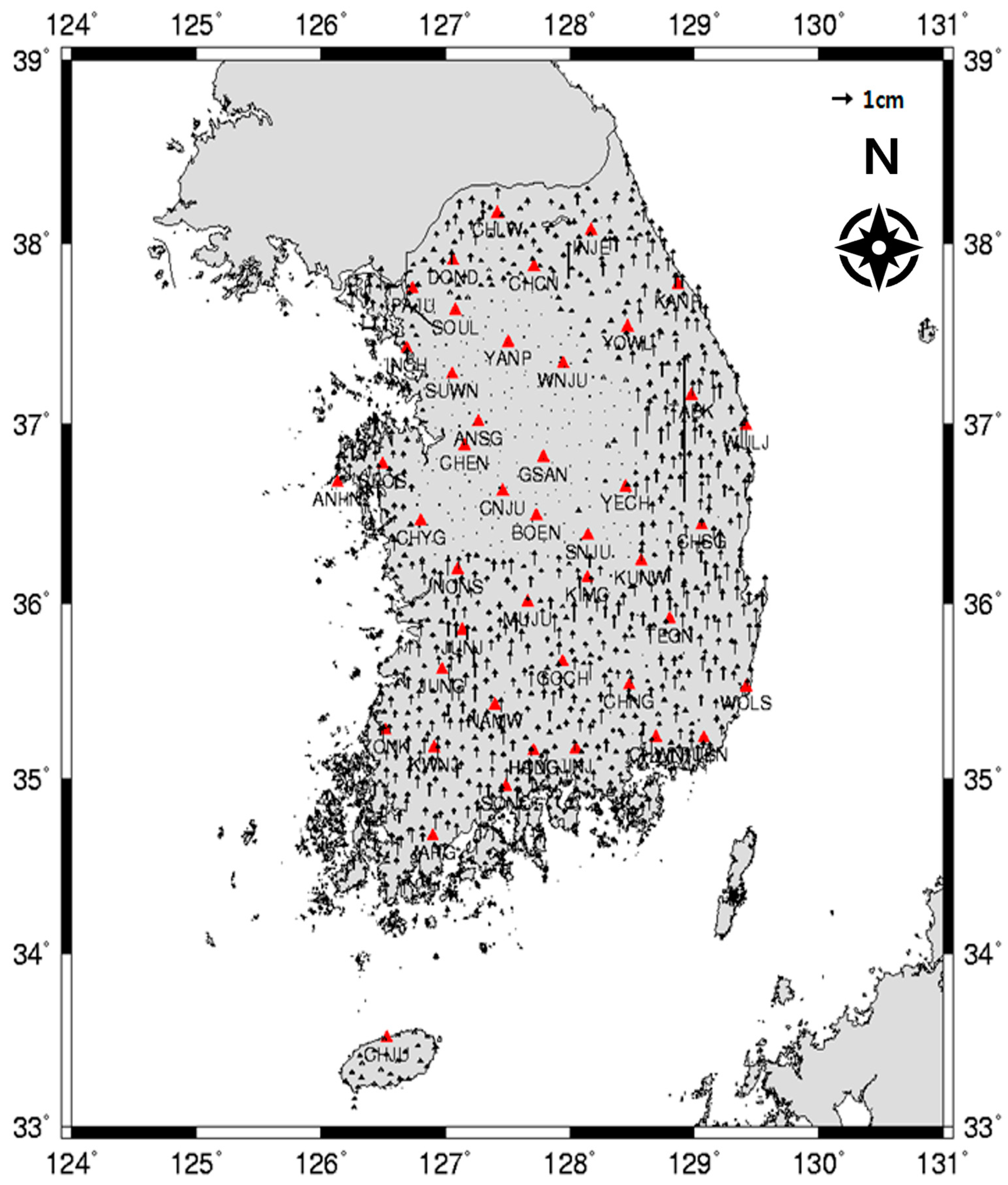
3.1. Fixed Point Selection and Baseline Network Diagram
- i.
- Continuous and stable GNSS observations suitable for long-term positioning applications.
- ii.
- No undocumented hardware changes during the adjustment period.
- iii.
- Complete and validated station metadata including antenna, receiver, and site information.
- iv.
- Even and appropriate spatial distribution across the national territory.
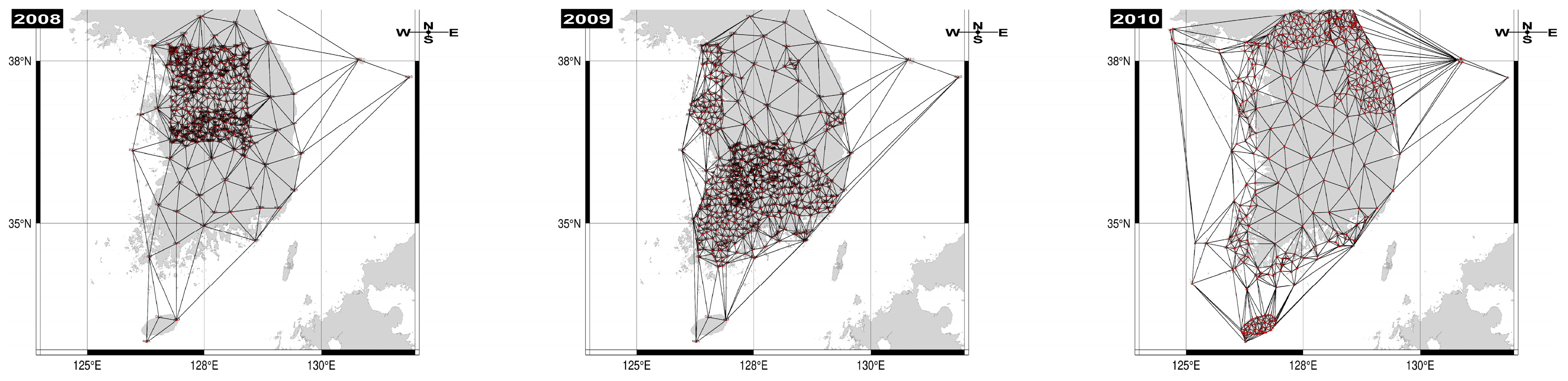
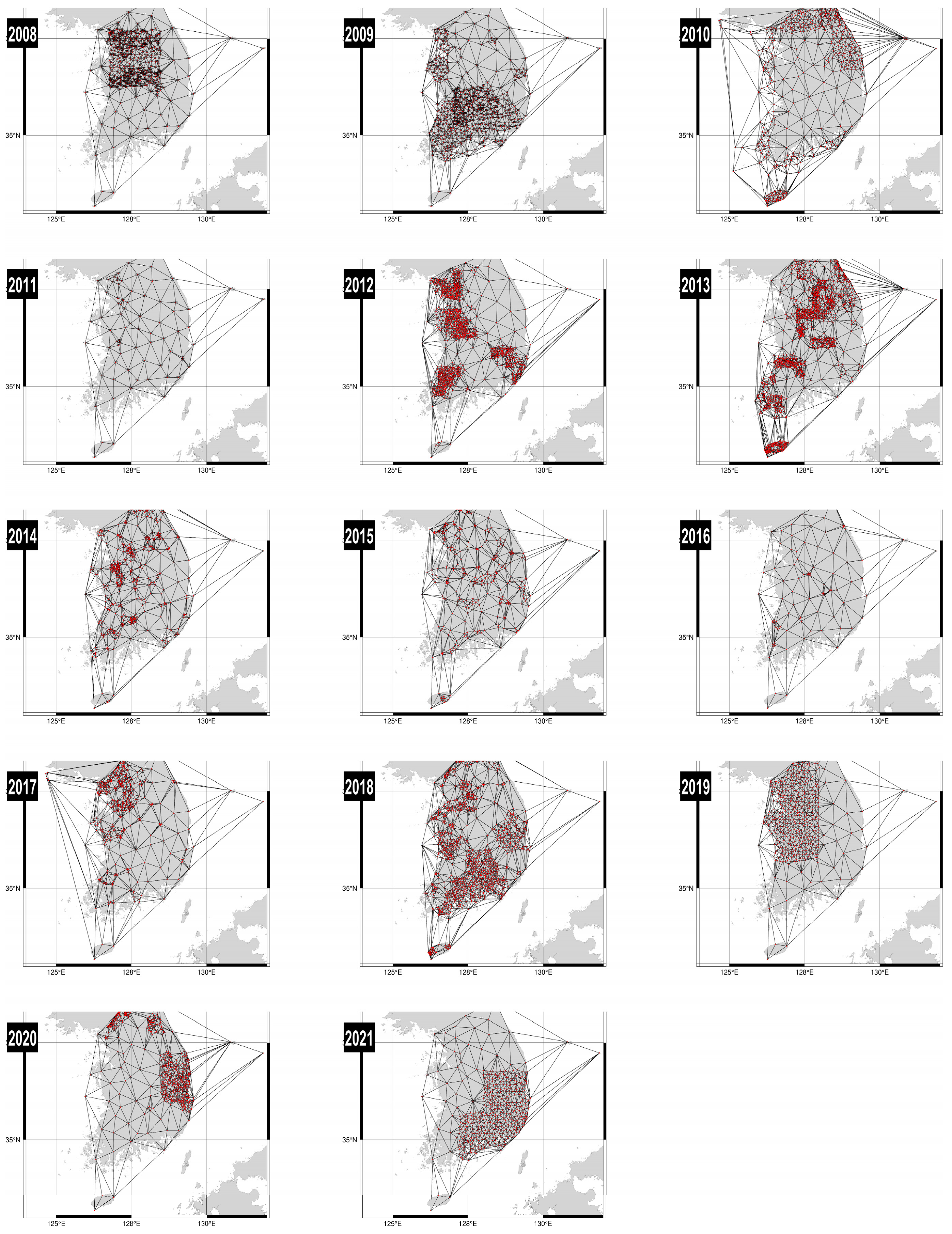
3.2. Pilot Adjustment of Early Unified Control Points (2008–2010) for Strategy Validation
3.3. Full Network Adjustment of 5560 Unified Control Points (2008–2021)
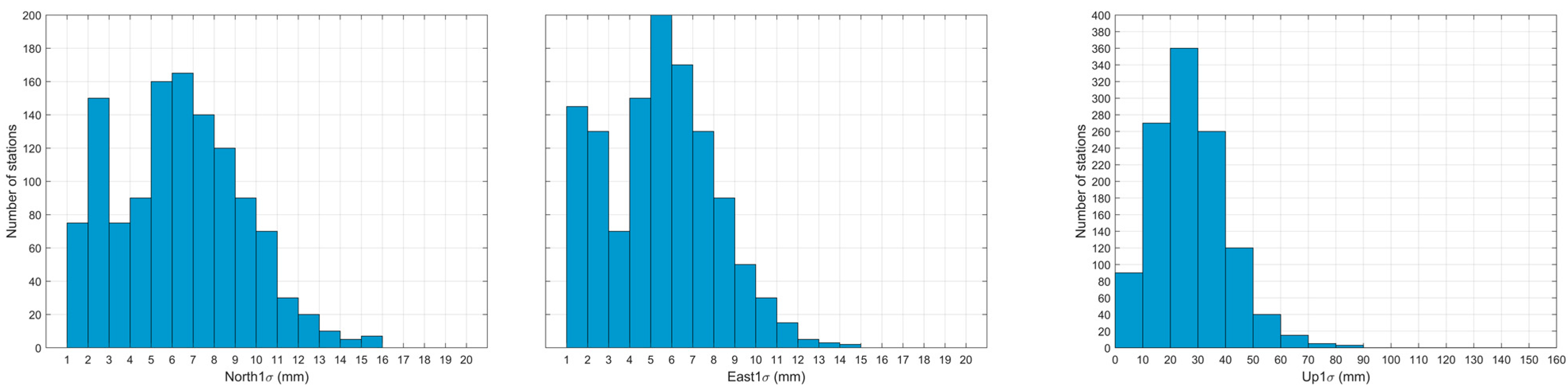
3.4. Accuracy Assessment of GAMIT/GLOBK Adjustment Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Choi, J.H.; Choi, Y.S. Performance Analysis of the First-Order Geodetic Control Survey in Korea. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 1994, 12, 15–24. [Google Scholar]
- Fedman, D. Triangulating Chōsen: Maps, Mapmaking, and the Land Survey in Colonial Korea. Cross-Curr. East Asian Hist. Cult. Rev. 2012, 1, 205–234. [Google Scholar] [CrossRef]
- Central Intelligence Agency. KOREA: Evaluation of Maps; CIA-RDP79-00976A000100070001-1; Central Intelligence Agency: Washington, DC, USA, 1948. Available online: https://www.cia.gov/readingroom/document/cia-rdp79-00976a000100070001-1 (accessed on 13 April 2025).
- University of Texas at Austin. Korea Maps—Perry-Castañeda Library Map Collection; University of Texas Libraries: Austin, TX, USA, 1945; Available online: https://maps.lib.utexas.edu/maps/korea.html (accessed on 13 April 2025).
- National Archives and Records Administration (NARA). Records of U.S. Army Operational, Tactical, and Support Organizations (World War II and Thereafter); Record Group 338; National Archives: Washington, DC, USA. Available online: https://www.archives.gov/research/guide-fed-records/groups/338.html (accessed on 13 April 2025).
- Choi, J.H.; Choi, Y.S. Simultaneous Adjustment of the Korea Precise Primary Geodetic Network by Development Method. KSCE J. Civ. Environ. Eng. Res. 1993, 13, 151–159. [Google Scholar]
- Ministry of Land, Infrastructure and Transport (MOLIT). Disaster Management Geospatial Information; MOLIT: Sejong, Republic of Korea, 2020. Available online: https://www.molit.go.kr (accessed on 13 April 2025).
- Manfré, L.; Santana, R.; Haddad, A.; Campos, M.B.; da Fonseca, L.M.G.; Cartaxo, R. An Analysis of Geospatial Technologies for Risk and Natural Disaster Management. ISPRS Int. J. Geo-Inf. 2012, 1, 166–185. [Google Scholar] [CrossRef]
- World Bank. The Power of Effective Geospatial Information Management in South Korea: Development and Application; World Bank Group Korea Office: Seoul, Republic of Korea, 2020. Available online: https://documents1.worldbank.org/curated/en/716801606984840817/pdf/The-Power-of-Effective-Geospatial-Information-Management-in-South-Korea-Development-and-Application.pdf (accessed on 13 April 2025).
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2—Documentation; Astronomical Institute, University of Bern: Bern, Switzerland, 2015; Available online: https://www.bernese.unibe.ch/docs/DOCU52.pdf (accessed on 13 April 2025).
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Teunissen, P.J.G.; Montenbruck, O. (Eds.) Springer Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to GAMIT/GLOBK; MIT Department of Earth, Atmospheric, and Planetary Sciences: Cambridge, MA, USA, 2018. [Google Scholar]
- International GNSS Service (IGS). Data Transmission Guidelines; IGS: Bern, Switzerland, 2024; Available online: https://igs.org/data-access/ (accessed on 25 March 2025).
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products; IGS: Bern, Switzerland, 2009; Available online: http://acc.igs.org/UsingIGSProductsVer21.pdf (accessed on 25 March 2025).
- Langley, R.B. GPS Receivers and the Observables. In GPS for Geodesy, 2nd ed; Teunissen, P.J.G., Kleusberg, A., Eds.; Springer: Berlin, Heidelberg, 1998; pp. 151–185. [Google Scholar] [CrossRef]
- Rapiński, J.; Tomaszewski, D.; Pelc-Mieczkowska, R. Analysis of Multipath Changes in the Polish Permanent GNSS Stations Network. Remote Sens. 2024, 16, 1617. [Google Scholar] [CrossRef]
- Blewitt, G. Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km. J. Geophys. Res. 1989, 94, 10187–10203. [Google Scholar] [CrossRef]
- Blewitt, G. An Automatic Editing Algorithm for GPS Data. In IAG Symposia; Springer: Ottawa, ON, Canada, 1990. [Google Scholar] [CrossRef]
- Lee, D.; Cho, J.; Suh, Y.; Hwang, J.; Yun, H. A New Window-Based Program for Quality Control of GPS Sensing Data. Remote Sens. 2012, 4, 3168–3183. [Google Scholar] [CrossRef]
- Han, J.; Lee, S.J.; Yun, H.S.; Kim, K.B.; Bae, S.W. PyRINEX: A New Multi-Purpose Python Package for GNSS RINEX Data. PeerJ Comput. Sci. 2024, 10, e1800. [Google Scholar] [CrossRef]
- Estey, L.H.; Meertens, C.M. TEQC: The Multi-Purpose Toolkit for GPS/GLONASS Data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- Kim, M.; Seo, J.; Lee, J. A Comprehensive Method for GNSS Data Quality Determination to Improve Ionospheric Data Analysis. Sensors 2014, 14, 14971–14993. [Google Scholar] [CrossRef]
- Lee, J.; Kim, M. Optimized GNSS Station Selection to Support Long-Term Monitoring of Ionospheric Anomalies for Aircraft Landing Systems. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 236–246. [Google Scholar] [CrossRef]
- Kowalczyk, K.; Rapiński, J. Robust Network Adjustment of Vertical Movements with GNSS Data. Geofizika 2017, 34, 45–65. [Google Scholar] [CrossRef]
- Xu, Y.; Ji, S. Data Quality Assessment and the Positioning Performance Analysis of BeiDou in Hong Kong. Surv. Rev. 2015, 47, 446–457. [Google Scholar] [CrossRef]
- Yigit, C.O.; Gikas, V.; Alçay, S.; Ceylan, A. Performance Evaluation of Short- to Long-Term GPS, GLONASS and GPS/GLONASS Post-Processed PPP. Surv. Rev. 2014, 46, 155–166. [Google Scholar] [CrossRef]
- Grafarend, E.W. Optimization of geodetic networks. Can. Surv. 1974, 28, 716–723. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS: Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Gurtner, W.; Estey, L. The International GNSS Service (IGS): An introduction. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar] [CrossRef]
- Van Hien, N.; Falco, G.; Falletti, E.; Nicola, M.; La, T.V. A Linear Regression Model of the Phase Double Differences to Improve the D3 Spoofing Detection Algorithm. In Proceedings of the 2020 European Navigation Conference (ENC), Dresden, Germany, 23–24 November 2020; pp. 1–14. [Google Scholar] [CrossRef]
- Xu, G. GPS: Theory, Algorithms and Applications; Springer: Berlin, Germany, 2007. [Google Scholar]
- Teunissen, P.J.G.; Kleusberg, A. (Eds.) GPS for Geodesy, 2nd ed.; Springer: Berlin, Germany, 1998. [Google Scholar] [CrossRef]
- Dong, D.; Bock, Y. Global positioning system network analysis with phase ambiguity resolution applied to crustal deformation studies in California. J. Geophys. Res. Solid Earth 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- Schaffrin, B. Reliability measures for correlated observations. J. Surv. Eng. 1997, 123, 126–137. [Google Scholar] [CrossRef]
- Snow, K.B. Notes on Adjustment Computations: Parts I and II; School of Earth Sciences, The Ohio State University: Columbus, OH, USA, 2021; Available online: https://earthsciences.osu.edu/sites/default/files/2021-09/osu_adjustment_computation_notes_parts_1_and_2.pdf (accessed on 15 April 2025).
- Soler, T.; Marshall, J. Rigorous transformation of variance–covariance matrices of GPS-derived coordinates and velocities. GPS Solut. 2002, 6, 76–90. [Google Scholar] [CrossRef]
- Wang, P.; Cetin, E.; Dempster, A.G.; Wang, Y.; Wu, S. GNSS interference detection using statistical analysis in the time-frequency domain. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 416–428. [Google Scholar] [CrossRef]
- Du, Y.; Li, Y.; Wang, J.; Zhang, Y.; Xu, Y. Vulnerabilities and integrity of precise point positioning for intelligent transportation systems. Satell. Navig. 2021, 2, 3. [Google Scholar] [CrossRef]
- Sun, R.; Qiu, M.; Liu, F.; Wang, Z.; Ochieng, W.Y. A Dual w-Test Based Quality Control Algorithm for Integrated IMU/GNSS Navigation in Urban Areas. Remote Sens. 2022, 14, 2132. [Google Scholar] [CrossRef]
- Tiberius, C.C.J.M.; de Jonge, P.J. Fast ambiguity resolution for real-time applications. In Proceedings of the 9th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1996), Kansas City, MO, USA, 17–20 September 1996; pp. 1077–1084. [Google Scholar]
- Gargula, T. Adjustment of an Integrated Geodetic Network Composed of GNSS Vectors and Classical Terrestrial Linear Pseudo-Observations. Appl. Sci. 2021, 11, 4352. [Google Scholar] [CrossRef]
- Karsznia, K.; Osada, E.; Muszyński, Z. Real-Time Adjustment and Spatial Data Integration Algorithms Combining Total Station and GNSS Surveys with an Earth Gravity Model. Appl. Sci. 2023, 13, 9380. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to GAMIT/GLOBK; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010; Available online: http://www-gpsg.mit.edu/gg/docs/Intro_GG.pdf (accessed on 15 April 2025).
- National Geodetic Survey (NGS). Standards and Specifications for Geodetic Control Networks; Federal Geodetic Control Committee: Silver Spring, MD, USA, 1984. Available online: https://www.ngs.noaa.gov/FGCS (accessed on 15 April 2025).
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual, GPS Analysis at MIT, Release 10.7; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018; Available online: http://www-gpsg.mit.edu/gg/docs/GAMIT_Ref.pdf (accessed on 15 April 2025).
- Herring, T.A.; King, R.W.; McClusky, S.C. GLOBK Reference Manual, Global Kalman Filter VLBI and GPS Analysis Program, Release 10.7; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018; Available online: http://www-gpsg.mit.edu/gg/docs/GLOBK_Ref.pdf (accessed on 15 April 2025).
- Rebischung, P.; Altamimi, Z.; Ray, J.; Garayt, B. The IGS contribution to ITRF2014. J. Geod. 2016, 90, 611–630. [Google Scholar] [CrossRef]
- International GNSS Service (IGS). Guidelines for Continuously Operating Reference Stations in the IGS; International GNSS Service: Pasadena, CA, USA, 2023; Available online: https://igs.org/news/igs-cors-guidelines/ (accessed on 15 April 2025).
- Intergovernmental Committee on Surveying and Mapping (ICSM). Guideline for Continuously Operating Reference Stations—SP1 Version 2.2; Intergovernmental Committee on Surveying and Mapping: Symonston, Australia, 2017. Available online: https://icsm.gov.au/sites/default/files/2020-12/Guideline-for-Continuously-Operating-Reference-Stations_v2.2.pdf (accessed on 15 April 2025).
- National Geodetic Survey (NGS). NGS Guidelines for Real-Time GNSS Networks v2.2; National Geodetic Survey: Silver Spring, MD, USA, 2011. Available online: https://www.ngs.noaa.gov/PUBS_LIB/NGSGuidelinesForRealTimeGNSSNetworksV2.2.pdf (accessed on 15 April 2025).
- Altamimi, Z.; Sillard, P.; Boucher, C. ITRF2000: A new release of the International Terrestrial Reference Frame for earth science applications. J. Geophys. Res. Solid Earth 2002, 107, ETG 2-1–ETG 2-19. [Google Scholar] [CrossRef]
- King, R.W.; Bock, Y. Documentation for the GAMIT GPS Analysis Software. Massachusetts Institute of Technology: Cambridge, MA, USA, 2003. [Google Scholar]
- Abdalla, A.; Mustafa, M. Horizontal displacement of control points using GNSS differential positioning and network adjustment. Measurement 2021, 174, 108965. [Google Scholar] [CrossRef]
- Kanhere, A.; Gupta, S.; Shetty, A.; Gao, G. Improving GNSS positioning using neural-network-based corrections. Navigation 2021, 69, 857–873. [Google Scholar] [CrossRef]
- Mohanty, A.; Gao, G. Learning GNSS positioning corrections for smartphones using graph convolution neural networks. Navigation 2022, 70, 1–15. [Google Scholar] [CrossRef]
- Tang, Y.; Sun, J.; Li, Y.; Zhou, J. Improving GNSS positioning correction using deep reinforcement learning with an adaptive reward augmentation method. Navigation 2024, 71, 1–17. [Google Scholar] [CrossRef]
- Jalalirad, A.; Belli, D.; Major, B.; Jee, S.; Shah, H.; Morrison, W. GNSS positioning using cost function regulated multilateration and graph neural networks. arXiv 2024, arXiv:2402.18630. Available online: https://arxiv.org/abs/2402.18630 (accessed on 15 April 2025).




| Index | Function |
|---|---|
| first EPOCH | GNSS observation start time (year/month/day/hour) |
| last EPOCH | GNSS observation end time (year/month/day/hour) |
| hrs | Total observation duration [unit: hours] |
| dt | Data reception interval [unit: seconds] |
| expt | Estimated total number of observations (elevation angle applied) |
| have | Actual number of observations |
| Average multipath length of L1 signal [unit: m] | |
| Average multipath length of L2 signal [unit: m] | |
| o/slps | (Actual number of observations)/(number of cycle slips) |
| slps | Number of cycle slips |
| non_slps | Percentage of observations without cycle slip [unit: %] |
| Satellite | Total Observations | Acquisitions | Acquisition Rate | Threshold | Cycle Slip | Comparison |
|---|---|---|---|---|---|---|
| G02 | 141 | 19 | 13.5% | 70% | 0 | unpassed |
| G03 | 522 | 481 | 92.1% | 70% | 0 | passed |
| G04 | 374 | 274 | 73.3% | 70% | 0 | passed |
| … | … | … | … | … | … | … |
| G06 | 448 | 405 | 90.4% | 70% | 1 | passed |
| G07 | 594 | 473 | 79.6% | 70% | 2 | unpassed |
| Satellite | MP1 | MP2 | Comparison |
|---|---|---|---|
| G02 | 0.41(m) | 0.45(m) | passed |
| G03 | 0.31 | 0.41 | passed |
| G04 | 0.26 | 0.40 | passed |
| … | … | … | … |
| G06 | 0.47 | 0.74 | unpassed |
| G07 | 0.40 | 0.49 | passed |
| Year | 08 | 09 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|
| Observation point | 886 | 1407 | 820 | 23 | 2396 | 3382 | 1089 |
| Outlier | 48 | 61 | 208 | 1 | 604 | 554 | 422 |
| Rate | 5.4% | 4.3% | 25.3% | 4.3% | 25.1% | 16.4% | 38.8% |
| Year | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Observation point | 488 | 647 | 1941 | 1770 | 774 | 741 | 668 |
| Outlier | 23 | 188 | 923 | 251 | 370 | 328 | 319 |
| Rate | 29.1% | 29.1% | 47.6% | 14.1% | 47.8% | 44.2% | 47.2% |
| Year | Region (Example) | Adjustment Software | UCPs |
|---|---|---|---|
| 2008 | Seoul, Gyeonggi, Gangwon | GAMIT/GLOBK | ~300 |
| 2009 | Gyeongsang, Jeolla | Bernese | ~600 |
| 2010 | Gangwon, Jeju | GAMIT/GLOBK | ~300 |
| SITE | N | E | H | dN | dE | dH |
|---|---|---|---|---|---|---|
| UCP001 | 518,199.1056 | 202,524.8082 | 69.6456 | 0.0069 | 0.0011 | −0.0046 |
| UCP002 | 632,748.5197 | 300,213.5836 | 450.1037 | −0.0009 | 0.0027 | 0.0142 |
| UCP003 | 649,301.4179 | 326,825.3849 | 31.0333 | −0.0066 | −0.0060 | 0.0350 |
| UCP004 | 642,899.4686 | 327,998.3013 | 49.0462 | −0.0039 | −0.0057 | 0.0404 |
| UCP005 | 630,251.8133 | 320,260.1322 | 610.8182 | −0.0048 | −0.0068 | 0.0137 |
| … | … | … | … | … | … | … |
| Mean | 0.00073 | −0.0019 | 0.0190 | |||
| STD | 0.0047 | 0.0035 | 0.0237 | |||
| RMSE | 0.0047 | 0.0039 | 0.0304 | |||
| Max. | 0.0123 | 0.0087 | 0.4566 |
| Direction | RMSE (cm) | Coordinate Difference (cm) Min/Max/Mean | Standard Deviation (cm) |
|---|---|---|---|
| East (E) | 1.4 | 0.00/85.69/0.63 | 1.25 |
| North (N) | 1.33 | 0.00/81.09/0.60 | 1.18 |
| Vertical (U) | 64.8 | 0/4826.36/3.49 | 64.71 |
| Direction | RMSE (cm) | Coordinate Difference (cm) Min/Max/Mean | Standard Deviation (cm) |
|---|---|---|---|
| East (E) | 0.79 | 0.00/2.48/0.61 | 0.5 |
| North (N) | 50.0 | 0.00/2.35/0.58 | 0.48 |
| Vertical (U) | 64.8 | 0.00/9.46/2.35 | 1.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-J.; Yun, H.-S. Nationwide Adjustment of Unified Geodetic Control Points for the Modernization of South Korea’s Spatial Reference Frame. Appl. Sci. 2025, 15, 5500. https://doi.org/10.3390/app15105500
Lee S-J, Yun H-S. Nationwide Adjustment of Unified Geodetic Control Points for the Modernization of South Korea’s Spatial Reference Frame. Applied Sciences. 2025; 15(10):5500. https://doi.org/10.3390/app15105500
Chicago/Turabian StyleLee, Seung-Jun, and Hong-Sik Yun. 2025. "Nationwide Adjustment of Unified Geodetic Control Points for the Modernization of South Korea’s Spatial Reference Frame" Applied Sciences 15, no. 10: 5500. https://doi.org/10.3390/app15105500
APA StyleLee, S.-J., & Yun, H.-S. (2025). Nationwide Adjustment of Unified Geodetic Control Points for the Modernization of South Korea’s Spatial Reference Frame. Applied Sciences, 15(10), 5500. https://doi.org/10.3390/app15105500







