High-Precision Positioning Method for Robot Acoustic Ranging Based on Self-Optimization of Base Stations
Abstract
1. Introduction
2. High-Precision Confidence Interval Weight Assignment Method for Acoustic Ranging
2.1. Acoustic Localization Error Factors
2.2. Preprocessing Methods for Sound Signals
2.3. High-Precision Confidence Interval Weight Assignment Method
3. Base Station Deployment and Self-Optimization Positioning Method
3.1. Trilateration Positioning
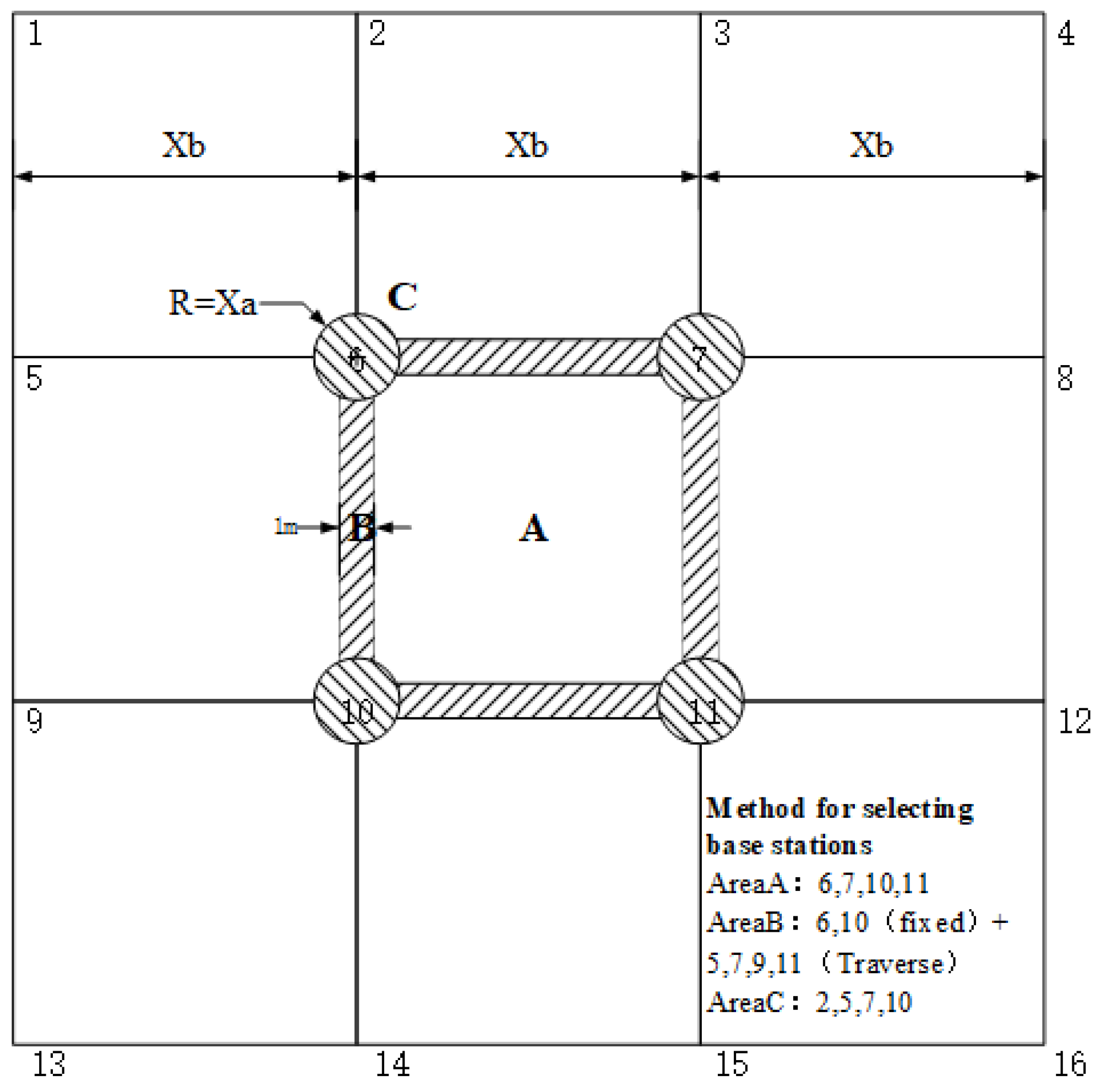
3.2. Base Station Deployment and Transition Zone Division Method
3.3. Self-Optimization Positioning Method for Base Stations
3.3.1. A-Type Central Area
- (1)
- There are four distance measurements with weights greater than or equal to 0.5;
- (2)
- There are only three distance measurements with weights greater than or equal to 0.5;
- (3)
- There are only two distance measurements with weights greater than or equal to 0.5.
3.3.2. B-Type Transition Area
3.3.3. C-Type Transition Area
3.3.4. Judgment Logic
| Algorithm 1 Base station self optimization algorithm | |
| 1: | Input: Distance set d, Time t−1 coordinate set pointt−1 |
| 2: | Output: Time t coordinate set pointt |
| 3: | d_min ← min(d) |
| 4: | If d_min < xa |
| 5: | AreaC; |
| 6: | else |
| 7: | Dis ← dist(d, pointt−1) |
| 8: | If dis < 0.5 |
| 9: | AreaB; |
| 10: | else |
| 11: | AreaA; |
| 12: | End if |
| 13: | End if |
3.4. Experiment and Results
3.4.1. Simulation Experiment on Positioning Accuracy of A-Type Central Area
3.4.2. Cross-Regional Positioning Accuracy Comparison Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TOF | Time of Flight |
| GPS | Global Positioning System |
| UWB | Ultra-Wide Band |
| SLAM | Simultaneous Localization and Mapping |
| GCC | Generalized Cross-Correlation |
| CC | Cross-Correlation |
| TDOA | Time Difference in Arrival |
References
- Li, S.; Chang, X.; Yang, C.; Jiang, K.; Wang, Z.; Wang, L.; Li, X. A Fast Vehicle Horn Sound Location Method with Improved SRP-PHAT. In Proceedings of the 2018 IEEE International Conference on Progress in Informatics and Computing (PIC), Suzhou, China, 14–16 December 2018. [Google Scholar]
- Dibiase, J.H. A High-Accuracy, Low-Latency Technique for Talker Localization in Reverberant Environments. Ph.D. Thesis, Brown University, Providence, RI, USA, 2000. [Google Scholar]
- Sieriebriakov, A.; Hospodarchuk, O.; Lakhtyr, D.; Simakhin, V.; Bondar, S. Technology of sound source localization based on incoming sound intensity. In Proceedings of the 2023 IEEE 18th International Conference on Computer Science and Information Technologies (CSIT), Lviv, Ukraine, 19–21 October 2023. [Google Scholar]
- Wang, J.; Guo, Y.; Lu, S.; Zhang, Y.; Shu, H. An Acoustic Indoor Localization Method Based on Directional Variability for Mobile Robot. In Proceedings of the 2024 IEEE International Conference on Industrial Technology (ICIT), Bristol, UK, 25–27 March 2024. [Google Scholar]
- Wu, S.; Zhang, S.; Huang, D. A TOA-Based Localization Algorithm With Simultaneous NLOS Mitigation and Synchronization Error Elimination. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Tong, K.; Wang, X.; Khabbazibasmenj, A.; Dounavis, A. Optimum reference node deployment for TOA-based localization. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015. [Google Scholar]
- Zhu, K.; Wei, Y.; Xu, R. TOA-based localization error modeling of distributed MIMO radar for positioning accuracy enhancement. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016. [Google Scholar]
- Koohzadi, M.; Ebadollahi, S.; Vahidnia, R.; Dian, F.J. Implementation and Comparison of Different Tropospheric Models to Reduce Error Low-cost Real-time GPS Positioning. In Proceedings of the 2019 IEEE 10th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 17–19 October 2019. [Google Scholar]
- Yan, Z.; Wan-Fang, Z.; Li-Li, C. Design of Robot Positioning System Based on the Integration of Slam System and Inertial System. In Proceedings of the 2022 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Hengyang, China, 26–27 March 2022. [Google Scholar]
- Wu, F.; Liu, Z. Research on UWB/IMU Fusion Positioning Technology in Mine. In Proceedings of the 2020 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Vientiane, Laos, 11–12 January 2020. [Google Scholar]
- Zhang, Z.; Han, X.; Shi, Y.; Wang, Y.; Ma, L.; Yin, J. Acoustic Positioning System Beneath the Arctic Ice and Its Experimental Verification. In Proceedings of the 2024 OES China Ocean Acoustics (COA), Harbin, China, 29–31 May 2024. [Google Scholar]
- Goldoni, E.; Savioli, A.; Risi, M.; Gamba, P. Experimental analysis of RSSI-based indoor localization with IEEE 802.15.4. In Proceedings of the 2010 European Wireless Conference (EW), Lucca, Italy, 12–15 April 2010. [Google Scholar]
- Banda, S.; Hemanth, K.; Karanam Uma Maheshwar, R. A robust approach for WSN localization for underground coal mine monitoring using improved RSSI technique. Math. Model. Eng. Probl. 2018, 5, 225–231. [Google Scholar]
- Zhou, Y.; Qiu, T.; Xia, F.; Hou, G. N-Times Trilateral Centroid Weighted Localization Algorithm of Wireless Sensor Networks. In Proceedings of the Internet of Things (iThings/CPSCom), 2011 International Conference on and 4th International Conference on Cyber, Physical and Social Computing, Dalian, China, 19–22 October 2011. [Google Scholar]
- Fang, H.; Li, Y. Wireless Basestation Location Algorithm based on Clustering and TDOA. Commun. Technol. 2019, 311–317. [Google Scholar] [CrossRef]
- Bao, J.; Huo, Z.; Xu, W.; Zhao, Y. A Wireless Location Method with High Precision for Underground Personnel Tracking. Ind. Mine Autom. 2009, 10, 18–21. [Google Scholar]
- Zu, M.; Rong, X. UWB Indoor Localization Algorithm Based on Inner Triangle Centroid Correction and Taylor. Nat. Sci. J. Harbin Norm. Univ. 2018, 42–47. [Google Scholar] [CrossRef]

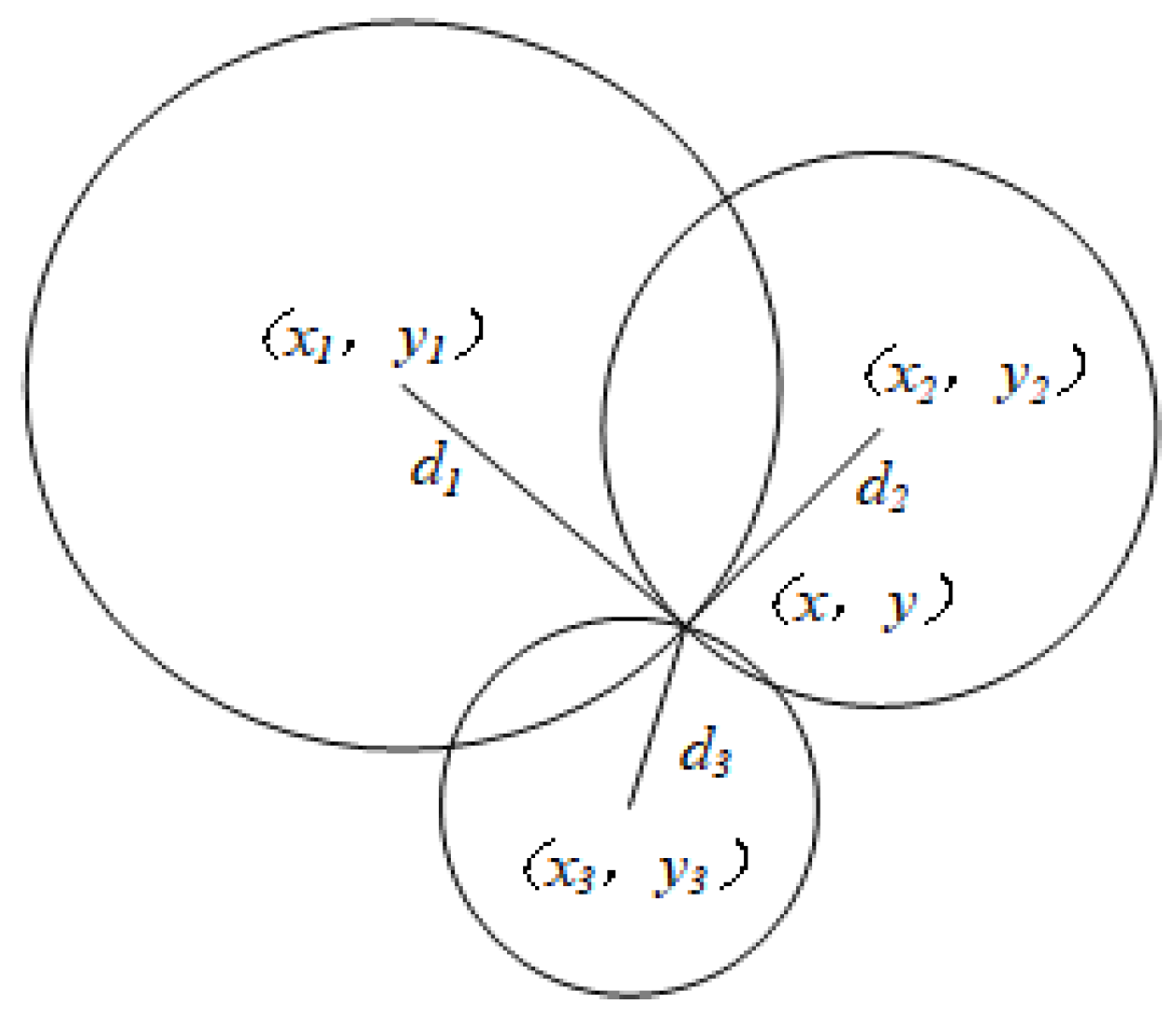


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Chen, J.; Gao, B.; Sun, Y.; Ling, X.; Li, Z.; Gong, L. High-Precision Positioning Method for Robot Acoustic Ranging Based on Self-Optimization of Base Stations. Appl. Sci. 2025, 15, 5478. https://doi.org/10.3390/app15105478
Zhang Z, Chen J, Gao B, Sun Y, Ling X, Li Z, Gong L. High-Precision Positioning Method for Robot Acoustic Ranging Based on Self-Optimization of Base Stations. Applied Sciences. 2025; 15(10):5478. https://doi.org/10.3390/app15105478
Chicago/Turabian StyleZhang, Zekai, Jiayu Chen, Bishu Gao, Yefeng Sun, Xiaofeng Ling, Zheyuan Li, and Liang Gong. 2025. "High-Precision Positioning Method for Robot Acoustic Ranging Based on Self-Optimization of Base Stations" Applied Sciences 15, no. 10: 5478. https://doi.org/10.3390/app15105478
APA StyleZhang, Z., Chen, J., Gao, B., Sun, Y., Ling, X., Li, Z., & Gong, L. (2025). High-Precision Positioning Method for Robot Acoustic Ranging Based on Self-Optimization of Base Stations. Applied Sciences, 15(10), 5478. https://doi.org/10.3390/app15105478







