Modeling and Analysis of Dynamics of Rigid–Flexible Coupled Parallel Robots
Abstract
1. Introduction
2. Modal Vector Bond Graph
2.1. Modal Vector Bond Graph Concepts
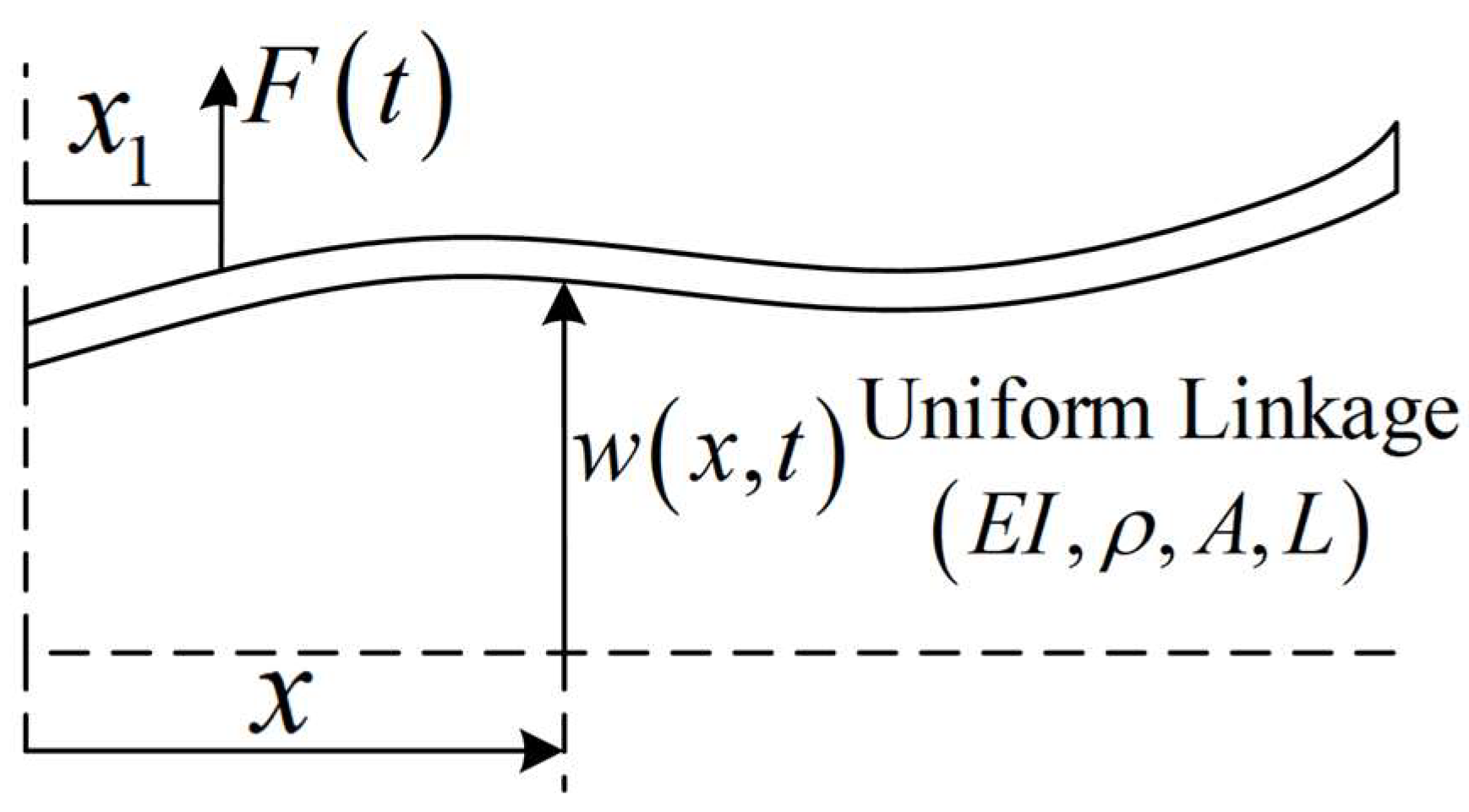
2.2. Flexible Connecting Rod Bond Graph Modeling
2.3. Hybrid Bond Graph Rigid–Flexible Coupled Rod System
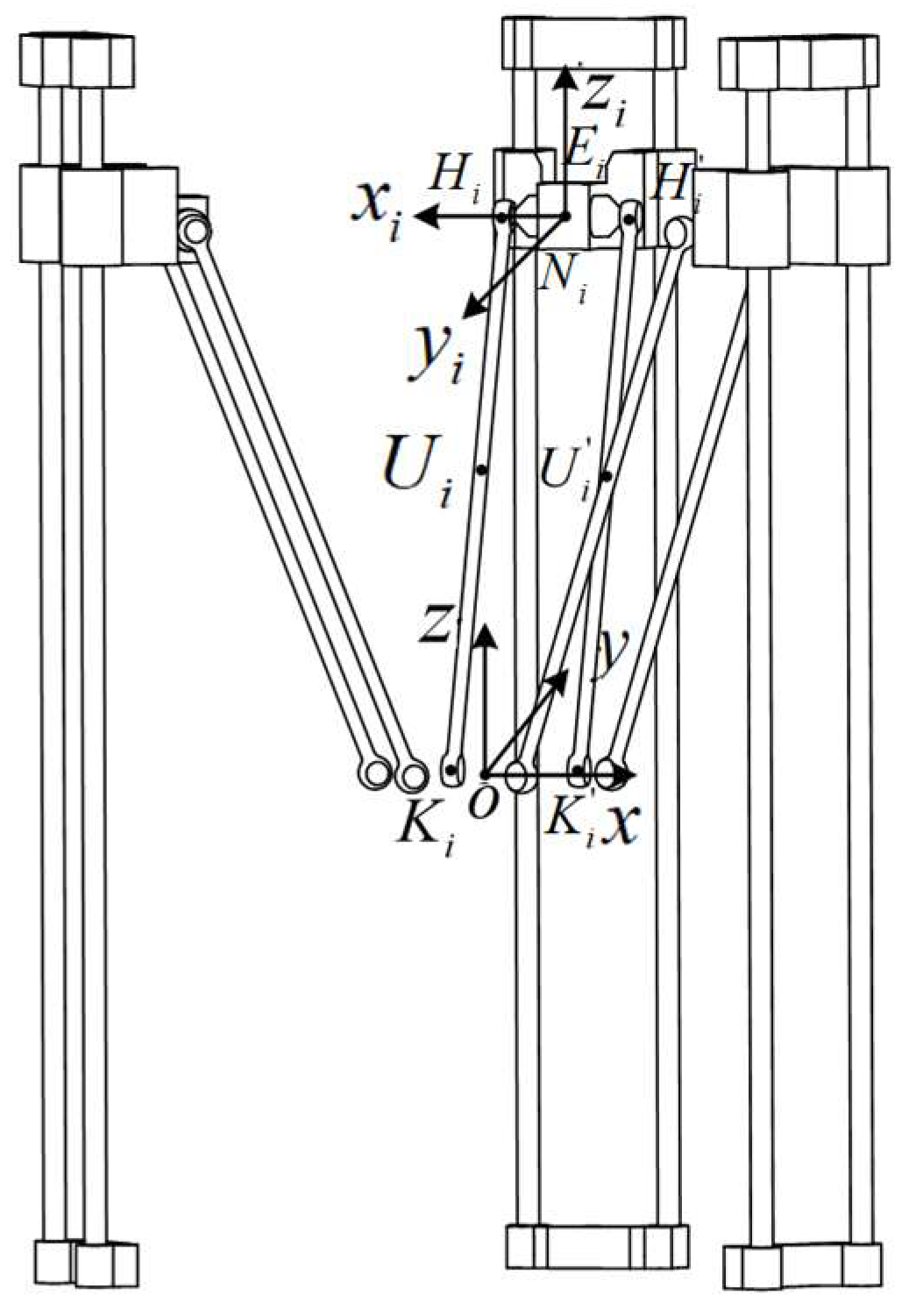
3. Modeling of Spatial Delta-Type Robot Dynamics Considering Linkage Flexibility
3.1. Introduction to the Organization
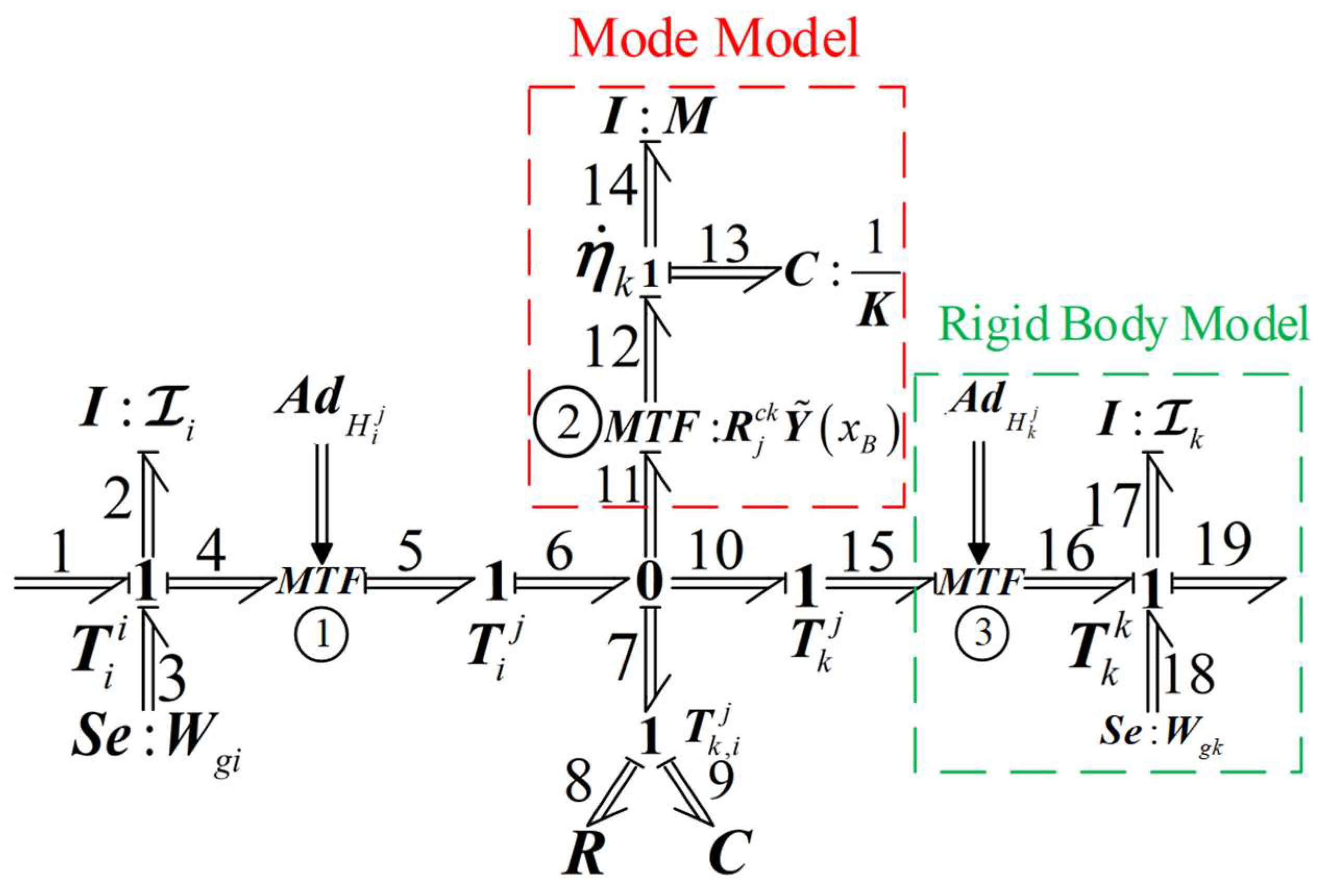
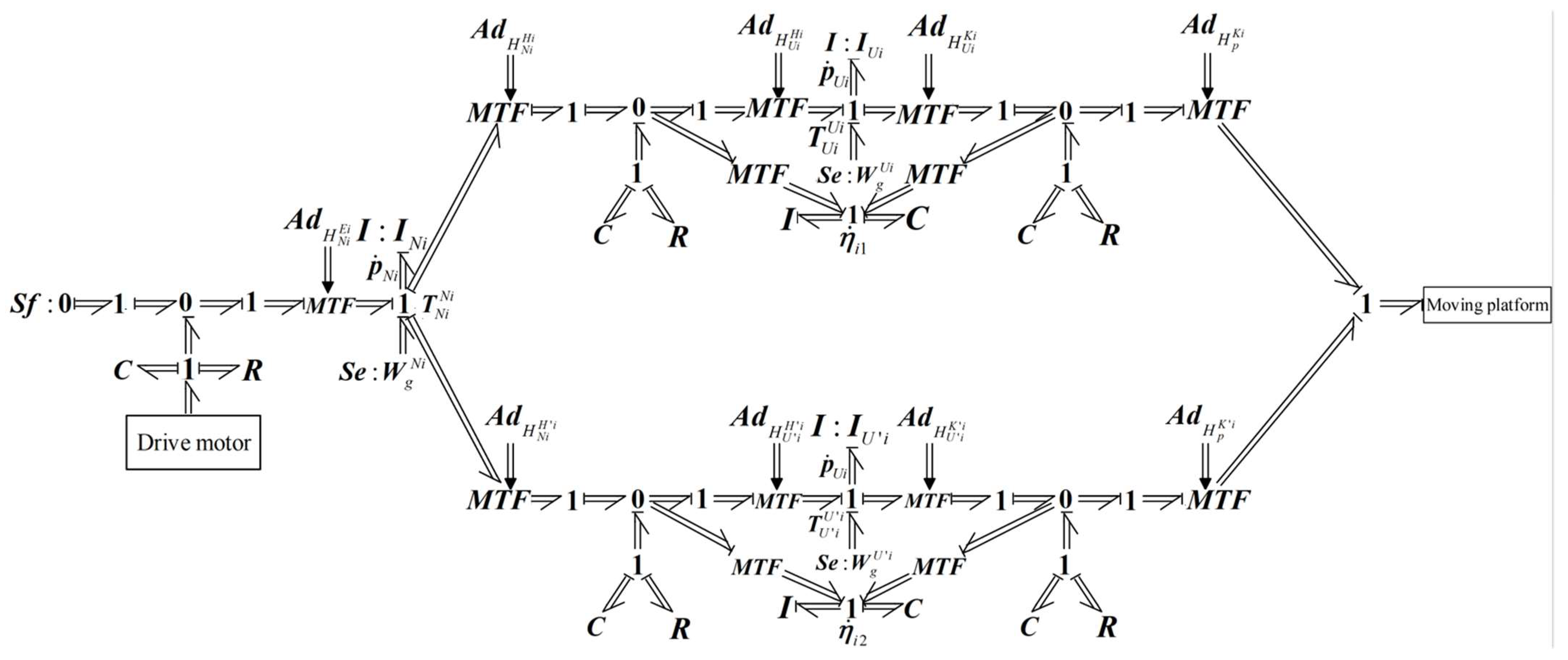
3.2. Rigid–Flexible Coupling Bond Graph Model of Parallel Mechanism
3.3. Constructing a Multi-Energy Domain Rigid–Flexible Coupling Dynamics Model for Robotic Systems
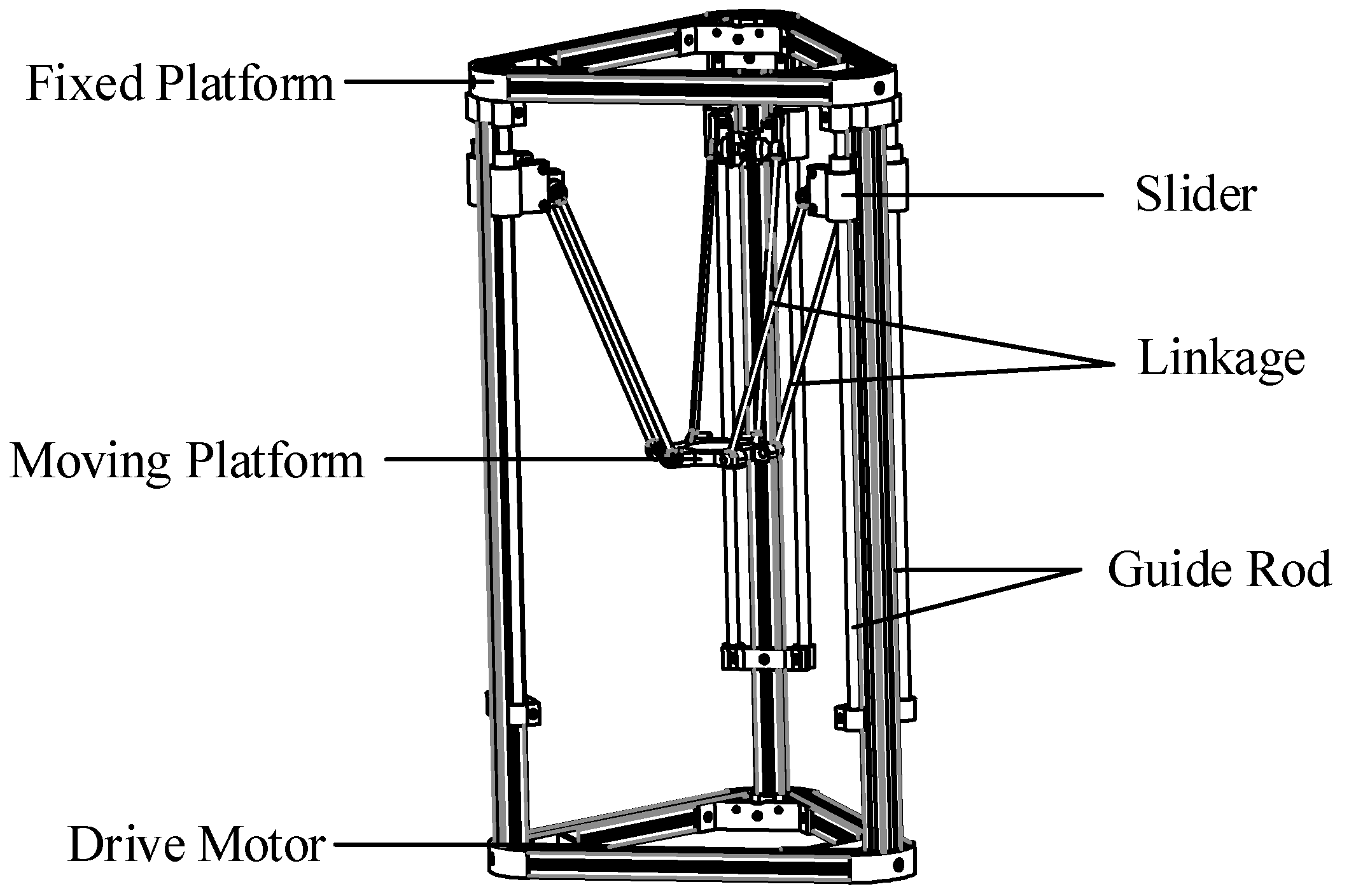
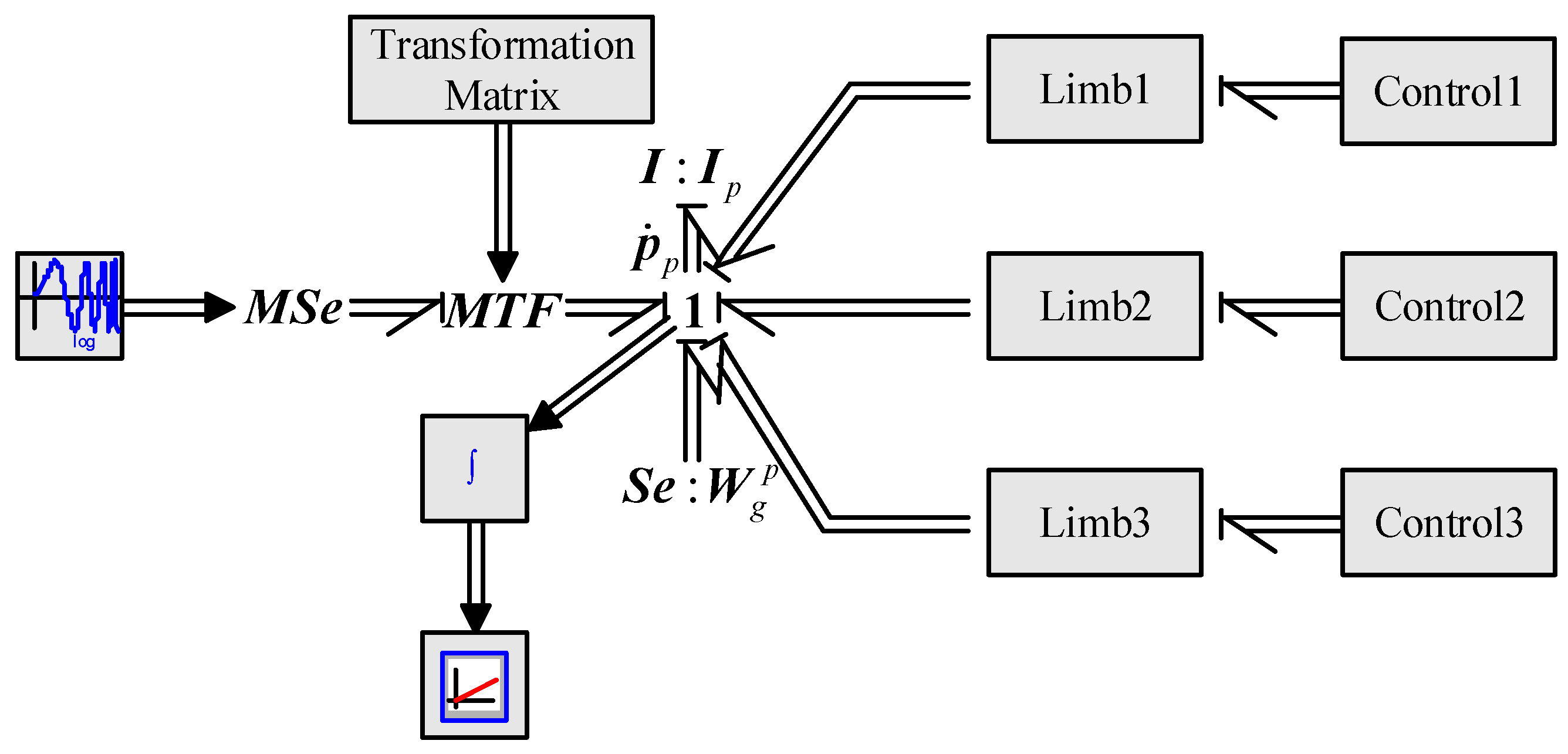
3.4. Arithmetic Examples
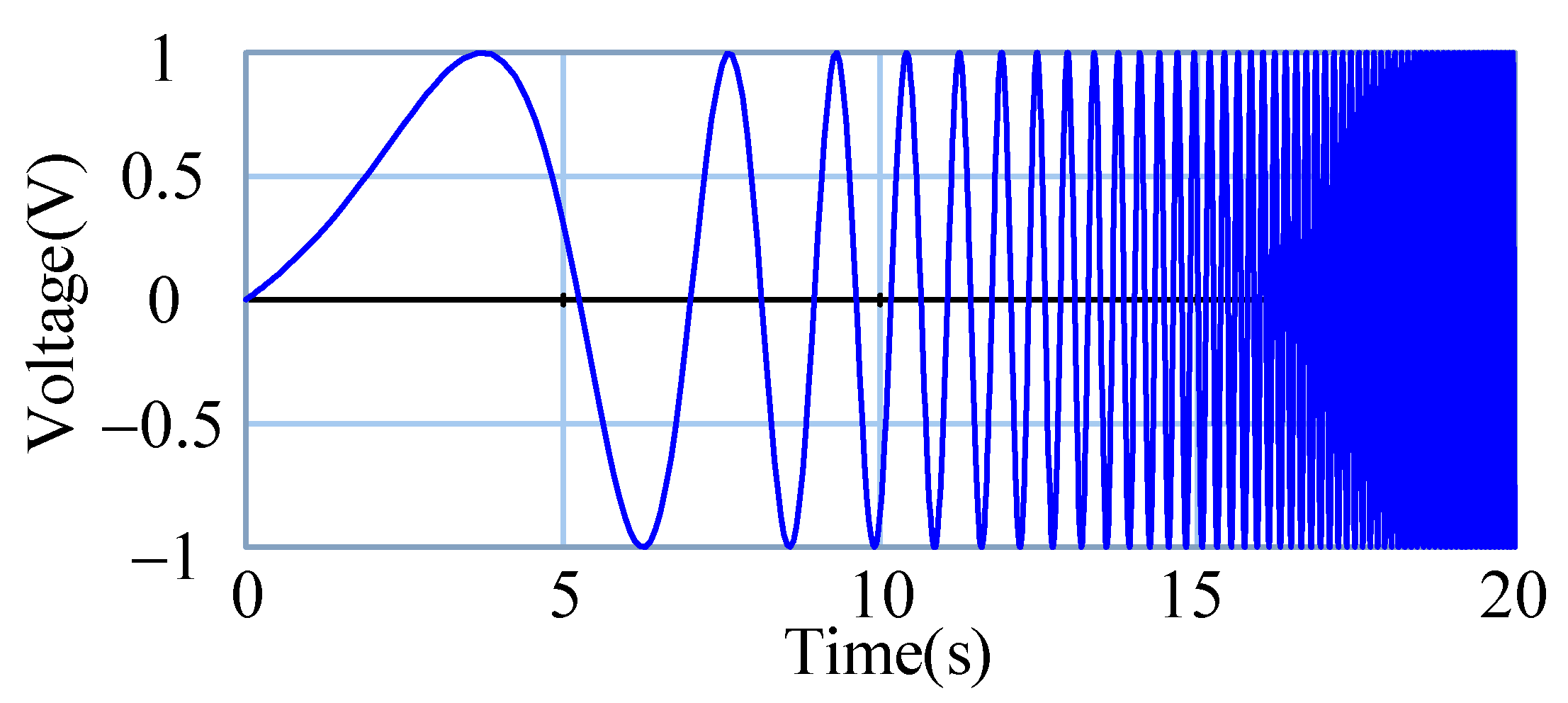
4. Simulation-Based Vibration Analysis
5. Conclusions
- (1)
- In this study, the expression form and graphical modeling of the unified essential elements of the bond graph are used to establish a system model containing multiple energy domains and rigid–flexible coupling. The structural form of the model corresponds to the physical structure. A computer simulation model is generated; in addition, there is a unified mathematical description between the equations of state of various energy domains, and it is easy to establish a functional relationship between the desired outputs of the system and the equations of state so that the outputs are observable.
- (2)
- Simulation analysis was carried out based on the model. From the simulation results, the model’s first-order and second-order intrinsic frequencies are 229.09 Hz and 524.80 Hz, respectively, and the mechanical subsystems’ first-order and second-order intrinsic frequencies are 234.7 Hz and 531.3 Hz, respectively. Therefore, it can be concluded that the relative deviations of the simulated frequency of the 20-sim simulation from the simulated frequency of ADAMS are, respectively, 2.45% and 1.24%, which verifies the reasonableness of the bond graph models and derives the influence of different control system parameters on the system, laying a foundation for the subsequent control system design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, B.; Zhang, L.; Zhang, Y.; Sang, D. Joint simulation analysis of rigid flexible coupling of Delta parallel robot. Mod. Mach. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Sheng, L.; Li, W.; Wang, Y.; Yang, X.; Fan, M. Rigid-flexible coupling dynamic model of a flexible planar parallel robot for modal characteristics research. Adv. Mech. Eng. 2019, 11, 1687814018823469. [Google Scholar] [CrossRef]
- Shang, L.; Huang, X.; Huang, Y.; Zhang, T. Nonlinear Hybrid Control of Rigid Flexible Coupling Delta Robot Based on Singular Perturbation. J. Mech. Eng. 2024, 60, 124–133. [Google Scholar]
- Shang, D.; Huang, Y.; Huang, X.; Pan, Z. Research on Rigid-flexible Coupling Dynamics of Delta Parallel Robot Based on Kane Equation Perturbation. J. Mech. Eng. 2024, 60, 95–106. [Google Scholar]
- Zhang, Q.; Zhao, X.; Liu, L.; Dai, T. Dynamic Modeling and Vibration Simulation of Spatial Flexible Closed-chain Robot. Trans. Chin. Soc. Agric. Mach. 2021, 52, 401–409. [Google Scholar]
- Chen, P.; Zhang, H. Optimal Control of Motion Stability of Parallel Robot. Comput. Simul. 2018, 35, 291–295. [Google Scholar]
- Liu, L.; Zhao, X.; Zhou, H.; Wang, J. Dynamic Solution for Spatial Rigid-flexible Parallel Robot. Trans. Chin. Soc. Agric. Mach. 2018, 49, 376–384. [Google Scholar]
- Kang, B.; Mills, J.K. Vibration control of a planar parallel manipulator using piezoelectric actuators. J. Intell. Robot. Syst. 2005, 42, 51–70. [Google Scholar] [CrossRef]
- Kang, B.; Mills, J.K. Dynamic modeling of structurally-flexible planar parallel manipulator. Robotica 2002, 20, 329–339. [Google Scholar] [CrossRef]
- Briot, S.; Khalil, W. Recursive and symbolic calculation of the elastodynamic model of flexible parallel robots. Int. J. Robot. Res. 2013, 33, 469–483. [Google Scholar] [CrossRef]
- Sun, T.; Song, Y.-M.; Yan, K. Kineto-static analysis of a novel high-speed parallel manipulator with rigid-flexible coupled links. J. Cent. South Univ. 2011, 18, 593–599. [Google Scholar] [CrossRef]
- Yu, Y.-Q.; Du, Z.-C.; Yang, J.-X.; Li, Y. An Experimental Study on the Dynamics of a 3-RRR Flexible Parallel Robot. IEEE Trans. Robot. 2011, 27, 992–997. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, Q. Dynamic Modeling and Characteristic Analysis of Compliant Mechanisms Based on PR Pseudo-rigid-body Model. Trans. Chin. Soc. Agric. Mach. 2013, 44, 225–229. [Google Scholar]
- Sun, Z.H.; Cheng, M.L. Mechanical Characteristics Analysis on Flexible Mattress in Downstream Sinking Based on Lumped Mass Method. Appl. Mech. Mater. 2014, 580–583, 1910–1917. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X. Dynamic analysis of planar 3-RRR flexible parallel robots under uniform temperature change. J. Vib. Control 2013, 21, 81–104. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X. Dynamic modelping and analysis of planar 3-RRR flexible parallel robots. J. Vib. Eng. 2013, 26, 239–245. [Google Scholar] [CrossRef]
- Karnopp, D.C.; Margolis, D.L.; Rosenberg, R.C. System Dynamics: Modeling and Simulation of Mechatronic Systems; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Yazman, M.A.; Servettaz, G.; Maschke, B. Bond-Graph Modelling of Flexible Robotic Manipulators. IFAC Proc. Vol. 1989, 22, 327–332. [Google Scholar] [CrossRef]
- Damić, V. Modelling flexible body systems: A bond graph component model approach. Math. Comput. Model. Dyn. Syst. 2006, 12, 175–187. [Google Scholar] [CrossRef]
- Lynch, S. Dynamical Systems with Applications Using Mathematica; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Chen, Y.; Chen, X.; Guo, F.; Meng, C.; Zhang, C.; Chen, Y. Dynamic full solution modeling of HDPE film welding robot thermal-mechanical-electric coupled energy domain system. J. Ration Shock 2022, 41, 60–68. [Google Scholar] [CrossRef]
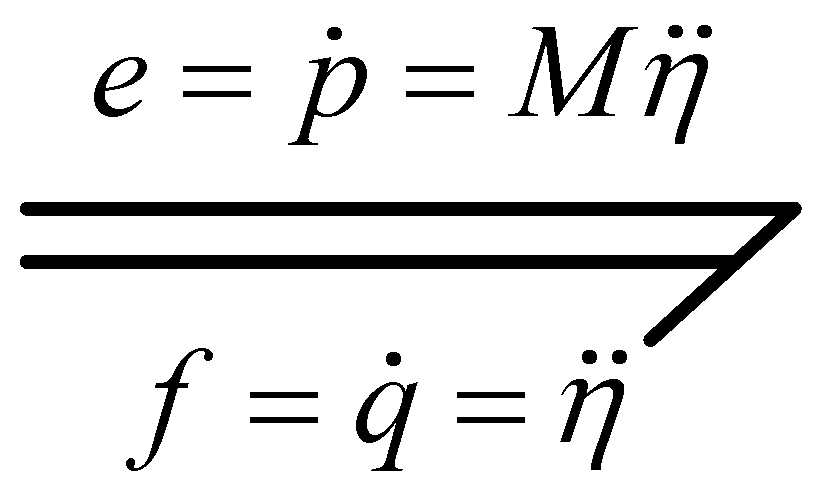




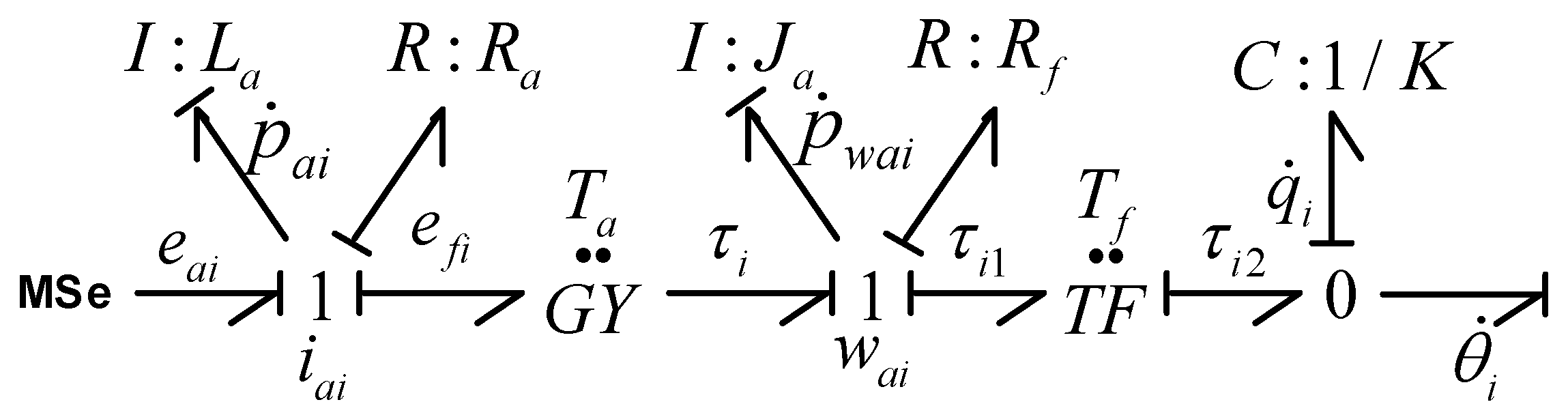

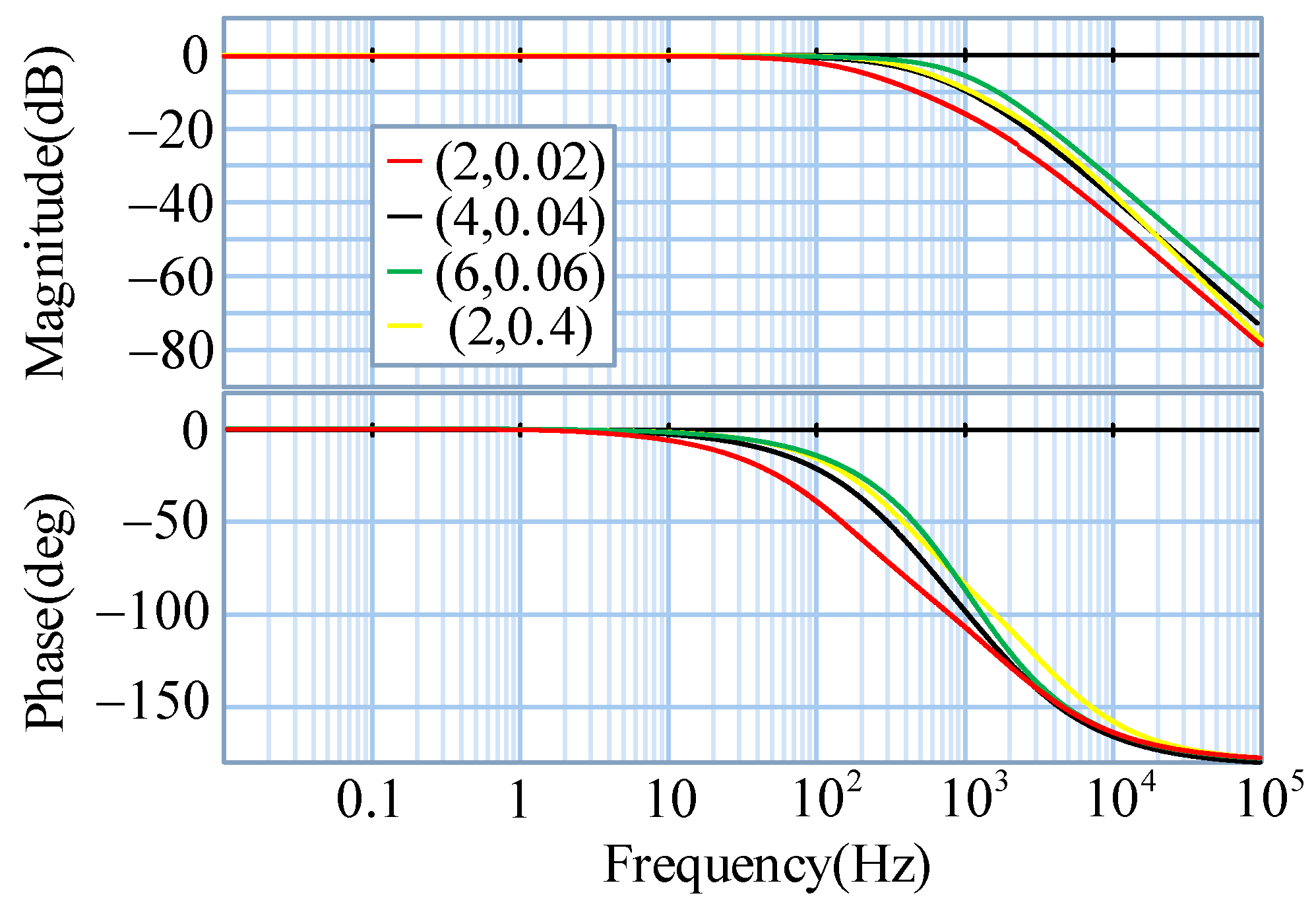
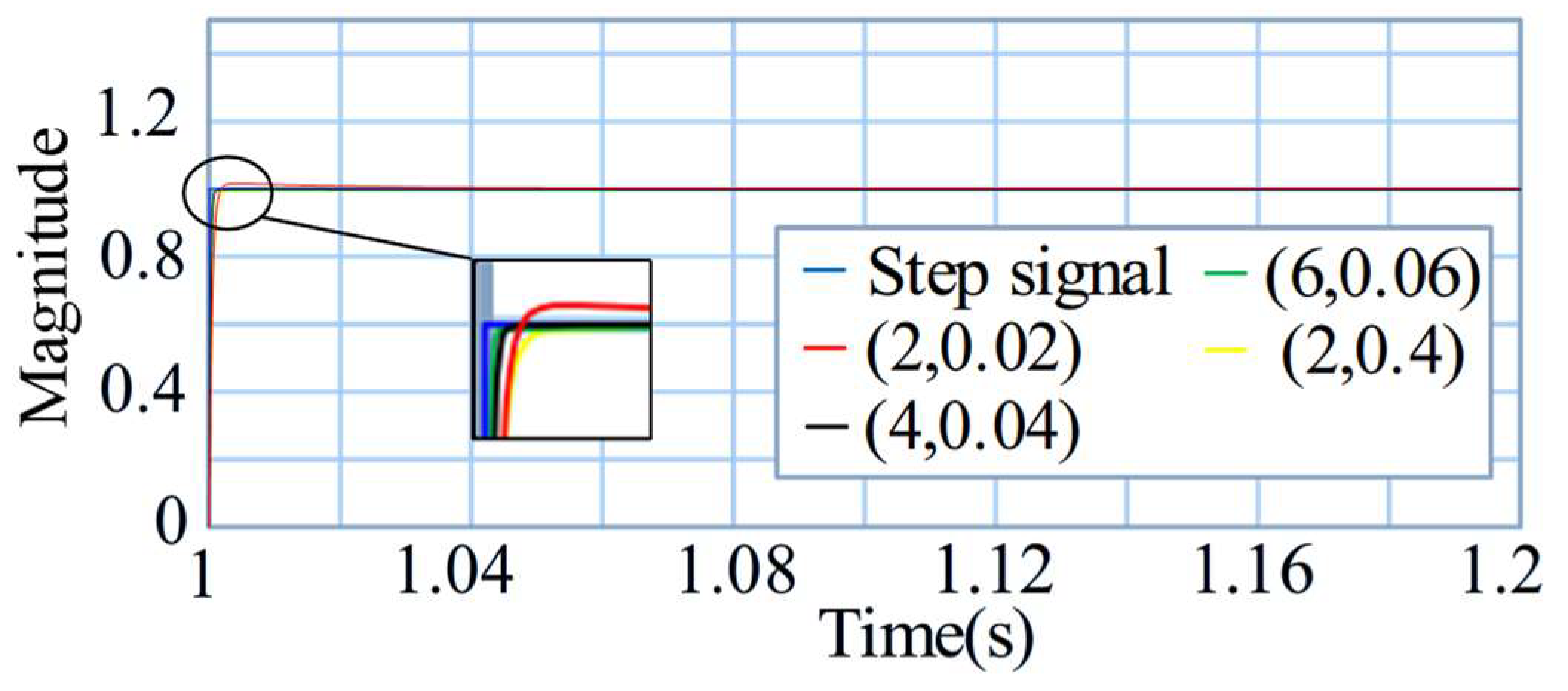

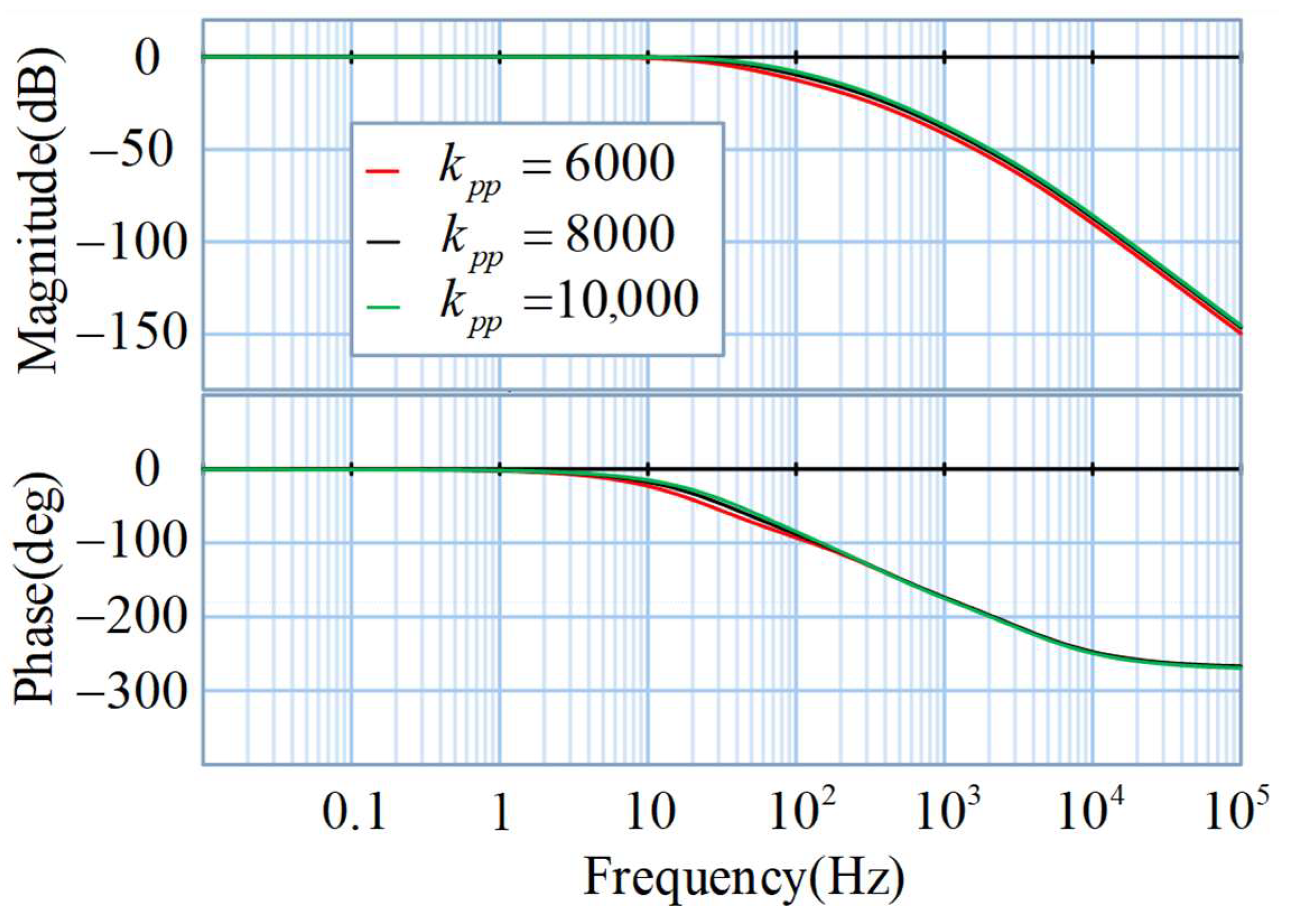

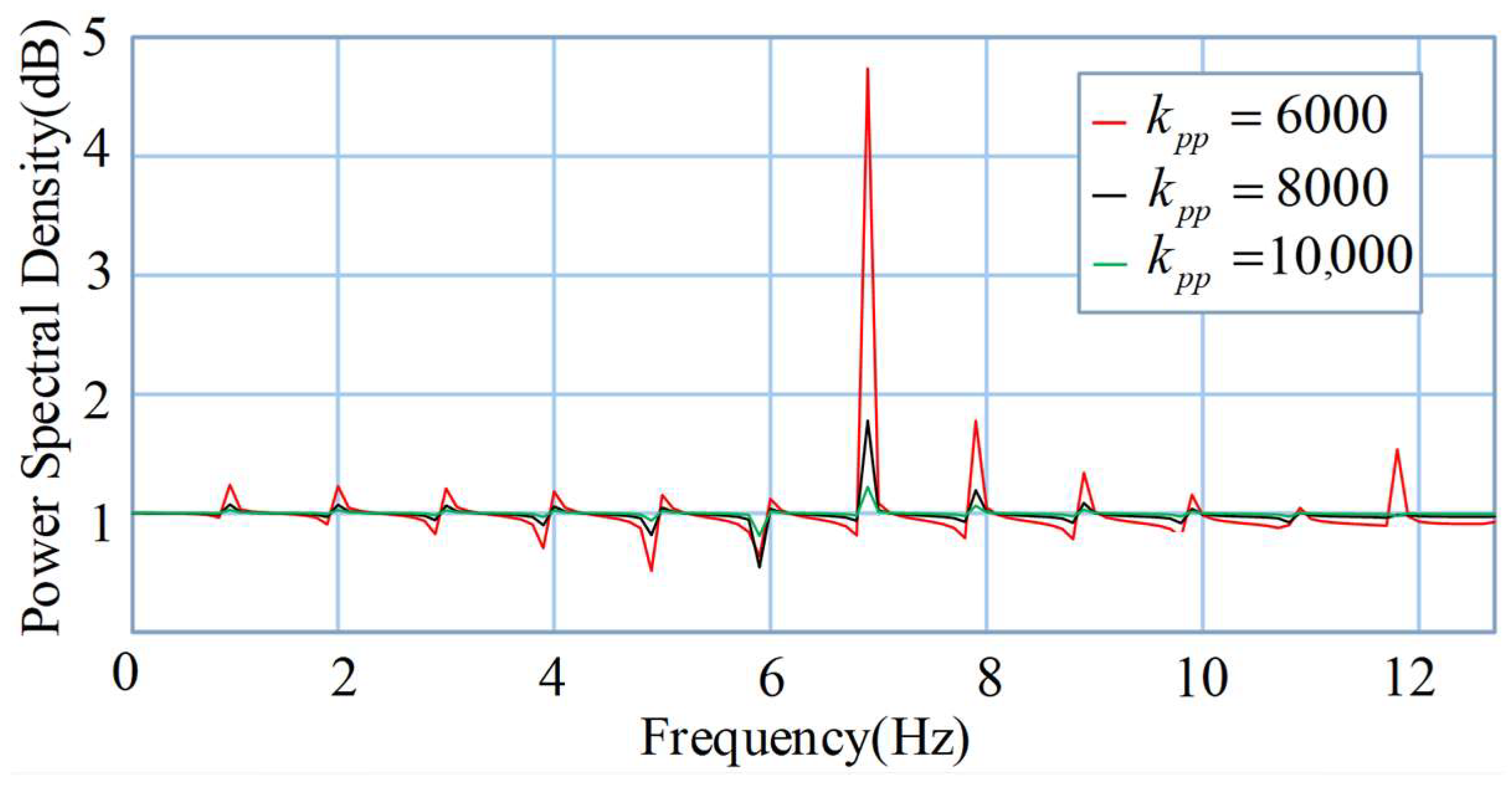






| Parameters | Value |
|---|---|
| Radius of fixed platform (R/m) | 0.233 |
| Length of flexible linkage (L/m) | 0.213 |
| Radius of moving platform (r/m) | 0.073 |
| Mass of slider (/kg) | 0.397 |
| Mass of flexible linkage (/kg) | 0.032 |
| Mass of moving platform (/kg) | 0.195 |
| Young’s modulus of flexible linkage (E/(pa)) | 2 × 1011 |
| Density of flexible linkage (ρ/(kg/m3)) | 7.85 × 103 |
| Parameters | Value |
|---|---|
| Winding inductance (H) | 1.58 × 10−3 |
| Operating voltage (V) | 200 |
| Rotor inertia of motor (kg·m2) | 3.12 × 10−4 |
| Winding resistance (Ω) | 0.32 |
| Electromagnetic torque constant (N·m/A) | 0.34 |
| Equivalent friction torque of motor (N·m) | 0.003 |
| Reduction ratio of reducer | 0.025 |
| Torque stiffness of reducer (N·m/arcmin) | 1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Xu, W.; Guo, F.; Yan, H.; Wang, Y. Modeling and Analysis of Dynamics of Rigid–Flexible Coupled Parallel Robots. Appl. Sci. 2025, 15, 5471. https://doi.org/10.3390/app15105471
Wang L, Xu W, Guo F, Yan H, Wang Y. Modeling and Analysis of Dynamics of Rigid–Flexible Coupled Parallel Robots. Applied Sciences. 2025; 15(10):5471. https://doi.org/10.3390/app15105471
Chicago/Turabian StyleWang, Leilei, Wei Xu, Fei Guo, Hao Yan, and Yunxue Wang. 2025. "Modeling and Analysis of Dynamics of Rigid–Flexible Coupled Parallel Robots" Applied Sciences 15, no. 10: 5471. https://doi.org/10.3390/app15105471
APA StyleWang, L., Xu, W., Guo, F., Yan, H., & Wang, Y. (2025). Modeling and Analysis of Dynamics of Rigid–Flexible Coupled Parallel Robots. Applied Sciences, 15(10), 5471. https://doi.org/10.3390/app15105471






