Abstract
The complexity of mathematical formulas in scientific documents makes efficient formula similarity computation a critical task in information retrieval. Approaches based on text or structure matching cannot fully capture the inherent semantic and hierarchical properties of formulas. Although large language models (LLM) made significant progress in formula similarity comparison, the linear processing may ignore the structure information of formulas. In contrast, GNN excel at modeling the structure relationships of formulas, but still face challenges in accurately defining nodes and edges in a formula tree, especially in distinguishing between nodes at different levels and modeling edge relationships. In this paper, we propose a formula-structure-embedding based GNN (FSCMGNN), and it is integrated with formula structure embedding, structure standardization and attention mechanism. The model is designed for semantic equivalence comparison. Experimental results show that the model outperforms existing models in formula equivalence determination in calculus.
1. Introduction
Mathematical formulas, as structured information in scientific literature, constitute a fundamental part of scientific literature and serve as abstract representations of domain-specific knowledge. Different from texts, mathematical formulas have the advantage of accurately conveying complex mathematical meaning and logical relationships. Correct understanding of mathematical formulas not only helps to grasp the core content of scientific literature, but also is significant for knowledge extraction, automatic reasoning, and literature retrieval. Formula equivalence determination refers to the process of determining whether two or more formulas are equivalent under specific conditions, which facilitates researchers in overcoming superficial symbolic differences to semantically grasp the underlying meaning of formulas. It not only can help to improve the accuracy of mathematical information retrieval, but also can provide a solid foundation for intelligent processing tasks, e.g., mathematical text analysis and automatic reasoning, which has significant research value and potential for broad applications.
The methods for math formula equivalence determination can be divided into three categories: one is a category of methods based on symbolic reasoning [1,2], where a logic system or a computer algebra system is used to perform precise mathematical reasoning to determine formula equivalence. The methods of this category show a high degree of accuracy and interpretability, but have high requirements for professional mathematical knowledge and a low degree of automation. This makes it difficult to adapt to the needs of large-scale data processing. The second category of methods is mainly based on formula structure comparison [3,4]. These methods reduce manual intervention by defining structural similarities. However, explicitly representing and comparing all substructures demands significant computational resources, which limits their scalability and efficiency in practical applications. The third category of methods is based on machine learning [5]. These methods encode formulas into low-dimensional vectors via word embeddings or by pre-trained language models. Compared with the methods of two previous categories, methods of this category have the advantages of high computational efficiency and low computing resource requirements. However, their structure information is often lost during formula embedding.
In order to eliminate the effect of formula structure information losing in machine-learning-based methods, this paper proposes a multi-level node feature embedding based GNN (FSCMGNN) for formula equivalence determination. It integrates with formula standardization, formula node structure embedding and attention mechanisms to extract structure information effectively. Experiments show that this method achieves a significant performance improvement in the task of formula equivalence determination in calculus.
2. Related Work
Mathematical formulas are a special form of description. Early equivalence determinations are commonly used for information retrieval. Miner and Munavalli construct a mathematical n-gram-index to query similarities between mathematical expressions [6]. Yokoi and Aizawa improve the accuracy of formula similarity calculation by using a tree-structured formula representation method, in which they extract sets of sub-paths and computed their similarities [3]. Richard and Yuan use the vector space model with the TF-IDF algorithm and cosine similarity to assess the similarity between mathematical formulas [5]. Zanibbi and Blostein transform mathematical formulas into canonical sorted text strings with indexes, and the matching of sub-expressions is used as a judgement condition for similarity [7]. Kamali and Tompa propose a tree edit distance method that calculates formula structure similarity through node insertion and deletion operations [4].
The above methods define similarities between formulas, but they mainly focus on symbol-level similarity, lacking deeper semantic understanding. Therefore, they are not quite suitable for formula equivalence determination and mathematical automated reasoning. Zaremba et al. make initial progress in the search for mathematical identities. They propose TreeNNs to generate leaf node embeddings, which are recursively combined to obtain parent node vectors [8]. Lrving et al. unify character-level and word-level models and introduce a semantic embedding approach to enhance the generalization of automated reasoning [9]. Allamanis et al. propose a neural equivalence network based on TreeNN. This network is designed to learn semantic representations of successive algebraic and logical expressions. It can capture the semantic equivalence between expressions, even when they differ in grammatical form [10]. Davila and Zanibbi propose Symbol Layout Tree and Operator Tree for formulas representations. These representations provide options for subsequent formula tree parsing [11]. Gao et al. treat LaTeX formulas as linear text and develop Symbol2Vec based on the CBOW model to learn embeddings for LaTeX mathematical symbols [12]. Arashahi et al. apply Tree-LSTM to model the syntactic structure of differential equations, overcoming limitations in generality and scalability found in traditional numerical approaches [13]. Lample and Charton employ sequence-to-sequence models to solve symbolic mathematical tasks such as integration and ordinary differential equations [14]. Zhong et al. perform structural analysis of formulas by designing complex tree matching and pruning rules [15]. Peng et al. introduce MathBERT, a BERT-based model fine-tuned for mathematical formula understanding and applies it to multiple downstream tasks [16]. Li et al. leverage the Z3 theorem prover to assess symbolic equivalence, enabling identification of logically equivalent formulas with different symbols [17]. Raz et al. discover the intrinsic connection between formulas through matrix transformations. They propose that the equivalence of two mathematical formulas can be determined if their recurrence matrices satisfy a specific co-boundary condition. This approach effectively solves the equivalence determination problem related to mathematical constants [18].
3. Method
To address the limitations of existing methods in extracting structural features from mathematical formulas, this paper proposes a multi-level node feature embedding based GNN for formula equivalence determination. The model uses multi-level node feature embedding to capture structure features from different levels, providing a strong support for equivalence determination.
The model follows a typical encoder–processor–decoder architecture (see in Figure 1). The encoder consists of a formula standardization module, a multi-level node feature embedding module, a node-level embedding module that encodes each node’s representation, and a graph-level embedding module that captures the overall structure of the formula graph. The processor includes both graph-level and node-level similarity comparison modules, which determine formula equivalence from both global and local perspectives. Specifically, the graph-level similarity comparison module adopts the corresponding module of SimGNN to evaluate the overall structural similarity between formulas. The node-level similarity comparison module incorporates an attention mechanism that dynamically adjusts interaction weights between nodes, enabling more accurate determination of key structure components. Finally, in the decoder, the model employs a cross-attention mechanism to integrate similarity vectors from both levels and outputs the final equivalence prediction. The integration of formula standardization, multi-level node feature embedding, and attention mechanisms together enhances the model’s capability to effectively extract formula structure information and improve its scalability and accuracy in practical applications.
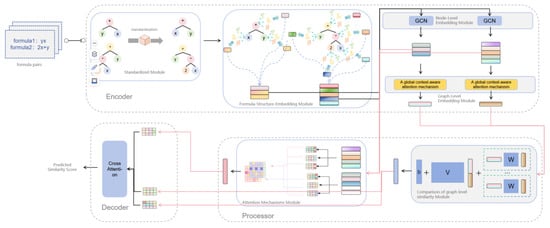
Figure 1.
A multi-level node feature embedding-based GNN. The symbol ‘*’ denotes multiplication throughout the paper.
3.1. Encoder
The key components of the Encoder consist of a formula standardization module, a multi-level node feature embedding module, a node embedding module, a graph embedding module, and four sub-modules.
3.1.1. Formula Standardization Module
There are basic algebraic laws for formula transformation, e.g., associative law and commutative law, which make algebraic computation more flexible but increase the diversity of formula expressions, e.g., formulas in Figure 2 have the same mathematical meaning but different abstract syntax trees (ASTs). However, the diversity in form do not reflect any further information about domain knowledge. In order to eliminate the structure differences brought by using the basic algebraic laws, the formula standardization module is introduced to uniform the different abstract syntax trees caused by the use of these algebraic laws. In this module, the following typical operations are performed on each AST:
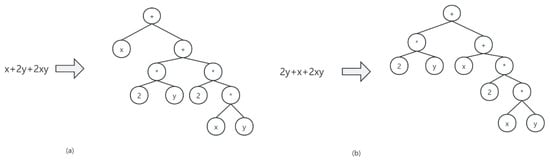
Figure 2.
(a) Abstract syntax trees of ‘x + 2y + 2xy’; (b) Abstract syntax trees of ‘2y + x + 2xy’.
- When processing operators with associative property (such as addition or multiplication), this method examines whether the operators of the current node and its child nodes are the same: if yes, the associative law can be used on these two nodes, and other sub-trees of the current node and the two sub-trees of the child node will be set as the next children of the current node. This operation will be performed recursively operations until all operator nodes have been examined. After this step, the AST will become an N-ary tree (see in Figure 3).
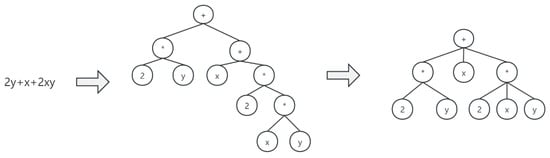 Figure 3. N-ary tree generation based on the associative law.
Figure 3. N-ary tree generation based on the associative law. - To process an operator with commutative property (such as addition or multiplication), we first provide a unique value for each type of operators or operands, then recursively calculate the dictionary order of each sub-tree, and rearrange the order of all sub-trees of the operator in ascending order of the sub-tree dictionary orders. The dictionary order is defined as a unique sequence obtained by recursively performing a breadth-first traversal, where the value of corresponding operator, the number of its sub-trees and the orders of all its sub-trees are sequentially recorded during the traversal process (see Figure 4).
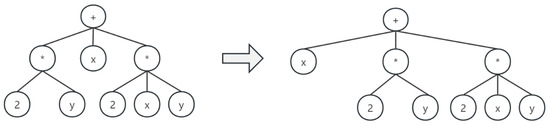 Figure 4. AST reordering based on the commutative law.
Figure 4. AST reordering based on the commutative law.
By using the above operations, different forms of formulas caused by the application of algebraic laws can be standardized, which improves the accuracy of formula equivalence determination.
3.1.2. Multi-Level Node Feature Embedding Module
In mathematics, formulas can be represented as graphs, where nodes represent operators and operands, and edges represent operational relations between them. This graph preserves the hierarchical structure and logical relations of formulas. However, if we use the GNN model for formula equivalence determination directly, nodes are represented by their IDs. This representation fails to adequately use use the positional information of each node, resulting in an imprecise understanding of the formula’s overall structure. In order to solve this problem, we improve the representation of formulas based on the node structure information. In this paper, each operator or operand, such as ‘+’, ‘sin’, etc., is represented by a fixed number which is called the Node Type Identifier T); Node Level Information (L) refers the level at which the node is located in its formula tree; Node Intra-Level Number (N) records the relative position of the node at its level. The operations of formula structure embedding are as follows:
- Each node’s ‘Token T’, ‘Level L’, and ‘Number N’ are converted into corresponding vectors by embedding, such that each embedding vector contains all structure information of corresponding node.
- The three embedding vectors of a node are fused to form a node feature vector that contains all structure information of corresponding node (see Figure 5).
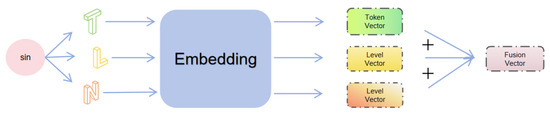 Figure 5. Feature embedding and fusion.
Figure 5. Feature embedding and fusion. - A breadth-first traversal is performed on the formula tree to aggregate all node vectors, generating a vector that represents the structure information of the formula tree (see Figure 6).
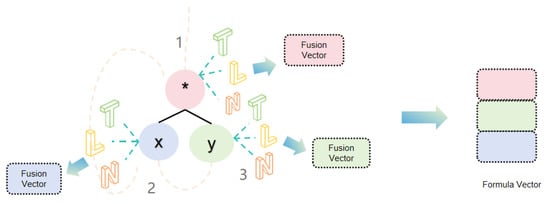 Figure 6. Breadth first traversal and generation of formula vector.
Figure 6. Breadth first traversal and generation of formula vector.
Take ‘’ as an example, Table 1 shows its structure information of each node. By encoding such structural information into node representations, the model incorporates hierarchical and positional details into computation, ensuring the accuracy and reliability of formula equivalence determination.

Table 1.
Characteristic representation of the formula.
3.1.3. Node Embedding Module
In this paper, Neighbor-Aggregation-based Graph Convolution Network (GCN) [19] is used to capture the local structure of the graph. GCN performs convolution operations on each node by aggregating its own features with those of its neighboring nodes. As a result, each updated node representation encodes both the node’s original information and the structural context provided by its neighbors. The update process of node features in GCN can be represented as:
Here, denotes the node feature matrix of layer l, is the adjacency matrix plus the self-loop, is the degree matrix of , defined as , is the weight matrix of the lth level, and is a nonlinear activation function, usually using ReLU. After multiple levels of GCN, the node embeddings are ready for inputing into the next stages.
3.1.4. Graph Embedding Module
In order to capture global features and combine node importance, a global context-aware attention mechanism is introduced to generate the global graph context vector by averaging and non-linearly transforming all node embedding vectors. Different attention weights W are assigned to the global context, and the global graph context vector calculated by Equation (2) reflects the overall structure information of the formula.
In Equation (2), N is the total number of nodes, is an embedding of node n, is a simple average of node embedding, is the learnable weight matrix, is the sigmoid activation function. This global context-based attention mechanism has an advantage of reflecting the overall structure features of formulas by flexible adjustment of node weights.
3.2. Processor
3.2.1. Graph–Graph Interaction Module
A simple way to model the relation between the graph-level embeddings is to calculate the inner product of the two. However, this often leads to insufficient interactions between graphs and makes it difficult to accurately measure the equivalence determination. To solve this problem, our method adopt the Neural Tensor Network (NTN) proposed by [20] to model the relation between two graph-level embeddings (see in Figure 7), i.e.,
Here, and are the graph-level vector representations of two formulas, is tensor parameters used to capture quadratic interactions between the vectors, V and b are weight matrices and bias terms for NTN, is a nonlinear activation function, and K is a hyperparameter that controls the number of interaction scores for each graph embedding pair.
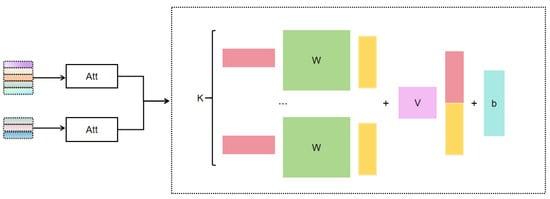
Figure 7.
Graph level equivalence determination module.
3.2.2. Node–Node Interaction Module
Similar to the equivalence determination score in the graph–graph interaction module, we use a cross-attention mechanism instead of the inner product to calculate the node-level equivalence determination score (see in Figure 8). Unlike the inner product, which only captures the linear relationships between node feature vectors, the cross-attention mechanism introduces non-linear transformations that better capture complex interactions between node representations. The equations for the cross-attention mechanism are listed as follows:
Here, z denotes the probability of formula equivalence, i and j denote the ith and jth nodes, represents the attention that node i pays to node j, indicates the attention from node j to node i, and X denotes the embedding of the input sequence, and denote the weights learn from matrices Q and K, respectively.
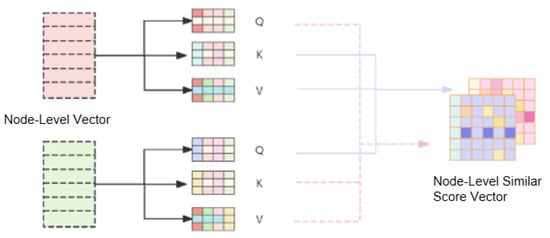
Figure 8.
Graph–graph interaction module.
3.3. Decoder
In the formula equivalence determination module, the graph level similarity score vectors and node level similarity score vectors are integrated by a cross-attention mechanism (see in Figure 9). The cross-attention mechanism can deeply interact with the two score vectors to capture the subtle relationship between them. The final score s for formula equivalence determination can be calculated as follows:
where is the Q matrix of the graph-level similarity vector , is the K matrix of the node-level similarity vector , and is the V matrix of the node-level similarity vector.
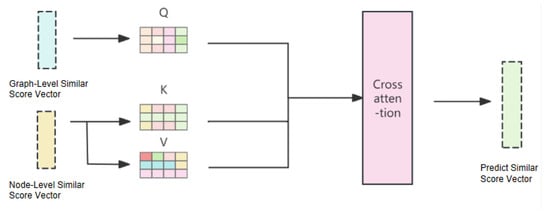
Figure 9.
Formula determination score calculation module.
4. Experiments and Analysis
4.1. Dataset
To the best of our current knowledge, most of the existing research focus on the matching of formula symbols, and less on formula equivalence determination. Therefore, we construct a dataset from equivalent formulas in calculus, as calculus is not only an important part of higher mathematics and has a wide range of applications, but also involves a large number of equivalent transformations, i.e., derivative and integral transformation, Taylor expansion, trigonometric identity transformation, etc. These advantages allows us to easily obtain a large number of equivalent calculus formulas.
To obtain positive and negative samples for formula equivalence determination, a large number of mathematical expressions from several widely used calculus textbooks, i.e., Calculus and Its Applications [21] by Bittinger et al., Single Variable Calculus: Early Transcendentals [22] by Anton et al., and CALCULUS EARLY TRANSCENDENTALS [23] by Jon et al. are curated.
To generate positive samples, we applied four common mathematically equivalent transformations: algebraic expansions and simplifications, derivatives and integral calculations, substitution of variables, and trigonometric constant transformations to the extracted expressions, and used the Python’s SymPy tool (version 1.12) to generate equivalent formulas. These transformations were chosen because, firstly, algebraic expansion and simplification operations, e.g., , are the common equivalence operations in elementary algebra, and are suitable for assessing the model’s understanding of the underlying transformations; secondly, derivative and integral calculations, e.g., , help to test the model’s grasp of the semantics of core operations in calculus; thirdly, variable substitution, e.g., and , can verify whether the model has the ability to deal with the generalization of variable change without semantic change; lastly, the triangular constant transformations, e.g., and , are highly structurally variable, which help to enhance the robustness of the model to complex structure deformations. These operations cover the most common cases of equivalent transformations in the field of calculus, reflecting both equivalence relations in the mathematical sense and structure diversity, which helps to train the model to maintain stable semantic comprehension under different structures.
To construct negative samples, we selected formulas with completely different mathematical meanings, e.g., and , which may have structure similarities, but are unequivalent.
By the above method, a dataset of formula equivalence determination from calculus is constructed (see in Table 2).

Table 2.
Table of data set structure.
4.2. Evaluation Indicators
The metrics used in the experiments are , , and score. Accuracy measures the proportion of samples correctly predicted by the model out of the total samples. Precision measures the proportion of correctly identified entities out of the identified entities. Recall evaluates the proportion of correctly identified entities out of all actual entities. F1 score is calculated as the reconciled mean of precision and recall as a combined indicator of model performance.
where denotes positive instances correctly predicted, denotes negative instances misclassified as positive, denotes positive instances misclassified as negative, and denotes negative instances correctly predicted.
4.3. Experimental Results
To demonstrate the training process and convergence behavior of the proposed model, the training loss curve in Figure 10 is analyzed: the curve exhibits a consistent downward trend, indicating that the model is effectively minimizing the objective function; during the initial stages of training, the loss decreases rapidly, suggesting a quick learning from the training data by the model, while as the number of epochs increases, the rate of decrease in the loss slows down and gradually stabilizes, reflecting that the model parameters are approaching an optimal solution. This steady decline and plateau in the loss curve provide empirical evidence that the training process is both stable and effective, ensuring the reliability of the learned representations.
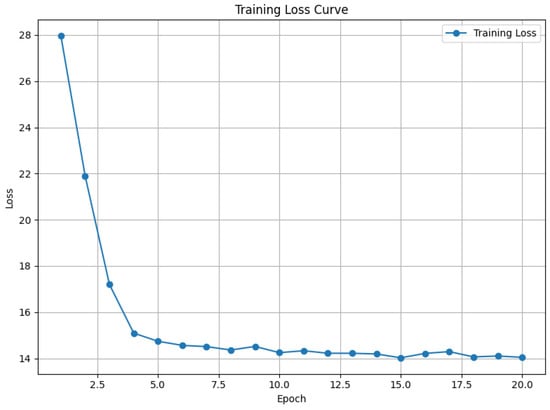
Figure 10.
Training loss curve of FSCMGNN.
To demonstrate the superiority of our proposed model, comparative experiments among the pre-trained Bert model, the baseline model SimGNN, the GNN model NAGSL, and our proposed model FSCMGNN are conducted. As shown in Figure 11. The accuracy of the Bert model is 5.29%, 7.04%, and 13.31% lower than that of NAGSL, SimGNN, and FSCMGNN, respectively. This performance gap can be attributed to the nature of the models and the data: Bert, being optimized for natural language processing, excels at capturing semantic relationships in linearly structured text. However, when dealing with formulas represented as ASTs, its capabilities are limited. In contrast, GNNs are inherently better suited for such structure representations, as they operate directly on graph structures and can effectively aggregate both local and global structural information through message-passing mechanisms. These findings validate the suitability and effectiveness of GNN-based models for formula equivalence determination tasks.
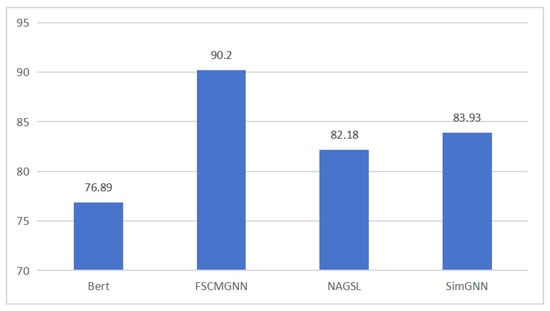
Figure 11.
Accuracy of Bert, NAGSL, SimGNN, and FSCMGNN.
To verify the effectiveness of each structural pre-processing module, we introduced Formula Structure Embedding (FSE) and Standardization (SD) operations in the Bert and SimGNN models, respectively, and conducted comparative experiments. The experimental results show that with only the introduction of formula structure embedding module, all indicators of SimGNN model have been improved, among which the F1 value has increased by 2.62%. Furthermore, after adding standardized operations on this basis, the F1 value increased by 2.1% again (see in Table 3). Similarly, the Bert model also shows some improvement after incorporating the same module, but overall performance still lags significantly behind the SimGNN model that introduced the same module. These results indicate that pre-processing structure information has a positive effect on improving model performance, especially in the graph neural network architecture. FSE and SD can more fully explore the structural and semantic features of formulas, further confirming the significant advantages of graph neural network-based models in mathematical formula equivalence determination.

Table 3.
Comparison of Bert and SimGNN with FSE and SD.
To verify the effectiveness of our optimization modules, we conducted an ablation experiment based on the baseline model SimGNN, with results shown in Figure 12. Specifically, FSCMGNN integrates multi-level node feature embedding and several optimisation modules. To examine the impact of each component, we designed different variants: one without formula structure embedding (FSCMGNN-ff), one without the node-level similarity module (FSCMGNN-node), one without the similarity score calculation module (FSCMGNN-score), and one without standardisation processing (FSCMGNN-sd). As the results indicate, the formula structure embedding module contributes the most significantly to the overall performance, demonstrating that effectively incorporating structural information of formulas can greatly enhance similarity measurement. Standardization also plays a notable role by reducing redundant information and improving the consistency of feature representations, thereby facilitating better learning. Although the attention mechanism contributes relatively less to performance improvement, its ability to introduce non-linearity and enable the model to learn the relative importance of different features still brings observable effect.
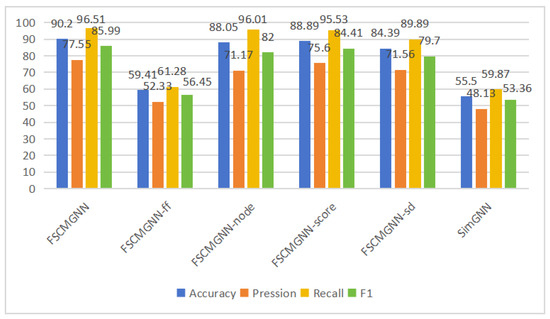
Figure 12.
Ablation experiment.
5. Conclusions
In this paper, we propose a formula equivalence determination based on GNN. Specifically, the architecture of SimGNN combined with multi-level node feature embedding and standardization operation are used to effectively enhance the structure information extraction and processing capabilities of the model. In addition, by replacing linear operations with the attention mechanism for formula equivalence determination computation, the model’s ability to interact with global and local information is enhanced, thus improving the accuracy of similarity computation. In this paper, 5623 formulas in the field of calculus are extracted to form a dataset and validated on this dataset. The experimental results show that the proposed GNN-based method outperforms the baseline model in terms of accuracy and F1 value, showing that GNNs are more effective than large language models in handling mathematical formulas, which are highly structured data. In addition, by introducing structure information pre-processing, the accuracy of formula equivalence judgment is further improved, verifying both the advantage of GNN-based approaches and the importance of structure information enhancement for formula equivalence determination.
In future work, we plan to develop a context-combining retrieval framework that integrates both formula structure and its textual environment, aiming to support more accurate and semantically rich mathematical information retrieval.
Author Contributions
Conceptualization, D.J.; Methodology, D.J. & S.L.; Software, S.L.; Validation, S.L.; Formal analysis, S.L. & D.J.; Investigation, S.L.; Resources, S.L.; Data curation, S.L.; Writing—original draft, S.L.; Writing—review & editing, D.J. & S.L.; Visualization, S.L.; Supervision, D.J.; Project administration, D.J.; Funding acquisition, D.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported Beijing Advanced Innovation Center for Future Blockchain and Privacy-Computing.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflict of interest.
References
- Garcez, A.d.; Gori, M.; Lamb, L.C.; Serafini, L.; Spranger, M.; Tran, S.N. Neural-symbolic computing: An effective methodology for principled integration of machine learning and reasoning. arXiv 2019, arXiv:1905.06088. [Google Scholar]
- Besold, T.R.; Bader, S.; Bowman, H.; Domingos, P.; Hitzler, P.; Kühnberger, K.U.; Lamb, L.C.; Lima, P.M.V.; de Penning, L.; Pinkas, G.; et al. Neural-symbolic learning and reasoning: A survey and interpretation 1. In Neuro-Symbolic Artificial Intelligence: The State of the Art; IOS Press: Amsterdam, The Netherlands, 2021; pp. 1–51. [Google Scholar]
- Yokoi, K.; Aizawa, A. An approach to similarity search for mathematical expressions using MathML. In Towards a Digital Mathematics Library. Grand Bend, Ontario, Canada, July 8–9th, 2009; Masaryk University Press: Brno, Czech Republic, 2009; pp. 27–35. [Google Scholar]
- Kamali, S.; Tompa, F.W. Structural similarity search for mathematics retrieval. In Proceedings of the International Conference on Intelligent Computer Mathematics, Bath, UK, 8–12 July 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 246–262. [Google Scholar]
- Zanibbi, R.; Yuan, B. Keyword and image-based retrieval of mathematical expressions. In Proceedings of the Document Recognition and Retrieval XVIII, San Francisco, CA, USA, 23–27 January 2011; Volume 7874, pp. 141–149. [Google Scholar]
- Miner, R.; Munavalli, R. An approach to mathematical search through query formulation and data normalization. In Proceedings of the International Conference on Mathematical Knowledge Management, Hagenberg, Austria, 27–30 June 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 342–355. [Google Scholar]
- Zanibbi, R.; Blostein, D. Recognition and retrieval of mathematical expressions. Int. J. Doc. Anal. Recognit. (IJDAR) 2012, 15, 331–357. [Google Scholar] [CrossRef]
- Zaremba, W.; Kurach, K.; Fergus, R. Learning to discover efficient mathematical identities. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Irving, G.; Szegedy, C.; Alemi, A.A.; Eén, N.; Chollet, F.; Urban, J. Deepmath-deep sequence models for premise selection. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Allamanis, M.; Chanthirasegaran, P.; Kohli, P.; Sutton, C. Learning continuous semantic representations of symbolic expressions. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 80–88. [Google Scholar]
- Davila, K.; Zanibbi, R. Layout and semantics: Combining representations for mathematical formula search. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Tokyo, Japan, 7–11 August 2017; pp. 1165–1168. [Google Scholar]
- Gao, L.; Jiang, Z.; Yin, Y.; Yuan, K.; Yan, Z.; Tang, Z. Preliminary Exploration of Formula Embedding for Mathematical Information Retrieval: Can mathematical formulae be embedded like a natural language? arXiv 2017, arXiv:1707.05154. [Google Scholar]
- Arabshahi, F.; Singh, S.; Anandkumar, A. Towards solving differential equations through neural programming. In Proceedings of the ICML Workshop on Neural Abstract Machines and Program Induction (NAMPI), Stockholm, Sweden, 14 July 2018. [Google Scholar]
- Lample, G.; Charton, F. Deep learning for symbolic mathematics. arXiv 2019, arXiv:1912.01412. [Google Scholar]
- Zhong, W.; Rohatgi, S.; Wu, J.; Giles, C.L.; Zanibbi, R. Accelerating substructure similarity search for formula retrieval. In Proceedings of the Advances in Information Retrieval: 42nd European Conference on IR Research, ECIR 2020, Lisbon, Portugal, 14–17 April 2020; Proceedings, Part I 42. Springer: Berlin/Heidelberg, Germany, 2020; pp. 714–727. [Google Scholar]
- Peng, S.; Yuan, K.; Gao, L.; Tang, Z. Mathbert: A pre-trained model for mathematical formula understanding. arXiv 2021, arXiv:2105.00377. [Google Scholar]
- Li, Z.; Wu, Y.; Li, Z.; Wei, X.; Zhang, X.; Yang, F.; Ma, X. Autoformalize mathematical statements by symbolic equivalence and semantic consistency. Adv. Neural Inf. Process. Syst. 2025, 37, 53598–53625. [Google Scholar]
- Raz, T.; Shalyt, M.; Leibtag, E.; Kalisch, R.; Hadad, Y.; Kaminer, I. From Euler to AI: Unifying Formulas for Mathematical Constants. arXiv 2025, arXiv:2502.17533. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Bai, Y.; Ding, H.; Bian, S.; Chen, T.; Sun, Y.; Wang, W. Simgnn: A neural network approach to fast graph similarity computation. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, Melbourne, Australia, 11–15 February 2019; pp. 384–392. [Google Scholar]
- Bittinger, M.L.; Ellenbogen, D.; Surgent, S.A. Calculus and Its Applications; Pearson: London, UK, 2016. [Google Scholar]
- Stewart, J.; Clegg, D.; Watson, S. Single Variable Calculus: Early Transcendentals, 2nd ed.; Brooks/Cole Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Zill, D.G.; Wright, W.S. Calculus: Early Transcendentals; Jones & Bartlett Publishers: Burlington, MA, USA, 2009. [Google Scholar]
- Jimidovich, B.P. Mathematical Analysis Exercise Set; MIR Publishers: Moscow, Russia, 2002. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).