A Stair-Climbing Wheelchair with Novel Spoke Wheels for Smooth Motion
Abstract
1. Introduction
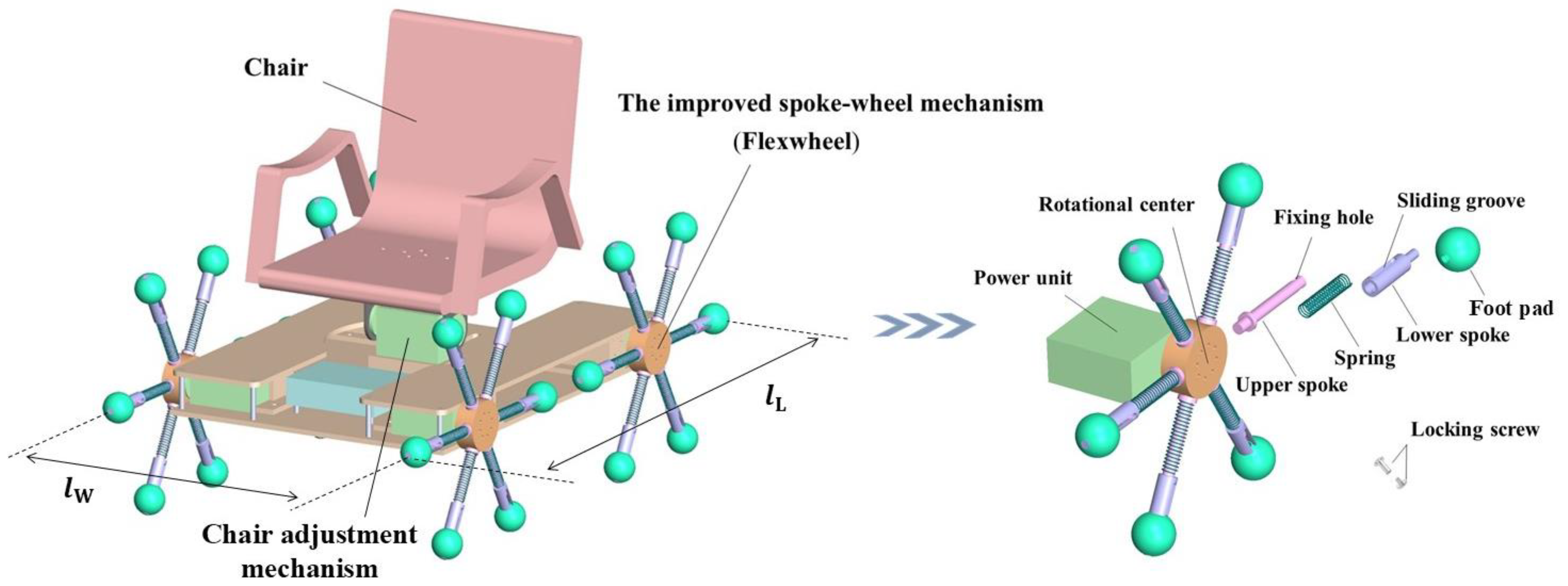
2. Mechanism Design
3. Theoretical Analysis
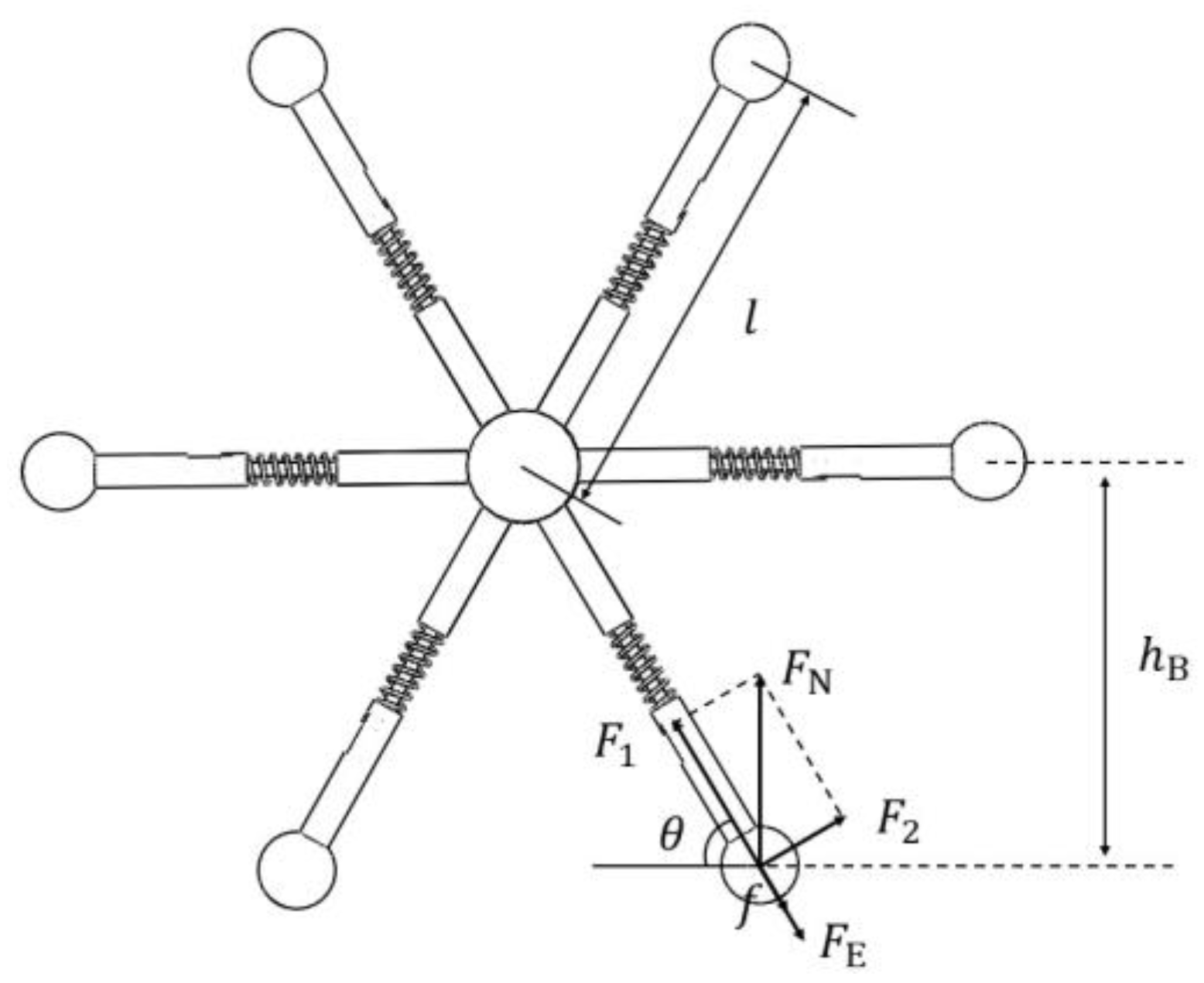
3.1. Spring Configuration
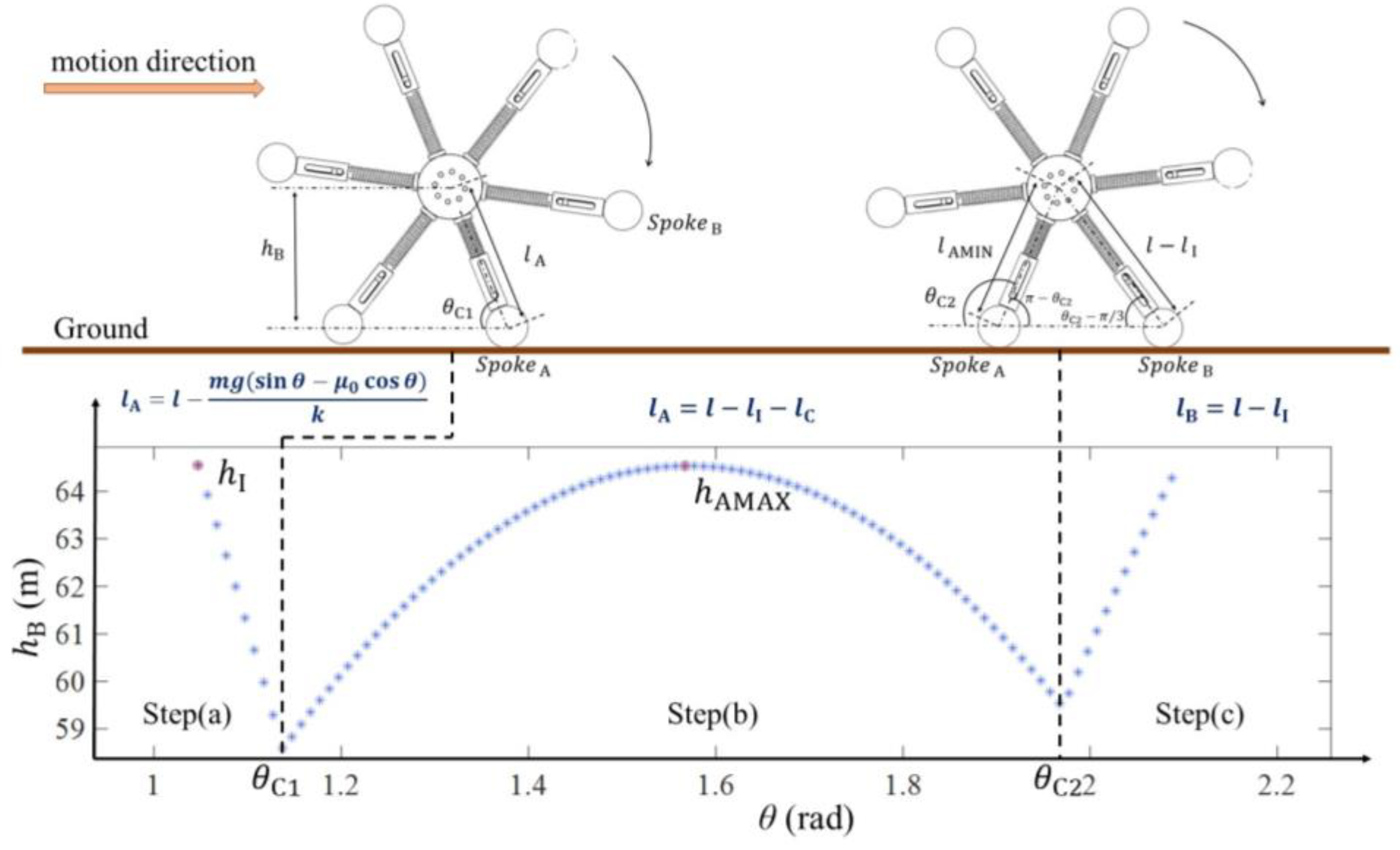
3.1.1. Spoke Deformation Analysis
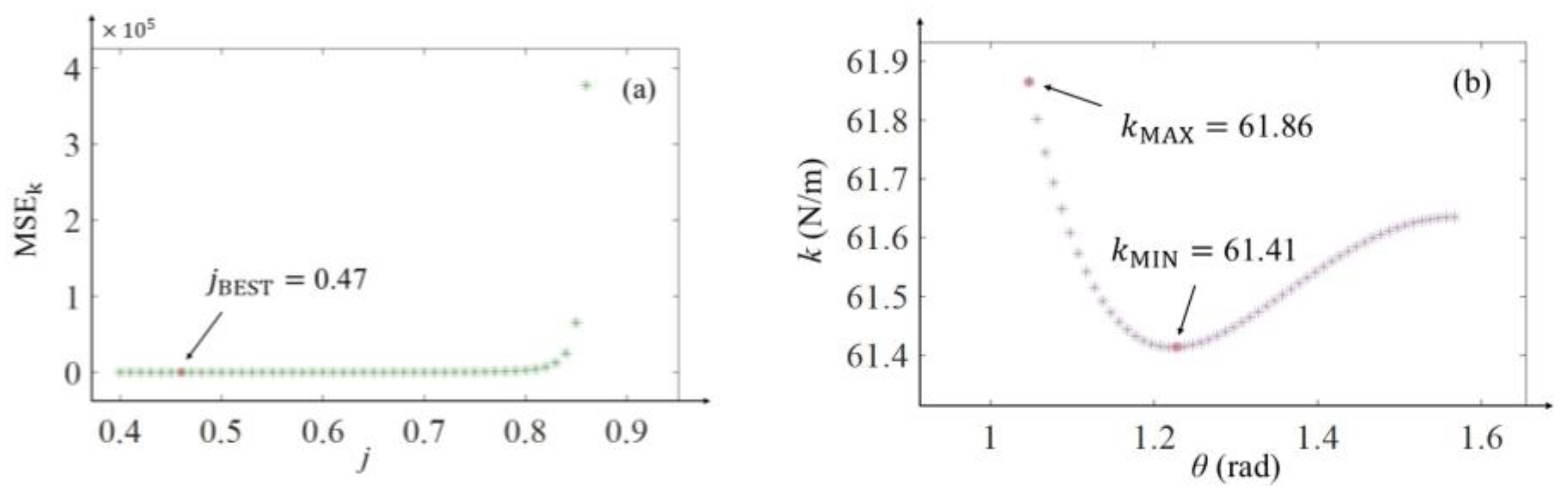
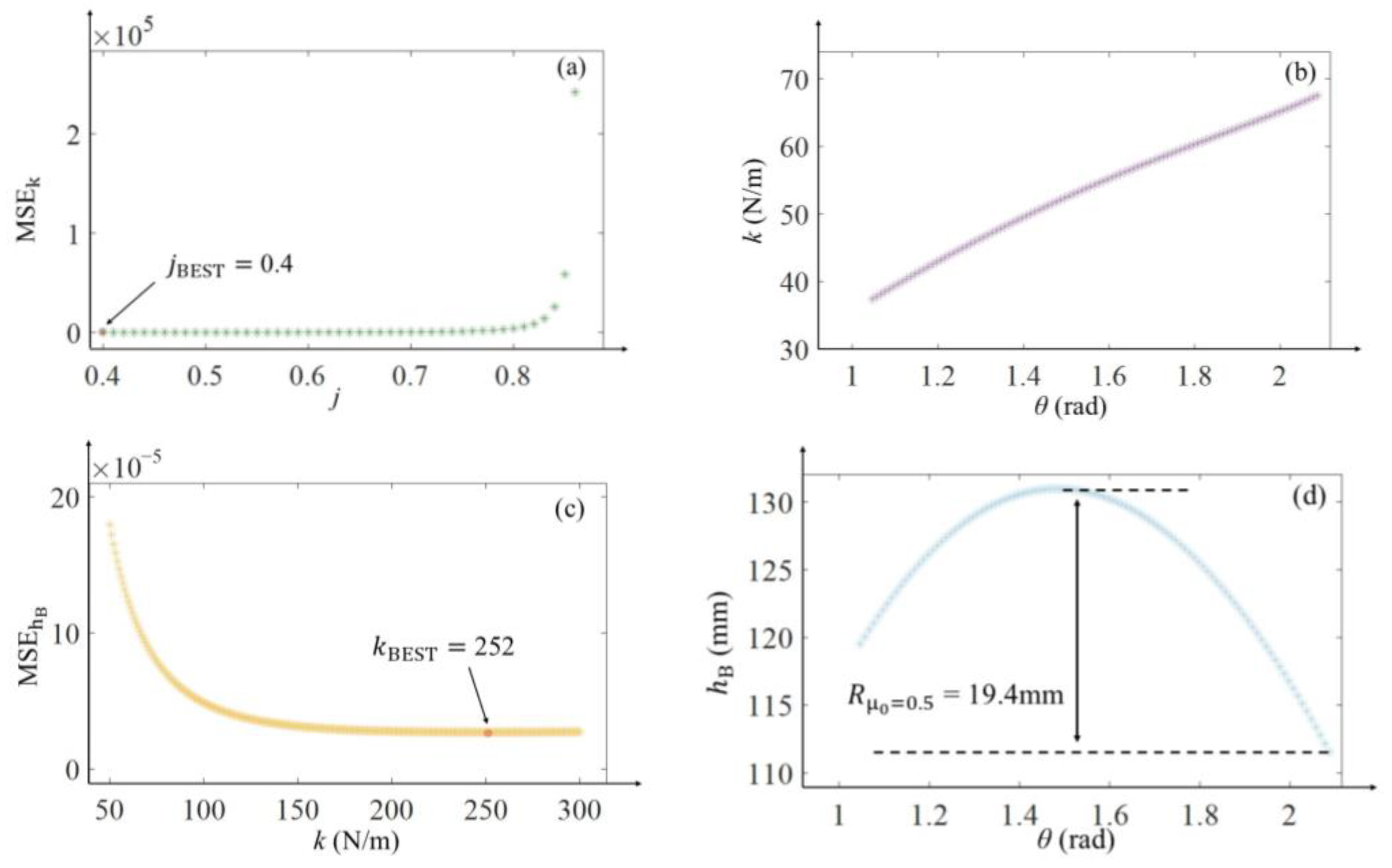
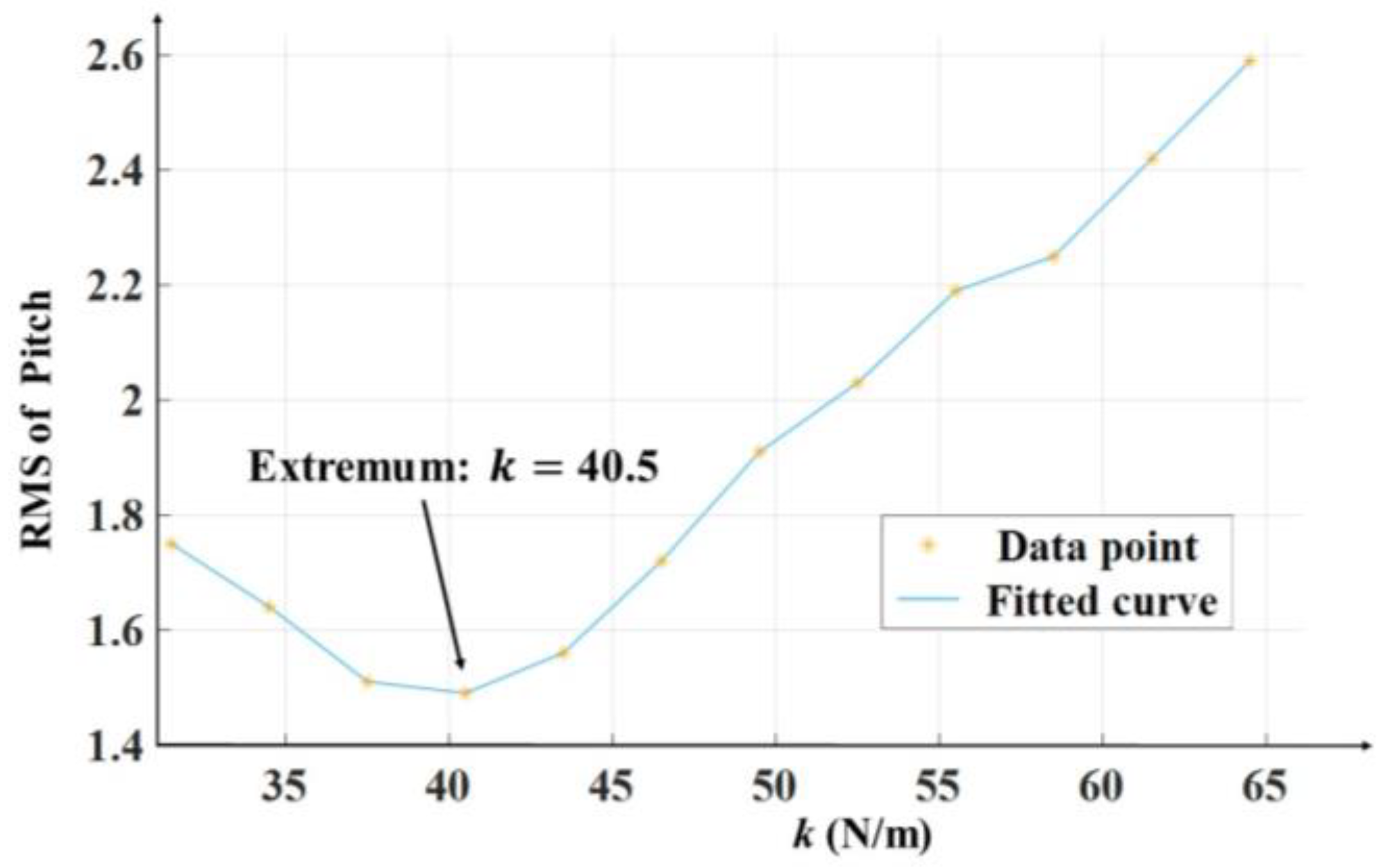
3.1.2. Selection Method for Spring Constant
- 1.
- Determine the optimal body height ratio;
- 2.
- Determine the range of when;
- 3.
- Determine the optimal spring constant;
- 4.
- Determine the range of when;
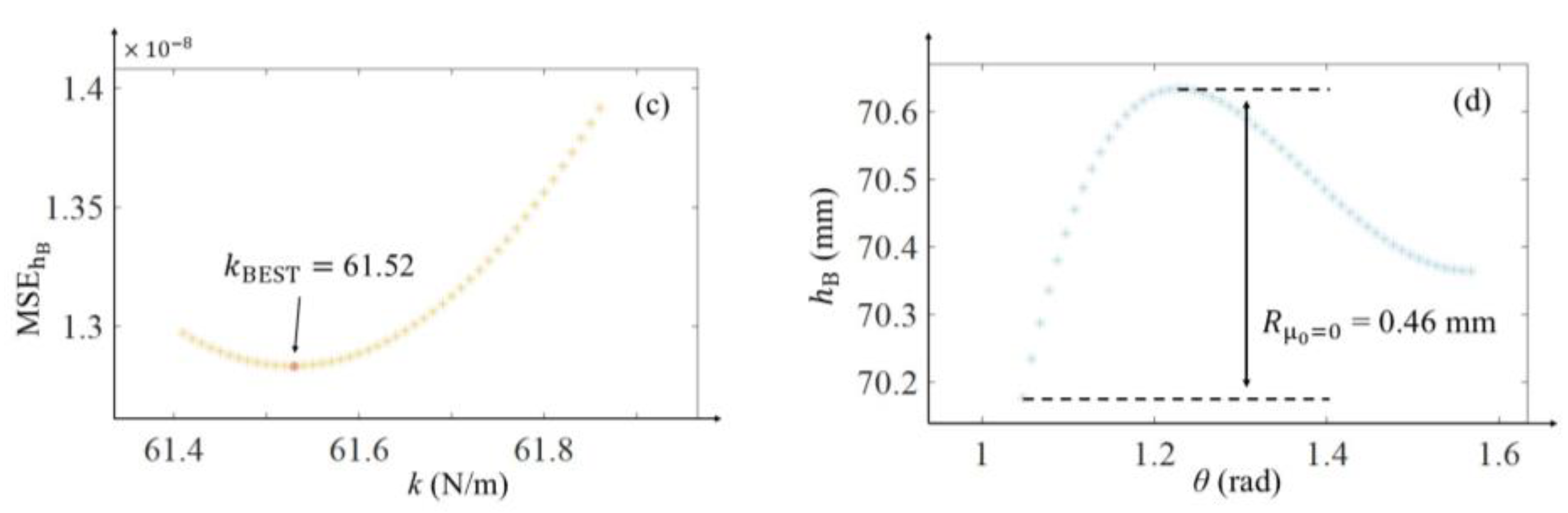
3.1.3. Pre-Compression Determination
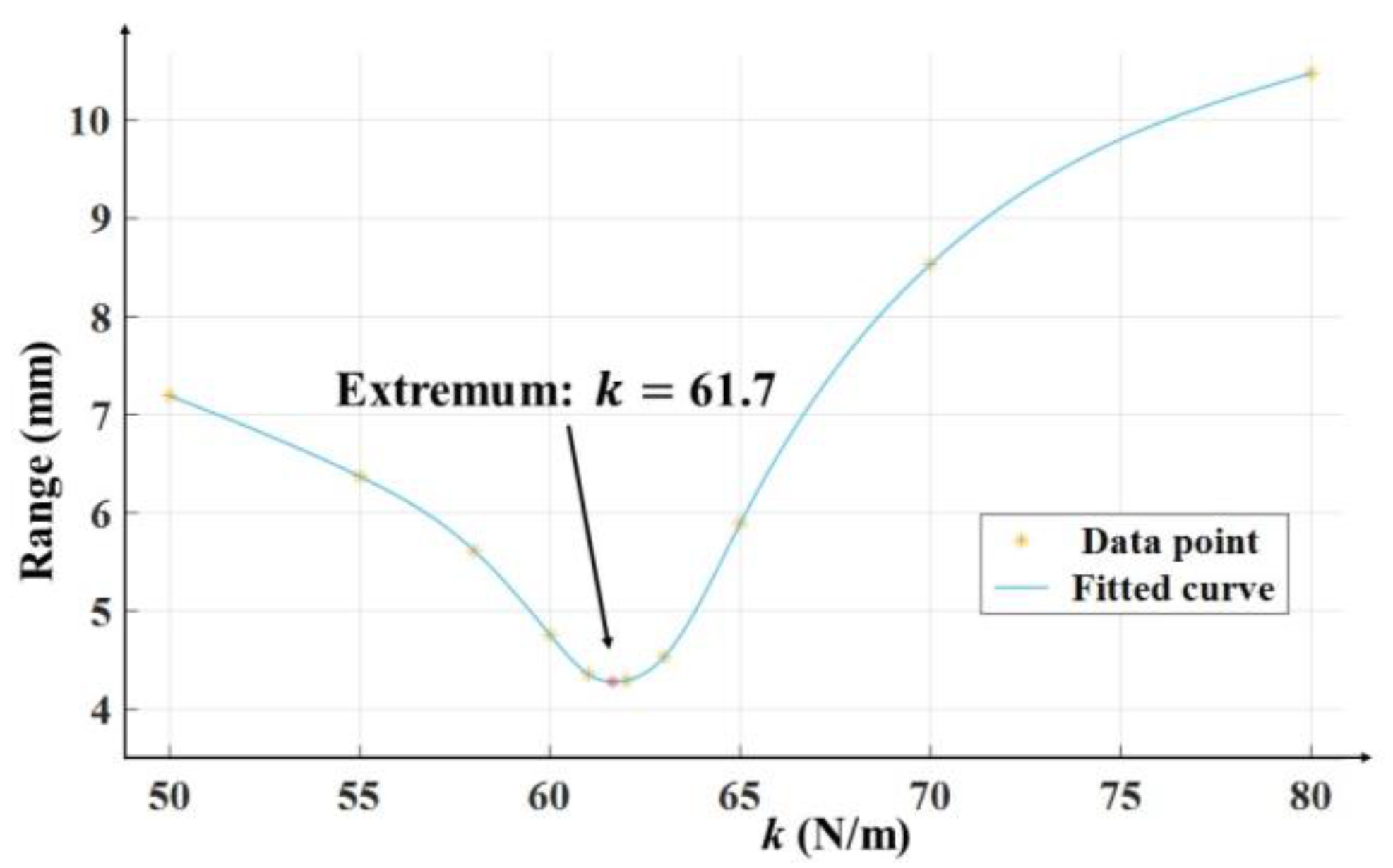
3.2. Theoretical Validation
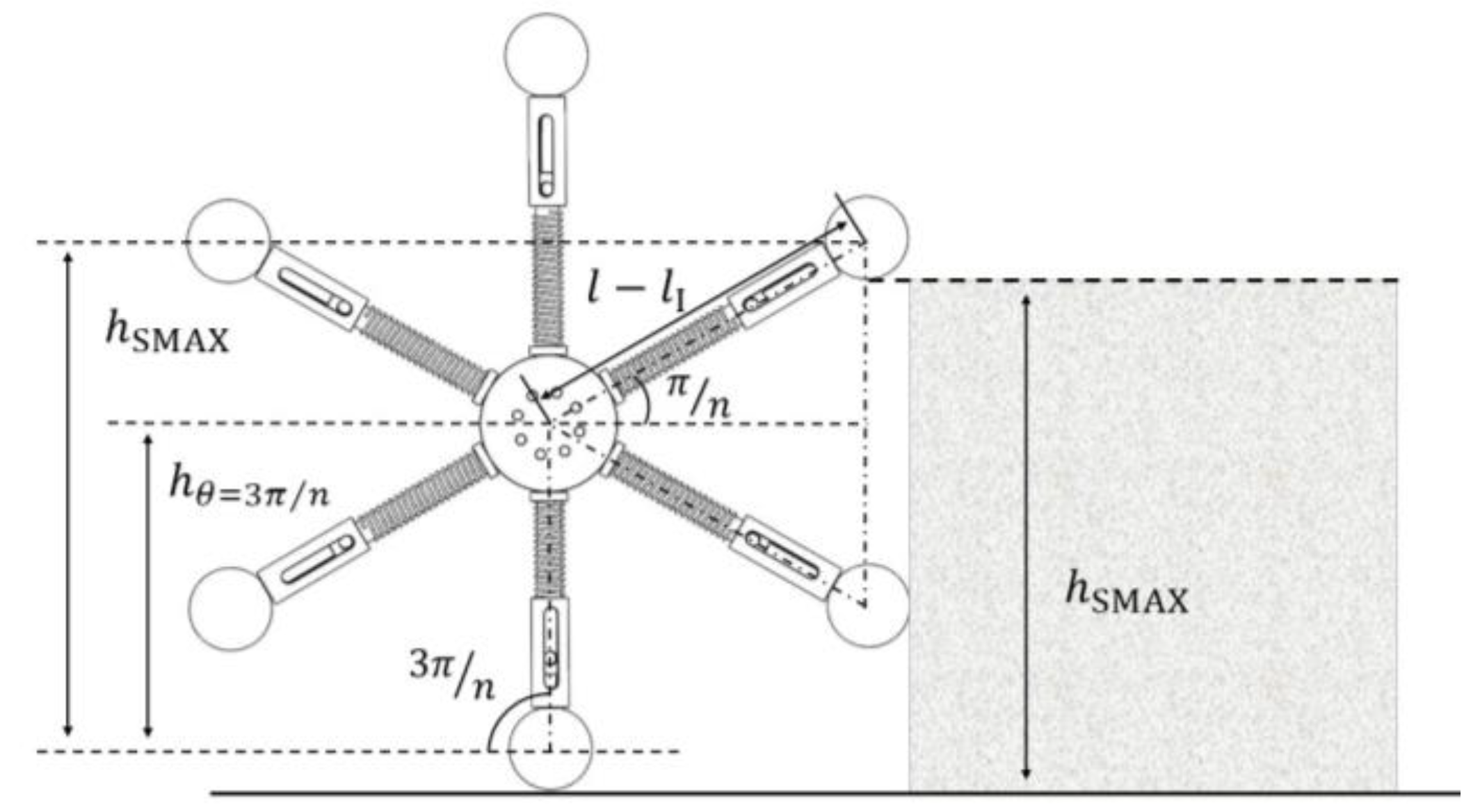
3.3. Maximum Climbing Height
4. Simulation Verification
- 3D Modeling
- 2.
- Simulation Environment Integration
- 3.
- Control Program Development
- 4.
- Physics Engine and Joint Configuration
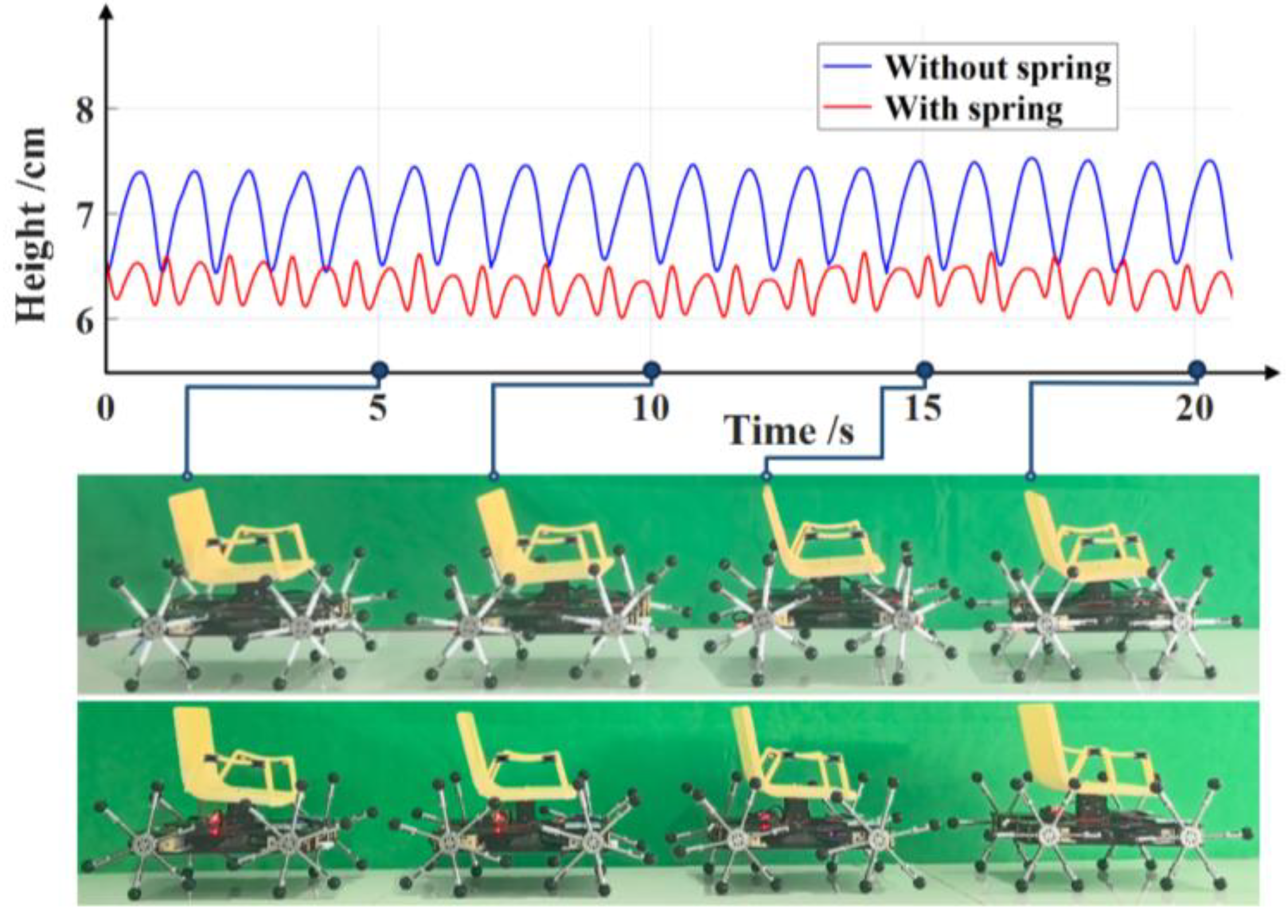
4.1. Flat Terrain Motion Simulation
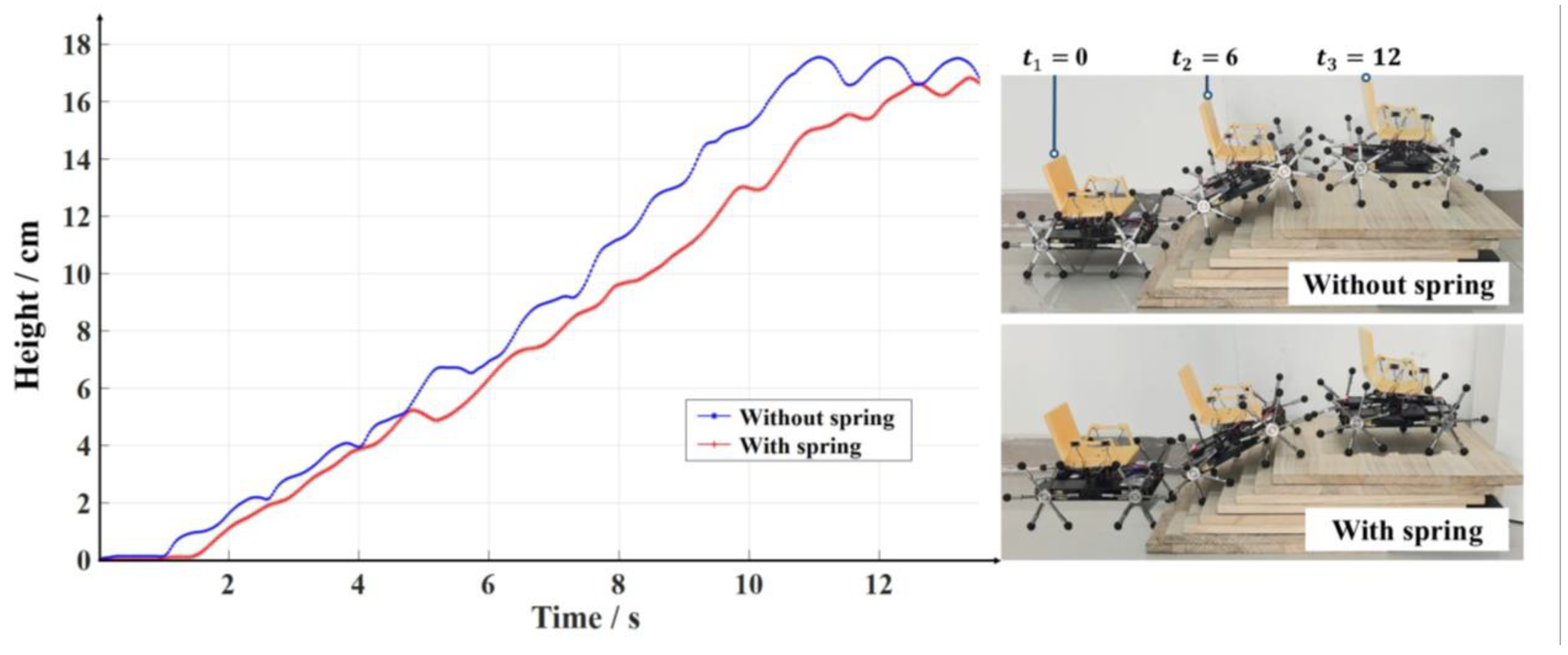
4.2. Stair Climbing Simulation
5. Experimental Validation
5.1. Prototype Fabrication
5.2. Flat Terrain Motion Experiment
5.3. Stair-Climbing Experiment
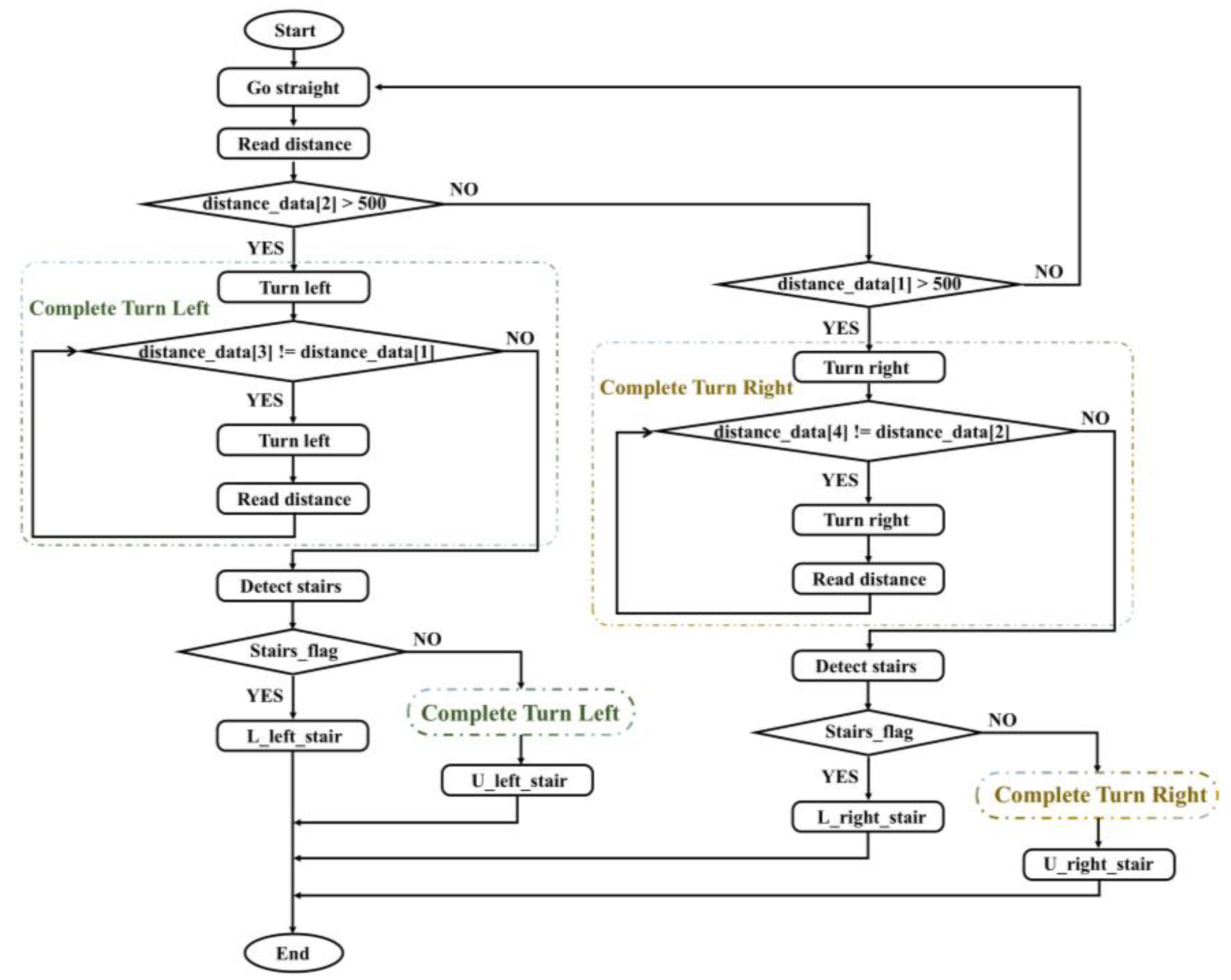
5.4. Multi-Sensor Fusion Stair Climbing Experiment
6. Conclusions
7. Patents
- Patent Number: CN115817066B.
- Applicant: Nanjing University of Information Science and Technology.
- Inventors: Yuting Li, Zhong Wei, Jiwen Zhang. et al.
- Filing Date: 24 November 2022.
- Publication Date: 16 August 2024.
- Status: Granted.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luoma-Halkola, H.; Häikiö, L. Independent living with mobility restrictions: Older people’s perceptions of their out-of-home mobility. Ageing Soc. 2022, 42, 249–270. [Google Scholar] [CrossRef]
- Sanderson, W.C.; Scherbov, S. A new perspective on population aging. Demogr. Res. 2007, 16, 27–58. [Google Scholar] [CrossRef]
- Wu, Y.; Xiong, Y.; Wang, P.; Liu, R.; Jia, X.; Kong, Y.; Li, F.; Chen, C.; Zhang, X.; Zheng, Y. Risk factors of cardiovascular and cerebrovascular diseases in young and middle-aged adults: A meta-analysis. Medicine 2022, 101, e32082. [Google Scholar] [CrossRef] [PubMed]
- Fang, L.; Lu, T.; He, W.; Yuan, K. Dynamic and Tip-Over Stability Analysis of a Planetary Wheeled Stair-Climbing Wheelchair. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, Chengdu, Sichuan, China, 5–8 August 2012; pp. 2541–2546. [Google Scholar]
- Cooper, R.A.; Boninger, M.L.; Cooper, R.; Kelleher, A. Use of the INDEPENDENCE 3000 IBOT™ transporter at home and in the community: A case report. Disabil. Rehabil. Assist. Technol. 2006, 1, 111–117. [Google Scholar] [CrossRef] [PubMed]
- Guarnieri, M.; Takao, I.; Debenest, P.; Takita, K.; Fukushima, E.; Hirose, S. HELIOS IX Tracked Vehicle for Urban Search and Rescue Operations: Mechanical Design and First Tests. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 1612–1617. [Google Scholar]
- Sugahara, Y.; Ohta, A.; Hashimoto, K.; Sunazuka, H.; Kawase, M.; Tanaka, C.; Lim, H.-o.; Takanishi, A. Walking Up and Down Stairs Carrying a Human By a Biped Locomotor with Parallel Mechanism. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 1489–1494. [Google Scholar]
- Baishya, N.J.; Bhattacharya, B.; Ogai, H.; Tatsumi, K. Analysis and design of a minimalist step climbing robot. Appl. Sci. 2021, 11, 7044. [Google Scholar] [CrossRef]
- Zhengyan, Q.; Hongbo, W.; Zhen, H. Kinematics of a Quadruped/Biped Reconfigurable Walking Robot with Parallel Leg Mechanisms. In Proceedings of the ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, London, UK, 22–24 June 2009; pp. 558–564. [Google Scholar]
- Yu, S.; Wang, T.; Wang, Y.; Zhi, D.; Yao, C.; Li, X.; Wang, Z.; Luo, Y.; Wang, Z. A Tip-Over and Slippage Stability Criterion for Stair-Climbing of a Wheelchair Robot with Variable Geometry Single Tracked Mechanism. In Proceedings of the 2012 IEEE International Conference on Information and Automation, Shenyang, China, 6–8 June 2012; pp. 88–93. [Google Scholar]
- Tao, W.; Jia, Y.; Liu, T.; Yi, J.; Wang, H.; Inoue, Y. A novel wheel-track hybrid electric powered wheelchair for stairs climbing. J. Adv. Mech. Des. Syst. Manuf. 2016, 10, JAMDSM0060. [Google Scholar] [CrossRef]
- Imaoka, N.; Kimura, K.; Noda, S.; Kakiuchi, Y.; Inaba, M.; Ando, T. A Transformable Human-Carrying Wheel–Leg Mobility for Daily Use. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3005–3011. [Google Scholar]
- Lee, J.-Y.; Han, S.; Kim, M.; Seo, Y.-S.; Park, J.; Park, D.I.; Park, C.; Seo, H.; Lee, J.; Kim, H.-S. Variable-stiffness–morphing wheel inspired by the surface tension of a liquid droplet. Sci. Robot. 2024, 9, eadl2067. [Google Scholar] [CrossRef] [PubMed]
- Tao, W.; Xu, J.; Liu, T. Electric-powered wheelchair with stair-climbing ability. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417721436. [Google Scholar] [CrossRef]
- Deng, Y.; Hua, Y.; Napp, N.; Petersen, K. A compiler for scalable construction by the termes robot collective. Robot. Auton. Syst. 2019, 121, 103240. [Google Scholar] [CrossRef]
- Schroer, R.T.; Boggess, M.J.; Bachmann, R.J.; Quinn, R.D.; Ritzmann, R.E. Comparing Cockroach and Whegs Robot Body Motions. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 3288–3293. [Google Scholar]
- Hidalgo, J. Navigation and Slip Kinematics for High Performance Motion Models. In Proceedings of the Symposium on Advanced Space Technologies in Robotics and Automation, Sydney, Australia, 2–4 December 2013. [Google Scholar]
- Ai, X.; Yue, H.; Wang, W.D. Crawling soft robot exploiting wheel-legs and multimodal locomotion for high terrestrial maneuverability. IEEE Trans. Robot. 2023, 39, 4230–4239. [Google Scholar] [CrossRef]
- Zheng, C.; Sane, S.; Lee, K.; Kalyanram, V.; Lee, K. α-WaLTR: Adaptive Wheel-and-Leg Transformable Robot for Versatile Multiterrain Locomotion. IEEE Trans. Robot. 2022, 39, 941–958. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, H.; Xiong, K.; Zhou, Q.; Guo, W. Design and Analysis of a Bi-Directional Transformable Wheel Robot Trimode. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 8396–8403. [Google Scholar]
- Sun, C.; Yang, G.; Yao, S.; Liu, Q.; Wang, J.; Xiao, X. Rhex-t3: A transformable hexapod robot with ladder climbing function. IEEE/ASME Trans. Mechatron. 2023, 28, 1939–1947. [Google Scholar] [CrossRef]
- Yoon, H.; Kim, S.; Park, I.; Heo, J.; Kim, H.S.; Seo, T. 2 DOF transformable wheel design based on geared 8 bar parallel linkage mechanism. Sci. Rep. 2024, 14, 379. [Google Scholar] [CrossRef] [PubMed]
- Murphy, D.; Giuliani, M.; Bremner, P. Evaluation and Design Recommendations for a Folding Morphing-Wheg Robot for Nuclear Characterisation. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 13–18 October 2024; pp. 9088–9093. [Google Scholar]
- Jeans, J.B.; Hong, D. IMPASS: Intelligent Mobility Platform with Active Spoke System. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1605–1606. [Google Scholar]
- Oh, S.; Kim, H.; Jeon, S.; Shin, B.; Ryu, B.; Kim, Y. Design of a mobile robot with 2-DOF compliant wheel-legs by using a linear spring. Microsyst. Technol. 2023, 29, 1189–1196. [Google Scholar] [CrossRef]
- Gillespie, T. Fundamentals of Vehicle Dynamics; SAE Int.: Warrendale, PA, USA, 2021; pp. 11–12. [Google Scholar]






| Number of Spokes n | The Range of the Body Height | Maximum Climbing Height | |
|---|---|---|---|
| 4 | 56.88 N/m | 2.3 mm | 120.27 mm |
| 6 | 61.52 N/m | 0.5 mm | 110.85 mm |
| 8 | 62.82 N/m | 0.1 mm | 103.00 mm |
| Description | Symbol | Value |
|---|---|---|
| Length | 380 mm | |
| Width | 200 mm | |
| Number of spokes | 6 | |
| Original spoke length | 150 mm | |
| Spring free length | 100 mm | |
| Rigid segment length | 50 mm | |
| Sliding groove length | 10 mm | |
| Body mass | 2 kg |
| Joints | Parameter | Value |
|---|---|---|
| Revolute joints | Speed [rad/s] | 1.2 |
| Prismatic joints | Pos. min [m] | 0.069 |
| Pos. range [m] | 0.010 | |
| Position [m] | 0.069 | |
| Front prismatic joints | Spring constant K [N/m] | 40.5 |
| Spring constant C [N·s/m] | 9.0 | |
| Rear prismatic joints | Spring constant K [N/m] | 61.7 |
| Spring constant C [N·s/m] | 11.1 |
| Motion Mechanism | Stair Specifications | RMS of Z-Axis Acceleration |
|---|---|---|
| Traditional spoke wheels | 2 cm × 4 cm | 0.48 m/s2 |
| Flexwheels | 2 cm × 4 cm | 0.39 m/s2 |
| Traditional spoke wheels | 3 cm × 10 cm | 0.51 m/s2 |
| Flexwheels | 3 cm × 10 cm | 0.42 m/s2 |
| Traditional spoke wheels | 4 cm × 8 cm | 0.52 m/s2 |
| Flexwheels | 4 cm × 8 cm | 0.47 m/s2 |
| Motion Mechanism | Stair Specifications | RMS of Z-Axis Acceleration |
|---|---|---|
| Traditional spoke wheels | 2 cm × 4 cm | 0.45 m/s2 |
| Flexwheels | 2 cm × 4 cm | 0.36 m/s2 |
| Flexwheels | 4 cm × 8 cm | 0.43 m/s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wei, Z.; Guo, J.; Ren, J.; Ding, Y.; Wang, W.; Liu, J.; Song, A. A Stair-Climbing Wheelchair with Novel Spoke Wheels for Smooth Motion. Appl. Sci. 2025, 15, 5433. https://doi.org/10.3390/app15105433
Li Y, Wei Z, Guo J, Ren J, Ding Y, Wang W, Liu J, Song A. A Stair-Climbing Wheelchair with Novel Spoke Wheels for Smooth Motion. Applied Sciences. 2025; 15(10):5433. https://doi.org/10.3390/app15105433
Chicago/Turabian StyleLi, Yuting, Zhong Wei, Jinlin Guo, Jinyao Ren, Yu Ding, Weixi Wang, Jia Liu, and Aiguo Song. 2025. "A Stair-Climbing Wheelchair with Novel Spoke Wheels for Smooth Motion" Applied Sciences 15, no. 10: 5433. https://doi.org/10.3390/app15105433
APA StyleLi, Y., Wei, Z., Guo, J., Ren, J., Ding, Y., Wang, W., Liu, J., & Song, A. (2025). A Stair-Climbing Wheelchair with Novel Spoke Wheels for Smooth Motion. Applied Sciences, 15(10), 5433. https://doi.org/10.3390/app15105433





