Dynamic Characterization and Parametric Optimization of Secondary Cushioned Pump Valves in Drilling Systems: A 3D Transient Fluid–Structure Interaction Study
Abstract
1. Introduction
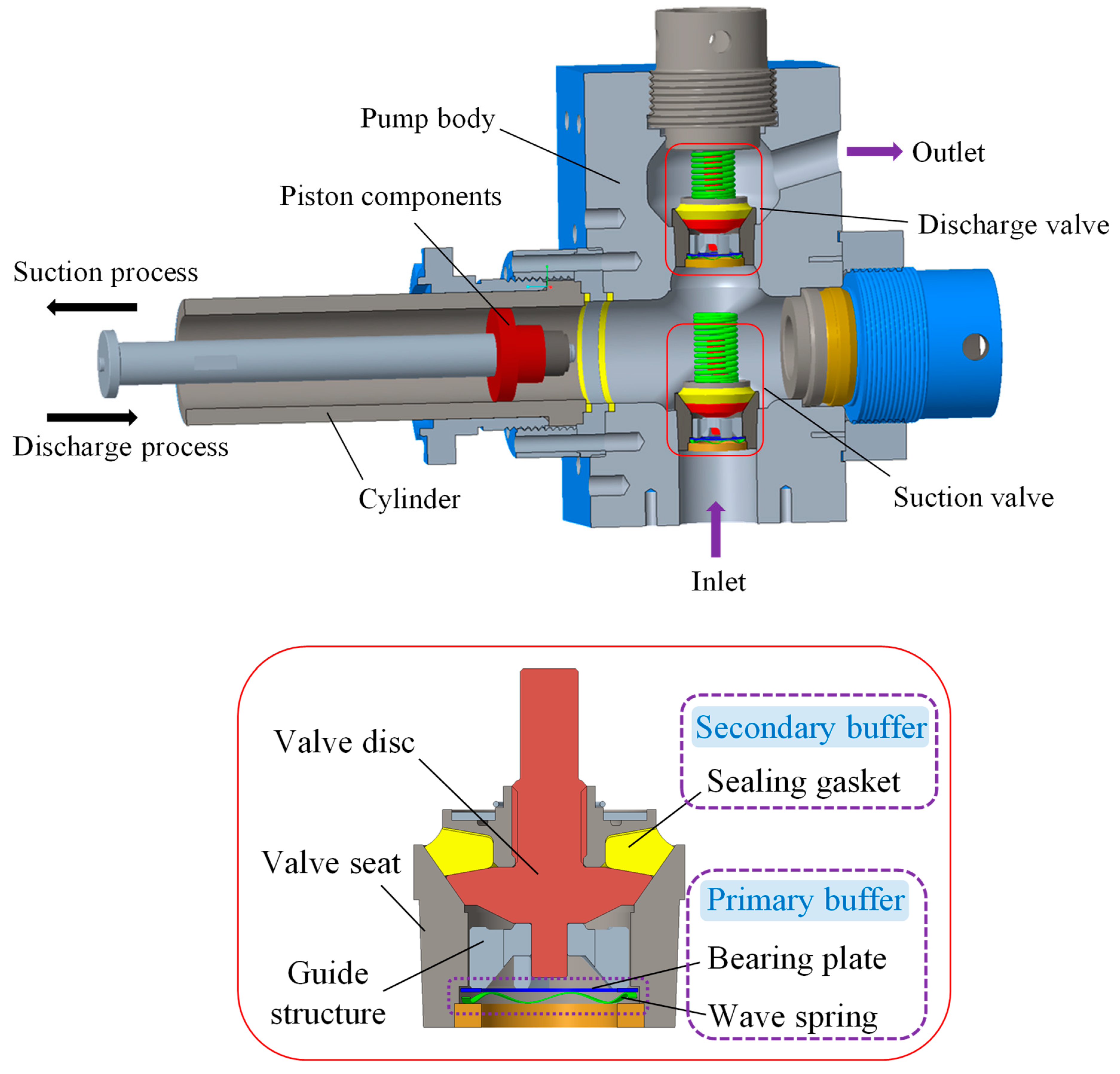
2. Basic Dimensions of Drilling Pump
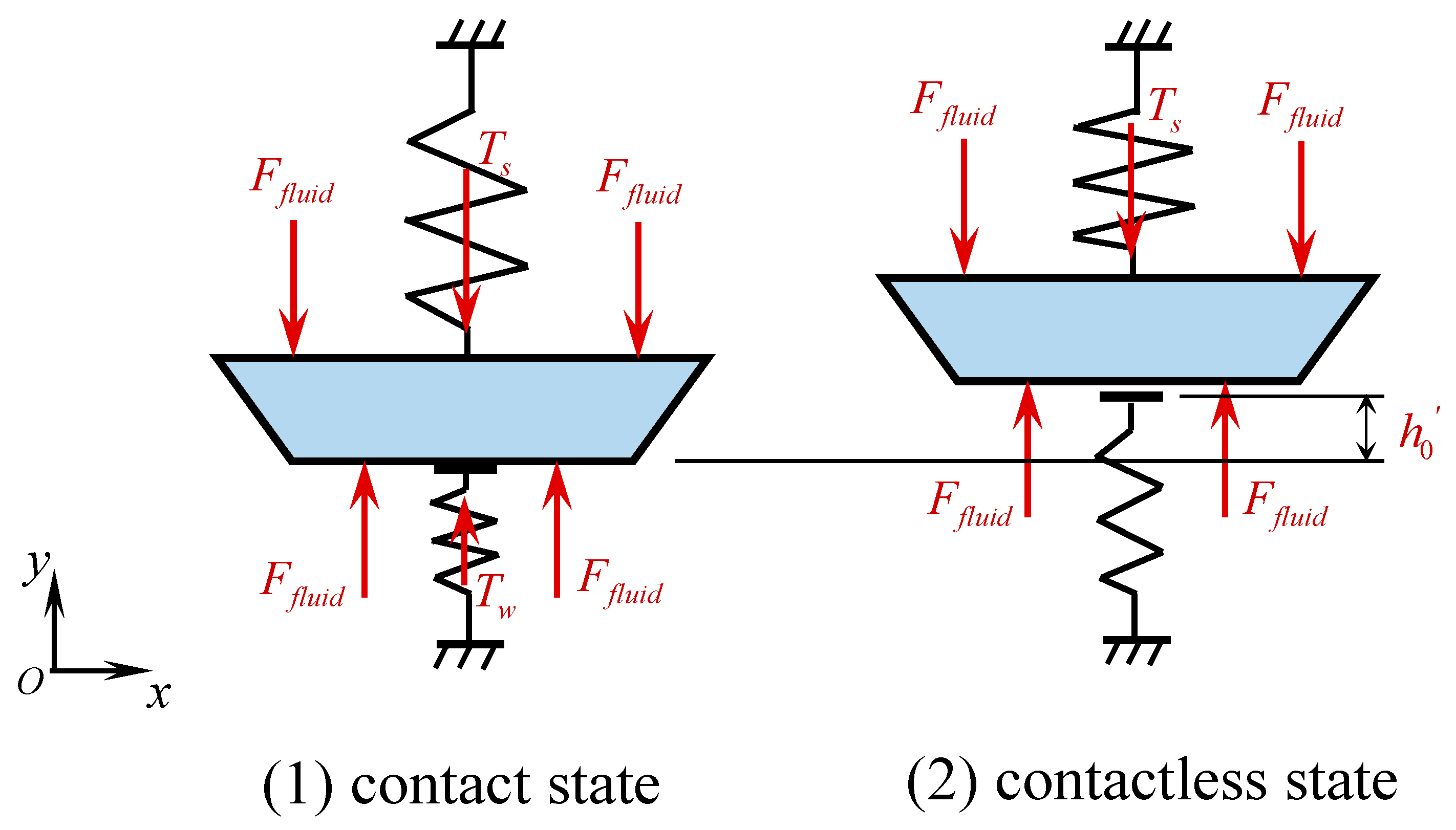
3. Mathematical Model of the Valve Disc Motion
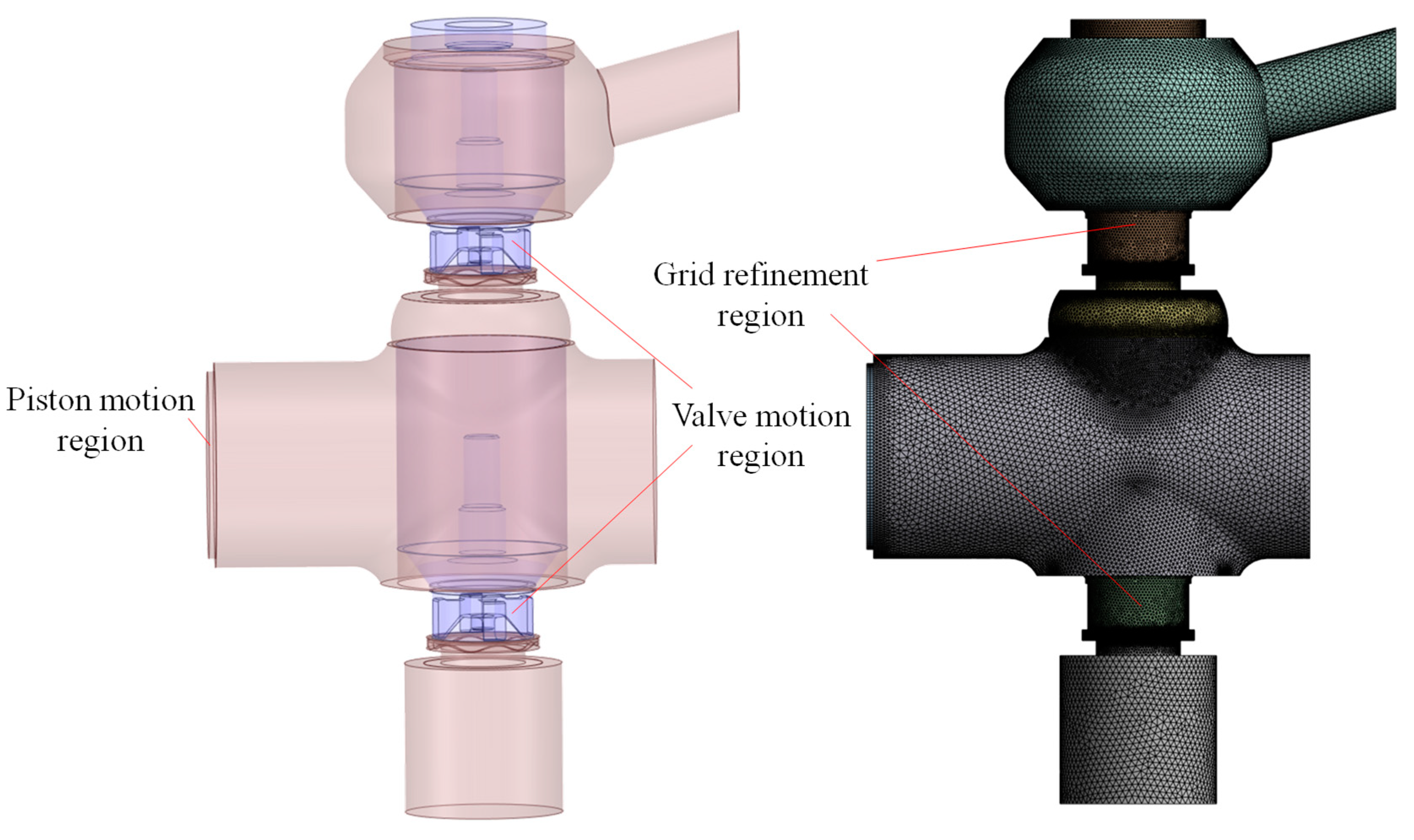
4. Numerical Model and Simulation
5. Results
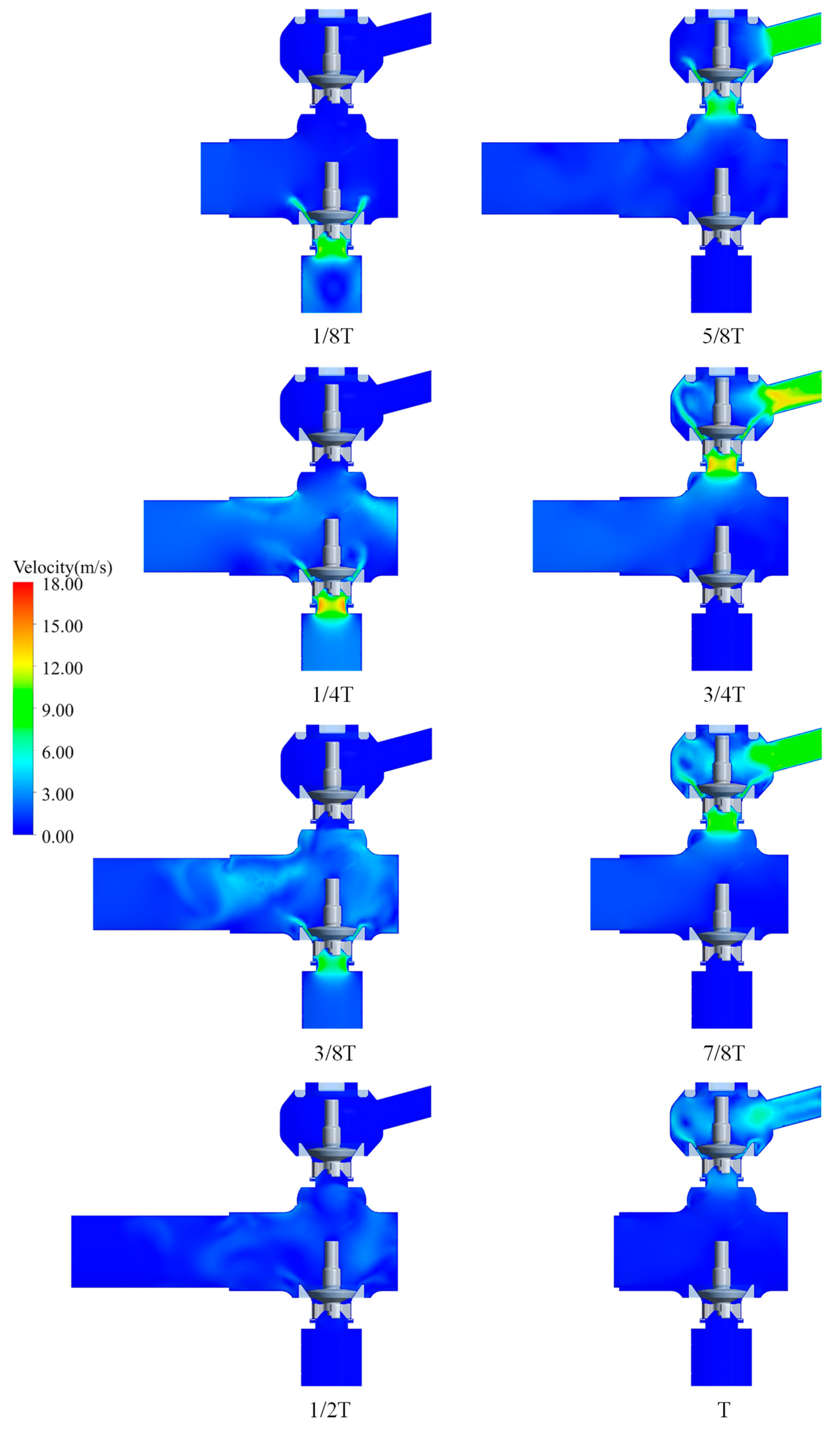
5.1. Coupled Flow–Valve Dynamics
5.1.1. Sealing Integrity
5.1.2. Jet-Driven Valve Motion
5.1.3. Pressure Differential Effects on Closure Hysteresis
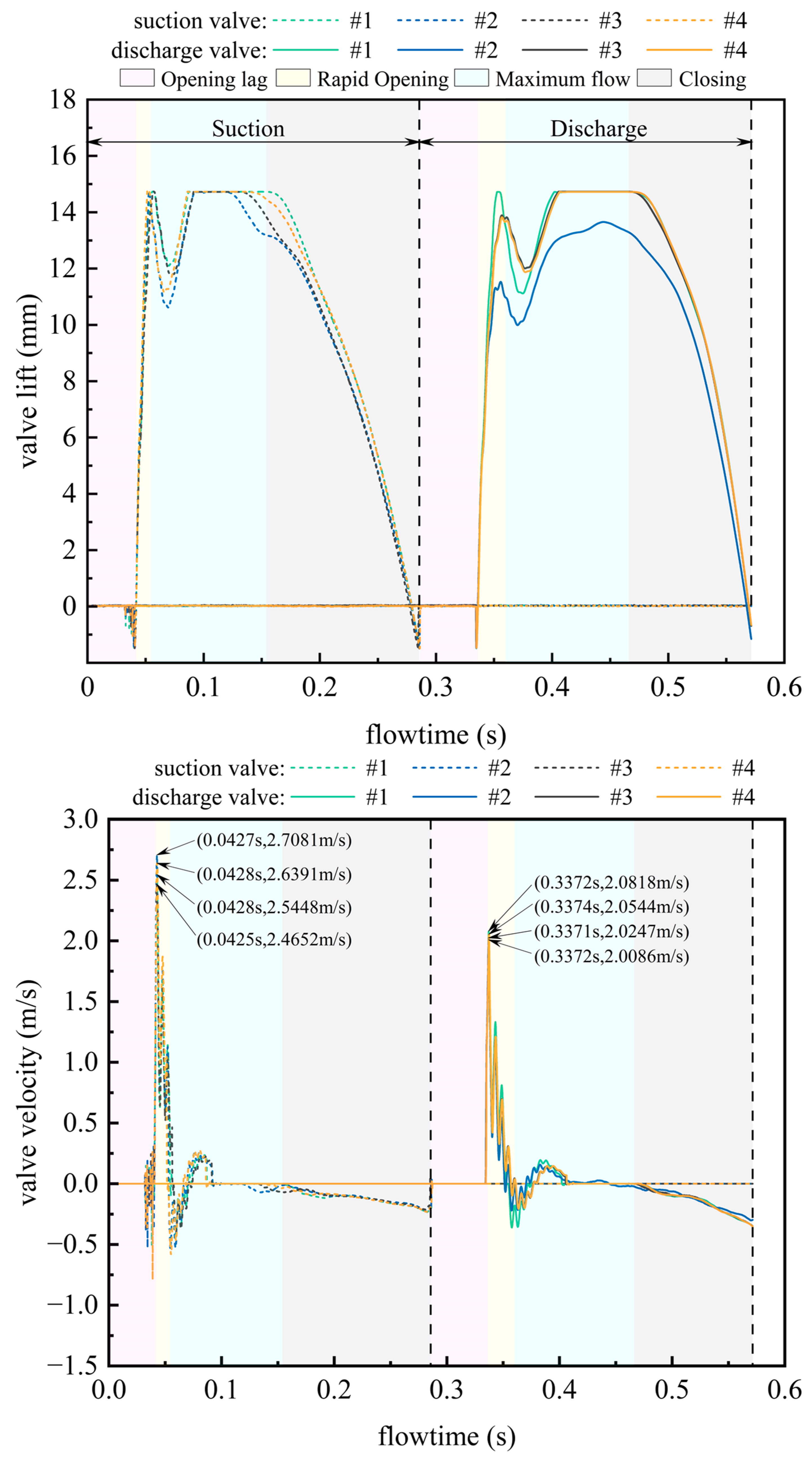
5.2. The Motion Characteristics of Pump Valves
5.2.1. Dynamic Response Characteristics of Valve Operation
5.2.2. Structural Parametric Sensitivity Analysis
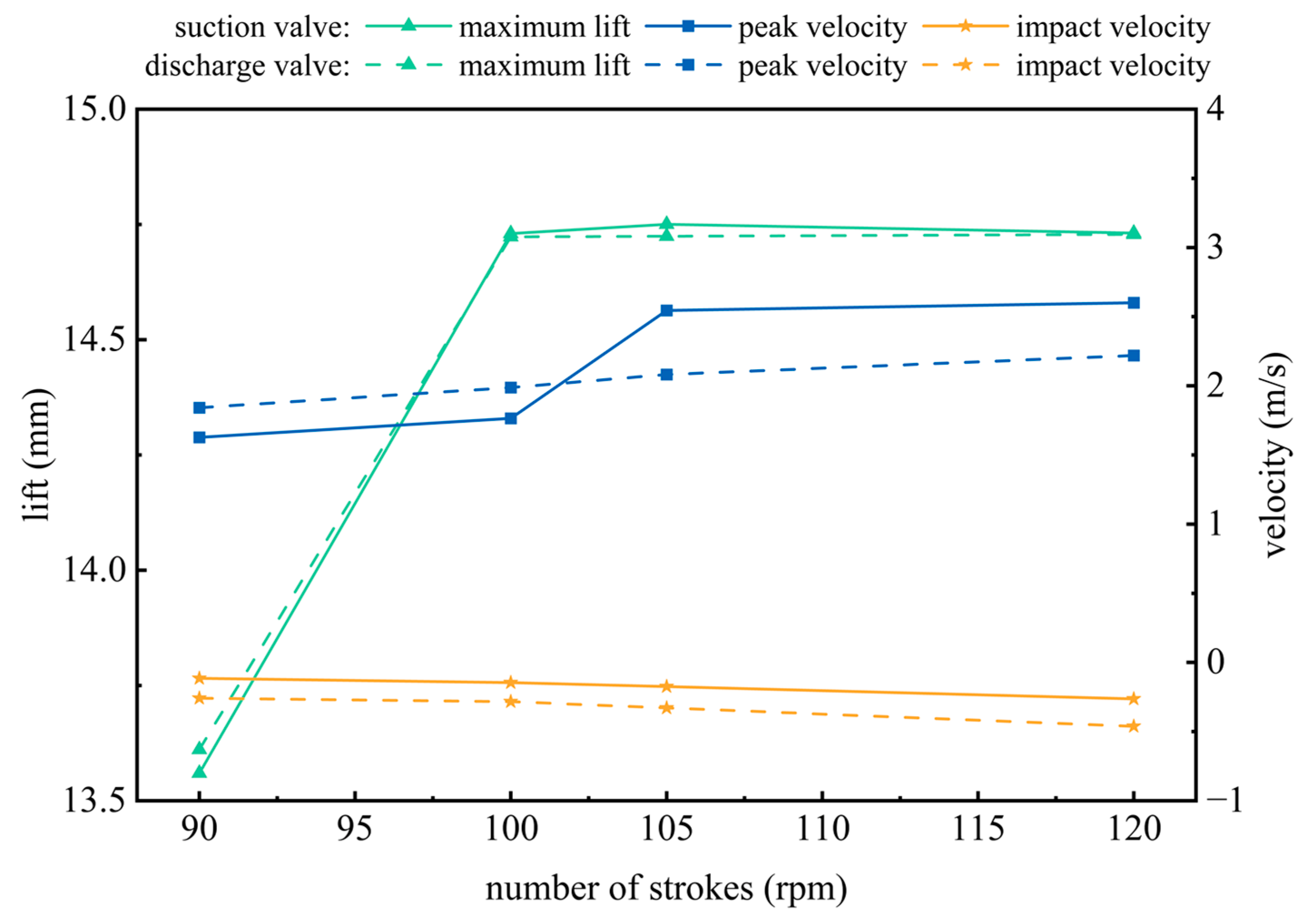
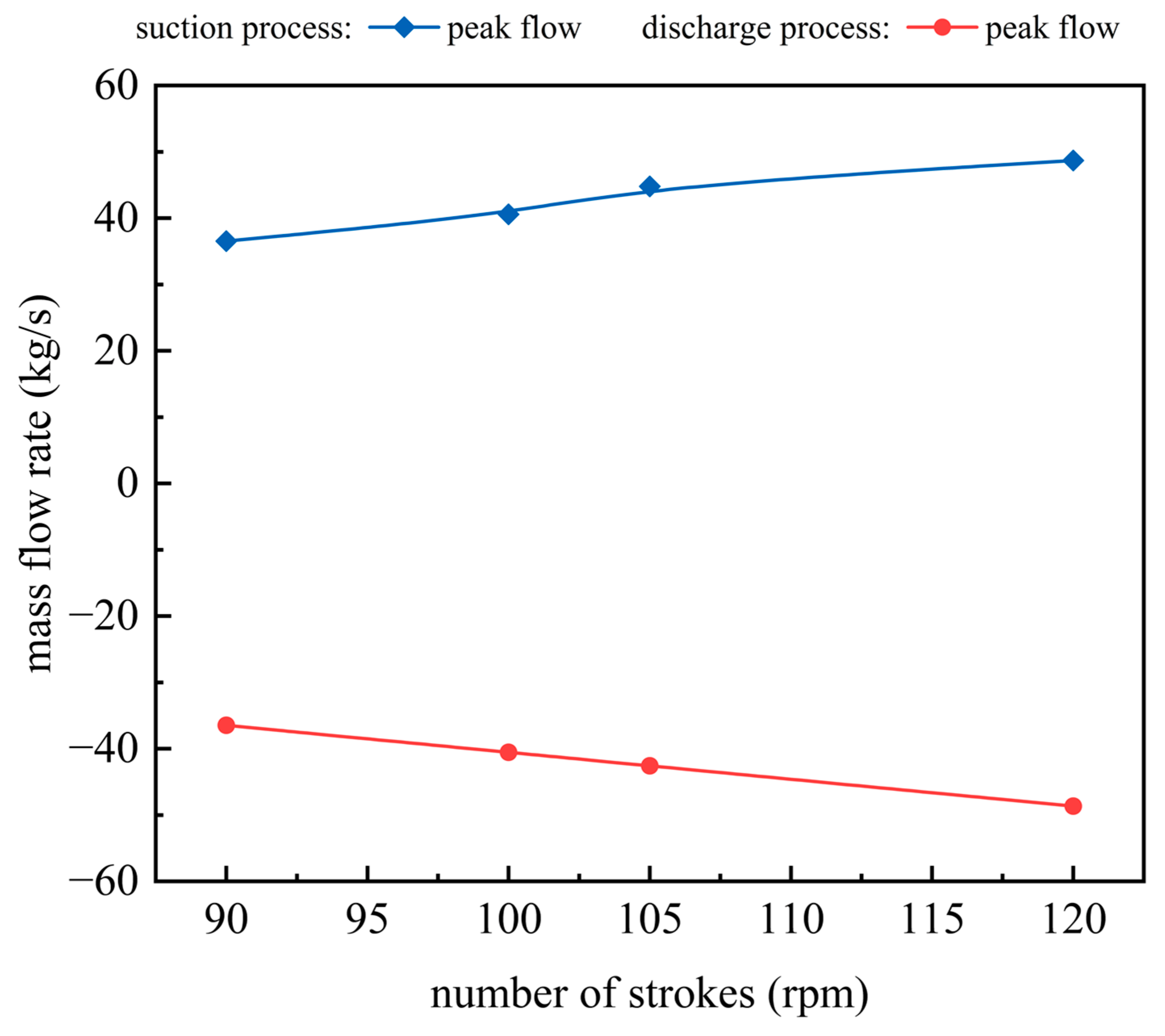
5.2.3. Operating Condition Sensitivity Analysis
5.3. Comparative Performance Analysis
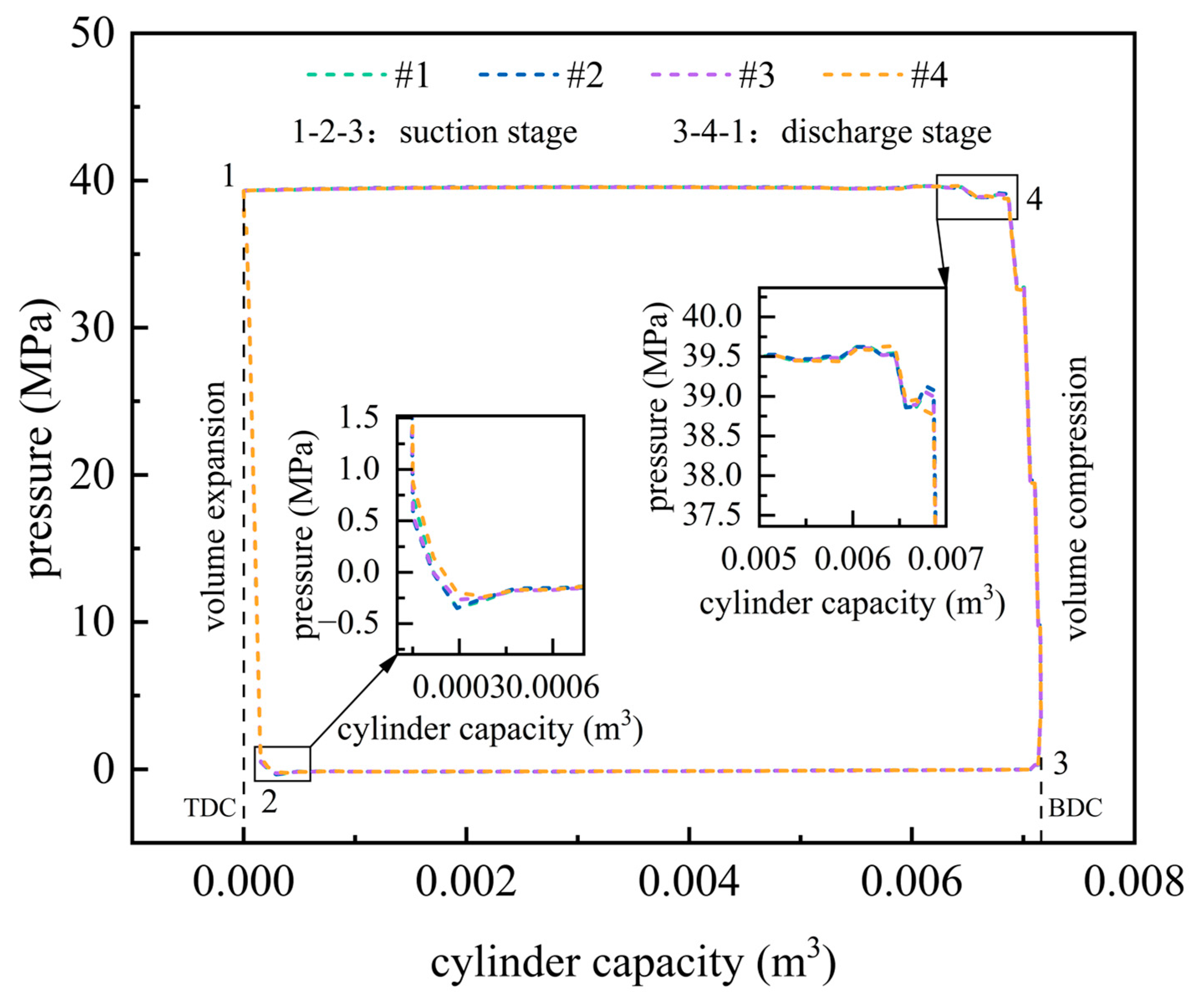
5.3.1. Dynamic P-V Characteristics Across Operational Phases
5.3.2. Parametric Modulation of Pressure Stability
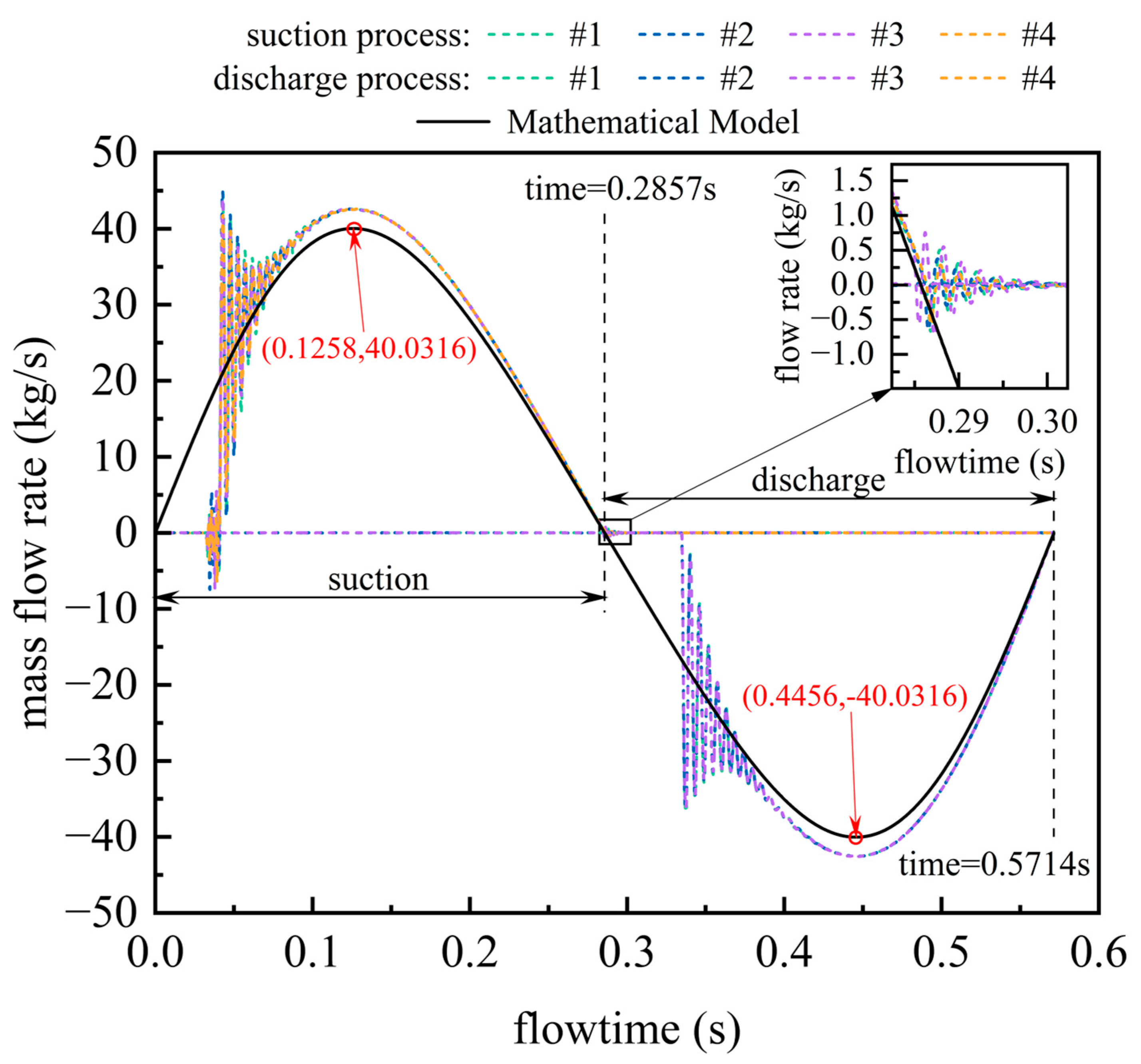
5.4. Flow Characteristic Analysis
6. Discussion
6.1. Valve–Flow Interaction Dynamics
6.1.1. Sealing Performance Validation
6.1.2. Jet-Induced Valve Actuation Mechanism
6.1.3. Pressure-Driven Closure Optimization
6.2. Parametric Control of Valve Dynamics
6.2.1. Dynamic Response Characteristics
6.2.2. Spring Parameter Sensitivity
6.3. System-Level Performance Evaluation
6.3.1. Phase-Synchronized P-V Behavior
6.3.2. Flow Stability Enhancement
7. Conclusions
- Sealing Efficacy Verification: complete sealing integrity was demonstrated through near-zero clearance flow velocities, validated by symmetrical flow suppression patterns.
- Hysteresis Mitigation Strategy: the secondary cushioned mechanism design reduces closure delays by 22%, directly enhancing volumetric efficiency.
- Parametric Optimization Guidelines: spring stiffness and preload were established as primary control parameters, with structural factors dominating closing dynamics. A wave spring stiffness enhancement of 24% achieves pressure stability through optimized damping, reducing perturbations by 90%. Increasing the number of strokes can effectively increase drilling pump displacement while exacerbating critical component failures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Josifovic, A.; Roberts, J.J.; Corney, J.; Davies, B.; Shipton, Z.K. Reducing the environmental impact of hydraulic fracturing through design optimisation of positive displacement pumps. Energy 2016, 115, 1216–1233. [Google Scholar] [CrossRef]
- Pei, J.; He, C.; Lv, M.; Huang, X.; Shen, K.; Bi, K. The valve motion characteristics of a reciprocating pump. Mech. Syst. Signal Process. 2016, 66–67, 657–664. [Google Scholar] [CrossRef]
- Brazhenko, V.; Cai, J.-C.; Fang, Y. Utilizing a Transparent Model of a Semi-Direct Acting Water Solenoid Valve to Visualize Diaphragm Displacement and Apply Resulting Data for CFD Analysis. Water 2024, 16, 3385. [Google Scholar] [CrossRef]
- Shu, Z.; Liang, W.; Qin, B.; Lei, G.; Wang, T.; Huang, L.; Che, B.; Zheng, X.; Qian, H. Transient Flow Dynamics Behaviors during Quick Shut-off of Ball Valves in Liquid Hydrogen Pipelines and Storage Systems. J. Energy Storage 2023, 73, 109049. [Google Scholar] [CrossRef]
- Yao, H.; Ye, Q.; Wang, C.; Yuan, P. CFD Dynamic Mesh-Based Simulation and Performance Investigation of Combined Guided Float Valve Tray. Chem. Eng. Process.-Process Intensif. 2023, 193, 109523. [Google Scholar] [CrossRef]
- Neyestanaki, M.K.; Dunca, G.; Jonsson, P.; Cervantes, M.J. A Comparison of Different Methods for Modelling Water Hammer Valve Closure with CFD. Water 2023, 15, 1510. [Google Scholar] [CrossRef]
- Wang, T.; Wang, G.R.; Dai, L.M.; Chen, L.Y.; Qiu, S.Z.; Li, R. Motion mechanism study on the valve disc of an ultra-high pressure reciprocating pump. Mech. Syst. Signal Process. 2021, 160, 107942. [Google Scholar] [CrossRef]
- Wang, G.R.; Zhong, L.; He, X.; Lei, Z.; Hu, G.; Li, R.; Wang, Y. Dynamic behavior of reciprocating plunger pump discharge valve based on fluid structure interaction and experimental analysis. PLoS ONE 2015, 10, e0140396. [Google Scholar] [CrossRef]
- Lian, Z.H.; Liu, Y.; Lin, T.; Li, L.; Lei, Z.; Han, C.J. Study on the fluid flow rule of five-cylinder plunger pump hydraulic end. Petroleum 2018, 4, 457–465. [Google Scholar] [CrossRef]
- Beune, A.; Kuerten, J.G.M.; van Heumen, M.P.C. CFD analysis with fluid-structure interaction of opening high-pressure safety valves. Comput. Fluids 2012, 64, 108–116. [Google Scholar] [CrossRef]
- Qian, J.; Wei, L.; Jin, Z.; Wang, J.; Zhang, H.; Lu, A. CFD analysis on the dynamic flow characteristics of the pilot-control globe valve. Energy Convers. Manag. 2014, 87, 220–226. [Google Scholar] [CrossRef]
- Zhang, S.C.; Zhang, Y.L.; Fang, Z.M. Numerical simulation and analysis of ball valve three-dimensional flow based on CFD. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 052024. [Google Scholar] [CrossRef]
- Song, X.G.; Wang, L.; Park, Y.C. Transient Analysis of a spring-loaded pressure safety valve using computational fluid dynamics (CFD). J. Press. Vessel. Technol.-Trans. ASME 2010, 132, 054501. [Google Scholar] [CrossRef]
- Ma, Y.; Luo, H.; Gao, T.; Zhang, Z. Transient Flow Study of a Novel Three-Cylinder Double-Acting Reciprocating Multiphase Pump. J. Fluids Eng. 2017, 139, 101101. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, Y.; Zhang, H.; Luo, H.; Deng, H. Instability Prediction of Valve Motion and Internal Flow in Novel Large-scale Reciprocating Pump. Int. J. Fluid Mach. Syst. 2019, 12, 1–11. [Google Scholar] [CrossRef]
- Hwang, I.S.; Park, S.J.; Oh, W.; Lee, Y.L. Linear compressor discharge valve behavior using a rigid body valve model and a FSI valve model. Int. J. Refrig. 2017, 82, 509–519. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Cai, S.; Zhu, H.; Zhang, Y. Investigation of gas–liquid two-phase flow in a three-stage rotodynamic multiphase pump via numerical simulation and visualization experiment. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Iannetti, A.; Stickland, M.T.; Dempster, W.M. A CFD model to evaluate the inlet stroke performance of a positive displacement reciprocating plunger pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 5, 574–584. [Google Scholar] [CrossRef]
- Pan, X.; Yang, S.; Shi, Y.; Liu, Y. Investigation on the dynamic characteristics of port valves in a diaphragm pump for exhaust gas treatment system by FSI modeling. IEEE Access 2019, 7, 57238–57250. [Google Scholar] [CrossRef]
- Tao, W.; Guo, Y.; He, Z.; Peng, X. Investigation on the delayed closure of the suction valve in the refrigerator compressor by FSI modeling. Int. J. Refrig 2018, 91, 111–121. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, Y.; Tang, B.; Li, L. Dynamic performance of suction valve in stepless capacity regulation system for large-scale reciprocating compressor. Appl. Therm. Eng. 2016, 96, 167–177. [Google Scholar] [CrossRef]
- Suh, J.; Kim, J.; Choi, Y.; Joo, W.; Lee, K. A study on numerical optimization and performance verification of multiphase pump for offshore plant. Proc. Inst. Mech. Eng. Part A J. Power Energy 2017, 231, 382–397. [Google Scholar] [CrossRef]
- Ma, Y.; Ni, Y.; Zhang, H.; Zhou, S.; Deng, H. Influence of valve’s lag characteristic on pressure pulsation and performance of reciprocating multiphase pump. J. Pet. Sci. Eng. 2018, 164, 584–594. [Google Scholar] [CrossRef]
- Zhu, G.; Dong, S.M. Analysis on the Performance Improvement of Reciprocating Pump with Variable Stiffness Valve using CFD. J. Appl. Fluid Mech. 2020, 13, 387–400. [Google Scholar] [CrossRef]
- Menéndez-Blanco, A.; Oro, J.M.F.; Meana-Fernández, A. Unsteady three-dimensional modeling of the Fluid–Structure Interaction in the check valves of diaphragm volumetric pump. J. Fluids Struct. 2019, 90, 432–449. [Google Scholar] [CrossRef]

| Crank radius (mm) | 178 |
| Connecting rod length (mm) | 890 |
| Strokes (rpm) | 105 |
| Cylinder diameter (mm) | 160 |
| Piston stroke (mm) | 356 |
| Valve seat bore diameter (mm) | 90 |
| Cylindrical spring stiffness (N/mm) | 11 |
| Cylindrical spring preload (N) | 110 |
| Wave spring stiffness (N/mm) | 175.0548 (D100) 217.0437 (D110) |
| Wave spring pre-compression (mm) | 1 |
| Test No. | Cylindrical Spring | Wave Spring | ||
|---|---|---|---|---|
| Stiffness (N/mm) | Preload (N) | Stiffness (N/mm) | Pre-Compression (mm) | |
| #1 | 11 | 110 | 175.054 | 1 |
| #2 | 15 | 110 | 175.054 | 1 |
| #3 | 11 | 150 | 175.054 | 1 |
| #4 | 11 | 110 | 217.044 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Hou, Y. Dynamic Characterization and Parametric Optimization of Secondary Cushioned Pump Valves in Drilling Systems: A 3D Transient Fluid–Structure Interaction Study. Appl. Sci. 2025, 15, 5431. https://doi.org/10.3390/app15105431
Wu Y, Hou Y. Dynamic Characterization and Parametric Optimization of Secondary Cushioned Pump Valves in Drilling Systems: A 3D Transient Fluid–Structure Interaction Study. Applied Sciences. 2025; 15(10):5431. https://doi.org/10.3390/app15105431
Chicago/Turabian StyleWu, Yi, and Yongjun Hou. 2025. "Dynamic Characterization and Parametric Optimization of Secondary Cushioned Pump Valves in Drilling Systems: A 3D Transient Fluid–Structure Interaction Study" Applied Sciences 15, no. 10: 5431. https://doi.org/10.3390/app15105431
APA StyleWu, Y., & Hou, Y. (2025). Dynamic Characterization and Parametric Optimization of Secondary Cushioned Pump Valves in Drilling Systems: A 3D Transient Fluid–Structure Interaction Study. Applied Sciences, 15(10), 5431. https://doi.org/10.3390/app15105431





