A Dissipative Particle Dynamics Study on the Formation of the Water-In-Petroleum Emulsion: The Contribution of the Oil
Abstract
1. Introduction
1.1. General Overview
1.2. Literature Review
1.3. Gap and Novelty
2. Methodology
3. Physics-Based Particle Simulation Approach
3.1. Overview of the DPD Simulation Method
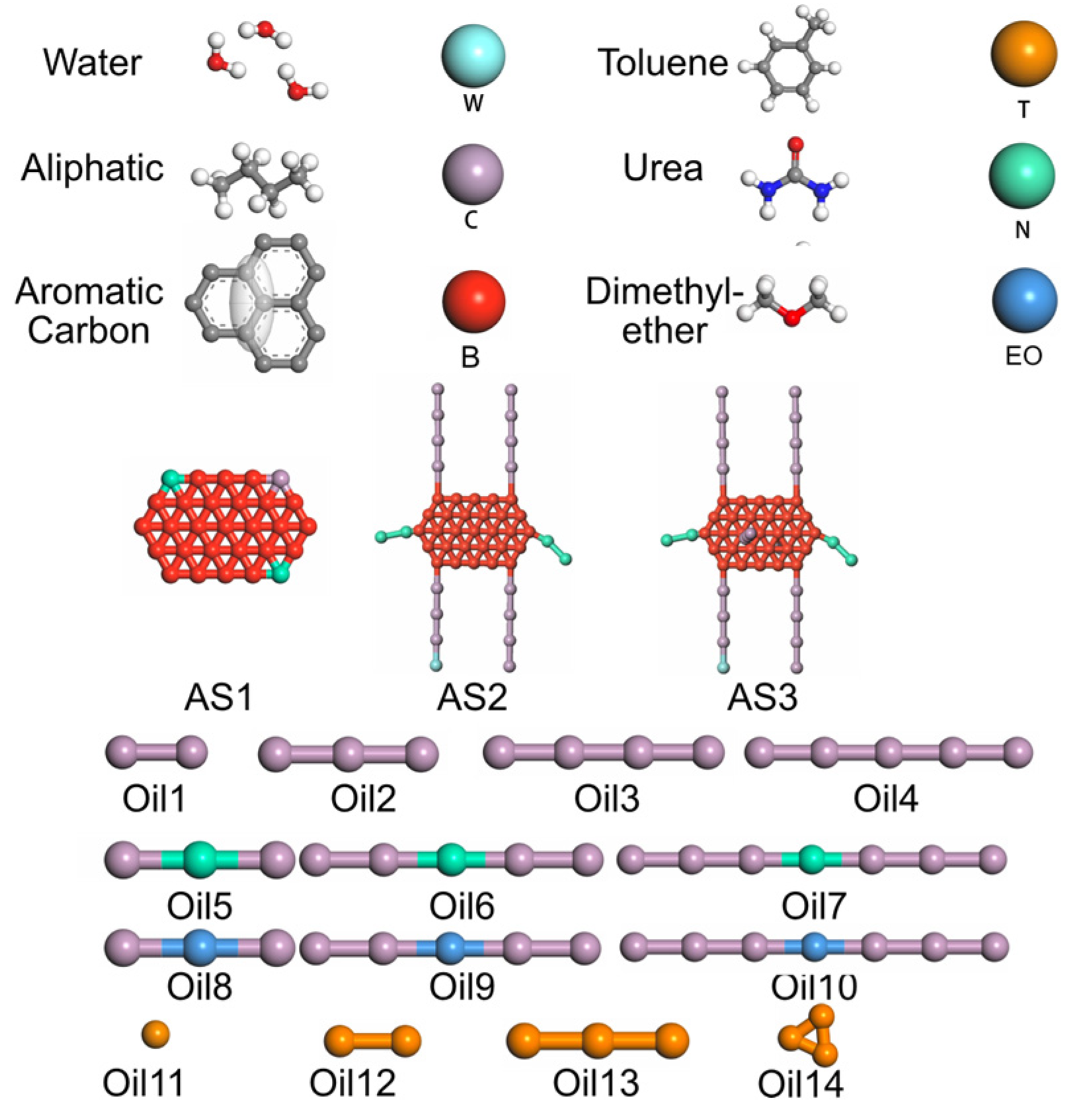
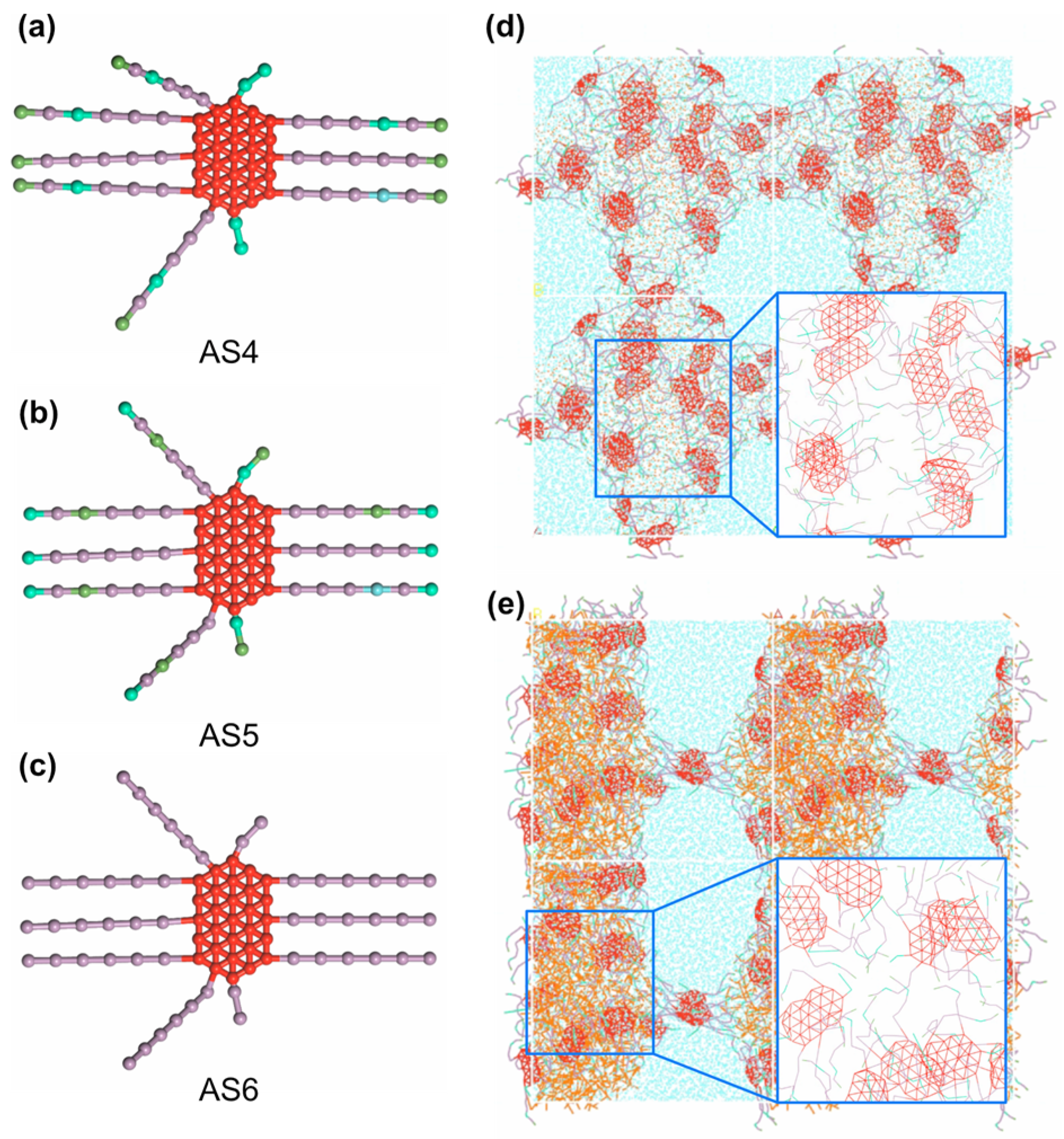
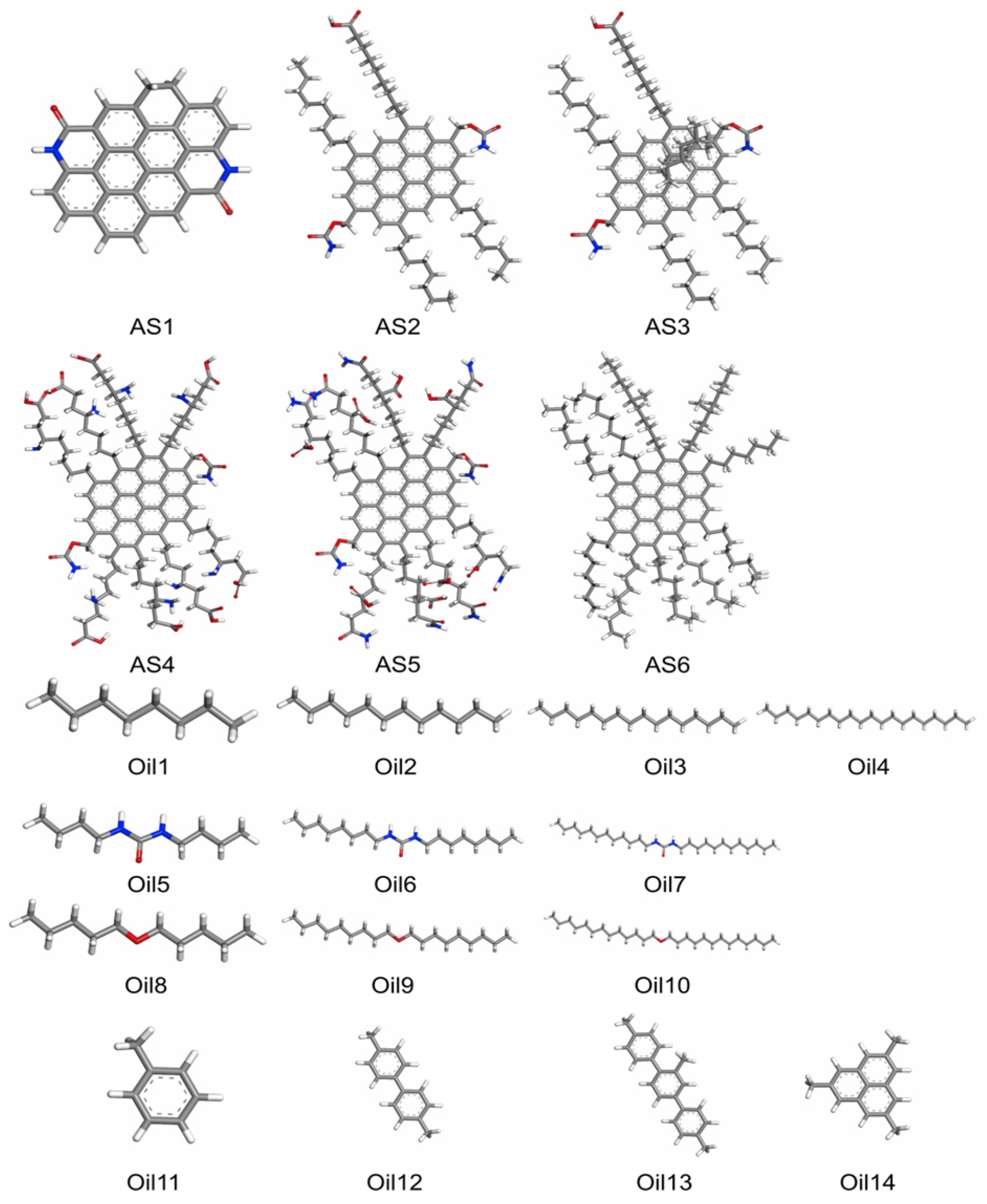
3.2. Molecular Mapping and Coarse-Graining
- AS1: PAC with no side chains;
- AS2: PAC with 4 aliphatic + 2 heteroatom side chains;
- AS3: AS2 with 2 added perpendicular aliphatic chains.
- Oil1–4: Alkanes;
- Oil5–7: Amides;
- Oil8–10: Ethers;
- Oil11–14: Aromatics.
3.3. Force Parameter Derivation from MD
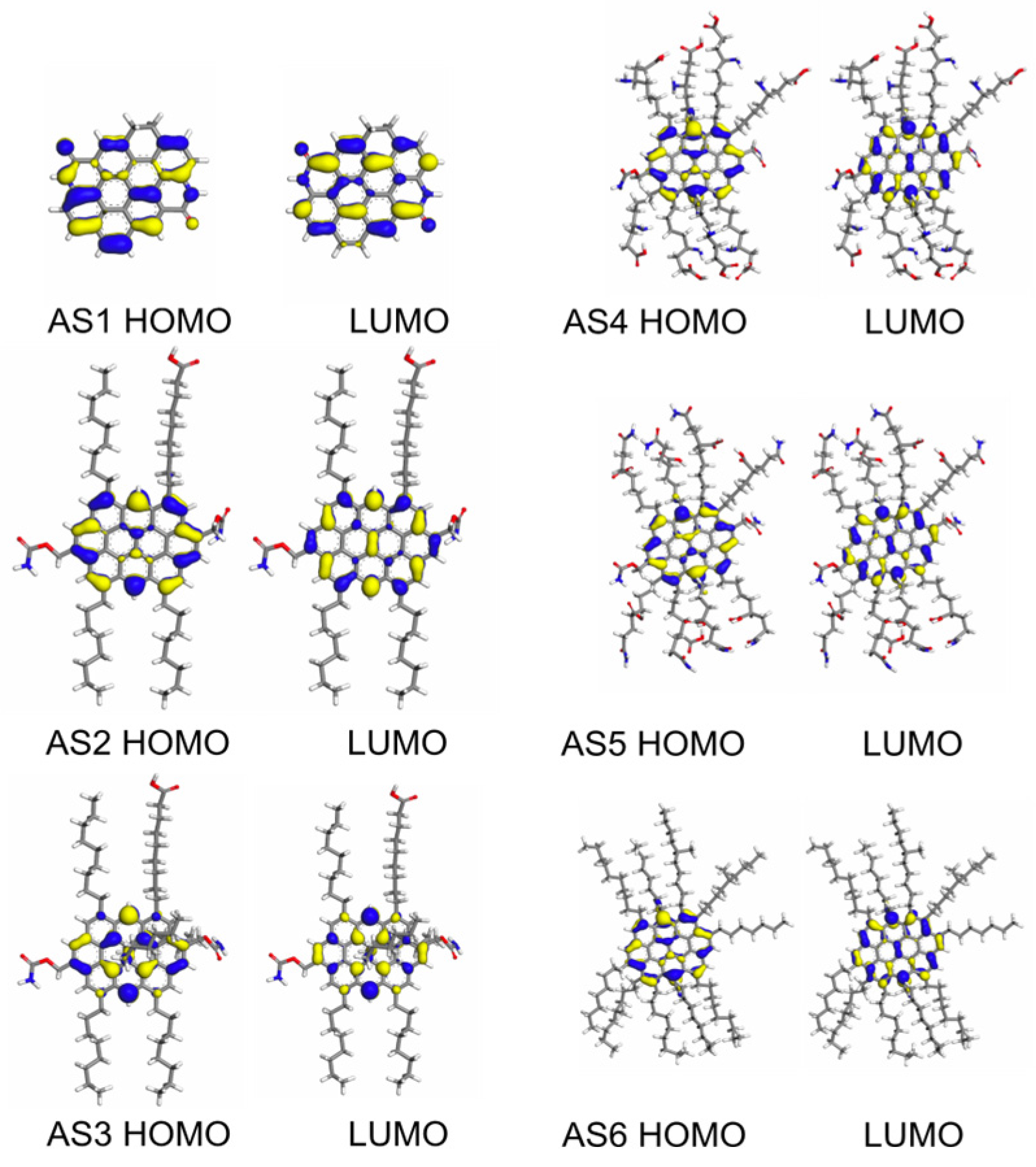
3.4. Density Functional Theory (DFT) Calculations for Molecular Descriptors
- Highest Occupied Molecular Orbital (HOMO) energy;
- Lowest Unoccupied Molecular Orbital (LUMO) energy;
- Energy gap (ELUMO-HOMO);
- Dipole moment (Debye).
3.5. Simulation Model Configuration and IFT Calculation
3.6. Validation and Assumptions
4. Results and Discussion
4.1. Interfacial Activity and Aggregation Behavior of Emulsifiers
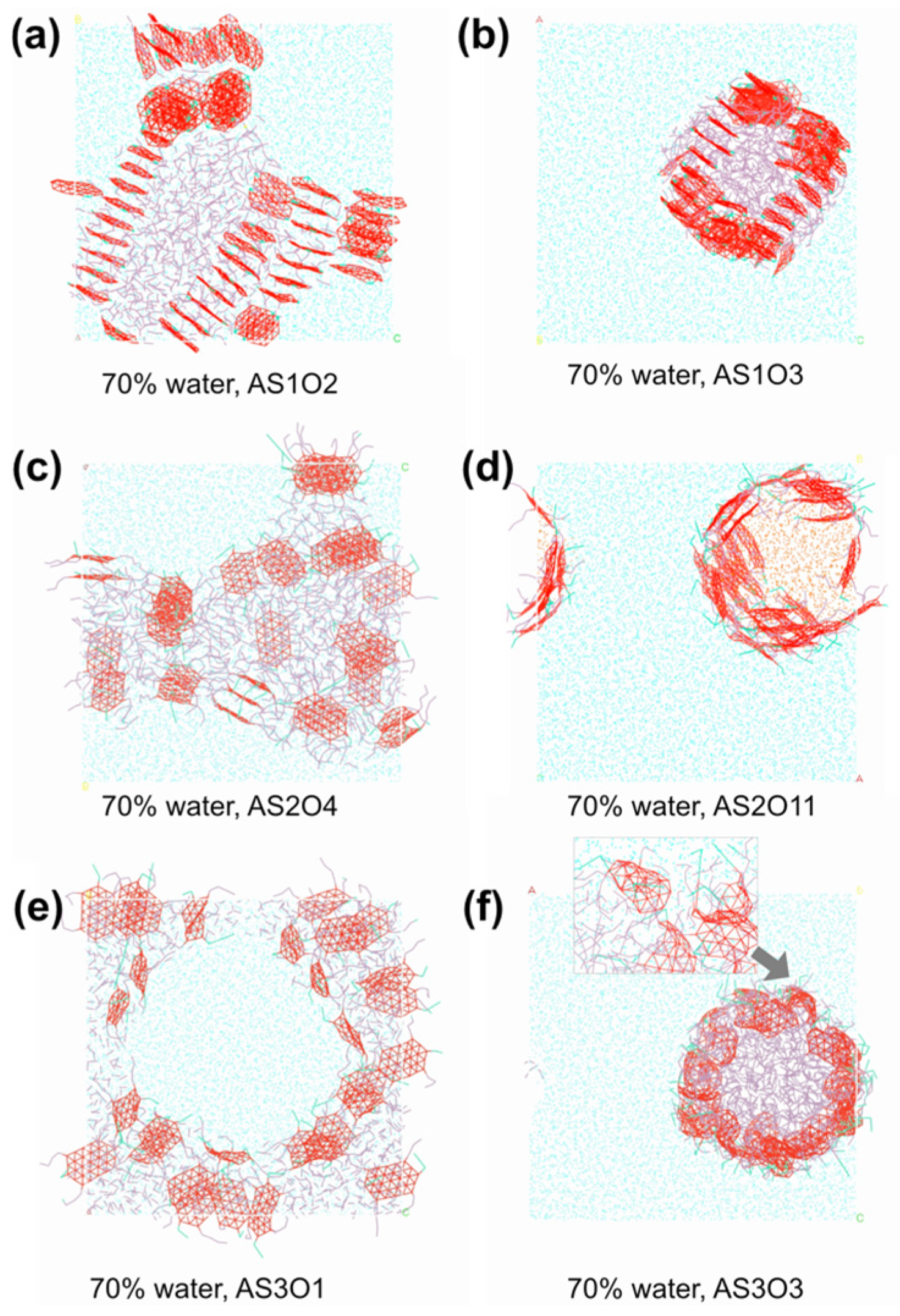
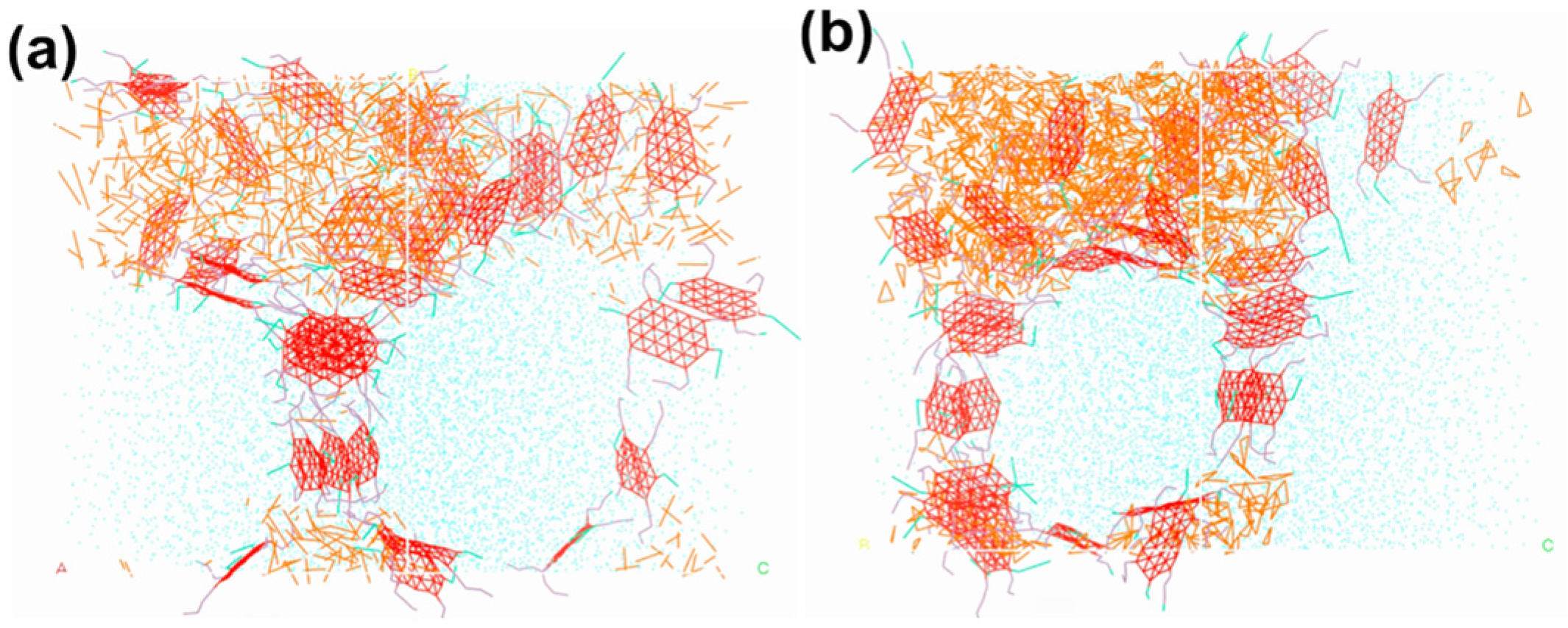
4.2. Structural Evolution and Formation Conditions of High Internal Phase Emulsions
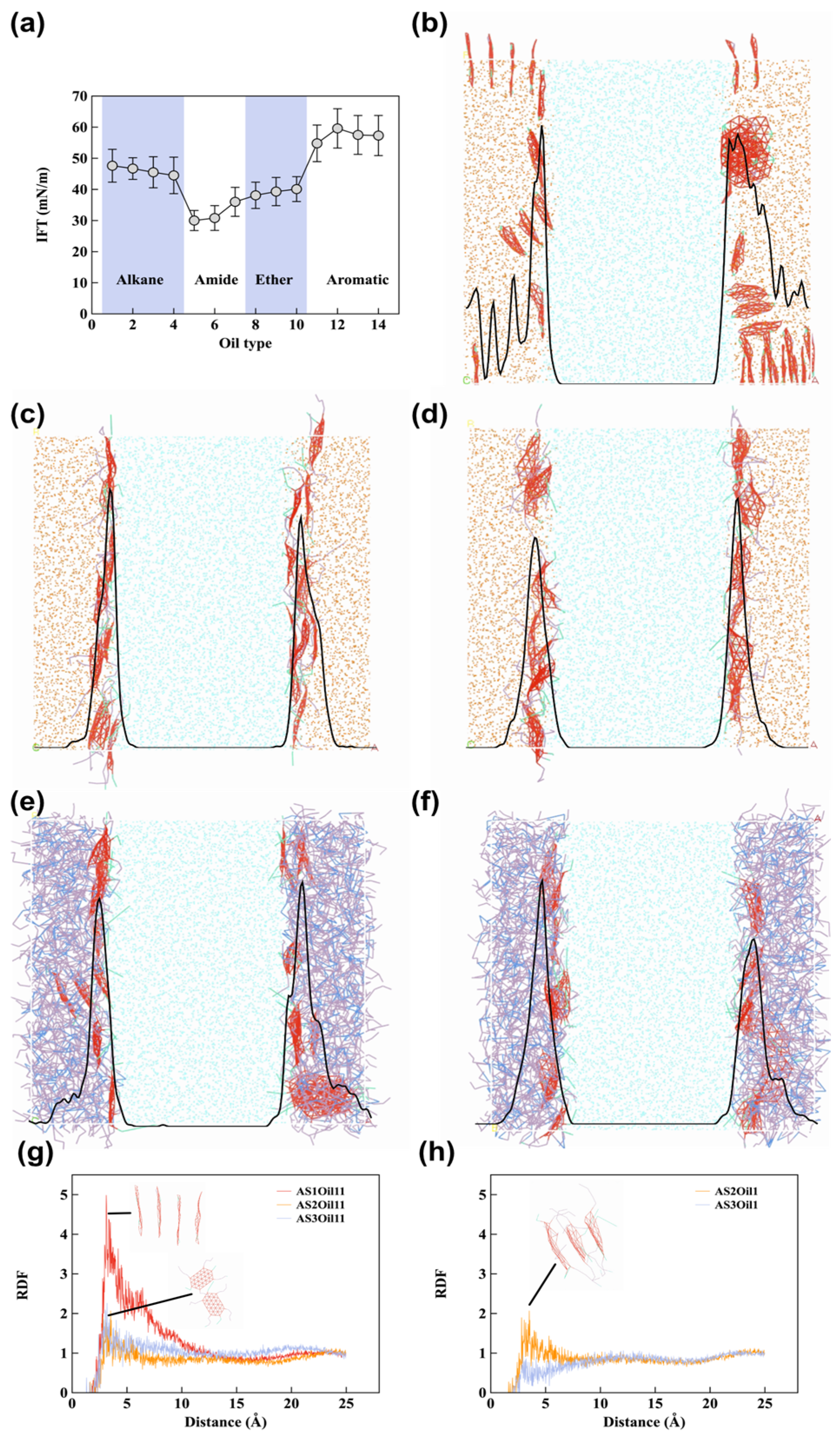
4.3. Influence of Oil Type and Emulsifier Structure on Emulsion Formation
4.3.1. Effect of Oil Polarity on HIPE Morphology
4.3.2. Effect of Emulsifier Structure on Interfacial Stabilization
4.4. Influence of Emulsifier Diffusion and Association on Emulsion Stabilization
4.5. Influence of System Size on HIPE Formation
4.6. Enhanced Performance of Structurally Modified Emulsifiers
4.7. Correlation Between Molecular Electronic Properties and Emulsification Stability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sousa, A.M.; Pereira, M.J.; Matos, H.A. Oil-in-Water and Water-in-Oil Emulsions Formation and Demulsification. J. Pet. Sci. Eng. 2022, 210, 110041. [Google Scholar] [CrossRef]
- Ariffin, T.S.T.; Yahya, E.; Husin, H. The Rheology of Light Crude Oil and Water-In-Oil-Emulsion. Procedia Eng. 2016, 148, 1149–1155. [Google Scholar] [CrossRef]
- Keleşoğlu, S.; Pettersen, B.H.; Sjöblom, J. Flow Properties of Water-in-North Sea Heavy Crude Oil Emulsions. J. Pet. Sci. Eng. 2012, 100, 14–23. [Google Scholar] [CrossRef]
- Romanova, Y.N.; Koroleva, M.Y.; Musina, N.S.; Maryutina, T.A. Ultrasonic Demulsification of Water-in-Crude Oil Emulsions: Influence of Rheological Properties. Chem. Eng. Process.-Process Intensif. 2025, 211, 110242. [Google Scholar] [CrossRef]
- Wong, S.F.; Lim, J.S.; Dol, S.S. Crude Oil Emulsion: A Review on Formation, Classification and Stability of Water-in-Oil Emulsions. J. Pet. Sci. Eng. 2015, 135, 498–504. [Google Scholar] [CrossRef]
- Kolotova, D.S.; Kuchina, Y.A.; Petrova, L.A.; Voron’ko, N.G.; Derkach, S.R. Rheology of Water-in-Crude Oil Emulsions: Influence of Concentration and Temperature. Colloids Interfaces 2018, 2, 64. [Google Scholar] [CrossRef]
- Yonguep, E.; Kapiamba, K.F.; Kabamba, K.J.; Chowdhury, M. Formation, Stabilization and Chemical Demulsification of Crude Oil-in-Water Emulsions: A Review. Pet. Res. 2022, 7, 459–472. [Google Scholar] [CrossRef]
- Ghannam, M.T. Water-in-Crude Oil Emulsion Stability Investigation. Pet. Sci. Technol. 2005, 23, 649–667. [Google Scholar] [CrossRef]
- Umar, A.A.; Saaid, I.B.M.; Sulaimon, A.A.; Pilus, R.B.M. A Review of Petroleum Emulsions and Recent Progress on Water-in-Crude Oil Emulsions Stabilized by Natural Surfactants and Solids. J. Pet. Sci. Eng. 2018, 165, 673–690. [Google Scholar] [CrossRef]
- Xu, C.; Sun, Y.; Feng, C.; Zhang, S. Porous PEG Scaffold Fabricated via Emulsion-Templating Technique Towards Immobilization of Saccharomyces Cerevisiae Cells. Catalysts 2024, 14, 809. [Google Scholar] [CrossRef]
- Wagle, V.; AlYami, A.; Safran, A. Designing Invert Emulsion Drilling Fluids for High Temperature and High-Pressure Conditions. Sci. Rep. 2024, 14, 27748. [Google Scholar] [CrossRef]
- Ehyaie, D.; Zaheri, P.; Samadfam, M.; Zahakifar, F. Evaluation of Cyanex272 in the Emulsion Liquid Membrane System for Separation of Thorium. Sci. Rep. 2024, 14, 31897. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Huang, J.; Guo, Z.; Yang, Q.; Xia, C.; Zheng, Z. Preparation of Polymerized High Internal Phase Emulsion Membranes with High Open-Cellular Extent and High Toughness via RAFT Polymerization. Polymers 2025, 17, 515. [Google Scholar] [CrossRef]
- Sadeghi, S.; Zargarzadeh, L. Gibbsian Surface Thermodynamic Analysis of Emulsion Liquid Membranes. Sci. Rep. 2025, 15, 6401. [Google Scholar] [CrossRef]
- Liu, S.; Yao, T.; Xia, D.; Liu, Q.; Tian, G.; Liu, Y. The Development and Preparation of Novel Gel Emulsion Systems Based on a Cholesterol Star-Shaped Derivative. Molecules 2025, 30, 787. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Ge, J.; Wu, H.; Li, X.; Zhang, X.; Zhang, G. Study on Oil-in-Water Emulsions Stabilized by SiO2 Nanoparticles for Enhancing Oil Recovery in Harsh Reservoirs. Colloid. Polym. Sci. 2024, 302, 1985–1998. [Google Scholar] [CrossRef]
- Al-Haddad, L.A.; Mahdi, N.M. Efficient Multidisciplinary Modeling of Aircraft Undercarriage Landing Gear Using Data-Driven Naïve Bayes and Finite Element Analysis. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 3187–3199. [Google Scholar] [CrossRef]
- Al-Haddad, S.A.; Fattah, M.Y.; Al-Azawi, T.K.; Al-Haddad, L.A. Three-Dimensional Analysis of Steel Beam-Column Bolted Connections. Open Eng. 2024, 14, 20220579. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Al-Haddad, L.A.; Ayasrah, M.; Jaber, A.A.; Al-Haddad, S.A. Coupled Finite Element and Artificial Neural Network Analysis of Interfering Strip Footings in Saturated Cohesive Soils. Transp. Infrastruct. Geotechnol. 2024, 11, 2168–2185. [Google Scholar] [CrossRef]
- Al-Haddad, L.A.; Ibraheem, L.; EL-Seesy, A.I.; Jaber, A.A.; Al-Haddad, S.A.; Khosrozadeh, R. Thermal Heat Flux Distribution Prediction in an Electrical Vehicle Battery Cell Using Finite Element Analysis and Neural Network. Green Energy Intell. Transp. 2024, 3, 100155. [Google Scholar] [CrossRef]
- Abdul-Zahra, A.S.; Ghane, E.; Kamali, A.; Farhan Ogaili, A.A. Power Forecasting in Continuous Extrusion of Pure Titanium Using Naïve Bayes Algorithm. Terra Joule J. 2024, 1, 2. [Google Scholar]
- Al-Haddad, L.A.; Kahachi, H.A.H.; Ur Rehman, H.Z.; Al-Zubaidi, A.A.; Al-Karkhi, M.I.; Al-Oubaidi, B. Advancing Sustainability in Buildings Using an Integrated Aerodynamic Façade: Potential of Artificial Intelligence. Terra Joule J. 2024, 1, 1. [Google Scholar]
- Jiang, H.; Liu, X.; Liang, C.; Wang, Z.; Jia, Y. Dissipative Particle Dynamics to Study Asphaltenes and Surfactants Interactions at the Oil–Water Interface. J. Mol. Liq. 2023, 381, 121802. [Google Scholar] [CrossRef]
- Zhang, B.; Guan, B.; Liu, W.; Peng, B.; Cong, S. Dissipative Particle Dynamics Simulation and Microscopic Experimental Study of Emulsification Performance of Surfactant/Polymer Flooding. Processes 2023, 11, 1411. [Google Scholar] [CrossRef]
- Ruiz-Morales, Y.; Alvarez-Ramírez, F. Mesoscale Dissipative Particle Dynamics to Investigate Oil Asphaltenes and Sodium Naphthenates at the Oil−Water Interface. Energy Fuels 2021, 35, 9294–9311. [Google Scholar] [CrossRef]
- Liu, S.; Qiu, Y.; Liu, J.; Chen, X.; He, L.; Wang, Y.; Li, X.; Chao, L.; Yang, B.; Liu, T. Interfacial Competitive Behavior of Water/Oil/Surfactant Systems in Ultra-Deep Tight Reservoir—Insights from Dissipative Particle Dynamics. Colloids Surf. A Physicochem. Eng. Asp. 2025, 717, 136766. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, H.; Li, J.; Li, Y.; Xiang, D.; Wu, Y.; Wang, G.; Qin, M. Facile Fabrication of Superhydrophobic Graphene/Polystyrene Foams for Efficient and Continuous Separation of Immiscible and Emulsified Oil/Water Mixtures. Polymers 2022, 14, 2289. [Google Scholar] [CrossRef] [PubMed]
- Han, D.; Mao, J.; Zhao, J.; Zhang, H.; Yang, X.; Lin, C. Effect of Surfactant Hydrophobic Chain Equivalence on the Oil-Water Interface and Emulsion Stability: A Dissipative Particle Dynamics and Experimental Study. J. Mol. Liq. 2023, 382, 121781. [Google Scholar] [CrossRef]
- Alvarez, F.; Flores, E.A.; Castro, L.V.; Hernández, J.G.; López, A.; Vázquez, F. Dissipative Particle Dynamics (DPD) Study of Crude Oil−Water Emulsions in the Presence of a Functionalized Co-Polymer. Energy Fuels 2011, 25, 562–567. [Google Scholar] [CrossRef]
- Song, X.; Shi, P.; Duan, M.; Fang, S.; Ma, Y. Investigation of Demulsification Efficiency in Water-in-Crude Oil Emulsions Using Dissipative Particle Dynamics. RSC Adv. 2015, 5, 62971–62981. [Google Scholar] [CrossRef]
- Han, D.; Mao, J.; Zhao, J.; Zhang, H.; Wang, D.; Wang, C.; Xue, J.; Cao, H.; Yang, X.; Lin, C.; et al. Dissipative Particle Dynamics Simulation and Experimental Analysis of the Effect of Anionic/Cationic Mixed Surfactants on the Stability of Emulsions. J. Mol. Liq. 2022, 367, 120482. [Google Scholar] [CrossRef]
- Goodarzi, F.; Zendehboudi, S. Effects of Salt and Surfactant on Interfacial Characteristics of Water/Oil Systems: Molecular Dynamic Simulations and Dissipative Particle Dynamics. Ind. Eng. Chem. Res. 2019, 58, 8817–8834. [Google Scholar] [CrossRef]
- Han, D.; Mao, J.; Zhao, J.; Zhang, H.; Wang, D.; Cao, H.; Yang, X.; Lin, C.; Zhang, Y. Dissipative Particle Dynamics Simulation and Experimental Analysis of Effects of Gemini Surfactants with Different Spacer Lengths on Stability of Emulsion Systems. Colloids Surf. A Physicochem. Eng. Asp. 2022, 655, 130205. [Google Scholar] [CrossRef]
- Liang, C.; Liu, X.; Jia, Y.; Jiang, H.; Xu, Y. Mechanistic Study of the Effects of Surfactants and Asphaltenes on the Action of Emulsions with Different Water Contents: Based on Dissipative Particle Dynamics. Energy Fuels 2024, 38, 7758–7772. [Google Scholar] [CrossRef]
- Li, Q.; Cao, J.; Liu, Y.; Cheng, Q.; Liu, C. Effect of Dispersed Water on the Paraffin Crystallization and Deposition of Emulsified Waxy Crude Oil via Dissipative Particle Dynamics. J. Mol. Liq. 2021, 343, 117679. [Google Scholar] [CrossRef]
- Schäfer, G.; Jaranowski, P. Hamiltonian Formulation of General Relativity and Post-Newtonian Dynamics of Compact Binaries. Living Rev. Relativ. 2024, 27, 2. [Google Scholar] [CrossRef]
- Schneider, J.; Fleck, F.; Karimi-Varzaneh, H.A.; Müller-Plathe, F. Simulation of Elastomers by Slip-Spring Dissipative Particle Dynamics. Macromolecules 2021, 54, 5155–5166. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative Particle Dynamics: Bridging the Gap between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Ruiz-Morales, Y.; Mullins, O.C. Coarse-Grained Molecular Simulations to Investigate Asphaltenes at the Oil–Water Interface. Energy Fuels 2015, 29, 1597–1609. [Google Scholar] [CrossRef]
- Zhang, Y.; Feller, S.E.; Brooks, B.R.; Pastor, R.W. Computer Simulation of Liquid/Liquid Interfaces. I. Theory and Application to Octane/Water. J. Chem. Phys. 1995, 103, 10252–10266. [Google Scholar] [CrossRef]
- Abdulameer, A.G.; Mrah, M.M.; Bazerkan, M.; Al-Haddad, L.A.; Al-Karkhi, M.I. Machine Learning-Driven Power Prediction in Continuous Extrusion of Pure Titanium for Enhanced Structural Resilience under Extreme Loading. Discov. Mater. 2025, 5, 7. [Google Scholar] [CrossRef]
- Al-Haddad, L.A.; Łukaszewicz, A.; Majdi, H.S.; Holovatyy, A.; Jaber, A.A.; Al-Karkhi, M.I.; Giernacki, W. Energy Consumption and Efficiency Degradation Predictive Analysis in Unmanned Aerial Vehicle Batteries Using Deep Neural Networks. Adv. Sci. Technol. Res. J. 2025, 19, 21–30. [Google Scholar] [CrossRef]
- Al-Haddad, A.A.; Al-Haddad, L.A.; Al-Haddad, S.A.; Jaber, A.A.; Khan, Z.H.; Rehman, H.Z.U. Towards Dental Diagnostic Systems: Synergizing Wavelet Transform with Generative Adversarial Networks for Enhanced Image Data Fusion. Comput. Biol. Med. 2024, 182, 109241. [Google Scholar] [CrossRef]
- Al-Haddad, L.A.; Jaber, A.A.; Dhahir, M.K.; Nagim, H.Y.; Algburi, Z.I. Characterization and Prediction of Femtosecond Laser Induced Tracks in Silver-Containing Zinc Phosphate Glass. In Proceedings of the CEUR Workshop Proceedings, Bari, Italy, 14–18 October 2024; Volume 3870, pp. 10–19. [Google Scholar]
- Alawee, W.H.; Al-Haddad, L.A.; Basem, A.; Al-Haddad, A.A. A Data Augmentation Approach to Enhance Breast Cancer Detection Using Generative Adversarial and Artificial Neural Networks. Open Eng. 2024, 14, 20240052. [Google Scholar] [CrossRef]
- Von Lilienfeld, O.A.; Ramakrishnan, R.; Rupp, M.; Knoll, A. Fourier Series of Atomic Radial Distribution Functions: A Molecular Fingerprint for Machine Learning Models of Quantum Chemical Properties. Int. J. Quantum Chem. 2015, 115, 1084–1093. [Google Scholar] [CrossRef]
- Watanabe, N.; Hori, Y.; Sugisawa, H.; Ida, T.; Shoji, M.; Shigeta, Y. A Machine Learning Potential Construction Based on Radial Distribution Function Sampling. J. Comput. Chem. 2024, 45, 2949–2958. [Google Scholar] [CrossRef] [PubMed]
- Kelbaliev, G.I.; Safarov, F.F. Study of Interphase Film Thinning in Petroleum Emulsion Separation Processes. Chem. Technol. Fuels Oils 2011, 47, 268–277. [Google Scholar] [CrossRef]
- Jiao, B.; Shi, A.; Wang, Q.; Binks, B.P. High-internal-phase Pickering Emulsions Stabilized Solely by Peanut-protein-isolate Microgel Particles with Multiple Potential Applications. Angew. Chem. Int. Ed. 2018, 57, 9274–9278. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Dong, H.; Sun, Q.; Shen, Y.; Ji, R. A Three-Step Model for Submicron W/O Emulsion Formation in a Transitional-Phase Inversion Process. J. Dispers. Sci. Technol. 2016, 37, 1186–1191. [Google Scholar] [CrossRef]
- Wang, Z.; Li, N.; Sun, Z.; Wang, X.; Chen, Q.; Liu, W.; Qi, Z.; Wei, L.; Li, B. Molecular Dynamics Study of Droplet Electrocoalescence in the Oil Phase and the Gas Phase. Sep. Purif. Technol. 2021, 278, 119622. [Google Scholar] [CrossRef]



| Ref. | Application/Method | Key Finding | Limitation |
|---|---|---|---|
| [25] | DPD of asphaltenes and sodium naphthenates | Oxygenated asphaltenes form more stable interfacial films | Focused only on binary mixtures without complex multicomponent emulsions |
| [27] | Superhydrophobic foam for emulsion separation | Graphene/polystyrene foams effectively separate W/O emulsions | Experimental only; no molecular-level understanding |
| [28] | DPD + experimental on Gemini surfactants | Gemini surfactants stabilize emulsions more effectively | Concentration effect overlaps structural interpretation |
| [29] | DPD of copolymer–crude oil–water emulsions | Longer co-polymer chains improve coalescence control | Emulsion system limited to single polymer–oil configuration |
| [26] | DPD on interfacial behavior in ultra-deep reservoirs | Surfactants and crude components compete for interfacial adsorption | No discussion of performance under varying water contents |
| [30] | DPD study of polyether demulsifiers | PBO-based demulsifiers enhance coalescence via network formation | Mechanism valid only for ultra-heavy crude and certain polymer types |
| [31] | DPD on anionic/cationic mixed surfactants | Mixed surfactants reduce IFT (interfacial tension) and enhance emulsion stability | Spacer group effect needs more systematic quantification |
| [32] | Integrated MD–DPD for salt/surfactant effects | Salinity and temperature influence IFT and interfacial structure | Radius of gyration and χ parameter treated in ideal conditions |
| [33] | DPD on Gemini surfactants with variable spacers | Shorter spacers yield better interfacial activity and lower sedimentation | Aging behavior not fully validated experimentally |
| [23] | DPD of asphaltenes + surfactants | Synergistic adsorption reduces IFT, forming tight films | Focus limited to heavy oil and static systems |
| [34] | DPD on emulsion conformation at varying water contents | Adsorption energy and Rg changes affect emulsion stability | No extension to HIPEs |
| [35] | DPD of wax crystallization in emulsified waxy crude | Water cut alters paraffin nucleation pathways | No link to interfacial film or surfactant activity |
| [24] | DPD + experiment on S/P emulsification | Stable S/P systems reduce IFT and improve oil recovery | Interfacial behavior not generalized across emulsifier types |
| aij | W | C | B | N | EO | T |
|---|---|---|---|---|---|---|
| W | 78 | |||||
| C | 129.78 | 78 | ||||
| B | 131.02 | 79.55 | 78 | |||
| N | 88.95 | 101.94 | 95.24 | 78 | ||
| EO | 101.12 | 82.69 | 79.55 | 83.79 | 78 | |
| T | 138.95 | 79.58 | 78 | 97.34 | 79.84 | 78 |
| Parameter | Value |
|---|---|
| Simulation ensemble | NVT |
| Temperature | 65 °C |
| Timestep | 0.005tc (≈15 fs) |
| Total steps | 1,000,000 |
| Simulation box size | |
| Emulsifier: Oil mass ratio | 1:1 |
| Water content (volume basis) | 70% and 80% |
| Initial configuration | Random packing |
| IFT slab configuration | Oil/Water/Oil layers (25:50:25 Rc) |
| Output analyses | Morphology, RDF, IFT, snapshots |
| Assumption | Description |
|---|---|
| Coarse-graining level | Each bead represents 2–3 molecules, enabling mesoscale behavior capture |
| No reactive chemistry | DPD does not account for chemical bond formation or reaction kinetics |
| Isothermal system | Constant temperature (65 °C) maintained in all simulations |
| Constant mass ratio (Emulsifier/Oil) | Held at 1:1 for all systems |
| Initial molecular distribution | Randomized distribution assumed to reflect emulsification via shearing |
| Fixed simulation duration | One million steps assumed sufficient for equilibrium morphology observation |
| Coarse-graining level | Each bead represents 2–3 molecules, enabling mesoscale behavior capture |
| No reactive chemistry | DPD does not account for chemical bond formation or reaction kinetics |
| Isothermal system | Constant temperature (65 °C) maintained in all simulations |
| Constant mass ratio (Emulsifier/Oil) | Held at 1:1 for all systems |
| Oil Type | Functional Group Type | Simulated IFT Trend (This Study) | Reported IFT Range (Literature) | Ref. | Consistency |
|---|---|---|---|---|---|
| Oils 5–7 | Amides (polar) | ~38–41 mN/m | 35–40 mN/m | [23,25] | High |
| Oils 8–10 | Ethers (less polar) | ~43–46 mN/m | ~40–45 mN/m | [23,32] | Moderate |
| Oils 1–4 | Alkanes (non-polar) | ~50–52 mN/m | >50 mN/m | [23,26] | High |
| Oils 11–14 | Aromatics (non-polar) | ~51–54 mN/m | >50 mN/m | [23,25] | High |
| Water Content | Oil | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | Counts | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Emulsifier | |||||||||||||||||
| 70% | AS1 | + | + | + | 3 | ||||||||||||
| AS2 | + | + | + | + | + | + | + | + | + | + | + | + | 12 | ||||
| AS3 | + | + | + | + | + | + | + | + | + | 9 | |||||||
| Counts | 2 | 3 | 1 | 2 | 3 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 0 | 1 | |||
| Oil | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | Counts | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Emulsifier | ||||||||||||||||
| AS4 | + | + | + | + | + | + | + | + | + | + | + | + | + | + | 14 | |
| AS5 | + | + | + | + | + | + | + | + | + | + | + | + | + | + | 14 | |
| AS6 | + | + | + | + | + | + | 6 | |||||||||
| Sample | EHOMO (Ha) | ELUMO (Ha) | ELUMO-HOMO (Ha) | ELUMO-HOMO (eV) |
|---|---|---|---|---|
| AS1 | −0.183 | −0.100 | 0.082 | 2.239 |
| AS2 | −0.170 | −0.102 | 0.068 | 1.853 |
| AS3 | −0.142 | −0.113 | 0.029 | 0.791 |
| AS4 | −0.158 | −0.099 | 0.059 | 1.610 |
| AS5 | −0.164 | −0.102 | 0.062 | 1.679 |
| AS6 | −0.139 | −0.080 | 0.060 | 1.626 |
| Oil1 | −0.260 | 0.067 | 0.327 | 8.901 |
| Oil2 | −0.252 | 0.066 | 0.318 | 8.649 |
| Oil3 | −0.248 | 0.066 | 0.313 | 8.528 |
| Oil4 | −0.245 | 0.066 | 0.310 | 8.447 |
| Oil5 | −0.192 | 0.024 | 0.216 | 5.876 |
| Oil6 | −0.191 | 0.023 | 0.215 | 5.844 |
| Oil7 | −0.189 | 0.022 | 0.212 | 5.756 |
| Oil8 | −0.203 | 0.063 | 0.266 | 7.250 |
| Oil9 | −0.202 | 0.061 | 0.263 | 7.154 |
| Oil10 | −0.202 | 0.061 | 0.263 | 7.166 |
| Oil11 | −0.210 | −0.028 | 0.182 | 4.962 |
| Oil12 | −0.128 | −0.050 | 0.077 | 2.107 |
| Oil13 | −0.184 | −0.058 | 0.126 | 3.426 |
| Oil14 | −0.135 | −0.112 | 0.023 | 0.623 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, P.; Ogail, M.H.O.; Feng, X.; Fang, S.; Duan, M.; Pu, W.; Liu, R. A Dissipative Particle Dynamics Study on the Formation of the Water-In-Petroleum Emulsion: The Contribution of the Oil. Appl. Sci. 2025, 15, 5422. https://doi.org/10.3390/app15105422
Shi P, Ogail MHO, Feng X, Fang S, Duan M, Pu W, Liu R. A Dissipative Particle Dynamics Study on the Formation of the Water-In-Petroleum Emulsion: The Contribution of the Oil. Applied Sciences. 2025; 15(10):5422. https://doi.org/10.3390/app15105422
Chicago/Turabian StyleShi, Peng, Murtaja Hamid Oudah Ogail, Xinxin Feng, Shenwen Fang, Ming Duan, Wanfen Pu, and Rui Liu. 2025. "A Dissipative Particle Dynamics Study on the Formation of the Water-In-Petroleum Emulsion: The Contribution of the Oil" Applied Sciences 15, no. 10: 5422. https://doi.org/10.3390/app15105422
APA StyleShi, P., Ogail, M. H. O., Feng, X., Fang, S., Duan, M., Pu, W., & Liu, R. (2025). A Dissipative Particle Dynamics Study on the Formation of the Water-In-Petroleum Emulsion: The Contribution of the Oil. Applied Sciences, 15(10), 5422. https://doi.org/10.3390/app15105422







