Abstract
The advancement of digital technologies has revolutionized the medical field, offering new opportunities for the biomechanical analysis and simulation of anatomical structures. This study explored the modeling of mandibular and dental components using advanced methods such as finite element analysis (FEA) and three-dimensional modeling. Special attention was given to the distribution of masticatory forces and their impact on premolars, highlighting the biomechanical differences between restorative materials such as amalgam and composites. The results indicate that each material presents specific advantages depending on the loading conditions, emphasizing the need for personalized dental treatments. This study confirms the effectiveness of numerical methods in optimizing the design of dental structures and supports the applicability of these techniques in orthodontics, maxillofacial surgery, and dental prosthetics.
1. Introduction
Modeling a system represents a fundamental step in understanding it while also providing a means to anticipate its future, yet-unknown behavior. With the advancement of information technology and computational systems, medical research has increasingly focused on developing sophisticated mathematical models capable of simulating the evolution of complex biomedical structures and processes. The biomechanics of the mandible, along with its mathematical modeling, are an emerging field of interest. This domain has captured the attention of scientists since the 1970s [1], marking the beginning of research in this direction. To obtain conclusive results, researchers today study this bony and articular component by considering physical elements, such as geometry, mechanical properties, and muscle activities, as well as pathological factors, such as bruxism, that contribute to the degradation of dental units [2].
The biomechanics of mastication and dental surfaces represent another field in which research through modeling and numerical simulation provides a means for observing and investigating biomechanical aspects characterized by a high degree of intra- and inter-individual variability [3]. These are biologically complex systems from a morpho-functional perspective, which, due to their small dimensions and limited accessibility, are not well-suited for direct investigations of patients [4,5].
The loss of dental substance is a frequently encountered phenomenon with multiple causes, including oral parafunctional behaviors, particularly bruxism. Bruxism, characterized by clenching or grinding of the teeth, generates excessive forces that can lead to various hard tissue lesions, including occlusal surface wear, tooth fractures, or restoration failures [6]. Understanding how these parafunctional forces contribute to tissue damage requires a detailed biomechanical analysis of mechanical stress distribution. The three-dimensional modeling of mandibular and dental structures, combined with the finite element analysis (FEA) method, provides an effective approach for simulating and quantifying these mechanical loads. FEA enables the assessment of the impact of occlusal forces generated by bruxism on teeth, contributing to a better understanding of pathological mechanisms and optimizing the selection process of the materials used in dental restoration reconstructions.
Three-dimensional modeling and finite element analysis (FEA) provide a powerful tool for investigating the biomechanical behavior of structures, allowing for the study of an unlimited number of variations [3]. By modifying different parameters, new models can be created—a process that would be impossible using traditional investigation methods. A major advantage of this approach is its ability to visualize internal stress distributions within structures, offering a detailed perspective on functional mechanisms [7].
The primary objective of this research was to develop and experimentally validate an innovative analog model correlated with a dedicated numerical model. Through these methodological tools, this study aimed to investigate and evaluate the forces exerted on medium- and large-sized dental restorations located at the level of the mandibular second premolar. The comparative analysis focused on two distinct types of restorative materials (amalgam and composite), along with the assessment of orthodontic biomechanics. This was achieved by simulating tooth displacement and the distribution of periodontal pressures through the application of orthodontic forces, either individually or in combination with an anti-rotational force coupler.
Finite element analysis (FEA) involves a large number of equations and is based on several key principles, including object modeling, defining the material and contact parameters, discretizing the model and determining the element types (meshing), applying constraints and loads on the object, defining the contact types, solving the resulting mathematical equation systems, and displaying the simulation results [8].
Once the model is created, it requires discretization, which involves dividing it into regular geometric elements of selectable sizes. These elements, although they behave similarly to the overall structure, become easier to analyze due to their standardized geometry, imposed by the software. The choice of element type (tetrahedral, hexahedral, etc.) is often arbitrary, as the polymorphic structures of anatomical models necessitate a combination of these elements, sometimes constrained by software limitations [9].
The greater the number of elements in a discretized model (mesh), the higher the accuracy of the final analysis. However, an increased number of elements will lead to a larger system of equations, resulting in longer processing times, sometimes excessively so. Simplifying the model reduces the computational power requirements but also decreases the accuracy of the analysis. Subsequently, material properties and boundary conditions are defined for each element. This results in a system of n equations with n unknowns, where n represents the number of nodes. Consequently, the computational capacity required is significant, but modern processing speeds and advanced algorithms enable the efficient management of this complexity [7].
The software includes a material database characterized by key parameters. If the materials of interest are not included in the database, the user can define them by inputting the relevant constants for this study. These constants typically include Poisson’s ratio, the modulus of elasticity, density, compressive strength, tensile strength, or melting temperature. Depending on the type of experiment—whether mechanical stress (tension, compression, impact) or thermal studies—some analyses may require only two or three material properties.
2. Materials and Methods
Three-dimensional modeling and finite element analysis (FEA) enable the investigation of an unlimited range of clinical scenarios. The major advantage of these methods lies in their ability to visualize internal stresses within dental structures. The aim of this research was to develop and validate an analog model used for investigating and evaluating dental forces and biomechanics by simulating tooth movements and the distribution of periodontal pressures at the contact surfaces of the premolars during bruxism. Assessing the forces involved is essential for understanding clinical consequences and for developing an effective therapeutic plan. The forces generated during bruxism result from involuntary muscular contractions of the masticatory muscles, particularly the masseter, temporalis, and medial and lateral pterygoid muscles. These muscles produce high-magnitude forces through involuntary contractions, which are responsible for abnormal mandibular movements. These forces may be vertical (axial) or lateral (tangential) in nature. In bruxism, their magnitude can exceed 500–1000 N, compared with 70–200 N during normal mastication. In this study, force intensities of 200 N, 400 N, 600 N, and 800 N were used—values most commonly encountered and known to induce changes in the alveolar bone and gingival tissues. These alterations can be addressed through the use of occlusal splints, relaxation techniques, behavioral therapy, and the correction of occlusal imbalances [10].
The directions and magnitudes of these forces influence the degree of dental wear and the stress exerted on the temporomandibular joint. These muscular contractions lead to increased pressure on both dental and periodontal structures, resulting in clinical manifestations such as dental erosion, fractures, or temporomandibular joints. During bruxism, direct contact between premolars transmits forces across the occlusal surfaces, generating localized stress and deformation within the dental tissues and their supporting structures.
The interaction between dental surfaces is a complex process influenced by the irregular morphology of cusps, the lubricating role of saliva, and the distinct behavior of dental tissue compared to engineering materials, which is characterized by anisotropy and reduced elasticity. Under static contact conditions (tooth clenching), the forces are predominantly distributed along the vertical axis, whereas dynamic contact (tooth grinding) introduces tangential components and frictional forces that significantly contribute to occlusal wear. In this context, the contact modeling between the occlusal surfaces incorporated friction coefficients ranging from 0.2 to 0.3, corresponding to enamel–enamel and enamel–food interactions. These coefficients affected the tangential components of the applied force and allowed for a more realistic simulation of the force transmission and dental wear processes.
The mandibular second premolar is regarded as a composite system consisting of dentin, enamel, and restorative materials such as amalgam and composite resin. For the purpose of simplifying this analysis, this model assumes linear elastic behavior, isotropic material properties, and perfect adhesion at the interfaces between the constituent phases [11].
The analysis described below focused on evaluating the biomechanical responses of restored dental structures under the influences of four distinct masticatory loading intensities: 200 N, 400 N, 600 N, and 800 N. The selection of these values was grounded in existing data from the scientific literature [12], which delineate the range of masticatory forces under both physiological and pathological conditions. Thus, a 200 N load is representative of normal masticatory forces, while a value of 800 N simulates excessive occlusal loading conditions associated with bruxism.
In addition, the value of 600 N was included in the analysis in accordance with the findings of previous studies conducted by Imanishi et al. [13] and Nakamura et al. [14], being considered representative of the maximum masticatory force typically developed under normal conditions [15]. The inclusion of an intermediate value of 400 N allowed for the investigation of the structural response to an increased masticatory force situated between the physiological norm and the maximum threshold reached under parafunctional conditions.
The masticatory forces were virtually applied to two types of dental reconstructions. These reconstructions, characterized by medium and large dimensions, are located at the mandibular second premolar level. The objective was to comparatively assess the biomechanical performance of these reconstructions based on the type of restorative material used. In this context, two commonly used clinical restorative materials were analyzed: dental amalgam and composite resins.
Dental amalgam is one of the most versatile materials used in restorative dentistry. It continues to be widely employed, accounting for approximately 75% of all restorative materials used in dental practice. With a history of over 165 years of clinical application, dental amalgam remains, to this day, without an economically equivalent alternative [16]. Its long-term effectiveness in areas subjected to mechanical stress, combined with low cost, has not been matched by other restorative materials. Among its advantages are low technique sensitivity, self-sealing capability, and remarkable longevity, which provide it with a broad range of clinical applications [17].
Dental composites are frequently used in dentistry due to their remarkable mechanical properties, such as compressive strength, durability, and an appropriate elastic modulus, which enable them to withstand the functional demands of the oral cavity. These characteristics make them suitable for durable restorations while also maintaining an aesthetic appearance closely resembling natural dentition. However, despite their high mechanical performance, composites may develop microcracks over time as a result of repeated loading or thermal fluctuations, which can compromise their structural integrity. The detection of these microcracks is challenging and, in some cases, impossible using conventional diagnostic methods [18].
Thus, the inclusion of both materials in such a study not only allowed for a comparison of their ability to withstand occlusal forces but also highlights the differences in their long-term mechanical behavior, thereby supporting the selection of restorative materials based on specific clinical requirements.
Through this approach, this study aimed to obtain detailed information regarding the distribution of stresses and strains within restored dental structures under various masticatory loading scenarios, depending on the size of the defect and the properties of the restorative material.
To facilitate visualization and analysis, this study began with an anatomical model of the premolar (Figure 1), which was used to create a three-dimensional model (Figure 2). The file generated from the scanning process was produced in the form of a mesh, providing information solely regarding the surface geometry of the analyzed structure without including any details about its internal composition. The reconstruction of the morphological stratification characteristic of the dental structure was carried out in a CAD environment, using a sequence of scaling operations and Boolean subtraction. Through this method, both the superficial and intermediate layers of the tooth were obtained. The resulting enamel layer thickness ranged from 0.9 mm to 0.5 mm, with the minimum value located at the coronal extremity of the tooth. The dentin exhibited a thickness of between 1.21 mm and 0.7 mm, also registering a minimum in the apical region. The dental crown was modeled with a constant thickness of approximately 0.7 mm [19].
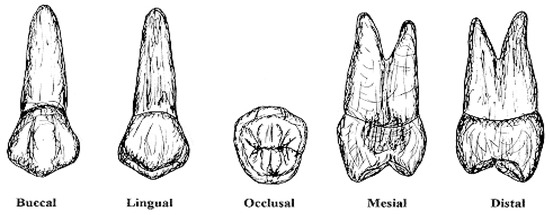
Figure 1.
Visualization of the anatomical model of the mandibular second premolar from five distinct morphological analysis angles [20].
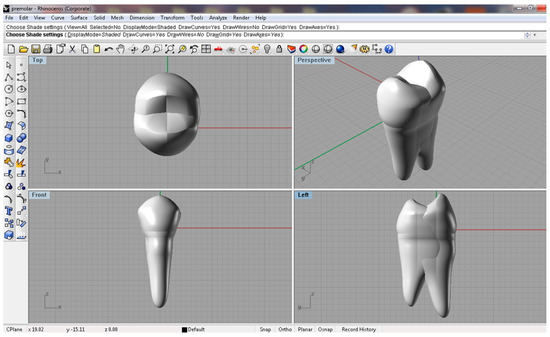
Figure 2.
Three-dimensional model of the mandibular second premolar, anatomically described using Rhinoceros 3D software, version 7, presented from the following perspectives: occlusal view, oblique perspective, frontal view, and left lateral view.
After the creation of the geometric structure of the model, it had to be exported in a solid-specific format (e.g., *.x_t, *.x_b, *.sat) to allow for further analysis. The stress analysis was performed using the finite element method (FEM), which is well-suited for biological structures due to its ability to model domains with high diversity of materials and complex geometric structures.
The finite element platform used was SolidWorks Simulation 2021, where the discretized model was generated, consisting of 9638 nodes and 6217 elements (Figure 3).
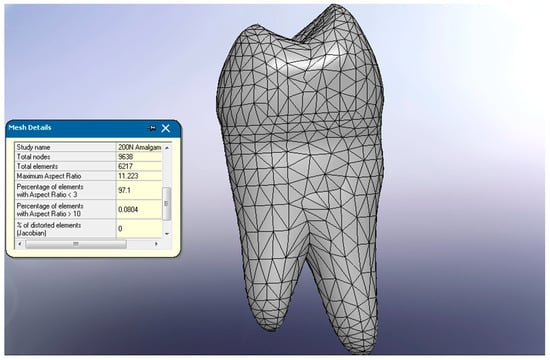
Figure 3.
Meshing of the mandibular second premolar.
Following each FEA simulation, the software generated a von Mises stress distribution field, which expressed a scalar equivalent value of mechanical stress by integrating all components of the stress tensor. This type of stress is commonly used for evaluating ductile materials, such as metal alloys and dental composites, and serves as a direct indicator of the risk of plastic deformation. The data were exported in tabular format for each volumetric mesh element, thus providing a detailed foundation for the subsequent analysis of the stress distribution within the restorative mass.
This step was essential for identifying areas with high potential for stress concentration, which were susceptible to the formation of microcracks or other forms of structural damage—information with direct relevance to clinical practice.
In order to quantitatively assess the overall mechanical behavior of the restoration under functional load, a volumetric integration of the von Mises stresses was performed across the entire volume of the restorative material. This integration was based on the following formula:
where is the von Mises stress recorded in element i, is the volume of that element, and represents the total volume of the restoration.
This method provides a global and objective assessment of the stress level experienced by the material, avoiding interpretations based solely on isolated peak values, which may arise as numerical artifacts. The weighted average stress reflects the deformation energy accumulated throughout the entire restorative body and allows for rigorous comparisons between different materials.
To determine the structural stability of the restorations, the safety factor (SF) was calculated for each material, defined as the ratio between the material’s compressive strength and the maximum von Mises stress obtained from the simulation:
The interpretation of safety factor (SF) values provides important insights into the structural integrity of dental restorations under functional loading. SF values of below 1 indicate a high likelihood of material failure, either through plastic deformation or fracture, suggesting that the restorative material cannot safely withstand the applied stress. SF values of close to 1 reflect a borderline mechanical condition, where even minor variations in loading or material defects could precipitate failure. Conversely, SF values exceeding 1.5 are generally regarded as indicative of a safe operational regime, ensuring adequate mechanical performance and clinical reliability under masticatory forces.
The materials used in this analysis, along with their characteristic parameters, were stored in a material library from which they could be accessed. In this specific study, three types of materials were defined: amalgam, dental enamel, and a composite.
To conduct this study and obtain conclusive results, the analysis focused on the forces involved during the mastication process as applied to the models, depending on the size and type of material used.
A crucial aspect in achieving a realistic simulation is the precise definition of material parameters [21]. In the proposed study, specific numerical values were established for the elastic modulus, Poisson’s ratio, and the compressive strength, which are essential parameters for characterizing the behavior of the analyzed materials (Table 1).

Table 1.
The numerical values corresponding to each analyzed material [22].
During mastication, occlusal contact generates both horizontal and axial forces, which can displace teeth in any direction. The consistency of the food influences the frequency and degree of the dental contact. Soft foods require less chewing, whereas hard foods lead to more frequent dental contacts as they are broken down. The physiological mobility of teeth, measured at 28 µm axially and 72–108 µm horizontally, allows them to withstand occlusal stress [23].
The forces applied (Figure 4) in this study exhibited variable magnitudes and orientations, selected based on data from the scientific literature. In dental biomechanics, the forces acting on teeth can be classified according to their direction and nature of application, directly influencing the stability, structural integrity, and longevity of prosthetic restorations. Axial forces, which are applied along the longitudinal axis of the tooth, are biomechanically the most favorable. These forces are efficiently absorbed by the dento–periodontal system and play a significant role in maintaining the stability of the tooth within the alveolus, representing a type of loading for which the supporting tissues are both morphologically and functionally adapted [24].
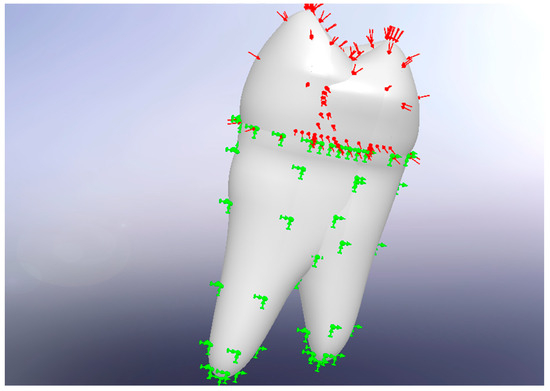
Figure 4.
Application of forces and constraints. Red arrows represent the resultant masticatory force vector inclined at 15° to the long axis of the tooth. Green arrows indicate boundary conditions mimicking the periodontal ligament–bone interface.
In contrast, lateral forces—whether oblique or horizontal—are applied at various angles relative to the tooth axis and generate considerable stress on the periodontal ligament and alveolar bone. Over time, such forces may lead to dental migration or tipping, particularly in the absence of adequate biomechanical control. Moreover, torsional forces, which arise during the rotational movements associated with mastication, produce shear stress on the dental roots and restorative materials. These types of forces are especially relevant in premolars, which, due to their anatomical position and functional role, are frequently exposed to such complex loading conditions. In the absence of biomechanically compatible restorations, torsional forces may promote the formation of microcracks, loss of material adhesion, and even structural fracture of the dental unit [24].
The masticatory force vector was defined with an inclination of 15° relative to the tooth’s longitudinal axis to simulate the oblique direction of occlusal contact typically observed during bruxism episodes. This orientation allowed for the integration of both axial and tangential force components, providing a more accurate representation of the actual trajectory of the mandibular movements. The direction of the force was set between the occlusal plane and the center of the pulp chamber using the External Loads → Force function. The load application area was located at the central occlusal fossa of the mandibular second premolar, a region physiologically involved in the transmission of masticatory forces. The force was applied as a resultant to the nodes corresponding to this region and was uniformly distributed to ensure a functionally realistic contact [5].
According to these sources, pathological bruxism forces of up to 800 N may occur at the level of the premolar. This value was considered the pathological upper limit in the present study. An important aspect of research in this field is the evaluation of the effects of these forces not only on the dental crown but also along the entire axis of the tooth, including the supporting structures.
Additionally, it is important to note that the upper limit of axial force that the periodontium can withstand without causing irreversible changes is approximately 200 N. Exceeding this threshold may lead to periodontal damage [25].
Among the occlusal parameters involved in the dynamics of bruxism, the contact angle plays a significant role, influencing both the distribution of masticatory forces and the degree of dental wear. This angle reflects the geometry of the guidance provided by occlusal morphology during mandibular movements such as lateral excursions, protrusion, and retrusion. In the context of bruxism, the contact angle becomes particularly relevant, as the abnormal and repetitive trajectory of the mandible leads to pathological contact between opposing surfaces. Therefore, the contact angle indicates the direction and intensity of the parafunctional forces exerted on the teeth and periodontium. In the case of premolars, the contact angle plays a crucial role in determining the directions and magnitudes of the parafunctional forces generated during bruxism. Even a minor change in this angle can lead to a significant redistribution of force vectors, increasing tangential components and favoring the emergence of shear stress. These stresses, when applied repeatedly and in unfavorable directions, can exceed the resistance capacity of dento–periodontal tissues and restorative materials, increasing the risk of microcracks, material debonding, and structural failure. Particularly, when forces are directed obliquely to the tooth axis, they may be amplified by the specific geometry of the cusps, leading to localized stress concentrations with disproportionate impacts on the root and ligament attachment areas. Therefore, the magnitudes of parafunctional forces should not be evaluated in isolation but rather in correlation with occlusal morphology and the direction of force application in order to fully understand the biomechanical risks associated with bruxism [26].
In this study, the application of forces of 400 N, 600 N, and 800 N—values exceeding the maximum physiological threshold of 200 N—revealed the occurrence of cracks within restored dental structures, particularly in the context of minor variations in the contact angle obtained through modeling (Table 2). These observations are especially relevant in cases of eccentric bruxism, characterized by lateral mandibular movements (grinding), where the effects of the applied forces become disproportionate. In such scenarios, the cusps of opposing teeth tend to “slide” over each other at biomechanically unfavorable angles, generating horizontal components of force that are transmitted to the dental roots and periodontal ligaments [27].
These horizontal forces may exceed the physiological adaptive capacity of the tooth’s supporting apparatus, which, over time, can lead to the development of extensive occlusal wear surfaces and dentin exposure accompanied by dentin hypersensitivity, as well as chronic periodontal inflammation due to the constant transmission of para-axial forces to the alveolar bone [28].
The highest stress levels have been observed in patients with bruxism, where occlusal stress can reach values of up to 1000 N. Due to the dynamic, unpredictable, and variable nature of mastication, accurately assessing actual stress levels remains a major challenge in biomechanical analysis. In this context, to ensure a relevant and reproducible comparison of the analyzed scenarios, a standardized loading model was adopted, allowing for linear parametric analysis. This model incorporates both vertical (axial) and horizontal (lateral) components, applied at the occlusal contact point, in accordance with data from the scientific literature [26].

Table 2.
Material behavior as a function of applied forces [29,30].
Table 2.
Material behavior as a function of applied forces [29,30].
| Applied Forces (N) | Amalgam | Composite |
|---|---|---|
| 200 | Stable, no risk of fracture, good tolerance | Stable, no risk of cracking, effective bonding |
| 400 | Stable, microcracks possible near margins | Possible microcracks if bonding is suboptimal |
| 600 | Risk of marginal fracture, especially in large cavities | Potential debonding or marginal microcracking, bonding under stress |
| 800 | Increased risk of coronal and marginal fracture, brittle behavior | Bonding fails, risk of internal cracks, less brittle than amalgam |
To accurately replicate the biomechanical behavior of the dento–periodontal system, the constraints applied in the simulation were designed to mimic the anchorage (fixation) of the premolar within the dental alveolus. The external surface of the periodontal ligament was restricted in translation but allowed minor physiological rotations (<0.1°), reflecting its damping capacity. Additionally, the root apex was rigidly connected to a global reference point, simulating dental stabilization within the alveolar bone. This configuration enabled the identification of compression zones in the regions where the force was applied, as well as in the support area, through the analysis of the resulting images. Complemented by the adoption of a homogeneous loading model, this approach facilitated a linear parametric analysis of masticatory force distribution [26].
Additionally, both tensile and compressive zones were observed in the studied region. These findings support clinical observations indicating that improperly fabricated or applied materials may lead to the formation of cracks and, consequently, to erosion.
After the introduction of all necessary data, the next step involved solving the systems of differential equations that described the studied process. The results obtained could be visualized using a color-coded scale or presented in alphanumeric format. The correct interpretation of these data requires a thorough understanding of the mathematical principles underlying the analysis, as well as the theories of material strength, such as the von Mises and Mohr–Coulomb criteria or thermal analysis. These areas of knowledge are essential to ensure accurate and meaningful results [31].
The von Mises stress criterion is based on the Mises–Hencky theory, also known as the maximum distortion energy theory or the shear energy theory. By defining the principal stresses as σ1, σ2, and σ3, the von Mises stress is expressed as follows [32]:
This theory states that a ductile material begins to deform at the point where the von Mises stress exceeds the yield stress (). In most cases, the ultimate tensile strength is used as the limit stress. However, using specialized software allows for the input of a custom yield stress based on the following condition: (σvon Mises ≥ σlimit) [26].
Additionally, the shear stress (τ) is also a defining characteristic for , expressed as follows:
For τmax = 0.577 σ, the failure phenomenon occurs.
This analysis made a comparison of two types of materials, amalgam and a composite, in the case of two types of dental fillings (medium and large) (Figure 5a,b), by applying four different force intensities (200 N, 400 N, 600 N, and 800 N).
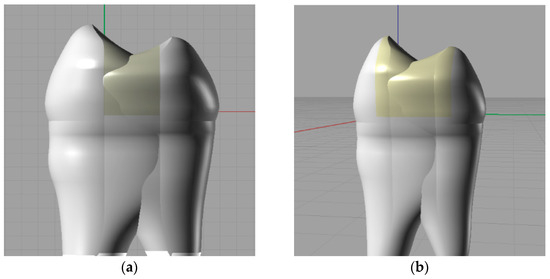
Figure 5.
(a) Modeling of a dental filling, medium-sized restoration. (b) Modeling of a dental filling, large-sized restoration.
3. Results
Following the pre-processing stage and the input of the data into the analysis system, the actual processing phase began, consisting of the simulation of stress distribution within the premolar during masticatory loading.
In the first stage, the stress distribution was analyzed for a premolar with a medium-sized restoration, which was restored using amalgam-based materials. This initial analysis provided insight into the mechanical behavior of the restored tooth under the action of masticatory forces (Figure 6a–d).
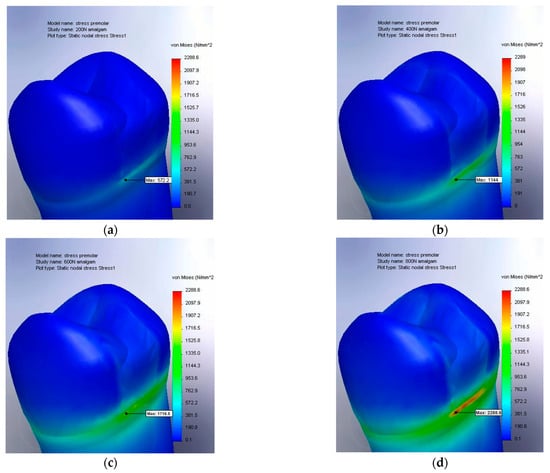
Figure 6.
(a) The von Mises stress result for amalgam at 200 N, medium-sized restoration; (b) von Mises stress result for amalgam at 400 N, medium-sized restoration; (c) von Mises stress result for amalgam at 600 N, medium-sized restoration; and (d) von Mises stress result for amalgam at 800 N, medium-sized restoration.
The simulation results for the stress distribution are represented on a value scale ranging from 0 to 2288.6 N/mm2. The maximum value, 2288.6 N/mm2, corresponds to the highest stress recorded under the application of an 800 N force (Figure 6d).
The visual representation of the stress distribution employs the ROYGBIV color spectrum (red, orange, yellow, green, blue, indigo, and violet), where red indicates the areas with the highest stress values. This color coding facilitates the rapid identification of the regions with the greatest stress concentrations.
A significant concentration of von Mises stresses was observed at the base of the dental crown, in the transition area toward the root. This phenomenon can be explained by the fact that although masticatory forces are applied to the upper part of the crown, the premolar is anchored in the dental alveolus. A more detailed analysis revealed a stress peak at the lower boundary of the dental restoration, particularly at the interface between the tooth and the filling material. This observation suggests that this region is prone to early changes in structural integrity. Moreover, the initial signs of material degradation (indicated in red, with stress values exceeding 1600 MPa) appeared under forces ranging between 600 and 800 N. This force range can be considered critical for the integrity of the restored tooth. The specific aspects of von Mises stress distribution for the extended occlusal cavity are illustrated in the simulations presented in the following figures (Figure 7a–d).
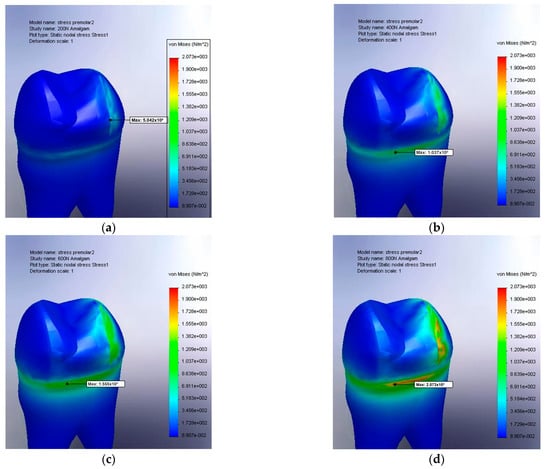
Figure 7.
(a) The von Mises stress result for amalgam at 200 N, large filling; (b) von Mises stress result for amalgam at 400 N, large filling; (c) von Mises stress result for amalgam at 600 N, large filling; and (d) von Mises stress result for amalgam at 800 N, large filling.
Increases in the von Mises stress were observed both on the occlusal lateral surface and at the level of the gingival wall. A detailed analysis highlighted more pronounced stress concentrations in the lower and lateral regions compared to the values recorded for a medium-sized occlusal cavity. Notably, the initial signs of material degradation (marked in red, with stress values exceeding 2073 MPa) appeared only under forces exceeding 800 N.
Another important aspect is the color gradient observed along the entire interface between the filling material and the dental tissue, suggesting elevated stress in this region. This observation is further supported by Figure 7a,b, which depict a premolar restored with the composite material. Increased stress (represented by progressively lighter shades of blue) can be observed both at the interface with the filling material and within its deeper structure. This indicates a stress distribution that affects not only the contact zone between the material and the tooth but also the internal structure of the restorative material itself.
By comparing Figure 6d and Figure 8a, it can be readily deduced that amalgam possesses physical properties more similar to those of living tissue. Furthermore, Figure 8a indicates that the resulting stresses are significantly higher under identical loading conditions (a maximum of 3047 MPa for the composite compared with 2288 MPa for the amalgam).
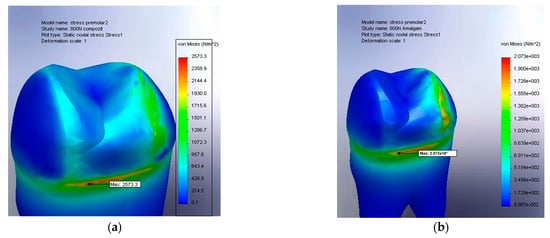
Figure 8.
(a) The von Mises stress result for amalgam at 800 N, large filling; (b) the von Mises stress result for the composite at 800 N, large filling.
In Figure 8a, a pronounced concentration of stress is observed at the base of the crown, specifically near the transition zone toward the tooth root. The maximum value of 2573.3 N/m2 indicates a deep accumulation of stress and a limited capacity of the composite material to effectively dissipate the applied forces, which favors the development of microcracks at the interface between the restorative material and the dental structure. Furthermore, the depth at which these stresses penetrate suggests an increased risk of internal damage and biomechanical decompensation under repeated loading conditions, such as those encountered in chronic bruxism.
In contrast, Figure 8b illustrates the behavior of an amalgam restoration under identical loading conditions, showing a more uniform and controlled stress distribution at the base of the crown, with a maximum value of 2073 N/m2. Although the affected area is similar in location, the stress intensity is significantly lower. This finding suggests that amalgam, having an elastic modulus close to that of dentin, forms a more rigid and better-integrated unit with the natural dental structure, thereby reducing the risk of excessive stress at the crown–root junction.
The comparative analysis of the stress distribution at the premolar level allowed for the differentiation of stress characteristics based on the applied force (Figure 9). It was observed that the stress values ranging between 200 and 400 N generated a von Mises distribution with values below 1500 MPa. Under these conditions, the physical alterations were relatively minimal, suggesting an elastic behavior of both the restorative materials and the dental tissue without significant structural changes (such as cracks or shrinkage) and with reversible deformations.
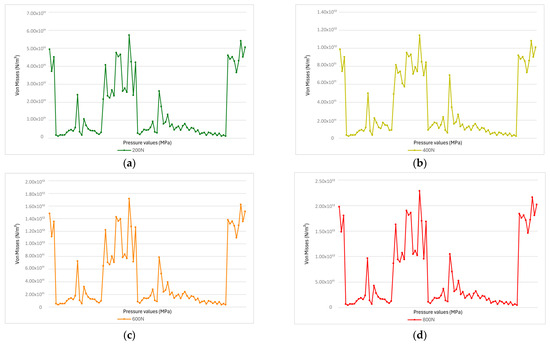
Figure 9.
(a) At a force of 200 N (a normal physiological value), the stress levels are relatively low, with most values below 5.00 × 1011 Pa. (b) At 400 N, several areas show increased stress, with peaks exceeding 1.00 × 1012 Pa. This indicates an uneven stress distribution and the beginning of localized accumulation, which may lead to fatigue over time. (c) At 600 N, the stress becomes more intense, with some values exceeding 1.50 × 1012 Pa. More peaks and abrupt variations appear, indicating that the material is being pushed beyond normal limits, increasing the risk of cracking. (d) At 800 N, stress levels are the highest—with peaks over 2.00 × 1012 Pa—and the distribution is highly fragmented. The material is under overload and faces a real risk of failure or fracture.
In contrast, pressures exceeding 600–800 N resulted in irreversible structural modifications. The analytical images highlight irreversible structural changes at the interface between the tooth and the restorative material, including erosion, microcracks, or even material detachment (Figure 10). These findings emphasize the critical importance of managing masticatory forces in order to preserve the integrity of dental restorations and adjacent tissues [33].
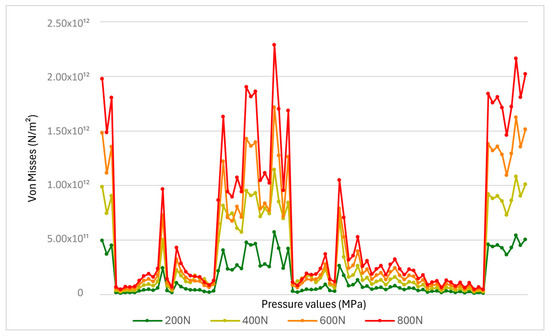
Figure 10.
The von Mises stress distribution on the premolar crown based on applied force.
To obtain a quantitative perspective on the overall mechanical behavior of dental restorations made with amalgam, a volumetric integration method of von Mises stress was applied. In the simulation process, the stress distribution was evaluated for each volumetric element (mesh), each having a constant volume, which allowed for the calculation of an arithmetic mean equivalent to a weighted integration. The resulting average stresses from this analysis reflect the ability of amalgam to distribute applied forces uniformly throughout a restorative mass, providing a more accurate overview of its biomechanical behavior than analyzing only local peak values.
Table 3 summarizes the values obtained for the integrated average stress and the safety factor (SF), calculated as the ratio between the compressive strength of the amalgam (483 MPa) and the average stress obtained in each loading scenario.

Table 3.
Average von Mises stress and safety factor (SF) values for amalgam restorations under increasing masticatory loads (200–800 N).
To evaluate the mechanical behavior of the restorations made with the composite material, the same methodology of volumetric integration of von Mises stresses was applied as for the amalgam (Table 4). The four axial loading scenarios were used to replicate the functional and parafunctional conditions within the oral cavity. The results indicated a higher average stress in the composite compared to the amalgam at all force levels, suggesting a reduced ability of the composite material to uniformly disperse mechanical stress. At a force of 800 N, the average stress in the composite mass was 7.2 × 108 Pa, compared with 6.08 × 108 Pa in the amalgam—a biomechanically significant difference.

Table 4.
Average von Mises stress and safety factor (SF) values for composite restorations under increasing masticatory loads (200–800 N).
These results highlight the superior mechanical stability of the amalgam compared to the composite under identical loading conditions. Although the calculated SF values remain below the ideal threshold, the amalgam consistently exhibited lower average von Mises stress values at all force levels, indicating a better ability to distribute and absorb mechanical loads. This suggests that amalgam has a higher resistance to repetitive or intense occlusal forces without approaching the material’s critical failure limits.
In the case of the composite material (Figure 11a), the stresses generated by the applied force penetrated deeply into the restoration, with the maximum values reaching 3.05 GPa. The stress distribution was clearly more extensive in depth, indicating the internal transmission of the mechanical loads throughout the restorative material mass. This characteristic suggests that the structure of the composite allows for more pronounced elastic deformations but also presents a potential for stress accumulation in regions farther from the contact surface. Such a phenomenon may increase the risk of internal microcrack formation or debonding at the interface with the dental tissue.
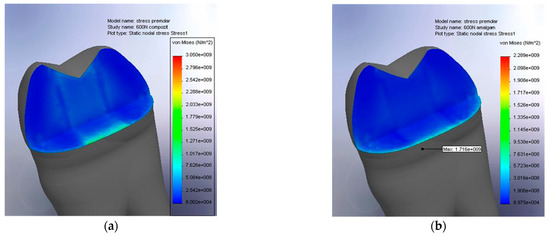
Figure 11.
(a) Stress absorption within the composite filling; (b) stress absorption within the amalgam filling.
In contrast, Figure 11b, corresponding to the amalgam restoration, shows a more superficial stress distribution, with a significantly lower maximum value of 1.716 GPa. The stress zone is concentrated almost exclusively in the upper layer of the material, confirming the more rigid behavior of the amalgam. This rigidity resulted in limited volumetric absorption of force but allowed for efficient surface-level dissipation, thereby reducing the risk of internal stress propagation. Consequently, the amalgam formed a more integrated assembly with the dental structure, functioning as a unified mechanical unit.
Based on this observation, it can be concluded that amalgam possesses advantageous properties, as its physical characteristics more closely match those of the natural tooth structure. However, it is important to note that this conclusion is based solely on the analysis of stress distribution and does not account for other critical factors, such as adhesive properties, aesthetics, or material biocompatibility. Therefore, a comprehensive evaluation of restorative materials should include an in-depth analysis of all relevant properties rather than relying solely on stress distribution models.
The global stress distribution within the restorative material was evaluated under a 200 N load, which falls within the normal physiological masticatory range. Although the results obtained at this level are not statistically significant, they offer relevant insight into the general mechanical behavior of the materials studied. As illustrated in Figure 12, which presents the spatial distribution of the safety factor (SF) in the amalgam restoration, the values remain predominantly in the favorable range, with large blue zones indicating the regions where the SF approaches 1. This reflects a low risk of mechanical failure and confirms the material’s ability to efficiently absorb applied forces without undergoing critical deformation. Nonetheless, the small red and orange areas—particularly at the margins—highlight localized stress concentrations where the safety factor may decrease to as low as 0.017.
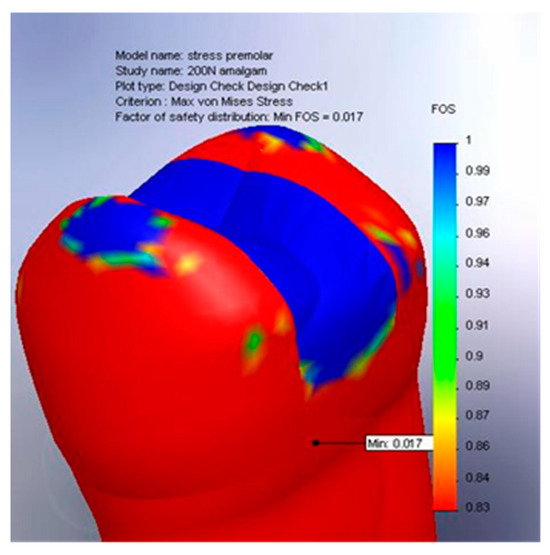
Figure 12.
Global stress distribution in the amalgam filling, 200 N.
Compared to the composite restorations, the critical stress accumulation was noticeably less pronounced in the amalgam, especially in the coronal–apical transition zone and along the tooth–restoration interface. Clinically, this translates into reduced risk of marginal breakdown, microcrack formation, and material fatigue, thus supporting the use of amalgam in high-load-bearing restorations, particularly in the posterior teeth or in patients exhibiting parafunctional habits such as bruxism.
In contrast, the application of an 800 N load resulted in extremely high stress values within the restorative material in both the composite and amalgam restorations, leading to the formation of cracks and accelerated degradation of the premolar–restoration complex. Although the maximum von Mises stress values were higher in the composite (reaching up to 3047 MPa, compared with 2288 MPa for the amalgam), the internal structure of the composite—due to its network of intermolecular bonds—enabled a deeper distribution of stress, reducing its concentration in critical areas. This differentiated behavior reflects the distinct ways in which the two materials absorb and manage occlusal loads, depending on their nature and the intensity of the forces involved.
4. Discussion
The present study adopted an integrative methodology, combining three-dimensional modeling with finite element analysis (FEA) to investigate the biomechanical behavior of mandibular second premolars restored with amalgam and a composite under varying masticatory forces. The results provide valuable insights into the complex interactions between the mandibular structure, the dynamics of the muscular forces, and the integrity of the restored tooth.
In the mathematical model presented, the muscular force was applied at a specific angle relative to the horizontal plane, and its transfer to the premolar was conceptualized as a lever system, with the temporomandibular joint functioning as the fulcrum—a model similar to that described by Gupta and collaborators as early as the 1970s [1].
The vectorization of the masticatory force enabled the differentiation between its vertical component—responsible for the axial loading of the tooth—and its horizontal component, which contributes to the lateral displacement of the dental surface. This distinction is essential for rigorous biomechanical analysis, as each component induces distinct stress responses within the dental and restorative structures. Correlations with clinical studies and FEA simulations, such as those conducted by Liu et al. [3], confirm that vertical forces, while essential for efficient mastication, generate significant stress at the base of restorations and at the restorative interface, whereas horizontal forces substantially contribute to the occurrence of marginal fractures and delamination, particularly in patients with bruxism [6].
The comparison of the mechanical behavior of the amalgam and composite under these loads revealed significant differences. The amalgam, characterized by rigidity and an elastic modulus closely matching that of dentin, demonstrated a more homogeneous stress distribution, with reduced concentration in high-risk areas. This behavior supports the hypothesis of the functional integration of amalgam into the dental structure, forming a biomechanically cohesive unit capable of withstanding high loads without excessive deformation—a fact also confirmed by Bharti et al., who highlighted its remarkable clinical durability in posterior restorations [16].
In contrast, the composite—despite its aesthetic advantages and clinical manageability—exhibited a more complex internal stress distribution, with a pronounced tendency for stress accumulation at deeper levels, particularly in the case of extensive restorations. This finding aligns with the results reported by Iftikhar [15], who demonstrated an increased susceptibility of composites to microcracks and progressive deterioration under the conditions of repetitive loading.
The mandible, as a mobile and adaptable structure, directly influences stress distribution within restorations, especially under conditions of bruxism or parafunctional activity. In such cases, sudden increases in masticatory force magnitude, combined with atypical angles of application, can exacerbate stress in the basal region of the dental crown—a zone also identified as vulnerable in a study by Ceddia et al. [26]. The FEA simulations in the present study indicated that the maximum stresses recorded for the composite (3047 MPa) significantly exceeded the material’s strength limits, suggesting increased structural vulnerability in patients subjected to extreme occlusal loads.
This study also emphasizes that the interface between the dental tissue and the restorative material represents the area most prone to deterioration, regardless of the type of material used. The difference between the elastic moduli of the dentin and the restorative material governs the transfer of stress, and a significant mismatch may lead to the accumulation of residual stresses. This factor was also highlighted by Fok and Chew [34], who analyzed the critical relationship between structural inhomogeneities and failures at the contact zone.
The technological contribution of this study is reflected in the use of a high-fidelity discretized model (9638 nodes, 6217 elements), allowing for a detailed visualization of the stress distribution. The use of the ROYGBIV color spectrum for data interpretation facilitated the precise identification of the zones with the maximum stress concentrations, contributing to the assessment of the structural risks. Furthermore, the application of the forces in simulated scenarios with clinically relevant thresholds (200–800 N), as defined in the specialized literature [12,15], ensured direct applicability to dental practice.
An additional significant finding of this study is the distinct difference in stress absorption mechanisms between the two materials. Specifically, the amalgam exhibited a tendency to concentrate stress at the surface, whereas the composite material facilitated deeper stress dissipation. This observation is corroborated by the findings of Gönder et al. [17], who investigated the mechanical behavior of restorations as a function of the elastic modulus and the thickness of the cementation layer. Furthermore, recent research on self-healing smart composites [18] presents promising advancements in addressing the functional limitations inherent to conventional composite materials.
Consequently, the results of this study underscore the necessity of a personalized restorative approach that accounts not only for the morphological characteristics of the cavity but also for the patient’s individual biomechanical profile. Factors such as masticatory forces, a history of bruxism, and occlusal type should be considered to optimize the long-term success of restorations. In this regard, advanced digital modeling and finite element analysis serve as essential tools, offering predictive and objective methodologies to enhance clinical decision-making. The integration of these techniques facilitates the transition toward modern, evidence-based dentistry tailored to the specific needs of each patient [33].
5. Conclusions
The present study highlights the fundamental relevance of three-dimensional biomechanical modeling and finite element analysis (FEA) in investigating the dynamic behavior of dento–maxillary structures subjected to masticatory forces. Through the use of an integrated approach, it was possible not only to accurately simulate the interaction between various components of the masticatory system but also to critically evaluate the mechanical performance of two commonly used restorative materials—amalgam and a composite.
The analysis of the von Mises stress distribution revealed significant differences between the two materials studied. The amalgam, due to its mechanical properties being similar to those of dentin, demonstrated a superior ability to distribute mechanical stress uniformly, thereby reducing stress concentration in critical areas, such as the interface between the restorative material and the dental tissue. In contrast, the composite exhibited a tendency to absorb and internally propagate stress, which, under conditions of overload (forces > 600 N), may promote the development of microcracks or delamination. These findings underscore the need for an informed selection of restorative materials, taking into account not only aesthetic considerations but also their specific mechanical behavior under both functional and parafunctional loading conditions.
This study also demonstrated that the magnitude and direction of applied forces, particularly in the context of bruxism, decisively influence the risk of the structural failure of restorations. Specifically, forces exceeding 800 N were associated with stress values surpassing the strength thresholds of the materials, particularly in the case of the composite, indicating the need for personalized preventive and therapeutic strategies for patients with parafunctional habits.
Another essential conclusion derives from the analysis of the behavior at the dentin–restorative material interface. Differences in the elastic modulus between the two materials and the dental tissue generated local stress imbalances, which can serve as initiation points for structural degradation. Therefore, the optimization of restorations should not focus solely on the restorative material itself but also on application techniques, layer thickness, and mechanical compatibility with the biological substrate.
The significance of digital technologies, particularly finite element analysis (FEA), is underscored by their capacity to produce high-fidelity predictive models that closely replicate real-world loading conditions within the oral cavity. These methodologies offer a robust foundation for experimental validation and are pivotal in advancing modern dentistry, particularly in the areas of personalization, prediction, and prevention.
In conclusion, the present research supports the implementation of clinically guided protocols based on biomechanical analysis and digital simulation, aimed at improving the longevity of dental restorations. In an increasingly complex clinical context, the integration of advanced modeling tools has become not only beneficial but essential for maximizing long-term therapeutic success.
Author Contributions
Conceptualization, M.T. and I.D.; methodology, M.R. and C.M.; software, M.T., I.D. and C.M.; validation, I.D. and M.R.; formal analysis, M.T. and C.M.; investigation, M.T.; resources, I.D.; data curation, M.R. and C.M.; writing—original draft preparation, I.D.; writing—review and editing, M.R.; visualization, C.M.; supervision, M.T.; project administration, M.R. and M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gupta, K.K.; Knoell, A.C.; Grenoble, D.E. Mathematical modeling and structural analysis of the mandible. Biomater. Med. Devices Artif. Organs 1973, 1, 469–479. [Google Scholar] [CrossRef] [PubMed]
- Sierwald, I.; John, M.T.; Schierz, O.; Hirsch, C.; Sagheri, D.; Jost-Brinkmann, P.-G.; Reissmann, D.R. Association of temporomandibular disorder pain with awake and sleep bruxism in adults. J. Orofac. Orthop. Fortschritte Kieferorthopadie OrganOfficial J. Dtsch. Ges. Kieferorthopadie 2015, 76, 305–317. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-F.; Wang, R.; Baur, D.A.; Jiang, X.-F. A finite element analysis of the stress distribution to the mandible from impact forces with various orientations of third molars. J. Zhejiang Univ. Sci. B 2018, 19, 38–48. [Google Scholar] [CrossRef] [PubMed]
- Costa, A.K.F.; Xavier, T.A.; Paes-Junior, T.J.A.; Andreatta-Filho, O.D.; Borges, A.L.S. Influence of occlusal contact area on cusp defection and stress distribution. J. Contemp. Dent. Pract. 2014, 15, 699–704. [Google Scholar] [CrossRef]
- Lee, J.-H.; Seo, J.-H.; Park, S.-W.; Kim, W.-G.; Jung, T.-G.; Lee, S.-J. A Finite Element Analysis Study of Edentulous Model with Complete Denture to Simulate Masticatory Movement. Bioengineering 2024, 11, 336. [Google Scholar] [CrossRef]
- Thayer, M.L.T.; Ali, R. The dental demolition derby: Bruxism and its impact—Part 1: Background. Br. Dent. J. 2022, 232, 515–521. [Google Scholar] [CrossRef]
- Zheng, B.; Ran, J.; He, J.; Al-Yafrusee, E.S.A.M.; Zhao, Y.; Liu, Y. Three-dimensional finite element analysis of the uprighting movement of mandibular mesially inclined second molars. Am. J. Orthod. Dentofac. Orthop. Off. Publ. Am. Assoc. Orthod. Its Const. Soc. Am. Board Orthod. 2024, 165, 314–320. [Google Scholar] [CrossRef]
- Jager, N.D.E. 13—Finite element analysis of stresses in dental crowns. In Dental Biomaterials; Curtis, R.V., Watson, T.F., Eds.; Woodhead Publishing Series in Biomaterials; Academic Center for Dentistry Amsterdam (ACTA): Amsterdam, The Netherlands, 2008; pp. 343–359. ISBN 978-1-84569-296-4. [Google Scholar]
- Zhong, Z.; Kiong Yip, P. Finite element analysis of a three-dimensional package. Solder. Surf. Mt. Technol. 2003, 15, 21–25. [Google Scholar] [CrossRef]
- Todić, J.; Mitić, A.; Lazić, D.; Radosavljević, R.; Staletović, M. Effects of bruxism on the maximum bite force. Vojnosanit. Pregl. 2017, 74, 138–144. [Google Scholar] [CrossRef]
- Alkan, A.; Celebi, N.; Ozden, B.; Baş, B.; Inal, S. Biomechanical comparison of different plating techniques in repair of mandibular angle fractures. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endod. 2007, 104, 752–756. [Google Scholar] [CrossRef]
- Awasthi, M.P.; Sharma, L.C.S.; Kaur, M.S. Three-dimensional finite element analysis of class 2 inlay on mandibular molar using various materials. Int. J. Res.-Granthaalayah 2018, 6, 272–277. [Google Scholar] [CrossRef]
- Imanishi, A.; Nakamura, T.; Ohyama, T.; Nakamura, T. 3-D Finite element analysis of all-ceramic posterior crowns. J. Oral Rehabil. 2003, 30, 818–822. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Imanishi, A.; Kashima, H.; Ohyama, T.; Ishigaki, S. Stress analysis of metal-free polymer crowns using the three-dimensional finite element method. Int. J. Prosthodont. 2001, 14, 401–405. [Google Scholar] [PubMed]
- Iftikhar, N. Three-Dimensional Finite Element Analysis of the Stress Distribution Pattern in a Mandibular First Molar Tooth Restored with Three Different Restorative Materials. Saudi J. Oral Dent. Res. 2019, 160–163. [Google Scholar] [CrossRef]
- Bharti, R.; Wadhwani, K.K.; Tikku, A.P.; Chandra, A. Dental amalgam: An update. J. Conserv. Dent. JCD 2010, 13, 204–208. [Google Scholar] [CrossRef]
- Gönder, H.Y.; Demirel, M.G.; Mohammadi, R.; Alkurt, S.; Fidancioğlu, Y.D.; Yüksel, I.B. The Effects of Using Cements of Different Thicknesses and Amalgam Restorations with Different Young’s Modulus Values on Stress on Dental Tissue: An Investigation Using Finite Element Analysis. Coatings 2023, 13, 6. [Google Scholar] [CrossRef]
- Tavasolikejani, S.; Farazin, A. Explore the most recent advancements in the domain of self-healing intelligent composites specifically designed for use in dentistry. J. Mech. Behav. Biomed. Mater. 2023, 147, 106123. [Google Scholar] [CrossRef]
- Bramanti, E.; Cervino, G.; Lauritano, F.; Fiorillo, L.; D’Amico, C.; Sambataro, S.; Denaro, D.; Famà, F.; Ierardo, G.; Polimeni, A.; et al. FEM and Von Mises Analysis on Prosthetic Crowns Structural Elements: Evaluation of Different Applied Materials. Sci. World J. 2017, 2017, 1029574. [Google Scholar] [CrossRef]
- Elaborare Metodica Nr. 12. Available online: https://ro.scribd.com/document/207547461/Elaborare-Metodica-Nr-12 (accessed on 2 April 2025).
- di Lauro, A.E.; Ciaramella, S.; Tribst, J.P.M.; Aliberti, A.; Ausiello, P. Comparison of Bulk Polymeric Resin Composite and Hybrid Glass Ionomer Cement in Adhesive Class I Dental Restorations: A 3D Finite Element Analysis. Polymers 2024, 16, 2525. [Google Scholar] [CrossRef]
- Davies, R.A.; Ardalan, S.; Mu, W.-H.; Tian, K.; Farsaikiya, F.; Darvell, B.W.; Chass, G.A. Geometric, electronic and elastic properties of dental silver amalgam γ-(Ag3Sn), γ1-(Ag2Hg3), γ2-(Sn8Hg) phases, comparison of experiment and theory. Intermetallics 2010, 18, 756–760. [Google Scholar] [CrossRef]
- Okenson, J.P. Management of Temporomandibular Disorders and Occlusion, 8th ed.; Elsevier Inc.: Lexington, KY, USA, 2019; ISBN 978-0-323-58210-0. [Google Scholar]
- Hazem, A.; Mărășescu, F.I.; Țuculină, M.J.; Popescu, A.D.; Popa, D.L.; Mihai, L.L.; Cumpătă, C.N.; Iliescu, A.; Mărășescu, P.; Dascălu, I.T. Orthodontic System Modeled and Simulated with the Lingual Technique to Assess Tooth Forces. Diagnostics 2024, 14, 1171. [Google Scholar] [CrossRef] [PubMed]
- Nanci, A. Ten Cate’s Oral Histology—Pageburst on VitalSource: Development, Structure, and Function; Elsevier Health Sciences: Amsterdam, The Netherlands, 2007; ISBN 978-0-323-05848-3. [Google Scholar]
- Ceddia, M.; Lamberti, L.; Trentadue, B. FEA Comparison of the Mechanical Behavior of Three Dental Crown Materials: Enamel, Ceramic, and Zirconia. Materials 2024, 17, 673. [Google Scholar] [CrossRef] [PubMed]
- Archangelo, C.M.; Rocha, E.P.; Anchieta, R.B.; Martin, M.; Freitas, A.C.; Ko, C.-C.; Cattaneo, P.M. Influence of buccal cusp reduction when using porcelain laminate veneers in premolars. A comparative study using 3-D finite element analysis. J. Prosthodont. Res. 2011, 55, 221–227. [Google Scholar] [CrossRef]
- Doğan, Ö. Stress Distribution of Pediatric Zirconia and Stainless Steel Crowns after Pulpotomy Procedure under Vertical Loading: A Patient-Specific Finite Element Analysis. J. Funct. Biomater. 2024, 15, 268. [Google Scholar] [CrossRef]
- Boțilă, M.-R.; Popa, D.L.; Mercuț, R.; Iacov-Crăițoiu, M.M.; Scrieciu, M.; Popescu, S.M.; Mercuț, V. A Finite Element Method Study of Stress Distribution in Dental Hard Tissues: Impact of Access Cavity Design and Restoration Material. Bioengineering 2024, 11, 878. [Google Scholar] [CrossRef]
- Gönder, H.Y.; Fidancıoğlu, Y.D.; Fidan, M.; Mohammadi, R.; Karabekiroğlu, S. Comparison of Resin Cement’s Different Thicknesses and Poisson’s Ratios on the Stress Distribution of Class II Amalgam Restoration Using Finite Element Analysis. Appl. Sci. 2023, 13, 4125. [Google Scholar] [CrossRef]
- Gere, J.M. Mechanics of Materials; Cengage Learning: Stamford, CT, USA, 2013; ISBN 978-1-111-57773-5. [Google Scholar]
- Mali, S.Y.; Kondhalkar, G.E. Force analysis of grinding wheel on different material. Int. J. Creat. Res. Thoughts IJCRT 2020, 8, 1242–1254. [Google Scholar]
- Aldowish, A.F.; Alsubaie, M.N.; Alabdulrazzaq, S.S.; Alsaykhan, D.B.; Alamri, A.K.; Alhatem, L.M.; Algoufi, J.F.; Alayed, S.S.; Aljadani, S.S.; Alashjai, A.M.; et al. Occlusion and Its Role in the Long-Term Success of Dental Restorations: A Literature Review. Cureus 2024, 16, e73195. [Google Scholar] [CrossRef]
- Fok, A.; Chew, H.P. Mechanical Failure of Dental Restorations: The Weakest-Link Theory. In Mathematical Models for Dental Materials Research; Fok, A., Chew, H.P., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 47–53. ISBN 978-3-030-37849-3. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).