The Analysis of the Possibility to Conduct Orbital Manoeuvres of Nanosatellites in the Context of the Maximisation of a Specific Operational Task
Abstract
1. Introduction
- Different types of orbital manoeuvres of nanosatellites differ significantly in terms of fuel consumption, depending on the scale of change in the required parameter. For example, the altitude change manoeuvre is characterised by relatively low fuel consumption when the impulses are precisely planned, but the consumption of fuel for additional orbital manoeuvres is significantly limited by performing regular orbit adjustments.
- Parameters, such as altitude, inclination, and the tilt of the satellite have a major influence on the fuel and energy requirements of the manoeuvres. The optimum strategies vary depending on the specific requirements of the given mission, such as the need for the precise coverage of target areas or to maintain the orbit for a longer period.
- Impulsive manoeuvres proved to be an effective method to modify the parameters of the orbit, enabling precise control over the trajectory with a minimum time required to perform the manoeuvre. However, the manoeuvre of tilting the nanosatellite, with the telescope, with the use of reaction wheels, enables to prolong the time of observation of a specific area without the need to consume fuel. In this case, the satellite uses the energy generated by solar panels, which significantly lowers operating costs and improves the flexibility of the mission.
- The research results may be used to improve the planning of nanosatellite missions, in particular, by identifying the manoeuvres that are the most cost-effective in terms of fuel and energy, which will allow to maximise their operational efficiency.
- Combining orbital manoeuvres (such as changing the altitude or inclination) with the satellite tilting manoeuvre ensures the best balance between fuel and energy efficiency and operational precision. However, in order to effectively combine these two types of manoeuvres, it is necessary to ensure the appropriate amounts of fuel and energy. Therefore, when planning a satellite mission, one should take into consideration both the fuel resources that are necessary to conduct impulse orbital manoeuvres and the appropriate availability of electric power for propulsion systems, such as reaction wheels. For future nanosatellite missions, in particular, those devoted to long-term observations, it is recommended to increase the focus on the accurate planning of fuel and energy consumption. This will allow the use of tilting manoeuvres efficiently together with the change in the inclination of the orbit.
2. Materials and Methods
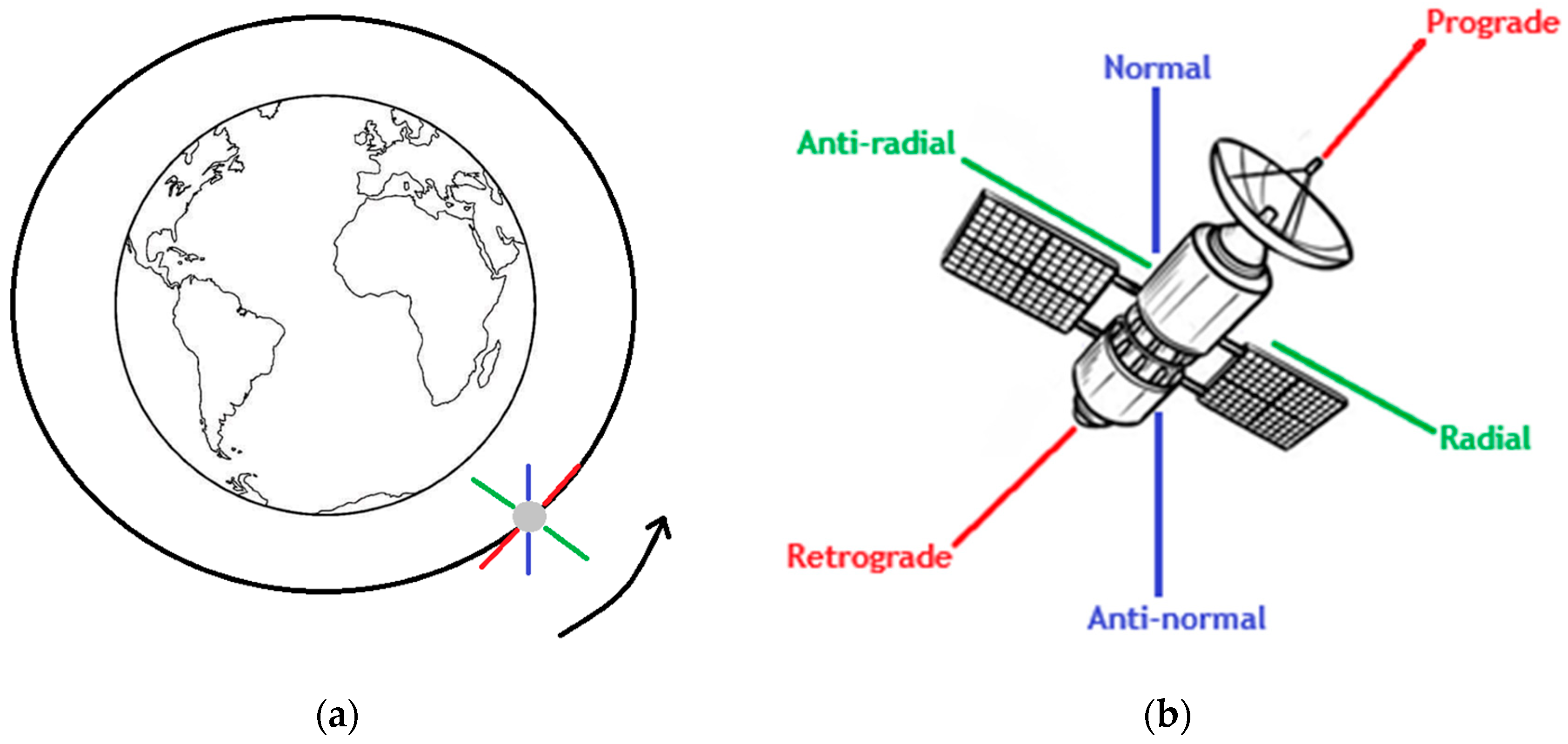
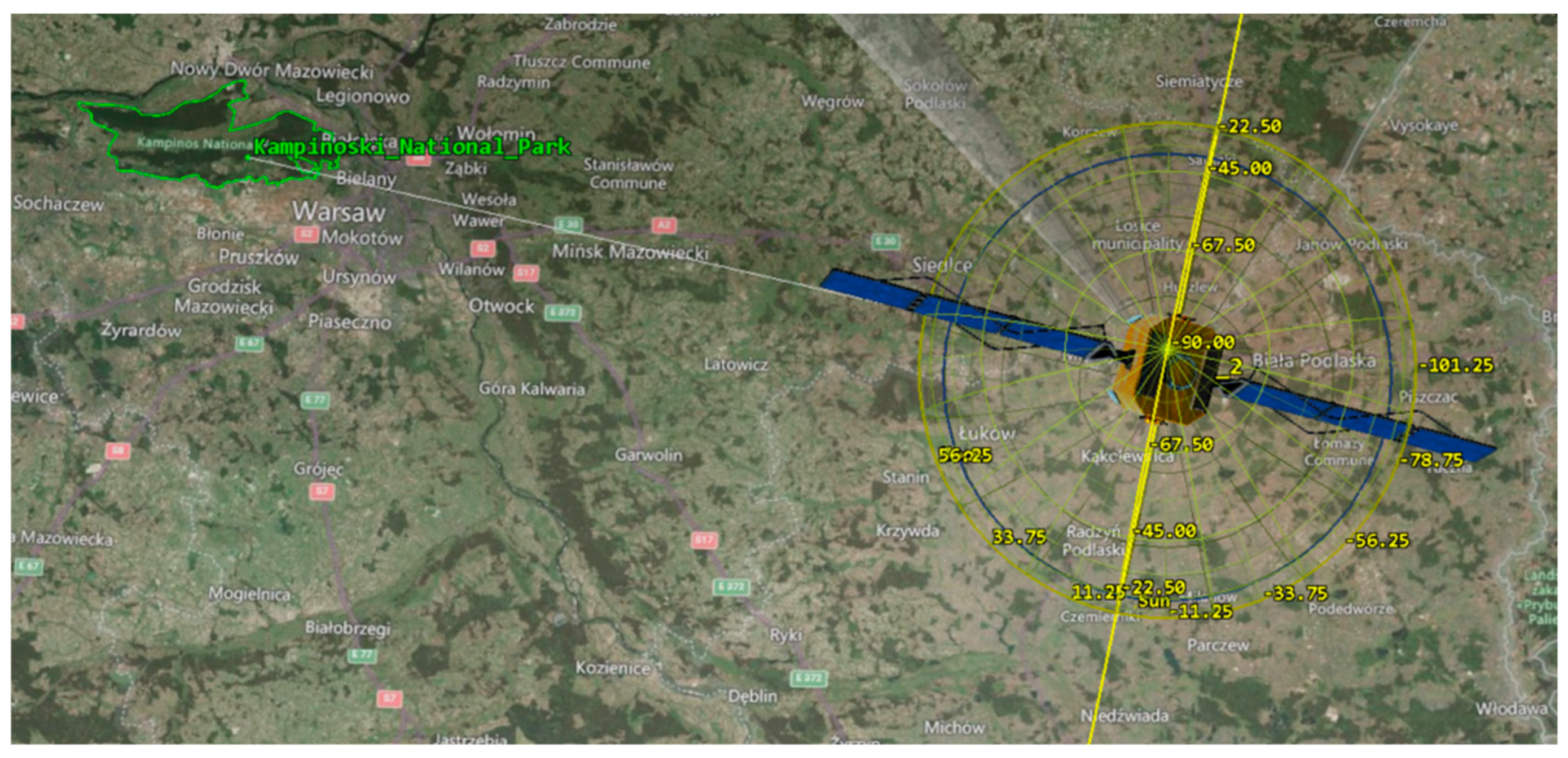
2.1. Directions of the Thrusters During Orbital Manoeuvres
2.2. Impulsive Manoeuvres
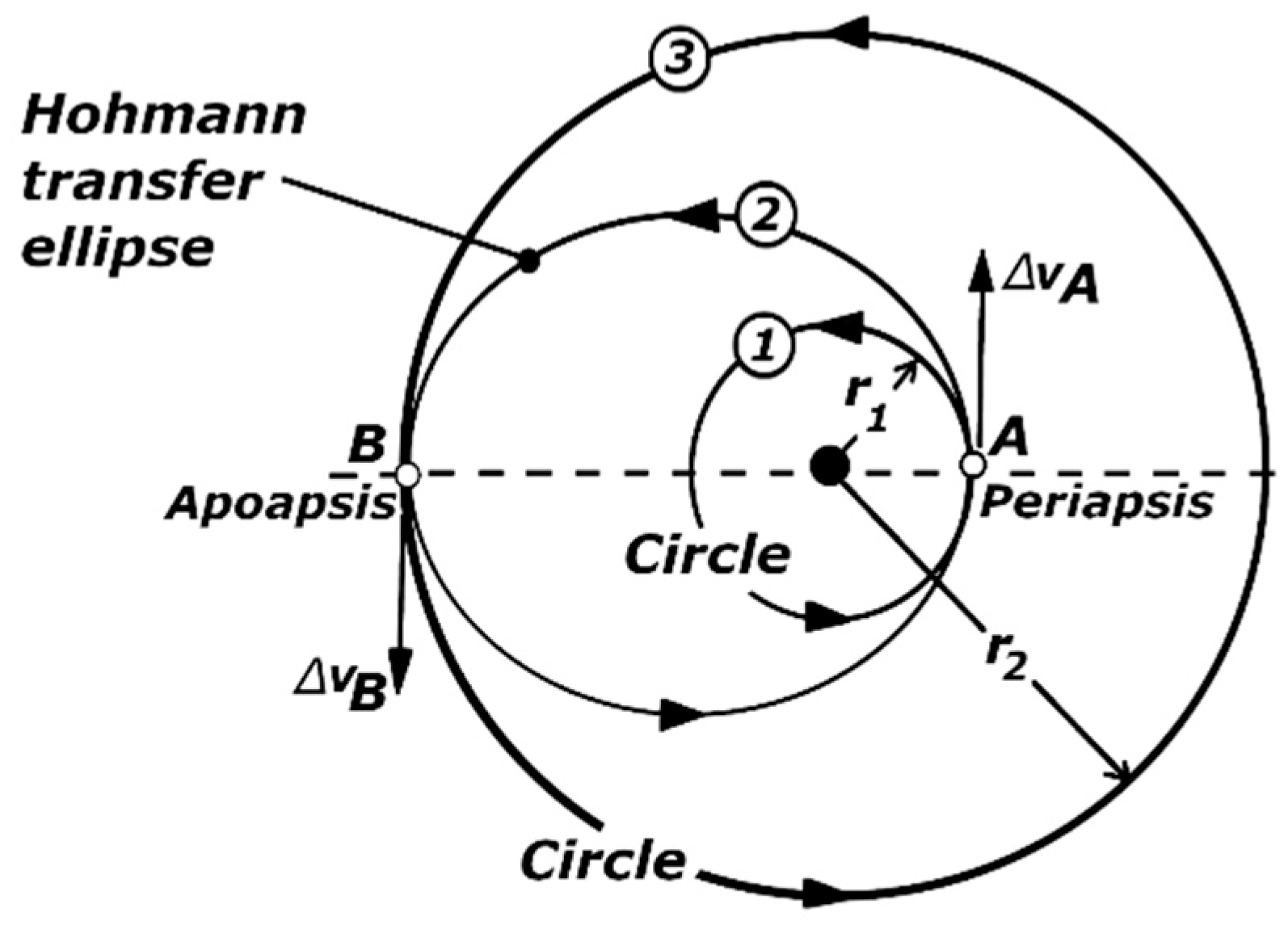
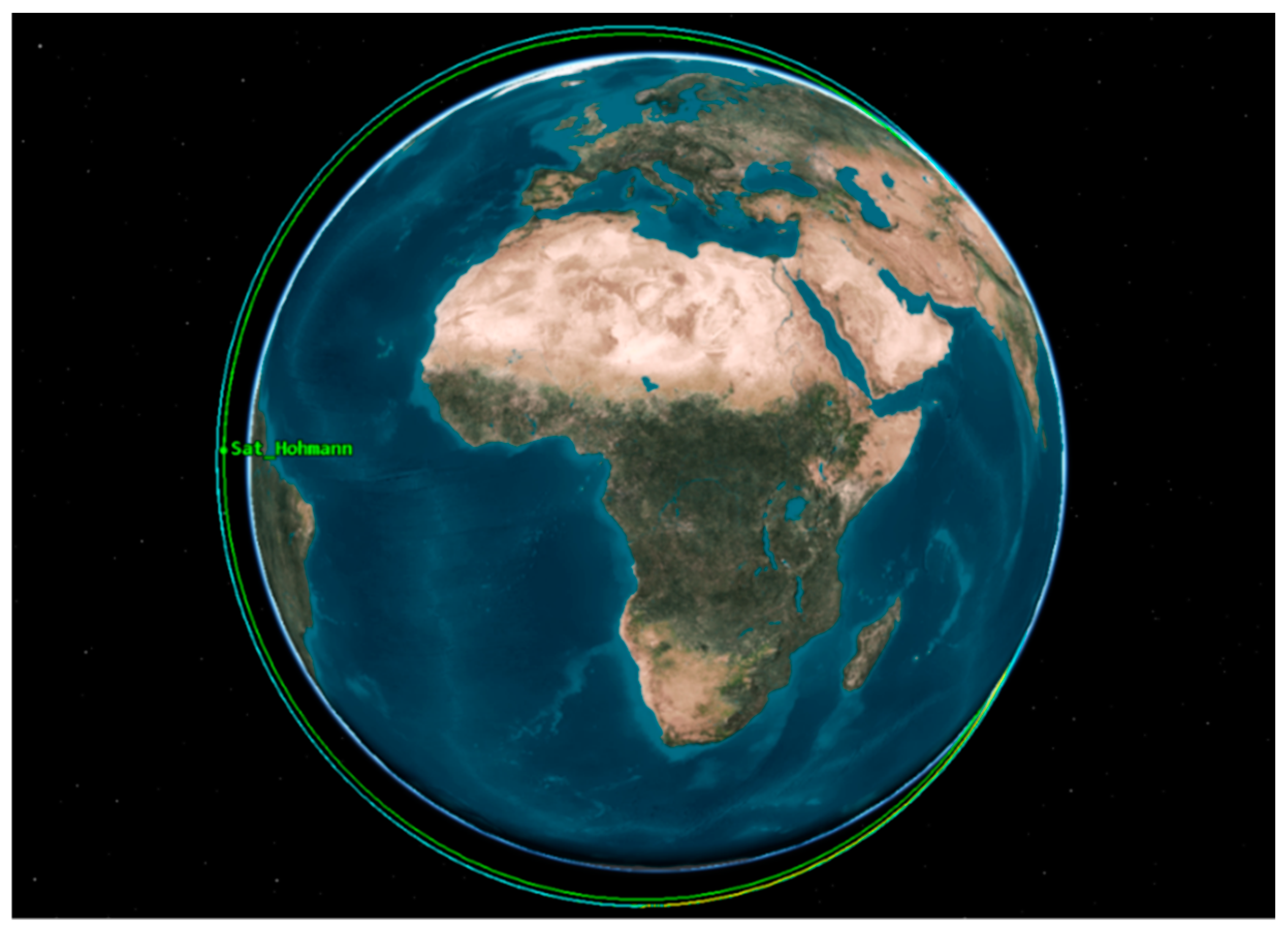
2.2.1. Hohmann Transfer
- Calculating ∆v
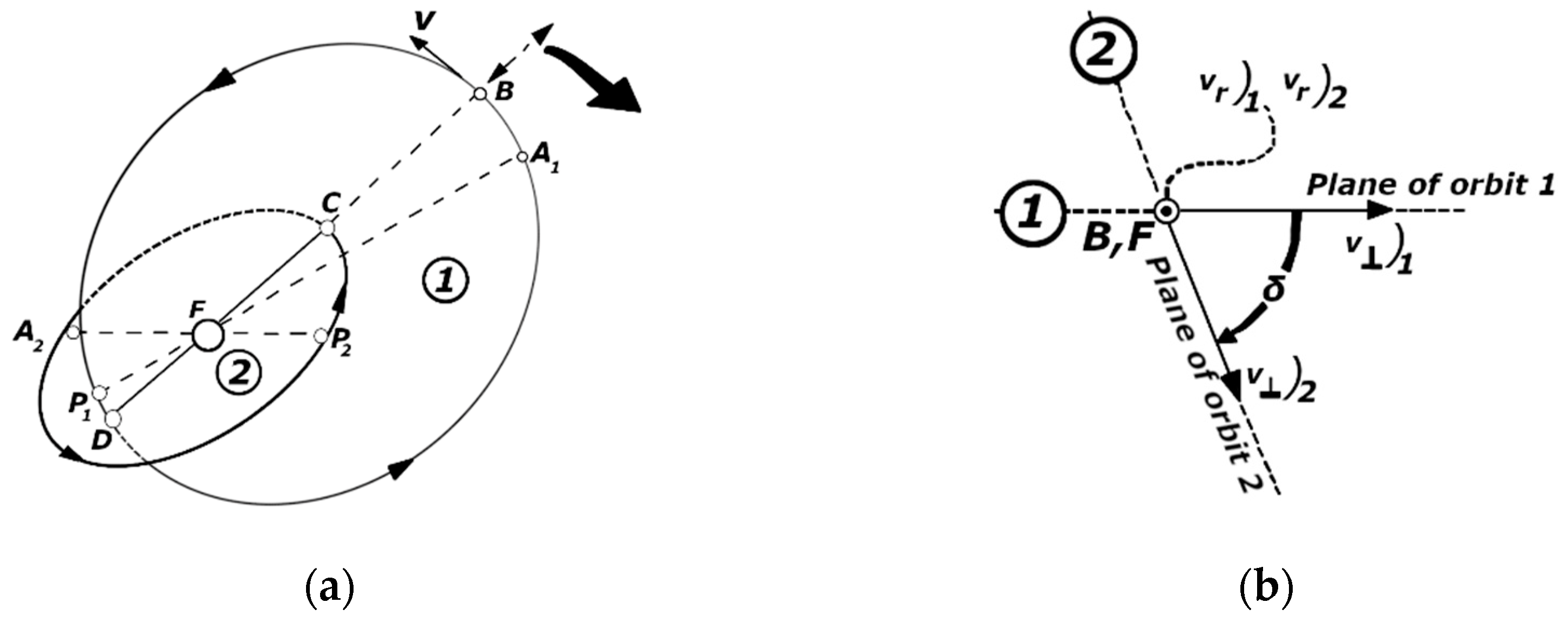
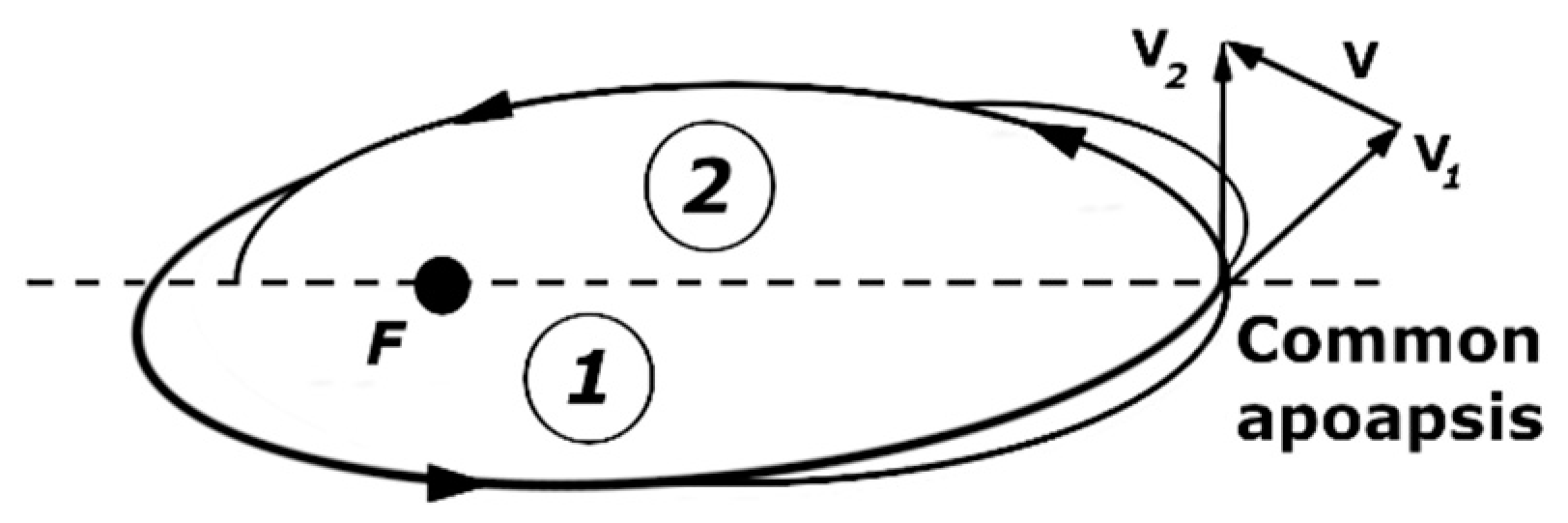
2.2.2. Manoeuvre of Changing the Orbital Plane
- Required change in velocity
- The radial velocity component should remain constant, i.e., ;
- The perpendicular velocity component should be as small as possible.
2.3. Methodology
- Equations used
- Duration of the satellite’s flight over a given area
- Determining the possible change in inclination
- Determination of the weight of fuel necessary to perform the Hohmann transfer
- Calculating the energy required to tilt the satellite
- Presentation of the constant parameters for the analysed manoeuvres
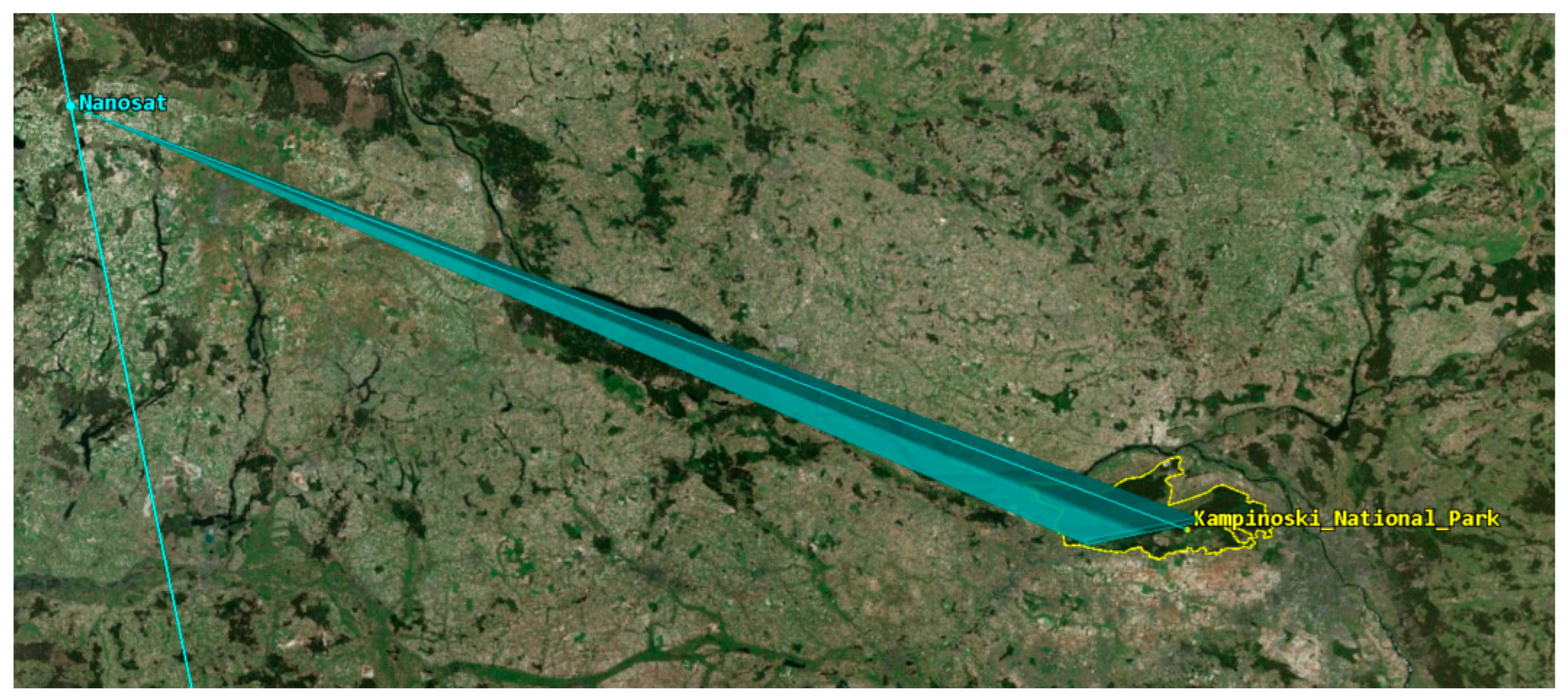
- Duration of the satellite’s flight over a given area
- Case with a variable weight of the satellite
- Case with variable fuel weight
- Determining the possible change in inclination
- Determination of the weight of fuel necessary to perform the Hohmann transfer
- Calculating the energy required to tilt the satellite
3. Results
3.1. Analysis for a Variable Weight of the Satellite
3.2. Analysis for a Variable Weight of Fuel
3.3. Analysis of the Possible Change in Inclination
3.4. Analysis of the Weight of Fuel Necessary to Perform the Hohmann Transfer
3.5. Analysis of the Energy Required to Tilt the Satellite by a Specific Angle
3.6. Selection of the Optimum Nanosatellite Dedicated to Maximise the Specific Operational Task
4. Discussion
4.1. Discussion of the Results of the Analysis for a Variable Weight of the Satellite
- The increase in the weight of the satellite limits the potential increase in orbital velocity, which means that heavier satellites require more efficient propulsion systems or larger amounts of fuel;
- Higher specific impulses result in higher effective exhaust velocity, which improves the efficiency of fuel consumption;
- Heavier satellites require more time to perform the manoeuvres, which may limit the number of operations during the mission and increase the demand for energy;
- The satellite’s mass is positively correlated with observational capability, not directly due to the mass itself, but because of the ability to implement more advanced observation systems (e.g., sensors with greater swath width);
- The sensor’s swath width increases on average by 0.5–1 km for every additional kilogram of the satellite’s mass, reflecting the possibility of installing better optical systems;
- Observation time (pass over the Area of Interest, AOI) increases with swath width and decreases with the rise in orbital velocity, which in turn, depends on orbital altitude;
- The duration of the satellite’s flight over the given area is directly related to the angle of inclination of the trajectory in reference to the equator θ and the swath width L.
4.2. Discussion of the Results of the Analysis for a Variable Fuel Weight
- Higher values of specific impulse and effective exhaust velocity improve the efficiency of propulsion, enabling a larger increase in velocity at lower fuel consumption. This makes it possible to perform more demanding manoeuvres.
- Larger weight of fuel allows to achieve a larger increase in velocity, which is beneficial when planning more demanding changes of the orbit.
- The duration of the manoeuvre increases significantly with the weight of fuel, which may affect planning satellite operations, e.g., the need to store energy and the availability of the propulsion system.
- Selecting the appropriate weight of fuel and specific impulse is crucial for nanosatellite systems, to ensure the maximum efficiency of the mission while complying with energy limitations.
- There is no universally optimal fuel mass. It should be carefully selected based on specific mission requirements, such as the number of planned manoeuvres, the precision of orbital changes, and time constraints.
4.3. Discussion of the Results of the Analysis of the Possible Change in Inclination
- The ability to change orbital inclination is strongly dependent on both fuel mass and specific impulse. Even a slight increase in available ∆v allows for more advanced manoeuvres.
- An increase in specific impulse by 10 s results in an increase in exhaust gas velocity by approximately 85 , improving fuel utilisation efficiency.
- Even small changes in inclination (≈0.5–0.8°) may significantly influence the coverage of the target area.
- A longer duration of flight over the given area may be beneficial for observation missions, but it requires more precise manoeuvres.
- The optimum orbit should take into account the compromise between the amount of fuel, efficiency of the manoeuvre, and the required duration of the flight over the area.
4.4. Discussion of the Results of the Analysis of the Weight of Fuel Necessary to Perform the Hohmann Transfer
- The weight of the necessary fuel increases with the increase in the initial weight of the satellite. Heavier satellites require more fuel to generate the same increase in velocity.
- Higher specific impulse leads to a reduction in the required amount of fuel. This results from a higher effective exhaust velocity, which improves the efficiency of the thruster.
- Higher effective exhaust velocity leads to a reduction in the required amount of fuel.
- The value of the total increase in velocity remains constant, regardless of the weight of the satellite or other parameters, since it is determined by the geometry and altitude of the orbits.
- Higher values of specific impulse lead to a significant reduction in the required amount of fuel; an increase in specific impulse by 10 s allows for a reduction in fuel demand by approximately 15 g, which is essential for missions with limited weight resources, such as nanosatellites.
- The optimum choice for satellites weighing up to 15 kg are propulsion systems with a high specific impulse to minimise the weight of fuel.
4.5. Discussion of the Comparative Analysis of Hohmann Transfers and Inclination Change Maneuvers in Terms of Energy Requirements and Mission Efficiency
4.6. Discussion of the Results of the Analysis of the Energy Required to Tilt the Satellite by a Specific Angle
- The analysis revealed that the power system of the nanosatellite with the selected parameters is suitable for performing short tilt manoeuvres. Thanks to the high charging power of the solar panels equal to 70 W, energy recovery time is less than 0.04 s; the satellite is able to quickly recover the energy required for further manoeuvres.
- Assuming that regular tilt manoeuvres of a maximum angle of 30° are performed, the satellite may perform these operations with a minimum influence on the availability of power, which is crucial for missions that require a large number of spot observations. Reaction manoeuvres using the reaction wheels are highly energy-efficient; even a full assumed pivot (30°) requires only 2.7 J.
- The results of the analysis suggest that the M6P satellite may be used in intensive observational operations, such as the monitoring of selected areas of the Earth, without the risk of running out of energy. The short charging time after each manoeuvre allows to increase the frequency of operational activities.
4.7. Discussion of the Results of the Selection of the Optimum Nanosatellite Dedicated to Maximise the Specific Operational Task
- Although heavier satellites offer more advanced functional capabilities, their fuel requirements are increasing. Based on the data analysis, one may assume that the optimum configuration is a satellite weighing 5 kg. This range of weight ensures a proper balance between the capacity and orbital stability, while, at the same time, enabling the installation of an advanced sensor.
- The specific impulse of 220 s guarantees high fuel efficiency with moderate technical requirements. Higher values of the specific impulse might reduce fuel consumption, yet they are less cost-efficient for satellites in this weight category.
- The weight of fuel of 0.5 kg is perfectly suitable for missions lasting up to six months, provided that the amount of fuel spent on manoeuvres to adjust the orbit is moderate. This amount allows six manoeuvres to be performed, increasing the altitude of the orbit by 643 m, which effectively prevents orbit degradation.
- The drag force increases in proportion to the face area, which in turn, scales with the mass of the satellite. The frontal surface of 0.02 m2 that is determined by the satellite’s dimensions minimises the influence of drag, which translates into lower energy losses and a more stable trajectory.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roshan, S.; Raunak, S.; Kaushik, D. Constellation Design of Remote Sensing Small Satellite for Infrastructure Monitoring in India. arXiv 2021, arXiv:2107.09253. [Google Scholar]
- Luo, Q.; Peng, W.; Wu, G.; Xiao, Y. Orbital Maneuver Optimization of Earth Observation Satellites Using an Adaptive Differential Evolution Algorithm. Remote Sens. 2022, 14, 1966. [Google Scholar] [CrossRef]
- Banks, B.A.; Miller, S.K.; de Groh, K.K. Low Earth Orbital Atomic Oxygen Interactions with Materials. MRS Proc. 2004, 851, 426–437. [Google Scholar] [CrossRef]
- It’s Some Kind of Space. Available online: https://www.youtube.com/watch?v=DvO3FLcLC88&t=1360s (accessed on 17 January 2024).
- Nunes Vaz, B.; Bertachini De Almeida Prado, A.F. Sub-Optimal Orbital Maneuvers for Artificial Satellites. WSEAS Trans. Appl. Theor. Mech. 2008, 3, 769. Available online: https://www.wseas.us/e-library/transactions/mechanics/2008/28-469.pdf (accessed on 10 January 2025).
- Butikov, E.I. Orbital maneuvers and space rendezvous. Adv. Space Res. 2015, 56, 2582–2594. [Google Scholar] [CrossRef]
- Curtis, H.D. Orbital Mechanics for Engineering Students, 4th ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Chen, Y.; Mahalec, V.; Chen, Y.; He, R.; Liu, X. Optimal Satellite Orbit Design for Prioritized Multiple Targets with Threshold Observation Time Using Self-Adaptive Differential Evolution. J. Aerosp. Eng. 2015, 28, 04014066. [Google Scholar] [CrossRef]
- Savitri, T.; Kim, Y.; Jo, S.; Bang, H. Satellite Constellation Orbit Design Optimization with Combined Genetic Algorithm and Semianalytical Approach. Int. J. Aerosp. Eng. 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- Sengupta, P.; Vadali, S.R.; Alfriend, K.T. Satellite Orbit Design and Maintenance for Terrestrial Coverage. J. Spacecr. Rocket. 2010, 47, 177–187. [Google Scholar] [CrossRef]
- Graham, K.F.; Rao, A.V. Minimum-Time Trajectory Optimization of Low-Thrust Earth-Orbit Transfers with Eclipsing. J. Spacecr. Rocket. 2016, 53, 289–303. [Google Scholar] [CrossRef]
- Zhang, C.; Topputo, F.; Bernelli-Zazzera, F.; Zhao, Y.S. Low-Thrust Minimum-Fuel Optimization in the Circular Restricted Three-Body Problem. J. Guid. Control. Dyn. 2015, 38, 1501–1510. [Google Scholar] [CrossRef]
- Wang, Z.; Grant, M.J. Optimization of Minimum-Time Low-Thrust Transfers Using Convex Programming. J. Spacecr. Rocket. 2017, 55, 586–598. [Google Scholar] [CrossRef]
- Sadegh Mohammadi, M.; Naghash, A. Robust optimization of impulsive orbit transfers under actuation uncertainties. Aerosp. Sci. Technol. 2019, 85, 246–258. [Google Scholar] [CrossRef]
- Morante, D.; Sanjurjo-Rivo, M.; Soler, M.; Sánchez-Pérez, J.M. Hybrid multi-objective orbit-raising optimization with operational constraints. Acta Astronaut. 2020, 175, 447–461. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, Z.; Jiang, F.; Zhou, C. Real-Time Optimal Control for Spacecraft Orbit Transfer via Multiscale Deep Neural Networks. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 2436–2450. [Google Scholar] [CrossRef]
- Song, Z.; Chen, X.; Luo, X.; Wang, M.; Dai, G. Multi-objective optimization of agile satellite orbit design. Adv. Space Res. 2018, 62, 3053–3064. [Google Scholar] [CrossRef]
- Appel, L.; Guelman, M.; Mishne, D. Optimization of satellite constellation reconfiguration maneuvers. Acta Astronaut. 2014, 99, 166–174. [Google Scholar] [CrossRef]
- Paek, S.W.; Kim, S.; de Weck, O. Optimization of Reconfigurable Satellite Constellations Using Simulated Annealing and Genetic Algorithm. Sensors 2019, 19, 765. [Google Scholar] [CrossRef]
- Sarno, S.; Guo, J.; D’Errico, M.; Gill, E. A guidance approach to satellite formation reconfiguration based on convex optimization and genetic algorithms. Adv. Space Res. 2020, 65, 2003–2017. [Google Scholar] [CrossRef]
- He, X.; Li, H.; Yang, L.; Zhao, J. Reconfigurable Satellite Constellation Design for Disaster Monitoring Using Physical Programming. Int. J. Aerosp. Eng. 2020, 2020, 8813685. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Bai, S.; Yue, Y. Design of agile satellite constellation based on hybrid-resampling particle swarm optimization method. Acta Astronaut. 2021, 178, 595–605. [Google Scholar] [CrossRef]
- Soleymani, M.; Fakoor, M.; Bakhtiari, M. Optimal mission planning of the reconfiguration process of satellite constellations through orbital maneuvers: A novel technical framework. Adv. Space Res. 2019, 63, 3369–3384. [Google Scholar] [CrossRef]
- Hu, J.; Huang, H.; Yang, L.; Zhu, Y. A multi-objective optimization framework of constellation design for emergency observation. Adv. Space Res. 2021, 67, 531–545. [Google Scholar] [CrossRef]
- Bate, R.; Mueller, D.; White, E.; Saylor, W. Fundamentals of Astrodynamics, 2nd ed.; Dover Publications: Garden City, NY, USA, 2020. [Google Scholar]
- Sutton, G.P.; Biblarz, O. Rocket Propulsion Elements, 9th ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Wertz, J.R. Mission Geometry; Orbit and Constellation Design and Management: Spacecraft Orbit and Attitude Systems; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Wertz, J.R.; Larson, W.J. Space Mission Analysis and Design, 3rd ed.; Space Technology Library; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- MultiScape100 CIS Product. Available online: https://simera-sense.com/products/multiscape100/ (accessed on 15 June 2024).
- CubeSat 6U CubeSat/ Nanosatellite M6P. Available online: https://nanoavionics.com/small-satellite-buses/6u-cubesat-nanosatellite-m6p/ (accessed on 6 October 2024).
- Sentinel-2 Operations. Available online: https://www.esa.int/Enabling_Support/Operations/Sentinel-2_operations (accessed on 10 January 2025).
- Successful Demonstration of Polish Missile Technologies. Flight of the ILR-33 “Amber” Missile”. Available online: https://ilot.lukasiewicz.gov.pl/udana-demonstracja-polskich-technologii-rakietowych-lot-rakiety-ilr-33-bursztyn/ (accessed on 10 January 2025).
- Why Do Starlink Satellites Use Krypton for Electric Propulsion Instead of Xenon? Available online: https://chimniii.com/news/Technology/Technology-Starlink-why-do-starlink-satellites-use-krypton-for-electric-propulsion-instead-of-xenon.html (accessed on 10 January 2025).
- Ruggiero, A.; Pergola, S.; Marcuccio, S.; Andrenucci, M. Low-Thrust Maneuvers for the Efficient Correction of Orbital Elements, IEPC-2011-102. In Proceedings of the 32nd International Electric Propulsion Conference, Wiesbaden, Germany, 11–15 September 2011. [Google Scholar]
- Derfel, G. From Orbit to Orbit, Institute of Physics, Lodz University of Technology. Available online: https://www.deltami.edu.pl/media/articles/2020/08/delta-2020-08-z-orbity-na-orbite.pdf (accessed on 13 January 2025).
- Michael, J.R.; Perkins, J. SpaceX Rocket Data Satisfies Elementary Hohmann Transfer Formula. Phys. Educ. 2020, 55, 025011. [Google Scholar]

| Parameter | Value | Unit |
|---|---|---|
| GSD at the altitude of 500 km | 4.75 | m |
| Swath width at the altitude of 500 km | 19.4 | km |
| Number of channels in the VNIR band | 7 | - |
| Spectral range | 450–900 | nm |
| Number of pixels | 4096 | pix |
| Pixel size | 5.5 | µm |
| Sensor type | “pushbroom” | - |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Fuel weight | mf | 0.5 | [kg] |
| Orbit altitude | h | 482 | [km] |
| Acceleration of gravity | g | 8.49 | |
| Orbital velocity | vo | 7.8 | |
| Thrust force | F | 1 | [N] |
| Weight of the fuel consumed to conduct the manoeuvre | mfspent | 0.5 | [kg] |
| Angle of inclination of the trajectory in reference to the equator at the orbit inclination of 97° | θ | 0.655 | [rad] |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Initial weight of the satellite | mp | 15 | [kg] |
| Orbit altitude | h | 482 | [km] |
| Acceleration of gravity | g | 8.49 | |
| Orbital velocity | vo | 7.8 | |
| Thrust force | F | 1 | [N] |
| Swath width | L | 19.4 | [km] |
| Angle of inclination of the trajectory in reference to the equator at the orbit inclination of 97° | θ | 0.655 | [rad] |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Initial inclination of the orbit | ip | 97 | [°] |
| Orbit altitude | h | 482 | [km] |
| Acceleration of gravity | g | 8.49 | |
| Orbital velocity | vo | 7.8 | ] |
| Thrust force | F | 1 | [N] |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Initial orbit altitude | hp | 482 | [km] |
| Target orbit altitude | hd | 550 | [km] |
| Radius of the Earth | RZ | 6371 | [km] |
| Acceleration of gravity | g | 8.49 | [] |
| Gravitational constant | G | 6.674 × 10−11 | [] |
| Weight of the Earth | MZ | 5.972 × 1024 | [kg] |
| Initial radius of the orbit | rp | 6853 | [km] |
| Target radius of the orbit | rd | 6921 | [km] |
| Velocity on the initial orbit | vp | 7626.45 | [] |
| Velocity on the target orbit | vd | 7588.89 | [] |
| Semi-major axis | a | 6887 | [km] |
| Velocity on the transfer orbit in perigee | vtp | 7645.25 | [] |
| Velocity on the transfer orbit in apogee | vta | 7570.14 | [] |
| First increase in velocity | ∆v1 | 18.80 | [] |
| Second increase in velocity | ∆v2 | 18.76 | [] |
| Total increase in velocity | Δvtotal | 37.56 | [] |
| Orbital velocity | vo | 7.8 | [] |
| Thrust force | F | 1 | [N] |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Weight of the satellite without fuel | ms | 4.5 | [kg] |
| Fuel weight | mf | 0.5 | [kg] |
| Weight of the satellite with fuel | msf | 5 | [kg] |
| Satellite size along the x axis | - | 0.1 | [m] |
| Satellite size along the y axis | - | 0.2 | [m] |
| Satellite size along the x axis | - | 0.3 | [m] |
| Moment of inertia | Iz | 0.021 | [kg·m2] |
| Slew rate | - | 5 | [°] |
| Power consumption in the stable state (1000 RPM) | P | 0.45 | [W] |
| Charging power of the solar panels | Pł | 70 | [W] |
| Initial Weight of the Satellite mp [kg] | End Weight of the Satellite mk [kg] | Specific Impulse Isp [s] | Effective Exhaust Velocity | Increase in Velocity | Impulse Duration t [s] | Swath Width L [km] | Duration of the Satellite’s Flight over the Area of Interest T [s] |
|---|---|---|---|---|---|---|---|
| 8 | 7.5 | 180 | 1528.20 | 98.63 | 764.10 | 15.0 | 2.44 |
| 9 | 8.5 | 190 | 1613.10 | 92.20 | 806.55 | 16.0 | 2.61 |
| 10 | 9.5 | 200 | 1698.00 | 87.10 | 849.00 | 17.0 | 2.77 |
| 11 | 10.5 | 210 | 1782.90 | 82.94 | 891.45 | 17.5 | 2.85 |
| 12 | 11.5 | 215 | 1825.35 | 77.69 | 912.67 | 18.0 | 2.93 |
| 13 | 12.5 | 220 | 1867.80 | 73.26 | 933.90 | 18.5 | 3.01 |
| 14 | 13.5 | 225 | 1910.25 | 69.47 | 955.13 | 19.0 | 3.10 |
| 15 | 14.5 | 230 | 1952.70 | 66.20 | 976.35 | 19.4 | 3.16 |
| 16 | 15.5 | 235 | 1995.15 | 63.34 | 997.58 | 19.8 | 3.23 |
| 17 | 16.5 | 240 | 2037.60 | 60.83 | 1018.80 | 20.2 | 3.29 |
| 18 | 17.5 | 250 | 2122.50 | 59.79 | 1061.25 | 21.0 | 3.42 |
| End Weight of the Satellite mk [kg] | Fuel Weight mf [kg] | Specific Impulse Isp [s] | Effective Exhaust Velocity | Increase in Velocity | Weight of Fuel Spent to Perform the Manoeuvre mfspent [kg] | Duration of the Impulse t [s] | Duration of the Satellite’s Flight over the Area of Interest T [s] |
|---|---|---|---|---|---|---|---|
| 14.70 | 0.30 | 200 | 1698.00 | 34.30 | 0.30 | 509.40 | 3.16 |
| 14.65 | 0.35 | 210 | 1782.90 | 42.09 | 0.35 | 624.01 | 3.16 |
| 14.60 | 0.40 | 215 | 1825.35 | 49.34 | 0.40 | 730.14 | 3.16 |
| 14.55 | 0.45 | 218 | 1850.82 | 56.37 | 0.45 | 832.87 | 3.16 |
| 14.50 | 0.50 | 220 | 1867.80 | 63.32 | 0.50 | 933.90 | 3.16 |
| 14.45 | 0.55 | 225 | 1910.25 | 71.36 | 0.55 | 1050.64 | 3.16 |
| 14.40 | 0.60 | 230 | 1952.70 | 79.71 | 0.60 | 1171.62 | 3.16 |
| 14.35 | 0.65 | 235 | 1995.15 | 88.39 | 0.65 | 1296.85 | 3.16 |
| 14.30 | 0.70 | 240 | 2037.60 | 97.38 | 0.70 | 1426.32 | 3.16 |
| Initial Weight of the Satellite mp [kg] | End Weight of the Satellite mk [kg] | Weight of Fuel mf [kg] | Specific Impulse Isp [s] | Effective Exhaust Velocity | Increase in Velocity | Possible Change in Inclination im [rad] | Possible Change in Inclination im2 [°] | Target Inclination id [rad] | Target Inclination id2 [°] | Inclination of the Trajectory in Reference to the Equator After the Manoeuvre θm [rad] | Swath Width L [km] | Duration of the Satellite’s Flight over the Area of Interest T [s] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 7.50 | 0.50 | 180 | 1528.20 | 98.63 | 0.013 | 0.72 | 1.680 | 96.28 | 0.752 | 15.0 | 2.63 |
| 9 | 8.50 | 0.50 | 190 | 1613.10 | 92.20 | 0.012 | 0.68 | 1.681 | 96.32 | 0.775 | 16.0 | 2.87 |
| 10 | 9.50 | 0.50 | 200 | 1698.00 | 87.10 | 0.011 | 0.64 | 1.682 | 96.36 | 0.797 | 17.0 | 3.12 |
| 11 | 10.50 | 0.50 | 210 | 1782.90 | 82.94 | 0.011 | 0.61 | 1.682 | 96.39 | 0.817 | 17.5 | 3.28 |
| 12 | 11.50 | 0.50 | 215 | 1825.35 | 77.69 | 0.010 | 0.57 | 1.683 | 96.43 | 0.845 | 18.0 | 3.48 |
| 13 | 12.50 | 0.50 | 220 | 1867.80 | 73.26 | 0.009 | 0.54 | 1.684 | 96.46 | 0.873 | 18.5 | 3.69 |
| 14 | 13.50 | 0.50 | 225 | 1910.25 | 69.47 | 0.009 | 0.51 | 1.684 | 96.49 | 0.899 | 19.0 | 3.91 |
| 15 | 14.50 | 0.50 | 230 | 1952.70 | 66.20 | 0.008 | 0.49 | 1.684 | 96.51 | 0.924 | 19.4 | 4.13 |
| 16 | 15.50 | 0.50 | 235 | 1995.15 | 63.34 | 0.008 | 0.47 | 1.685 | 96.53 | 0.949 | 19.8 | 4.36 |
| 17 | 16.50 | 0.50 | 240 | 2037.60 | 60.83 | 0.008 | 0.45 | 1.685 | 96.55 | 0.972 | 20.2 | 4.59 |
| 18 | 17.50 | 0.50 | 250 | 2122.50 | 59.79 | 0.008 | 0.44 | 1.685 | 96.56 | 0.982 | 21.0 | 4.85 |
| 15 | 14.65 | 0.35 | 210 | 1782.90 | 42.09 | 0.005 | 0.31 | 1.688 | 96.69 | 1.263 | 19.4 | 8.22 |
| 15 | 14.60 | 0.40 | 215 | 1825.35 | 49.34 | 0.006 | 0.36 | 1.687 | 96.64 | 1.114 | 19.4 | 5.64 |
| 15 | 14.55 | 0.45 | 218 | 1850.82 | 56.37 | 0.007 | 0.41 | 1.686 | 96.59 | 1.019 | 19.4 | 4.74 |
| 15 | 14.50 | 0.50 | 220 | 1867.80 | 63.32 | 0.008 | 0.47 | 1.685 | 96.53 | 0.949 | 19.4 | 4.27 |
| 15 | 14.45 | 0.55 | 225 | 1910.25 | 71.36 | 0.009 | 0.52 | 1.684 | 96.48 | 0.886 | 19.4 | 3.93 |
| 15 | 14.40 | 0.60 | 230 | 1952.70 | 79.71 | 0.010 | 0.59 | 1.683 | 96.41 | 0.834 | 19.4 | 3.70 |
| 15 | 14.35 | 0.65 | 235 | 1995.15 | 88.39 | 0.011 | 0.65 | 1.682 | 96.35 | 0.791 | 19.4 | 3.54 |
| 15 | 14.30 | 0.70 | 240 | 2037.60 | 97.38 | 0.012 | 0.72 | 1.680 | 96.28 | 0.756 | 19.4 | 3.42 |
| Initial Weight of the Satellite mp [kg] | Specific Impulse Isp [s] | Effective Exhaust Velocity | Fuel Weight Required mtotal [kg] |
|---|---|---|---|
| 8 | 180 | 1527.69 | 0.194 |
| 9 | 190 | 1612.57 | 0.207 |
| 10 | 200 | 1697.44 | 0.219 |
| 11 | 210 | 1782.31 | 0.229 |
| 12 | 215 | 1824.75 | 0.244 |
| 13 | 220 | 1867.18 | 0.259 |
| 14 | 225 | 1909.62 | 0.273 |
| 15 | 230 | 1952.05 | 0.286 |
| 16 | 235 | 1994.49 | 0.298 |
| 17 | 240 | 2036.93 | 0.311 |
| 18 | 250 | 2121.80 | 0.316 |
| 15 | 200 | 1697.44 | 0.328 |
| 15 | 210 | 1782.31 | 0.313 |
| 15 | 215 | 1824.75 | 0.306 |
| 15 | 218 | 1850.21 | 0.301 |
| 15 | 220 | 1867.18 | 0.299 |
| 15 | 225 | 1909.62 | 0.292 |
| 15 | 230 | 1952.05 | 0.286 |
| 15 | 235 | 1994.49 | 0.280 |
| 15 | 240 | 2036.93 | 0.274 |
| Tilt Angle Δθ [°] | Duration of the Manoeuvre t [s] | Energy Consumed by Reaction Wheels E [J] | Charging Time tł [s] |
|---|---|---|---|
| 1 | 0.20 | 0.09 | 0.00129 |
| 2 | 0.40 | 0.18 | 0.00257 |
| 3 | 0.60 | 0.27 | 0.00386 |
| 4 | 0.80 | 0.36 | 0.00514 |
| 5 | 1.00 | 0.45 | 0.00643 |
| 6 | 1.20 | 0.54 | 0.00771 |
| 7 | 1.40 | 0.63 | 0.00900 |
| 8 | 1.60 | 0.72 | 0.01029 |
| 9 | 1.80 | 0.81 | 0.01157 |
| 10 | 2.00 | 0.90 | 0.01286 |
| 11 | 2.20 | 0.99 | 0.01414 |
| 12 | 2.40 | 1.08 | 0.01543 |
| 13 | 2.60 | 1.17 | 0.01671 |
| 14 | 2.80 | 1.26 | 0.01800 |
| 15 | 3.00 | 1.35 | 0.01929 |
| 16 | 3.20 | 1.44 | 0.02057 |
| 17 | 3.40 | 1.53 | 0.02186 |
| 18 | 3.60 | 1.62 | 0.02314 |
| 19 | 3.80 | 1.71 | 0.02443 |
| 20 | 4.00 | 1.80 | 0.02571 |
| 21 | 4.20 | 1.89 | 0.02700 |
| 22 | 4.40 | 1.98 | 0.02829 |
| 23 | 4.60 | 2.07 | 0.02957 |
| 24 | 4.80 | 2.16 | 0.03086 |
| 25 | 5.00 | 2.25 | 0.03214 |
| 26 | 5.20 | 2.34 | 0.03343 |
| 27 | 5.40 | 2.43 | 0.03471 |
| 28 | 5.60 | 2.52 | 0.03600 |
| 29 | 5.80 | 2.61 | 0.03729 |
| 30 | 6.00 | 2.70 | 0.03857 |
| Initial Weight of the Satellite mp [kg] | Fuel Weight mf [kg] | Specific Impulse Isp [s] | Frontal Surface of the Satellite A [m2] | Drag Force FD [N] | Loss of Orbital Energy ΔE [J] | Drop in Altitude in One Month ∆h [m] | Total Drop in Altitude in Six Months ∆htotal [m] | Required Weight of Fuel Δm [kg] | Total Required Weight of Fuel Δmtotal [kg] |
|---|---|---|---|---|---|---|---|---|---|
| 8 | 0.50 | 180 | 0.02 | 0.00000135 | 27,306.86 | −402 | −2412 | 0.050 | 0.301 |
| 9 | 0.50 | 190 | 0.02 | 0.00000135 | 27,306.86 | −357 | −2144 | 0.053 | 0.321 |
| 10 | 0.50 | 200 | 0.02 | 0.00000135 | 27,306.86 | −322 | −1930 | 0.056 | 0.338 |
| 11 | 0.50 | 210 | 0.03 | 0.00000203 | 40,960.29 | −439 | −2632 | 0.059 | 0.355 |
| 12 | 0.50 | 215 | 0.03 | 0.00000203 | 40,960.29 | −402 | −2412 | 0.063 | 0.378 |
| 13 | 0.50 | 220 | 0.03 | 0.00000203 | 40,960.29 | −371 | −2227 | 0.067 | 0.400 |
| 14 | 0.50 | 225 | 0.03 | 0.00000203 | 40,960.29 | −345 | −2068 | 0.070 | 0.421 |
| 15 | 0.50 | 230 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.074 | 0.442 |
| 16 | 0.50 | 235 | 0.04 | 0.00000270 | 54,613.72 | −402 | −2412 | 0.077 | 0.461 |
| 17 | 0.50 | 240 | 0.04 | 0.00000270 | 54,613.72 | −378 | −2270 | 0.080 | 0.480 |
| 18 | 0.50 | 250 | 0.04 | 0.00000270 | 54,613.72 | −357 | −2144 | 0.081 | 0.488 |
| 15 | 0.30 | 200 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.085 | 0.508 |
| 15 | 0.35 | 210 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.081 | 0.483 |
| 15 | 0.40 | 215 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.079 | 0.472 |
| 15 | 0.45 | 218 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.078 | 0.466 |
| 15 | 0.50 | 220 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.077 | 0.462 |
| 15 | 0.55 | 225 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.075 | 0.451 |
| 15 | 0.60 | 230 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.074 | 0.442 |
| 15 | 0.65 | 235 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.072 | 0.432 |
| 15 | 0.70 | 240 | 0.03 | 0.00000203 | 40,960.29 | −322 | −1930 | 0.071 | 0.423 |
| 5 | 0.50 | 220 | 0.02 | 0.00000135 | 27,306.86 | −643 | −3860 | 0.026 | 0.154 |
| Type of Orbital Manoeuvre | Demand for Speed Change | Impact on Flight Time and AOI | Flexibility of Land Cover | Comments |
|---|---|---|---|---|
| Hohmann manoeuvre (in one plane) | Low () | Slightly extended (due to lower velocity in higher orbit) | Restricted (ground track unchanged) | Simple, energy-efficient, extends observation time |
| Change in inclinations | Very high ( per °) | Varies (depending on direction and extent of change) | High (change in geometry of ground track) | Costly, justified only by the requirements of the specific mission |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewinska, M.; Kedzierski, M. The Analysis of the Possibility to Conduct Orbital Manoeuvres of Nanosatellites in the Context of the Maximisation of a Specific Operational Task. Appl. Sci. 2025, 15, 5360. https://doi.org/10.3390/app15105360
Lewinska M, Kedzierski M. The Analysis of the Possibility to Conduct Orbital Manoeuvres of Nanosatellites in the Context of the Maximisation of a Specific Operational Task. Applied Sciences. 2025; 15(10):5360. https://doi.org/10.3390/app15105360
Chicago/Turabian StyleLewinska, Magdalena, and Michal Kedzierski. 2025. "The Analysis of the Possibility to Conduct Orbital Manoeuvres of Nanosatellites in the Context of the Maximisation of a Specific Operational Task" Applied Sciences 15, no. 10: 5360. https://doi.org/10.3390/app15105360
APA StyleLewinska, M., & Kedzierski, M. (2025). The Analysis of the Possibility to Conduct Orbital Manoeuvres of Nanosatellites in the Context of the Maximisation of a Specific Operational Task. Applied Sciences, 15(10), 5360. https://doi.org/10.3390/app15105360







