Research on Fleet Size of Demand Response Shuttle Bus Based on Minimum Cost Method
Abstract
1. Introduction
2. Cost Model of DRC
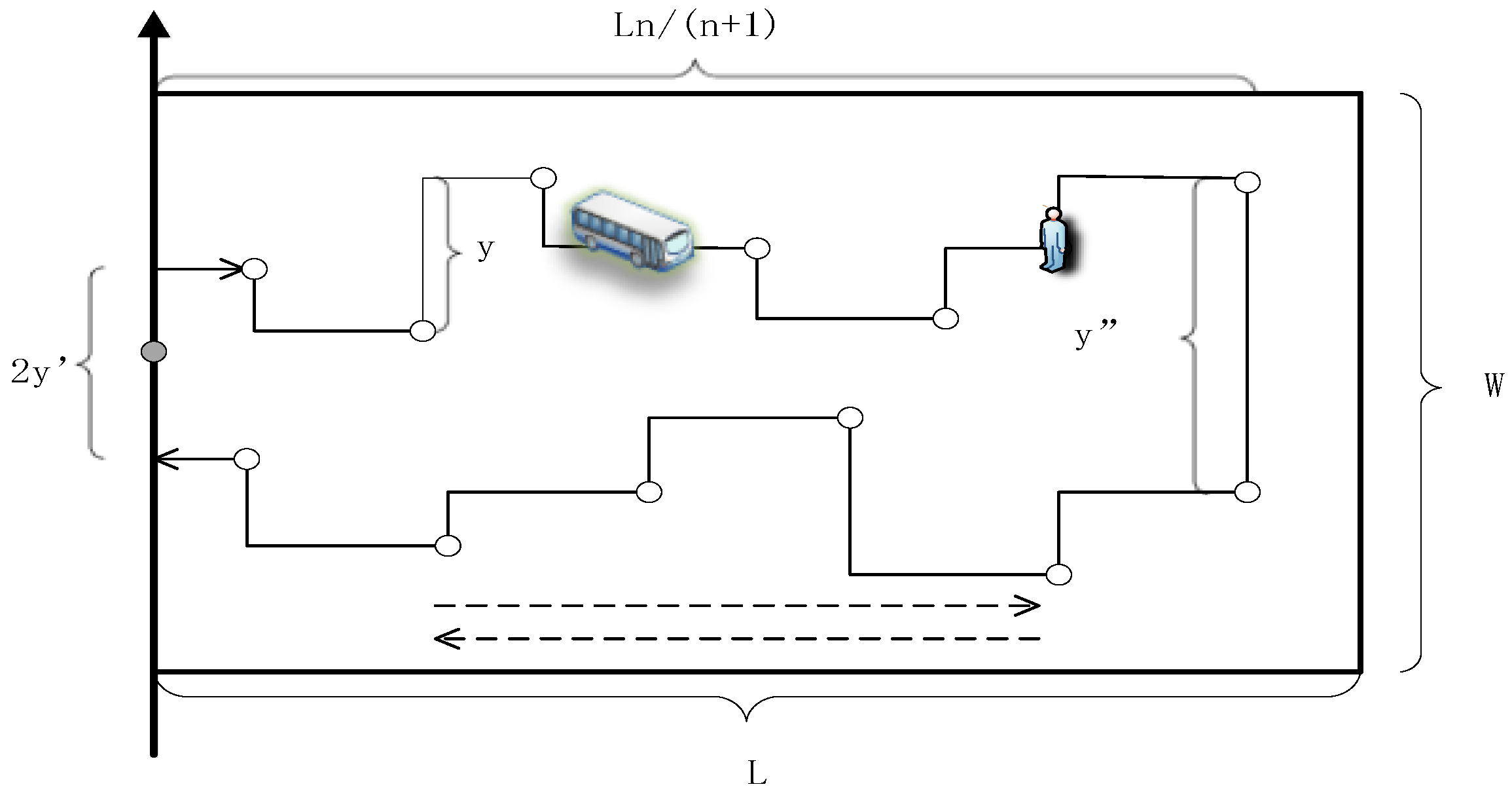
2.1. Assumptions of DRC Vehicle Operation
- (1)
- The service area is a rectangle of length L and width W, with the start and end points located at W/2;
- (2)
- Within the service area, travel demand conforms to a Poisson distribution;
- (3)
- The vehicle maintains a uniform speed and its average operating speed is v;
- (4)
- The boarding and alighting demands of each passenger do not overlap, i.e., the number of stops of the vehicle is equal to the number of traveling demands.
2.2. Definition of Variables
2.3. User Cost Modeling
2.4. Vehicle Operating Cost Modeling
3. Cost-Based Fleet Size Model
4. Numerical Simulation
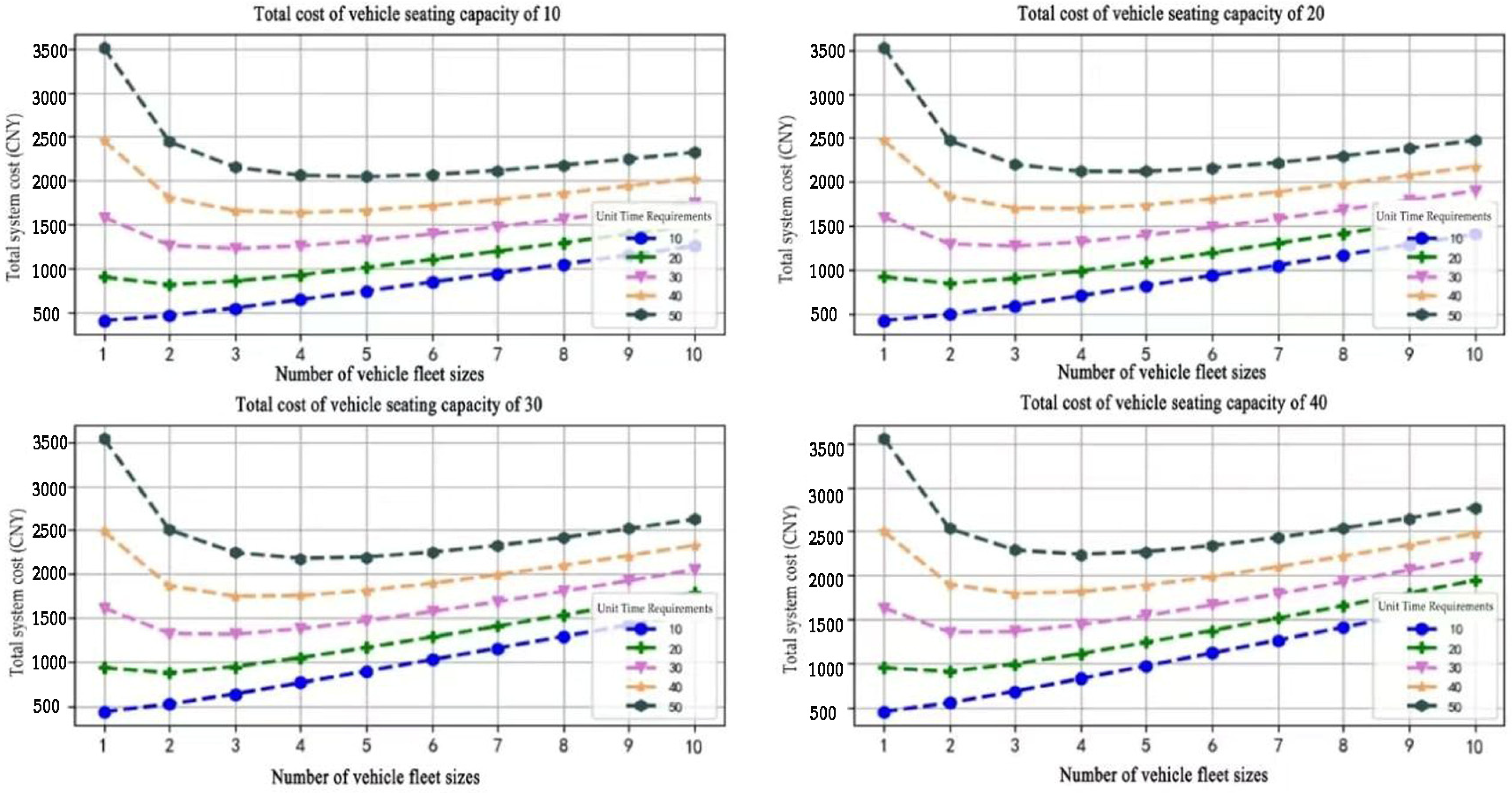
4.1. Overall Simulation Results
4.2. Optimal Fleet Size Analysis
4.3. Impact of Different Fleet Sizes on Operation
4.3.1. Traveling Distance
4.3.2. Average Waiting Time
4.3.3. Average In-Vehicle Time
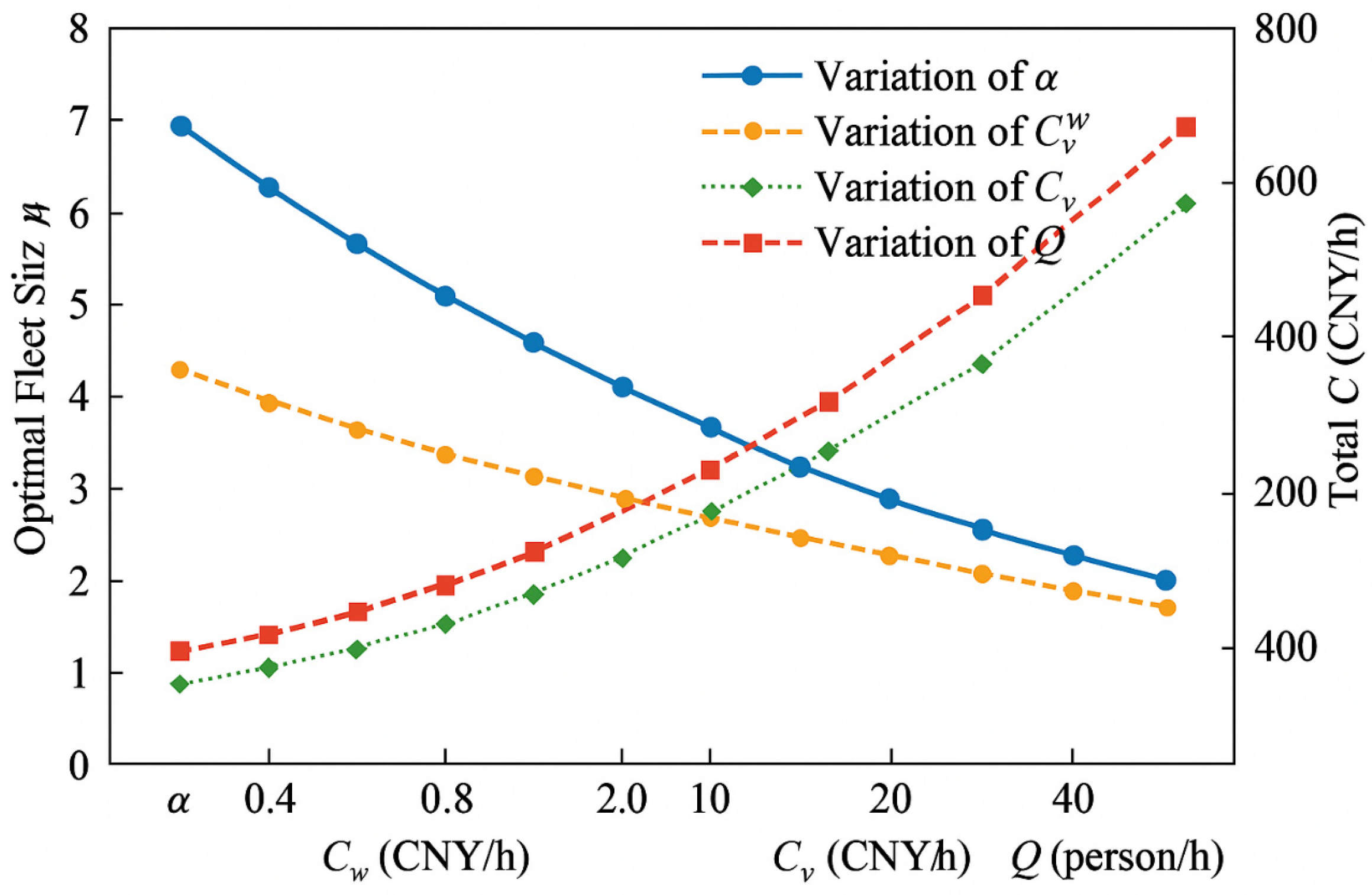
4.4. Analysis of Key Influencing Factors
4.5. Case Illustration: Application Scenario in a City Fringe of Heilongjiang
4.6. Comparison of Different DRC
5. Conclusions
- The study introduces a hybrid optimization approach that integrates both user costs and operational costs, offering an enhancement over traditional fleet allocation strategies, which typically consider only a single perspective.
- The study reveals a linear relationship between the optimal fleet size and demand density, while also examining the effect of vehicle capacity variations on this relationship. These findings possess notable generality and practical applicability.
- The developed model is highly adaptable to various operational scenarios and serves as an effective decision support tool for Demand-Responsive Transit (DRT) systems. It provides quantitative insights that can assist public transportation operators and urban transportation planners in formulating effective scheduling strategies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jokinen, J. Why urban mass demand responsive transport? In Proceedings of the 2011 IEEE Forum on Integrated and Sustainable Transportation Systems, Vienna, Austria, 29 June–1 July 2011; pp. 317–322. [Google Scholar]
- Balac, M. Fleet Sizing for Pooled (Automated) Vehicle Fleets. Transp. Res. Rec. 2020, 2674, 168–176. [Google Scholar] [CrossRef]
- Leich, G.; Bischoff, J. Should autonomous shared taxis replace buses? A simulation study. Transp. Res. Proc. 2019, 41, 450–460. [Google Scholar] [CrossRef]
- Khanal, M. Estimating Demand for a New Travel Mode in Boise, Idaho. Sustainability 2021, 13, 1209. [Google Scholar] [CrossRef]
- Ambrosino, G.; Nelson, J.; Romanazzo, M. Demand Responsive Transport Services: Towards the Flexible Mobility Agency; ENEA, Italian National Agency for New Technologies, Energy and the Sustainable Economic Development: Stockholm, Sweden, 2004. [Google Scholar]
- Avermann, N.; Schlüter, J. Determinants of Customer Satisfaction with a True Door-To-Door Drt Service in Rural Germany. Res. Transp. Bus. Manag. 2019, 32, 100420. [Google Scholar] [CrossRef]
- Berg, J.; Ihlstrom, J. The importance of public transport for mobility and everyday activities among rural residents. Soc. Sci. 2019, 8, 58. [Google Scholar] [CrossRef]
- Boarnet, M.G.; Giuliano, G.; Hou, Y.; Shin, E.J. First/last mile transit access as an equity planning issue. Transp. Res. Pol. Pract. 2017, 103, 296–310. [Google Scholar] [CrossRef]
- Noussan, M.; Tagliapietra, S. The effect of digitalization in the energy consumption of passenger transport: An analysis of future scenarios for Europe. J. Clean. Prod. 2020, 258, 120926. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Cats, O. Public transport planning adaption under the COVID-19 pandemic crisis: Literature review of research needs and directions. Transp. Rev. 2021, 41, 374–392. [Google Scholar] [CrossRef]
- Storme, T.; De Vos, J.; Paepe, L.D.; Witlox, F. Limitations to the car-substitution effect of MaaS. Findings from a Belgian pilot study. Transp. Res. Part A Policy Pract. 2020, 131, 196–205. [Google Scholar] [CrossRef]
- Clewlow, R.R.; Mishra, G.S. Disruptive Transportation: The Adoption, Utilization and Impacts of Ride-Hailing in the United States; Research Report UCD-ITS-RR-17-07; University of California. Institute of Transportation Studies: Davis, CA, USA, 2017. [Google Scholar]
- Davison, L.; Enoch, M.; Ryley, T.; Quddus, M.; Wang, C. Identifying potential market niches for demand responsive transport. Res. Transp. Bus. Manag. 2012, 3, 50–61. [Google Scholar] [CrossRef]
- Oldfield, R.H.; Bly, P.H. An analytic investigation of optimal bus size. Transp. Res. Part B Methodol. 1988, 22, 319–337. [Google Scholar] [CrossRef]
- Yang, H.; Cherry, C.R.; Zaretzki, R.; Ryerson, M.S.; Liu, X.; Fu, Z. A GIS-based method to identify cost-effective routes for rural deviated fixed route transit. J. Adv. Transp. 2016, 50, 1770–1784. [Google Scholar] [CrossRef]
- Ciaffi, F.; Cipriani, E.; Petrelli, M. Feeder bus network design problem: A new Metaheuristic procedure and real size applications. Procedia-Soc. Behav. Sci. 2012, 54, 798–807. [Google Scholar] [CrossRef]
- Burris, M.; Pendyala, R. Discrete choice models of traveler participation in difierential time of day pricing programs. J. Transp. Policy 2002, 9, 241–251. [Google Scholar] [CrossRef]
- Kaddoura, I.; Kickhöfer, B.; Neumann, A.; Tirachini, A. Optimal public transport pricing: Towards an agent-based marginalsocial cost approach. J. Transp. Econ. Policy 2015, 49, 200–218. [Google Scholar]
- Roson, R. Social cost pricing when public transport is an option value. Innov. Eur. J. Soc. Sci. Res. 2000, 13, 81–94. [Google Scholar] [CrossRef]
- Qiu, C.; Yan, H.; Li, N.; Li, T. The optimal design of Beijing bus fares of transit system. Res. Appl. Econ. 2014, 2, 72–79. [Google Scholar]
- Szeto, W.; Wu, Y. A simultaneous bus route design and frequeney setting problem for Tin Shui Wai, Hong Kong. Eur. J. Oper. Res. 2011, 209, 141–155. [Google Scholar] [CrossRef]
- Zeng, Y.Z.; Ran, B.; Zhang, N.; Yang, X.; Shen, J.J.; Deng, S.J. Optimal pricing and service for the peak-period bus commuting inelicieney of boarding queuing congestion. Sustainability 2018, 10, 3497. [Google Scholar] [CrossRef]
- Wagale, M.; Singh, A.P.; Sarkar, A.K.; Arkatkar, S. Real-time optimal bus scheduling for a city using A DTR model. Procedia-Soc. Behav. Sci. 2013, 104, 845–854. [Google Scholar] [CrossRef]
- Avila, P.; lrarragorri, F.; Caballero, R. A bi-objective model for the integrated frequency-timetabling problem. J. WIT Trans. Built Environ. 2014, 138, 209–219. [Google Scholar]
- Huang, Z.; Gang, R.; Liu, H. Optimizing bus frequencies under uncertain demand: Case study of the transit network in a developing city. Math. Probl. Eng. 2013, 2013, 375084. [Google Scholar] [CrossRef]
- Li, X.; Liao, J.; Wang, T.; Lu, L. Integrated optimization of bus bridging route design and bus resource allocation in response to metro service disruptions. J. Transp. Eng. Part A Syst. 2022, 148, 04022050. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Liu, Z. Terminal-based zonal bus: A novel flexible transit system design and implementation. Expert Syst. Appl. 2024, 238, 121793. [Google Scholar] [CrossRef]
- Emami, B.D.; Zhang, Y.; Khani, A.; Song, Y. Towards an efficient electric bus system: Multi-phase optimization model for incremental electrification of bus network with uncertain energy consumption. Transp. Res. Part C Emerg. Technol. 2025, 173, 105011. [Google Scholar] [CrossRef]
- Yetkin, M.; Augustino, B.; Lamadrid, A.J.; Snyder, L.V. Co-optimizing the smart grid and electric public transit bus system. Optim. Eng. 2024, 25, 2425–2472. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, H. Path-choice-constrained bus bridging design under urban rail transit disruptions. Transp. Res. Part E Logist. Transp. Rev. 2024, 188, 103637. [Google Scholar] [CrossRef]
- Golbabaei, F.; Yigitcanlar, T.; Paz, A.; Bunker, J. Understanding Autonomous Shuttle Adoption Intention: Predictive Power of Pre-Trial Perceptions and Attitudes. Sensors 2022, 22, 9193. [Google Scholar] [CrossRef]
- Qu, B.; Mao, L.; Xu, Z.; Feng, J.; Wang, X. How Many Vehicles Do We Need? Fleet Sizing for Shared Autonomous Vehicles with Ridesharing. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14594–14607. [Google Scholar] [CrossRef]
- Winter, K.; Cats, O.; Correia, G.H.D.; van Arem, B. Designing an Automated Demand-Responsive Transport System Fleet Size and Performance Analysis for a Campus-Train Station Service. Transp. Res. Rec. 2016, 2542, 75–83. [Google Scholar] [CrossRef]
- Quadrifoglio, L.; Dessouky, M. Insertion heuristic for scheduling mobility allowance shuttle transit services: Sensitivity to service area. In Computer-Aided Systems in Public Transport; Springer Series: Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 2007; Volume 600, pp. 419–437. [Google Scholar]
- Quadrifoglio, L.; Dessouky, M. Sensitivity analyses over the service area for mobility allowance shuttle transit (MAST) services. In Computer-Aided Systems in Public Transport; Springer: Berlin/Heidelberg, Germany, 2018; Volume 600, pp. 419–432. [Google Scholar]
- Kim, M.E.; Schonfeld, P.; Kim, E. Switching service types for multi-region bus systems. Transp. Plan. Technol. 2018, 41, 617–643. [Google Scholar] [CrossRef]
- Takeuchi, R.; Okura, I.; Nakamura, F.; Hiraishi, H. Feasibility Study on Demand Responsive Transport Systems (Drts). In Proceedings of the 5th Eastern Asia Society for Transportation Studies Conference, Hokkaido, Japan, 12 November 2003. [Google Scholar]
- Velaga, N.R.; Beecroft, M.; Nelson, J.D.; Corsar, D.; Edwards, P. Transport poverty meets the digital divide: Accessibility and connectivity in rural communities. J. Transp. Geogr. 2012, 21, 102–112. [Google Scholar] [CrossRef]
- Liu, Z.; Shen, J. Regional bus operation bi-level programming model integrating timetabling and vehicle scheduling. Syst. Eng.-Theory Pract. 2007, 27, 135–141. [Google Scholar] [CrossRef]
- Yu, H.; Mu, D. Carbon Emission Research of Beijing Transportation System Based on SD. In Proceedings of the 2016 International Conference on Logistics, Informatics and Service Sciences (LISS), Sydney, Australia, 24–27 July 2016; pp. 1–4. [Google Scholar]
- Wang, L.; Fan, J.; Wang, J.; Zhao, Y.; Li, Z.; Guo, R. Spatio-Temporal Characteristics of the Relationship between Carbon Emissions and Economic Growth in China’s Transportation Industry. Environ. Sci. Pollut. Res. 2020, 27, 32962–32979. [Google Scholar] [CrossRef] [PubMed]
- Shan, Y.; Guan, D.; Zheng, H.; Ou, J.; Li, Y.; Meng, J.; Mi, Z.; Liu, Z.; Zhang, Q. China CO2 Emission Accounts 1997–2015. Sci. Data 2018, 5, 1–14. [Google Scholar] [CrossRef]
- Pan, X.; Wei, Z.; Han, B.; Shahbaz, M. The Heterogeneous Impacts of Interregional Green Technology Spillover on Energy Intensity in China. Energy Econ. 2021, 96, 105133. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, F. An Inquiry into the Characteristics of Carbon Emissions in Inter-Provincial Transportation in China: Aiming to Typological Strategies for Carbon Reduction in Regional Transportation. Land 2024, 13, 15. [Google Scholar] [CrossRef]
- Wang, D.; Han, B. Effects of Indigenous R&D and Foreign Spillover on Energy Intensity in China. J. Renew. Sustain. Energy 2017, 9, 035901. [Google Scholar]

| Symbol | Full Name | Unit |
|---|---|---|
| Q | Demand per hour | person/hour |
| K | Vehicle capacity | seats/vehicle |
| P | Cost coefficient | RMB (yuan)/hour |
| V | Average vehicle speed | km/h |
| L | Length of the service area | km |
| W | Width of the service area | km |
| Proportion of boarding passengers | - | |
| T | Operation cycle time | hours |
| B | Number of vehicles in operation | vehicles |
| f | Frequency of vehicle departures | departures/hour |
| Vehicle utilization rate | - | |
| S | Total distance traveled by a vehicle | km |
| Cu | User cost | RMB (yuan) |
| Co | Operational cost | RMB (yuan) |
| Ct | Total system cost | RMB (yuan) |
| Demand density | person/km2 | |
| Tw | Total waiting time of the passenger | hours |
| Tv | Total in-vehicle time of the passenger | hours |
| Model | Dimension (M) | Rated Passenger Capacity | Fuel Consumption (100 km/L) |
|---|---|---|---|
| SC6608BC5 | 5.99 × 2.12 × 2.665 | 10–19 | 13.4 |
| DD6701K01F | 7.49 × 2.32 × 2.9 | 10–23 | ≤13 |
| XML6602 | 5.99 × 2.28 × 2.85 | 10–19 | ≤12.5 |
| JS6608 | 5.99 × 2.25 × 2.76 | 12–19 | 12 |
| YS6718 | 5.99 × 2.19 × 2.85 | 10–20 | 10 |
| MD6873 | 8.72 × 2.50 × 3.2 | 24–49 | 18 |
| XQ6892SH2 | 8.99 × 2.48 × 3.25 | 33 | 20 |
| L(km) | W(km) | c0 (CNY/h) | c1 (CNY/h/car) | Pw (CNY/h) | Pv (CNY/h) | v (km/h) | tn (h) | ts (h) |
|---|---|---|---|---|---|---|---|---|
| 10 | 5 | 90 | 1.5 | 30 | 10 | 30 | 1/200 | 1/1200 |
| Variable | Maximum Value | Minimum Value | Mean | Median | Standard Deviation |
|---|---|---|---|---|---|
| Traveling distance (km) | 66.71 | 14.45 | 27.55 | 24.89 | 10.13 |
| Average waiting time (h) | 1.68 | 0.61 | 0.78 | 0.70 | 0.21 |
| Average in-vehicle time | 1.12 | 0.40 | 0.52 | 0.47 | 0.14 |
| Total system cost (CNY) | 3560.44 | 408.85 | 1628.62 | 1638.52 | 623.20 |
| Q | k = 10 | k = 20 | k = 30 | k = 40 | ||||
|---|---|---|---|---|---|---|---|---|
| B | minC | B | minC | B | minC | B | minC | |
| 10 | 0.96 | 408.68 | 0.89 | 409.18 | 0.84 | 410.39 | 0.80 | 411.98 |
| 20 | 1.92 | 616.42 | 1.79 | 637.76 | 1.69 | 658.73 | 1.60 | 678.00 |
| 30 | 2.88 | 1220.98 | 2.69 | 1277.04 | 2.53 | 1330.93 | 2.39 | 1379.64 |
| 40 | 3.83 | 1522.29 | 3.58 | 1526.96 | 3.37 | 1626.92 | 3.19 | 1716.86 |
| 50 | 4.79 | 2020.34 | 4.47 | 2087.51 | 4.21 | 2146.70 | 3.99 | 2189.65 |
| B | Q | ||||
|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | |
| 1 | 30.34 | 39.92 | 48.97 | 57.87 | 66.71 |
| 2 | 24.51 | 30.34 | 35.26 | 39.92 | 44.47 |
| 3 | 21.81 | 26.67 | 30.34 | 33.67 | 36.84 |
| 4 | 20.00 | 24.51 | 27.64 | 30.34 | 32.85 |
| 5 | 18.63 | 22.99 | 25.84 | 28.21 | 30.34 |
| 6 | 17.52 | 21.81 | 24.51 | 26.67 | 28.57 |
| B | Q | ||||
|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | |
| 1 | 0.80 | 1.02 | 1.24 | 1.46 | 1.68 |
| 2 | 0.69 | 0.80 | 0.91 | 1.02 | 1.13 |
| 3 | 0.66 | 0.73 | 0.80 | 0.88 | 0.95 |
| 4 | 0.64 | 0.69 | 0.75 | 0.80 | 0.86 |
| 5 | 0.63 | 0.67 | 0.71 | 0.76 | 0.80 |
| 6 | 0.62 | 0.66 | 0.69 | 0.73 | 0.77 |
| B | Q | ||||
|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | |
| 1 | 0.53 | 0.68 | 0.83 | 0.97 | 1.12 |
| 2 | 0.46 | 0.53 | 0.61 | 0.68 | 0.75 |
| 3 | 0.44 | 0.49 | 0.53 | 0.58 | 0.63 |
| 4 | 0.43 | 0.46 | 0.50 | 0.53 | 0.57 |
| 5 | 0.42 | 0.45 | 0.48 | 0.51 | 0.53 |
| 6 | 0.41 | 0.44 | 0.46 | 0.49 | 0.51 |
| Q | k = 10 | k = 20 | k = 30 | k = 40 | ||||
|---|---|---|---|---|---|---|---|---|
| B | minC | B | minC | B | minC | B | minC | |
| 10 | 0.96 | 408.68 | 0.89 | 409.18 | 0.84 | 410.39 | 0.80 | 411.98 |
| 20 | 1.92 | 916.42 | 1.79 | 937.76 | 1.69 | 958.73 | 1.60 | 978.00 |
| 30 | 2.88 | 1620.98 | 2.69 | 1677.04 | 2.53 | 1730.93 | 2.39 | 1779.64 |
| 40 | 3.83 | 2522.29 | 3.58 | 2626.96 | 3.37 | 2726.92 | 3.19 | 2816.86 |
| 50 | 4.79 | 3620.34 | 4.47 | 3787.51 | 4.21 | 3946.70 | 3.99 | 4089.65 |
| Mode Type | Key Features | Advantages | Limitations | Suitable Scenarios |
|---|---|---|---|---|
| order-bus | Passengers reserve departure time and stop in advance | Reduces idle operation | Poor responsiveness | Medium- to low-density areas with regular commuting demand |
| dial-a-ride, | Passengers request door-to-door service via phone or app | High flexibility | High dispatching cost | Medical trips, elderly communities, small zones |
| microtransit | Small vehicles with flexible routing; complements transit | Urban supplement to conventional transit | Limited capacity | Urban sub-centers and transit hub catchment areas |
| Connector-Type DRC | Real-time response | Flexible service | Requires well-planned transfer points and smart routing | Urban fringes and suburban areas connecting to trunk lines |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Zu, Y. Research on Fleet Size of Demand Response Shuttle Bus Based on Minimum Cost Method. Appl. Sci. 2025, 15, 5350. https://doi.org/10.3390/app15105350
Sun X, Zu Y. Research on Fleet Size of Demand Response Shuttle Bus Based on Minimum Cost Method. Applied Sciences. 2025; 15(10):5350. https://doi.org/10.3390/app15105350
Chicago/Turabian StyleSun, Xianglong, and Yucong Zu. 2025. "Research on Fleet Size of Demand Response Shuttle Bus Based on Minimum Cost Method" Applied Sciences 15, no. 10: 5350. https://doi.org/10.3390/app15105350
APA StyleSun, X., & Zu, Y. (2025). Research on Fleet Size of Demand Response Shuttle Bus Based on Minimum Cost Method. Applied Sciences, 15(10), 5350. https://doi.org/10.3390/app15105350






