Research on Dynamic Modeling and Vibration Characterization of Integrated Bearings
Abstract
1. Dynamic Modeling of Integrated Bearing Systems
1.1. Specialized Structure of Integrated Bearings
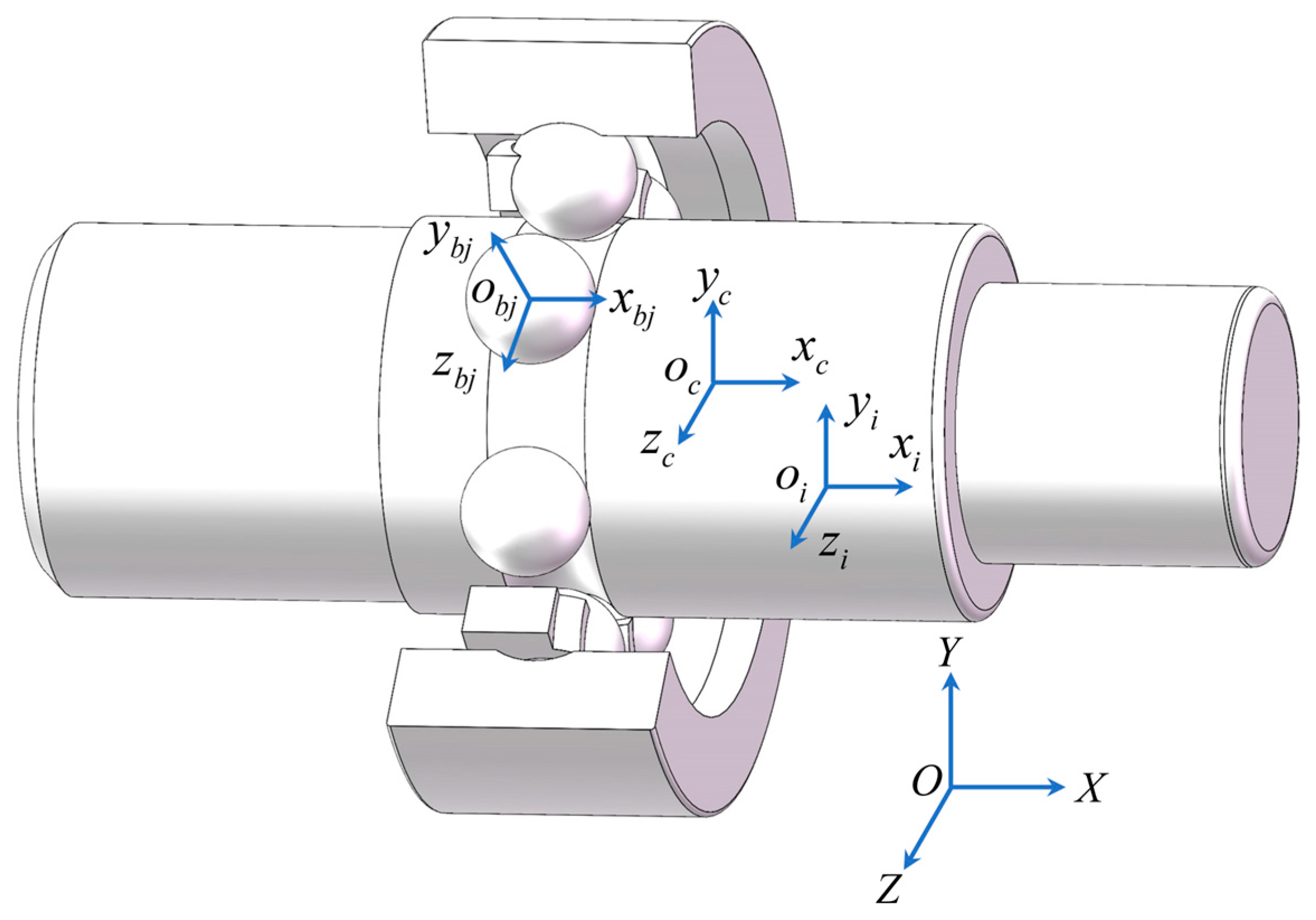
1.2. Coordinate System of Integrated Bearings
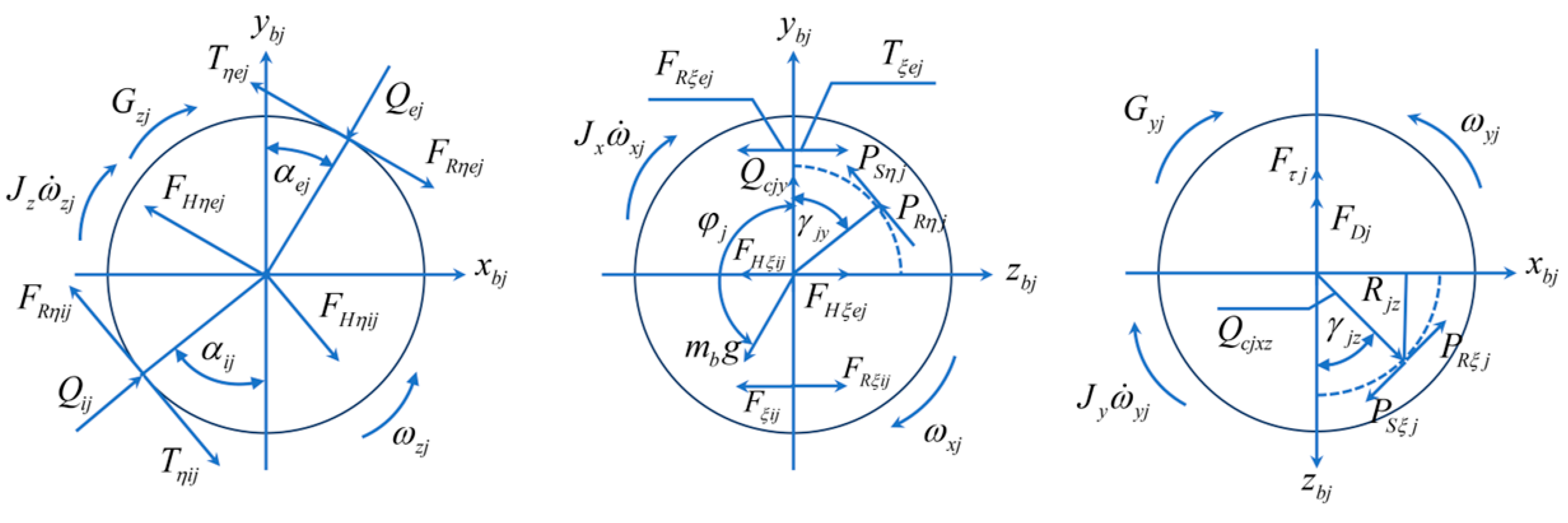
1.3. Dynamical Differential Equations of Balls
1.4. Dynamical Differential Equations of Cage
1.5. Dynamical Differential Equations of Spindle
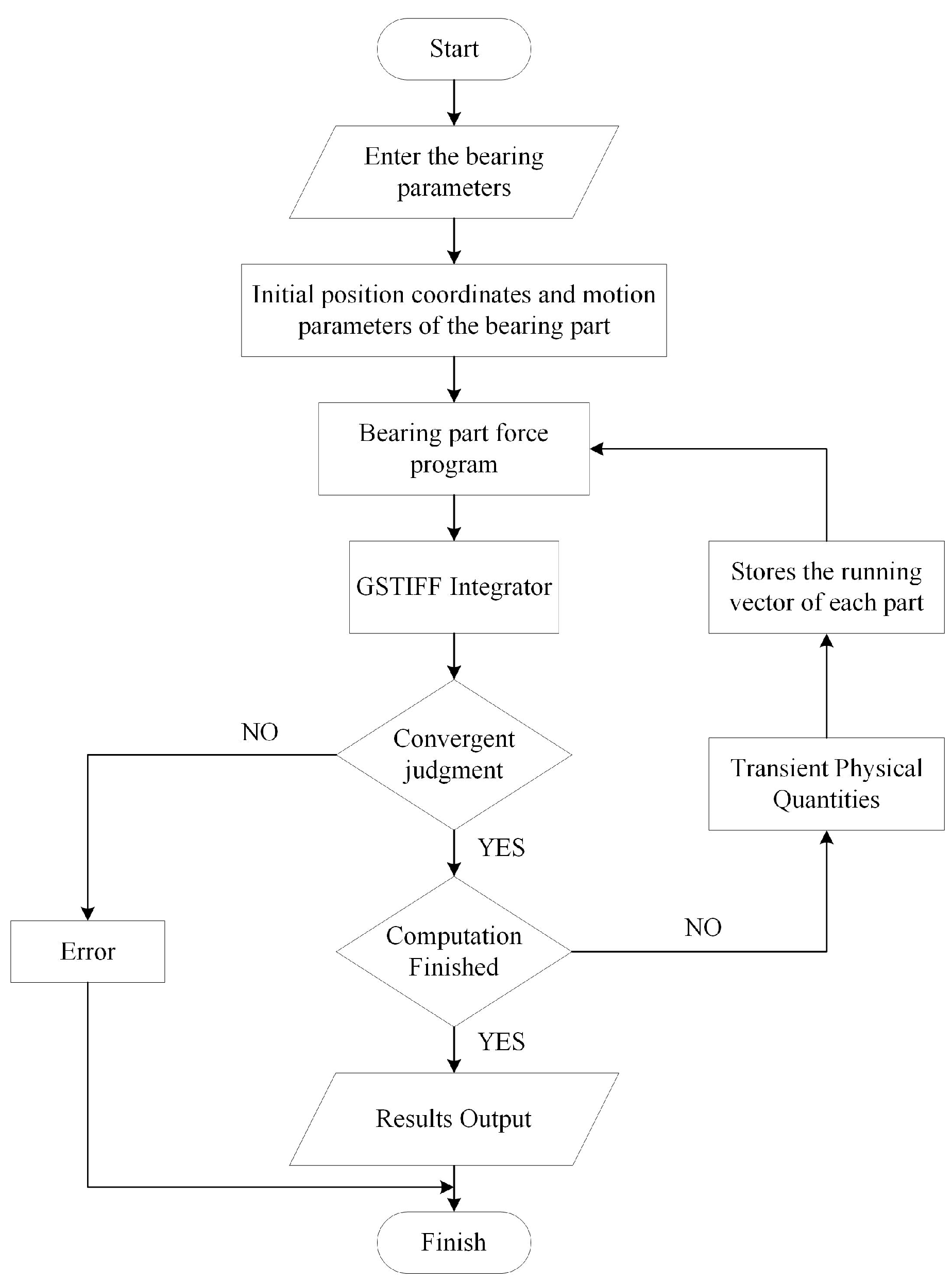
1.6. Solution Process of the System of Dynamical Differential Equations
2. Integrated Bearing Dynamic Performance Analysis
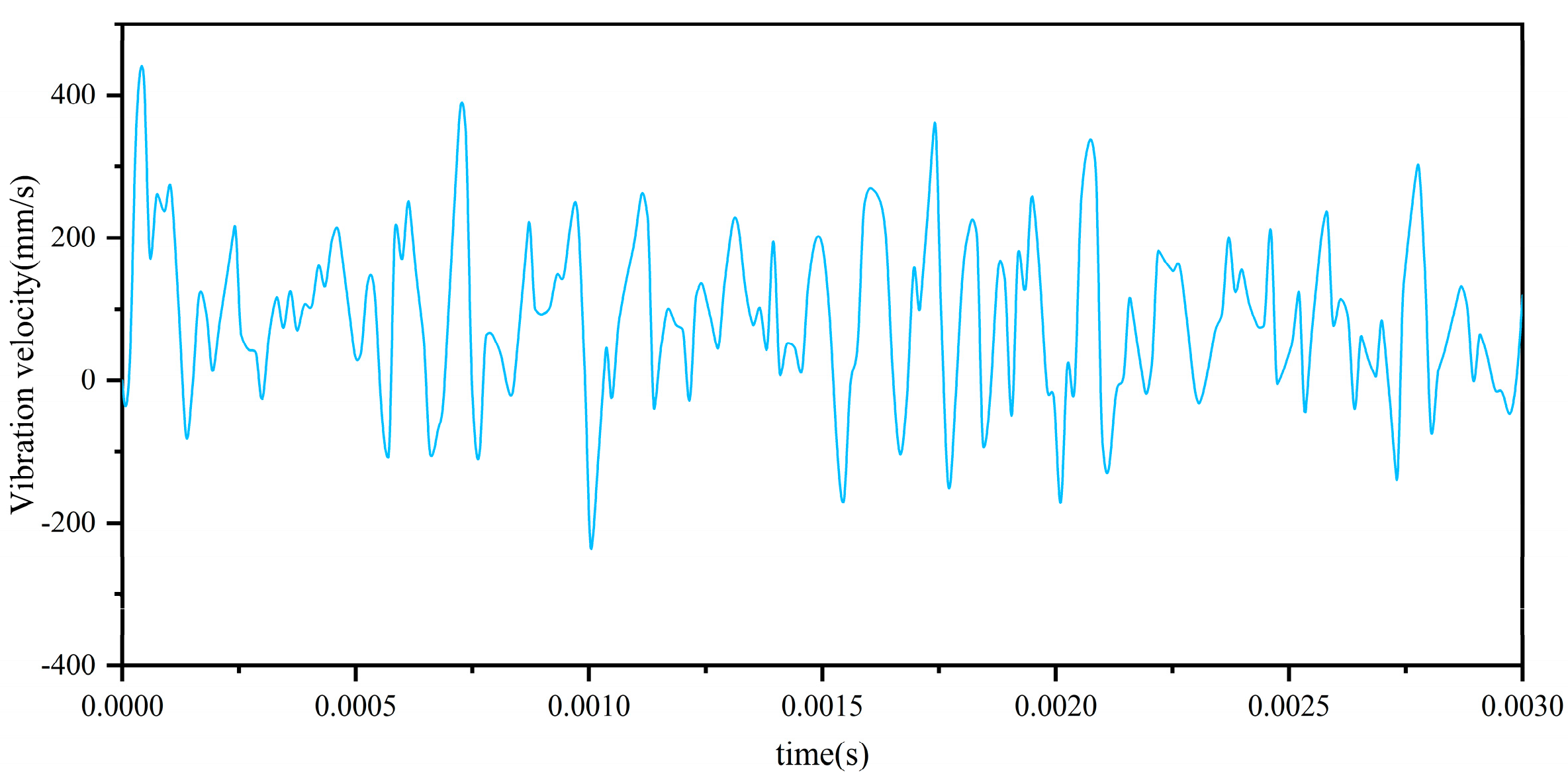
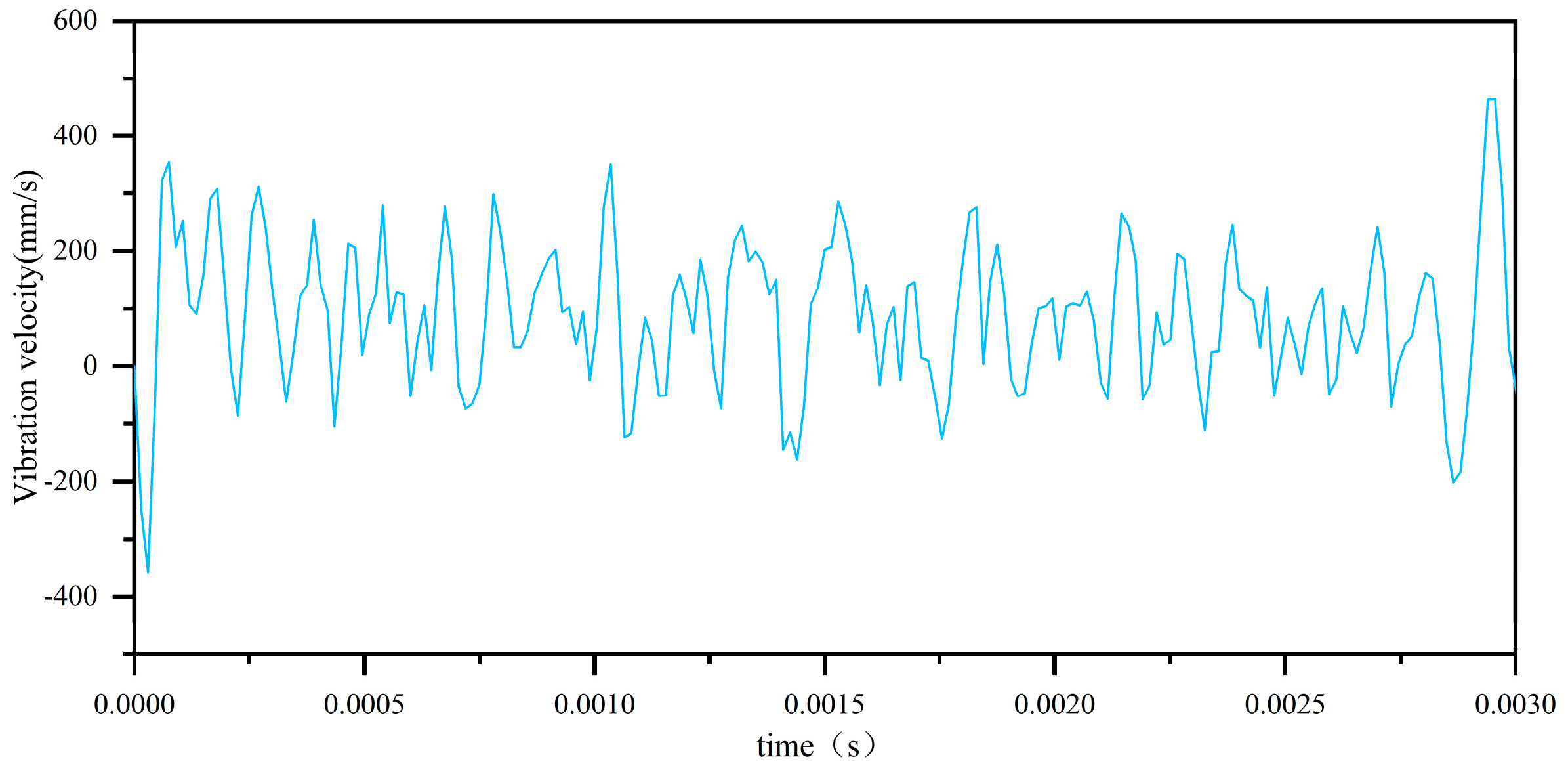
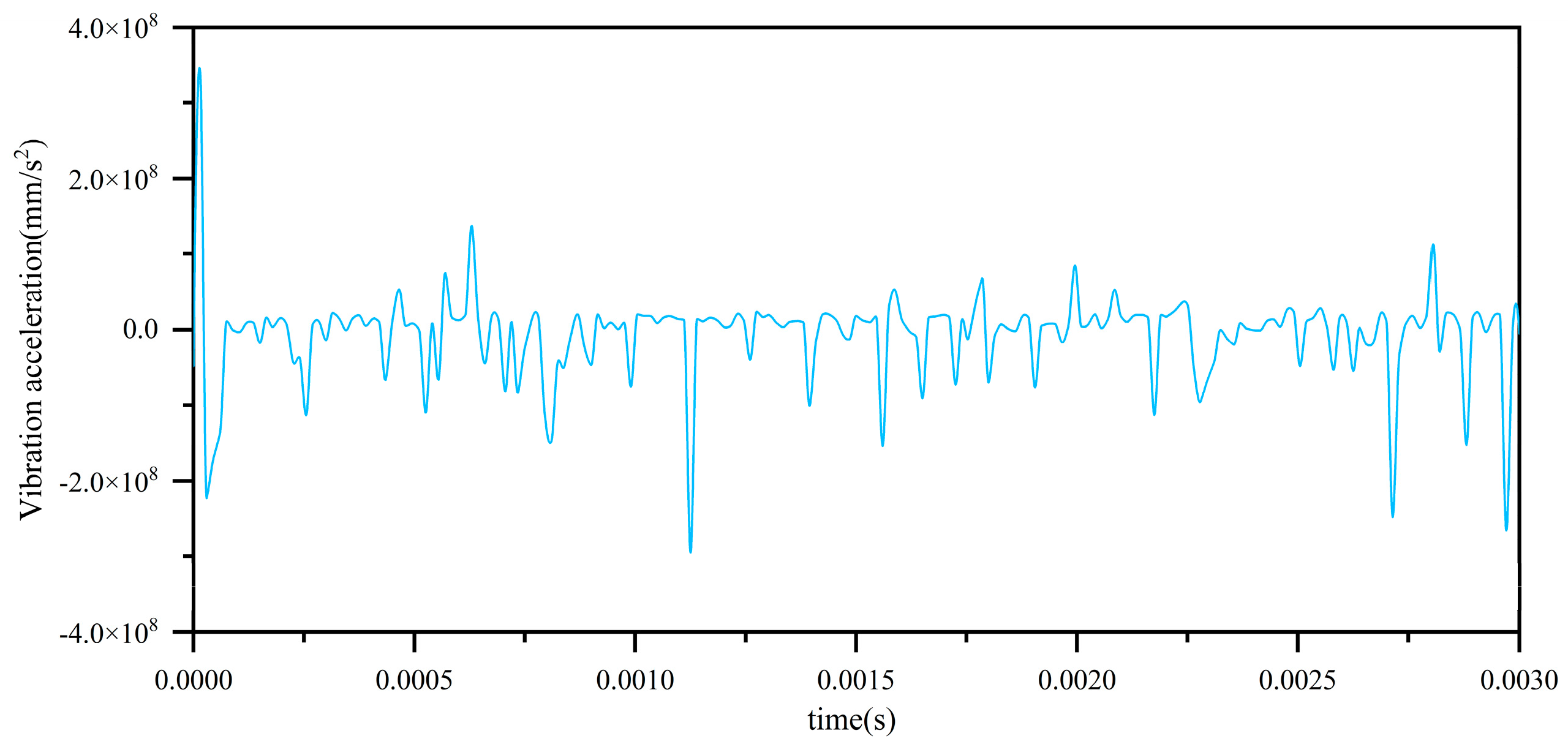
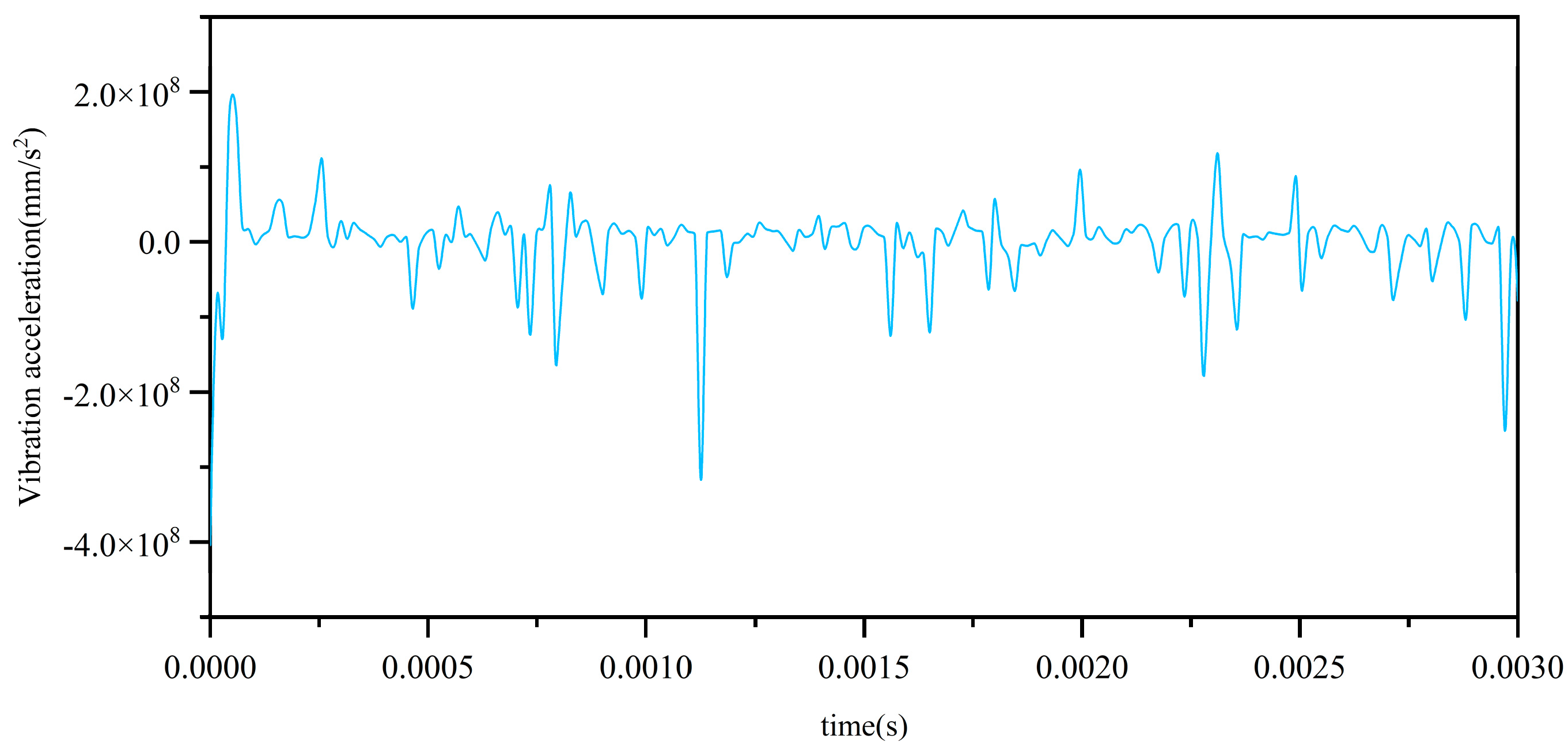
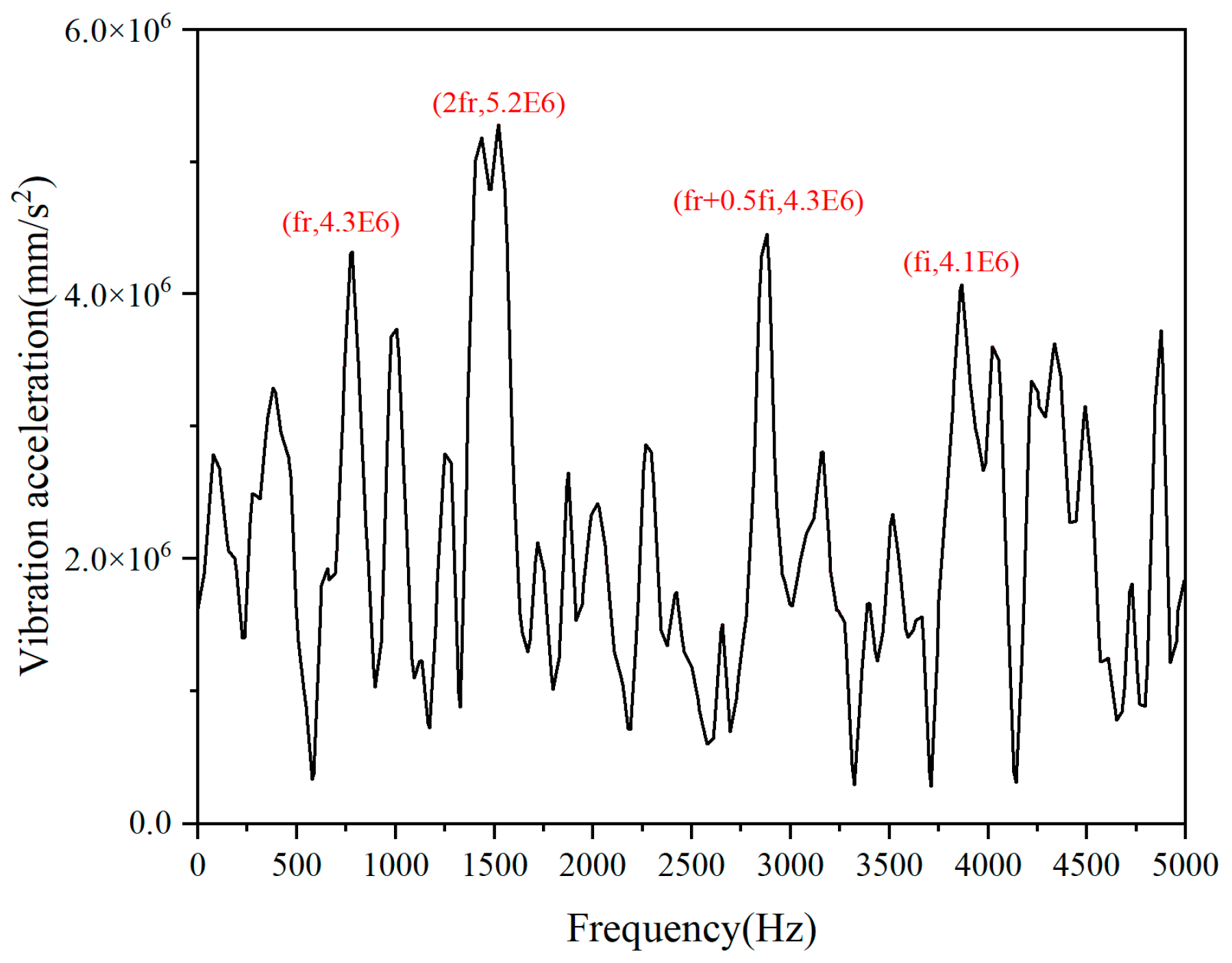
2.1. Results of the Integrated Bearing Dynamics Model
2.2. Influence of Structural Parameters on Vibration in Integrated Bearings
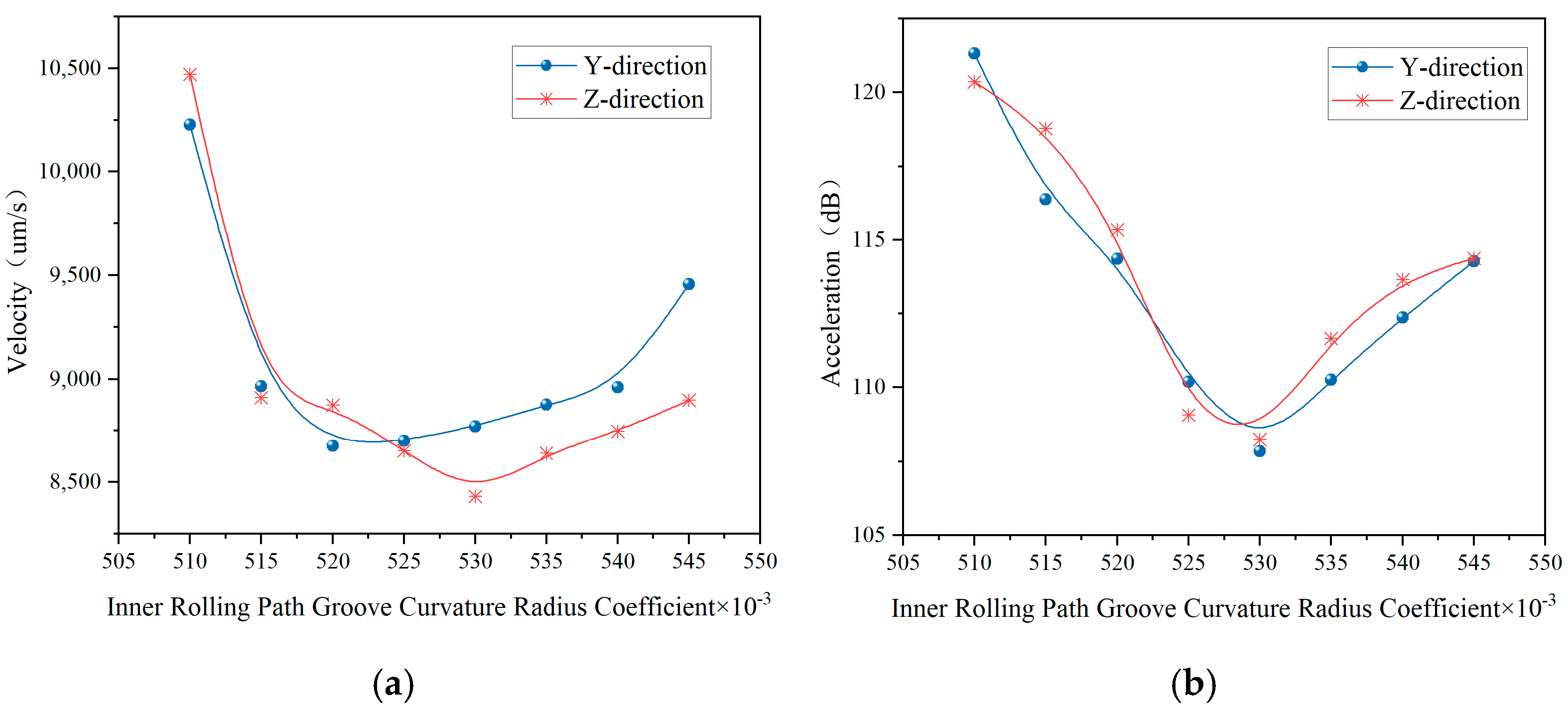
2.2.1. Influence of Inner Groove Curvature Radius Coefficients on Vibration Value
2.2.2. Influence of Outer Groove Curvature Radius Coefficients on Vibration Value
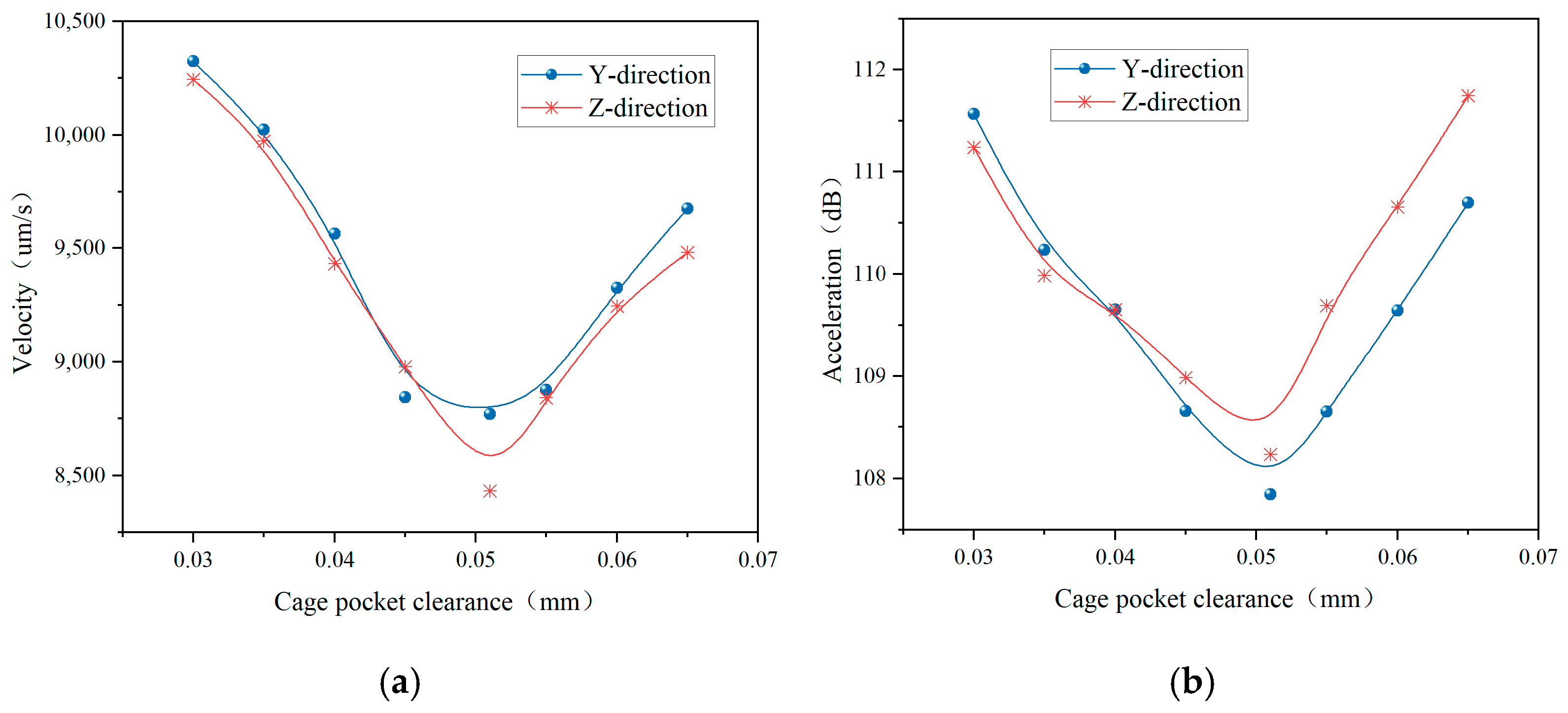
2.2.3. Effect of Cage Pocket Clearance on Vibration of Integrated Bearings
2.3. Impact of Operating Conditions on Vibration of Integrated Bearings
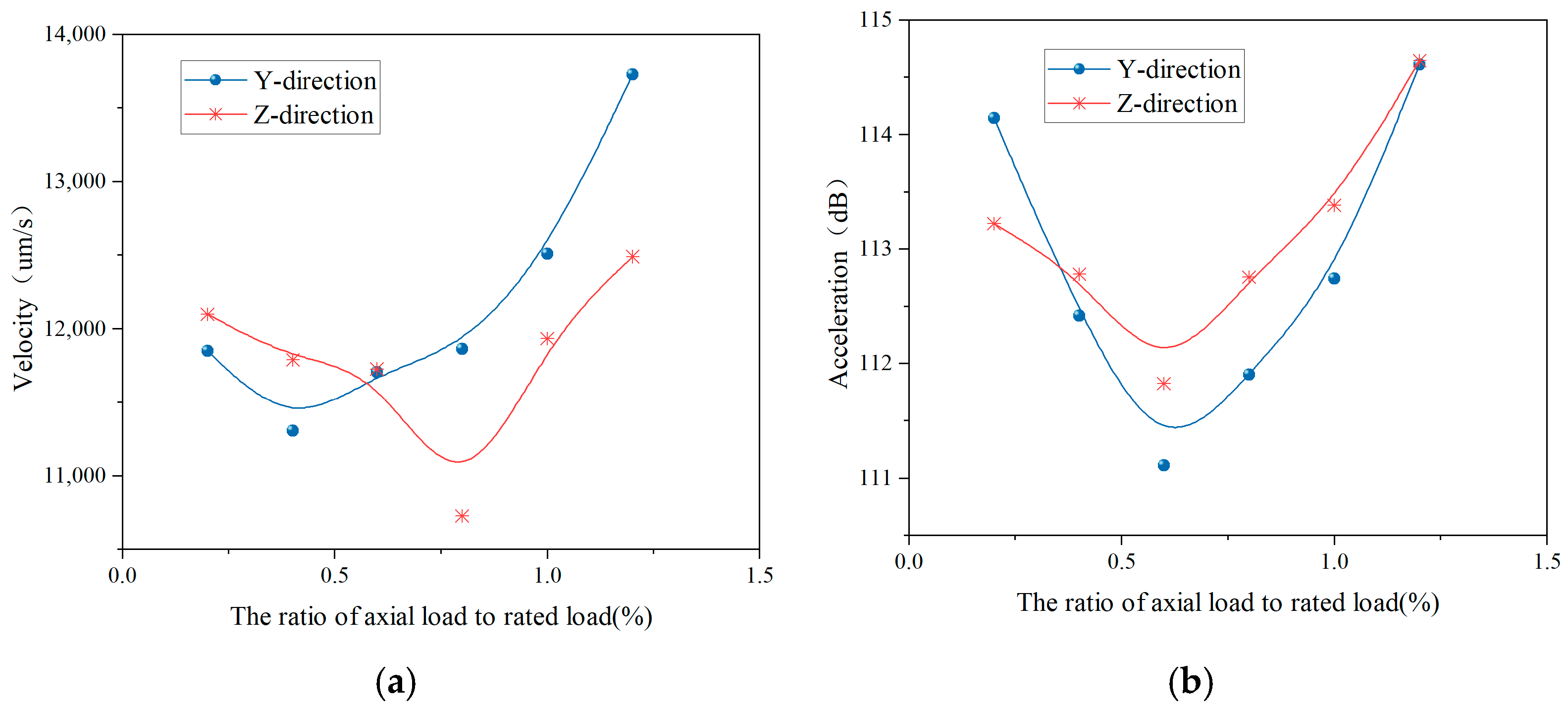
2.3.1. Impact of Axial Preload on the Vibration of Integrated Bearings
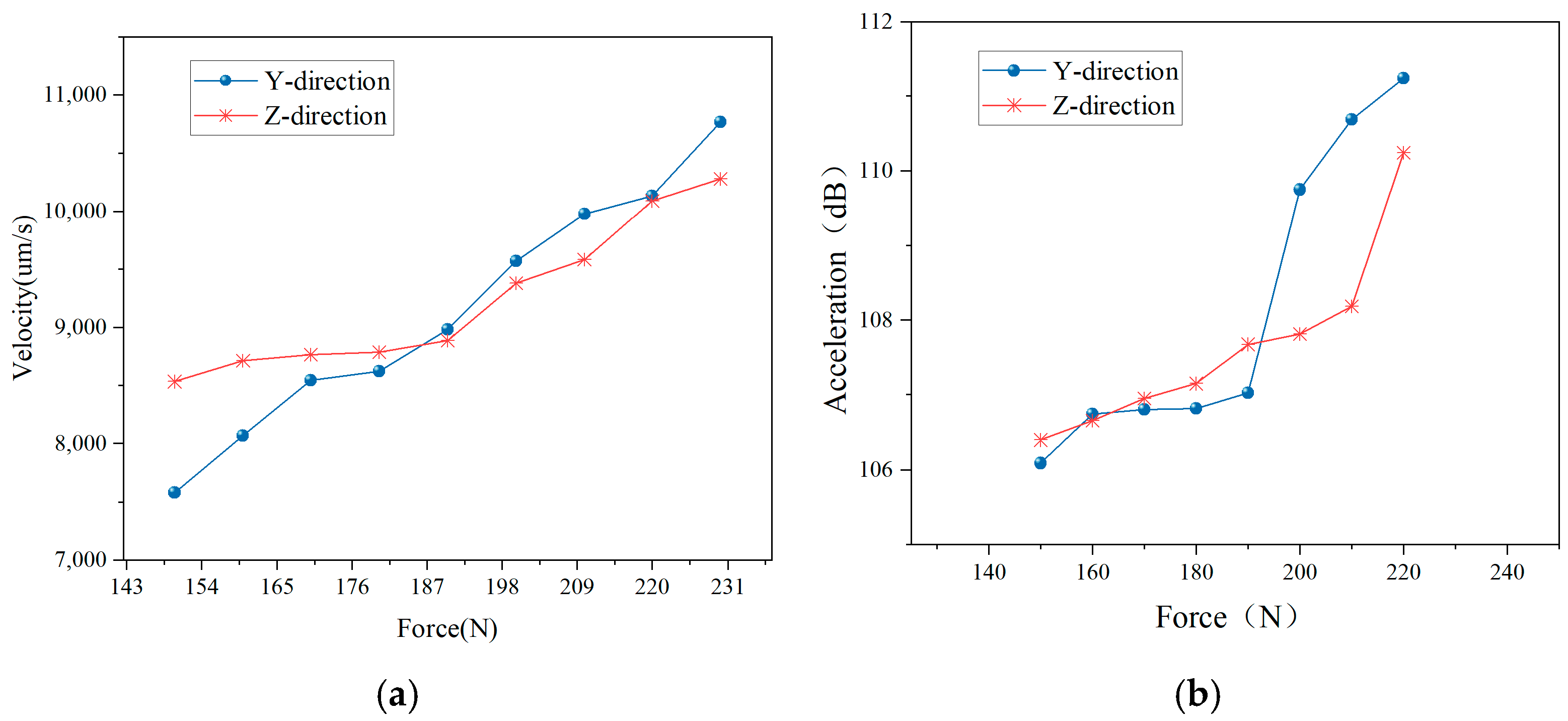
2.3.2. Impact of Radial Load on the Vibration of Integrated Bearings
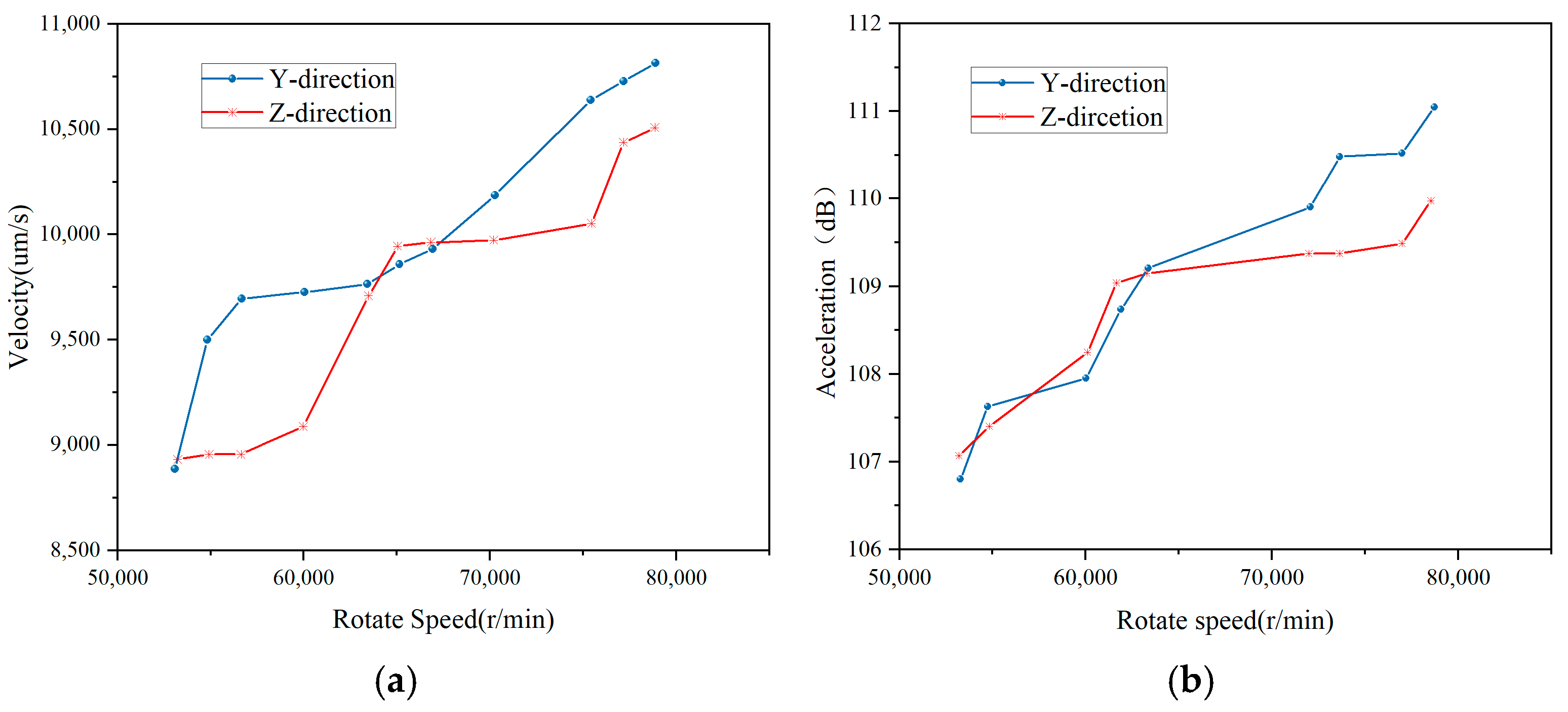
2.3.3. Impact of Bearing Speed on the Vibration of Integrated Bearings
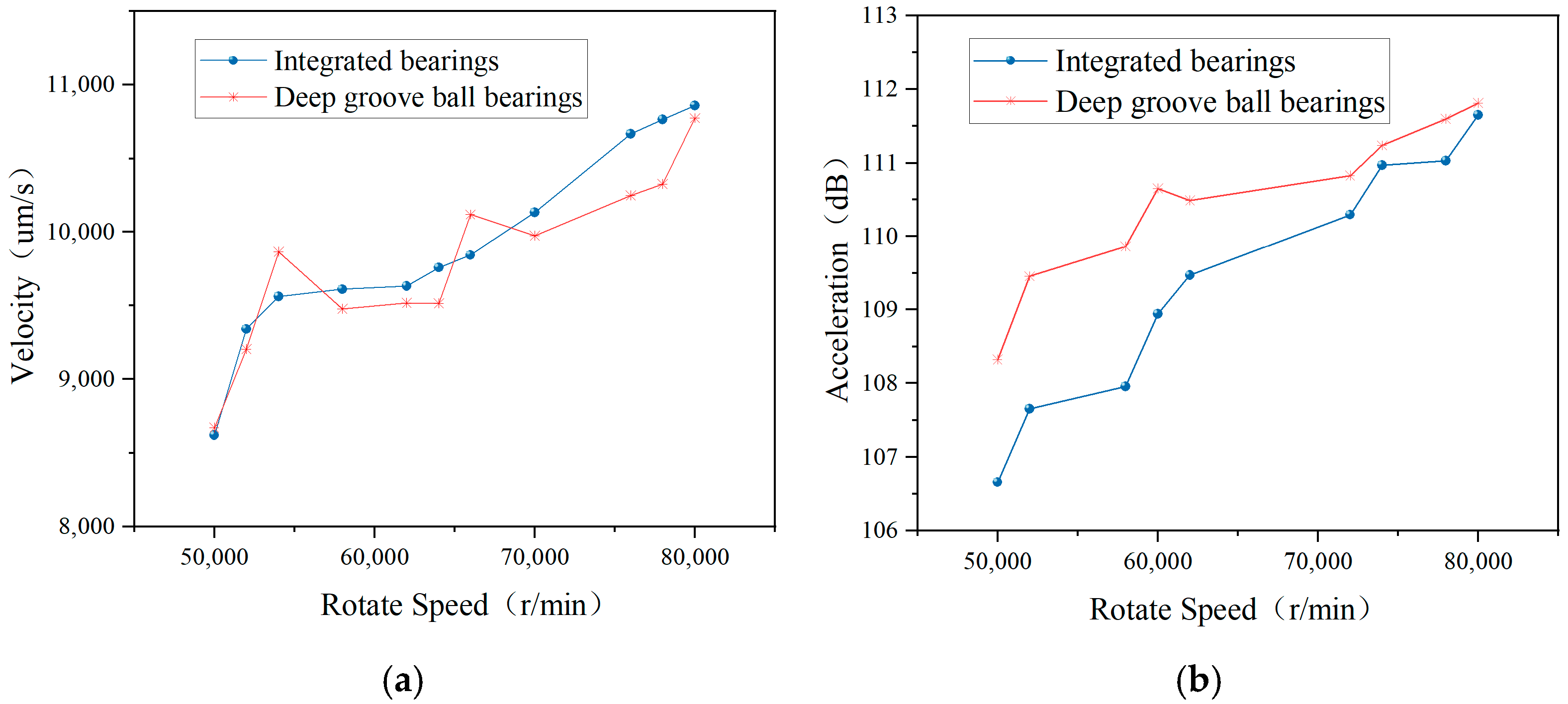
2.4. Comparison Between Integrated Bearings and Deep-Groove Ball Bearings
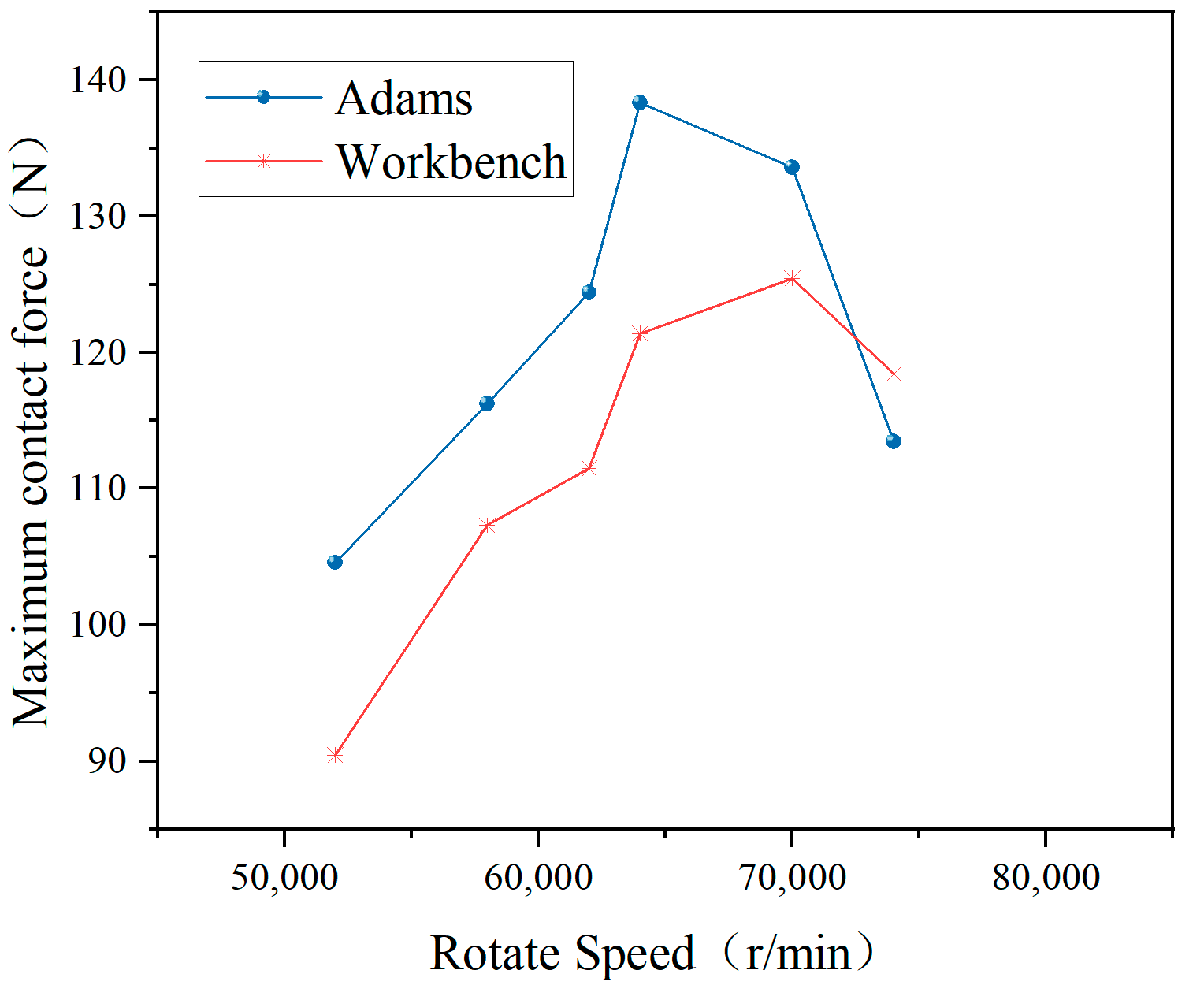
2.5. Calculation Result Verification
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ambrozkiewicz, B.; Litak, G.; Georgiadis, A.; Meier, N.; Gassner, A. Analysis of Dynamic Response of a Two Degrees of Freedom (2-DOF) Ball Bearing Nonlinear Model. Appl. Sci. 2021, 11, 787. [Google Scholar] [CrossRef]
- Lin, S.; Sun, J.; Zhao, C.; Peng, Y. Research on Dynamic Characteristics of the RBBH System Based on Dynamics Model and Vibration Data Fusion-Web of Science Core Collection. Sensors 2022, 22, 3806. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Wang, L.; Zhang, C. Study on the Load Distribution and Dynamic Characteristics of a Thin-Walled Integrated Squirrel-Cage Supporting Roller Bearing. Appl. Sci. 2016, 6, 415. [Google Scholar] [CrossRef]
- Questa, H.; Mohammadpour, M.; Theodossiades, S.; Garner, C.P.; Bewsher, S.R.; Offner, G. Tribodynamic Modelling of High-Speed Rolling Element Bearings in Flexible Multi-Body Environments. Machines 2023, 11, 93. [Google Scholar] [CrossRef]
- Xu, M.; Feng, G.; He, Q.; Gu, F.; Ball, A. Vibration Characteristics of Rolling Element Bearings with Different Radial Clearances for Condition Monitoring of Wind Turbine. Appl. Sci. 2020, 10, 4731. [Google Scholar] [CrossRef]
- Ambrozkiewicz, B.; Syta, A.; Georgiadis, A.; Gassner, A.; Meier, N. Experimental Verification of the Impact of Radial Internal Clearance on a Bearing’s Dynamics. Sensors 2022, 22, 6366. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. An Analytical Model for the Prediction of The Vibration Response of Rolling Element Bearings Due to a Localized Defect. J. Sound Vib. 1997, 205, 275–292. [Google Scholar] [CrossRef]
- Wang, H.; Gong, J.; Chen, G. Characteristics analysis of aero-engine whole vibration response with rolling bearing radial clearance. J. Mech. Sci. Technol. 2017, 31, 2129–2141. [Google Scholar] [CrossRef]
- Liu, Y.; Han, J.; Zhao, S.; Meng, Q.; Shi, T.; Ma, H. Study on the Dynamic Problems of Double-Disk Rotor System Supported by Deep Groove Ball Bearing. Shock Vib. 2019, 2019, 8120569. [Google Scholar] [CrossRef]
- Yhland, E.M. Paper 29: Waviness Measurement-An Instrument for Quality Control in Rolling Bearing Industry. Arch. Proc. Inst. Mech. Eng. Conf. Proc. 1967, 182, 438–445. [Google Scholar] [CrossRef]
- Akturk, N.; Uneeb, M.; Gohar, R. The Effects of Number of Balls and Preload on Vibrations Associated with Ball Bearings. J. Tribology 1997, 119, 747–753. [Google Scholar] [CrossRef]
- Deng, S.-E.; Sun, C.-Y.; Gu, J.-F.; Cui, Y.-C. Vibration characteristics of low-noise deep groove ball bearings. J. Vib. Shock 2015, 34, 12–19. [Google Scholar]
- Shah, D.S.; Patel, V.N. Theoretical and experimental vibration studies of lubricated deep groove ball bearings having surface waviness on its races. Measurement. 2018, 129, 405–423. [Google Scholar] [CrossRef]
- Xu, H.; Yang, Y.; Ma, H.; Luo, Z.; Li, X.; Han, Q.; Wen, B. Vibration characteristics of bearing-rotor systems with inner ring dynamic misalignment. Int. J. Mech. Sci. 2022, 230, 107536. [Google Scholar] [CrossRef]
- Jia, X.; Deng, K.; Tang, Z.; Cui, Y.; Zhang, W.; Deng, S. A study on vibration characteristics of crown cages in high speed ball bearings. Zhendong Yu Chongji. J. Vib. Shock 2022, 41, 16–23+30. [Google Scholar]
- Wang, P.; Yang, Y.; Ma, H.; Xu, H.; Li, X.; Luo, Z.; Wen, B. Vibration characteristics of rotor-bearing system with angular misalignment and cage fracture: Simulation and experiment. Mech. Syst. Signal Proc. 2023, 182, 109545. [Google Scholar] [CrossRef]
- Li, Y.; Cao, H.; Tang, K. A general dynamic model coupled with EFEM and DBM of rolling bearing-rotor system. Mech. Syst. Signal Proc. 2019, 134, 106322. [Google Scholar] [CrossRef]
- Li, F.; Li, X.; Shang, D. Dynamic Modeling and Vibration Characteristics Analysis of Deep-Groove Ball Bearing, Considering Sliding Effect. Mathematics 2021, 9, 2408. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y. Modeling of a deep-groove ball bearing with waviness defects in planar multibody system. Multibody Syst. Dyn. 2015, 33, 229–258. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Zhou, X.; Zhang, H.; Lin, Z.; Jia, S. Dynamic analysis of deep groove ball bearing with localized defects and misalignment. J. Sound Vibr. 2024, 568, 118071. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sadeghi, F.; Stacke, L.-E. Surface defects effects on bearing dynamics. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 25–35. [Google Scholar] [CrossRef]
- Shah, D.S.; Patel, V.N. A dynamic model for vibration studies of dry and lubricated deep groove ball bearings considering local defects on races. Measurement 2019, 137, 535–555. [Google Scholar] [CrossRef]
- Weinzapfel, N.; Sadeghi, F. A Discrete Element Approach for Modeling Cage Flexibility in Ball Bearing Dynamics Simulations. J. Tribol. Trans. ASME 2009, 131, 021102. [Google Scholar] [CrossRef]
- Sopanen, J.; Mikkola, A. Dynamic model of a deep-groove ball bearing including localized and distributed defects. Part 2: Implementation and results. Proc. Inst. Mech. Eng. Pt. K J. Multi-Body Dyn. 2003, 217, 213–223. [Google Scholar] [CrossRef]
- Sopanen, J.; Mikkola, A. Dynamic model of a deep-groove ball bearing including localized and distributed defects. Part 1: Theory. Proc. Inst. Mech. Eng. Pt. K J. Multi-Body Dyn. 2003, 217, 201–211. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Outer Diameter (mm) | 18 |
| Inner Diameter (mm) | 8.5 |
| Width (mm) | 5.9 |
| Number of Steel Balls | 7 |
| Diameter of Steel Balls (mm) | 2.778 |
| Pitch Circle Diameter (mm) | 13 |
| Property | Value | Unit |
|---|---|---|
| Density | 7.83 × 10−6 | kg/mm3 |
| Elastic Modulus | 2.19 × 105 | MPa |
| Poisson’s Ratio | 0.3 |
| Property | Value | Unit |
|---|---|---|
| Density | 1.1 × 10−6 | kg/mm3 |
| Elastic Modulus | 1000 | MPa |
| Poisson’s Ratio | 0.39 |
| Parameter | Value |
|---|---|
| Outer Diameter (mm) | 20 |
| Inner Diameter (mm) | 8 |
| Width (mm) | 6.3 |
| Number of Steel Balls | 7 |
| Diameter of Steel Balls (mm) | 2.38 |
| Pitch Circle Diameter (mm) | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhi, C.; Zhai, J.; Wen, B.; Li, N. Research on Dynamic Modeling and Vibration Characterization of Integrated Bearings. Appl. Sci. 2025, 15, 98. https://doi.org/10.3390/app15010098
Zhi C, Zhai J, Wen B, Li N. Research on Dynamic Modeling and Vibration Characterization of Integrated Bearings. Applied Sciences. 2025; 15(1):98. https://doi.org/10.3390/app15010098
Chicago/Turabian StyleZhi, Chuanxiao, Jingyu Zhai, Baogang Wen, and Ning Li. 2025. "Research on Dynamic Modeling and Vibration Characterization of Integrated Bearings" Applied Sciences 15, no. 1: 98. https://doi.org/10.3390/app15010098
APA StyleZhi, C., Zhai, J., Wen, B., & Li, N. (2025). Research on Dynamic Modeling and Vibration Characterization of Integrated Bearings. Applied Sciences, 15(1), 98. https://doi.org/10.3390/app15010098






