Abstract
Highly polarized high-energy photons demonstrate potential application in the efficient detection of strong-field quantum electrodynamics effects. Currently, polarized -rays are mostly generated in conventional particle accelerators, which are typically huge and expensive. This study proposes a scheme for generating linearly polarized photons from the interaction of a GeV-level unpolarized electron bunch with currently available laser pulses at moderate intensity. We investigate the scheme by considering the electron bunch of various initial energies and various laser intensities using two-dimensional particle-in-cell simulation and the theory of quantum electrodynamics. Results show that GeV-level linearly polarized photons were generated from the interaction with a high polarization degree of and brightness of at 1 GeV. Moreover, it is also shown that the photon generation rate was enhanced with higher laser intensity and electron bunch energy, whereas the polarization degree decreased with higher laser intensities. Our scheme can be realized experimentally at currently available laser wakefield electron acceleration facilities.
1. Introduction
Laser technology has significantly evolved in recent years, with intensities having reached [1]. Intensities are further expected to reach by the next-generation ultra-intense laser facilities [2], such as extreme light infrastructure [3], EP-OPAL, and SEL [4]. Future advancements in laser intensities may provide opportunities and platforms for nonlinear quantum electrodynamics (QED) physics [5,6,7,8], laser–plasma interaction physics [9,10], and other related domains such as high-energy-density physics and laboratory astrophysics [11,12,13]. Although the required strong field intensity for vacuum decay (termed the Schwinger limit , where the corresponding laser intensity is ) is beyond the current and near-future capability of contemporary laser facilities [14], electron–positron pair production via laser collision using a high-energy electron beam was realized 27 years ago at SLAC [15,16], and several promising QED experiments are currently being conducted based on the current laser technology and GeV-level electron beam [17,18,19] plan to measure the transition of nonlinear Compton scattering (NCS) to the nonperturbative regime.
Polarization is an important intrinsic property of a photon and has crucial applications in QED experiments and other widespread research fields. For instance, polarized -rays can excite the polarization-dependent photofission and photoproduction of muon [20,21]. Highly polarized high-energy photons are essential in generating polarized electron–positron pairs [22], probing radiation mechanisms, and the properties of dark matter and black holes [23,24]. Another important application is the detection of the vacuum birefringence effect using strong laser and polarized high-energy photon collision [4]. Understanding the process of the photon polarization is essential in the high-precision detection of the high-field QED process and basis of the practical application of the polarization-dependent QED process.
Currently, polarized -rays are mostly generated in conventional particle accelerators, which are typically huge and expensive. In the bremsstrahlung process, polarized photons produced by a pre-polarized seed electron and the spin polarization of the seed electron determine the photon polarization [25,26]. Moreover, a high-energy pre-polarized seed electron beam is mostly produced by the Sokolov–Terno effect in a conventional storage ring [27], which is huge and has a long electron polarization time and low polarization degree. In linear Compton scattering, an unpolarized seed electron can produce polarized photons and the polarization of the photons is determined by an incident laser polarization [28]. However, for coherent bremsstrahlung, because of the threshold of crystal materials, the seed electron current density and the energy of the produced photons are limited [29]. The incoherent bremsstrahlung cannot generate linearly polarized photons, and the photon divergence angle and directivity are not very good [30]. In addition, polarized photons in bremsstrahlung and linear Compton scattering are not applicable in most leading studies. For example, the detection of the vacuum birefringence requires highly polarized high-flux high-energy photons [31].
With the rapid advancement in laser technologies, the laser plasma-based scheme is one of the preferred alternatives for high-energy electron acceleration and high-energy photon generation. Therefore, considerable theoretical and numerical studies on new physical mechanisms for producing highly polarized high energy photons have been conducted [30,32,33,34,35]. Among these schemes, the plasma-based all optical [17,34] and laser electron collision schemes [17,30,36] are the most fascinating for current laser intensities and upcoming laser electron QED experiments at high power laser platforms around the world [3,18,37,38,39,40]. When a high-energy electron (an electron bunch) collides with a high-intensity laser, the photons can be produced via the NCS process. For a high-intensity laser , where is the normalized laser intensity, the photon formation length is significantly smaller than the laser wavelength and the laser field can be approximated as a constant field for photon formation. The process can be addressed using the locally constant field approximation (LCFA) [41]. In the laser-based photon production schemes, the energy and polarization of the photon can be controlled by either incoming seed electron or incident laser parameters. Recently, several proposals have been put forward to detect vacuum birefringence using GeV-level highly polarized photons [31].
In this study, we investigated the generation of a linearly polarized photon with GeV energy by an intense laser colliding with an unpolarized electron bunch. We simulated the photon emission process of the laser–electron collision using QED particle-in-cell (PIC) simulation, and the photon polarization process was calculated by applying the QED theory. We considered incoming electron bunches with various initial energies within the range of 1–10 GeV, which can be obtained in present day laser wakefield acceleration experiments [9,42]. The results indicated that the production rate and energy of the produced photons could be enhanced by increasing the laser intensity and electron initial energies. However, high laser intensity and initial beam energy could not yield a high photon polarization degree. In particular, the photon polarization degree reached its maximum (approximately ) with an energy exceeding 1 GeV in the case of a low laser intensity of with an initial electron beam energy of 5 GeV.
The rest of this paper is organized as follows: In Section 2, we present the simulation model, simulation parameters, and simulation results for the laser–electron bunch collision process. In Section 3, we first briefly review and present key equations for the photon polarization process and develop a QED calculation model of the photon polarization. Subsequently, the results of QED calculations for different electron energies and laser intensities are presented and their physical implications are discussed. Comparisons of the results obtained from PIC simulation and QED calculation are presented in the final subsection of Section 3. Finally, the main conclusions are presented in Section 4.
2. Simulation of the High Energy Photon Production
2.1. Model and Simulation Parameters
The photon production process of an electron colliding with a laser field is referred to as NCS (). We focused on the production of a linearly polarized photon by an unpolarized electron bunch interacting with a linearly polarized laser pulse in the NCS process. Our physical model is shown in Figure 1a. The photon production process is tested by conducting a set of 2D-QED-PIC simulations using the code EPOCH [43]. The simulation size is set as , which corresponds to the grid cell number of . We considered a linearly polarized laser pulse with a Gaussian intensity profile entering the simulation region from the right boundary at . For the test simulation, the laser intensity is , and the corresponding normalized field amplitude is , where e and are the electron charge and rest mass, respectively; c is the speed of light in a vacuum; and and are the laser electric field strength and laser frequency, respectively. The laser pulse duration, wavelength, and pulse spot size are fs, , and , respectively, in all simulations. To verify the effects of laser intensity on photon energy and polarization degree, the laser intensity was varied in the simulation as .
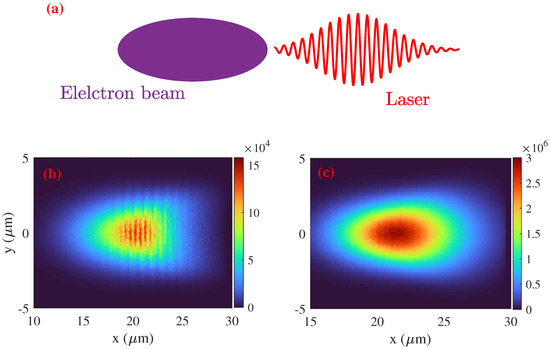
Figure 1.
(a) Schematic of the laser electron bunch collision scheme. Density distribution of electron (b) and produced photons (c) following laser electron collision at time fs. Laser normalized intensity and electron bunch initial energy are (laser intensity of ) and 2 GeV, respectively. Other laser electron bunch parameters are given in the text.
The electron beam enters the simulation region from the left boundary at . The electron density has a transversely Gaussian and longitudinally uniform distribution with a transverse size (FWHM) , and the duration is fs (beam length of 9 m), which is represented by of the total macroscopic particles and total charge of 1 pC. The energy spread of each electron beam is fixed to 0.06 in all calculations. The longitudinal and transverse initial temperatures of the electrons are set to 1 and 0.01 MeV, respectively. We set 100 macro electrons in each cell of the electron bunch. Periodic and simple-outflow boundary conditions are used in the transverse and longitudinal direction, respectively. To investigate the influence of the electron initial energy on the final photon production rate, energy, and polarization degree, the electron bunch energy changes from to . Such a high energy compact electron bunch can be obtained via laser wakefield acceleration experiments [9,42].
In the EPOCH code, the emission of photons via the NCS process is controlled using the key quantum nonlinear parameter . Here, is the electromagnetic field tensor, is the four-momentum of electron, is the electron relativistic factor, and is the Schwinger critical field strength, corresponding to the laser intensity of far beyond the currently available laser intensity. The photon emission can be considerable and dominate the dynamics of the electron only if [44,45]. Notably, for a high-energy electron bunch co-propagating with a laser pulse, the parameter can be approximated as , which requires the laser intensity to be extremely high to satisfy . Here, is the perpendicular electric field that is experienced by the electron. However, for a high-energy electron head-on colliding with a laser pulse, the QED parameter becomes comparable to a unit including the currently available lasers because of the boosted electric field. Therefore, the photon emission rate can efficiently be enhanced via the laser–electron colliding NCS process. We take in to account the radiation reaction in all simulations and calculations. In the Epoch code, we not implemented the electron spin polarization and photon polarization because of the complexity of the process. However, in Section 3, we introduced a simple and quick method to calculate the photon polarization by corporation of the PIC simulation and QED calculation. We theoretically calculate the photon polarization probability and polarization degree based on the data of the electron beam with acquired in the simulation [35].
2.2. Simulation Results
In this section, we first demonstrate the 2D-QED-PIC simulation results of the photon production via the NCS process, and the photon polarization is discussed in the next section. We begin with a simulation of a laser pulse with a normalized intensity of interacting with a 2 GeV electron bunch. Figure 1b,c show the distribution of the electron and produced photon number density. During the interaction, the dynamics of the electrons are highly affected by the laser field. The laser field is equivalent to a natural undulator, and most of the electrons oscillate perpendicularly, as illustrated in Figure 1b. The electrons absorb laser energy, accelerated higher energy than its initial energy and emit high-energy photons via the NCS process. Because the electron dynamics determine the photon emission and photons are emitted on the electron trajectories, the photons have an identical density distribution with the seed electron bunch, as illustrated in Figure 1c. Numerous photons are produced at the central region because of the Gaussian distribution of the electron beam density and laser intensity, corresponding to high laser intensity and energetic electrons at the central region.
Figure 2 illustrates the energy spectrum of the electron spectrum after interaction and produced photons for different electron energies with a fixed laser intensity of . As the initial energy of the electron increases, high-energy photons can be produced. The energy of the beam is determined by that of the seed electron and is, at most, radiated with an energy of for ultra-relativistic electrons [45]. Therefore, the photons cutoff energies are approximately , and GeV for initial electron energies of , and 10 GeV, respectively, as shown in Figure 2. Notably, the photon cutoff energies were comparable with the electron energies for electrons with initial energies of 5 and 10 GeV. However, the photon cutoff energies exceeded electron energies for electrons with initial energies of 1 and 2 GeV. This can be explained as follows: because the laser exists during the interaction, some electrons accelerated to higher energy by laser electric field after laser-electron interaction and effective electron cutoff energy higher than incoming electron energy, as shown in Figure 2a. For example, with the low initial energy of the electron bunch (indicating low electron momentum) in our simulation, the electrons could stay in the high field region for a long time (indicating a long interaction time), and accelerated to energies higher than the initial incoming energy as shown in Figure 2a. This accounts for the high energy of the generated photons. Therefore, emitted photon final energy lager than electron beam initial energy but not exceed the electron final cut of energy after acceleration, this result is consistent with previous results [46]. However, for electrons with high initial energies (5 and 10 GeV), the momenta were also high, and they rapidly penetrated the high field region and pass through the laser (referring to a short interaction time) with less chance for additional acceleration in the laser field. Thus, the photon cutoff energy was comparable with the initial energy of the electron.
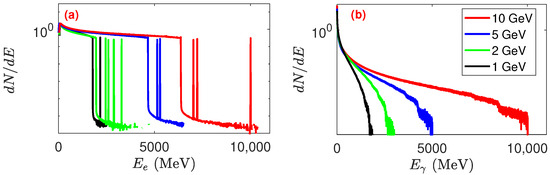
Figure 2.
(a) The energy spectrum of electrons with different initial energies after interacting with the laser, (b) produced photon energy spectrum for different electron bunch initial energy with a fixed laser intensity of . The other parameters are the same as in Figure 1.
Figure 3 illustrates the energy angular distribution of the produced photons for the different initial energies of the electron bunches. Here, with increasing electron bunch initial energy for a fixed laser intensity (), the divergence angle of the photons decreases. As aforementioned, electrons with low energy could easily be maintained in the high field region for a long time but were scattered at large angles with higher than initial energy by the laser ponderomotive force. Therefore, the divergence angles of the photons increased for low electron energies. The photon divergence angles were approximately and for initial electron energies of 1 and 2 GeV, as shown in Figure 3a,b, respectively. However, for high-electron initial energies, the momentum of the electron was high and well-directed to the propagation direction. Parent electrons maintained their initial directions and had fewer chances to be scattered to other angles. Because the photons were mostly produced in the direction of electron motion, they had low divergence angles. For the 5 and 10 GeV electron initial energies, the divergence angle of the photon is approximately , as shown in Figure 3c,d.
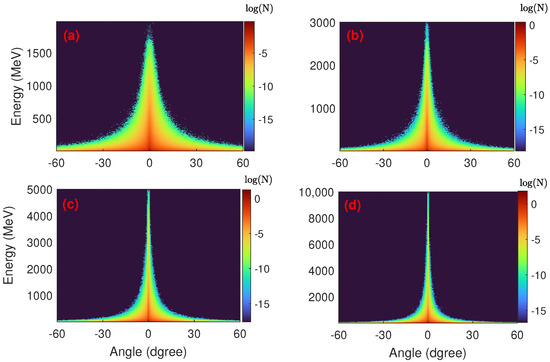
Figure 3.
Energy angular distribution of the produced photons for different electron initial energy with a fixed laser intensity of , the (a–d) represents the results for electron initial energy of 1, 2, 5, and 10 GeV, respectively. The other parameters are the same as in Figure 1.
Several practical applications of photons require high energy and the high brightness of the photon source. We estimate the brightness of the high-energy photon source in our scheme. The angular divergence, total number, and source size of the photon beam are determined by the electron bunch. The photon spectrum (see Figure 2) shows that for a photon beam with an energy of 1 GeV, the total number of photons (approximately ) is approximately the same for different initial electron energies. Most of the photons are concentrated within a source size of approximately for all cases (see Figure 1). However, the divergence angle is different for different electron initial energies, as shown in Figure 3, accounting for the different photon beam brightness. The photon number in a bandwidth (BW) at 1 GeV is obtained by averaging the total number of photons. We predict the brightness of the 2 GeV electron initial energy to be approximately at 1 GeV, which is more than two orders of magnitude brighter than recently suggested high energy polarized photon sources [30]. If we consider a high initial electron energy of 10 GeV, which is similar to that of the electron source of the FACET II [42], the brightness would be approximately one order higher as at 1 GeV.
3. Photon Polarization
When a high-energy electron bunch scatters off a laser pulse of sufficient intensity, high-energy photons are produced as demonstrated in the previous section. We focus on photon polarization theoretically. Polarization is an important feature of photons, and high-energy polarized photons show potential applications in many research fields. Correct and high-precision calculations of photon polarization using the QED theory are necessary in the theoretical investigations of upcoming QED experiments. In this section, we theoretically calculate the photon polarization probability and polarization degree.
3.1. Theory
When an unpolarized electron bunch collides with a linearly polarized laser pulse, the photon polarization is determined by the laser field. For the intense laser field in this study, as the radiation formation length is significantly smaller than the laser wavelength, the laser field can be considered constant during the photon formation interval. Therefore, we use an LCFA [41] and Nikishov–Ritus method for the QED calculations, photon production probability, and polarization degree. The detailed derivation of the basic formulas is given in Refs. [32,33], so we will briefly introduce the ideas and key points below. The probability of emitting a photon in the polarization state with a momentum k via the NCS process can be expressed as [32,33]
corresponding to the photon scattered by an unpolarized electron onto the polarization state and :
where is the photon momentum, is the laser wave vector, , and . The Airy functions are defined as follows:
where is the derivative of the Airy function Ai(x).
For small-angle collision , () indicates polarization in the y-direction (z-direction). The total yield is
where is the fine-structure constant, , is the light-front momentum fraction of the scattered photon, , , , and is the field intensity parameter ( is the laser pulse phase). is the momentum distribution of the electron bunch and satisfies the normalization condition .
The polarization degree can be determined by the probability change () and total probability () of photon scattering to a linearly polarized state as
Notably, for the intense laser field in this study, as the radiation formation length is significantly smaller than the laser wavelength, the laser field can be considered constant during the photon formation interval. Therefore, we use an LCFA [41] for the QED calculations, photon production probability, and polarization degree.
The momentum distribution of an accelerated high-energy electron bunch can be expressed as
Herein, we consider a head-on collision between a high-energy electron bunch and an intense laser field, as illustrated in Figure 1a. For the high-energy electron and , we have . Therefore, the two-dimensional density distribution of the high-energy electron bunch in our PIC simulation can be approximated to a one-dimensional representation as
Because of the head-on collision, we have
The probability of generating photons for the differently polarized states can be expressed as
3.2. Calculation Results
Figure 4 presents the energy distribution of the scattered photons by the electron bunch with different initial energies while the laser pulse intensity is fixed to . With an increase in the initial energy of the electron bunch, the electron Lorenz factor and QED parameter increase. The production rate of the photon is proportional to the parameter , and thus the energy of the photon is given as . Therefore, the production rate and energy of photon increases with the initial electron energy, as shown in Figure 4. However, Figure 4 shows that most of the photons are linearly polarized in the y-direction () for different electron initial energies because the photon polarization mainly transfers from background field polarization for an unpolarized initial electron. In this study, the linearly polarized laser pulse is in the y direction and, therefore, the linearly polarized photons are parallel to the laser field.
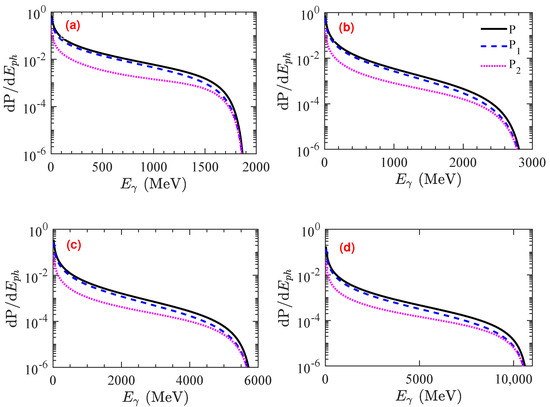
Figure 4.
Energy distribution of the different polarized photons from QED calculations with different initial energies, (a) 1, (b) 2, (c) 5, and (d) 10 GeV. Solid dashed and dotted lines represent total y- and z-direction polarization probabilities of the photons, respectively. Other parameters are the same as presented in Figure 1.
To validate the feasibility of our scheme, we compared the energy spectrum of the photons from the PIC simulations and spectrum from QED calculations shown in Figure 5 for different electron initial energies and fixed laser intensity. The results show that the energy spectra of the PIC simulation and QED calculation are consistent for low electron energies (for initial electron energies 1 and 2 GeV), whereas for high electron energies, a slight difference is observed at the tail of the photon spectrum, as illustrated in Figure 5. This indicates that our scheme and the theoretical calculation are consistent.
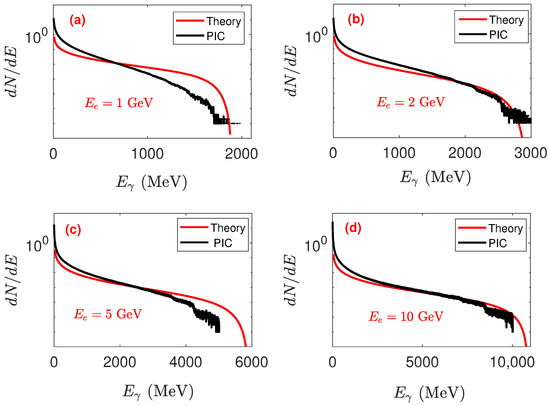
Figure 5.
photon energy spectrum from theoretical QED calculation (red curves) and PIC simulations (black curves) for different electron bunch initial energies, (a) 1, (b) 2, (c) 5, and (d) 10 GeV. with a fixed laser intensity of . Other parameters are the same as in Figure 1.
To discuss the photon polarization degree, first, we consider different initial electron energies and fixed laser intensity, as shown in Figure 6. Here, for electron bunches with low initial energies (1 and 2 GeV), the polarization degree of the photon increases as the photon energy increases and reaches its maximum at approximately and , respectively, at a photon energy of approximately 700 MeV. However, for high electron bunch initial energies (5 and 10 GeV), the peak photon polarization degree is only approximately at the same energy level (700 MeV) with the low initial energy cases. For photon energy exceeding 700 MeV, the photon polarization degree significantly decreases with a further increase in photon energy. This indicates that highly polarized photons are produced only at low photon energy regions, and high-electron initial energies only maintain the polarization unchanged in a broader photon energy range but do not increase the polarization. Notably, in our unpolarized initial electron bunch case, the photon polarization is transferred from the linearly polarized background field. Here, the polarization degree of the background field decreases with an increase in the energy absorbed by the scattered photon from the incident electron. The higher the photon energy, the lower the field polarization degree and polarization transfer efficiency to the photon. This results in a significant decrease in the photon polarization degree at high energy levels. For the initial electron energies of 5 and 10 GeV, the laser–electron interaction times may be shorter than those of the low electron initial energy cases. This results in the low photon polarization degree for the high initial electron energies, as illustrated in Figure 6.
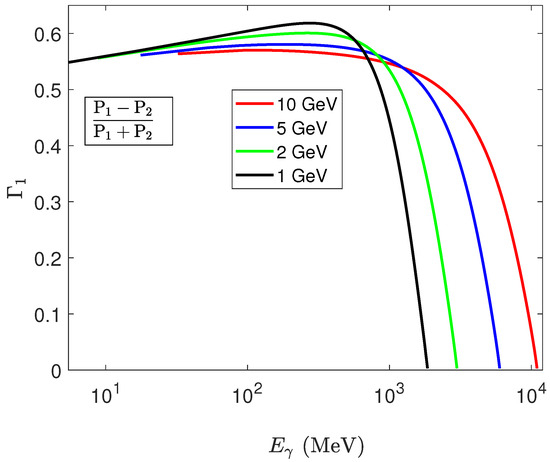
Figure 6.
photon polarization degree for different electron bunch initial energies (1, 2, 5, and 10 GeV) with a fixed laser intensity of . Other parameters are the same as in Figure 1.
Finally, we discuss the effect of the laser field intensity on the photon spectrum and photon polarization degree. In this case, we fixed the initial electron energy to 5 GeV, and the normalized laser intensity changes from 50 to 1000. The QED parameter and produced photon energy increase with increasing laser intensity. Similarly, the photon production rate and cutoff energy increase with increasing laser intensity, as shown in Figure 7a. However, the photon polarization degree decreases with increasing laser intensity, as shown in Figure 7b. For the high electron energy (5 GeV) and high laser intensity () case, the electron Lorentz factor and QED parameter are efficiently enhanced and the NCS process is triggered with high efficiency. However, at an extremely high laser intensity, the ponderomotive force acting on an electron is extremely high, thereby scattering high-speed electrons. This results in a short interaction time and low polarization conversion rate. Therefore, the photon polarization degree is only approximately for the extremely high laser intensity of , as shown in Figure 7b. For the low laser intensity (), the ponderomotive force acting on an electron is lower than that acting in the high-intensity laser case. High-energy electrons can penetrate the high field region and stay for a long time in this region (indicating a long interaction time). This may result in a high polarization conversion rate. Thus, 1 GeV level linearly polarized photons with a high polarization degree of are produced in the low laser intensity configuration, as shown in Figure 7b.
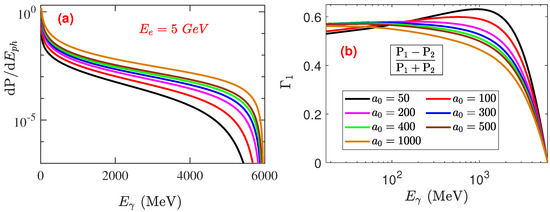
Figure 7.
(a) photon energy spectrum and (b) polarization degree from theoretical QED calculation for different laser intensities with a fixed electron bunch initial energy of 5 GeV. Other parameters are the same as in Figure 1.
Notably, in the theoretical calculation of the photon polarization in Section 3, we considered the photon energy distribution only from single Compton scattering. However, in a simulation, an electron can experience multiple Compton scattering, which would change the energy of the acquired electron bunch, causing the theoretical results slightly different from our simulation result shown in Figure 5.
4. Conclusions
This study proposed a scheme that can produce linearly polarized photons in an unpolarized electron bunch interacting with a linearly polarized laser pulse. The normal and polarization properties of the emitted photons were investigated using 2D-QED-PIC simulation and a theoretical model. The simulation results indicated that the properties of the photons could be varied by changing either the laser intensity or electron bunch initial energy. The cutoff energy, brightness, and polarization degree of the photons were enhanced by properly choosing the laser intensity and electron bunch initial energy. Highly collimated (a divergence angle of ) rays were emitted with a brightness of at 1 GeV. Further, the photons had high probabilities of being emitted into a polarization state parallel to the polarization of the background field and possessed a positive polarization degree, which attained its maximum ∼63% at a photon energy of approximately 1 GeV. Moreover, results showed that the low-intensity laser and high-energy electron bunch could generate highly polarized photons with high energies, and the extremely intense laser could not achieve this effect. Our findings point to potential application in theoretical studies on upcoming QED experiments. The well-collimated, high-energy, ultrabright, and linearly polarized photon beam obtained using our scheme may be suitable for the generation of energetic polarized positrons and laboratory astrophysics research.
Author Contributions
Conceptualization, M.A.B.; methodology, M.A.B.; formal analysis, Y.H., B.Y. and M.A.B.; investigation, Y.H. and M.A.B.; data curation, Y.H., B.Y. and M.A.B.; writing—original draft, Y.H. and M.A.B.; visualization, Y.H. and B.Y.; supervision, M.A.B.; project administration, M.A.B.; funding acquisition, M.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Special Training Program of Science and Technology Department of Xinjiang China (Grant No. 2024D03007) and the National Natural Science Foundation of China (NSFC) under Grant No. 12265024.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yoon, J.W.; Kim, Y.G.; Choi, I.; Sung, J.H.; Lee, H.W.; Lee, S.K.; Nam, C.H. Realization of laser intensity over 1023W/cm2. Optica 2021, 8, 630–635. [Google Scholar] [CrossRef]
- Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.C.F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I.; et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 2019, 7, e54. [Google Scholar] [CrossRef]
- Turcu, I.C.E.; Negoita, F.; Jaroszynski, D.A.; Mckenna, P.; Balascuta, S.; Ursescu, D.; Dancus, I.; Cernaianu, M.O.; Tataru, M.V.; Ghenuche, P.; et al. High field physics and QED experiments at ELI-NP. Rom. Rep. Phys. 2016, 68, S145. [Google Scholar]
- Shen, B.; Bu, Z.; Xu, J.; Xu, T.; Ji, L.; Li, R.; Xu, Z. Exploring vacuum birefringence based on a 100 PW laser and an x-ray free electron laser beam. Plasma Phys. Control. Fusion 2018, 60, 044002. [Google Scholar] [CrossRef]
- Bulanov, S.S.; Mur, V.D.; Narozhny, N.B.; Nees, J.; Popov, V.S. Multiple Colliding Electromagnetic Pulses: A Way to Lower the Threshold of e+e− Pair Production from Vacuum. Phys. Rev. Lett. 2010, 104, 220404. [Google Scholar] [CrossRef]
- Di Piazza, A.; Mueller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177. [Google Scholar] [CrossRef]
- Gonoskov, A.; Blackburn, G.; Marklund, M.; Bulanov, S.S. Charged particle motion and radiation in strong electromagnetic fields. Rev. Mod. Phys. 2022, 94, 045001. [Google Scholar] [CrossRef]
- Fedotov, A.; Ilderton, A.; Karbstein, F.; King, B.; Seipt, D.; Taya, H.; Torgrimsson, G. Advances in QED with intense background fields. Phys. Rep. 2023, 1010, 1–138. [Google Scholar]
- Gonsalves, A.J.; Nakamura, K.; Daniels, J.; Benedetti, C.; Pieronek, C.; de Raadt, T.C.H.; Steinke, S.; Bin, J.H.; Bulanov, S.S.; van Tilborg, J.; et al. Petawatt laser guiding and electron beam acceleration to 8 GeV in a laser-heated capillary discharge waveguid. Phys. Rev. Lett. 2019, 122, 084801. [Google Scholar] [CrossRef]
- Tajima, T.; Malka, V. Laser plasma accelerators. Plasma Phys. Control. Fusion 2020, 62, 034004. [Google Scholar] [CrossRef]
- Albert, F.; Thomas, A.G.R. Applications of laser wakefield accelerator-based light sources. Plasma Phys. Control. Fusion 2016, 58, 103001. [Google Scholar] [CrossRef]
- Gales, S.; Balabanski, D.L.; Negoita, F.; Tesileanu, O.; Ur, C.A.; Ursescu, D.; Zamfir, N.V. New frontiers in nuclear physics with high-power lasers and brilliant monochromatic gamma beams. Phys. Scr. 2016, 91, 093004. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Molina-Terriza, G.; Anzolin, G. Twisting of light around rotating black holes. Nat. Phys. 2011, 7, 195. [Google Scholar] [CrossRef]
- Schwinger, J.S. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664. [Google Scholar] [CrossRef]
- Burke, D.L.; Field, R.C.; HortonSmith, G.; Spencer, J.E.; Walz, D.; Berridge, S.C.; Bugg, W.M.; Shmakov, K.; Weidemann, A.W.; Bula, C.; et al. Positron production in multiphoton light-by-light scattering. Phys. Rev. Lett. 1997, 79, 1626. [Google Scholar] [CrossRef]
- Bamber, C.; Boege, S.J.; Koffas, T.; Kotseroglou, T.; Melissinos, A.C.; Meyerhofer, D.D.; Reis, D.A.; Ragg, W.; Bula, C.; McDonald, K.T.; et al. Studies of nonlinear QED in collisions of 46.6 GeV electrons with intense laser pulses. Phys. Rev. D 1999, 60, 092004. [Google Scholar] [CrossRef]
- Mirzaie, M.; Hojbota, C.I.; Kim, D.Y.; Pathak, V.B.; Pak, T.G.; Kim, C.M.; Lee, H.W.; Yoon, J.W.; Lee, S.K.; Rhee, Y.J.; et al. All-optical nonlinear Compton scattering performed with a multi-petawatt laser. Nat. Photonics 2024, 18, 1212. [Google Scholar] [CrossRef]
- Abramowicz, H.; Acosta, U.; Altarelli, M.; Assmann, R.; Bai, Z.; Behnke, T.; Benhammou, Y.; Blackburn, T.; Boogert, S.; Borysov, O.; et al. Conceptual design report for the LUXE experiment. Eur. Phys. J. Spec. Top. 2021, 230, 2445–2560. [Google Scholar] [CrossRef]
- Meuren, S.; Bucksbaum, P.H.; Fisch, N.J.; Fiúza, F.; Glenzer, S.; Hogan, M.J.; Qu, K.; Reis, D.A.; White, G.; Yakimenko, V. On seminal HEDP research opportunities enabled by colocating multi-petawatt laser with high-density electron beams. arXiv 2020, arXiv:2002.10051. [Google Scholar]
- Speth, J.; Vander Woude, A. Giant resonances in nuclei. Rep. Prog. Phys. 1981, 44, 719–786. [Google Scholar] [CrossRef]
- Akbar, Z.; Roy, P.; Park, S.; Crede, V.; Anisovich, A.V.; Denisenko, I.; Klempt, E.; Nikonov, V.A.; Sarantsev, A.V.; Adhikari, K.P.; et al. Measurement of the helicity asymmetry E in ω→π+π−π0 photoproduction. Phys. Rev. C 2017, 96, 065209. [Google Scholar] [CrossRef]
- Moortgat-Pick, G.; Abe, T.; Alexander, G.; Ananthanarayan, B.; Babich, A.A.; Bharadwaj, V.; Barber, D.; Bartl, A.; Brachmann, A.; Chen, S.; et al. Polarized positrons and electrons at the linear collider. Phys. Rep. 2008, 460, 131–243. [Google Scholar] [CrossRef]
- Boehm, C.; Degrande, C.; Mattelaere, O.; Vincent, A.C. Circular polarisation: A new probe of dark matter and neutrinos in the sky. J. Cosmol. Astropart. Phys. 2017, 5, 043. [Google Scholar] [CrossRef]
- Laurent, P.; Rodriguez, J.; Wilms, J.; Bel, M.C.; Pottschmidt, K.; Grinberg, V. Polarized Gamma-Ray Emission from the Galactic Black Hole Cygnus X-1. Science 2011, 332, 438–439. [Google Scholar] [CrossRef]
- Olsen, H.; Maximon, L.C. Photon and Electron Polarization in High-Energy Bremsstrahlung and Pair Production with Screening. Phys. Rev. 1959, 114, 887. [Google Scholar] [CrossRef]
- Abbott, D.; Adderley, P.; Adeyemi, A.; Aguilera, P.; Ali, M.; Areti, H.; Baylac, M.; Benesch, J.; Bosson, G.; Cade, B.; et al. Production of Highly Polarized Positrons Using Polarized Electrons at MeV Energies. Phys. Rev. Lett. 2016, 116, 214801. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Ternov, I.M. On polarization and spin effects in the theory of synchrotron radiation. Sov. Phys. Dokl. 1964, 8, 1203. [Google Scholar]
- Omori, T.; Fukuda, M.; Hirose, T.; Kurihara, Y.; Kuroda, R.; Nomura, M.; Ohashi, A.; Okugi, T.; Sakaue, K.; Saito, T.; et al. Efficient propagation of polarization from laser photons to positrons through Compton scattering and electron-positron pair creation. Phys. Rev. Lett. 2006, 96, 114801. [Google Scholar] [CrossRef]
- Lohmann, D.; Peise, J.; Ahrens, J.; Anthony, I.; Arends, H.J.; Beck, R.; Crawford, R.; Hunger, A.; Kaiser, K.H.; Kellie, J.D.; et al. Linearly polarized photons at mami (mainz). Nucl. Instrum. Methods Phys. Res. Sect. A 1994, 343, 494. [Google Scholar] [CrossRef]
- Li, Y.; Shaisultanov, R.; Chen, Y.; Wan, F.; Hatsagortsyan, K.Z.; Keitel, C.H.; Li, J. Polarized ultrashort brilliant multi-GeV γ rays via single-shot laser-electron interaction. Phys. Rev. Lett. 2020, 124, 014801. [Google Scholar] [CrossRef]
- Bragin, S.; Meuren, S.; Keitel, C.H.; Di Piazza, A. High energy vacuum birefringence and dichroism in an ultrastrong laser field. Phys. Rev. Lett. 2017, 119, 250403. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; King, B.; Hu, H. Highly polarised gamma photons from electron-laser collisions. Phys. Lett. B 2020, 809, 135701. [Google Scholar] [CrossRef]
- King, B.; Tang, S. Nonlinear Compton scattering of polarized photons in plane-wave backgrounds. Phys. Rev. A 2020, 102, 022809. [Google Scholar] [CrossRef]
- Xue, K.; Dou, Z.; Wan, F.; Yu, T.; Wang, W.; Ren, J.; Zhao, Q.; Zhao, Y.; Xu, Z.; Li, J. Generation of highly-polarized high-energy brilliant γ-rays via laser-plasma interaction. Matter Radiat. Extrem. 2020, 5, 054402. [Google Scholar] [CrossRef]
- Elaji, A.; Bake, M.A.; Tang, S.; Xie, B. Bright attosecond polarized γ-ray emission from the interaction of an intense laser pulse with non-uniform near-critical-density plasma. Chin. J. Phys. 2022, 77, 2751. [Google Scholar] [CrossRef]
- Yan, W.; Fruhling, C.; Golovin, G.; Haden, D.; Luo, J.; Zhang, P.; Zhao, B.; Zhang, J.; Liu, C.; Chen, M.; et al. High-order multiphoton Thomoson scattering. Nat. Photonics 2017, 11, 541. [Google Scholar] [CrossRef]
- Miller, K.G.; Pierce, J.R.; Ambat, M.V.; Shaw, J.L.; Weichman, K.; Mori, W.B.; Froula, D.H.; Palastro, J.P. Dephasingless laser wakefield acceleration in the bubble regime. Sci. Rep. 2023, 13, 21306. [Google Scholar] [CrossRef]
- Burdonov, K.; Fazzini, A.; Lelasseux, V.; Albrecht, J.; Antici, P.; Ayoul, Y.; Beluze, A.; Cavanna, D.; Ceccotti, T.; Chabanis, M.; et al. Characterization and performance of the Apollon short-focal-area facility following its commissioning at 1 PW level. Matter Radiat. Extrem. 2021, 6, 064402. [Google Scholar] [CrossRef]
- Mohammad, R.P.; Mirzaie, M.; Hojbota, C.I.; Pak, T.G.; Kim, S.B.; Lee, G.W.; Massudi, R.; Niknam, A.R.; Lee, S.K.; Kim, K.Y.; et al. Laser wakefield electron acceleration with polarization-dependent ionization injection. Phys. Rev. Apll. 2023, 20, 034026. [Google Scholar]
- Kettle, B.; Hollatz, D.; Gerstmayr, E.; Samarin, G.M.; Alejo, A.; Astbury, S.; Baird, C.; Bohlen, S.; Campbell, M.; Colgan, C.; et al. A laser-plasma platform for photon-photon physics: The two photon Breit-Wheeler process. New J. Phys. 2021, 23, 115006. [Google Scholar] [CrossRef]
- Ilderton, A.; King, B.; Seipt, D. Extended locally constant field approximation for nonlinear compton scattering. Phys. Rev. A 2019, 99, 042121. [Google Scholar] [CrossRef]
- Joshi, C.; Adli, E.; An, W.; Clayton, C.E.; Corde, S.; Gessner, S.; Hogan, M.J.; Litos, M.; Lu, W.; Marsh, K.A.; et al. Plasma wakefield acceleration experiments at FACET II. Plasma Phys. Control. Fusion 2018, 60, 034001. [Google Scholar] [CrossRef]
- Arber, T.D.; Bennett, K.; Brady, C.S.; Lawrence-Douglas, A.; Ramsay, M.G.; Sircombe, N.J.; Gillies, P.; Evans, R.G.; Schmitz, H.; Bell, A.R.; et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys. Control. Fusion 2015, 57, 113001. [Google Scholar] [CrossRef]
- Jansen, O.; Wang, T.; Stark, D.J.; d’Humieres, E.; Toncian, T.; Arefiev, A.V. Leveraging extreme laser-driven magnetic fields for gamma-ray generation and pair production. Plasma Phys. Control. Fusion 2018, 60, 054006. [Google Scholar] [CrossRef]
- Belland, A.R.; Kirk, J.G. Possibility of Prolific Pair Production with High-Power Lasers. Phys. Rev. Lett. 2008, 101, 200403. [Google Scholar]
- Bake, M.A.; Aimidula, A.; Zakir, A.; Abdukerim, N.; Ablat, A. Photon and positron generation by ultrahigh intensity laser interaction with electron beams. Front. Phys. 2018, 13, 135202. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).