Nesting Process Automation in the Footwear Industry: A Hybrid Approach to Minimize Material Waste

Abstract

In any industry, maximizing the use of raw materials is essential to reduce waste and costs, which also positively impacts the environment. In footwear production, components are typically derived from cutting processes, requiring optimized systems to maximize the use of different materials, minimize waste, and accelerate production. In this context, nesting is a technique that arranges shapes within a confined space to maximize area utilization and reduce unused space. As this problem is classified as NP-Hard, only algorithmic approximations can be employed. This paper focuses on optimizing the cutting of leather parts for shoe manufacturing. Footwear parts are cut from cattle hides, which are not only irregular in shape but also vary in resistance and quality across different areas of the same piece of leather. This study proposes automated nesting methods that aim to compete with current manual approaches, which are conducted exclusively by experts with deep knowledge of the characteristics of both the pieces and the leather, making the manual process time-intensive. This research reviews current methods and introduces hybrid ones, achieving up to 38.4× acceleration and up to 10.18% increase in nested pieces over manual methods.

1. Introduction

In any industrial sector, efficient use of materials, especially raw materials, and reduced waste and production costs are crucial, thus contributing to minimizing the environmental impact.

The final product in industrial manufacturing is typically composed of multiple components made from diverse materials, such as leather, wood, plastics, metal, and glass. These components are often obtained through precise cutting processes; for instance, metal parts are derived from metal foil. To maximize material utilization, companies must employ optimized cutting systems that minimize material waste and accelerate parts production.

Challenges associated with material optimization are prevalent across various sectors, including the furniture, automotive, and footwear industries. This article focuses specifically on the latter, examining methods to optimize leather parts production.

In traditional footwear manufacturing, various parts and components are precisely assembled to create a whole shoe. This process involves a wide array of materials, from leather or synthetic fabrics for the upper to different polymers for the sole. Additionally, various accessories and ornaments, such as laces, buckles, or decorative elements, are incorporated for aesthetic purposes.

Materials used for the upper and insole are usually leather or other flat fabrics, irregularly shaped in the case of leather, or regularly shaped in the case of fabrics or other synthetic materials. These materials are cut to match the shape of each piece in a shoe, which will then be assembled. During the cutting process, it is critical to maximize the use of these often-costly resources and to minimize waste or remaining offcuts that cannot be repurposed for other parts. This is where the concept of nesting becomes essential, as it optimizes the positioning of all parts to enhance material consumption.

Nesting is a process in which a set of shapes is arranged within a limited area to maximize available space and minimize unutilized space in the two-dimensional geometric plane. Typically, nesting incorporates a margin between parts to ensure that subsequent cutting does not compromise the integrity of adjacent parts.

This process is complex and, when performed manually, relies on skilled professionals who, through years of experience, can rapidly achieve the optimal positioning of parts of varying sizes and shapes, thus maximizing workspace efficiency and minimizing processing time. This expertise-driven nature underscores the need for automated nesting systems, and as a result, various algorithms have been developed to address this challenge with different success rates.

The implementation of automatic nesting solutions enhances the material utilization, reduces processing time and costs, and offers greater agility compared to manual methods. Additionally, it contributes to a reduced environmental impact by minimizing material waste.

In the footwear industry, the quality of the final product is significantly influenced by the use of leather animal hides and skins treated by a tanning process. Even leathers of the same origin (e.g., bovine and porcine) can vary in size and quality. Moreover, each leather contains areas of differing quality, which limits its use in obtaining specific pieces. For instance, parts that will be highly visible in the finished shoe must be cut from the highest-quality areas, typically located along the back of the animal. To achieve consistent quality across a pair of shoes, it is essential that the corresponding leather parts are obtained from the same leather, making optimal nesting both vital and complex. Furthermore, the footwear industry encompasses a wide variety of styles (e.g., boots, moccasins, and Strobel constructions), each with unique requirements regarding the shape and variety of parts. These differences require tailored approaches to obtain and assemble the components of each shoe model.

The main objective of this study is to identify and propose automated nesting methods suitable for the footwear sector that can effectively compete with the manual processes currently performed by skilled experts. Achieving this would lead to significant reductions in material waste and maximized material utilization, providing both economic and environmental benefits. Additionally, automating the nesting process would reduce the time required, addressing the inefficiencies of this traditionally labor-intensive task.

In line with these objectives, the research hypotheses are as follows:

• The application of various nesting algorithms will yield positioning outcomes comparable to those achieved by experts.
• Calculation time for positioning will be significantly reduced.

This article is structured in the following sections: Section 2 presents an analysis of the different nesting algorithms developed to date. Section 3 discusses the main types of footwear and their impact on nesting efficiency. Section 4 details the nesting algorithms employed in the testing phase and the results obtained. Finally, Section 5 summarizes the main conclusions of this research.

2. State of the Art

Cutting and packing problems are classified as NP-hard. NP problems are hard-to-solve decision problems studied by computational complexity theory. Within this framework, NP-hard problems are at least as challenging as NP problems. The two-dimensional rectangular nesting problem has been proven to be NP-complete [1]. Due to the added complexity of handling irregular parts, nesting problems are also considered NP-complete. Furthermore, the nesting problem encompasses considerable variability, with definitions that depend on the type of parts, containers, constraints, etc.

In studies where the master surface is typically a rectangle or an infinite strip, several common features are often overlooked:

• Convexity of the parts is frequently avoided.
• Free rotations are generally restricted, with only some specific rotation of the parts allowed in certain algorithms.
• Most solutions have been validated for both regular and irregular shapes or parts, on rectangular base surfaces, whether finite on both sides or infinite on one side. Nesting has even been studied on irregular base surfaces, such as leather in the footwear or fashion industries. However, no studies to date specifically address leather nesting for moccasin shoe parts or Strobel parts, marking this as a novel research area. Moccasin is a type of footwear in which a single piece of leather envelopes the entire foot. Strobel is another type of footwear, which takes its name from the method used to sew together the two pieces that conform it: the sole or lower part of the foot and the body, which covers the rest. Moccasins and Strobel shoes are unique in that they each incorporate either a single piece, or two or three smaller parts. During nesting, gaps of unused material typically appear between parts, which can accommodate smaller ones. However, the limited number of those parts in these types of shoes increases waste and complicates space optimization.

Most research articles focus on solutions for rolls of material with a fixed width and infinite length [2,3]. In this type of positioning, parts must be arranged to minimize both the area of material and the length of the roll used. This problem is commonly known in the literature as strip packing and is one of the most widely applied techniques for cutting parts on synthetic material.

One of the earliest algorithms proposed for strip packing was developed by Art [4], which introduced the concept of No-Fit-Polygon (NFP) to reduce the computational costs of intersections between two parts—a technique that remains in widespread use. In fact, among the different geometric tools developed to deal with nesting, the current mainstream method is NFP, as stated in [5].

Albano and Sapuppo [6] later presented highly influential algorithms for nesting problems, employing a tree-search-based method in Albano’s previous work with Adamowicz [7,8] and on the NFP concept. Tree searches are tree-type data structures used for search optimization, where efficiency is one of their main characteristics.

Most solutions proposed to minimize the space occupied in the placement of rely on heuristic algorithms (search for solutions that are not perfect, but good enough), as no exact algorithms have yet been developed. Only one approach in the literature, [9], proposes a mixed programming model (MIP) for parts with fixed orientation to solve the compaction and separation problem. This heuristic algorithm builds on the NFP concept and defines the inner-fit-rectangle approach, applying the same calculation rules as the NFP but on the inner side, thereby accelerating intersection calculations with the external edges. Following this, the Bottom-Left Greedy heuristic procedure is applied [2], introducing a random weighted length criterion that selects the longest parts with priority.

Additionally, the work by Lodi and Monaci [10] proposes integer linear programming models (programming problems where some or all of the variables are restricted to be integers), while Hifi and Roucairol [11] present an exact solution for the two-dimensional knapsack problem where the pieces are rectangular. This is one of the few examples of exact algorithms developed to address a subproblem within nesting, specifically the placement of small pieces in gaps left by larger ones. The previous study could only optimally prove a solution on two out of the three examples of broken crystals (up to 10 parts), concluding that the algorithm is unlikely to be viable for optimally solving nesting instances of manageable size. Consequently, it is recommended for use primarily in filling smaller cutouts and holes with the smallest pieces.

Heuristic solutions to the nesting problem can be approached either by generating partial solutions or by working directly toward global solutions. Various heuristic strategies have been applied to address the nesting problem, with the following being the most notable:

• The Bottom-Left strategy, first proposed by Albano and Sapuppo [6], arranges parts by placing each one “as low and as far to the left as possible”.
• The TOPOS algorithm [12] employs a strategy that iteratively builds a partial solution by adding the part that best satisfies the algorithm’s selected criteria from those proposed by it. Newly added parts are positioned around the already-placed set. An exhaustive analysis of algorithm performance is conducted, testing a combination of 126 possibilities, among the criteria proposed, and comparing these results with those obtained with other algorithms using a dataset common in the literature.
• The JOSTLE algorithm by Downsland et al. [3] introduces the possibility of placing parts behind those already positioned. This involves a series of iterations of a simple placement of parts, consecutively to the left and then to the right, resembling the effect of ‘shaking’ a box, the parts thus being rearranged in their best position.

Conversely, numerous publications propose solutions based on the linear programming (LP) technique for finding the best possible solution with an objective and a set of restrictions for the compaction and part separation techniques, often combined with various heuristic algorithms to achieve an improved initial solution.

The compaction technique can improve a valid initial nesting by applying a series of coordinated movements of the pieces to obtain an optimal arrangement. During these movements, no overlapping between parts is allowed and they must be continuous, so that parts cannot jump over each other. Furthermore, rotations are not allowed. The technique is repeated iteratively as long as improved nesting is obtained, with less than ten iterations usually being necessary to completely compact a design.

The separation technique focuses on resolving overlapping of parts in initial arrangements. As in compaction, it consists of applying coordinated movements to the parts. This technique is also iterative, and in most cases, fewer than ten iterations are required to fully eliminate overlaps.

In the application of metaheuristic algorithms for solving the nesting problem, several notable studies are as follows:

• Genetic algorithm (GA): This algorithm has been employed by researchers such as Kenmochi et al. [13] and Anand and Babu [14], among others. Recently, Martínez et al. [15] combined a genetic algorithm (the problem-solving technique that was inspired by biological evolution as a strategy for the resolution) with a greedy strategy to address the nesting of irregular parts on a rectangular master surface. Their approach includes a coding technique that significantly reduces the computations of the algorithm.
• Particle swarm algorithm (PSO): Developed by Kennedy and Eberhart [16], this algorithm is based on the collective movement of living organisms. Through a series of iterations, particles—representing candidate solutions—navigate the search space with defined velocities and directions, aiming for convergence on optimal solutions. The aim is for the swarm to converge toward the best solutions. Analyses of this technique can be found in studies such as [17] and the original authors’ own review [18].
• Greedy Randomized Adaptive Search Procedure (GRASP): Proposed by Hart and Shogan [19], it is a greedy randomized search method based on the repetition of two phases: a greedy construction followed by local search.
• Simulated Annealing (SA): As demonstrated in studies [20,21], this strategy explores the search for a solution in the neighborhood of a current solution, allowing probabilistic acceptance of suboptimal solutions. This strategy is especially effective in discrete search spaces.

Recent advancements in robust solutions for the nesting problem have increasingly focused on advanced image processing techniques [22] and neural networks [23]. Several recent studies regarding the application of artificial intelligence on nesting/packing are worth mentioning. In [24], a novel hierarchical reinforcement learning (RL) approach is proposed for packing irregular objects. The system employs a two-level architecture: a manager network that plans the packing sequence using object heightmaps, and a worker network that executes the placement of individual objects. This hierarchical structure is trained with a self-supervised Q-learning framework, using packing results to reward efficient packing (low top height, high volume utilization, and stable placements). The proposed method is demonstrated in both simulated and real-world robotic packing scenarios. Fang et al. [25] explore the application of RL for packing 2D irregular patterns. A mathematical model is formulated, and RL algorithms based on Monte Carlo, Q-learning, and Sarsa learning are implemented, incorporating a custom reward and strategy update mechanism tied to packing outcomes. Combining these RL-based sequence generation methods with a classical Bottom-Left positioning algorithm, the system achieves effective packing. Standard test cases validate the proposed method, showing competitive performance against traditional heuristic approaches. This work lays the groundwork for future packing solutions based on Deep Reinforcement Learning (DRL) and offers the potential for improved material efficiency. In [26], an end-to-end RL strategy for arranging scattered irregular objects within a crate using a series of pushing actions is proposed. A sparse reward function, based on object connectivity, guides the learning process. Proximal Policy Optimization is used to simultaneously train a convolutional neural network encoder and a fully connected actor-network. Evaluated in both simulation and real-world experiments with varying object numbers, shapes, and materials, the proposed method demonstrates efficient and flexible arrangement, achieving an 85% success rate in simulation and 75% in the real world. The trained network exhibits strong generalization capabilities to previously unconsidered objects. Xiong et al. [27] propose a novel robotic system for high-performance 3D bin packing using DRL. The system comprises three key components: first, a DRL agent that tackles the 3D bin packing problem, formulated as a Markov Decision Process, using a heightmap-based environment; second, a candidate map mechanism to efficiently explore the action space and improve DRL training; and third, a robotic system with a motion primitive and vision module to ensure robust real-world execution. The experimental results on two datasets show significant improvements in space utilization (over 2.7% and 3.8%) compared to baselines, with performance scaling to different container sizes. In [28], the first DL approach to predict scrap generated during nesting-based manufacturing is presented. The proposed framework estimates scrap based solely on part geometries, without needing prior nesting arrangements. This is achieved through three interconnected neural networks: a geometry encoder, an interdependence analyzer, and a scrap predictor. Key contributions include a novel sustainable manufacturing practice for pre-nesting scrap prediction; a DL framework considering the geometry of the entire nesting set; a real-world data-derived baseline for comparison; and experimental validation on a private sheet metal dataset, demonstrating at least twice the accuracy and 16 times better data fit compared to the baseline, achieving a mean absolute percentage error of 24.8%. Gahm et al. [29] address the challenge of integrating complex nesting problems (CNPs) into hierarchical production planning. The proposed solution is a machine learning-based anticipation method for batch feasibility. A prediction framework evaluates various machine learning techniques, using newly designed feature vectors to represent CNP instances generated by a novel procedure (88,200 instances from 6000 shapes). An artificial neural network is identified as the most effective predictor, achieving 98.8% accuracy in batch feasibility decisions. This approach offers a practical way to incorporate complex nesting constraints into higher-level scheduling problems, improving efficiency and solution quality.

A comprehensive review of the literature reveals that most studies concentrate on fitting both irregular and regular parts onto regular master parts. However, as previously noted, there is a lack of research specifically addressing the type of parts used in the assembly of moccasin and Strobel footwear, which are the focus of this study.

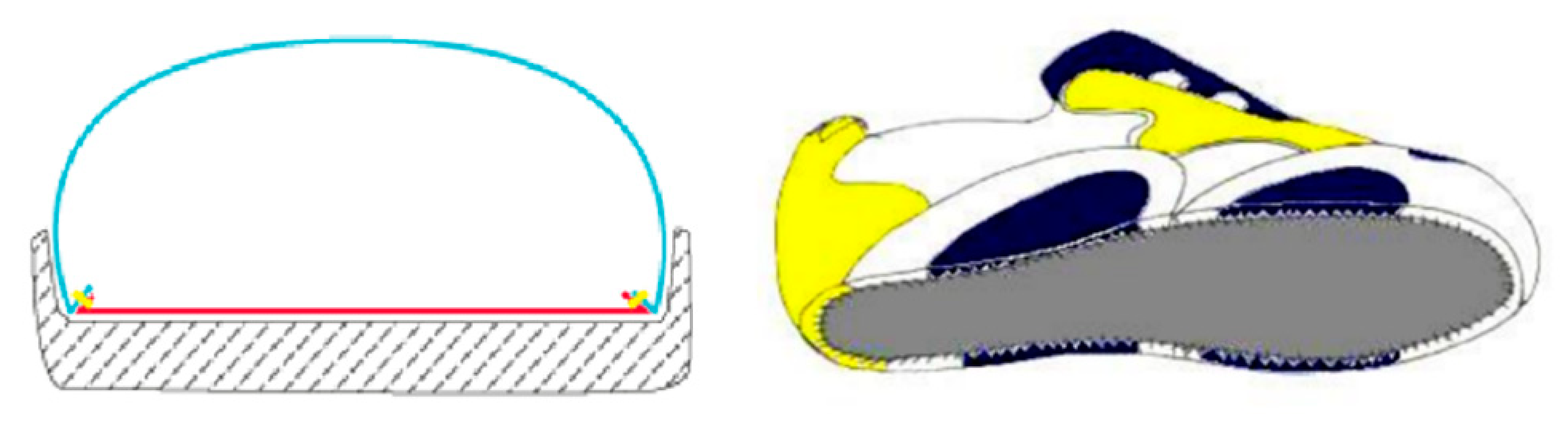
An additional challenge of interest is the nesting of irregularly shaped parts onto irregular surfaces, such as leather, as shown in Figure 1.

Leather contains varying quality areas, defects and even holes, all of which condition the positioning of parts. Figure 2 illustrates a nesting layout on leather with these characteristics. It can be observed that the area in red corresponds to the best quality of the leather, in which the most visible parts of the footwear are positioned, while the yellow area, being of a lower quality, is used for the rest of the pieces. The blue areas are discarded because of their low quality or because they are holes.

This issue has been less extensively explored in the literature. Among the studies identified, a classification can be made distinguishing those that consider variations in leather quality from those that do not.

Studies that do not consider leather quality include:

• Tan et al. [30] developed a hybrid genetic algorithm with SA (Simulated Annealing) that introduces a mutation operator to facilitate faster convergence and improve result accuracy, leveraging SA’s thorough exploration of the search space.
• Lee et al. [31] proposed a heuristic algorithm of quick location and movement (QLM) to solve the positioning of irregular shapes on multiple irregular sheets. The proposal includes two main parts: first, the approximation of irregular shapes to a polygon by means of a cluster of straight lines; second, the arrangement of the approximated shapes.
• Zhang et al. [32] introduced a new nesting algorithm for leather manufacturing that employs a bottom-left heuristic strategy to position parts on the leather. Optimal placement sequence, including rotation, is determined through a SA based on a genetic algorithm.

Other studies do consider leather quality, adding further variability to the problem:

• Heistermann et al. [33] account for four quality levels and a fifth for holes, using a greedy algorithm to solve the problem. To simplify the process, the algorithm first reduces the master surface’s polygons by calculating an outer and an inner polygon. The focus is defined as a specific edge location for positioning the next piece, with two modes: fixed focus, where parts are consistently positioned on the same side, and variable focus, where parts are placed in different areas of the master surface. The algorithm iteratively places parts in the best provisional position from all tests, followed by a compaction algorithm to optimize positioning.
• Crispin et al. [34] make significant contributions to genetic algorithms by presenting coding methodologies that, beyond standard parameters, incorporate both leather quality and specific quality requirements for the parts. Their approach also considers directionality, addressing stretching requirements for both the parts and the leather.
• Baldacci et al. [35] uses raster representation due to its lower computational cost, as polygonal solutions with free rotations hinder the use of NFPs, which expedite calculations in polygon-based heuristics (rotating a part invalidates the precomputed NFP). This study proposes generating global solutions through different constructive placement procedures, which are then employed in an iterative algorithm based on a Lagrangian relaxation approximation -a technique with proven effectiveness in heuristic frameworks [36] and widely applied in minimizing the traveling salesman problem.
• Rodríguez A et al. [37] conducted one of the most recent studies, with an in-depth exploration detailed in Rodriguez’s doctoral thesis [8,38]. This work presents a genetic algorithm to solve the nesting problem with the objective of waste minimization, and previous studies by the author also introduce a fitness function for this genetic algorithm [8,39].

The solutions presented in these studies, however, are not directly applicable to the cases examined in this article. As noted in much of the literature, part typology—particularly part size—is a critical consideration in nesting.

The nesting algorithms studied so far are designed for a varied set of input pieces in different sizes, especially medium and small. In these cases, the space between two neighboring pieces can be filled by a third, smaller one, thus improving the use of material and reducing its waste.

In the case studies of this article, the number of pieces found in non-conventional footwear types, such as moccasins and Strobel, is small and of large size. For these cases, the algorithms studied are not optimized, generating nestings with a higher wastage than those obtained with manual positioning. Moreover, these methods lack the possibility of limiting the range of solutions. This is especially important in the problem of nesting in footwear, since leather is a natural element, it is not homogeneous and does not have the same consistency over its entire surface. Experts know these characteristics and place the parts of the shoe that will suffer most from wear (e.g., the toe cap) in the strongest areas of the leather. With this algorithm, parts can be placed in a certain area; within this area, the algorithm will seek to place them in such a way as to produce the best nesting, although it will not allow them to move outside this area. This is not possible with the algorithms analyzed.

The use of a hybrid method allows the advantages of each of the algorithms to be combined, minimizing the calculation time and equaling the results of manual positioning in terms of wastage.

Because current automatic algorithms do not obtain good nesting results for these types of pieces, the positioning must be conducted manually, or by using dies for manual cutting. This has a negative economic impact, as the time taken to cut these types of construction is longer, and usually involves a higher consumption of material, as it generates more waste.

3. Nesting in the Footwear Sector

Minimizing material consumption to support green policies is a prominent priority in industry. In the footwear sector, many products are made from leather—an expensive resource that must be used as efficiently as possible. Additionally, leather undergoes chemical treatments that make it challenging to recycle.

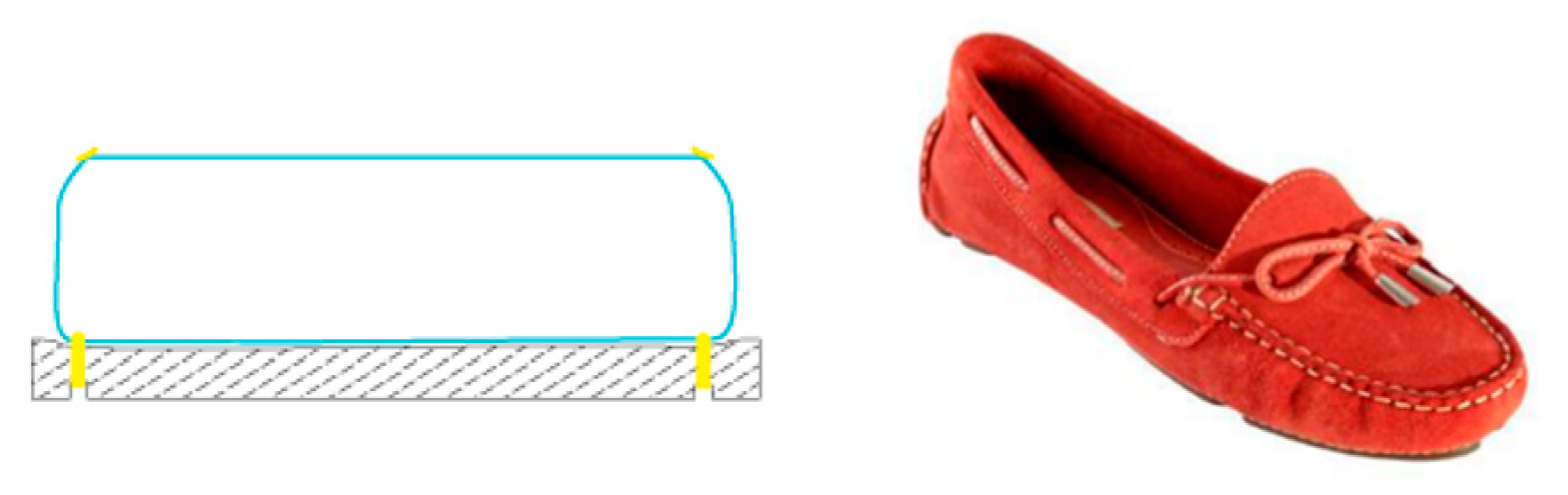
The footwear industry encompasses a wide variety of shoe types with different assembly methods. The most common and extensively used technique is the so-called ’glued construction’, as shown in Figure 3. The sole and cut are impregnated with contact glue, which is reacted by heat or light so that when pressed and joined together, it is sealed.

Beyond the conventional construction, there are other manufacturing techniques that, due to their specific characteristics, require distinct methodologies to achieve the desired result. Among the main manufacturing typologies in the market are the ‘moccasin’ or ‘Kiowa’ type and the ‘Strobel’ type, which are the focus of the nesting strategies discussed in this paper. Figure 4 depicts a Strobel shoe, while Figure 5 and Figure 6 illustrate a moccasin and a close-up of the assembled shoe.

It Is Important to note that moccasins can be further classified Into subtypes, including half moccasins or ‘car shoe’ style moccasins. Strobel shoes, similarly, can be categorized based on the stitching positioning: on the upper or on the bottom.

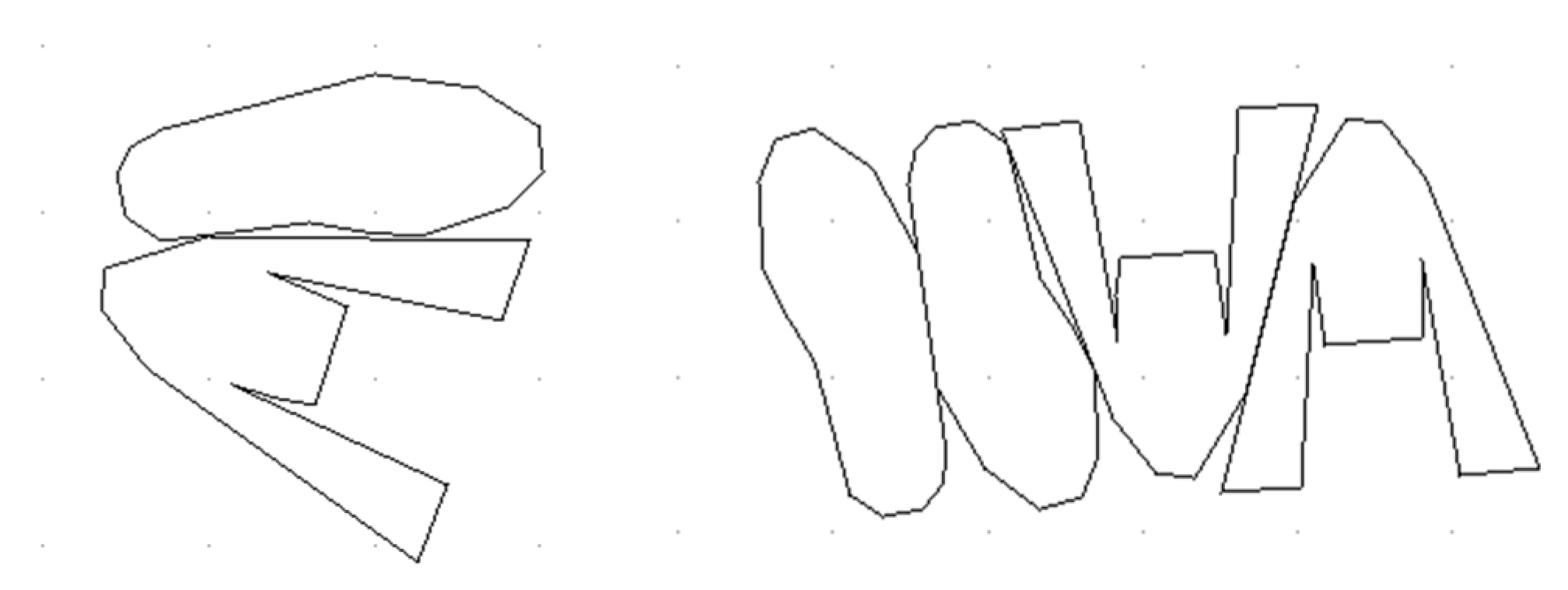
Unlike traditional or ‘cemented’ shoes, non-conventional footwear types—such as those discussed in this paper—consist of a reduced number of parts: a single part in the case of Strobel and three or four parts in the case of moccasins. Figure 7 shows the wide variety of parts typically required for traditionally assembled shoes, while Figure 8 highlights the significantly reduced number of parts in Strobel and moccasins.

In Strobel constructions, a single part is used to cover the whole upper of the shoe, serving as a base onto which the remaining parts are sewn. The entire assembly is then sewn to the sole using a stitching technique known as Strobel.

The main challenge, therefore, is the efficient nesting of moccasin and Strobel shoes as single-part constructions, which constrains the problem’s initial characteristics as follows:

For moccasins:

• Since these types of footwear are typically made of leather, the available space—or master part to be cut—will be, therefore, irregular in shape.
• The parts to be cut are generally large compared to parts used in other types of shoe constructions, except for smaller shoe parts that are occasionally added to these models, which help minimize material waste.
• The objective is to place as many complete pairs in one leather, filling any remaining space with as many pieces as possible to optimize material usage.

For Strobel, this study focuses on uppers comprised of a single part, which are typically used in sneakers, characterized by their comfort, sporty design, and ability to adapt to different clothing styles:

• These parts are usually made of synthetic material, providing regular, rectangular space.
• Each part to be cut is unique; for this study, a 2000 × 1000 mm measurement was used as a reference, with mirrored parts required for the left and right feet of each pair.
• The objective is to place as many complete pairs as possible on a single sheet of material, filling any remaining space with additional parts to optimize material utilization.

As highlighted in the previous section, the nesting of shoe parts on leather remains unexplored in the literature. Most research to date has focused on parts for traditionally constructed footwear. However, single-piece moccasin and Strobel parts differ significantly from these, necessitating a dedicated study, since the nesting of such moccasin and Strobel parts has not been thoroughly addressed in scientific literature.

In the following section, automatic nesting techniques will be applied to real footwear-cutting cases to evaluate whether material utilization rates comparable to manual positioning can be achieved. Additionally, the calculation times for these techniques will be assessed.

In this paper, areas of skin quality were not taken into account in the experiments carried out, but the method allows the selection of areas of low or no variability of the pieces.

4. Experimentation

This section presents the results from applying various algorithms that enable the automatic nesting of parts used in different footwear assembly cases: full moccasins, moccasins without wrinkles and half moccasins. Due to the NP-hard nature of these algorithms, they provide approximate rather than optimal solutions, which are validated against manual nesting results obtained by experts. The objective is to achieve automatically similar or superior outcomes in two key aspects: time efficiency and, with a focus on minimizing waste.

In a manual positioning, the expert initially places a cutting piece on the leather and after it he places another around it trying to minimize the use of the material. The process is repeated as long as he is able to position pieces. The selection of the next piece depends on its geometry and the skill the expert has acquired over the years. Automatic positioning allows all parts to be tested in all possible positions regardless of their geometry, selecting the positioning that generates the least waste of material.

The time required by an expert to perform manual nesting on a leather varies depending on the size and geometry complexity of both the leather and the parts to be positioned, generally ranging from two to five minutes. Figure 9 illustrates an example of manual nesting.

It is important to note that each different piece needed to form a complete set for footwear fabrication is represented by a distinct color. In the images showing the hybrid algorithm approach, the complete sets nested by the Jaya algorithm are represented in green, while the pieces nested by the NFP algorithm retain their original colors.

With regard to the selection of Jaya as the metaheuristic method for this study, according to [40], there are more than 500 of these metaheuristic algorithms documented in the literature. The authors have considered that it would be neither fair nor rigorous to select a small number of these algorithms for comparison with Jaya applied to nesting. The first remarkable advantage of Jaya over most other algorithms is that it does not require the setting of specific parameters at the beginning of the algorithm. In addition to this reason, the authors’ justification for the use of the Jaya algorithm is given by the numerous references documenting the benefits of using Jaya over other metaheuristic algorithms such as Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Differential Evolution (DE), and so on. Among these references, it would be useful to consult [41,42,43].

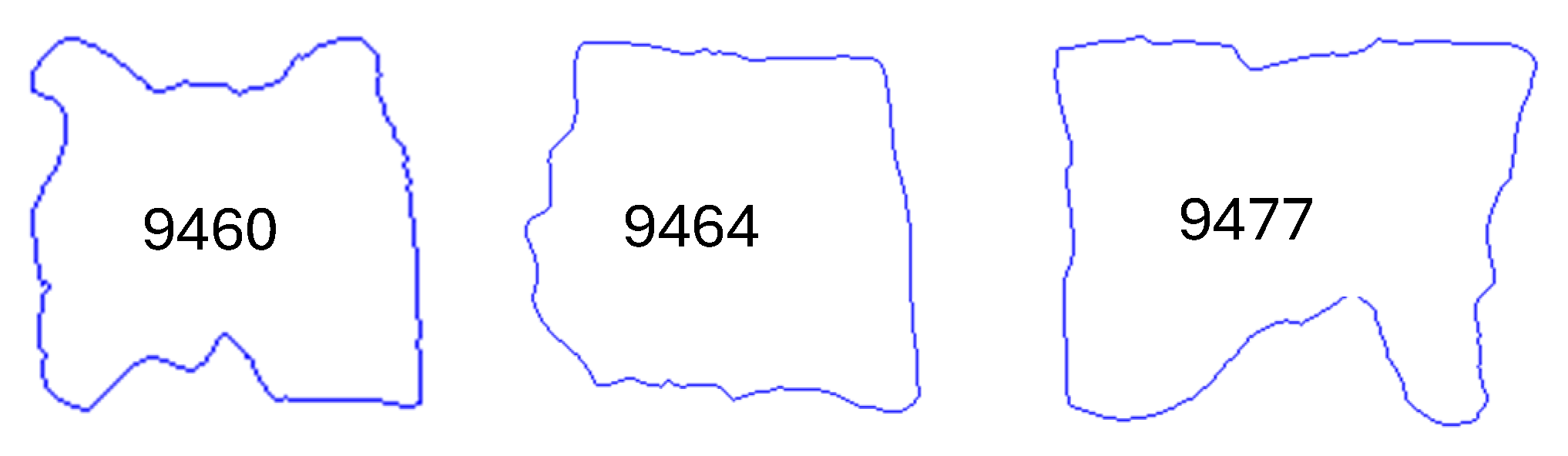
The results obtained in the different case studies are presented below. For this analysis, three different leathers have been used as references, as shown in Figure 10.

The selection of these three pieces of leather has been made based on the experience of the expert in manual positioning, representing the diversity that we can find according to their geometry. For each leather, three case studies have been carried out with sets of pieces for a full moccasin, a moccasin without wrinkles, and a half moccasin, all of them undergoing a first manual positioning and then comparing the result obtained with an automatic positioning, based on raw material usage and time spent.

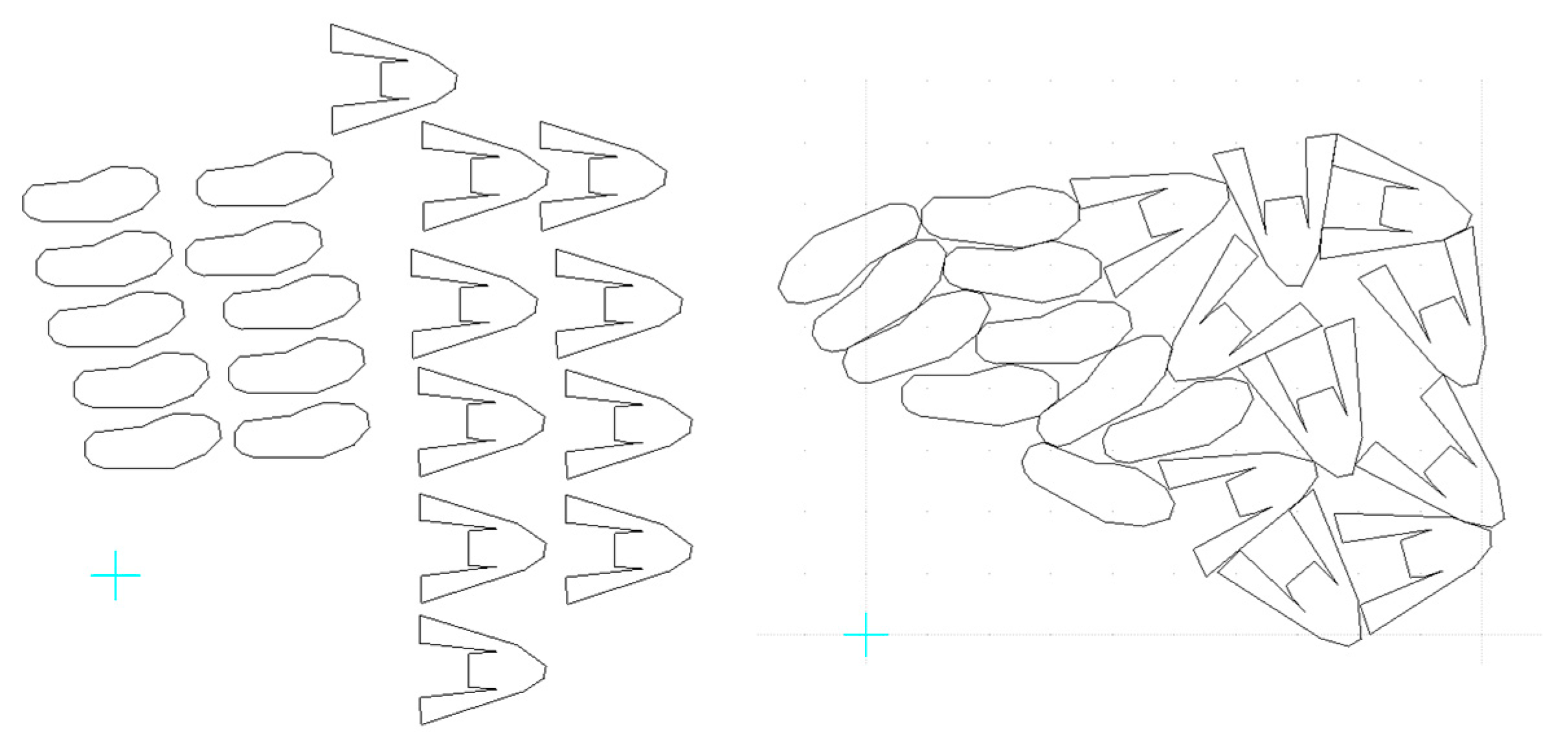
4.1. Case Study 1: Full Moccasin

In this case, a full moccasin consisting of two parts was used. The algorithm successfully identified the optimal placement without material constraints for one and two moccasins (Figure 11).

However, as the number of parts increases, the algorithm diverges from the optimal arrangement. To maximize material utilization, an optimal placement with few parts can be identified, establishing a pattern that guides the overall layout (Figure 12).

As shown in Figure 13, as the number of parts increases, the algorithm tends to maintain these parts in positions close to the original placement. This behavior is due to the expanding search space with each additional part, which increases the likelihood of collisions when parts are moved or rotated, leading to discarded solutions. With a larger number of parts, the algorithm favors configurations with minimal movements and rotations, which avoid collisions from the initial arrangement.

Utilizing the Jaya algorithm (powerful optimization algorithm proposed for solving the constrained and unconstrained optimization problems) to determine the relative placement of the set parts, followed by the NFP algorithm to maximize the number of sets positioned according to these relative coordinates, achieves leather utilization comparable to that of manual nesting, accommodating eighteen sets (Figure 14). The manual nesting includes four additional identical parts that cannot form a complete moccasin. Since these additional parts do not form complete sets and require spare complementary parts from other cuts, they are considered non-critical fillers.

Using another leather (9464, see Figure 15), the algorithm achieves the same result as the manual, fitting fifteen sets. Again, manual nesting adds three parts, while automatic nesting only includes one.

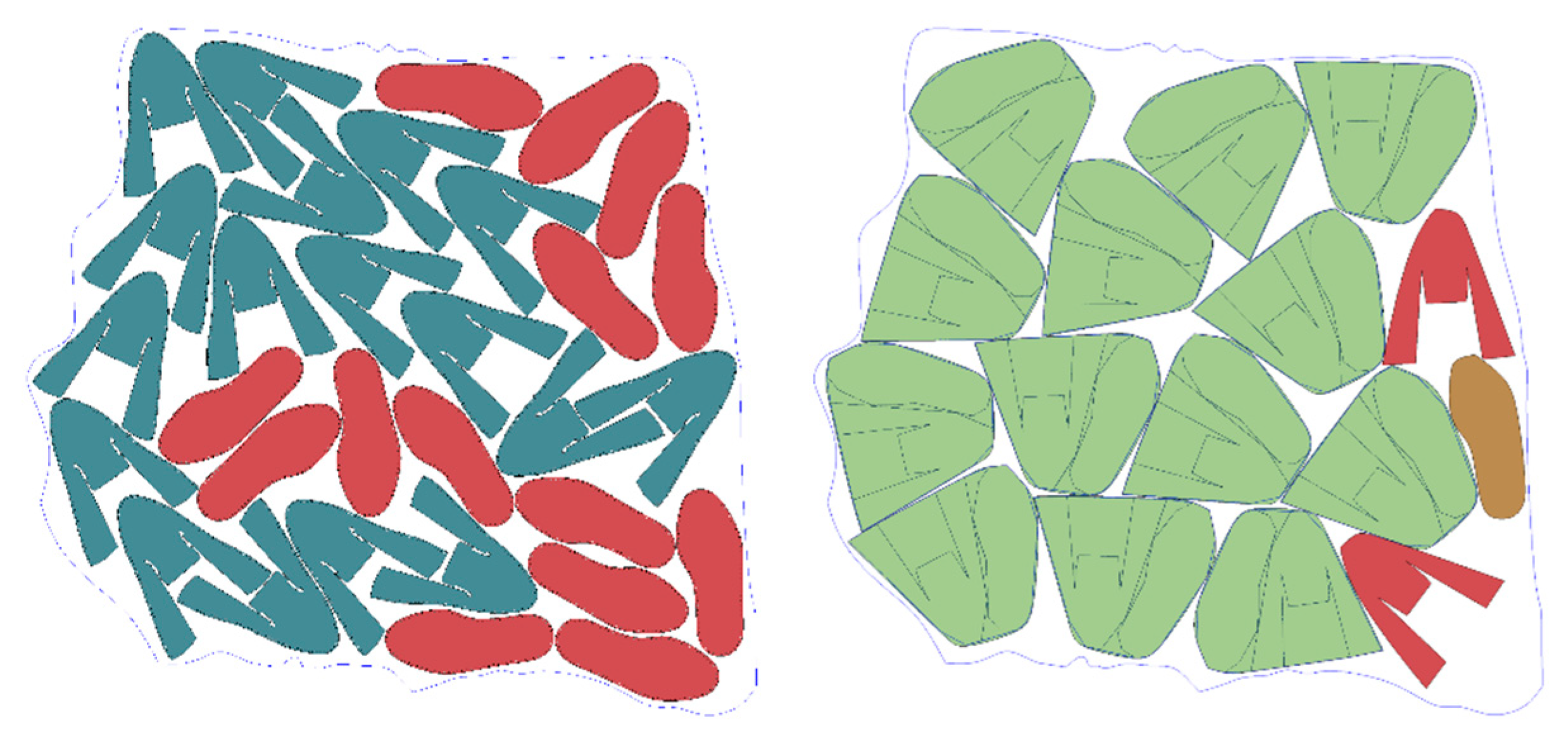
4.2. Case Study 2: Moccasin Without Wrinkles

This case study is focused on a moccasin without wrinkles, which consists of four different parts. As in case study 1, the automatic nesting solution generated by the Jaya algorithm (see Figure 16) can be used as a template to establish an effective placement pattern for manual nesting.

Applying the hybrid automatic nesting (Jaya + NFP) shown in Figure 17 yields results comparable to the previous case, accommodating fifteen sets and 36 parts.

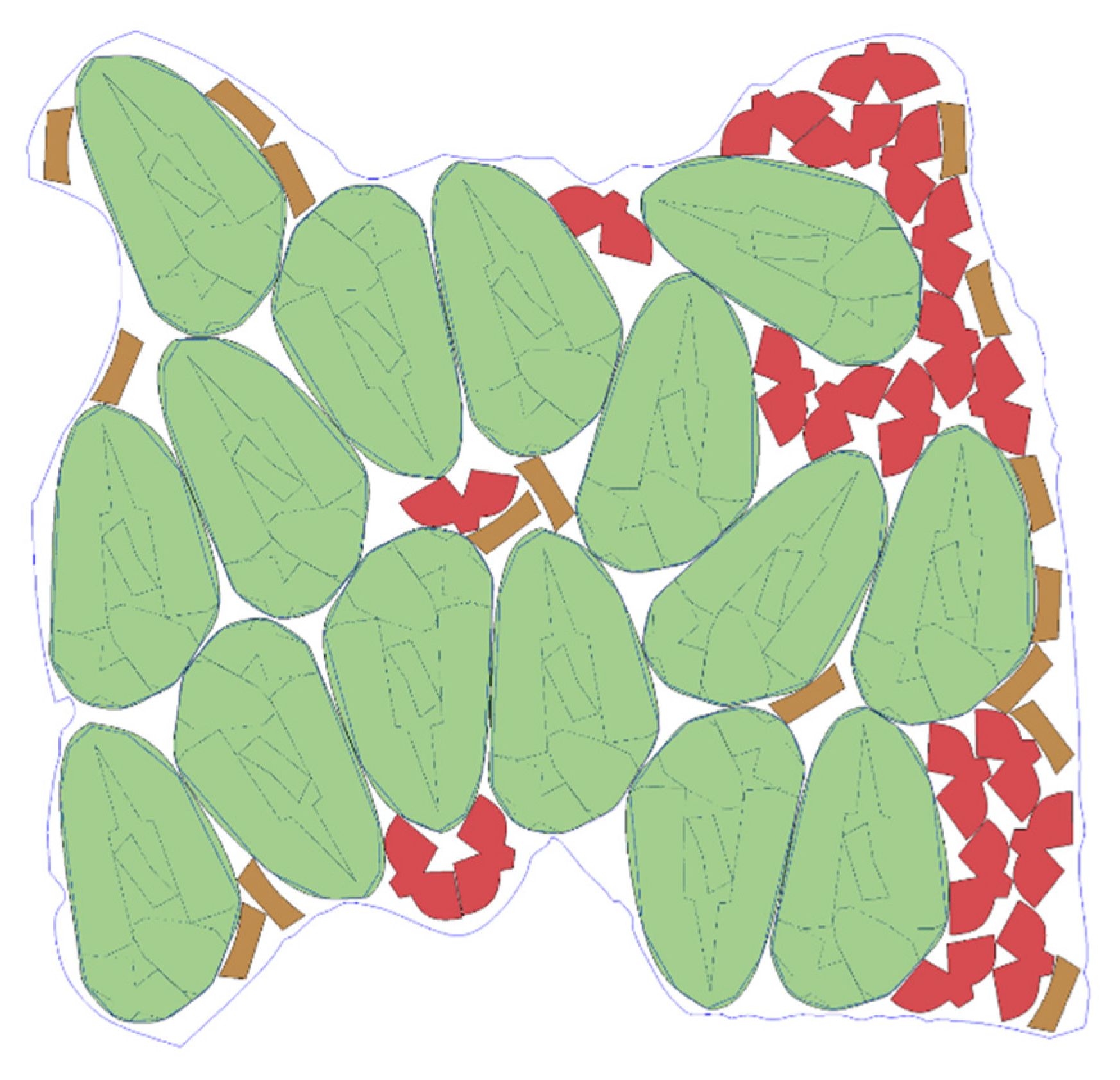
4.3. Case Study 3: Half Moccasin

In this case, we examine automatic nesting for a set of half-moccasin parts. As shown in Figure 18, the placement differs slightly from Case Study 2 due to variations in the larger part. Again, the automatic nesting placement produced by the Jaya algorithm suggests an optimal pattern for positioning the set of parts.

Alternatively, automatic nesting can be performed on parts of a set using only two parts, as shown in Figure 19. This placement allows for nesting on leather utilizing traditional heuristics, such as prioritizing the placement of the largest parts.

If we compare it with manual nesting, we can observe that in this case we obtain a slightly lower performance with automatic nesting, as shown in Figure 20. For the case of leather 9464, the manual nesting manages to fit 14 complete sets and 5 additional parts (see Figure 20). Automatic nesting using only the NFP algorithm fits 11 complete sets and 9 additional parts (see Figure 21), while automatic nesting using Jaya + NFP fits 13 complete sets and 16 additional parts (see Figure 20).

The data in

Table 1. Comparison of results.

		Nesting Jaya + NFP			Nesting NFP			Nesting Manual
Case	Leather	Sets	Parts	T (s.)	Sets	Parts	T (s.)	Sets	Parts	T (s.)
1	9460	18	36	2.547	19	39	3.922	18	40	*
1	9464	14	29	1.812	15	31	2.156	14	31	*
1	9477	17	34	2.296	18	38	3.535	19	38	*
2	9460	15	97	6.234	17	80	35.422	-	-	-
2	9464	12	60	4.891	13	67	17.625	-	-	-
2	9477	15	81	3.844	17	75	19.656	-	-	-
3	9460	16	87	5.703	18	86	15.842	19	78	*
3	9464	13	68	3.796	11	53	10.453	14	61	*
3	9477	15	88	4.062	16	74	15.016	16	72	*
Average		15	64.44	3.91	16	60.33	13.74	16.7	53.3	225

* The estimated time required by an expert, ranging from two to five minutes.

reveal three key trends across the different nesting approaches. First, the hybrid algorithm (Jaya + NFP) shows superior computational efficiency, completing operations in an average of 3.91 s, a 71.54% reduction (3.51× speedup) compared to NFP’s 13.74 s and a 98.26% reduction (57.54× speedup) versus manual nesting’s estimated average of 225 s. Second, while manual nesting achieves the highest average number of sets (16.7), the automated approaches perform comparably, with NFP averaging 16 sets and Jaya + NFP averaging 15 sets. Third, in terms of total parts placed, Jaya + NFP shows the highest efficiency, with an average of 64.44 parts per leather, compared to 60.33 for NFP and 53.3 for manual nesting. This higher total part count can be particularly advantageous in production scenarios where the extra individual pieces can still be utilized, unlike in set-based production, where incomplete sets have limited value. These findings indicate that automated approaches, particularly the hybrid algorithm, can match expert-level nesting efficiency while dramatically reducing processing time.

5. Discussion

This paper has analyzed nesting processes applied to real-world cases of footwear component cutting. This inherently complex process is further complicated by the unique characteristics of the sector, which relies on raw materials of animal origin that are irregular both in both shape and homogeneity. Moreover, the variability across footwear models limits the practicality of using expert rule-based systems.

The manual positioning used in our study has been carried out by a qualified expert with a high level of experience gained from years of practice. The learning curve depends very much on the individual’s skills and cannot be quantified. For the expert, the result obtained is the best solution, but for another expert, it may be different. There is no manual positioning methodology. The expert learns how to perform the positioning from the person who teaches him and from his own experience.

A comprehensive comparison has been conducted between nesting results achieved by human experts and those produced by the proposed automated systems. The results obtained by automatic positioning have achieved a similar or slightly lower use of the raw material compared to manual positioning, so that the initial objective has been met, but no improvement has been achieved in this aspect. However, the objective set with respect to the time spent on resolution has been amply met, as a drastic reduction in time has been achieved.

With the NFP algorithm, good results are obtained when we have a wide variety of pieces in different sizes, where the unused material areas between two pieces can be used to place another smaller piece. This is the case in traditional or ‘cemented’ shoes. However, in non-conventional footwear types—the object of this paper—the number of pieces is reduced, and hybrid algorithms are the ones that have adapted better to this problem, obtaining more optimal results.

The findings of this study are promising, suggesting that automated nesting systems overall can successfully match the material utilization efficiency of expert operators while offering significant advantages in processing speed, achieving a 98.26% reduction in processing time compared to manual operations. By employing hybrid algorithms based on metaheuristic approaches and greedy strategies, the study has proven that automated approaches can be particularly effective when applied to the footwear component nesting. The drastic reduction in processing time achieved by these automated systems enables manufacturers to significantly accelerate their cutting operations without sacrificing material optimization. This advancement is particularly valuable in an industry where rapid production cycles and material cost management are decisive competitive factors.

The application of the strategy applied to this paper could be useful in other fields, such as communications. There is a problem of a similar nature that tries to find the best location for an array of antennas or repeaters to maximize their coverage [44]. In this problem, there are also “forbidden” areas where it is not possible to locate antennas or limitations in the area where repeaters can be located. Genetic algorithms have already been implemented to provide a solution [45]; however, this algorithm would make it possible to fix these zones and evolve towards the optimal solution.

Future work will focus on expanding the range of nesting algorithms to further improve efficiency. Additionally, these algorithms will be used to develop a sufficiently comprehensive knowledge base, enabling the integration of neural networks capable of learning to construct even more efficient nesting configurations. To ensure that machine learning algorithms can effectively address this problem, it is essential to establish a sufficiently extensive training dataset. The primary challenge lies in obtaining this dataset for two main reasons. First, nesting experts are highly protective of their work, and they are generally reluctant to share it with other professionals, particularly if the goal is to replace them with AI algorithms. Secondly, the variability in models, sizes, and skin types is so significant that, even with the experts’ consent, the time required to collect several thousand samples would be considerable. One potential solution is to employ synthetic nesting generation techniques, although this approach may result in biased outcomes.