Study on the Multi-Hazard Responses of Transmission Tower-Line Systems Under Fire and Wind Loads Using ABAQUS
Abstract
1. Introduction
2. Failure Criteria for Components at High Temperatures
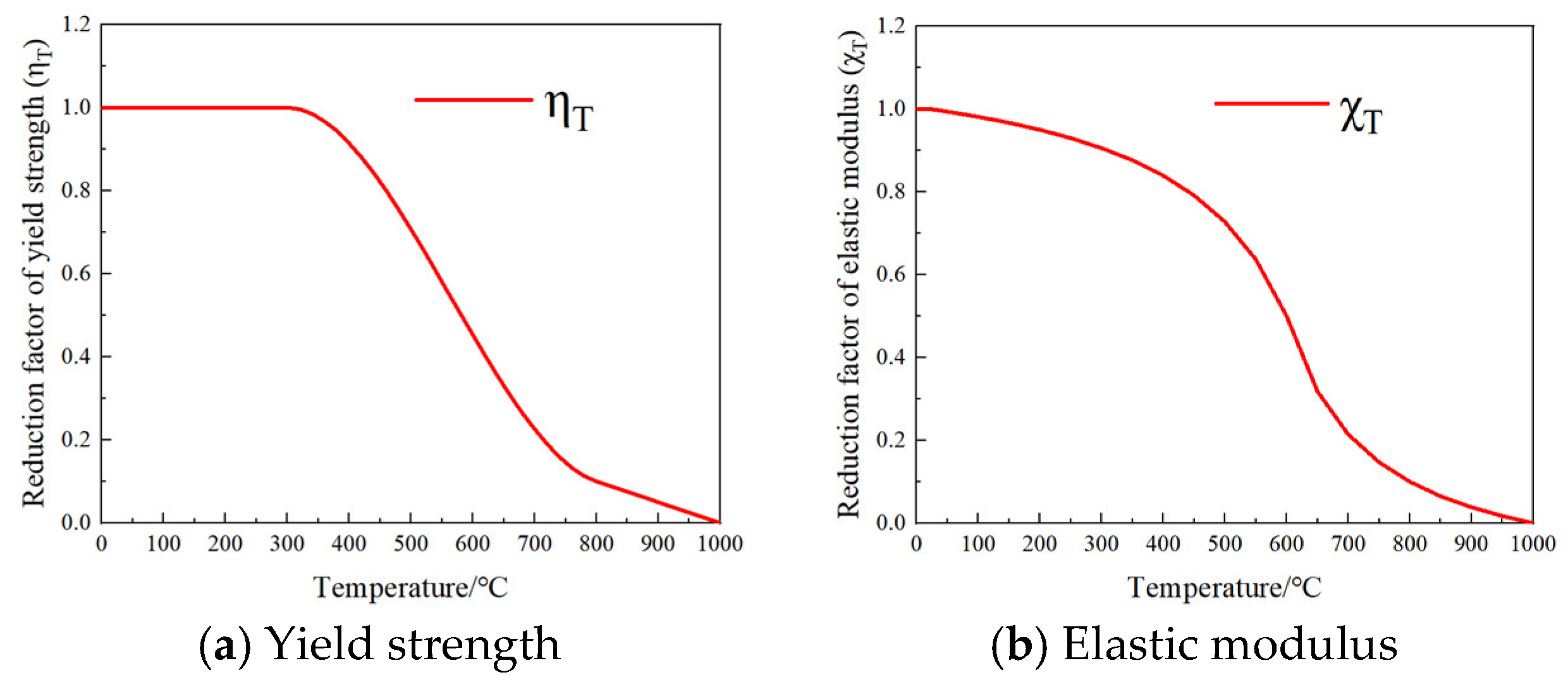
2.1. Reduction Factors for Yield Strength and Elastic Modulus
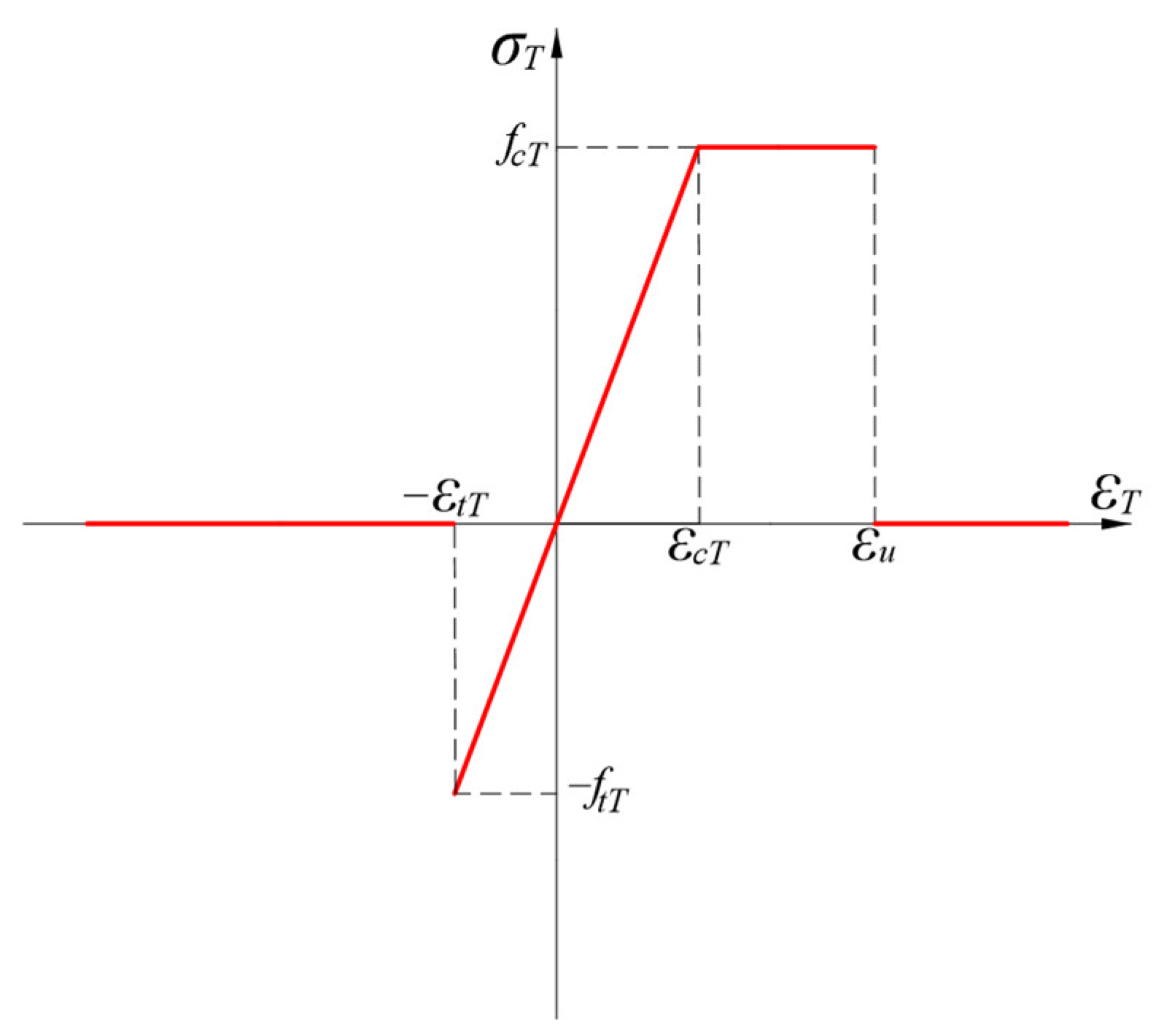
2.2. Failure Criteria of Materials
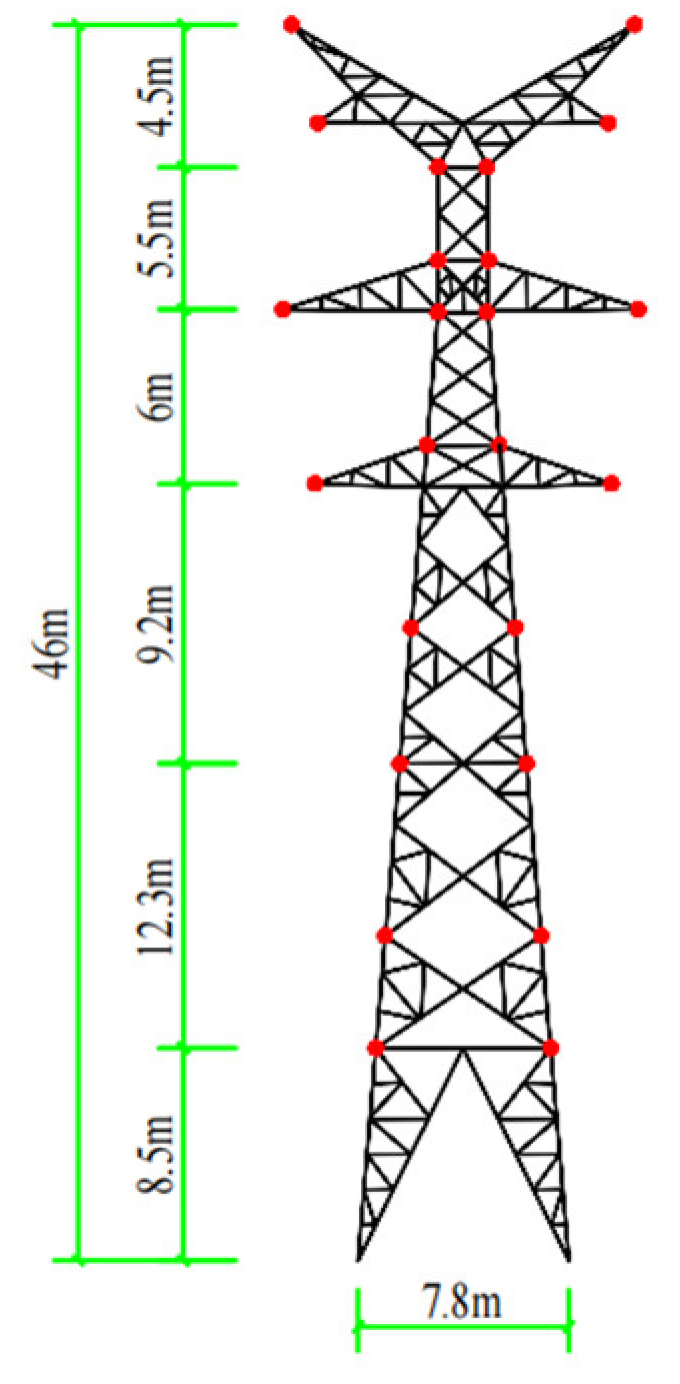
3. Project Overview
3.1. Finite Element Model
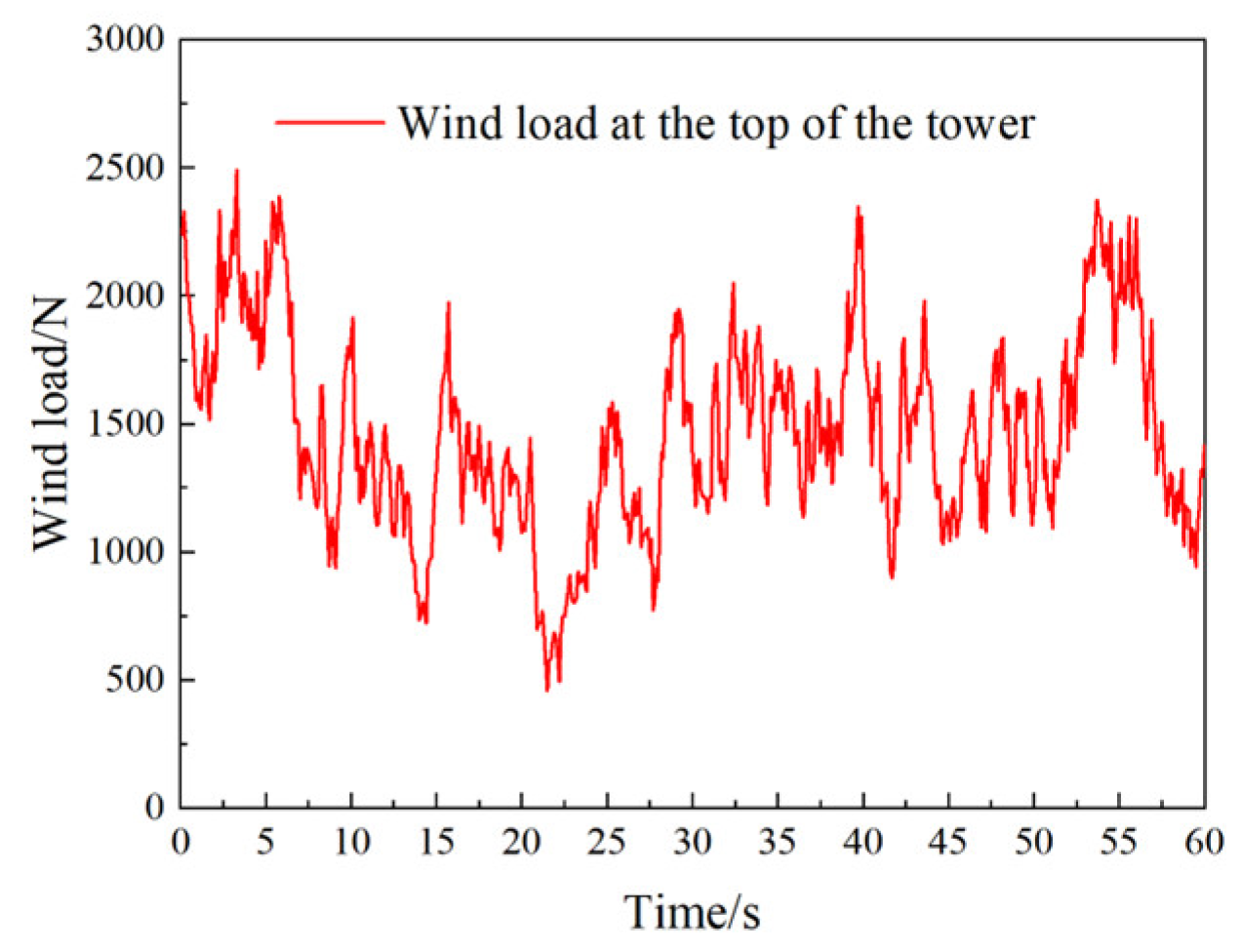
3.2. Load Application
4. Finite Element Simulation Results
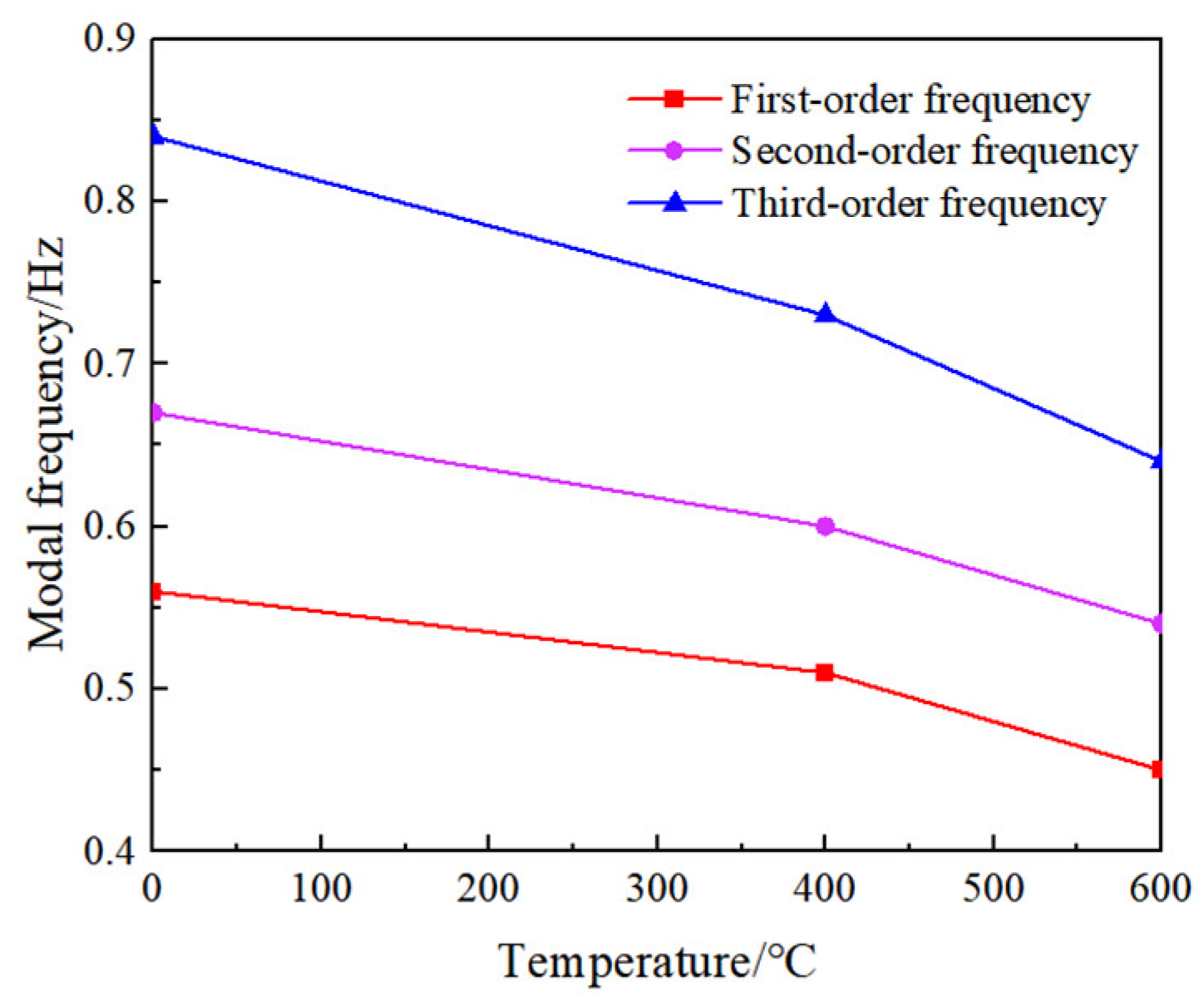
4.1. Modal Analysis
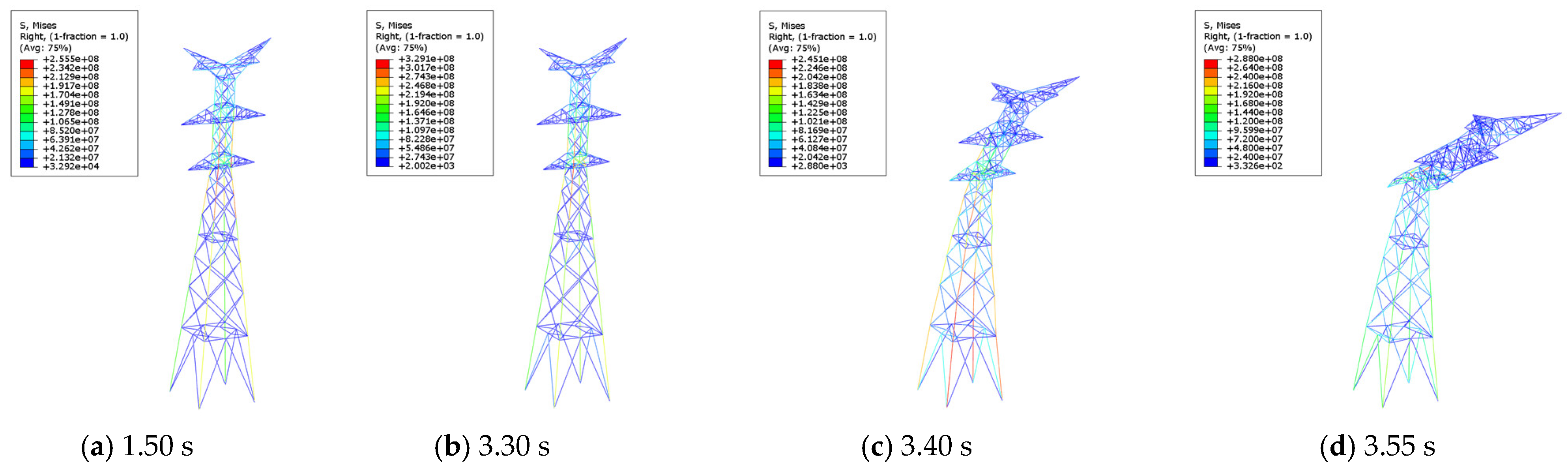
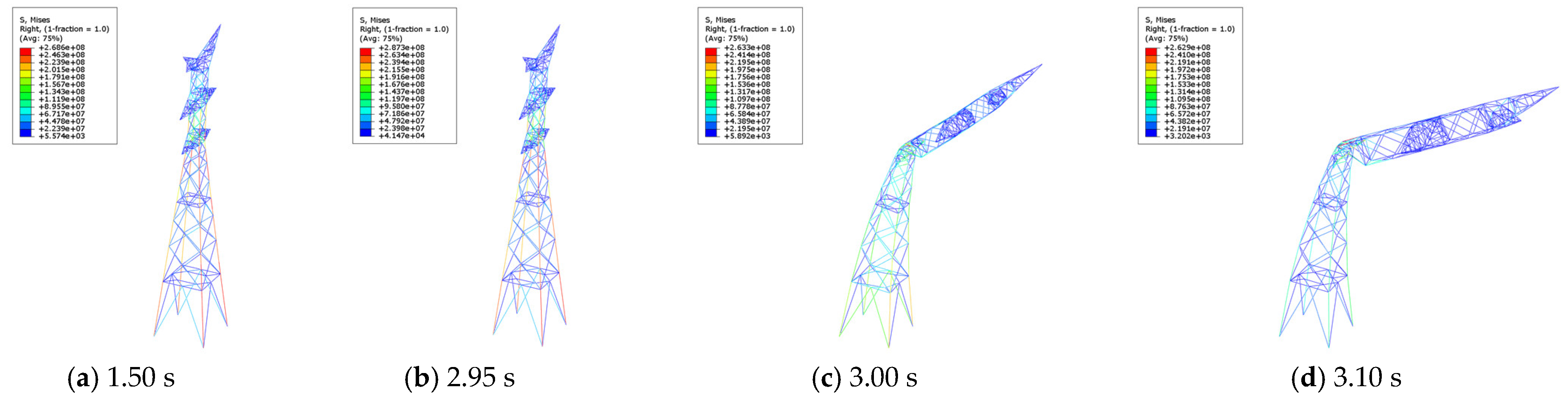
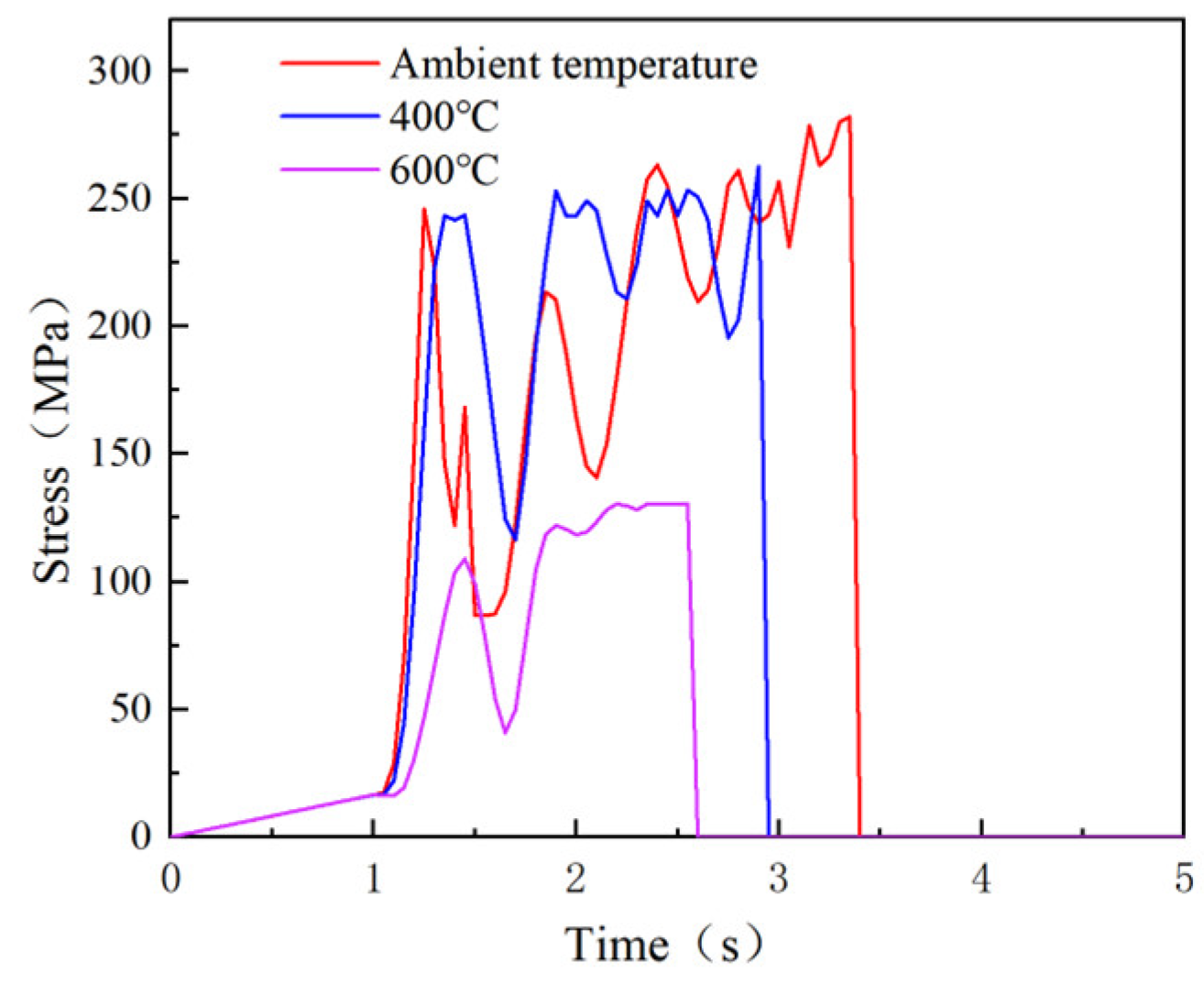
4.2. Collapse Analysis of Transmission Tower-Line System at Ambient Temperature
4.3. Collapse Analysis of Transmission Tower-Line System at High Temperature
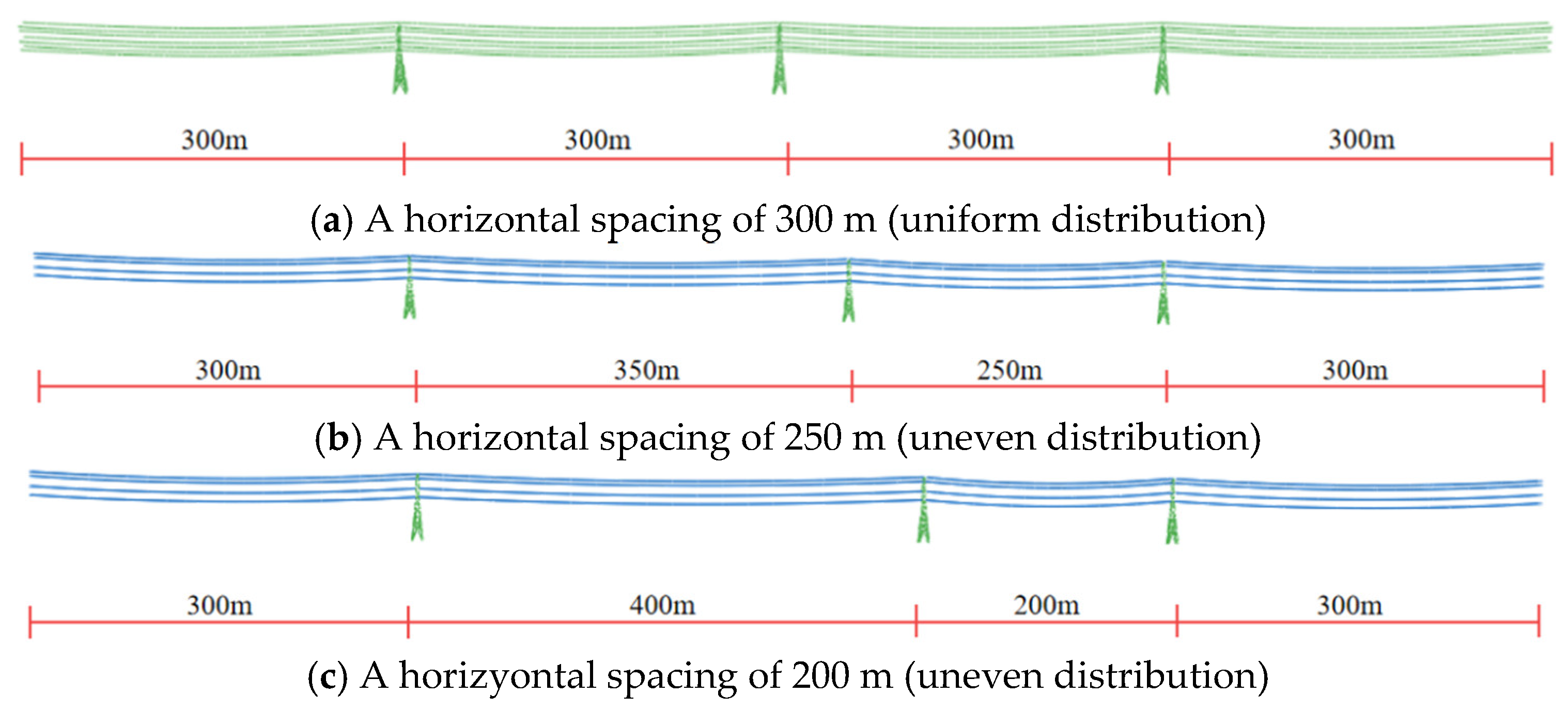
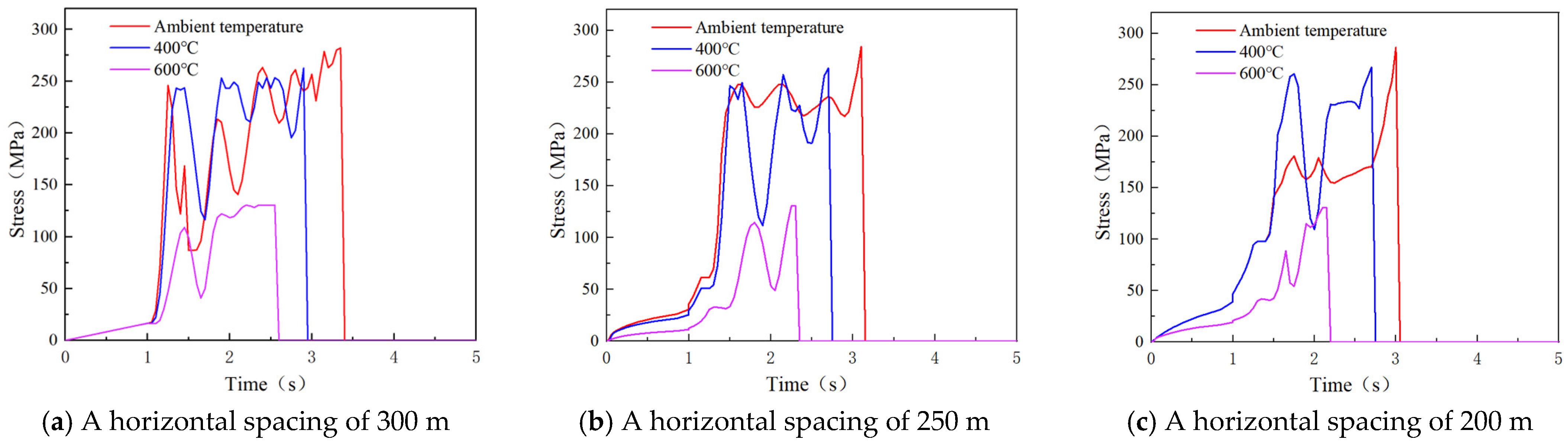
4.4. Study on the Influence of Horizontal Spacing
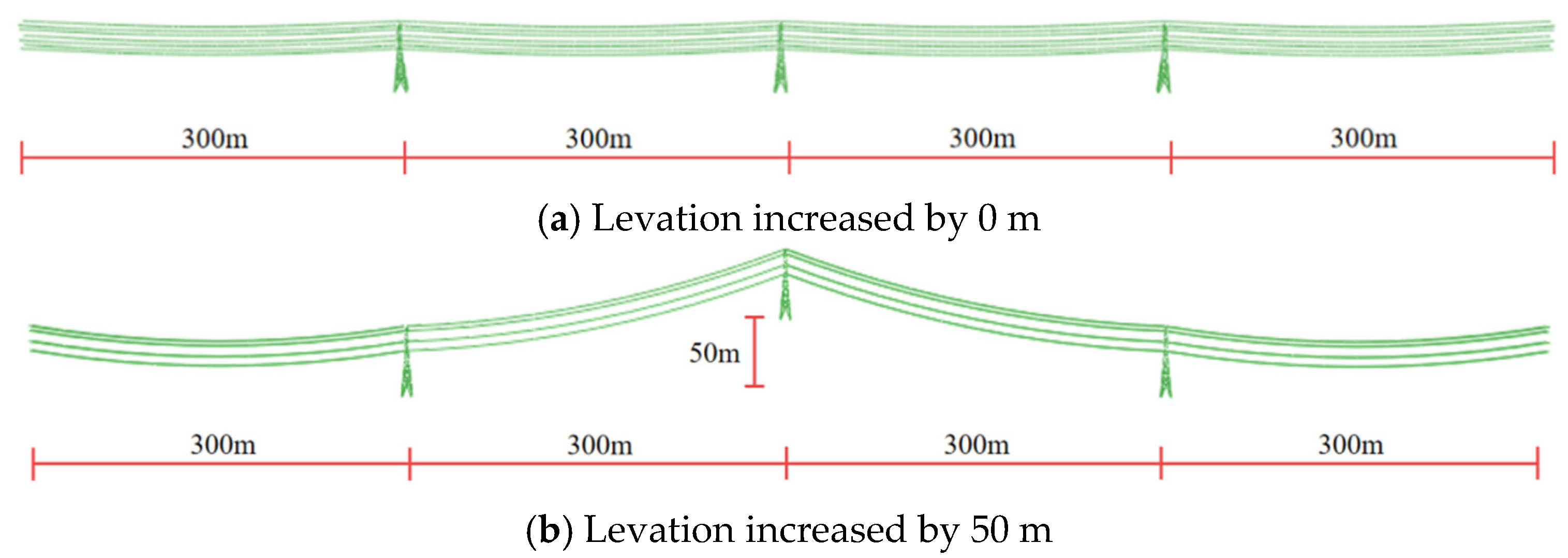
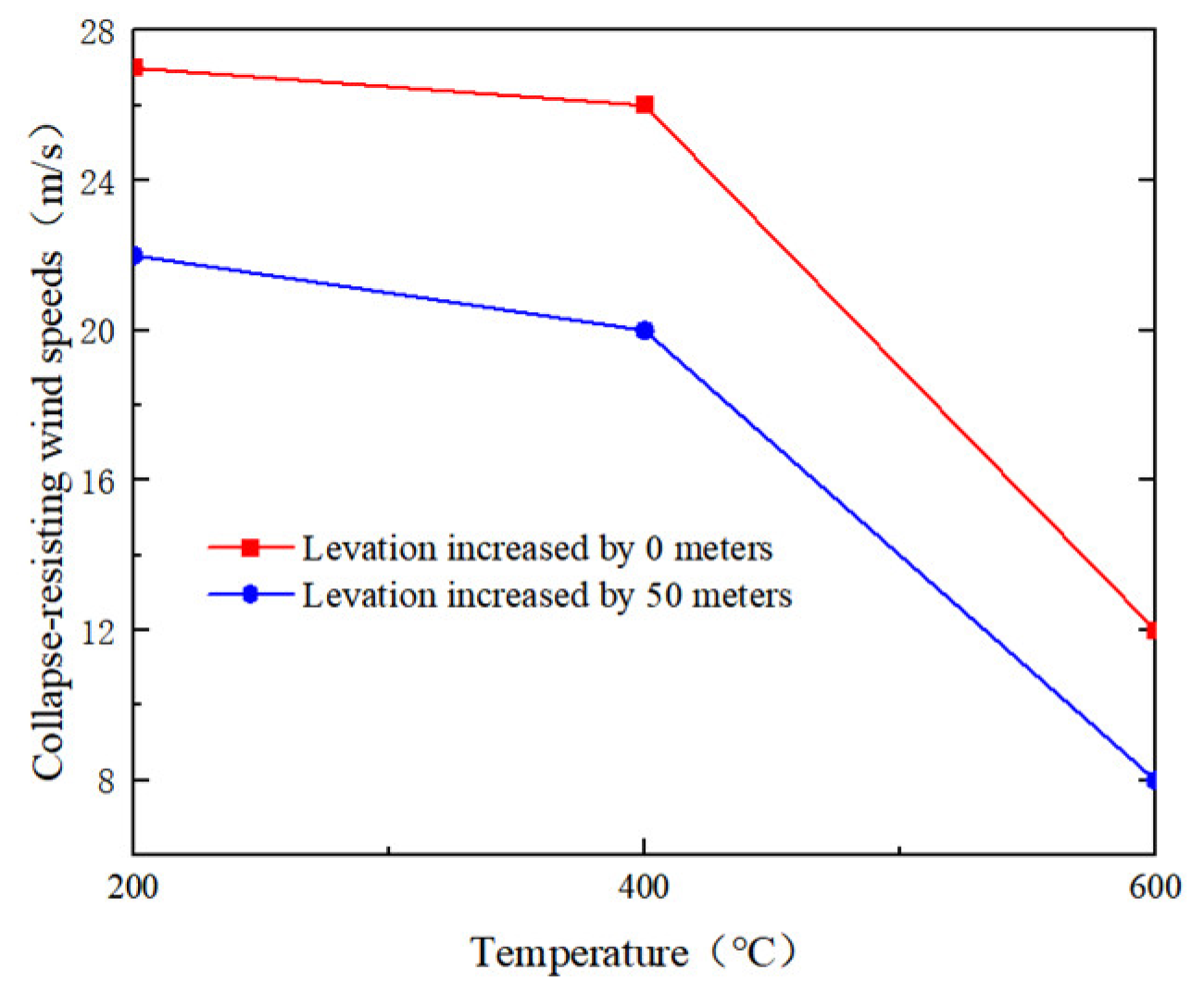
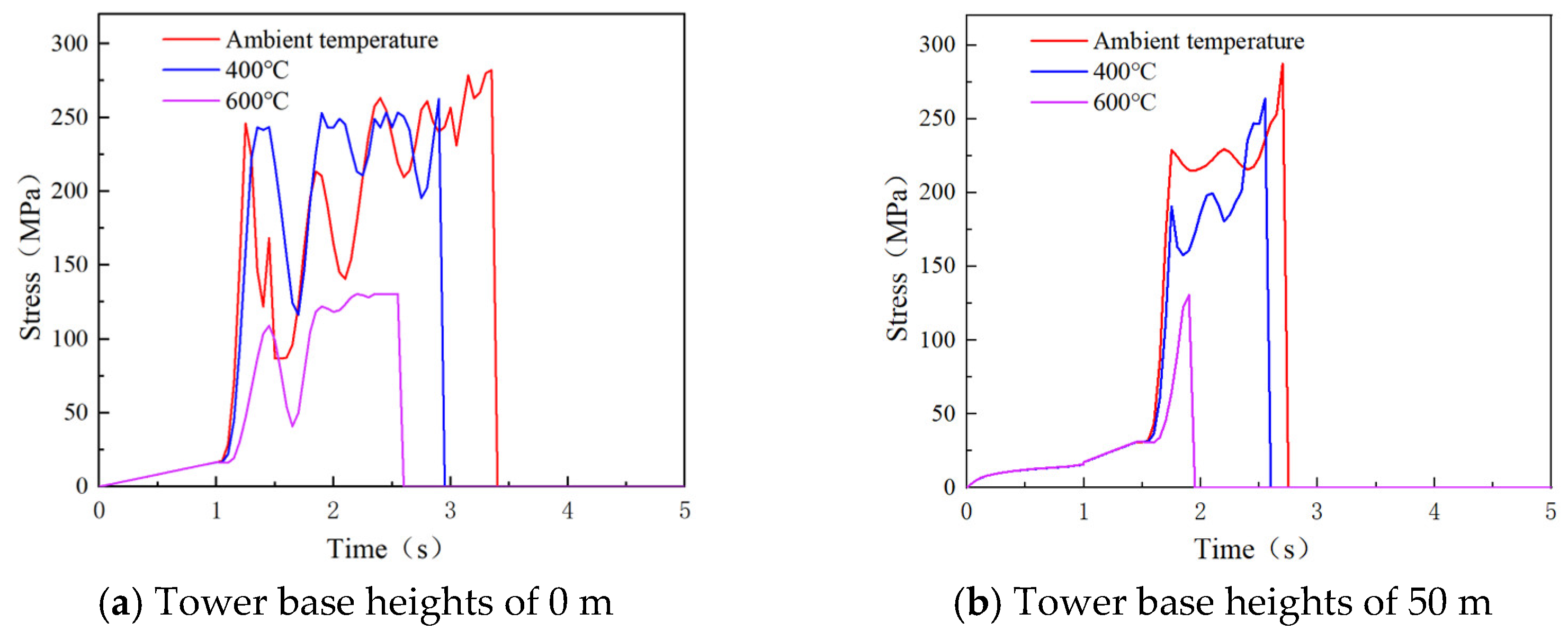
4.5. Study on the Influence of Elevation
5. Conclusions
- (1)
- The uneven horizontal spacing distribution reduces the stability of the transmission tower-line system. Compared to the condition with a horizontal spacing of 300 m (uniform distribution), the collapse-resisting wind speeds of the observed members are significantly reduced when the horizontal spacing is 250 m (uneven distribution). The more uneven the distribution of the horizontal spacing, the lower the stability of the transmission tower-line system. When the horizontal spacing is 200 m (uneven distribution), the collapse-resisting wind speeds of the observed members further decrease. During the design process, extreme uneven spacing distributions should be avoided to enhance the stability of the transmission tower.
- (2)
- The increase in the target tower height reduces the stability of the transmission tower-line system. Compared to the condition with a tower base height of 0 m, the collapse-resisting wind speeds of the observed members are significantly reduced when the tower base height is 50 m. During the design process, excessively high target towers should be avoided.
- (3)
- As the temperature increases, the adverse effects of uneven horizontal spacing distribution and increased target tower height on the transmission tower become more significant. With rising temperatures, the structural disaster resistance gradually weakens. It is recommended to choose steel materials with higher fire resistance or apply fire-resistant coatings to existing steel to enhance the bearing capacity of the transmission tower in high-temperature environments.
- (4)
- This paper investigates the disaster mechanism of transmission towers under the combined action of fire and wind loads, providing a reference for enhancing their disaster resistance and optimizing design schemes. Future research could further explore the impact of other disaster factors, such as ice and snow loads, seismic loads, etc., on transmission towers, offering insights for the design and safety assessment of transmission towers in complex environments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tian, L.; Yu, Q.; Ma, R.; Wang, C. The collapse analysis of a transmission tower under wind excitation. Open Civ. Eng. J. 2014, 8, 136–142. [Google Scholar] [CrossRef][Green Version]
- Zhang, W.; Zhu, J.; Liu, H.; Niu, H. Probabilistic capacity assessment of lattice transmission towers under strong wind. Front. Built Environ. 2015, 1, 20. [Google Scholar] [CrossRef]
- Savory, E.; Parke, G.A.R.; Zeinoddini, M.; Toy, N.; Disney, P. Modelling of tornado and microburst-induced wind loading and failure of a lattice transmission tower. Eng. Struct. 2001, 23, 365–375. [Google Scholar] [CrossRef]
- Li, H.; Bai, H. Research status and development trends of disaster resistance for high-voltage transmission tower-line systems. J. Civ. Eng. 2007, 2, 39–46. [Google Scholar]
- Wang, W.; Wang, G.; Sheng, H.; Gao, Y.; Lv, X. Research on multi-hazard response of transmission tower-line systems under rare earthquake-wind combined actions. World Earthq. Eng. 2023, 39, 165–173. [Google Scholar]
- Deng, H.Z.; Xu, H.J.; Duan, C.Y.; Jin, X.H.; Wang, Z.H. Experimental and numerical study on the responses of a transmission tower to skew incident winds. J. Wind. Eng. Ind. Aerodyn. 2016, 157, 171–188. [Google Scholar] [CrossRef]
- Cai, Y.; Xie, Q.; Xue, S.; Hu, L.; Kareem, A. Fragility modelling framework for transmission line towers under winds. Eng. Struct. 2019, 191, 686–697. [Google Scholar] [CrossRef]
- Edgar, T.H.; Sordo, E. Structural behaviour of lattice transmission towers subjected to wind load. Struct. Infrastruct. Eng. 2017, 13, 1462–1475. [Google Scholar] [CrossRef]
- Yan, B.; Sheng, J.; Jiang, K.; Qi, S.; Zhao, B.C. Dynamic stability of cat head type transmission towers under icing and wind loads. Sci. Technol. Eng. 2021, 21, 11166–11175. [Google Scholar]
- Zhang, J.; Xie, Q. Failure analysis of transmission tower subjected to strong wind load. J. Constr. Steel Res. 2019, 160, 271–279. [Google Scholar] [CrossRef]
- Fu, X.; Li, H.N.; Tian, L.; Wang, J.; Cheng, H. Fragility analysis of transmission line subjected to wind loading. J. Perform. Constr. Facil. 2019, 33, 04019044. [Google Scholar] [CrossRef]
- Okamura, T.; Ohkuma, T.; Hongo, E.; Okada, H. Wind response analysis of a transmission tower in a mountainous area. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 53–63. [Google Scholar] [CrossRef]
- Li, T.; Wang, Q.; Wu, D.; Su, J.; Cheng, Y.; Lou, W. Wind tunnel tests and wind vibration response analysis of 1000 kV transmission towers under typhoon wind field. J. Electr. Power Sci. Technol. 2021, 36, 76–82. [Google Scholar]
- Shehata, A.Y.; El Damatty, A.A. Behaviour of guyed transmission line structures under downburst wind loading. Wind. Struct. 2007, 10, 249–268. [Google Scholar] [CrossRef]
- Chen, B.; Wu, J.; Ouyang, Y.; Yang, D. Response evaluation and vibration control of a transmission tower-line system in mountain areas subjected to cable rupture. Struct. Monit. Maint. 2018, 5, 151–171. [Google Scholar]
- Guo, J.; Xiao, C.; Li, J. Wind tunnel tests and dynamic analysis of wind-induced response of a transmission tower on a hill. Adv. Struct. Eng. 2021, 24, 3594–3606. [Google Scholar] [CrossRef]
- Liang, B.; Xu, J. Numerical simulation of dynamic wind response of overhead transmission towers. J. Tongji Univ. Nat. Sci. 2002, 5, 583–587. [Google Scholar]
- Zhang, W.; Xiao, Y.; Li, C.; Zheng, Q.; Tang, Y. Wind load investigation of self-supported lattice transmission tower based on wind tunnel tests. Eng. Struct. 2022, 252, 113575. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, Q.; Li, J. Wind-induced dynamic response analysis of multi-tower coupled system in transmission lines. J. Disaster Prev. Mitig. Eng. 2006, 3, 261–267. [Google Scholar]
- Zhao, G.; Xie, Q.; Liang, S.; Li, J. Wind-induced nonlinear vibration aeroelastic model wind tunnel test of high-voltage transmission tower-line system. J. Tongji Univ. Nat. Sci. 2009, 37, 1157–1164. [Google Scholar]
- Jeddi, A.B.; Azzi, Z.; Shafieezadeh, A.; Elawady, A.; Chowdhury, A.G.; Irwin, P. Revisit of underestimated wind drag coefficients and gust response factors of lattice transmission towers based on aeroelastic wind tunnel testing and multi-sensor data fusion. Eng. Struct. 2023, 278, 115486. [Google Scholar] [CrossRef]
- Wu, C.; Yang, X.; Zhang, B.; Liu, Z.; Zhao, Y. Dynamic response of a cat head type transmission tower-line system under strong wind. J. Phys. Conf. Ser. 2021, 1986, 012098. [Google Scholar] [CrossRef]
- Savory, E.; Parke, G.A.R.; Disney, P.; Toy, N. Wind-induced transmission tower foundation loads: A field study-design code comparison. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1103–1110. [Google Scholar] [CrossRef]
- Liu, T.; Zhong, M.; Xing, J. Industrial accidents: Challenges for China’s economic and social development. Saf. Sci. 2005, 43, 503–522. [Google Scholar] [CrossRef]
- Lou, G.; Wang, C.; Jiang, J.; Jiang, Y.; Wang, L.; Li, G.Q. Experimental and numerical study on thermal-structural behavior of steel portal frames in real fires. Fire Saf. J. 2018, 98, 48–62. [Google Scholar] [CrossRef]
- Ren, W. Experimental and Theoretical Study on Catenary Mechanism of Steel Frame Beam Subject to Fire. Fire Technol. 2023, 59, 3493–3523. [Google Scholar] [CrossRef]
- Liu, H.; Chen, H.; Wang, L.; Li, Z.; Chen, Z. Fire resistance performance test study of full-scale steel frame structure under real fire. J. Build. Struct. 2024, 45, 14–24. [Google Scholar]
- Ruan, S.; Zhao, J.; Song, Z.; Duan, L. Fire resistance performance test study of steel frame structures under spreading fire. J. Build. Struct. 2022, 43, 103–114. [Google Scholar]
- Wang, W.; Zhou, H.; Zhou, Y.; Xu, L. A simplified approach for fire resistance design of high strength Q460 steel beams subjected to non-uniform temperature distribution. Fire Technol. 2018, 54, 437–460. [Google Scholar] [CrossRef]
- Yang, J.; Wang, W.; Shi, Y.; Xu, L. Experimental study on fire resistance of cold-formed steel built-up box columns. Thin Walled Struct. 2020, 147, 106564. [Google Scholar] [CrossRef]
- Wang, W.; Yan, S.; Zhang, L.; Wang, B. High-temperature creep tests of Q345 steel and study on fire resistance of steel columns considering creep effects. J. Build. Struct. 2016, 37, 47–54. [Google Scholar]
- Xue, X.; Wang, F.; Shi, Y.; Wang, W. Study on ultra-low cycle fatigue performance of Q690 high-strength steel after fire. J. Build. Struct. 2023, 44, 119–128. [Google Scholar]
- Ferraz, G.; Santiago, A.; Rodrigues, J.P.; Barata, P. Thermal analysis of hollow steel columns exposed to localised fires. Fire Technol. 2016, 52, 663–681. [Google Scholar] [CrossRef]
- Ragheb, W.F. Local buckling capacity of steel I-section beams subjected to uniform or linear temperature gradient. Thin Walled Struct. 2017, 119, 304–314. [Google Scholar] [CrossRef]
- Li, G.; Miao, J.; Song, L. Study on the influence parameters of residual axial compressive capacity of constrained high-strength steel columns after fire. J. Build. Struct. 2020, 41, 87–94. [Google Scholar]
- Li, X. Prediction Model of Yield Critical Temperature for Steel Components Under Sudden Temperature Changes. Ph.D. Thesis, Xinjiang University, Ürümqi, China, 2022. [Google Scholar]
- GB 51249-2017; Technical Specification for Fire Protection of Building Steel Structures. Ministry of Housing and Urban-Rural Development: Beijing, China, 2017.
- GB 50017-2017; Design Code for Steel Structures. China Planning Press: Beijing, China, 2017.








| Part | Material | Parameter | Numerical Value |
|---|---|---|---|
| Inclined member | Q235 | Density/kg·m−3 | 7850 |
| Elastic modulus/GPa | 200 | ||
| Yield stress/MPa | 235 | ||
| Coefficient of linear expansion/℃ | 1.17 × 10−5 | ||
| Main member | Q345 | Density/kg·m−3 | 7850 |
| Elastic modulus/GPa | 200 | ||
| Yield stress/MPa | 345 | ||
| Coefficient of linear expansion/℃ | 1.20 × 10−5 | ||
| Conductor | 2 × LGJ-400/50 | Density/kg·m−3 | 3333 |
| Elastic modulus/GPa | 69 | ||
| Yield stress/MPa | 700 | ||
| Ground wire | JLB-150 | Density/kg·m−3 | 6593 |
| Elastic modulus/GPa | 147 | ||
| Yield stress/MPa | 830 |
| Modal Order | Ambient Temperature | 400 °C | 600 °C | |||
|---|---|---|---|---|---|---|
| Frequency/Hz | Period/s | Frequency/Hz | Period/s | Frequency/Hz | Period/s | |
| First Order | 0.56 | 1.79 | 0.51 | 1.96 | 0.42 | 2.38 |
| Second Order | 0.67 | 1.49 | 0.62 | 1.61 | 0.53 | 1.89 |
| Third Order | 0.84 | 1.19 | 0.79 | 1.27 | 0.71 | 1.41 |
| Observed Members/Temperature | Ambient Temperature | 400 °C | 600 °C |
|---|---|---|---|
| Observed members 1 | 3.30 s | 2.95 s | 2.60 s |
| Observed members 2, 3, 4 | 3.55 s | 3.00 s | 2.75 s |
| Observed members 5, 6, 7, 8 | Intact | Intact | Intact |
| Horizontal Spacing/Temperature | Ambient Temperature | 400 °C | 600 °C |
|---|---|---|---|
| 300 m (uniform distribution)) | 27 m/s | 26 m/s | 12 m/s |
| 250 m (non-uniform distribution) | 25 m/s | 24 m/s | 10 m/s |
| 200 m (non-uniform distribution) | 24 m/s | 22 m/s | 9 m/s |
| Observed Members/Horizontal Spacing | 300 m (Uniform Distribution) | 250 m (Uneven Distribution) | 200 m (Uneven Distribution) |
|---|---|---|---|
| Observed members 1 | 3.30 s | 3.10 s | 3.00 s |
| Observed members 2, 3, 4 | 3.55 s | 3.25 s | 3.10 s |
| Observed members 5, 6, 7, 8 | Intact | Intact | Intact |
| Tower Base Height /Temperature | Ambient Temperature | 400 °C | 600 °C |
|---|---|---|---|
| 0 m | 27 m/s | 26 m/s | 12 m/s |
| 50 m | 22 m/s | 20 m/s | 8 m/s |
| Observed Members/Tower Base Height | 0 m | 50 m |
|---|---|---|
| Observed members 1 | 3.30 s | 2.75 s |
| Observed members 2, 3, 4 | 3.55 s | 2.85 s |
| Observed members 5, 6, 7, 8 | Intact | Intact |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Ma, H.; Zhang, S.; Wang, W.; Zhang, L. Study on the Multi-Hazard Responses of Transmission Tower-Line Systems Under Fire and Wind Loads Using ABAQUS. Appl. Sci. 2025, 15, 255. https://doi.org/10.3390/app15010255
He X, Ma H, Zhang S, Wang W, Zhang L. Study on the Multi-Hazard Responses of Transmission Tower-Line Systems Under Fire and Wind Loads Using ABAQUS. Applied Sciences. 2025; 15(1):255. https://doi.org/10.3390/app15010255
Chicago/Turabian StyleHe, Xiwei, Huichao Ma, Shibo Zhang, Wenming Wang, and Lijuan Zhang. 2025. "Study on the Multi-Hazard Responses of Transmission Tower-Line Systems Under Fire and Wind Loads Using ABAQUS" Applied Sciences 15, no. 1: 255. https://doi.org/10.3390/app15010255
APA StyleHe, X., Ma, H., Zhang, S., Wang, W., & Zhang, L. (2025). Study on the Multi-Hazard Responses of Transmission Tower-Line Systems Under Fire and Wind Loads Using ABAQUS. Applied Sciences, 15(1), 255. https://doi.org/10.3390/app15010255





