Calculations of Cross-Sections for Positron Scattering on Benzene
Abstract
1. Introduction
2. Theory and Computational Details
2.1. Molecular Structure
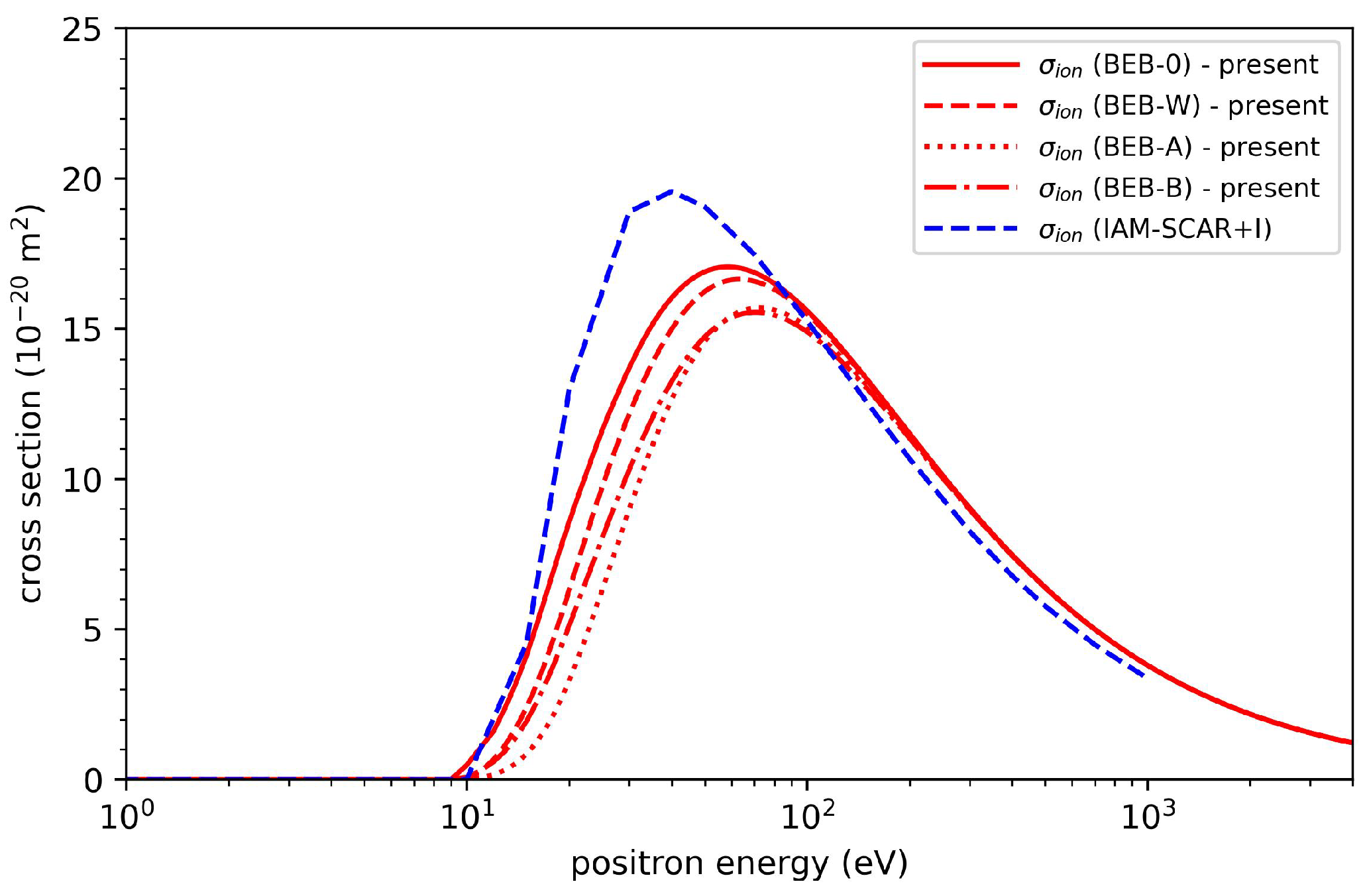
2.2. Model for Direct Ionization of Molecules by Positron Impact
- BEB-0 model: , , .
- BEB-W model: , , with the term
- BEB-A model: , , with the termwhere and to fulfill the threshold law of Jansen et al. [38].
- BEB-B model: , , and with the same values for and as in the BEB-A model.
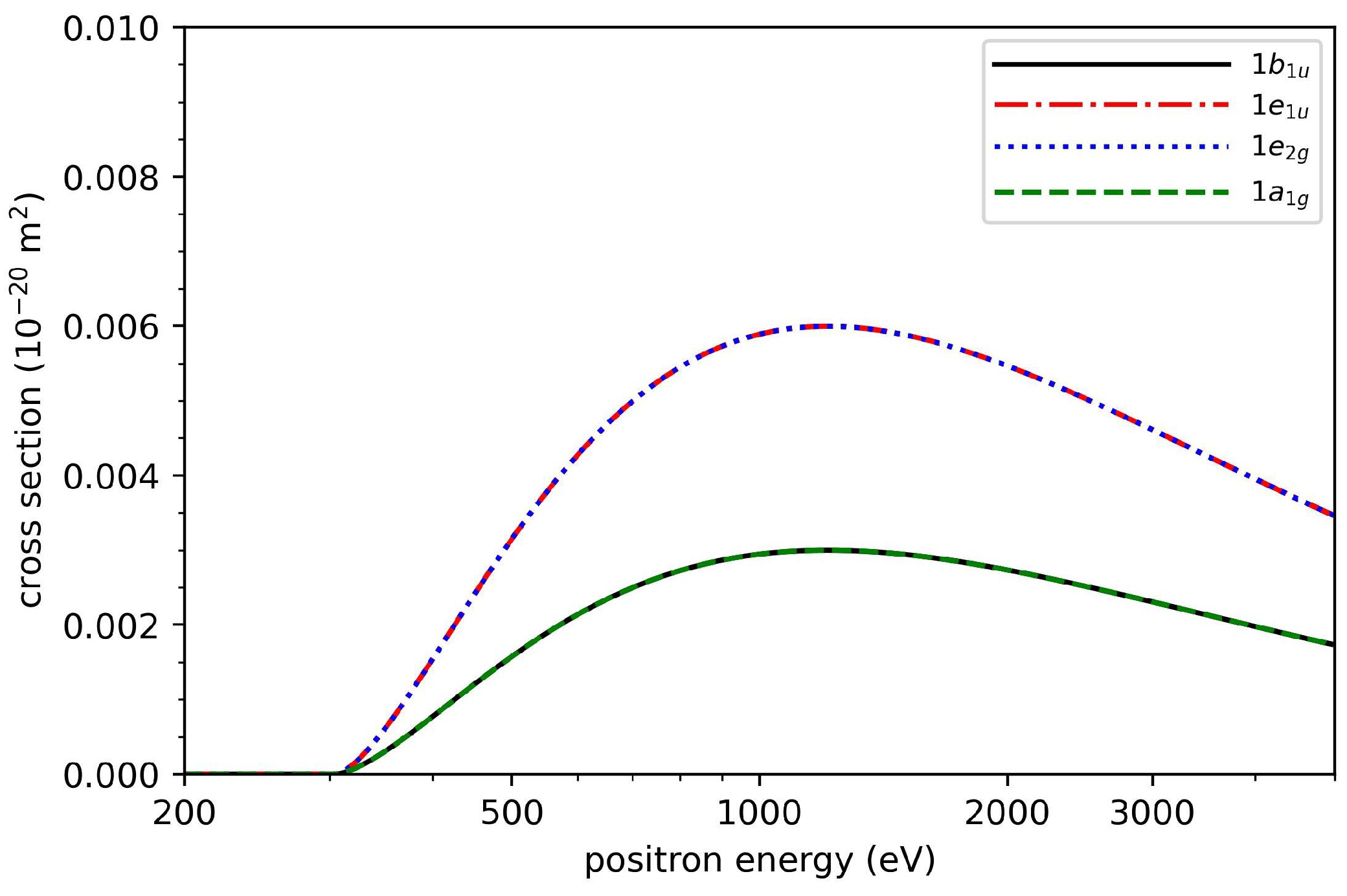
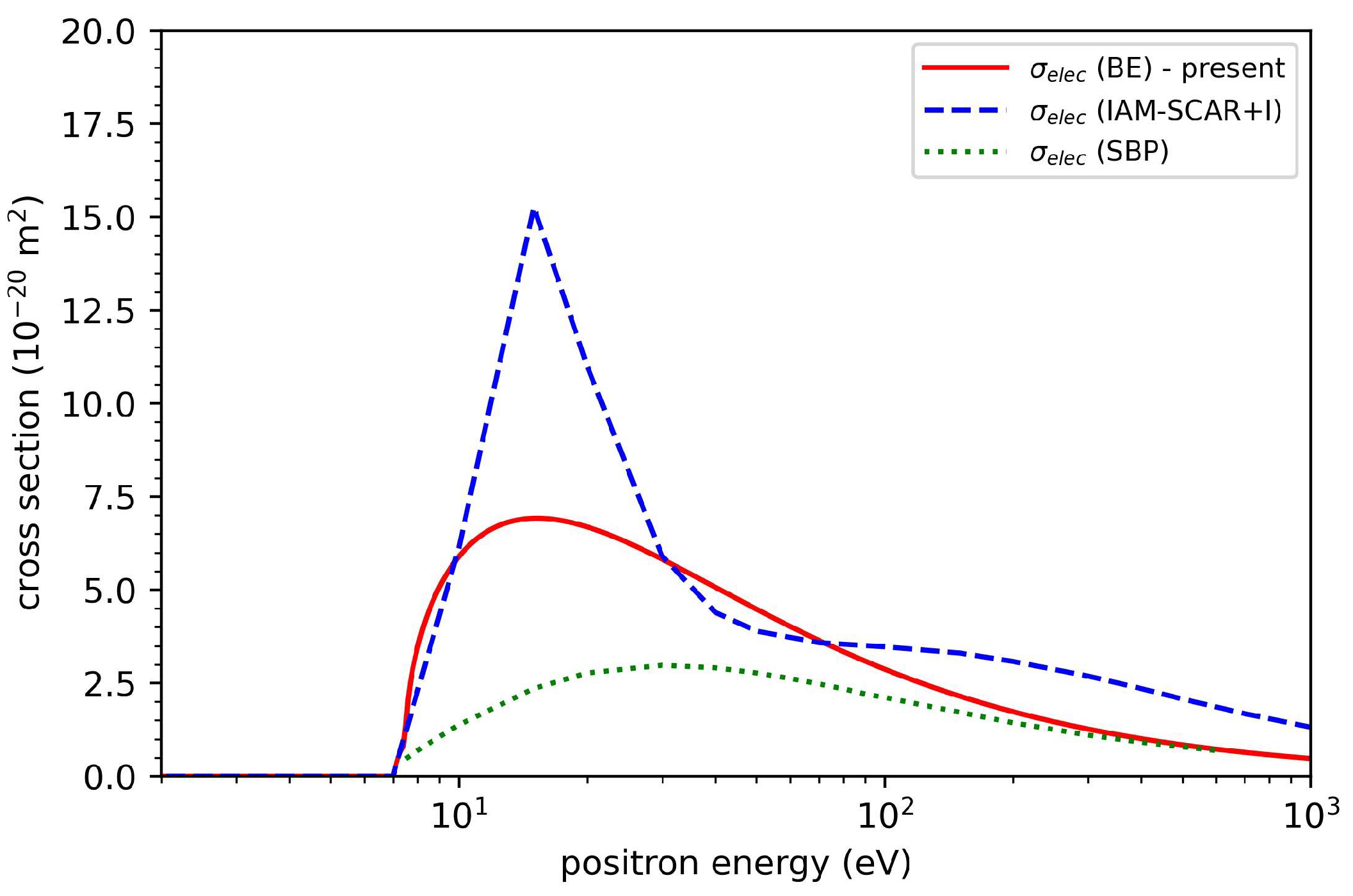
Cross-Sections for Electronic Excitation
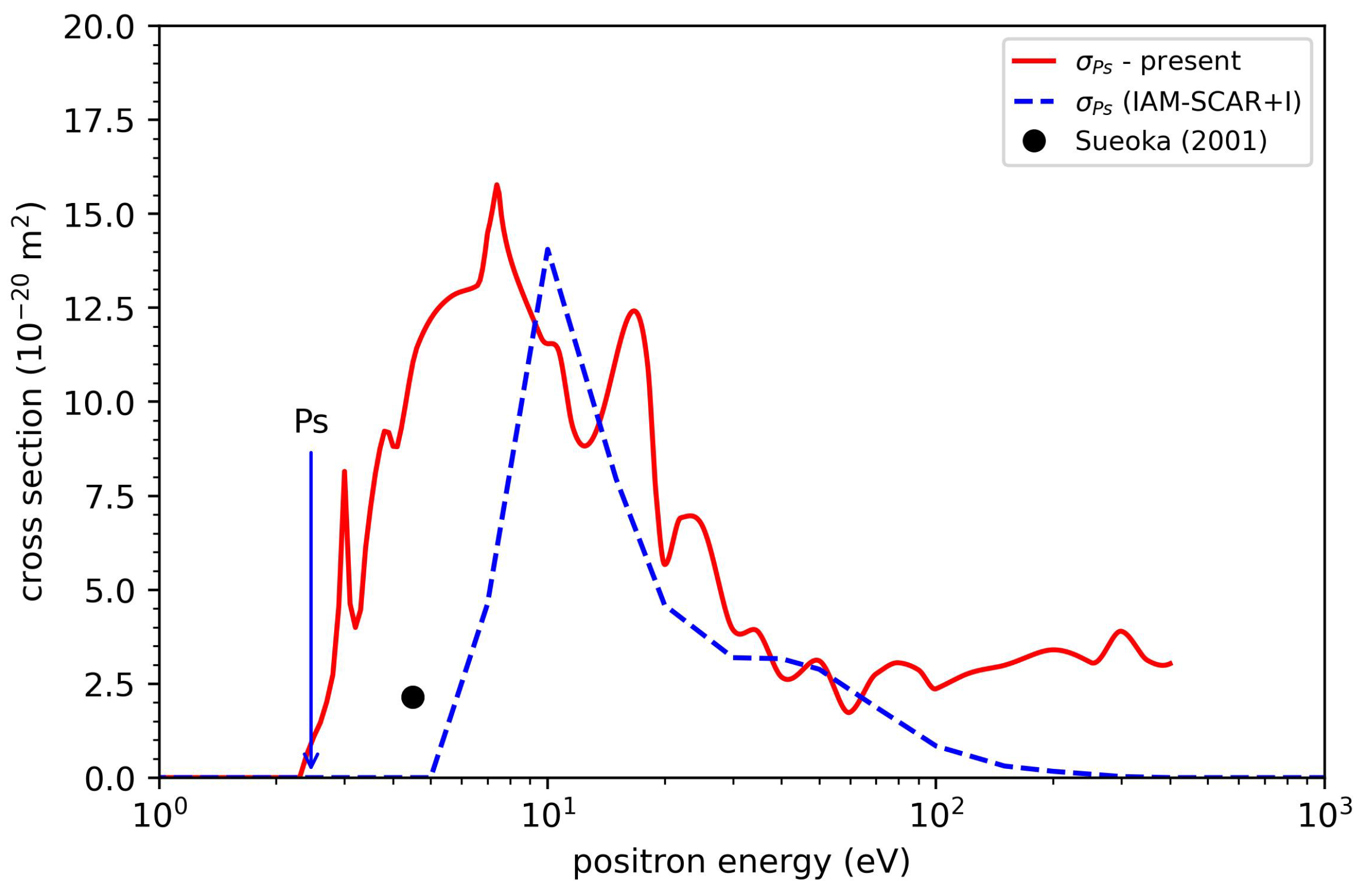
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BE | binary-encounter |
| BEB | binary-encounter Bethe |
| BEB-0 | binary-encounter Bethe for positrons |
| BEB-W | binary-encounter Bethe for positrons with Wannier-type threshold law |
| BEB-A | binary-encounter Bethe for positrons with Jansen-type threshold law, version A |
| BEB-B | binary-encounter Bethe for positrons with Jansen-type threshold law, version B |
| B3LYP | Becke, 3-parameter, Lee–Yang–Parr exchange-correlation functional |
| DFT | Density Functional Theory |
| eV | electron volt |
| IAM-SCAR+I | independent atom model with the screening corrected additivity rule, |
| including interference | |
| ISM | interstellar medium |
| OVGF | Outer Valence Green Function |
| PAH | polycyclic aromatic hydrocarbon |
| PET | positron emission tomography |
| Ps | positronium |
| SAC-CI | symmetry adapted cluster-configuration interaction |
| SBP | scaling Born positron |
References
- Bass, S.D.; Mariazzi, S.; Moskal, P.; Stepien, E. Positronium Physics and Biomedical Applications. Rev. Mod. Phys. 2023, 95, 021002. [Google Scholar] [CrossRef]
- Dryzek, J. Positron Profilometry Probing Material Depths for Enhanced Understanding, 1st ed.; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Keeble, D.J.; Wiktor, J.; Pathak, S.K.; Phillips, L.J.; Dickmann, M.; Durose, K.; Snaith, H.J.; Egger, W. Identification of lead vacancy defects in lead halide perovskites. Nat. Com. 2021, 12, 5566. [Google Scholar] [CrossRef] [PubMed]
- Prantzos, N.; Boehm, C.; Bykov, A.M.; Diehl, R.; Ferriére, K.; Guessoum, N.; Jean, P.; Knoedlseder, J.; Marcowith, A.; Moskalenko, I.V.; et al. The 511 keV emission from positron annihilation in the Galaxy. Rev. Mod. Phys. 2011, 83, 1001. [Google Scholar] [CrossRef]
- Casse, M.; Paul, J.; Bertone, G.; Sigl, G. Gamma Rays from the Galactic Bulge and Large Extra Dimensions. Phys. Rev. Lett. 2004, 92, 111102. [Google Scholar] [CrossRef] [PubMed]
- Boehm, C.; Hooper, D.; Silk, J.; Casse, M.; Paul, J. MeV Dark Matter: Has It Been Detected? Phys. Rev. Lett. 2004, 92, 101301. [Google Scholar] [CrossRef] [PubMed]
- Paul, J. Positrons in the universe. Nucl. Instrum. Methods Phys. Res. B 2004, 221, 215–224. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; Barrin, L.; et al. Towards Understanding the Origin of Cosmic-Ray Positrons. Phys. Rev. Lett. 2019, 122, 041102. [Google Scholar] [CrossRef] [PubMed]
- Guessoum, N.; Jean, P.; Prantzos, N. Microquasars as sources of positron annihilation radiation. Astron. Astrophys. 2006, 457, 753–762. [Google Scholar] [CrossRef]
- Guessoum, N.; Jean, P.; Gillard, W. Positron annihilation on polycyclic aromatic hydrocarbon molecules in the interstellar medium. Mon. Not. R. Astron. Soc. 2010, 402, 1171–1178. [Google Scholar] [CrossRef]
- Surko, C.M.; Gribakin, G.F.; Buckman, S.J. Low-energy positron interactions with atoms and molecules. J. Phys. B At. Mol. Phys. 2005, 38, R57. [Google Scholar] [CrossRef]
- Dapor, M. Transport of Energetic Electrons in Solids, 3rd ed.; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Franz, M.; Franz, J. A Monte Carlo strategy to simulate positrons and positronium in biological materials. Bio-Algorithms Med-Syst. 2023, 19, 40–42. [Google Scholar] [CrossRef]
- Brunger, M.J.; Buckman, S.J.; Ratnavelu, K. Positron Scattering from Molecules: An Experimental Cross Section Compilation for Positron Transport Studies and Benchmarking Theory. J. Phys. Chem. Ref. Data 2017, 46, 023102. [Google Scholar] [CrossRef]
- Moskal, P.; Stepien, E. Positronium as a biomarker of hypoxia. Bio-Algorithms Med-Syst. 2021, 17, 311–319. [Google Scholar] [CrossRef]
- Steinberger, W.M.; Mercolli, L.; Breuer, J.; Sari, H.; Parzych, S.; Niedzwiecki, S.; Lapkiewicz, G.; Moskal, P.; Stepien, E.; Rominger, A.; et al. Developing a Novel Positronium Biomarker for Cardiac Myxoma Imaging. EJNMMI Phys. 2023, 10, 76. [Google Scholar]
- Sueoka, O. Total cross section measurements for positron and electron scattering on benzene molecules. J. Phys. B At. Mol. Opt. Phys. 1988, 21, L631. [Google Scholar] [CrossRef]
- Makochekanwa, C.; Sueoka, O.; Kimura, M. Comparative study of electron and positron scattering from benzene (C6H6) and hexafluorobenzene (C6F6) molecules. Phys. Rev. A 2003, 68, 032707. [Google Scholar] [CrossRef]
- Karwasz, G.P.; Pliszka, D.; Zecca, A.; Brusa, R.S. Total cross sections for positron scattering on benzene and nitrogen. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 1–13. [Google Scholar]
- Karwasz, G.P.; Karbowski, A.; Idziaszek, Z.; Brusa, R.S. Total cross sections for positron scattering on benzene - angular resolution corrections. Nucl. Instrum. Methods Phys. Res. B 2008, 266, 471–477. [Google Scholar] [CrossRef]
- Zecca, A.; Moser, N.; Perazzolli, C.; Salemi, A.; Brunger, M.J. Total cross sections for positron scattering from benzene, cyclohexane, and aniline. Phys. Rev. A 2007, 76, 022708. [Google Scholar] [CrossRef]
- Kimura, M.; Makochekanwa, C.; Sueoka, O. Contrasting low-energy behaviour in total cross sections for electron and positron scattering from benzene molecules. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 1461. [Google Scholar] [CrossRef]
- Occhigrossi, A.; Gianturco, F.A. Low-energy positron dynamics in small hydrocarbon gases. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 1383. [Google Scholar] [CrossRef]
- Franz, J.; Franz, M. Low-energy positron scattering from gas-phase benzene. Eur. Phys. J. D 2019, 73, 192. [Google Scholar] [CrossRef]
- Karbowski, A.; Karwasz, G.P.; Franz, M.; Franz, J. Positron Scattering and Annihilation in Organic Molecules. Acta Phys. Pol. B 2020, 51, 207–212. [Google Scholar] [CrossRef]
- Barbosa, A.S.; Blanco, F.; Garcia, G.; Bettega, M.H.F. Theoretical study on positron scattering by benzene over a broad energy range. Phys. Rev. A 2019, 100, 062705. [Google Scholar] [CrossRef]
- Lino, J.L.S. Electronic excitation of C6H6 by positron impact. Rev. Mex. Fis. 2021, 67, 188–192. [Google Scholar] [CrossRef]
- Fedus, K.; Karwasz, G. Binary-encounter dipole model for positron-impact direct ionization. Phys. Rev. A 2019, 100, 062702. [Google Scholar] [CrossRef]
- Franz, M.; Wiciak-Pawlowska, K.; Franz, J. Binary-encounter model for direct ionization of molecules by positron-impact. Atoms 2021, 9, 99. [Google Scholar] [CrossRef]
- Kim, Y.-K. Scaled Born cross sections for excitations of H2 by electron impact. J. Chem. Phys. 2007, 126, 064305. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Raghavachari, K.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 20. Basis set for correlated wave-functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar]
- Kim, Y.-K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954–3967. [Google Scholar] [CrossRef]
- Hwang, W.; Kim, Y.-K.; Rudd, M.E. New model for electron-impact ionization cross sections of molecules. J. Phys. Chem. 1995, 104, 2956–2966. [Google Scholar] [CrossRef]
- Wannier, G.H. The Threshold Law for Single Ionization of Atoms or Ions by Electrons. Phys. Rev. 1953, 90, 817–825. [Google Scholar] [CrossRef]
- Jansen, K.; Ward, S.J.; Shertzer, J.; Macek, J.H. Absolute cross sections for positron impact ionization of hydrogen near threshold. Phys. Rev. A 2009, 79, 022704. [Google Scholar] [CrossRef]
- Ratnavelu, K.; Brunger, M.J.; Buckman, S.J. Recommended positron scattering cross sections for atomic systems. J. Phys. Chem. Ref. Data 2019, 48, 023102. [Google Scholar] [CrossRef]
- Utamuratov, R.; Kadyrov, A.S.; Fursa, D.V.; Zammit, M.C.; Bray, I. Two-center close-coupling calculations for positron-molecular-hydrogen scattering. Phys. Rev. A 2015, 92, 032707. [Google Scholar] [CrossRef]
- Koopmans, T. Ordering of Wave Functions and Eigenenergies to the Individual Electrons of an Atom. Physica 1933, 1, 104–113. [Google Scholar] [CrossRef]
- von Niessen, W.; Schirmer, J.; Cederbaum, L.S. Computational methods for the one-particle Green’s function. Comp. Phys. Rep. 1984, 1, 57–125. [Google Scholar] [CrossRef]
- Karlsson, L.; Mattsson, L.; Jadrny, R.; Bergmark, T.; Siegbahn, K. Valence Electron Spectra of Benzene and the Hexafluorides of Sulphur, Molybdenum, Tungsten and Uranium. Phys. Scr. 1976, 14, 230–241. [Google Scholar] [CrossRef]
- Lane, N.F. The theory of electron—Molecule collisions. Rev. Mod. Phys. 1980, 52, 29–119. [Google Scholar] [CrossRef]
- Li, Y.; Wan, J.; Xu, X. Theoretical study of the vertical excited states of benzene, pyrimidine, and pyrazine by the symmetry adapted cluster configuration interaction method. J. Comput. Chem. 2007, 28, 1658–1667. [Google Scholar] [CrossRef] [PubMed]
- Sueoka, O.; Kawada, M.K.; Kimura, M. Total and positronium formation cross-sections in polyatomic molecules. Nucl. Instrum. Methods Phys. Res. B 2000, 171, 96–102. [Google Scholar] [CrossRef]



| Orbital | /eV | /eV | |
|---|---|---|---|
| 9.26 a | 27.81 | 4 | |
| 12.16 a | 37.81 | 4 | |
| 12.45 a | 23.70 | 2 | |
| 14.47 a | 32.46 | 4 | |
| 14.90 a | 39.91 | 2 | |
| 15.82 a | 34.21 | 2 | |
| 17.40 a | 25.33 | 2 | |
| 22.44 b | 39.03 | 4 | |
| 27.64 b | 42.36 | 4 | |
| 31.36 b | 39.36 | 2 | |
| 305.62 b | 436.29 | 2 | |
| 305.64 b | 436.11 | 4 | |
| 305.68 b | 435.74 | 4 | |
| 305.69 b | 435.59 | 2 |
| Excited State Y | Description | ΔE/eV | |
|---|---|---|---|
| Rydberg | 0.2021 | 7.06 | |
| Valence | 0.6204 | 7.48 | |
| Rydberg | 0.0350 | 7.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franz, M.; Pastuszko, A.; Franz, J. Calculations of Cross-Sections for Positron Scattering on Benzene. Appl. Sci. 2025, 15, 153. https://doi.org/10.3390/app15010153
Franz M, Pastuszko A, Franz J. Calculations of Cross-Sections for Positron Scattering on Benzene. Applied Sciences. 2025; 15(1):153. https://doi.org/10.3390/app15010153
Chicago/Turabian StyleFranz, Małgorzata, Anna Pastuszko, and Jan Franz. 2025. "Calculations of Cross-Sections for Positron Scattering on Benzene" Applied Sciences 15, no. 1: 153. https://doi.org/10.3390/app15010153
APA StyleFranz, M., Pastuszko, A., & Franz, J. (2025). Calculations of Cross-Sections for Positron Scattering on Benzene. Applied Sciences, 15(1), 153. https://doi.org/10.3390/app15010153





