Structural Designing of Supersonic Swirling Devices Based on Computational Fluid Dynamics Theory
Abstract
1. Introduction
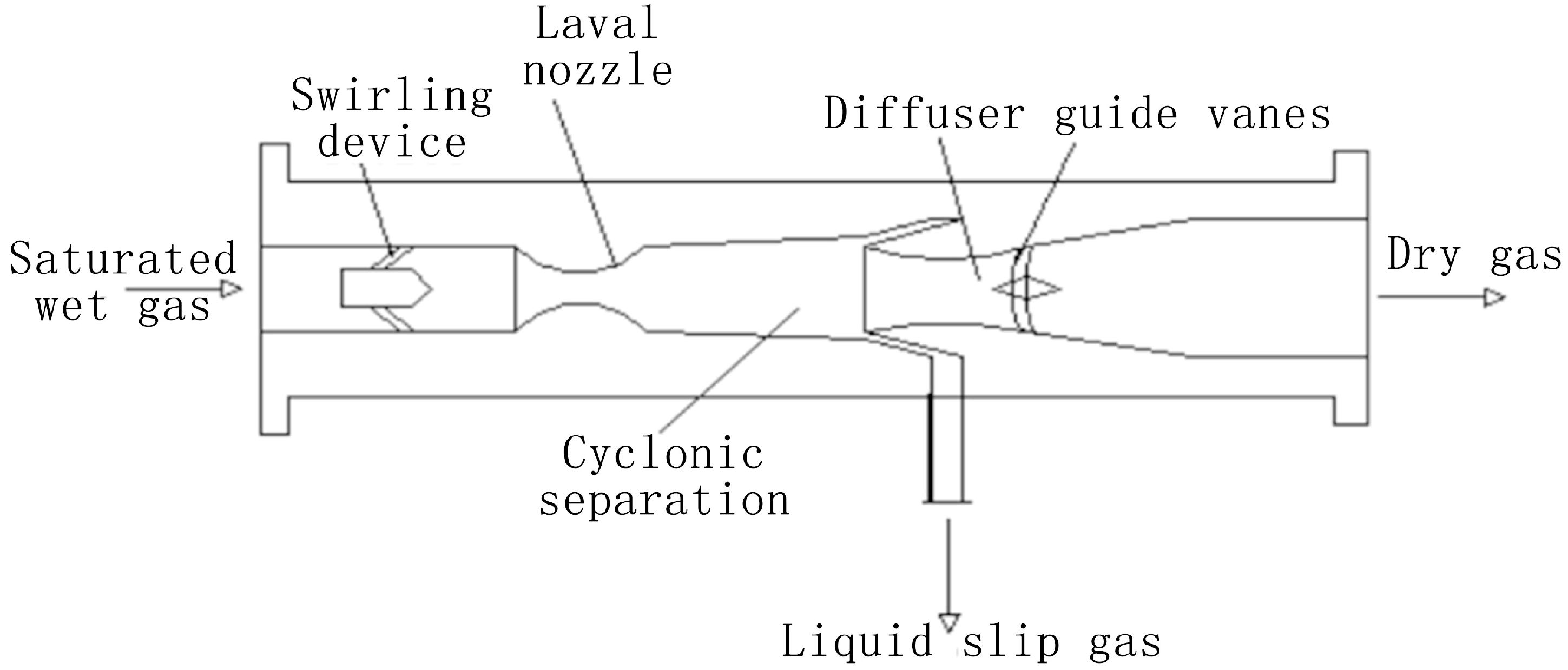
2. Structural Design Method of Supersonic Swirling Separator for Natural Gas Liquefaction
2.1. Design of Nozzle Structure
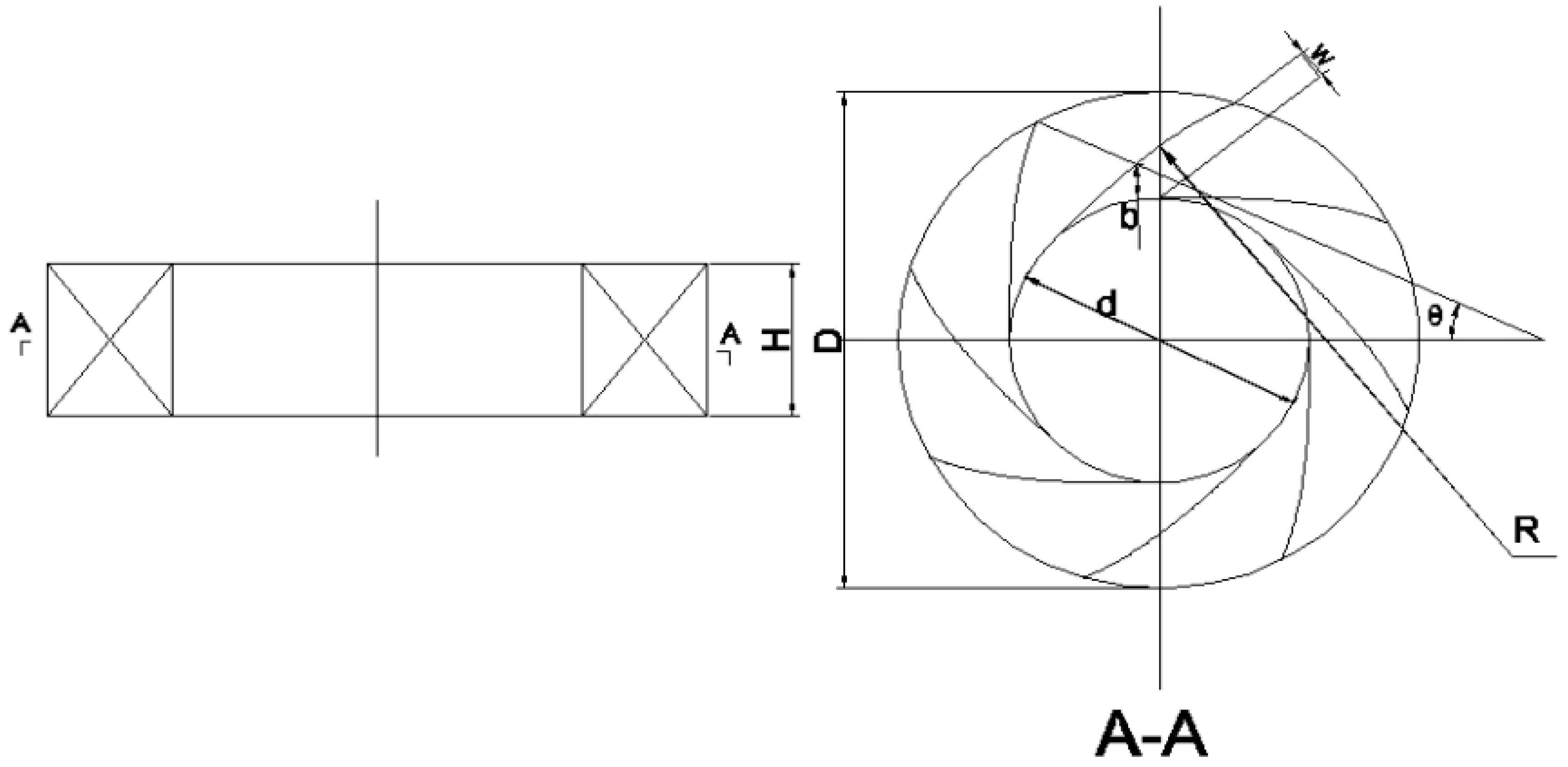
2.2. Design of Swirl Generator
2.3. Design of Diffuser
2.4. Design of Discharge Channel
3. Mathematical Modeling and Method of Calculation of Supersonic Condensation
3.1. Governing Equations
3.2. Turbulence Model
3.3. Real Gas Equation of State
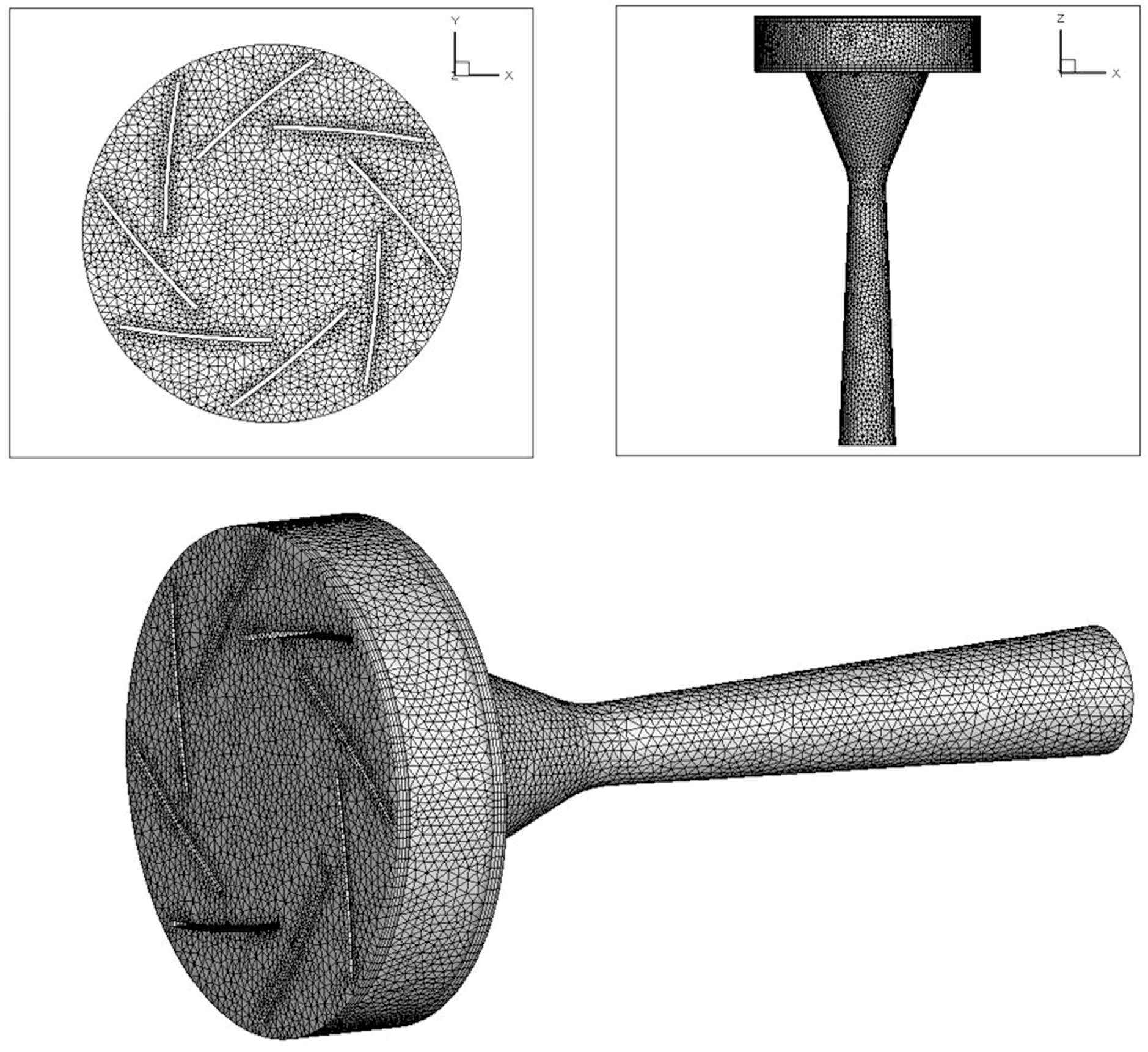
3.4. Numerical Solution
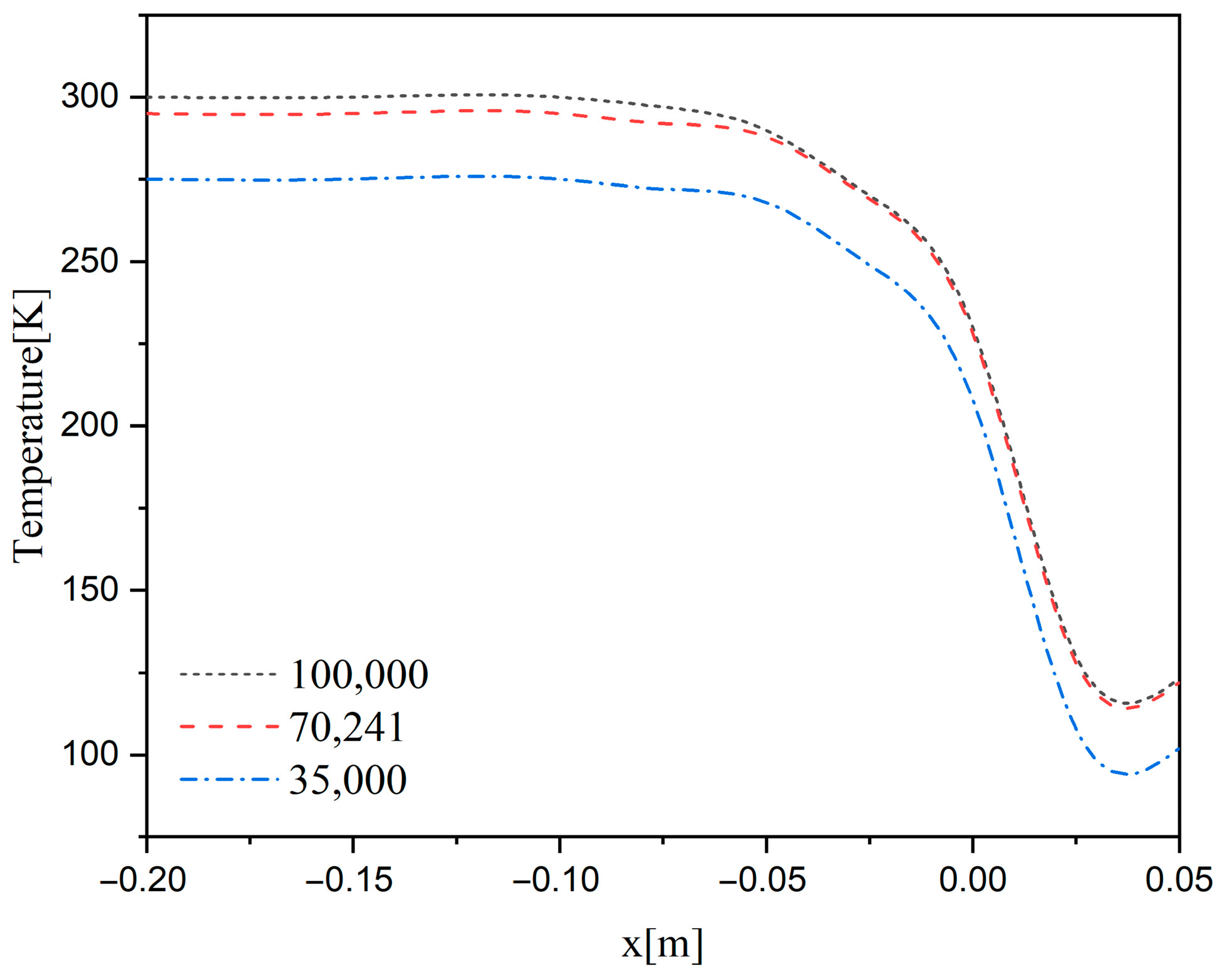
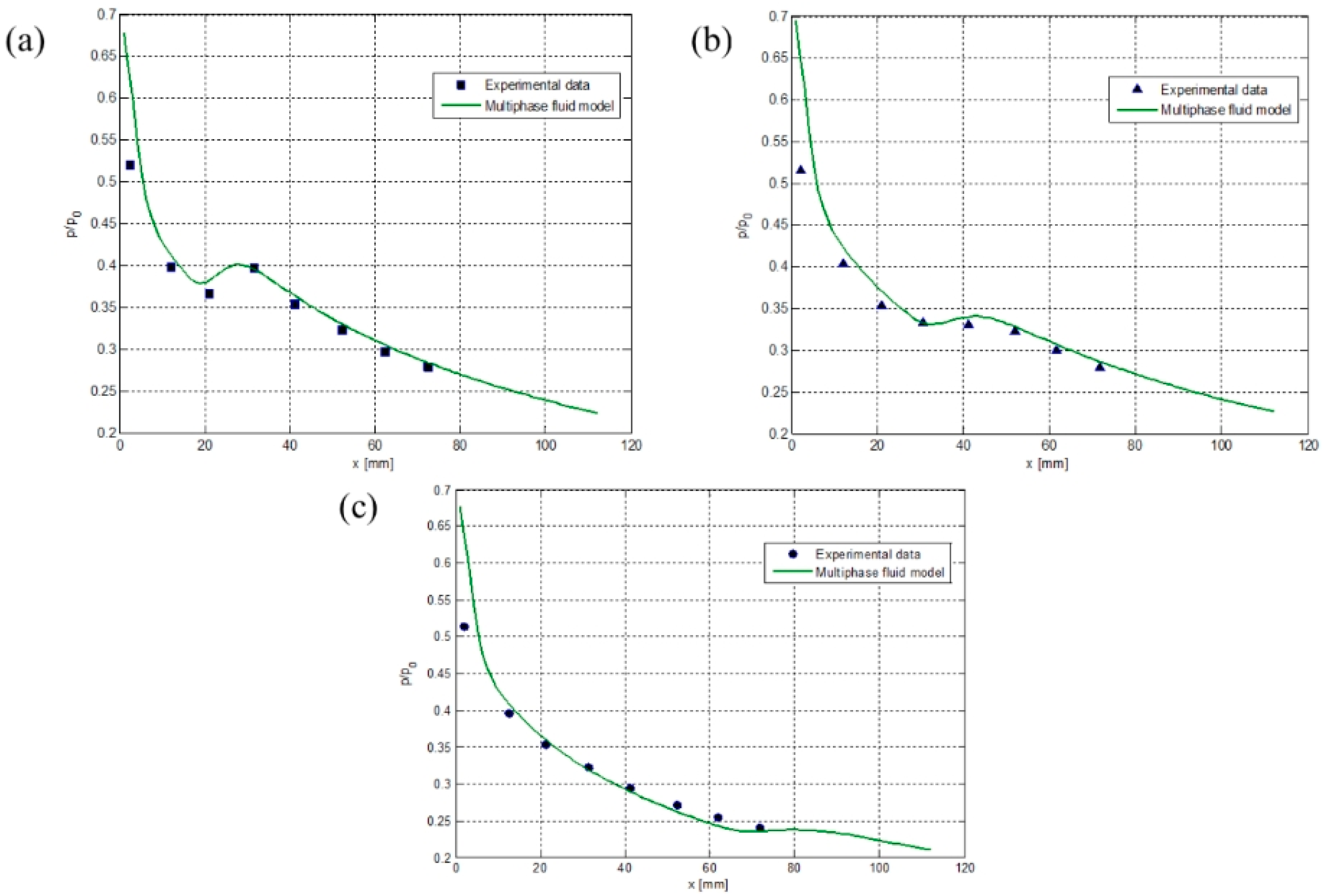
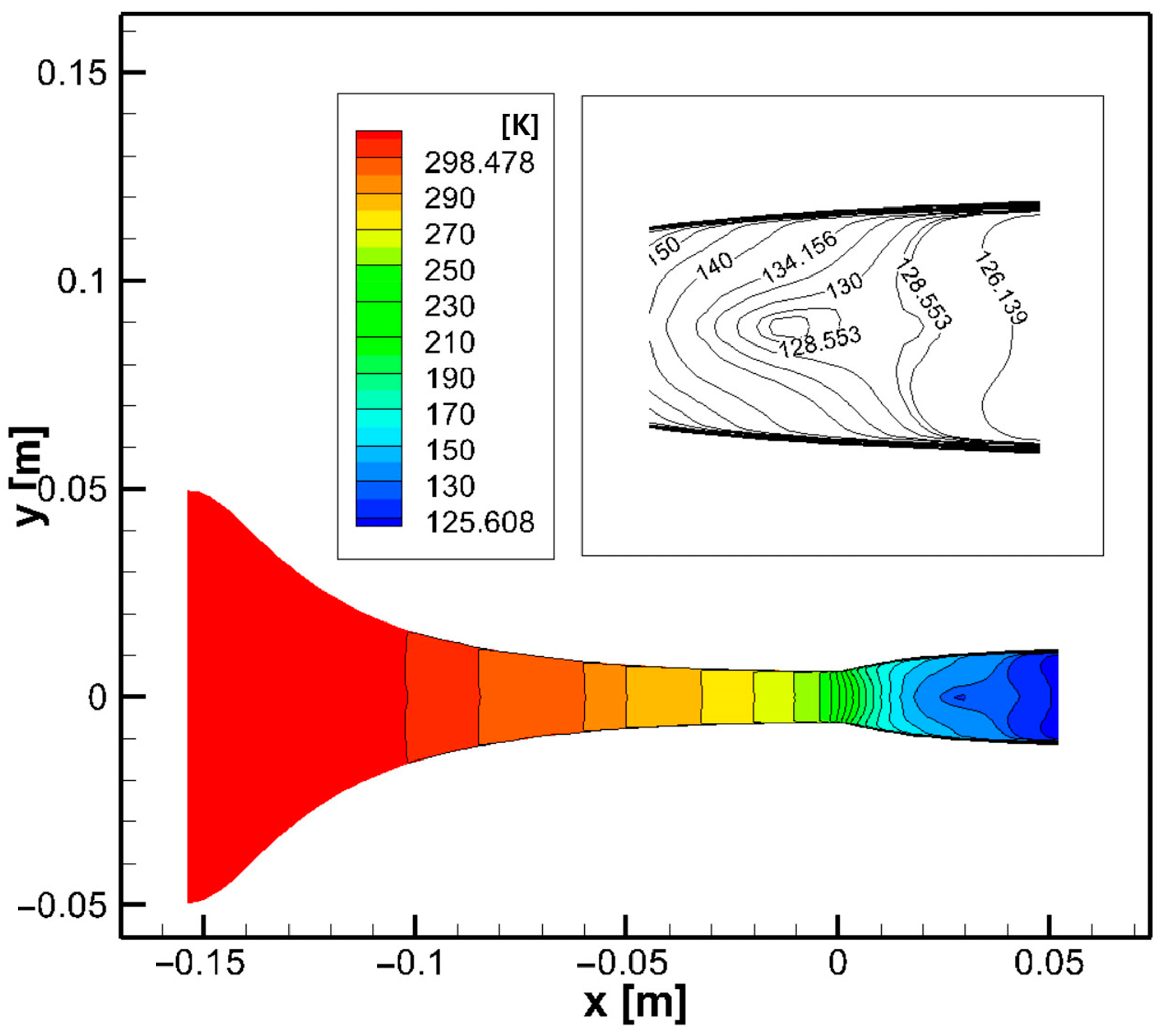
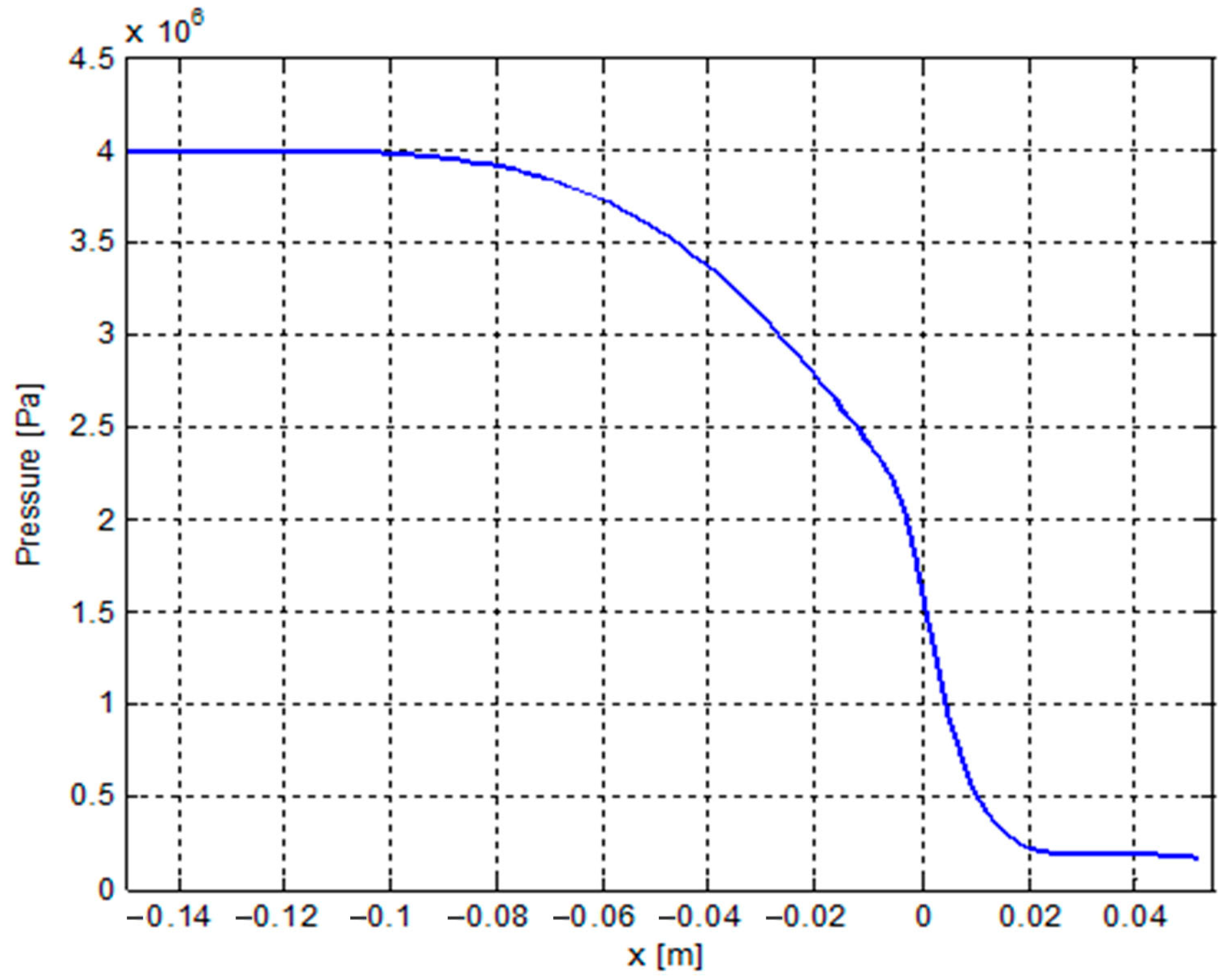
3.5. Model Verification
4. Structural Design Case and Analysis
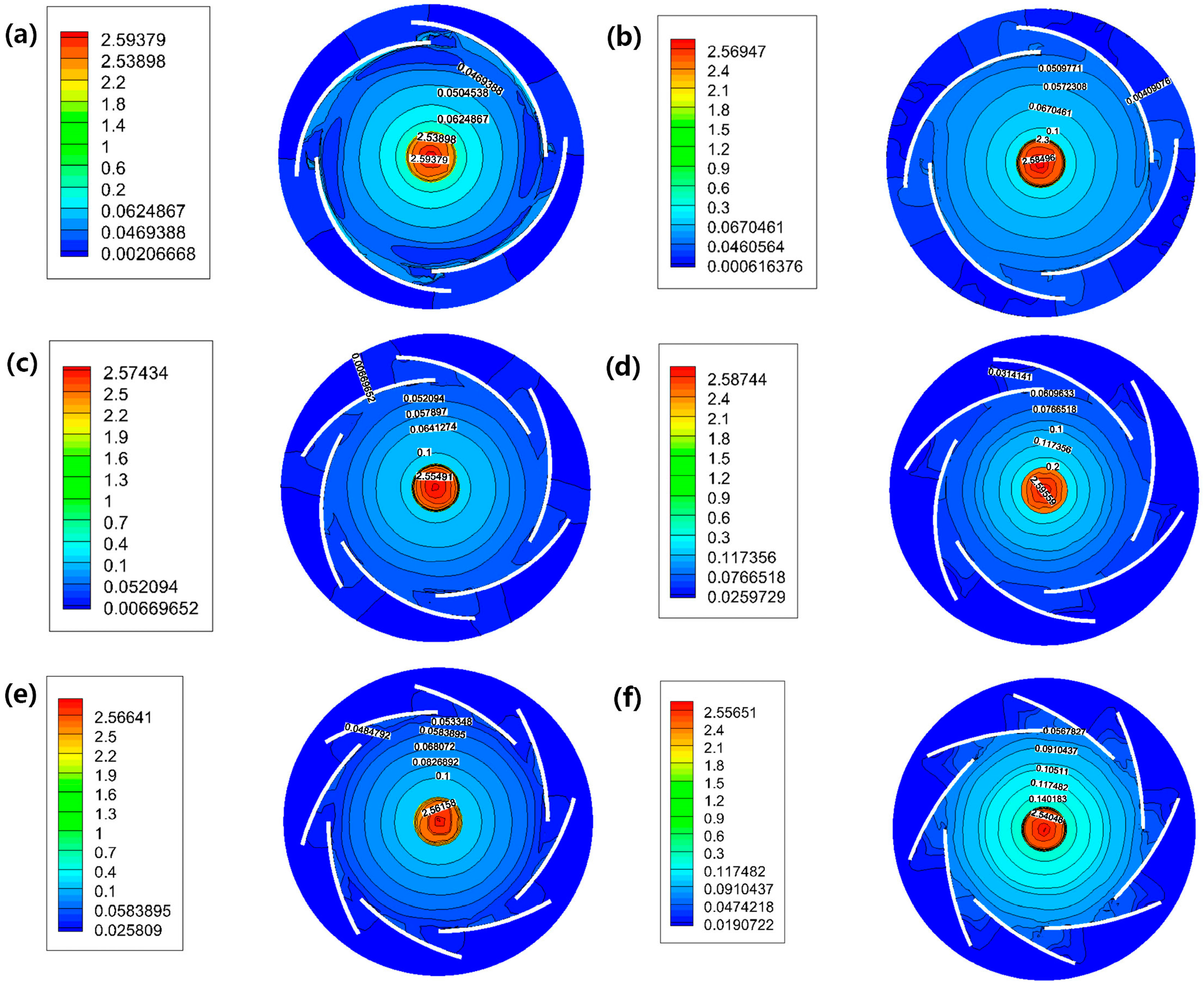
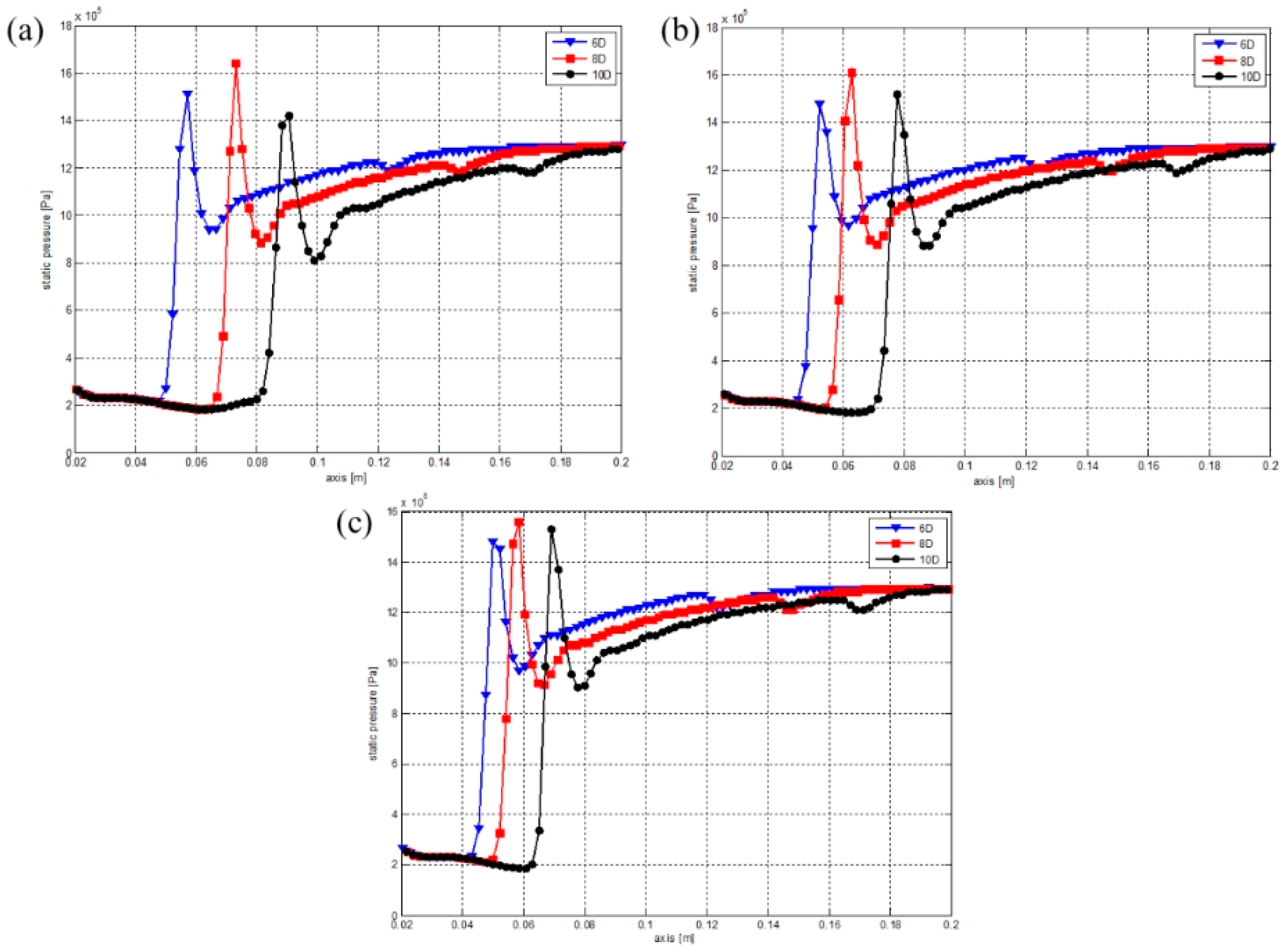
4.1. Swirler Design
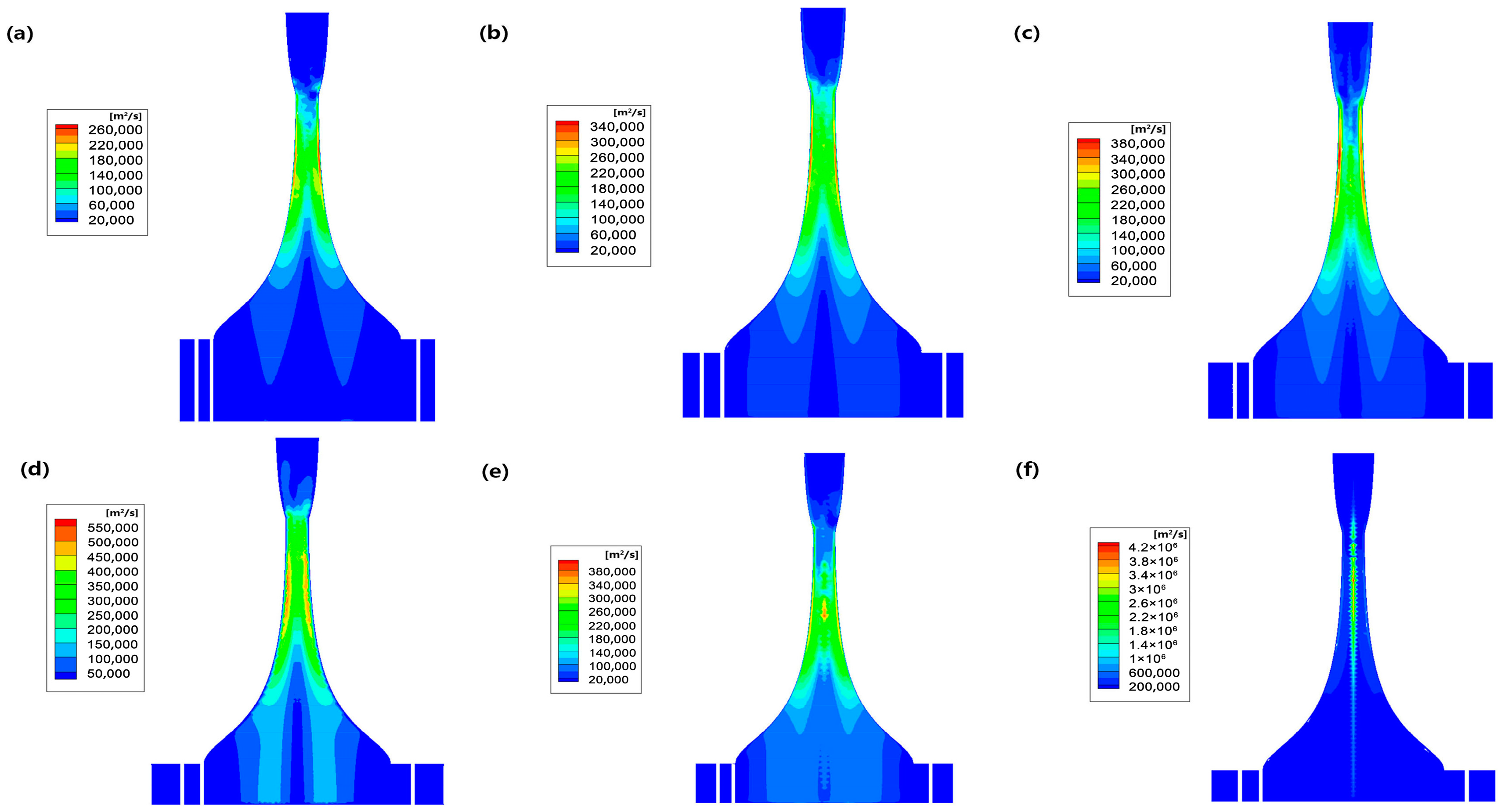
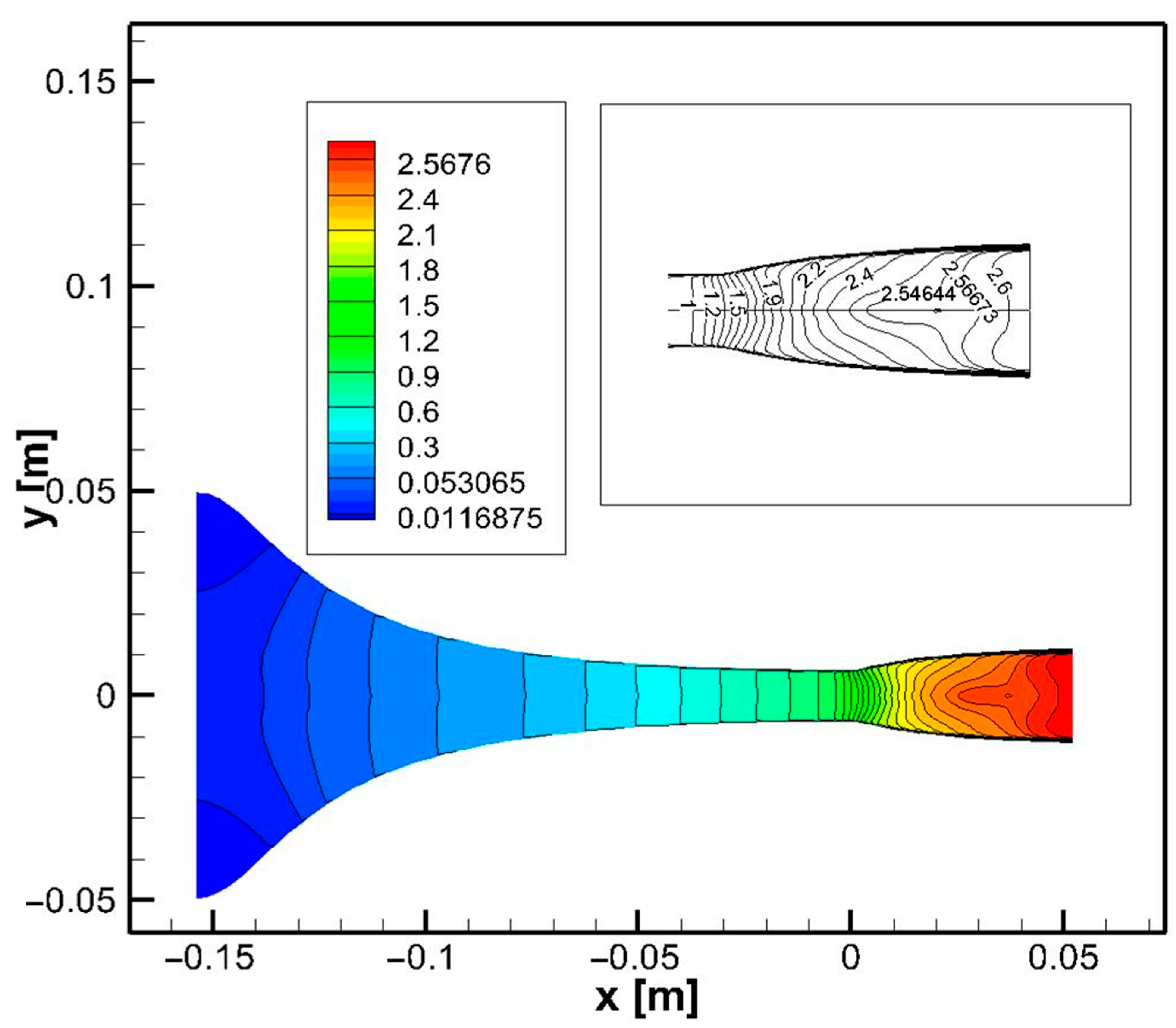
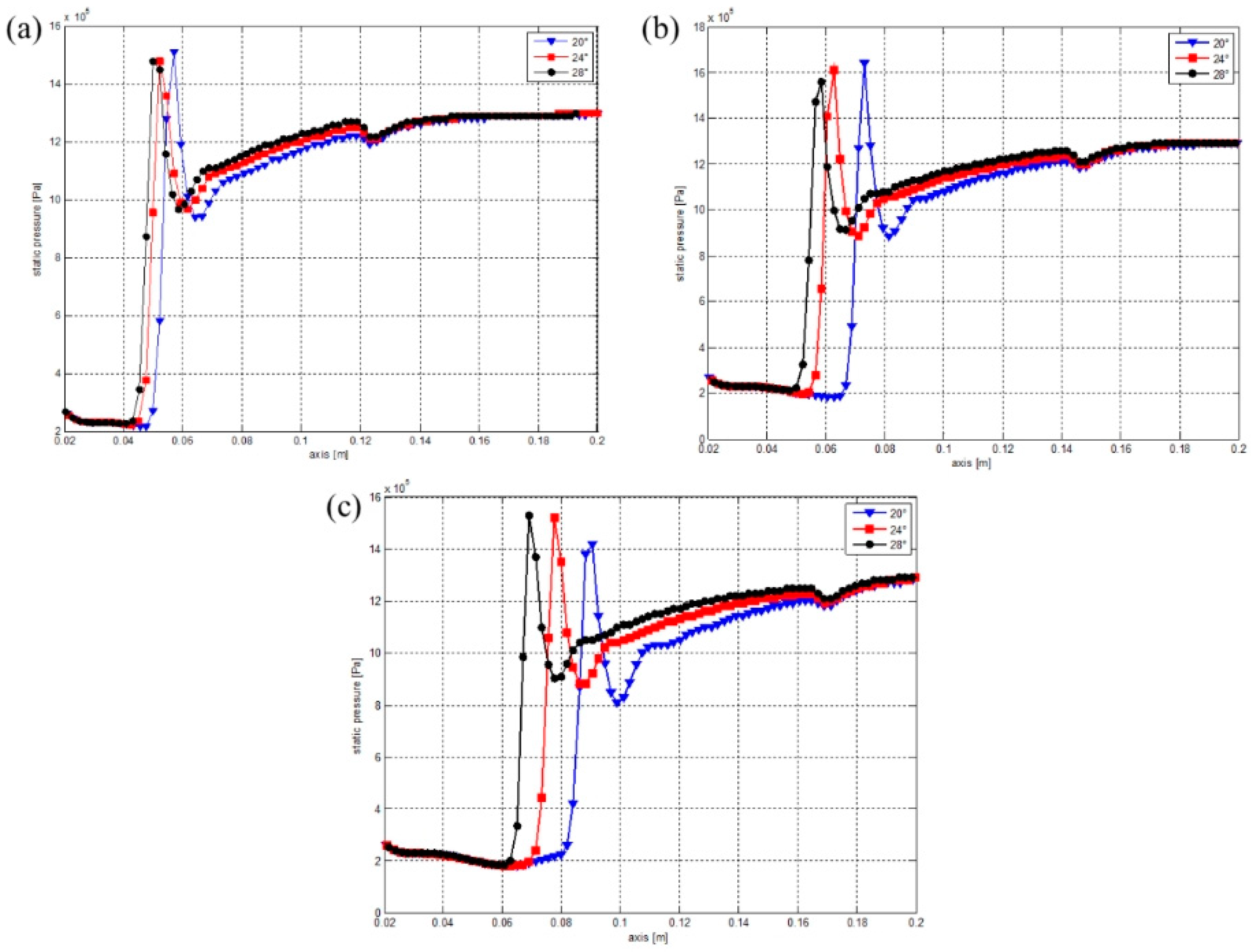
4.2. Nozzle Structure
4.3. Design of Diffuser and Straight Tube Section
4.4. Design of Discharge Gap
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gaidai, O.; Cao, Y.; Ashraf, A.; Sheng, J.; Zhu, Y.; Liu, Z. FPSO/LNG hawser system lifetime assessment by Gaidai multivariate risk assessment method. Energy Inform. 2024, 7, 51. [Google Scholar] [CrossRef]
- Long, X.; Huang, Q.; Tian, Y.; Mu, L. Effects of the operating parameters of supersonic separators on the supersonic liquefaction characteristics of natural gas. Energies 2022, 15, 2531. [Google Scholar] [CrossRef]
- Bian, J.; Cao, X.; Yang, W.; Du, H.; Yin, P. Effects of external particles on the liquefaction property of natural gas in a Laval nozzle. Powder Technol. 2018, 339, 894–902. [Google Scholar] [CrossRef]
- Bian, J.; Cao, X.; Yang, W.; Song, X.; Xiang, C.; Gao, S. Condensation characteristics of natural gas in the supersonic liquefaction process. Energy 2019, 168, 99–110. [Google Scholar] [CrossRef]
- Cao, X.; Bian, J. Supersonic separation technology for natural gas processing: A review. Chem. Eng. Process. Process Intensif. 2019, 136, 138–151. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, Y.; Sun, C.; Yang, Y.; Wen, C. Numerical simulation of supersonic condensation flows using Eulerian-Lagrangian and Eulerian wall film models. Energy 2022, 258, 124833. [Google Scholar] [CrossRef]
- Bian, J.; Jiang, W.; Teng, L.; Liu, Y.; Wang, S.; Deng, Z. Structure improvements and numerical simulation of supersonic separators. Chem. Eng. Process. Process Intensif. 2016, 110, 214–219. [Google Scholar] [CrossRef]
- Cao, X.; Yang, W. Numerical simulation of binary-gas condensation characteristics in supersonic nozzles. J. Nat. Gas Sci. Eng. 2015, 25, 197–206. [Google Scholar] [CrossRef]
- Wang, Y. Analysis for spiral vortex and effect of profile of nozzle and swirler on performance of supersonic separator. Chem. Eng. Process.-Process Intensif. 2020, 147, 107676. [Google Scholar] [CrossRef]
- Dengyu, J.; Eri, Q.; Wang, C.; Liu, H.; Yuan, Y. A fast and efficiency numerical simulation method for supersonic gas processing. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010; OnePetro: Richardson, TX, USA, 2010. [Google Scholar]
- Shoghl, S.N.; Naderifar, A.; Farhadi, F.; Pazuki, G. A novel strategy for comprehensive optimization of structural and operational parameters in a supersonic separator using computational fluid dynamics modeling. Sci. Rep. 2021, 11, 21850. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Yang, M.; Li, F. Investigation on Cryogenic Cavitation Characteristics of an Inducer Considering Thermodynamic Effects. Energies 2024, 17, 19961073. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Wu, J.; Li, L.; Tan, D. Machinability evolution of gas–liquid-solid three-phase rotary abrasive flow finishing. Int. J. Adv. Manuf. Technol. 2024, 131, 2145–2164. [Google Scholar] [CrossRef]
- Malyshkina, M. The procedure for investigation of the efficiency of purification of natural gases in a supersonic separator. High Temp. 2010, 48, 244–250. [Google Scholar] [CrossRef]
- Wen, C.; Cao, X.; Yang, Y.; Zhang, J. Supersonic swirling characteristics of natural gas in convergent-divergent nozzles. Pet. Sci. 2011, 8, 114–119. [Google Scholar] [CrossRef]
- Vlasenko, V.; Slesarenko, V.; Yudakov, A.; Gulkov, A.; Bashirov, K. Three-flow vortex tube: The effect of swirling method and separation insert gap on operational efficiency. Int. J. Therm. Sci. 2022, 173, 107399. [Google Scholar] [CrossRef]
- Wu, H.; Jurčević, M.; Ström, H.; Khurram, M.S.; Jin, H. Numerical simulation of condensation of supercritical water gasification products in a supersonic nozzle. Int. J. Fluid Eng. 2024, 1, 043903. [Google Scholar] [CrossRef]
- Chen, J.; Wang, T.; Li, A.; Huang, Z.; Jiang, W.; Xi, G. Effect of wall thermal condition on the nonequilibrium condensation of CO2 in supersonic flows. Int. J. Therm. Sci. 2024, 195, 108650. [Google Scholar] [CrossRef]
- Wen, C.; Cao, X.; Yang, Y.; Li, W. Numerical simulation of natural gas flows in diffusers for supersonic separators. Energy 2012, 37, 195–200. [Google Scholar] [CrossRef]
- Ren, H.Y.; Li, C.J.; Xie, G. Evaluation of state equations of natural gas in pipeline transportation. Adv. Mater. Res. 2012, 463, 936–939. [Google Scholar] [CrossRef]
- Foelsch, K. The analytical design of an axially symmetric Laval nozzle for a parallel and uniform jet. J. Aeronaut. Sci. 1949, 16, 161–166. [Google Scholar] [CrossRef]
- Bian, J.; Cao, X.; Yang, W.; Guo, D.; Xiang, C. Prediction of supersonic condensation process of methane gas considering real gas effects. Appl. Therm. Eng. 2020, 164, 114508. [Google Scholar] [CrossRef]
- Bakhtar, F.; Young, J.; White, A.; Simpson, D. Classical nucleation theory and its application to condensing steam flow calculations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 1315–1333. [Google Scholar] [CrossRef]
- Gyarmathy, G. Grundlagen Einer Theorie der Nassdampfturbine. Ph.D. thesis, ETH Zürich, Zürich, Switzerland, 1962. [Google Scholar]
- Li, C.; Huang, Q. Rheology-based computational fluid dynamics modeling for de-oiling hydrocyclone efficiency. Chem. Eng. Technol. 2016, 39, 899–908. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Y.; Wang, W.; Zhong, J.; Zhang, D. Application of BWRS equation of state for calculation of fluid density and viscosity. Pet. Sci. Technol. 2022, 40, 1423–1436. [Google Scholar] [CrossRef]
- Wyslouzil, B.E.; Heath, C.H.; Cheung, J.L.; Wilemski, G. Binary condensation in a supersonic nozzle. J. Chem. Phys. 2000, 113, 7317–7329. [Google Scholar] [CrossRef]
- Schinkelshoek, P.; Epsom, H. Supersonic gas conditioning-low pressure drop twister for NGL recovery. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006. [Google Scholar]



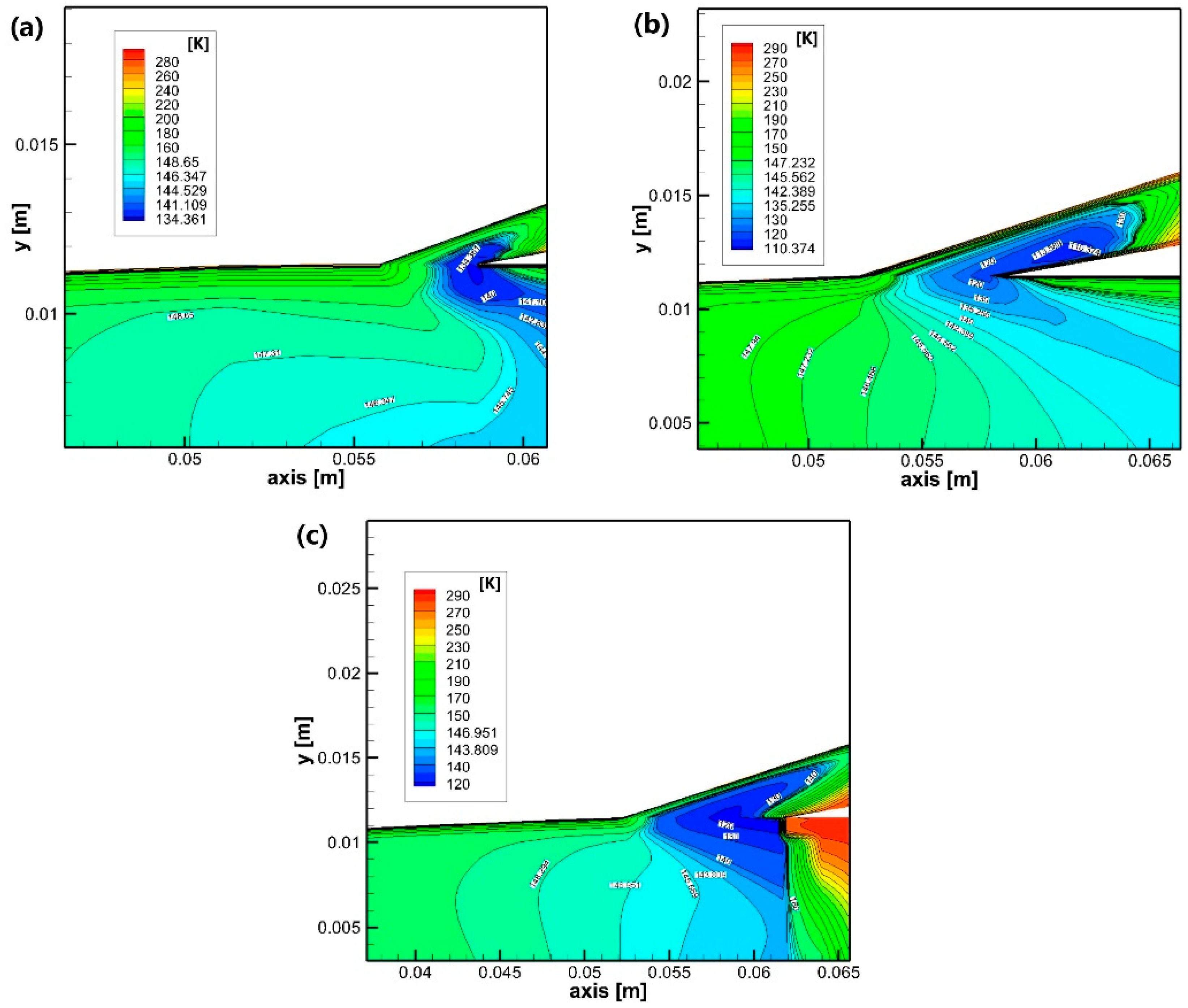
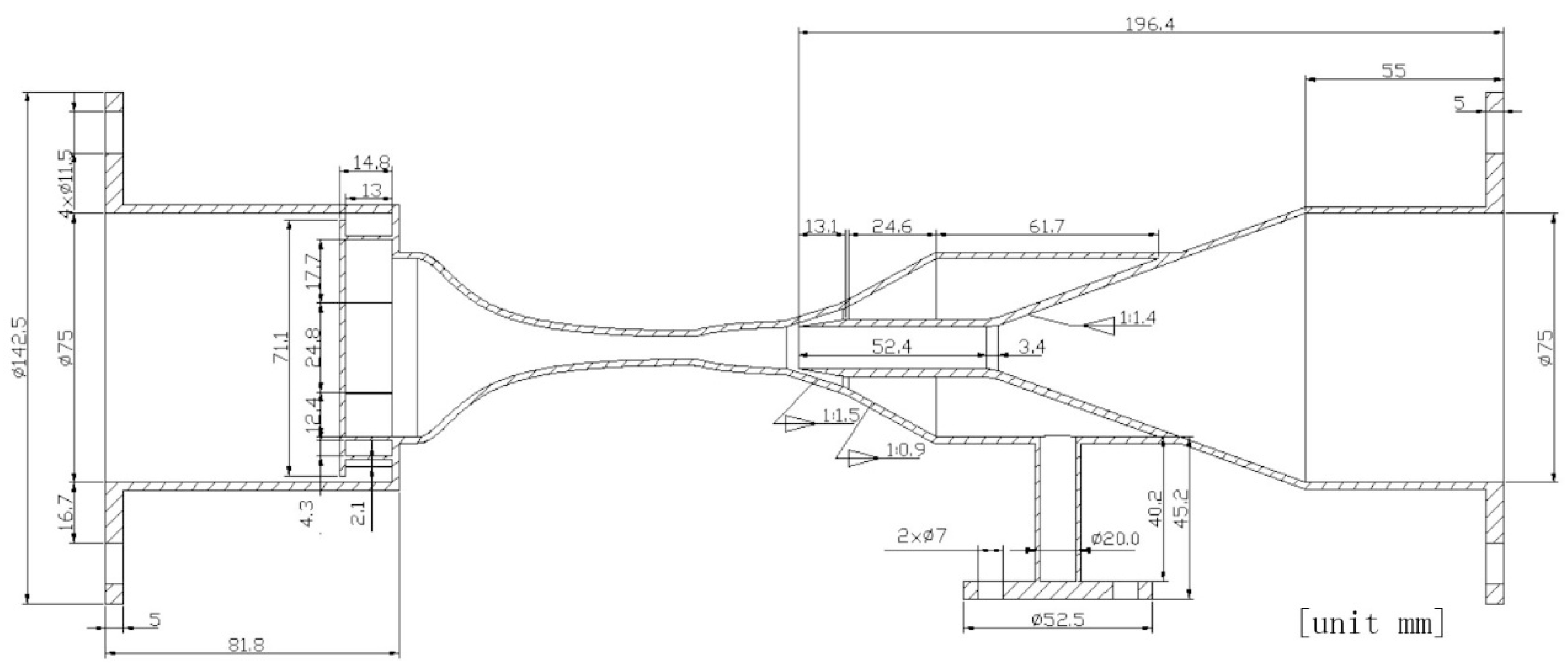
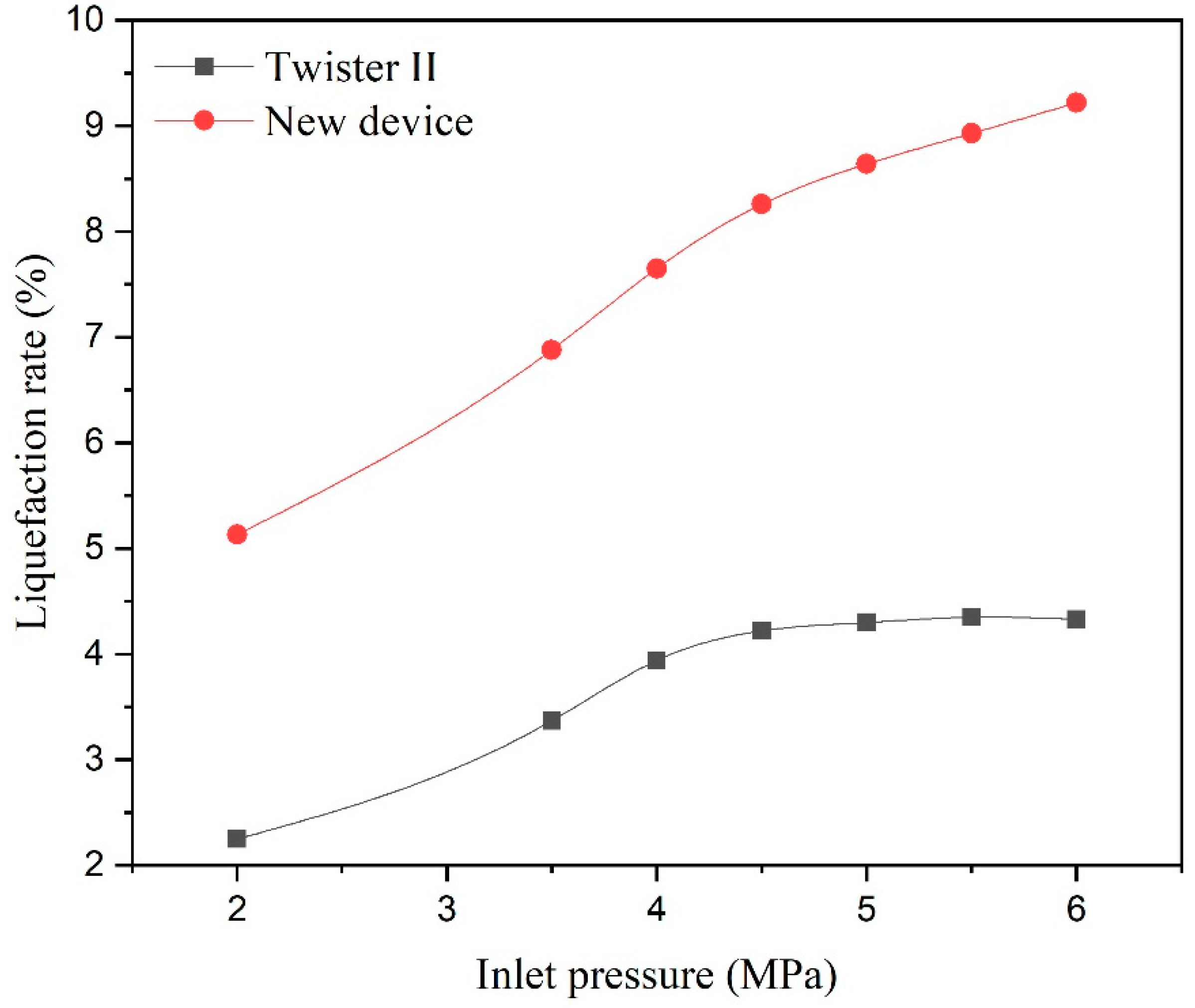
| Nozzle Structure | Experimental Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|
(mm) | (mm) | (mm) | (mm) | (kPa) | (K) | (kPa) | |||
| 38 | 95 | 1.58 | 5 | 12.7 | 60 | 287 | 1.00 | 0.50 | 0.26 |
| Chemical Component | C1 | C2 | C3 | iC4 | nC4 | iC5 | nC5 | N2 |
|---|---|---|---|---|---|---|---|---|
| Mole fraction (%) | 91.8 | 8.1 | 0.1 | 0 | 0 | 0 | 0 | 0 |
| Design | Number of Vanes | Channel Width (mm) | Swirler Height (mm) | Vane Arc Radius (mm) | Swirler Outer Diameter (mm) | Vane Arc Opening Angle (Degrees) |
|---|---|---|---|---|---|---|
| Design 1 | 4 | 6 | 52.00 | 58.39 | 135.00 | 90.00 |
| 8 | 39.00 | 60.85 | 141.00 | |||
| Design 2 | 6 | 6 | 34.00 | 71.04 | 145.00 | 60.00 |
| 8 | 26.00 | 79.13 | 155.00 | |||
| Design 3 | 8 | 6 | 26.00 | 103.13 | 143.00 | 30.00 |
| 8 | 20.00 | 140.60 | 155.00 | 25.00 |
| Convergent Section (mm) | Divergent Section (mm) | Throat Diameter (mm) | Inlet Diameter (mm) | Outlet Diameter (mm) |
|---|---|---|---|---|
| 153.93 | 52.21 | 12.42 | 99.3 | 15.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Huang, H.; Long, X.; Tian, Y.; Meng, J. Structural Designing of Supersonic Swirling Devices Based on Computational Fluid Dynamics Theory. Appl. Sci. 2025, 15, 151. https://doi.org/10.3390/app15010151
Huang Q, Huang H, Long X, Tian Y, Meng J. Structural Designing of Supersonic Swirling Devices Based on Computational Fluid Dynamics Theory. Applied Sciences. 2025; 15(1):151. https://doi.org/10.3390/app15010151
Chicago/Turabian StyleHuang, Qian, Huirong Huang, Xueyuan Long, Yuan Tian, and Jiang Meng. 2025. "Structural Designing of Supersonic Swirling Devices Based on Computational Fluid Dynamics Theory" Applied Sciences 15, no. 1: 151. https://doi.org/10.3390/app15010151
APA StyleHuang, Q., Huang, H., Long, X., Tian, Y., & Meng, J. (2025). Structural Designing of Supersonic Swirling Devices Based on Computational Fluid Dynamics Theory. Applied Sciences, 15(1), 151. https://doi.org/10.3390/app15010151





