Research on Orbital Angular Momentum Mode Detection in an Atmospheric Environment with Fusion Transfer Learning
Abstract
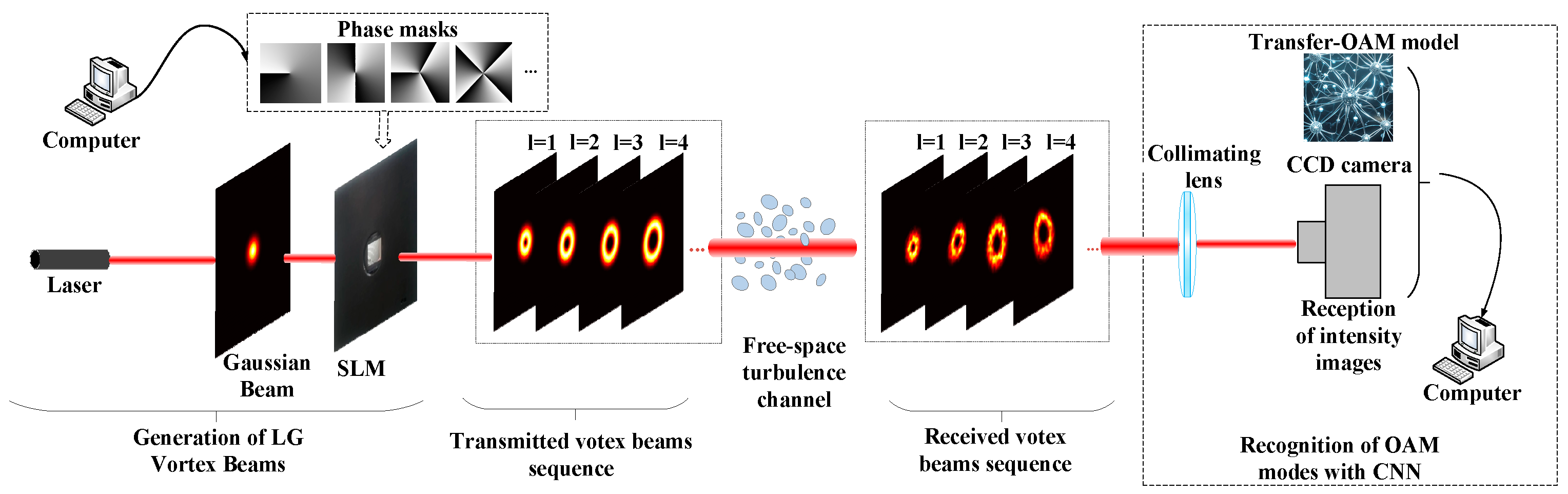
:1. Introduction
2. Theoretical Framework and Network
2.1. Laguerre Gaussian Beam with Orbital Angular Momentum
2.2. Atmospheric Turbulent Channel Model
2.3. Mode Classifier
3. Results and Discussion
3.1. OAM Detection Under Different Data Volumes
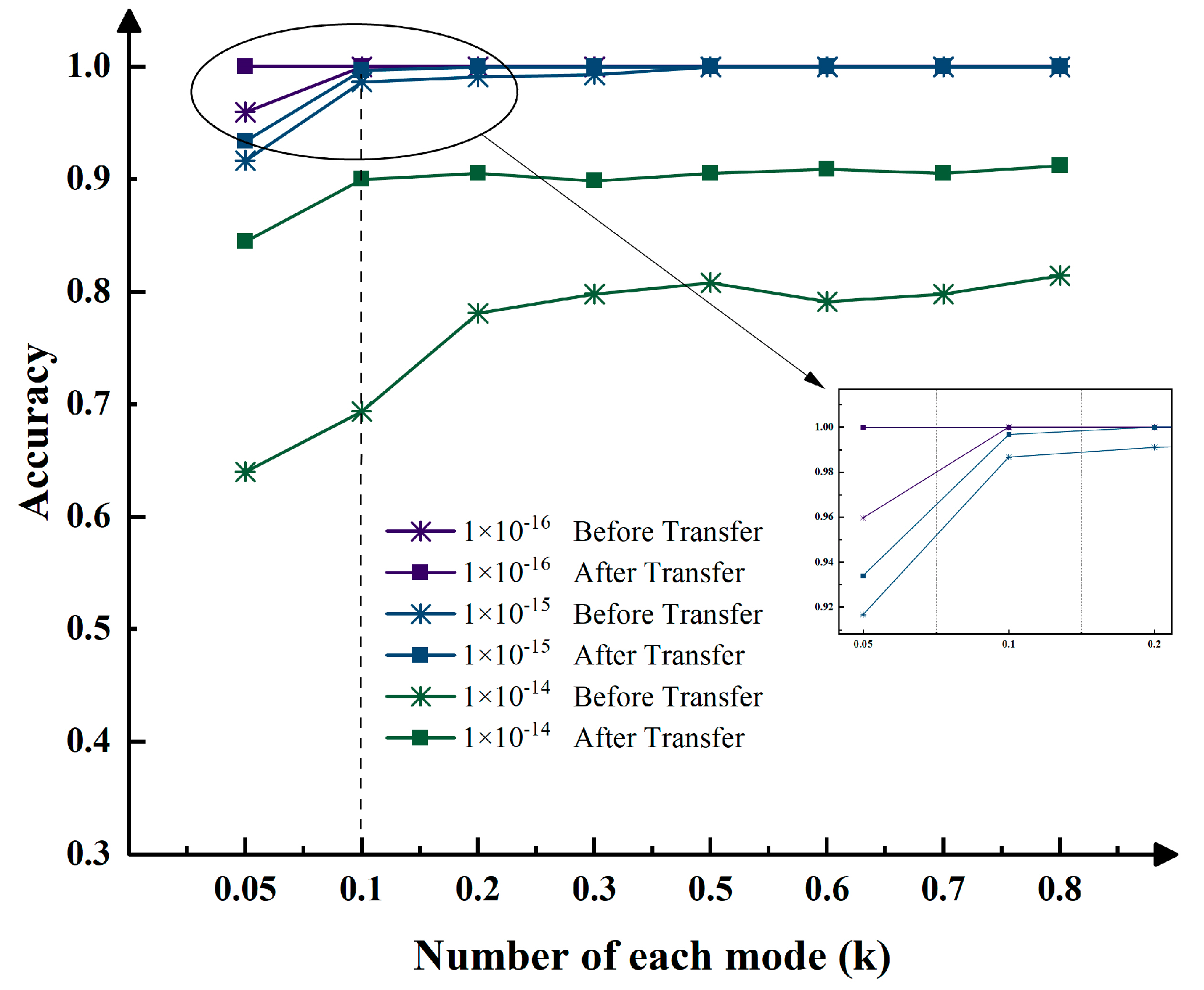
3.2. OAM Detection Under Different Turbulence Intensities
3.3. OAM Detection at Different Transmission Distances
3.4. Comparison of Different Networks
3.5. Analysis of Model Generalization Ability
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.X.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [PubMed]
- Li, X. Digital speckle correlation method based on phase vortices. Opt. Eng. 2012, 51, 077004. [Google Scholar] [CrossRef]
- Otte, E.; Denz, C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl. Phys. Rev. 2020, 7, 041308. [Google Scholar] [CrossRef]
- Li, Y.X.; Han, Y.P.; Cui, Z.W. Measuring the topological charge of vortex beams with gradually changing-period spiral spoke grating. IEEE Photonics Technol. Lett. 2020, 32, 101–104. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Astigmatic transforms of an optical vortex for measurement of its topological charge. Appl. Opt. 2017, 56, 4095–4104. [Google Scholar] [CrossRef]
- Taira, Y.; Zhang, S.K. Split in phase singularities of an optical vortex by off-axis diffraction through a simple circular aperture. Opt. Lett. 2017, 42, 13731376. [Google Scholar] [CrossRef] [PubMed]
- Emile, O.; Emile, J. Young’s double-slit interference pattern from a twisted beam. Appl. Phys. B 2014, 117, 487–491. [Google Scholar] [CrossRef]
- Zhou, H.L.; Shi, L.; Zhang, X.L.; Dong, J. Dynamic interferometry measurement of orbital angular momentum of light. Opt. Lett. 2014, 39, 6058–6061. [Google Scholar] [CrossRef] [PubMed]
- Leach, J.; Padgett, M.J.; Barnett, S.M.; Franke-Arnold, S.; Courtial, J. Measuring the orbital angular momentum of a single photon. Phys. Rev. Lett. 2002, 88, 257901. [Google Scholar] [CrossRef] [PubMed]
- Krenn, M.; Fickler, R.; Fink, M.; Handsteiner, J.; Malik, M.; Scheidl, T.; Ursin, R.; Zeilinger, A. Communication with spatially modulated light through turbulent air across Vienna. New J. Phys. 2014, 16, 113028. [Google Scholar] [CrossRef]
- Knutson, E.; Lohani, S.; Danaci, O.; Huver, S.D.; Glasser, R.T. Deep learning as a tool to distinguish between high orbital angular momentum optical modes. Opt. Photonics Inf. Process. X 2016, 9970, 997013–997020. [Google Scholar]
- Cui, X.; Yin, X.; Chang, H.; Liao, H.; Chen, X.; Xin, X.; Wang, Y. Experimental study of machine learning based orbital angular momentum shift keying decoders in optical underwater channels. Opt. Commun. 2019, 452, 116–123. [Google Scholar] [CrossRef]
- Wang, Z.; Dedo, M.I.; Guo, K.; Zhou, K.; Shen, F.; Sun, Y.; Liu, S.; Guo, Z. Efficient Recognition of the Propagated Orbital Angular Momentum Modes in Turbulences With the Convolutional Neural Network. IEEE Photonics J. 2019, 11, 236–237. [Google Scholar] [CrossRef]
- Dedo, K.G.Z. OAM mode recognition based on joint scheme of combining the Gerchberg–Saxton (GS) algorithm and convolutional neural network (CNN). Opt. Commun. 2020, 456, 124696. [Google Scholar] [CrossRef]
- Hao, Y.; Zhao, L.; Huang, T.; Wu, Y.; Jiang, T.; Wei, Z.; Deng, D.; Luo, A.P.; Liu, H. High-Accuracy Recognition of Orbital Angular Momentum Modes Propagated in Atmospheric Turbulences Based on Deep Learning. IEEE Access 2020, 8, 159542–159551. [Google Scholar] [CrossRef]
- Liu, W.; Jin, M.; Hao, Y.; Deng, D.; Wu, R.; Wei, Z.; Liu, H. Efficient identification of orbital angular momentum modes carried by Bessel Gaussian beams in oceanic turbulence channels using convolutional neural network. Opt. Commun. 2021, 498, 127251–127252. [Google Scholar] [CrossRef]
- Qian, Y.; Chen, H.; Huo, P.; Wang, X.; Gao, S.; Zhang, P.; Gao, H.; Liu, R.; Li, F. Towards fine recognition of orbital angular momentum modes through smoke. Opt. Express 2022, 30, 15172–15183. [Google Scholar] [CrossRef]
- Yang, L.; Huang, S.; Zhu, G. Jointly Detecting Atmospheric Turbulence and Recognizing OAM Modes Via a Residual Network. Wirel. Pers. Commun. 2023, 131, 187–196. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.; Tan, Z.; Wang, X.; Lei, S.; Wu, P.; Yang, C. Detection of orbital angular momentum carried high-order radial vortex beams using CNN-OAM mode classifier. Opt. Laser Technol. 2024, 169, 110027. [Google Scholar] [CrossRef]
- Elmabruk, K.; Kemal, A.; Serhat, K. Atmospheric turbulence recognition with deep learning models for sinusoidal hyperbolic hollow Gaussian beams-based free-space optical communication links. Phys. Scr. 2024, 99, 075404. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, D.; Sun, Y.; Nanehkaran, Y.A. Using deep transfer learning for image-based plant disease identification. Comput. Electron. Agric. 2020, 173, 105393. [Google Scholar] [CrossRef]
- Mathivanan, S.K.; Sonaimuthu, S.; Murugesan, S.; Rajadurai, H.; Shivahare, B.D.; Shah, M.A. Employing deep learning and transfer learning for accurate brain tumor detection. Sci. Rep. 2024, 14, 7232. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.C. An analytical model for the refractive index power spectrum and its application to optical scintillations in the atmosphere. J. Mod. Opt. 1992, 39, 1849–1853. [Google Scholar] [CrossRef]
- Berkhout, G.; Lavery, R.; Courtial, R.; Beijersbergen, M.W.; Padgett, M.J. Efficient sorting of orbital angular momentum states of light. Phys. Rev. Lett. 2010, 105, 153601. [Google Scholar] [CrossRef]
- Lane, R.G.; Glindemann, A.; Dainty, J.C. Simulation of a Kolmogorov phase screen. Waves Random Media 1992, 2, 209. [Google Scholar] [CrossRef]







| Parameter | Specification |
|---|---|
| 632.8 nm | |
| 0.05 m | |
| 512 | |
| 200 m | |
| 0.005 m | |
| 3 m | |
| Layer | Kernel Numbers | Kernel Size | Stride | Padding | Activation Function |
|---|---|---|---|---|---|
| Conv1 | 48 | 11 × 11 | 4 | 2 | MP (3 × 3) + ReLU |
| Conv2 | 128 | 3 × 3 | 1 | 2 | MP (3 × 3) + ReLU |
| Conv3 | 192 | 3 × 3 | 1 | 1 | ReLU |
| Conv4 | 192 | 3 × 3 | 1 | 1 | ReLU |
| Conv5 | 128 | 3 × 3 | 1 | 1 | MP (3 × 3) + ReLU |
| Conv6 | 128 | 3 × 3 | 1 | 1 | MP (3 × 3) + ReLU |
| Conv7 | 128 | 3 × 3 | 1 | 1 | ReLU |
| FC1 | 2048 | - | - | - | Dropout(0.5) + ReLU |
| FC2 | 2048 | - | - | - | Dropout(0.5) + ReLU |
| FC3 | 15 | - | - | - | ReLU |
| Types | AT | Net1 | Net2 | Transfer-OAM |
|---|---|---|---|---|
| Recognition accuracy | Weak | 1.0000 | 1.0000 | 1.0000 |
| Medium | 0.9562 | 1.0000 | 1.0000 | |
| Strong | 0.7489 | 0.8134 | 0.9073 | |
| Number of datasets per model/piece | / | 1000 | 1000 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, C.; Chen, Y.; Ke, X. Research on Orbital Angular Momentum Mode Detection in an Atmospheric Environment with Fusion Transfer Learning. Appl. Sci. 2025, 15, 15. https://doi.org/10.3390/app15010015
Ke C, Chen Y, Ke X. Research on Orbital Angular Momentum Mode Detection in an Atmospheric Environment with Fusion Transfer Learning. Applied Sciences. 2025; 15(1):15. https://doi.org/10.3390/app15010015
Chicago/Turabian StyleKe, Chenghu, Youmei Chen, and Xizheng Ke. 2025. "Research on Orbital Angular Momentum Mode Detection in an Atmospheric Environment with Fusion Transfer Learning" Applied Sciences 15, no. 1: 15. https://doi.org/10.3390/app15010015
APA StyleKe, C., Chen, Y., & Ke, X. (2025). Research on Orbital Angular Momentum Mode Detection in an Atmospheric Environment with Fusion Transfer Learning. Applied Sciences, 15(1), 15. https://doi.org/10.3390/app15010015





