Comparative Analysis of the Stability of Overlying Rock Mass for Two Types of Lined Rock Caverns Based on Rock Mass Classification
Abstract
1. Introduction
2. Rock Mass Classification
3. Analysis Method and Assumptions
3.1. Computational Model
3.2. Method for Solving Potential Failure Surfaces
3.3. Method for Solving the Factor of Safety
4. Computational Analysis and Discussion
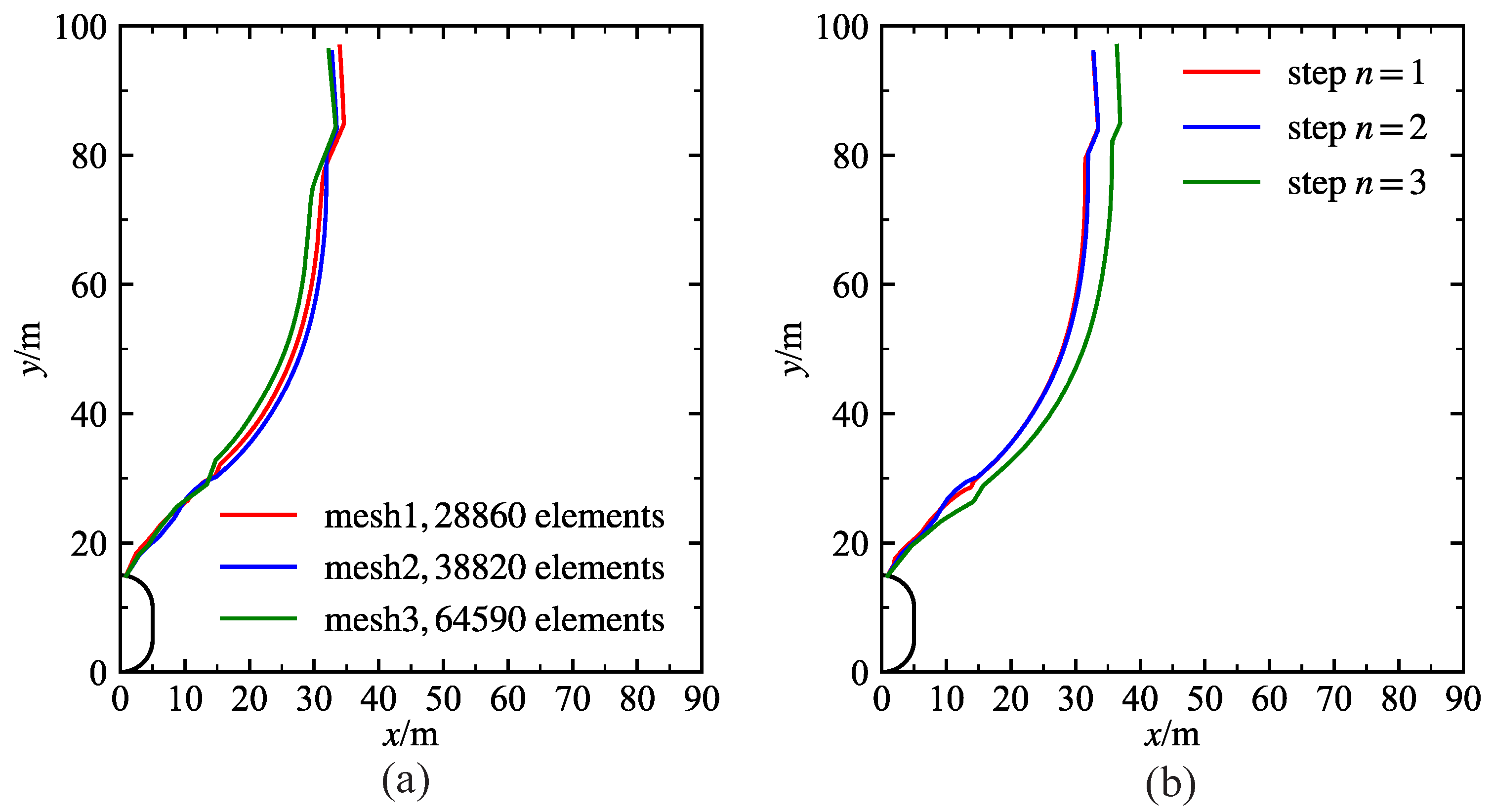
4.1. Potential Failure Surfaces
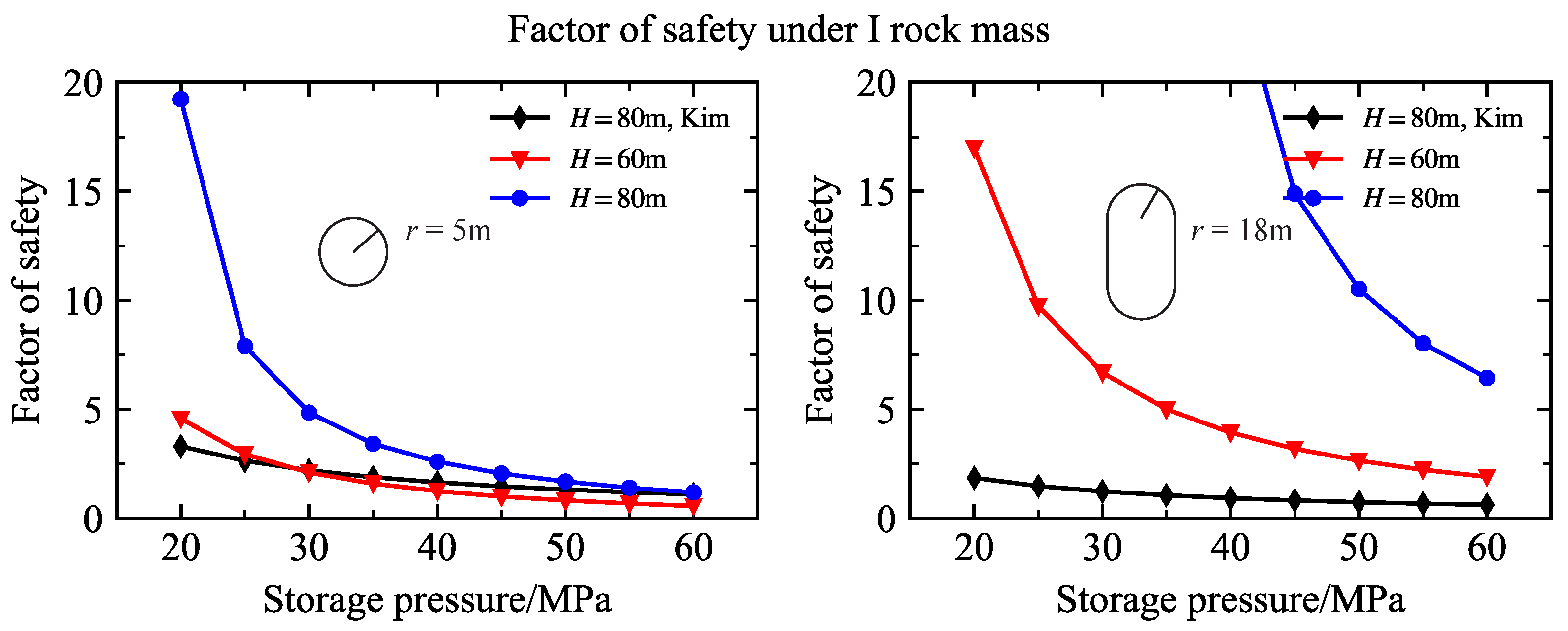
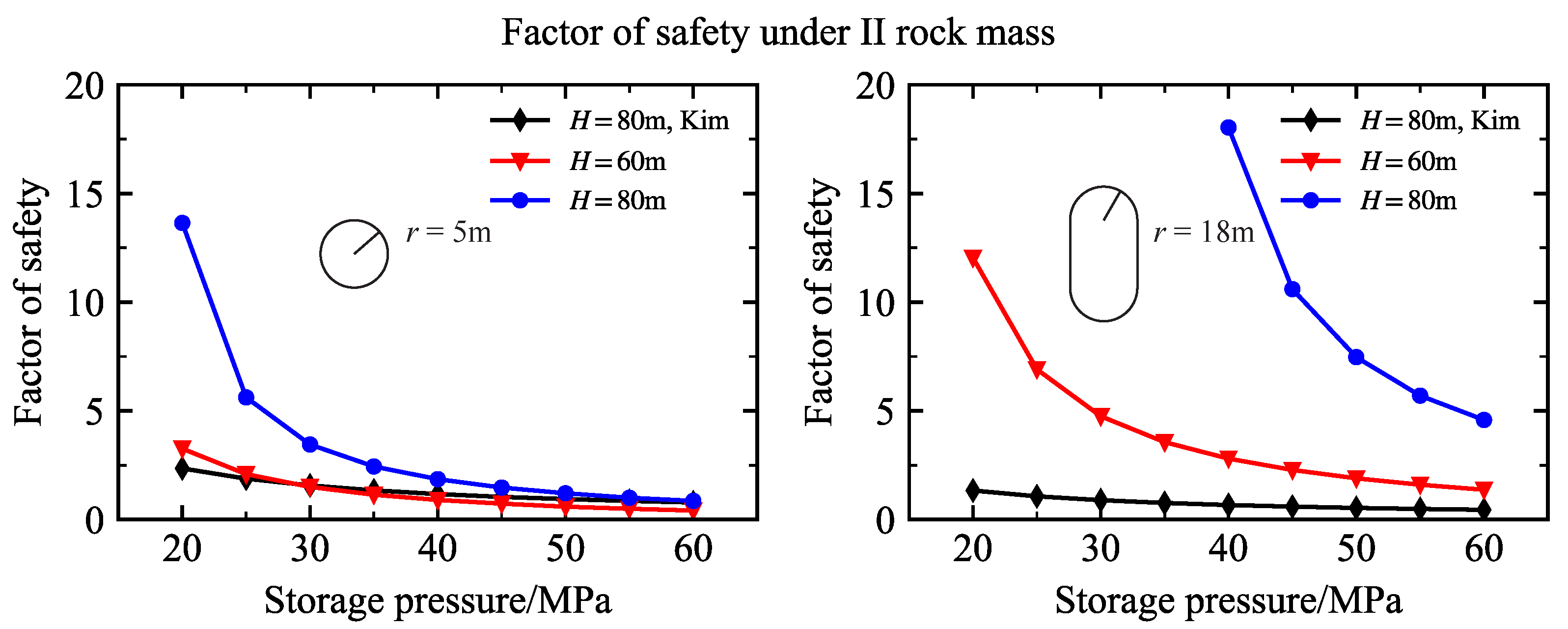
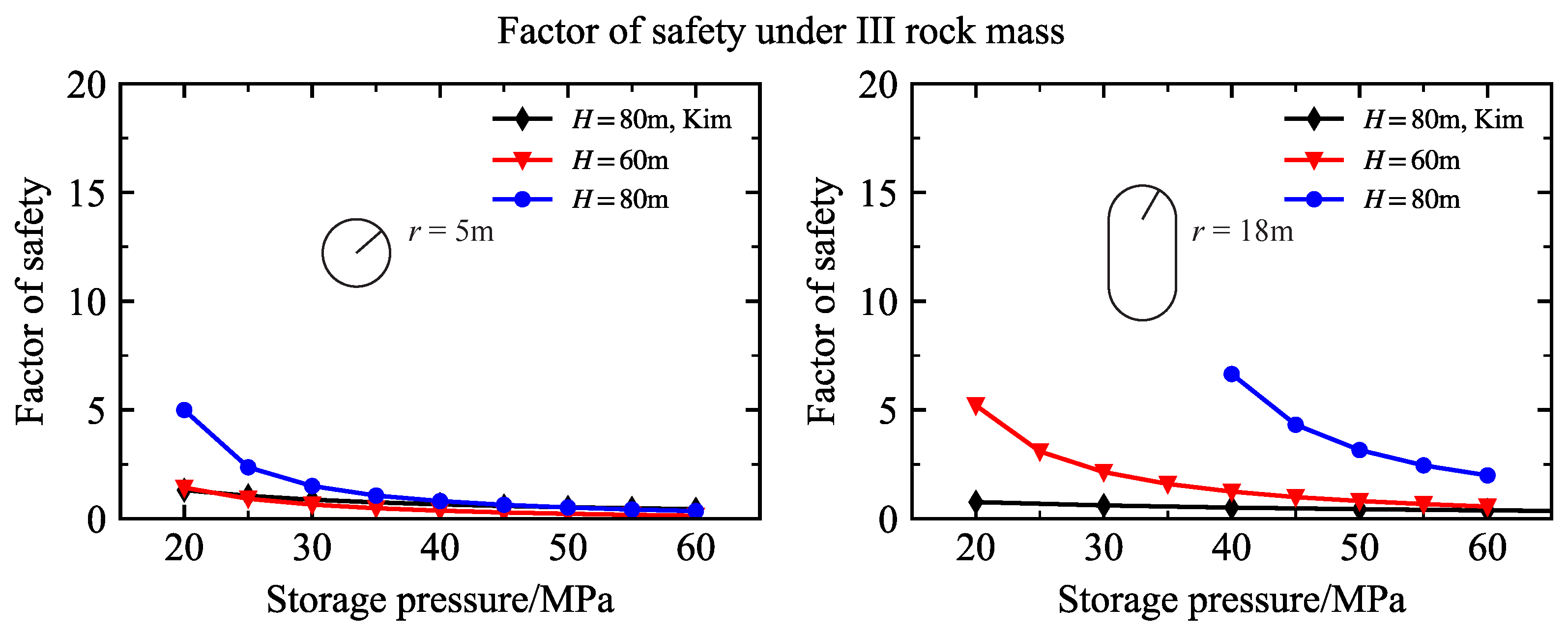
4.2. Factor of Safety
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAES | compressed air energy storage |
| LRC | lined rock cavern |
Appendix A
| Algorithm A1 Solving for potential fracture surfaces (taking two dimensions as an example) |
| Require: mesh information mesh, stress field stress, initial crack point , step n |
| Ensure: potential fracture surface |
| 1: // Current loop point |
| 2: |
| 3: while in model do // The point is within the model boundary |
| 4: |
| 5: Calculate the principal stress direction at point p; |
| 6: // It can be calculated through the known stress field and mesh node information. |
| 7: Calculate the crack direction |
| 8: = |
| 9: |
| 10: end while |
References
- Kim, H.M.; Rutqvist, J.; Ryu, D.W.; Choi, B.H.; Sunwoo, C.; Song, W.K. Exploring the Concept of Compressed Air Energy Storage (CAES) in Lined Rock Caverns at Shallow Depth: A Modeling Study of Air Tightness and Energy Balance. Appl. Energy 2012, 92, 653–667. [Google Scholar] [CrossRef]
- Kushnir, R.; Ullmann, A.; Dayan, A. Compressed Air Flow within Aquifer Reservoirs of CAES Plants. Transp. Porous Media 2010, 81, 219–240. [Google Scholar] [CrossRef]
- Lutyński, M.; Bartela, L.; Smolnik, G.; Waniczek, S. Underground Coal Mine Workings as Potential Places for Compressed Air Energy Storage. IOP Conf. Ser. Mater. Sci. Eng. 2019, 545, 012014. [Google Scholar] [CrossRef]
- Zhang, Q.; Duan, K.; Jiao, Y.; Xiang, W. Physical Model Test and Numerical Simulation for the Stability Analysis of Deep Gas Storage Cavern Group Located in Bedded Rock Salt Formation. Int. J. Rock Mech. Min. Sci. 2017, 94, 43–54. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, H.; Liu, Y.; Wang, T.; Wang, Z. Surrounding Rock Stability of Horizontal Cavern Reconstructed for Gas Storage. J. Energy Storage 2023, 59, 106534. [Google Scholar] [CrossRef]
- Li, H.; Ma, H.; Zhang, H.; Shi, X. A New Evaluation System for Feasibility and Stability Analyses of Ultra-Large Salt Caverns Gas Storage. Rock Mech. Rock Eng. 2024, 1–17. [Google Scholar] [CrossRef]
- Perazzelli, P.; Anagnostou, G. Design Issues for Compressed Air Energy Storage in Sealed Underground Cavities. Rock Mech. Rock Eng. 2016, 8, 314–328. [Google Scholar] [CrossRef]
- Barton, N.; Monsen, K.; Chryssanthakis, P.; Norheim, Ø. Rock mechanics design for high pressure gas storage in shallow lined caverns. In Storage of Gases in Rock Caverns, Proceedings of the International Conference on Storage of Gases in Rock Caverns, Trondheim, Norway, 26–28 June 1989; Routledge: London, UK, 2022; pp. 159–165. [Google Scholar]
- Brandshaug, T.; Christianson, M.; Damjanac, B.P. Technical Review of the Lined Rock Cavern Concept and Design Methodology: Mechanical Response of Rock Mass; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2001. [Google Scholar]
- Ghaly, A.; Hanna, A. Ultimate Pullout Resistance of Single Vertical Anchors. Can. Geotech. J. 1994, 31, 661–672. [Google Scholar] [CrossRef]
- Mandl, G. Mechanics of Tectonic Faulting: Models and Basic Concepts; Elsevier: Amsterdam, The Netherlands, 1988; pp. 391–401. [Google Scholar]
- Kim, H.M.; Park, D.; Ryu, D.W.; Song, W.K. Parametric Sensitivity Analysis of Ground Uplift above Pressurized Underground Rock Caverns. Eng. Geol. 2012, 135–136, 60–65. [Google Scholar] [CrossRef]
- Tunsakul, J.; Jongpradist, P.; Soparat, P.; Kongkitkul, W.; Nanakorn, P. Analysis of Fracture Propagation in a Rock Mass Surrounding a Tunnel under High Internal Pressure by the Element-Free Galerkin Method. Comput. Geotech. 2014, 55, 78–90. [Google Scholar] [CrossRef]
- Tunsakul, J.; Jongpradist, P.; Kim, H.M.; Nanakorn, P. Evaluation of Rock Fracture Patterns Based on the Element-Free Galerkin Method for Stability Assessment of a Highly Pressurized Gas Storage Cavern. Acta Geotech. 2018, 13, 817–832. [Google Scholar] [CrossRef]
- Tunsakul, J.; Jongpradist, P.; Kongkitkul, W.; Wonglert, A.; Youwai, S. Investigation of Failure Behavior of Continuous Rock Mass around Cavern under High Internal Pressure. Tunn. Undergr. Space Technol. 2013, 34, 110–123. [Google Scholar] [CrossRef]
- Jongpradist, P.; Tunsakul, J.; Kongkitkul, W.; Fadsiri, N.; Arangelovski, G.; Youwai, S. High Internal Pressure Induced Fracture Patterns in Rock Masses Surrounding Caverns: Experimental Study Using Physical Model Tests. Eng. Geol. 2015, 197, 158–171. [Google Scholar] [CrossRef]
- Thongraksa, A.; Punya-in, Y.; Jongpradist, P.; Kim, H.M.; Jamsawang, P. Failure Behaviors of Rock Masses around Highly Pressurized Cavern: Initiation and Modes of Failure. Tunn. Undergr. Space Technol. 2021, 115, 104058. [Google Scholar] [CrossRef]
- Perazzelli, P.; Anagnostou, G. Upper Bound Limit Analysis of Uplift Failure in Pressurized Sealed Rock Tunnels. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 719–735. [Google Scholar] [CrossRef]
- Wang, H.T.; Liu, P.; Li, S.C.; Li, X.J.; Zhang, X. Limit Analysis of Uplift Failure Mechanisms for a High-Pressure Gas Storage Tunnel in Layered Hoek-Brown Rock Masses. Eng. Fail. Anal. 2022, 138, 106274. [Google Scholar] [CrossRef]
- Perazzelli, P.; Anagnostou, G.; Amberg, J. Uplift Analysis for CAES Tunnels. In Computer Methods and Recent Advances in Geomechanics; Oka, F., Murakami, A., Uzuoka, R., Kimoto, S., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 1691–1696. [Google Scholar]
- Bieniawski, Z.T. Engineering Classification of Jointed Rock Masses. Civ. Eng. 1973, 15, 335–344. [Google Scholar]
- Button, E.; Riedmüller, G.; Schubert, W.; Klima, K.; Medley, E. Tunnelling in Tectonic Melanges—Accommodating the Impacts of Geomechanical Complexities and Anisotropic Rock Mass Fabrics. Bull. Eng. Geol. Environ. 2004, 63, 109–117. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Practical Estimates of Rock Mass Strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- GB/T 50218-2014; Standard for Engineering Classification of Rock Mass. National Standard of the People’s Republic of China, Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2014.
- Damasceno, D.R.; Spross, J.; Johansson, F. Rock Mass Response for Lined Rock Caverns Subjected to High Internal Gas Pressure. J. Rock Mech. Geotech. Eng. 2023, 15, 119–129. [Google Scholar] [CrossRef]
- Zhou, S.; Xia, C.; Zhou, Y. Long-term stability of a lined rock cavern for compressed air energy storage: Thermo-mechanical damage modeling. Eur. J. Environ. Civ. Eng. 2020, 24, 2070–2093. [Google Scholar] [CrossRef]
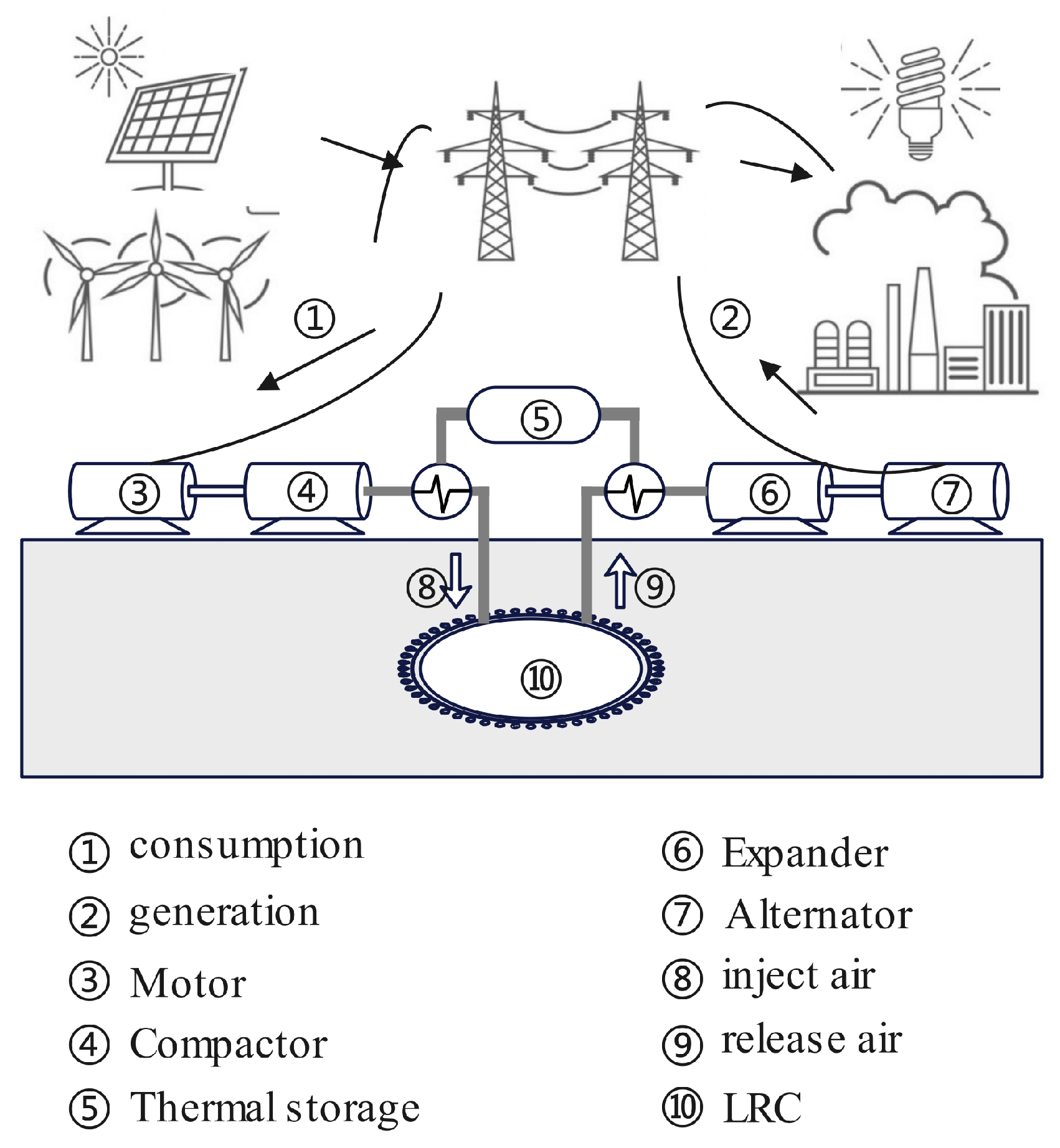
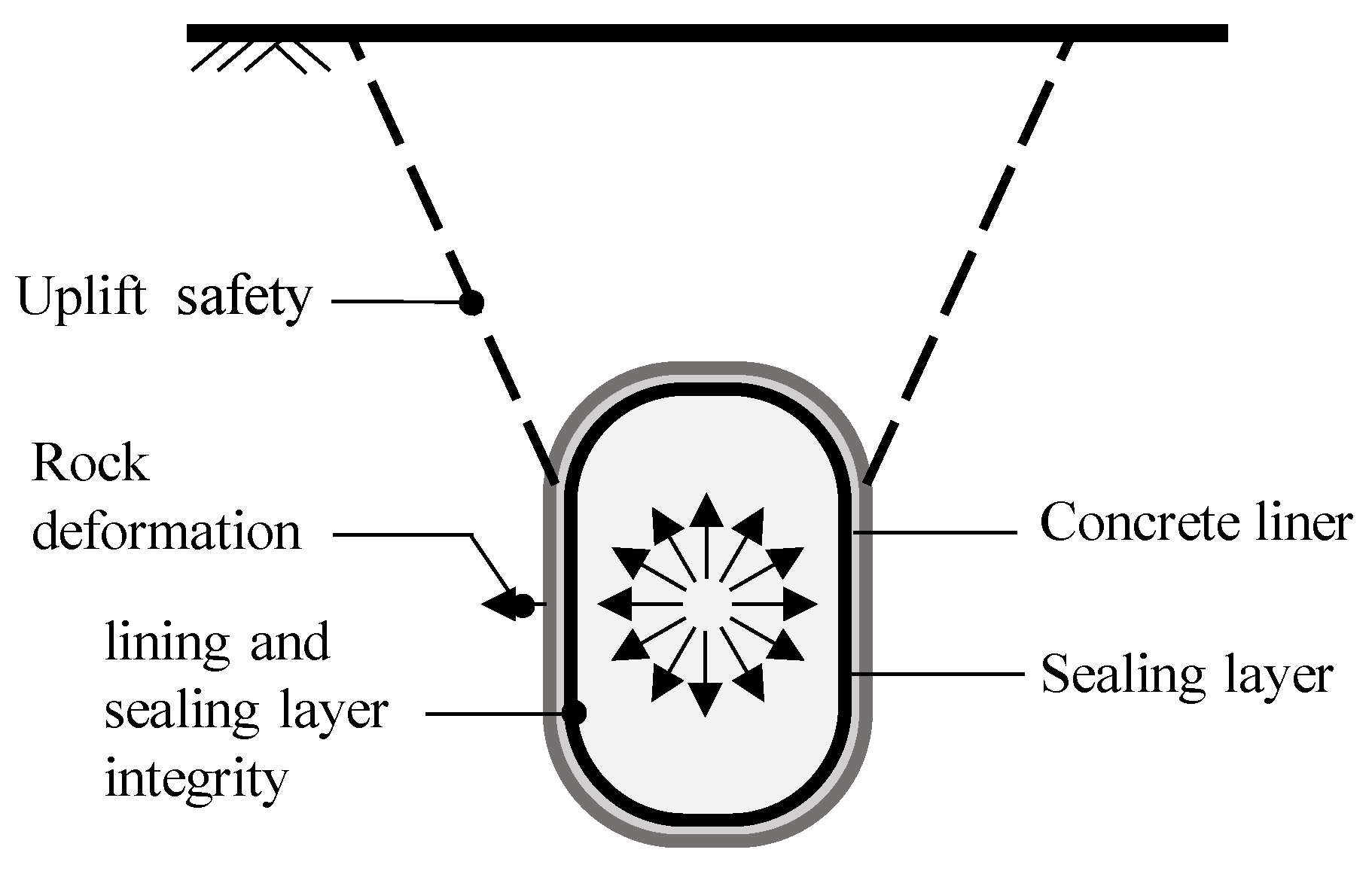
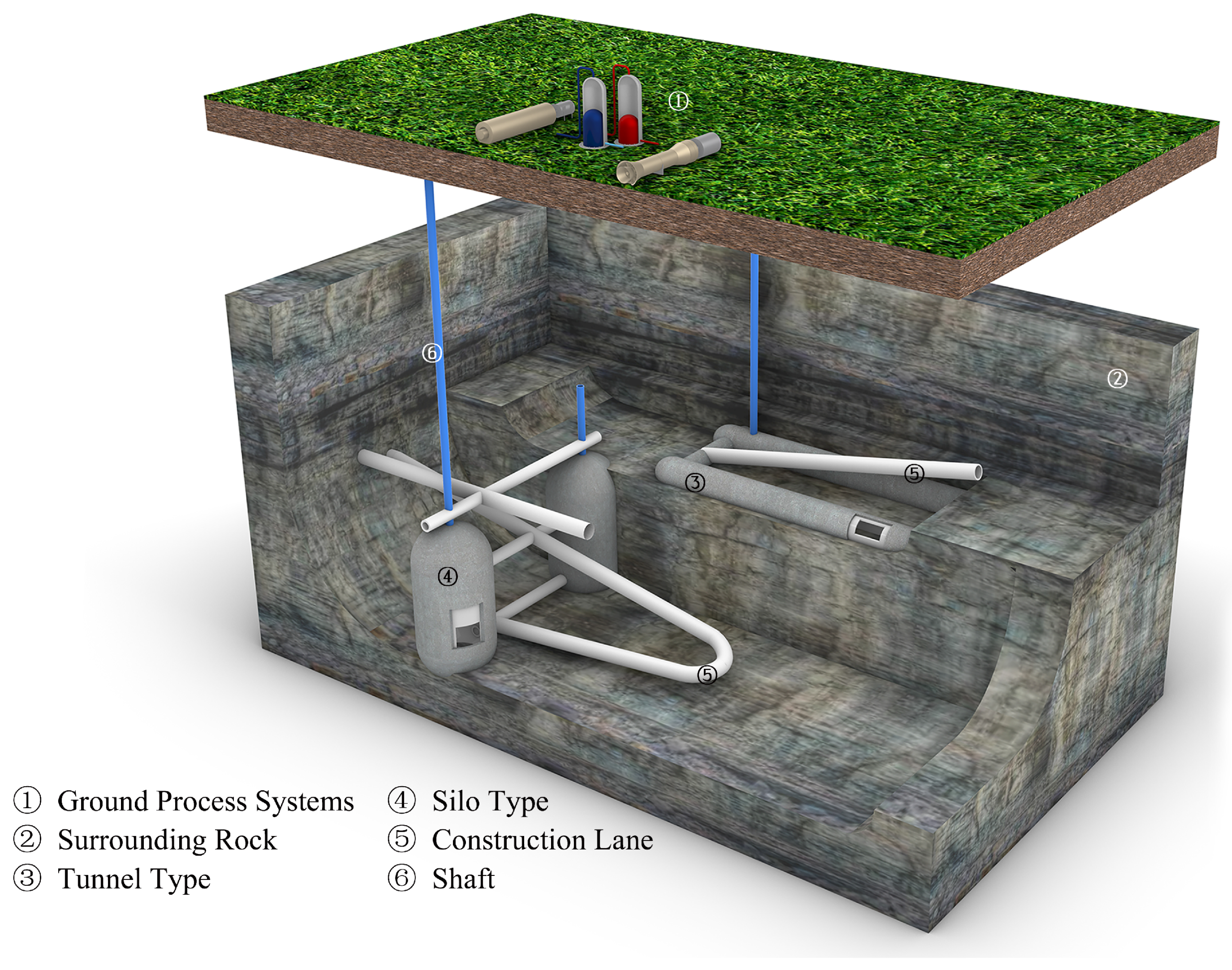
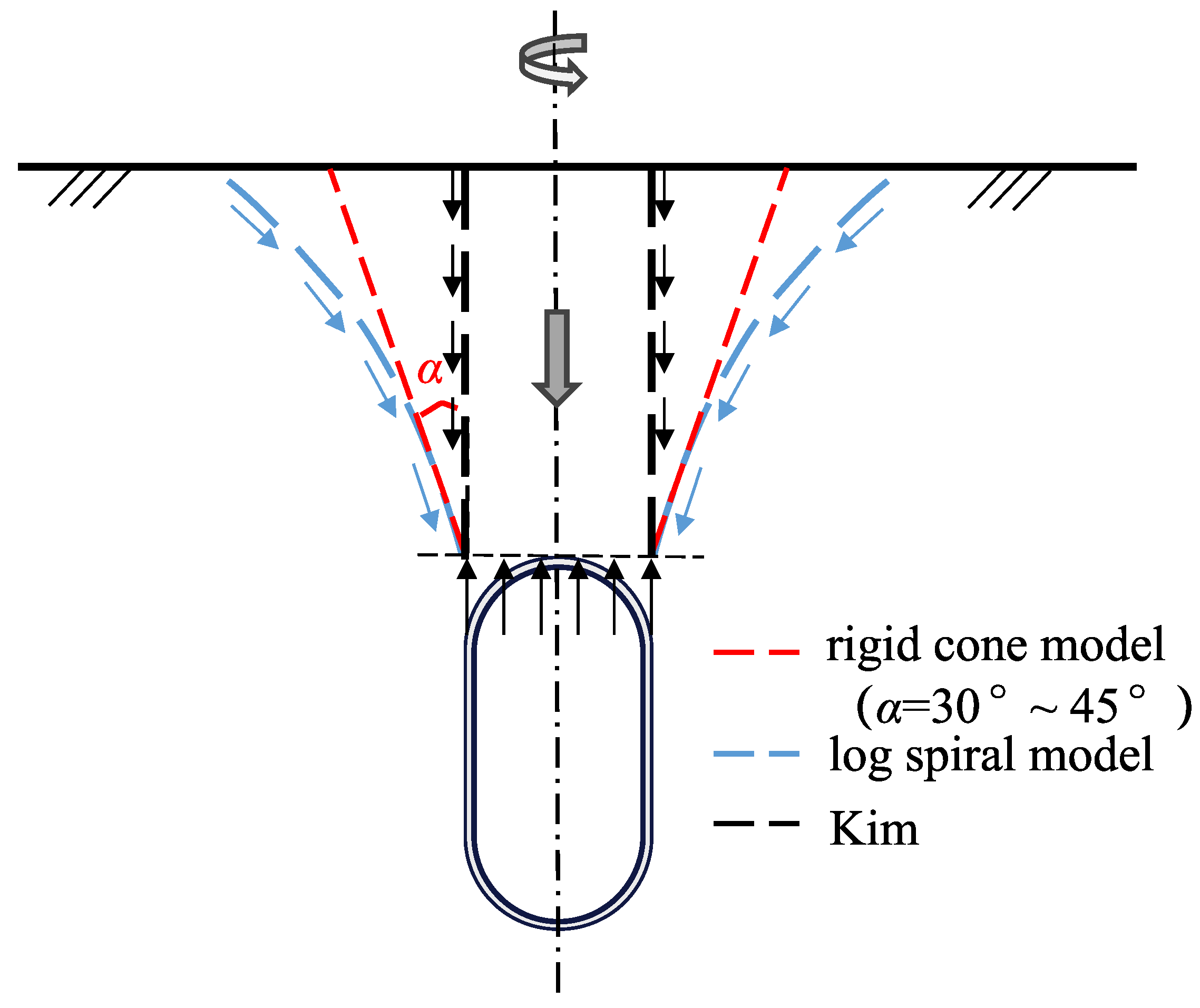
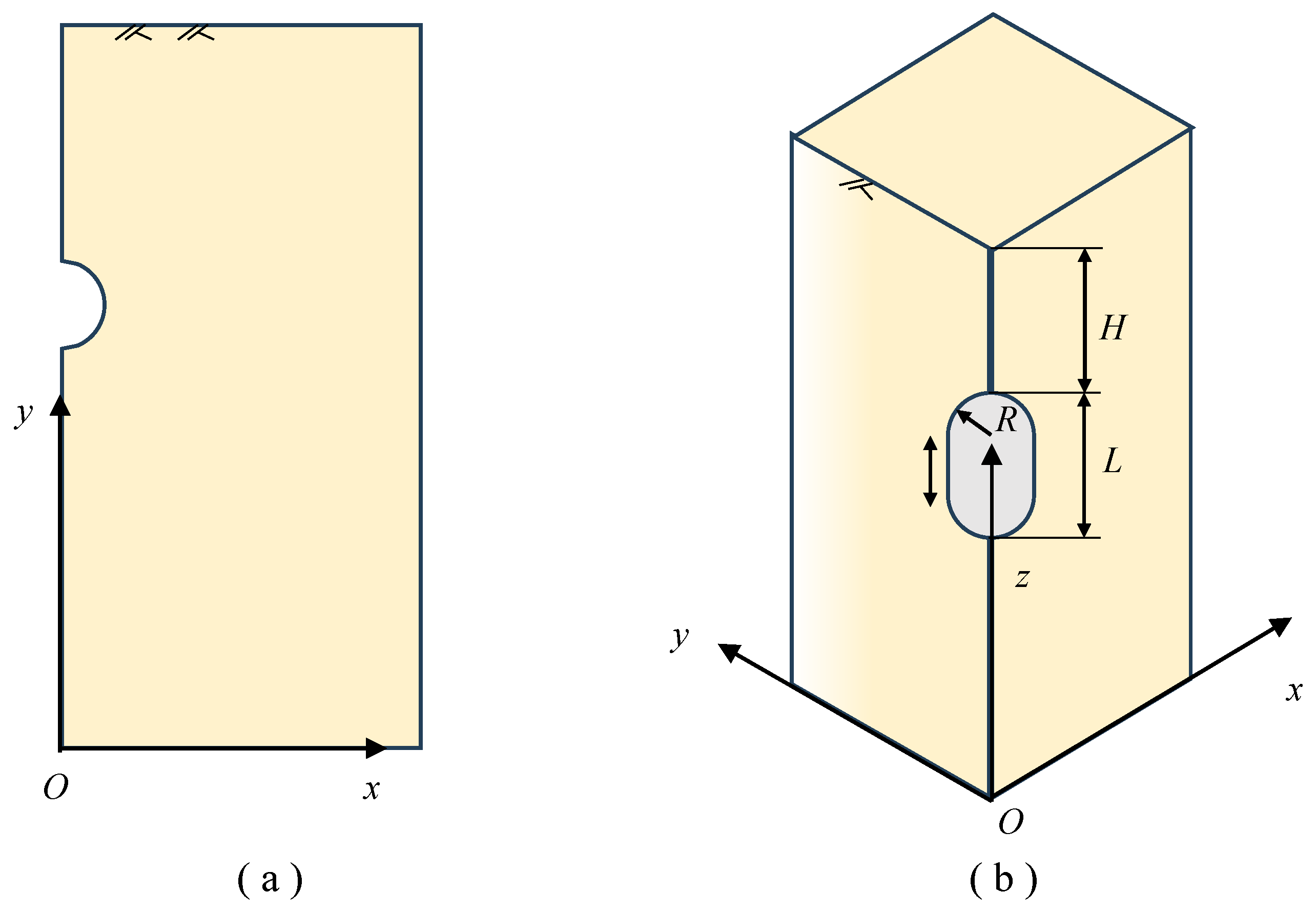
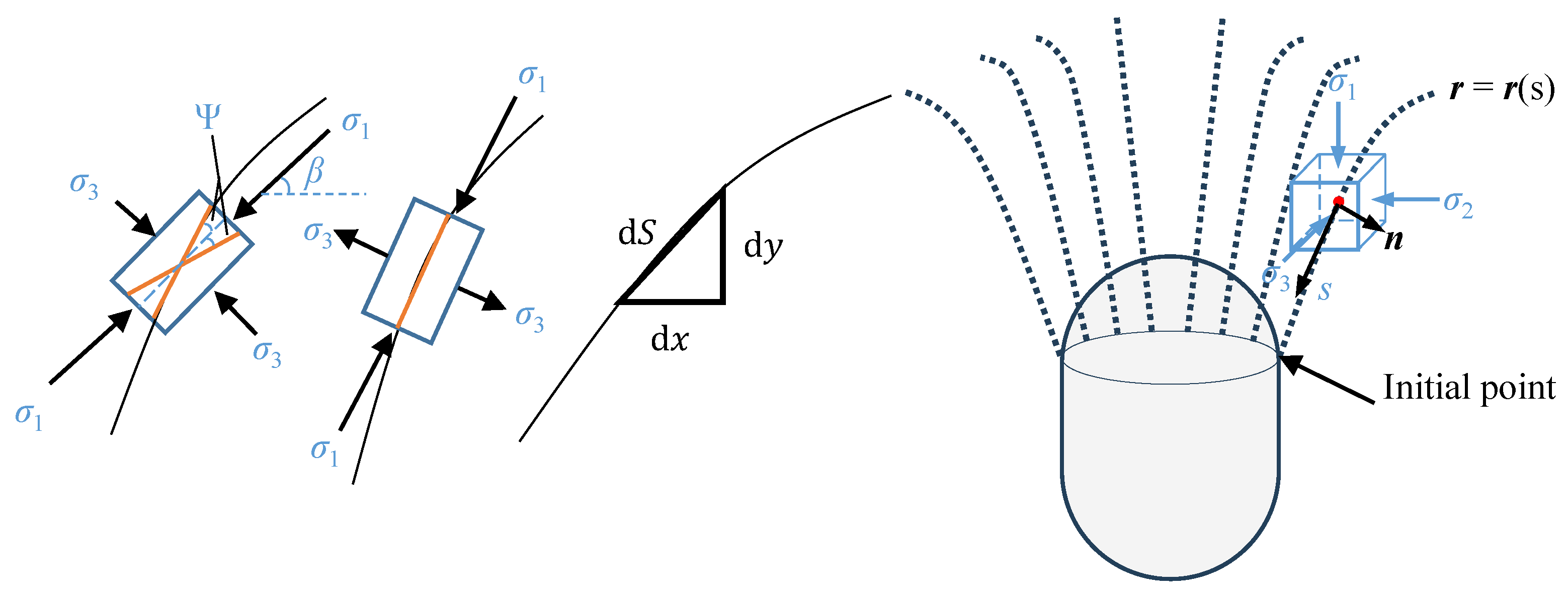
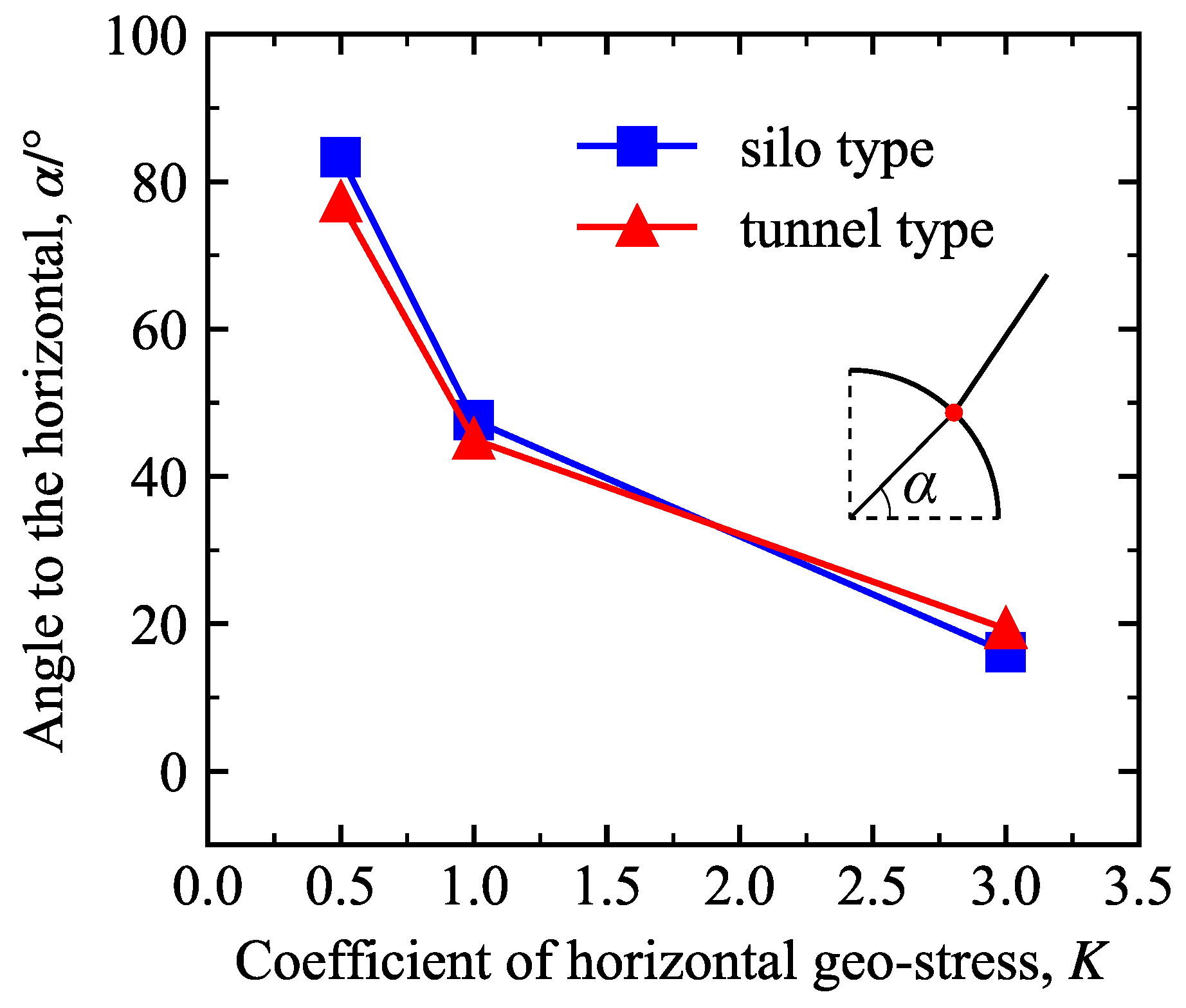
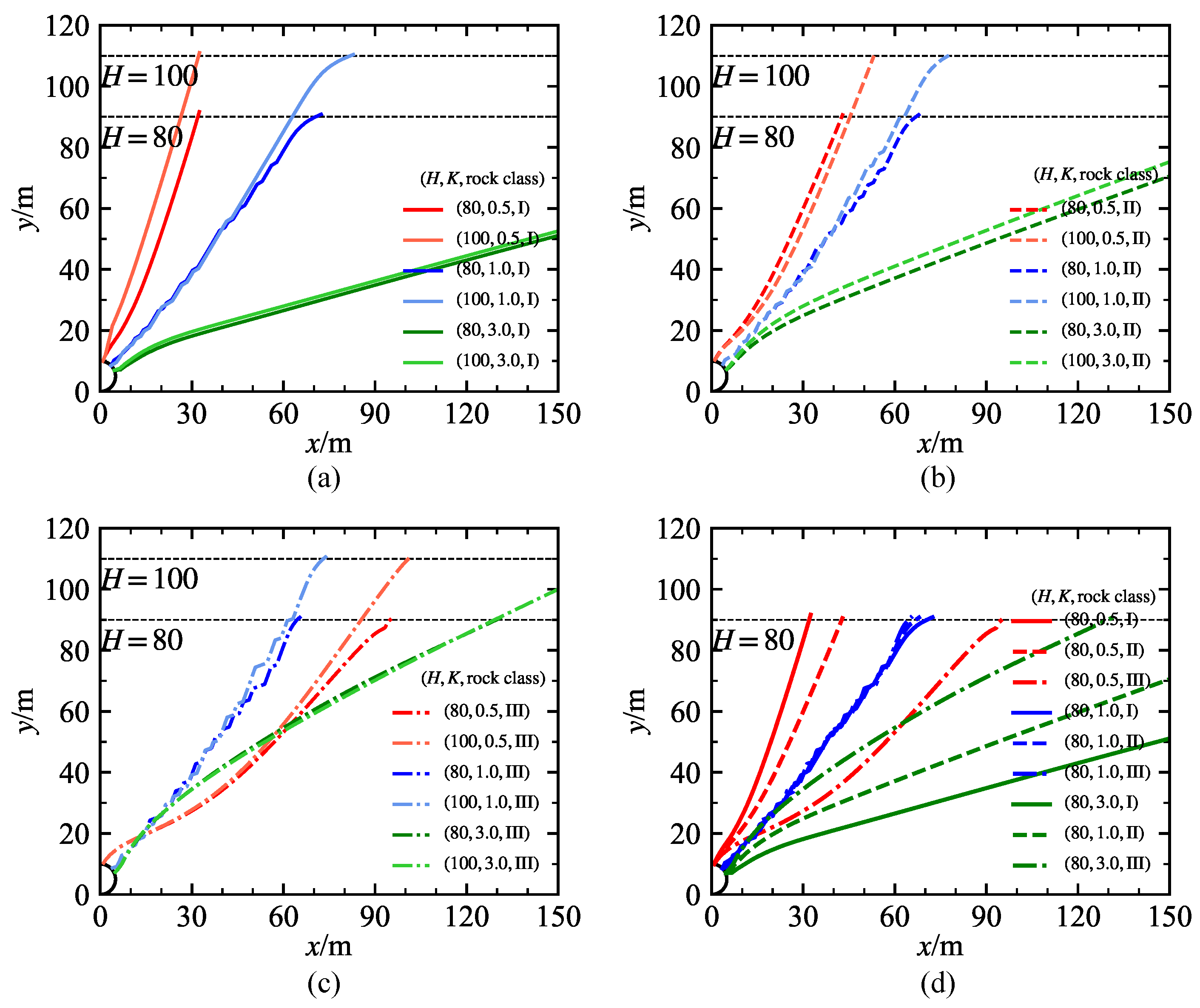
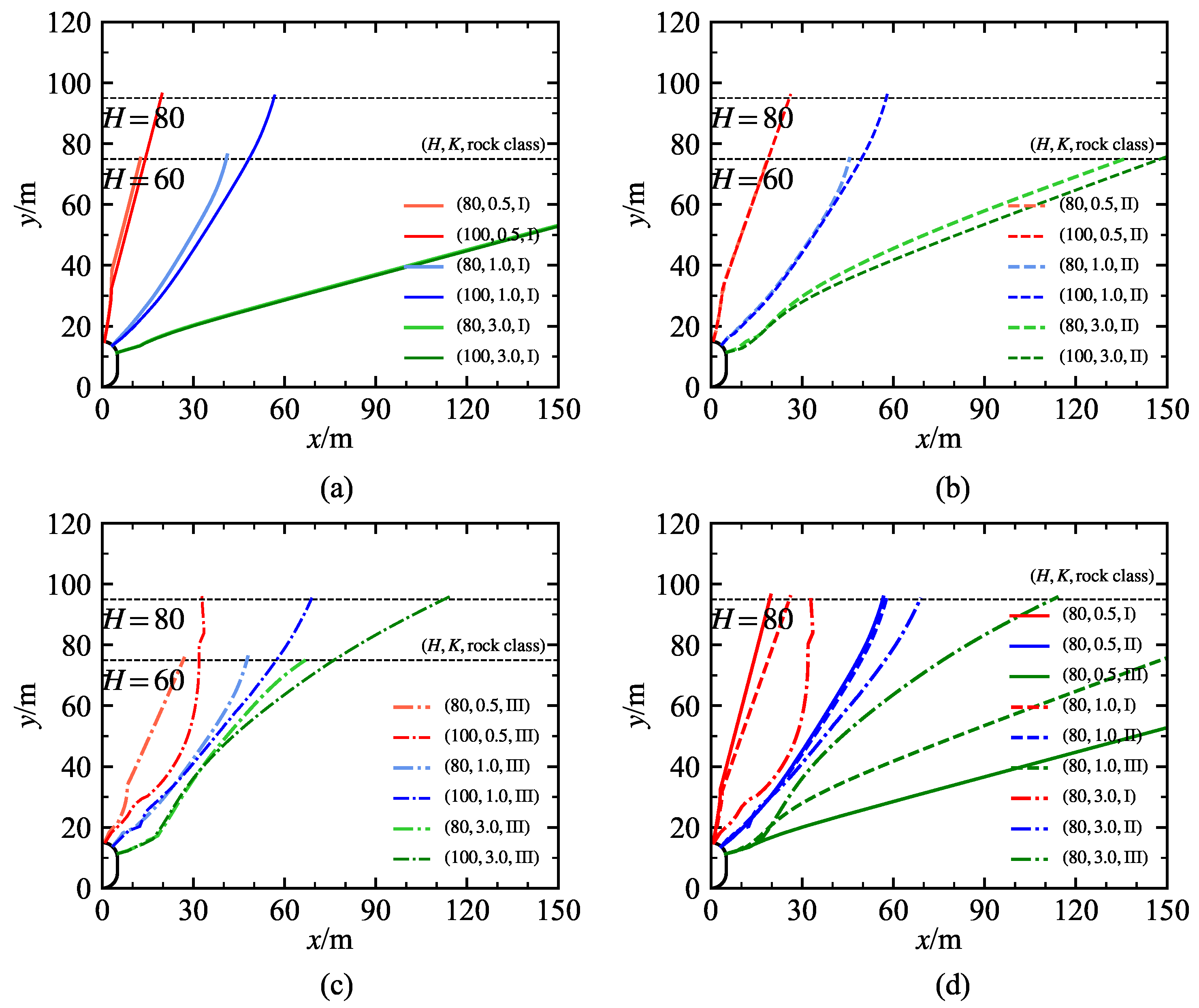
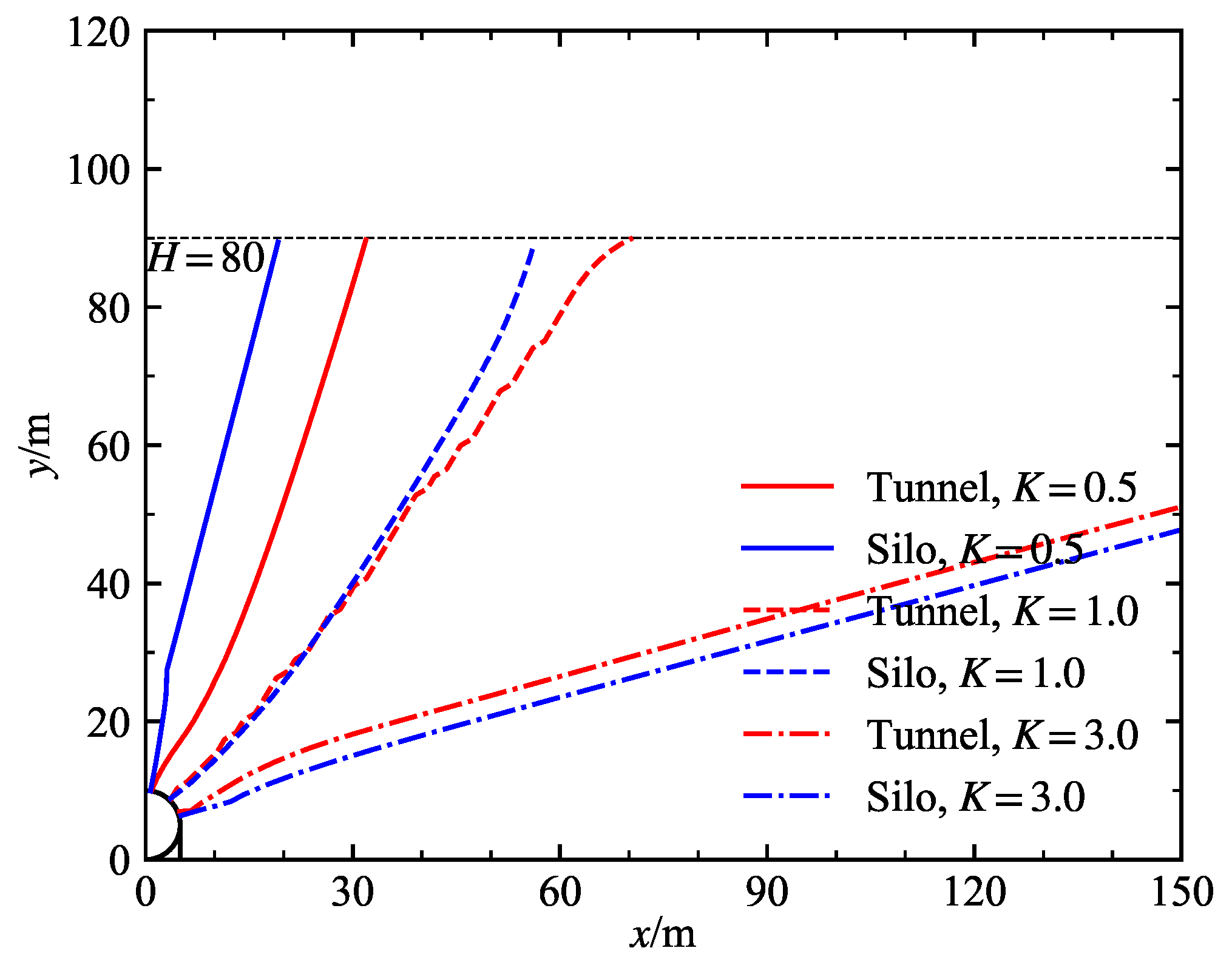
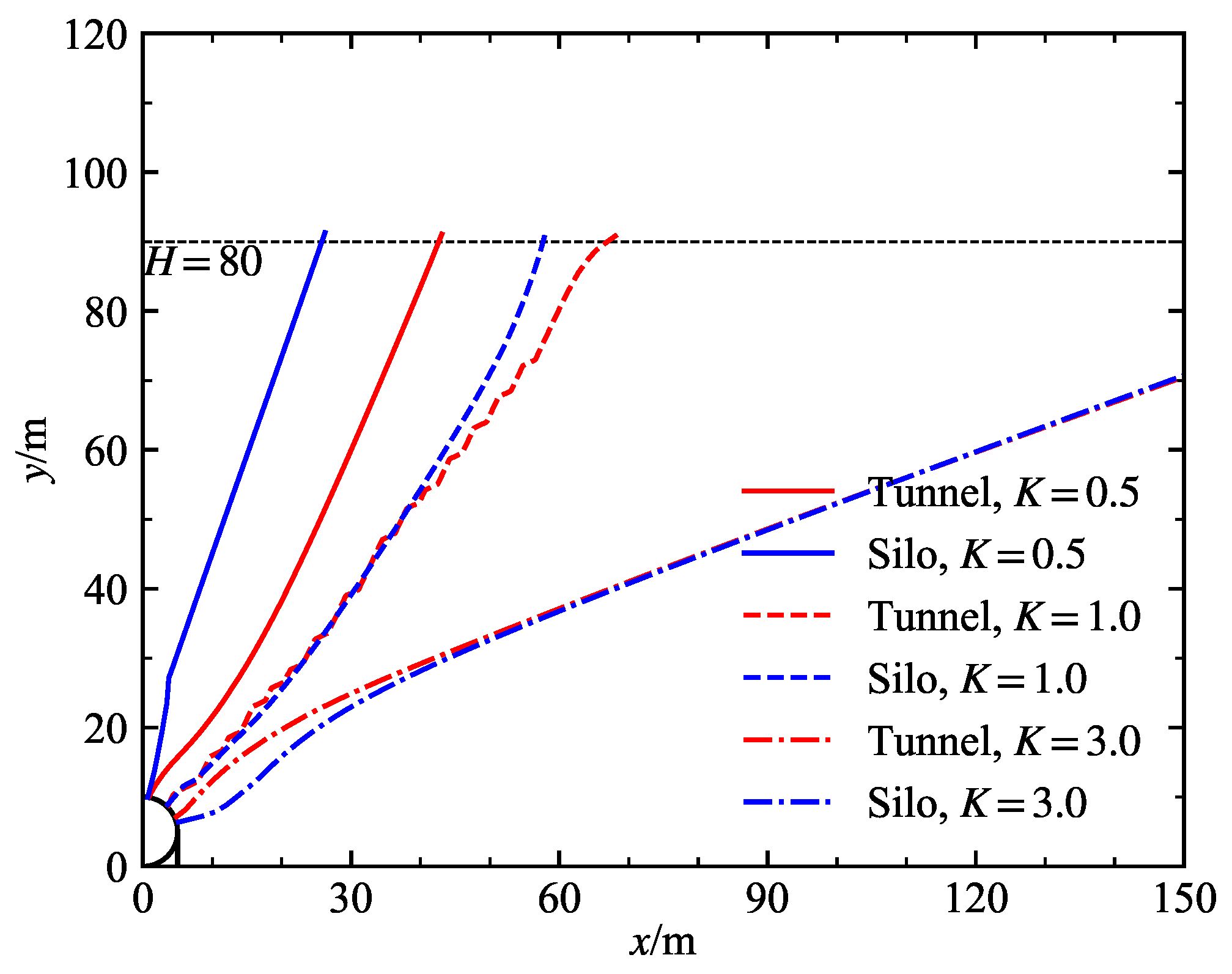
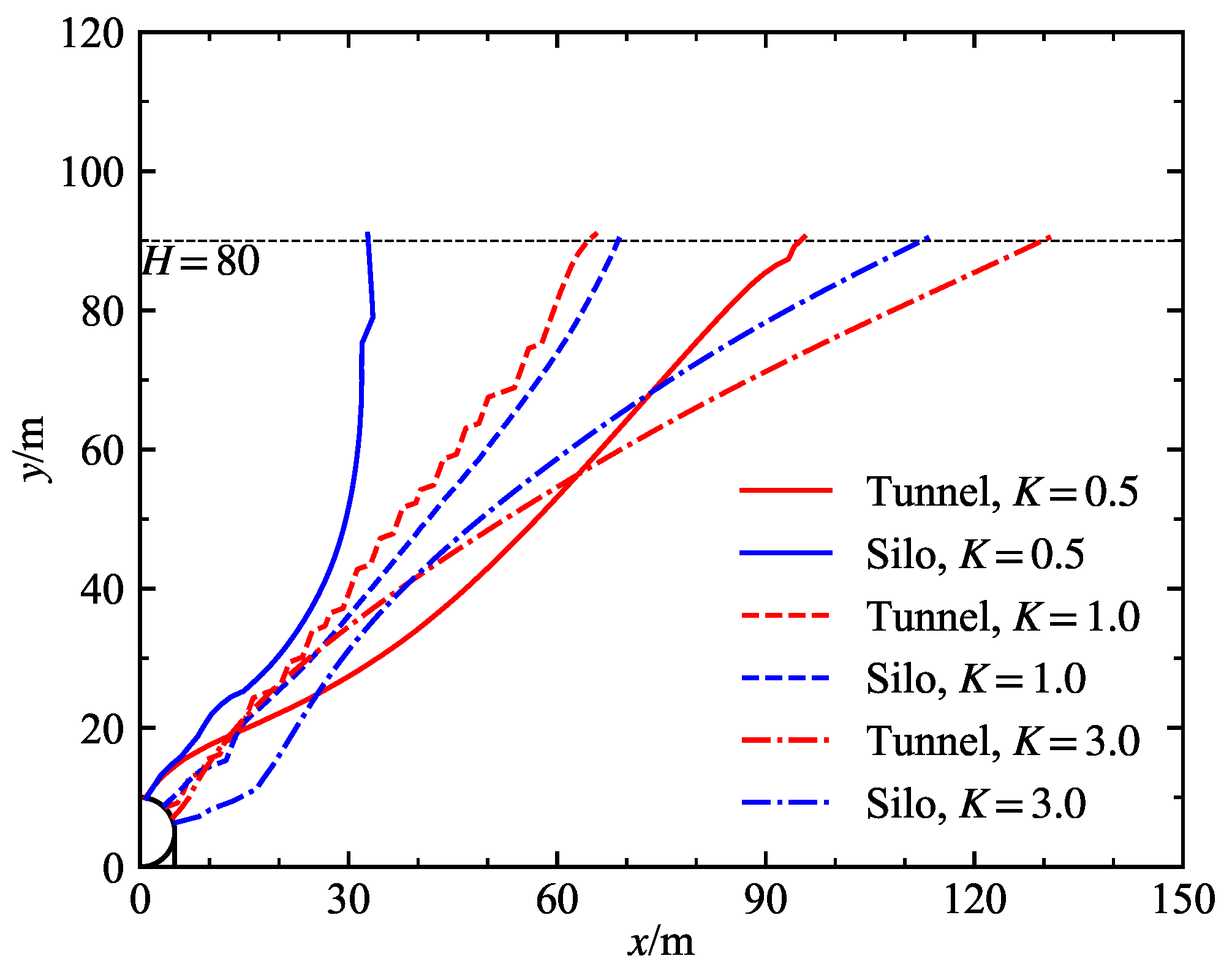
| Class | Unit Weight (kN/m3) | Internal Friction Angel (°) | Cohesion c (MPa) | Deformation Modulus E (GPa) | Poisson’s Ratio (-) |
|---|---|---|---|---|---|
| I | >26.5 | >60 | >2.1 | >33 | <0.20 |
| II | >26.5 | 60~50 | 2.1~1.5 | 33~16 | 0.20~0.25 |
| III | 26.5~24.5 | 50~39 | 1.5~0.7 | 16~ 6 | <0.25~0.30 |
| IV | 24.5~22.5 | 39~27 | 0.7~0.2 | 6~ 1.3 | <0.30~0.35 |
| V | <22.5 | <27 | <0.2 | <1.3 | >0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, Q.; Shen, Z.; Sun, G.; Lin, S.; Luo, H. Comparative Analysis of the Stability of Overlying Rock Mass for Two Types of Lined Rock Caverns Based on Rock Mass Classification. Appl. Sci. 2024, 14, 3525. https://doi.org/10.3390/app14083525
Yi Q, Shen Z, Sun G, Lin S, Luo H. Comparative Analysis of the Stability of Overlying Rock Mass for Two Types of Lined Rock Caverns Based on Rock Mass Classification. Applied Sciences. 2024; 14(8):3525. https://doi.org/10.3390/app14083525
Chicago/Turabian StyleYi, Qi, Zhen Shen, Guanhua Sun, Shan Lin, and Hongming Luo. 2024. "Comparative Analysis of the Stability of Overlying Rock Mass for Two Types of Lined Rock Caverns Based on Rock Mass Classification" Applied Sciences 14, no. 8: 3525. https://doi.org/10.3390/app14083525
APA StyleYi, Q., Shen, Z., Sun, G., Lin, S., & Luo, H. (2024). Comparative Analysis of the Stability of Overlying Rock Mass for Two Types of Lined Rock Caverns Based on Rock Mass Classification. Applied Sciences, 14(8), 3525. https://doi.org/10.3390/app14083525






