Hidden Markov Model-Based Dynamic Hard Shoulders Running Strategy in Hybrid Network Environments
Abstract
1. Introduction
1.1. Background
- (1)
- Modeling a mixed traffic flow expressway scenario and proposing a traffic breakdown prediction method based on a hidden Markov model;
- (2)
- Analyzing the characteristics of traffic breakdown in a hybrid network environment by comparing them with the logistic model-based prediction method;
- (3)
- Proposing a dynamic hard shoulder running method (HMMD-HSR) based on the traffic breakdown characteristics and verifying its effectiveness through a combined simulation of SUMO (1.9.2) and MATLAB (R2019b).
1.2. Literature Review
- (1)
- Traffic flow: Urban highway congestion is primarily caused by the traffic flow exceeding road capacity during peak hours. Therefore, many scholars consider traffic flow to be the key index for implementing the HSR strategy, which temporarily expands the road capacity by opening the hard shoulder. Carlson et al. [31] found that opening the hard shoulder when traffic exceeded a certain threshold helped alleviate congestion caused by heavy traffic flow. Cohen [32] also explored the effect of the dynamic opening of the hard shoulder on road bottlenecks, using traffic flow as a starting point. The hard shoulder increases the traffic capacity of bottleneck sections.
- (2)
- Safety: Extensive studies have been conducted on the safety impact of opening the hard shoulder [5,33,34,35,36], and the primary purpose of the hard shoulder is to serve as an emergency lane for vehicles that have broken down. If the goal is to maximize highway capacity, the hard shoulder will be in use throughout the simulation. However, it is important to consider the needs of accidents and not overuse the hard shoulder. In that case, Li et al. [6] introduced a safety weight to incorporate safety factors into the design of the hard shoulder open strategy. Other researchers believe that HSR can be used as a supplementary measure to VSL. The hard shoulder is only opened when VSL is unable to handle excessive traffic [19,20] in order to balance the negative impact on safety indicators.
- (3)
- Speed: Some researchers have explored the possibility of the open threshold of the hard shoulder from the angle of speed change characteristics. Ma et al. [37] introduced the concept of traffic breakdown as a threshold for hard shoulder opening. Chen et al. [38] argued that breakdown occurs when traffic flow switches from free to congested, which is frequently accompanied by continuous oscillation, resulting in large-scale congestion. Consequently, it becomes necessary to identify traffic breakdowns and manage them in advance. The definition of traffic breakdown has not been uniformly quantified. Many researchers have different definitions of breakdown based on the changing characteristics of road sections from free to congested, establishing a speed drop threshold or a density rise threshold [39,40]. Ma et al. [37] defined the critical vehicle speed and provided a method for calculating the drop threshold. However, most traffic breakdown studies have only focused on traditional human-driving scenarios, and it appears that few studies have examined mixed traffic flow scenarios.
2. Hybrid Network Expressway Scene Modeling
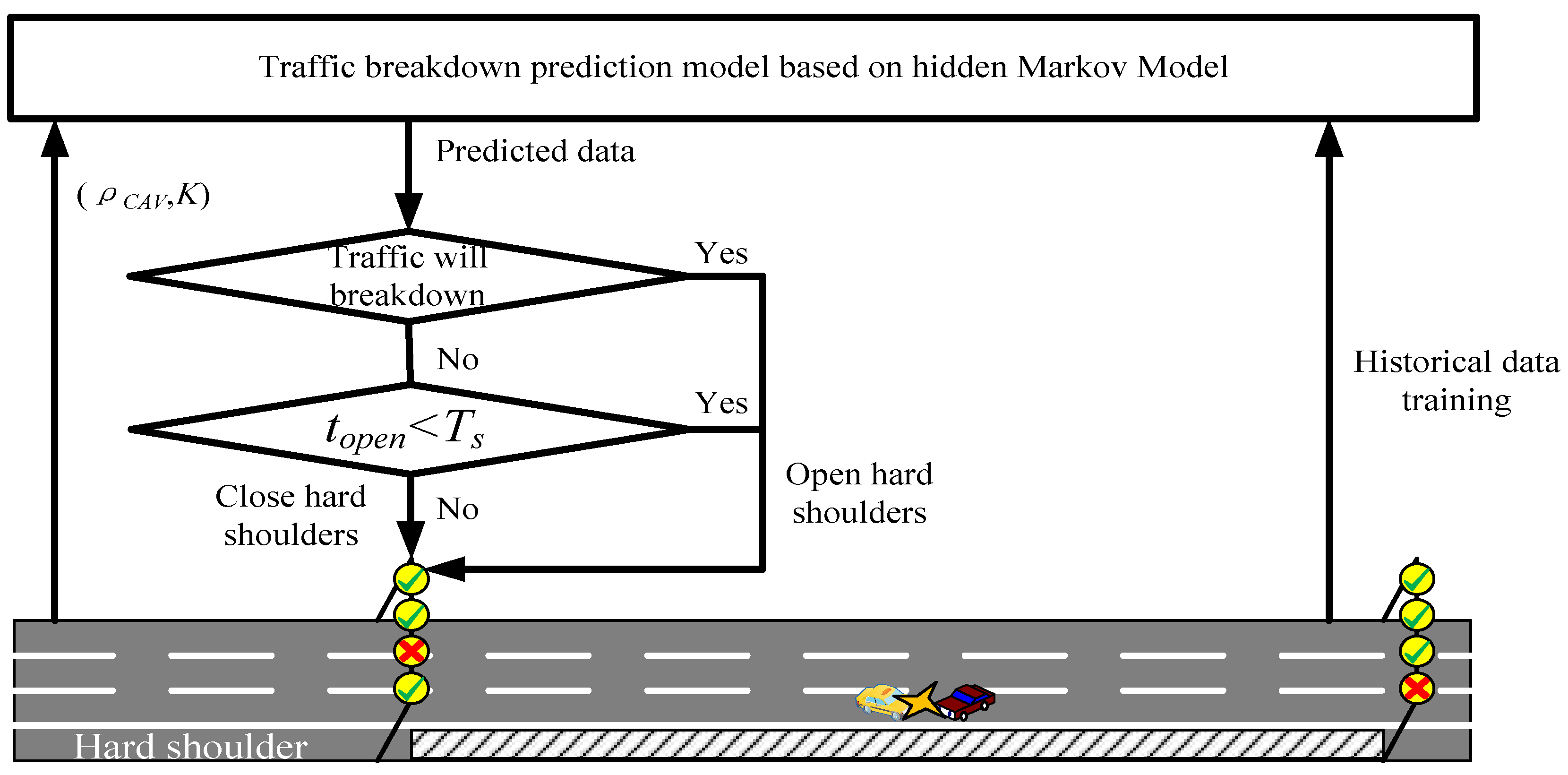
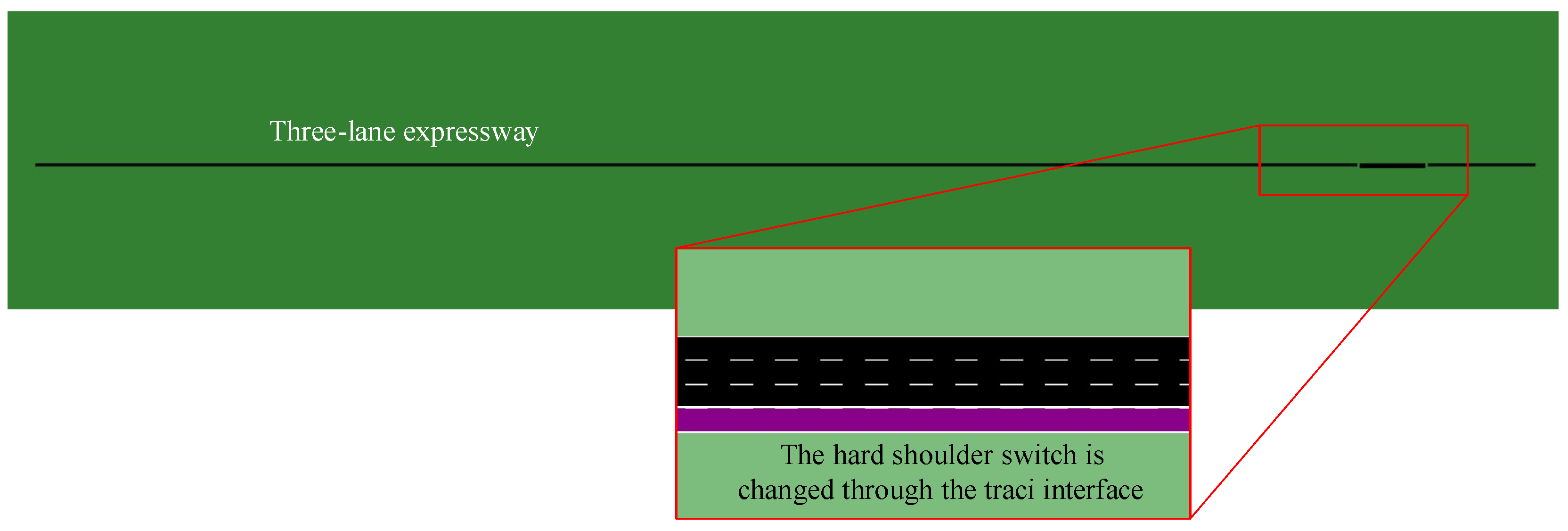
2.1. Dynamic Expressway Hard Shoulders Opening
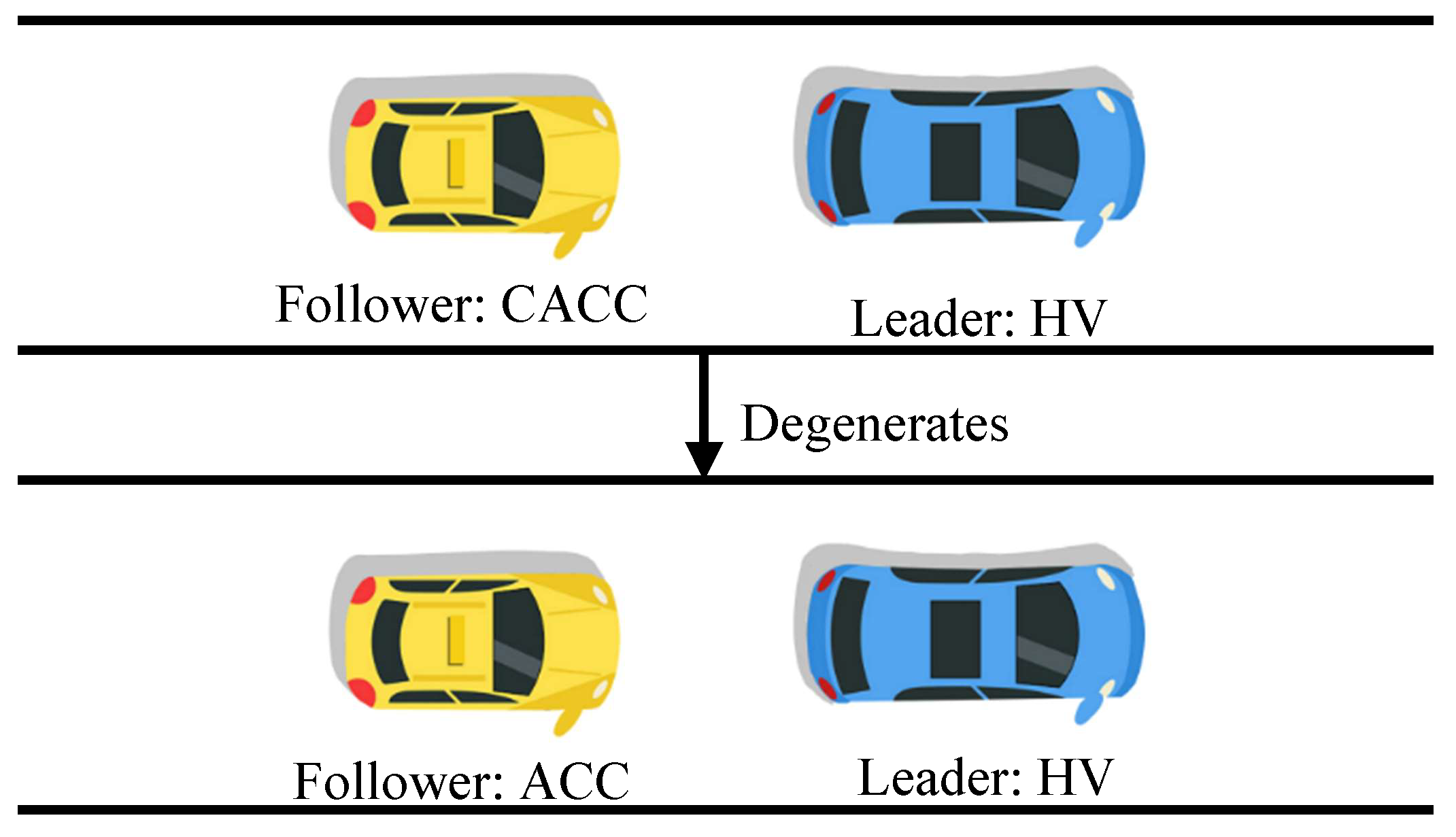
2.2. Hybrid Network Traffic Flow Modeling
- (1)
- HDV follows HDV.
- (2)
- HDV follows CAV.
- (3)
- CAV follows HDV.
- (4)
- CAV follows CAV.
3. Dynamic Hard Shoulder Running Strategy Based on Hidden Markov Model
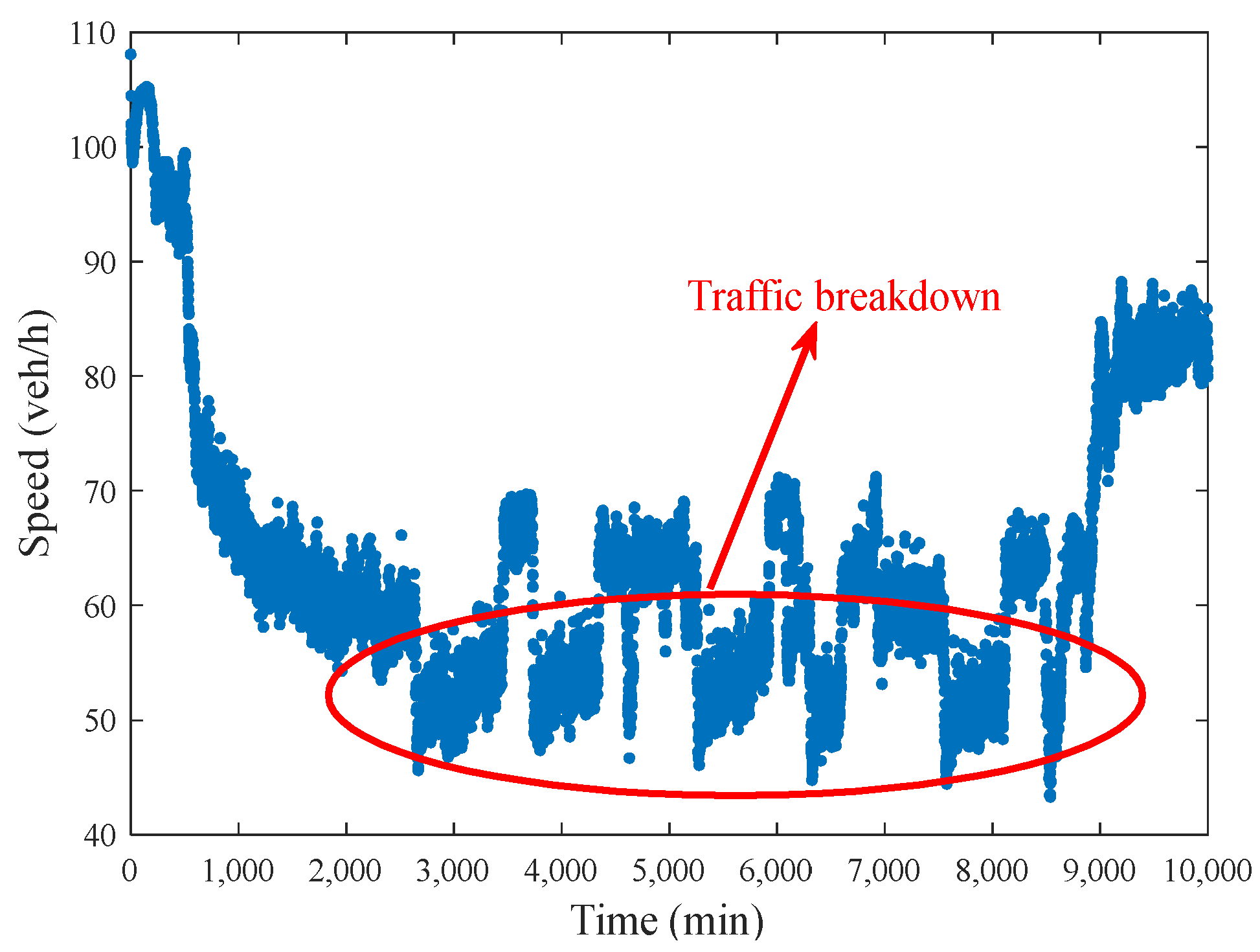
3.1. Traffic Breakdown Probability Calculation
- (1)
- Calculate the average speed for a continuous period of time (min);
- (2)
- Calculate the standard deviation of the speed in ;
- (3)
- Repeat the previous two steps to calculate the standard deviation of all average speeds , respectively. The critical speed is the corresponding to the greatest value of . The formulas for each parameter are as follows:where is the flow rate at moment ; is the average speed on the road at moment ; is the weighted average speed during period (min) starting at moment , and the weights are the traffic flow at the corresponding moments; is the weighted standard deviation of the speeds during period starting at moment , and the weights are .
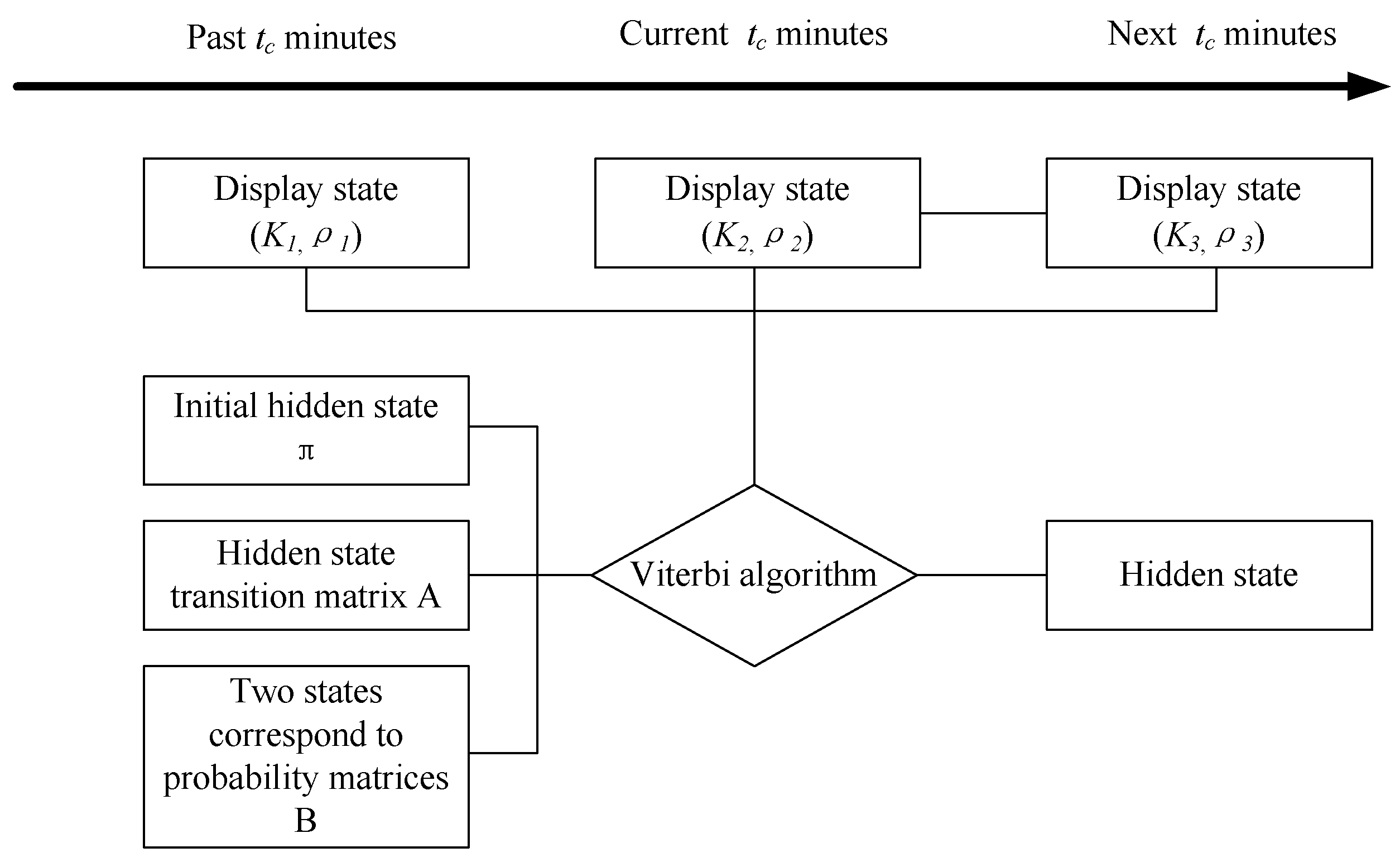
3.2. Traffic Breakdown Predict Model under Hybrid Network
- (1)
- Learning of hidden state transition probability matrix A:
- (2)
- Learning of two-state corresponding probability matrix B:
- (3)
- Learning of initial hidden state distribution:
3.3. Viterbi Algorithm Prediction
3.4. Control Process
4. Numerical Results and Discussion
4.1. Scene Introduction
4.1.1. Scene Characterization
4.1.2. Validation of a Hidden Markov Model-Based Traffic Breakdown Prediction Model
4.2. Experimental Analysis of Hard Shoulder Opening Strategies
4.2.1. Experimental Parameter Description
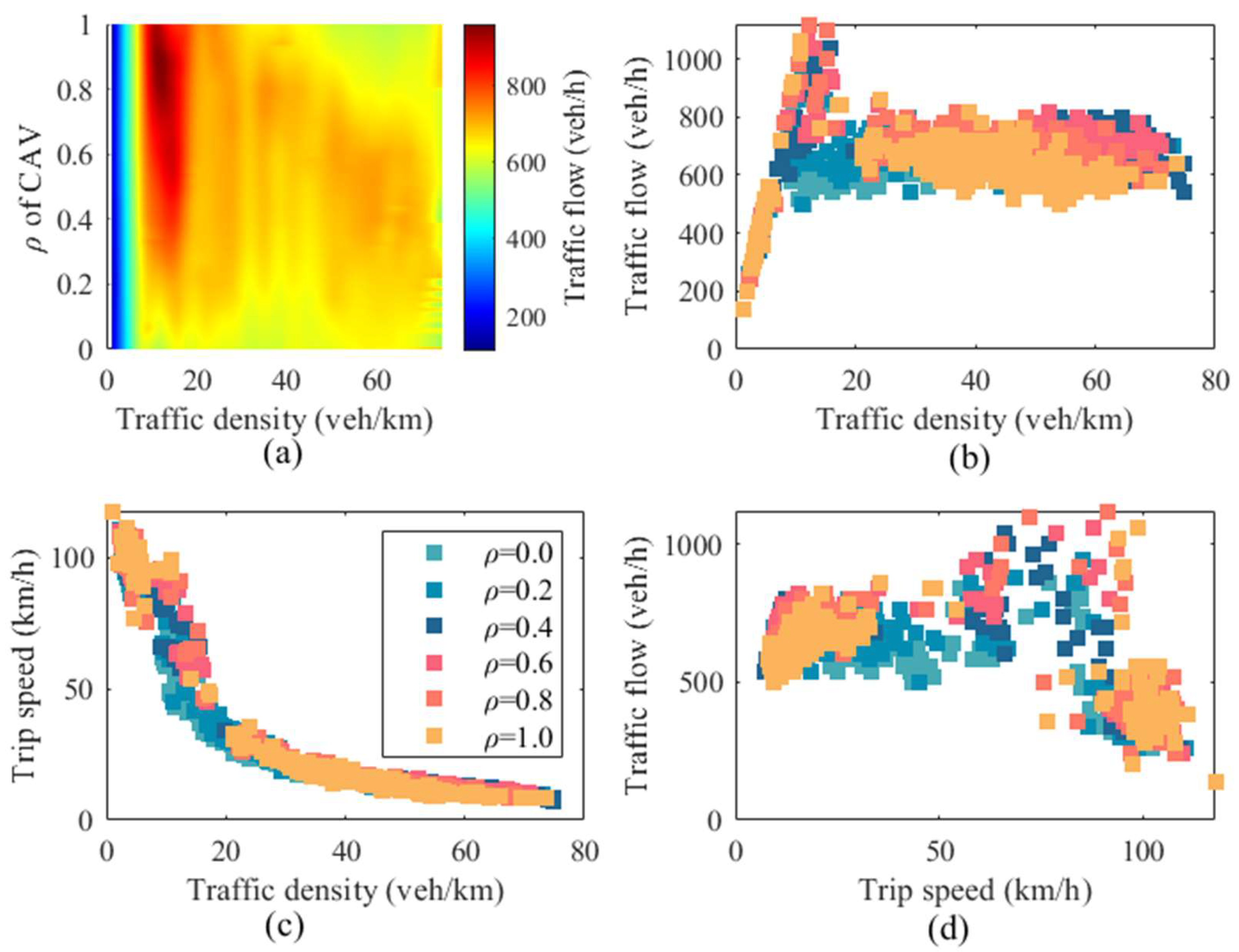
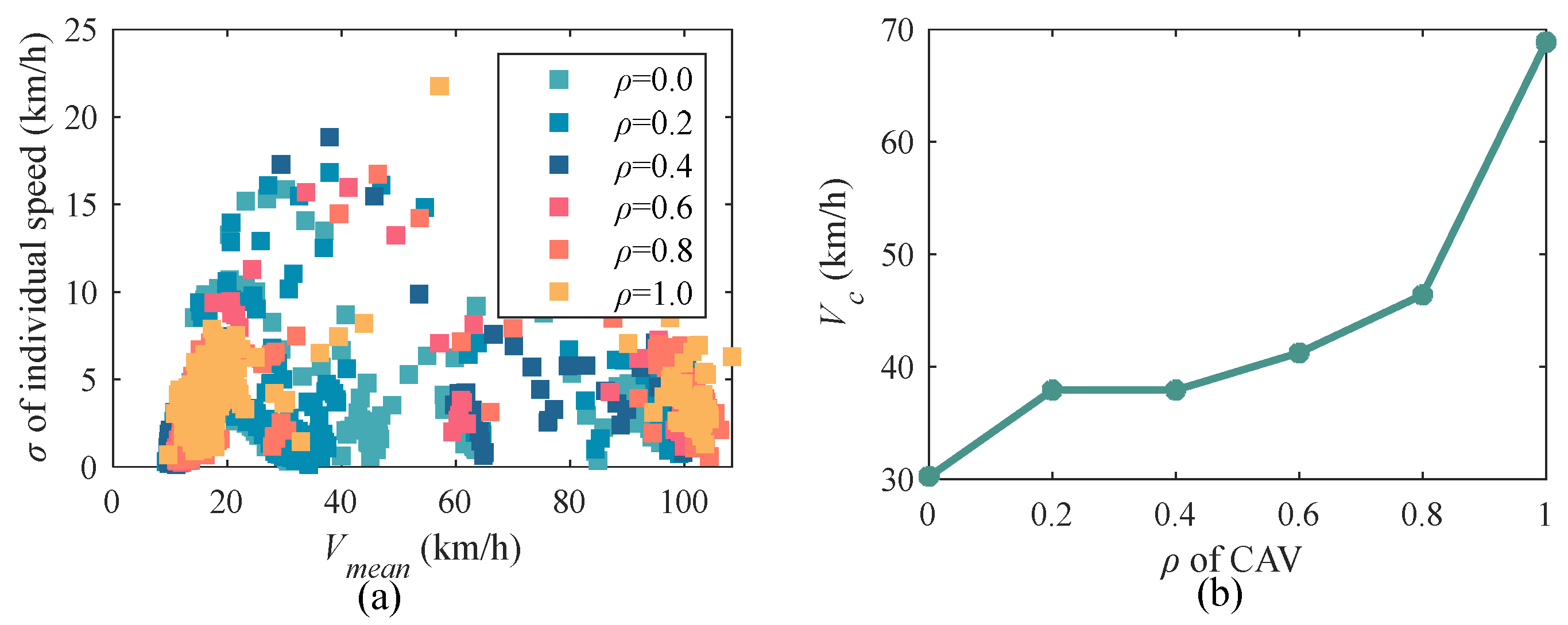
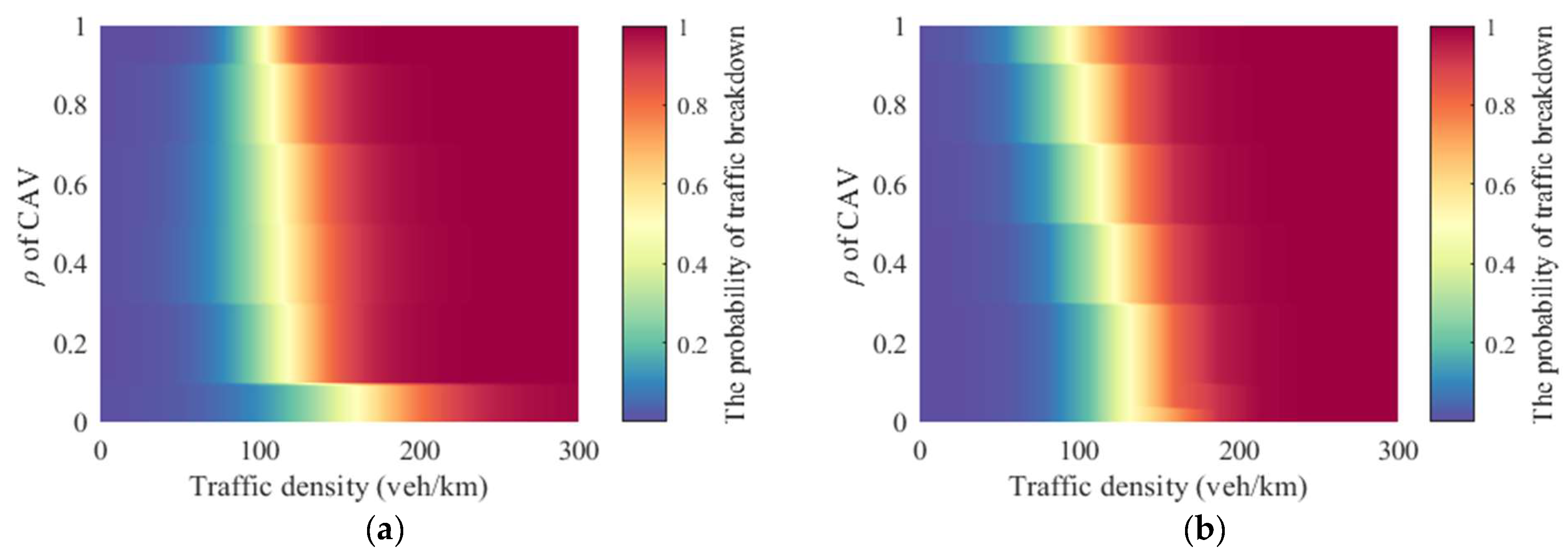
4.2.2. Analysis of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, Z.; Xu, T.; Jiang, Y.; Hu, R. Linear stability analysis of heterogeneous traffic flow considering degradations of connected automated vehicles and reaction time. Phys. A Stat. Mech. Its Appl. 2021, 561, 125218. [Google Scholar] [CrossRef]
- Calvert, S.C.; Schakel, W.J.; Van Lint, J.W.C. Will automated vehicles negatively impact traffic flow? J. Adv. Transp. 2017, 2017, 3082781. [Google Scholar] [CrossRef]
- Nitsche, P.; Olstam, J.; Taylor, N.; Reinthaler, M.; Ponweiser, W.; Bernhardsson, V.; van Dam, E. Pro-active management of traffic incidents using novel technologies. Transp. Res. Procedia 2016, 14, 3360–3369. [Google Scholar] [CrossRef]
- Fuhs, C.; Brinckerhoff, P. Synthesis of Active Traffic Management Experiences in Europe and the United States; No. FHWA-HOP-10-031; Federal Highway Administration: Washington, DC, USA, 2010. [Google Scholar]
- Coffey, S.; Park, S. State of the non-operations based research of hard shoulder running. Procedia Eng. 2016, 145, 693–698. [Google Scholar] [CrossRef][Green Version]
- Li, Y.; Chow, A.H.; Cassel, D.L. Optimal control of motorways by ramp metering, variable speed limits, and hard-shoulder running. Transp. Res. Rec. 2014, 2470, 122–130. [Google Scholar] [CrossRef]
- Su, H.; Zhong, Y.D.; Chow, J.Y.; Dey, B.; Jin, L. EMVLight: A multi-agent reinforcement learning framework for an emergency vehicle decentralized routing and traffic signal control system. Transp. Res. Part C Emerg. Technol. 2023, 146, 103955. [Google Scholar] [CrossRef]
- Farrag, S.G.; Outay, F.; Yasar, A.U.H.; El-Hansali, M.Y. Evaluating active traffic management (ATM) strategies under non-recurring congestion: Simulation-based with benefit cost analysis case study. Sustainability 2020, 12, 6027. [Google Scholar] [CrossRef]
- Geistefeldt, J. Operational experience with temporary hard shoulder running in Germany. Transp. Res. Rec. 2012, 2278, 67–73. [Google Scholar] [CrossRef]
- Dutta, N.; Boateng, R.A.; Fontaine, M.D. Safety and operational effects of the interstate 66 active traffic management system. J. Transp. Eng. Part A Syst. 2019, 145, 04018089. [Google Scholar] [CrossRef]
- Sullivan, A.; Fadel, G. Implementing Active Traffic Management Strategies in the US; No. FHWA/CA/OR; University Transportation Center for Alabama: Tuscaloosa, AL, USA, 2010. [Google Scholar]
- Ma, J.; Hu, J.; Hale, D.K.; Bared, J. Dynamic hard shoulder running for traffic incident management. Transp. Res. Rec. 2016, 2554, 120–128. [Google Scholar] [CrossRef]
- Yang, F.; Wang, F.; Ding, F.; Tan, H.; Ran, B. Identify Optimal Traffic Condition and Speed Limit for Hard Shoulder Running Strategy. Sustainability 2021, 13, 1822. [Google Scholar] [CrossRef]
- Li, R.; Ye, Z.; Li, B.; Zhan, X. Simulation of hard shoulder running combined with queue warning during traffic accident with CTM model. IET Intell. Transp. Syst. 2017, 11, 553–560. [Google Scholar] [CrossRef]
- Samoili, S.; Efthymiou, D.; Antoniou, C.; Dumont, A.G. Short-term lane flow distribution forecasting in hard shoulder running freeways. In Proceedings of the Optimum 2013 International Symposium on Recent Advances in Transport Modeling, Kingscliffe, SW, Australia, 21–23 April 2013. [Google Scholar]
- Samoili, S.; Efthymiou, D.; Antoniou, C.; Dumont, A.G. Investigation of lane flow distribution on hard shoulder running freeways. Transp. Res. Rec. 2013, 2396, 133–142. [Google Scholar] [CrossRef]
- Ma, J.; Smith, B.L.; Fontaine, M.D. Comparison of in-vehicle auditory public traffic information with roadside dynamic message signs. J. Intell. Transp. Syst. 2016, 20, 244–254. [Google Scholar] [CrossRef]
- Hussein, F.F.; Naik, B.; Süer, G.A. Development of Hybrid Hard Shoulder Running Operation System for Active Traffic Management. In Proceedings of the International Conference on Transportation and Development, Seattle, WA, USA, 26–29 May 2020; American Society of Civil Engineers: Reston, VA, USA, 2020; pp. 194–205. [Google Scholar]
- Arora, K.; Kattan, L. Operational and safety impacts of integrated variable speed limit with dynamic hard shoulder running. J. Intell. Transp. Syst. 2023, 27, 769–798. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, M.; Lee, M.; Zhang, L. Q-learning-based coordinated variable speed limit and hard shoulder running control strategy to reduce travel time at freeway corridor. Transp. Res. Rec. 2020, 2674, 915–925. [Google Scholar] [CrossRef]
- Vrbanić, F.; Ivanjko, E.; Mandžuka, S.; Miletić, M. Reinforcement learning based variable speed limit control for mixed traffic flows. In Proceedings of the 2021 29th Mediterranean Conference on Control and Automation (MED), Puglia, Italy, 22–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 560–565. [Google Scholar] [CrossRef]
- Vrbanić, F.; Tišljarić, L.; Majstorović, Ž.; Ivanjko, E. Reinforcement Learning-Based Dynamic Zone Placement Variable Speed Limit Control for Mixed Traffic Flows Using Speed Transition Matrices for State Estimation. Machines 2023, 11, 479. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, L.; Chen, J.; Zheng, X.; Pan, H.; Zhang, W. MPC-based dynamic speed control of CAVs in multiple sections upstream of the bottleneck area within a mixed vehicular environment. Phys. A Stat. Mech. Its Appl. 2023, 613, 128542. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Y.; Lee, J.; Yuan, C.; Wang, B. Safety Effects of Connected and Automated Vehicle-Based Variable Speed Limit Control near Freeway Bottlenecks considering Driver’s Heterogeneity. J. Adv. Transp. 2022, 2022, 7996623. [Google Scholar] [CrossRef]
- Gokasar, I.; Timurogullari, A.; Ozkan, S.S.; Deveci, M. IDILIM: Incident detection included linear management using connected autonomous vehicles. Ann. Oper. Res. 2023, 1–20. [Google Scholar] [CrossRef]
- Li, Y.; Pan, B.; Xing, L.; Yang, M.; Dai, J. Developing dynamic speed limit strategies for mixed traffic flow to reduce collision risks at freeway bottlenecks. Accid. Anal. Prev. 2022, 175, 106781. [Google Scholar] [CrossRef]
- Wu, W.; Sun, R.; Ni, A.; Liang, Z.; Jia, H. Simulation and evaluation of speed and lane-changing advisory of CAVS at work zones in heterogeneous traffic flow. Int. J. Mod. Phys. B 2020, 34, 2050201. [Google Scholar] [CrossRef]
- Ghiasi, A.; Hussain, O.; Qian, Z.S.; Li, X. A mixed traffic capacity analysis and lane management model for connected automated vehicles: A Markov chain method. Transp. Res. Part B Methodol. 2017, 106, 266–292. [Google Scholar] [CrossRef]
- Shang, M.; Wang, S.; Stern, R.E. Extending ramp metering control to mixed autonomy traffic flow with varying degrees of automation. Transp. Res. Part C Emerg. Technol. 2023, 151, 104119. [Google Scholar] [CrossRef]
- Silgu, M.A.; Erdağı, İ.G.; Göksu, G.; Celikoglu, H.B. Combined control of freeway traffic involving cooperative adaptive cruise controlled and human driven vehicles using feedback control through SUMO. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11011–11025. [Google Scholar] [CrossRef]
- Carlson, R.C.; Papamichail, I.; Papageorgiou, M.; Messmer, A. Optimal mainstream traffic flow control of large-scale motorway networks. Transp. Res. Part C Emerg. Technol. 2010, 18, 193–212. [Google Scholar] [CrossRef]
- Cohen, S. Using the hard shoulder and narrowing lanes to reduce traffic congestion some lessons from an experience on the Paris motorway network. In Proceedings of the 12th IEE International Conference on Road Transport Information & Control—RTIC 2004, London, UK, 20–22 April 2004; pp. 149–153. [Google Scholar]
- Kononov, J.; Hersey, S.; Reeves, D.; Allery, B.K. Relationship between freeway flow parameters and safety and its implications for hard shoulder running. Transp. Res. Rec. 2012, 2280, 10–17. [Google Scholar] [CrossRef]
- Choi, J.; Tay, R.; Kim, S.; Jeong, S.; Kim, J.; Heo, T.Y. Safety Effects of Freeway Hard Shoulder Running. Appl. Sci. 2019, 9, 3614. [Google Scholar] [CrossRef]
- Lemke, K. Hard shoulder running as a short-term measure to reduce congestion. In Proceedings of the 4th International Symposium on Highway Geometric Design, Valencia, Spain, 2–5 June 2010. [Google Scholar]
- Zhao, P.; Ma, J.; Xu, C.; Zhao, C.; Ni, Z. Research on the safety of the left hard shoulder in a multi-lane highway based on safety performance function. Sustainability 2022, 14, 15114. [Google Scholar] [CrossRef]
- Ma, D.; Nakamura, H.; Asano, M.; Axel, W. A Study on Expressway Breakdown Phenomenon Considering Flow Characteristics on Individual Lanes. In Proceedings of the 9th International Conference of Eastern Asia Society for Transportation Studies, Jeju, Republic of Korea, 20–23 June 2011; Volume 8, p. 279. [Google Scholar]
- Chen, X.Q. Modeling Traffic Flow Dynamic and Stochastic Evolutions. Ph.D. Thesis, Tsinghua University, Beijing, China, 2012; pp. 73–79. [Google Scholar]
- Brilon, W.; Geistefeldt, J.; Regler, M. Reliability of freeway traffic flow: A stochastic concept of capacity. In Proceedings of the 16th International Symposium on Transportation and Traffic Theory, College Park, MD, USA, 19–21 July 2005; Volume 125143. [Google Scholar]
- Kühne, R.; Mahnke, R.; Hinkel, J. Modelling the effects of corridor control systems on road capacity. In Proceedings of the 5th International Symposium on Highway Capacity and Quality of Service, Yokohama, Japan, 25–29 July 2006. [Google Scholar]
- Cvahte Ojsteršek, T.; Topolšek, D. Influence of drivers’ visual and cognitive attention on their perception of changes in the traffic environment. Eur. Transp. Res. Rev. 2019, 11, 45. [Google Scholar] [CrossRef]
- Aron, M.; Cohen, S.; Seidowsky, R. Two French Hard-Shoulder Running operations: Some comments on effectiveness and safety. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 230–236. [Google Scholar]
- Khattak, Z.H.; Fontaine, M.D. A Bayesian modeling framework for crash severity effects of active traffic management systems. Accid. Anal. Prev. 2020, 145, 105544. [Google Scholar] [CrossRef] [PubMed]
- Guerrieri, M.; Mauro, R. Capacity and safety analysis of hard-shoulder running (HSR). A motorway case study. Transp. Res. Part A Policy Pract. 2016, 92, 162–183. [Google Scholar] [CrossRef]
- Yu, Q.; Wu, L.; Zhang, H.; Lei, L.; Wang, L. The Impact of Automated Vehicles on Road and Intersection Capacity. Appl. Sci. 2023, 13, 5073. [Google Scholar] [CrossRef]
- Ma, Y.; Qi, S.; Zhang, Y.; Lian, G.; Lu, W.; Chan, C.Y. Drivers’ visual attention characteristics under different cognitive workloads: An on-road driving behavior study. Int. J. Environ. Res. Public Health 2020, 17, 5366. [Google Scholar] [CrossRef] [PubMed]
- Sedar, R.; Vázquez-Gallego, F.; Casellas, R.; Vilalta, R.; Muñoz, R.; Silva, R.; Alonso-Zarate, J. Standards-compliant multi-protocol on-board unit for the evaluation of connected and automated mobility services in multi-vendor environments. Sensors 2021, 21, 2090. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Lee, E.E.; Nejad, M.; Lee, J. Influence of CAV clustering strategies on mixed traffic flow characteristics: An analysis of vehicle trajectory data. Transp. Res. Part C Emerg. Technol. 2020, 115, 102611. [Google Scholar] [CrossRef]
- Tanveer, M.; Kashmiri, F.A.; Naeem, H.; Yan, H.; Qi, X.; Rizvi, S.M.A.; Lu, H. An assessment of age and gender characteristics of mixed traffic with autonomous and manual vehicles: A cellular automata approach. Sustainability 2020, 12, 2922. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, K.; Cheng, M.; Yang, M.; Cheng, Y.; Li, S. Safety evaluation for connected and autonomous vehicles’ exclusive lanes considering penetrate ratios and impact of trucks using surrogate safety measures. J. Adv. Transp. 2020, 2020, 5847814. [Google Scholar] [CrossRef]
- Zhu, W.X.; Zhang, H.M. Analysis of mixed traffic flow with human-driving and autonomous cars based on car-following model. Phys. A Stat. Mech. Its Appl. 2018, 496, 274–285. [Google Scholar] [CrossRef]
- Treiber, M.; Kesting, A.; Helbing, D. Influence of reaction times and anticipation on stability of vehicular traffic flow. Transp. Res. Rec. 2017, 1999, 23–29. [Google Scholar] [CrossRef]


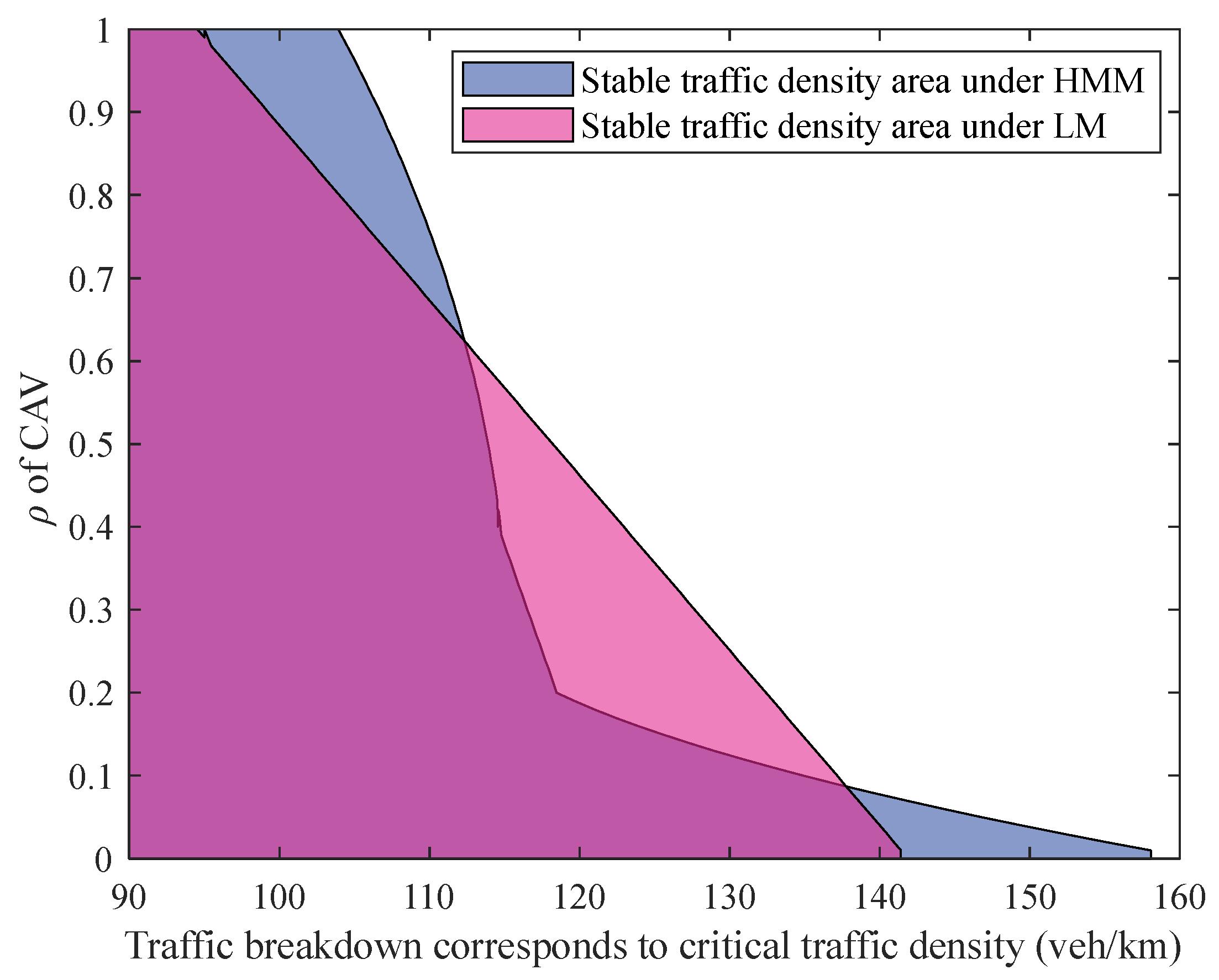
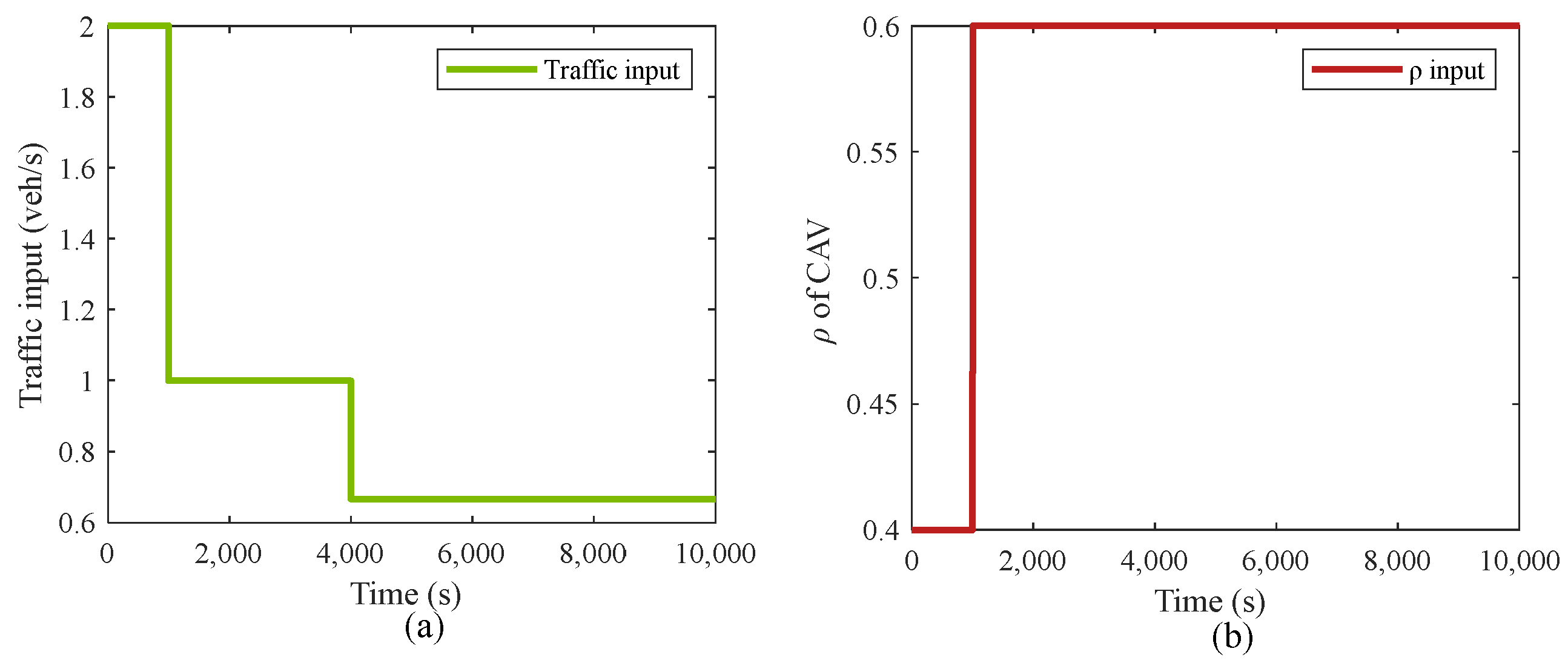

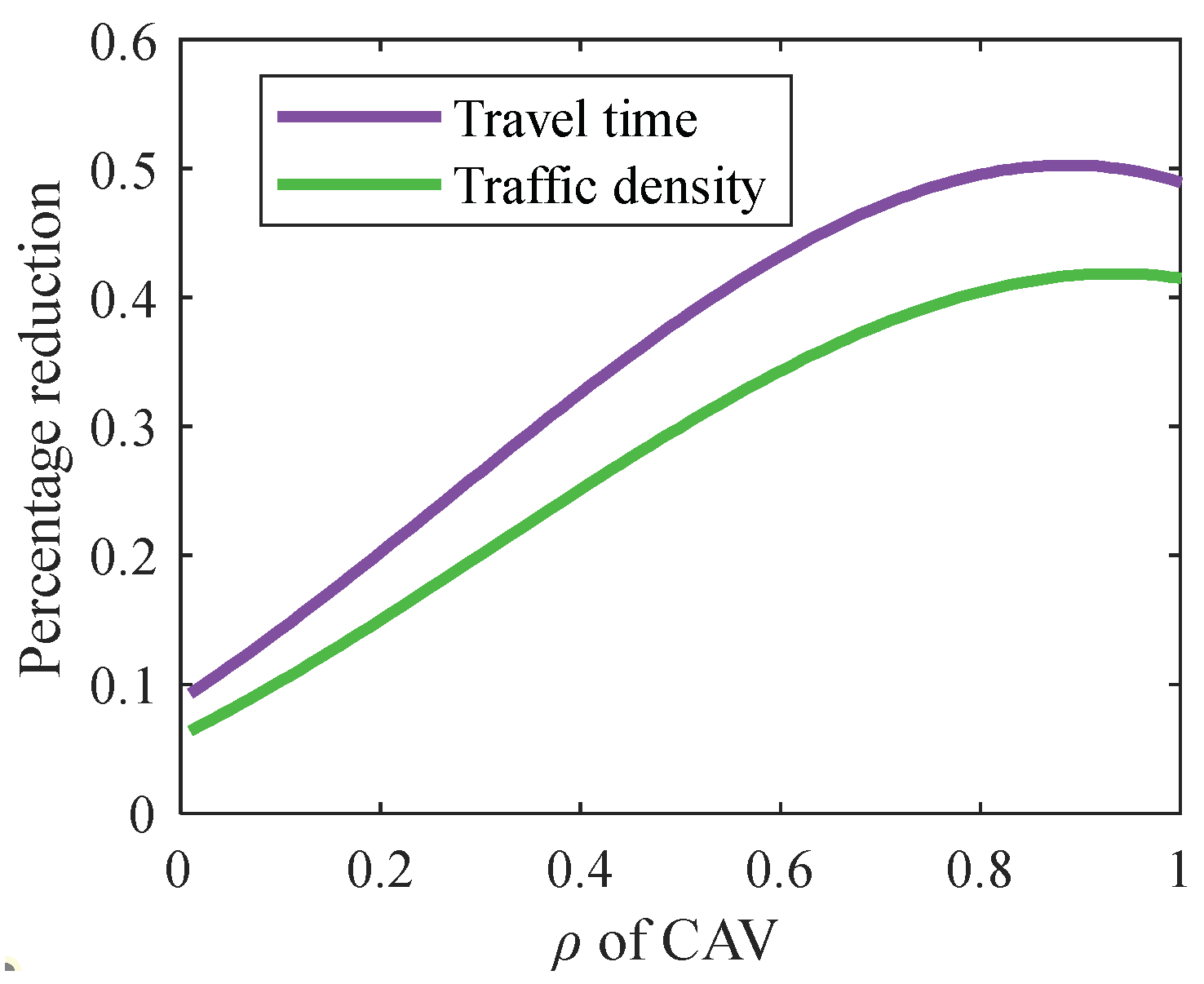
| 0 | 1 | |
|---|---|---|
| 0 | 0.6939 | 0.0170 |
| 1 | 0.0170 | 0.2721 |
| (0,0) | (1,0) | (2,0) | ... | (Zmax,1) | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ... | 0.0034 |
| 1 | 0 | 0 | 0 | ... | 0 |
| Prediction Method | Actual Number | Prediction Number | Errors | Accuracy Rate |
|---|---|---|---|---|
| HMMD | 1212 | 1235 | 23 | 0.9870 |
| LMD | 1212 | 1311 | 34 | 0.9438 |
| Accumulated Travel Time (s) | Accumulated Traffic Density (veh/km) | |
|---|---|---|
| 1.1151 × 107 | 1.1356 × 106 | |
| 9.3578 × 106 | 1.0145 × 106 | |
| 7.5665 × 106 | 8.9529 × 105 | |
| 7.3799 × 106 | 9.1256 × 105 | |
| 6.5766 × 106 | 8.5434 × 105 | |
| 5.5181 × 106 | 7.5571 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Qian, Y.; Feng, Z.; Zhang, J.; Zhang, H.; Chen, T.; Meng, S. Hidden Markov Model-Based Dynamic Hard Shoulders Running Strategy in Hybrid Network Environments. Appl. Sci. 2024, 14, 3145. https://doi.org/10.3390/app14083145
Yao J, Qian Y, Feng Z, Zhang J, Zhang H, Chen T, Meng S. Hidden Markov Model-Based Dynamic Hard Shoulders Running Strategy in Hybrid Network Environments. Applied Sciences. 2024; 14(8):3145. https://doi.org/10.3390/app14083145
Chicago/Turabian StyleYao, Jinqiang, Yu Qian, Zhanyu Feng, Jian Zhang, Hongbin Zhang, Tianyi Chen, and Shaoyin Meng. 2024. "Hidden Markov Model-Based Dynamic Hard Shoulders Running Strategy in Hybrid Network Environments" Applied Sciences 14, no. 8: 3145. https://doi.org/10.3390/app14083145
APA StyleYao, J., Qian, Y., Feng, Z., Zhang, J., Zhang, H., Chen, T., & Meng, S. (2024). Hidden Markov Model-Based Dynamic Hard Shoulders Running Strategy in Hybrid Network Environments. Applied Sciences, 14(8), 3145. https://doi.org/10.3390/app14083145







