Abstract
In integrated circuit (IC) design, floorplanning is an important stage in obtaining the floorplan of the circuit to be designed. Floorplanning determines the performance, size, yield, and reliability of very large-scale integration circuit (VLSI) ICs. The results obtained in this step are necessary for the subsequent continuous processes of chip design. From a computational perspective, VLSI floorplanning is an NP-hard problem, making it difficult to be efficiently solved by classical optimization techniques. In this paper, we propose a deep reinforcement learning floorplanning algorithm based on sequence pairs (SP) to address the placement problem. Reinforcement learning utilizes an agent to explore the search space in sequence pairs to find the optimal solution. Experimental results on the international standard test circuit benchmarks, MCNC and GSRC, demonstrate that the proposed deep reinforcement learning floorplanning algorithm based on sequence pairs can produce a superior solution.
1. Introduction
In recent years, the rapid advancement of integrated circuit technology has led to a significant increase in the complexity of very large-scale integrated circuit (VLSI) circuits. According to Moore’s law [1], the number of transistors on a chip doubles every 18 months. With the continuous advancement in semiconductor technology, the scale and complexity of integrated circuits have been increasing. Faced with such a vast scale of chip design, traditional manual design methods are no longer able to meet growing design demands. Therefore, electronic design automation (EDA) [2] technology has become an indispensable trend for the future. In the design and optimization process of VLSIs, physical design [3] plays a crucial role as an essential part of the VLSI design flow, serving as both a key link and the core of electronic design automation technology. The floorplan phase [4], as a critical part of the physical design flow, not only directly determines the area and overall floorplan of the integrated circuit chip, influencing the subsequent routing work, but also directly dictates the final performance of the entire circuit. The VLSI floorplanning problem, being a classic NP-hard problem, has a significant impact on performance metrics such as circuit delay, power consumption, congestion, and reliability [5]. Despite being a classical problem [6] and the subject of previous algorithms, block placement continues to pose significant challenges [7].
As the first stage of the physical design flow, the quality of floorplanning significantly impacts the subsequent floorplan and routing. Generally, research on floorplanning can be divided into two categories. One category is based on planar graph representations. For floorplan graphs with slicing structures [8], binary trees are widely used, where leaves correspond to blocks and internal nodes define the vertical or horizontal merge operations of their respective descendants. For more general non-slicing floorplan representations, several effective forms have been developed, including sequence pairs (SP) [9], the bounded slicing grid (BSG) [10], O-trees [11], transitive closure graphs with packed sequences (TCG-S) [12], and B*-trees [13]. Among these, the representation of block placement with sequence pairs, which uses positive and negative sequences to represent the geometric relationships between any two modules, has been extended in subsequent work to handle obstacles [14], soft modules, rectilinear blocks, and analog floorplans [15,16,17,18]. The decoding time complexity of the sequence pair representation is O(N2). In order to reduce the decoding complexity, Tang et al. [19]. utilized the longest common subsequence algorithm to decrease the decoding complexity to O(NlogN). Subsequently, Tang and Wong [20] proposed an enhanced Fast Sequence Pair (FSP) algorithm, further reducing the decoding time complexity to O(NloglogN). Another category involves the study of floorplanning algorithms. By employing suitable planar graph representations and/or efficient perturbation methods, high-quality floorplans can be achieved through linear programming [21] or some metaheuristic methods such as simulated annealing (SA) [22,23], genetic algorithms (GA) [24,25], memetic algorithms (MA) [26], and ant colony optimization [27].
Despite decades of research on VLSI floorplanning problems, the existing studies indicate that current EDA floorplan tools still struggle to achieve a floorplan close to optimal. These tools continue to face numerous limitations, making it challenging to obtain satisfactory design outcomes. Existing floorplan tools generally require long runtimes and experienced experts to spend weeks designing integrated circuit floorplans. Furthermore, these tools have a limited scalability and often require a time-consuming redesign when faced with new problems or different constraints. Reinforcement learning (RL) [28] provides a promising direction to address these challenges. Reinforcement learning possesses autonomy and generalization capabilities, allowing the agent in reinforcement learning, through interactions with the environment, to automatically extract knowledge about the space it operates in. In addition to breakthroughs in gaming [29] and robot control [30], reinforcement learning has been applied to solve combinatorial optimization problems. Ref. [31] proposed deep reinforcement learning (DRL) for solving the Traveling Salesman Problem (TSP). Moreover, significant progress has been made in the application of reinforcement learning to task scheduling [32], vehicle routing problems [33], graph coloring [34], and more. Recently, integrating reinforcement learning into electronic design automation (EDA) has become a trend. For example, the Google team [35] formulated macro-module placement as a reinforcement learning problem and trained an agent using reinforcement learning algorithms to place macro-modules on chips. He et al. [36] utilized the Q-learning algorithm to train an agent that selects the best neighboring solution at each search step. Cheng et al. [37] introduced cooperative learning to address floorplan and routing problems in chip design. Agnesina et al. [38] proposed a deep reinforcement learning method for VLSI placement parameter optimization. Vashisht et al. [39] utilized iterative reinforcement learning combined with simulated annealing to place modules. Xu et al. [40] employed graph convolutional networks and reinforcement learning methods for floorplanning under fixed-outline constraints.
This paper proposes a deep reinforcement learning-based floorplanning algorithm utilizing sequence pairs for the floorplanning problem. The algorithm aims to optimize the area and wirelength of the floorplan. To evaluate the effectiveness of our algorithm, we conduct experiments on the internationally recognized benchmark circuits MCNC and GSRC, comparing our approach with simulated annealing and the deep Q-learning algorithm proposed by He et al. [36]. In terms of dead space on the MCNC benchmark circuits, our algorithm outperforms simulated annealing and the literature [36] by an average improvement of 2.7% and 1.1%, respectively. Additionally, concerning wirelength, our algorithm shows an average improvement of 9.1% compared to simulated annealing. On the GSRC benchmark circuits, our algorithm demonstrates an average improvement of 7.0% and 3.7% in dead space to simulated annealing and the literature [36], respectively. Furthermore, for wirelength, our algorithm exhibits an average improvement of 8.8% over simulated annealing. These results validate the superior performance and robustness of our algorithm in handling ultra-large-scale circuit designs.
2. Description of Floorplanning Problem
Generally, floorplanning involves determining the relative positions of modules. Let B = {bi|1 ≤ i ≤ n} be a set of rectangular modules, where each module bi has a specified width wi and height hi. N = {ni|1 ≤ i ≤ m} represents a netlist that describes the connections between modules. The goal of floorplanning is to assign a set of coordinates to each module bi, while ensuring that no two modules overlap.
Let (xi, yi) denote the coordinates of the bottom-left corner of module bi. The floorplan area A is defined as the minimum rectangular area that encompasses all modules, and it can be calculated as follows:
We employ the widely used Half-Perimeter Wirelength (HPWL) model [41] as the method to estimate the total wirelength, which is defined as follows:
Based on the optimization objective defined by the minimum rectangle area A and the wirelength W, the formulation is as follows:
Among these, F is a feasible floorplan diagram, indicating the weighted sum of the total area A and the total wirelength W. The coefficients α and β are weight factors ranging from 0 to 1.
3. Sequence Pair Representation
Tamarana et al. [9] proposed a graph-encoding method called sequence pair (SP) for encoding non-sliced planar graphs. Given a non-sliced planar graph with n modules, a sequence pair consists of a positive sequence Г+ and a negative sequence Г−, which contains all the information about which subsets of modules are located above, below, to the right, and to the left of a given module. Through the analysis of different graph representation methods, we believe that sequence pair has unique advantages compared to other graph representations. Firstly, the sequence pair representation is concise and easy to understand, making it highly suitable for integration with reinforcement learning to jointly solve graph-planning problems. Secondly, it can represent the complete solution space and has a one-to-one correspondence with non-sliced graphs, allowing for the unique reconstruction of non-sliced graphs from it. Lastly, compared with other methods, the introduction of fast sequences significantly reduces the complexity of the decoding time.
3.1. Properties of Sequence Pair
Sequence pair is a method used to describe the relative order between sequences. In each pair of sequences, each sequence consists of a set of module names, where the module names are the same in the positive sequence Г+ and the negative sequence Г−, but their order is inconsistent between Г+ and Г−. For example, in a given pair of sequences (Г+, Г−), there are four possible positional relationships between any two modules, bi and bj:
- (1)
- If bi is positioned before bj in Г+, i.e., <....bi....bj....>, and bi is also positioned before bj in Г−, i.e., <....bi....bj....>, it indicates that bi is located on the left side of bj.
- (2)
- If bj is positioned before bi in Г+, i.e., <....bj....bi....>, and bj is also positioned before bi in Г−, i.e., <....bj....bi....>, it indicates that bi is located on the right side of bj.
- (3)
- If bi is positioned before bj in Г+, i.e., <....bi....bj....>, and bj is positioned before bi in Г−, i.e., <....bj....bi....>, it indicates that bi is located above bj.
- (4)
- If bj is positioned before bi in Г+, i.e., <....bj....bi....>, and bi is positioned before bj in Г−, i.e., <....bi....bj....>, it indicates that bi is located below bj.
As an example, Figure 1 shows an inclined grid representing the relative positions between modules in a sequence pair (Г+, Г−) = (<4, 3, 1, 6, 2, 5) and (<6, 3, 5, 4, 1, 2>).
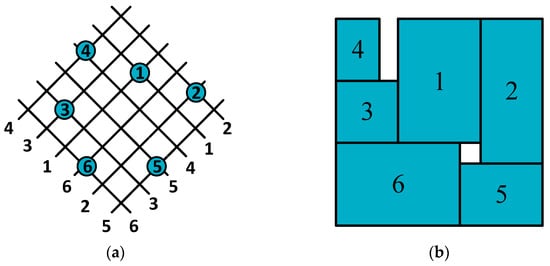
Figure 1.
(a) displays an inclined grid representing the relative positions between modules in a sequence pair (Г+, Г−) = (<4, 3, 1, 6, 2, 5) and (<6, 3, 5, 4, 1, 2>); (b) corresponds to the floorplan of the sequence pair. Each module has the following dimensions: 1 (4 × 6), 2 (3 × 7), 3 (3 × 3), 4 (2 × 3), 5 (4 × 3), 6 (6 × 4).
From the figure, it can be observed that all modules satisfy the requirements of sequence pairs. In fact, for any given sequence pair, the positions of each module can be efficiently determined by calculating the weighted longest common subsequence (LCS). The time complexity of this algorithm is O(nlog(logn)).
3.2. Sequence Pair Representation Floorplan
To obtain a floorplan from a sequence pair, we first construct a geometric constraint graph corresponding to the sequence pair. This constraint graph consists of a set of edges (E) and a set of vertices (V). The vertex set (V) represents nodes for each module name, source node S, and added receiving node T. A horizontal constraint graph (HCG) and a vertical constraint graph (VCG) can be constructed, based on the positional relationships of each module. The specific steps for construction are as follows:
- (1)
- For a given module x in the sequence pair (Г+, Г−), we obtain a list of modules that appear before x in Г+ and Г−. These modules are positioned to the left of x in the plane graph. A group of modules that appear after x in Г+ and Г− are positioned to the right of x in the plane graph. A group of modules that appear after x in Г+ and before x in Г− are positioned below x in the plane graph. Finally, a group of modules that appear before x in Г+ and after x in Г− are positioned above x in the plane graph.
- (2)
- Next, we construct a directed graph for the horizontal constraint graph based on the left and right relationships. A directed edge E (a, b) represents module a being positioned to the left of module b. We add a source node S connected to all nodes in the horizontal constraint graph, and we also add a receiving node T connected to all nodes. The longest path length from the source node S to each node in the horizontal constraint graph represents the x coordinate of the modules in the floorplan.
- (3)
- By computing the longest path length from the source node S to the added receiving node T, we can obtain the width of the floorplan. Similarly, we construct the vertical constraint graph based on the relationships above and below, and calculate the y coordinate of the modules and the height of the plane graph in a similar manner. Figure 2 illustrates the constructed horizontal and vertical constraint graphs for the sequence pair (Г+, Г−) = (<4, 3, 1, 6, 2, 5), (<6, 3, 5, 4, 1, 2>) as an example.
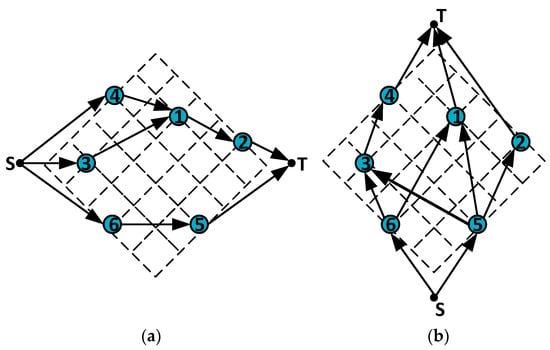 Figure 2. (a) represents the horizontal constraint graph and (b) represents the vertical constraint graph.
Figure 2. (a) represents the horizontal constraint graph and (b) represents the vertical constraint graph.
So, by constructing horizontal and vertical constraint graphs and calculating the longest path lengths for both directions, we can determine the width and height of the minimum bounding rectangle of the floorplan. Subsequently, floorplanning is performed for the pair of sequences, thereby determining the size and position of the non-slicing plane graph.
4. Reinforcement Learning
Reinforcement learning is a machine learning approach aimed at learning how to make decisions to achieve specific goals through interaction with the environment. In reinforcement learning, an agent observes the state of the environment, selects appropriate actions, and continuously optimizes its strategy based on feedback from the environment regarding its actions. This feedback is typically provided in the form of rewards [42,43] or penalties, and the agent’s objective is to learn the optimal strategy by maximizing the long-term cumulative reward.
Almost all reinforcement learning satisfies the framework of Markov Decision Processes (MDPs). A typical MDP, as shown in Figure 3, consists of four key elements:
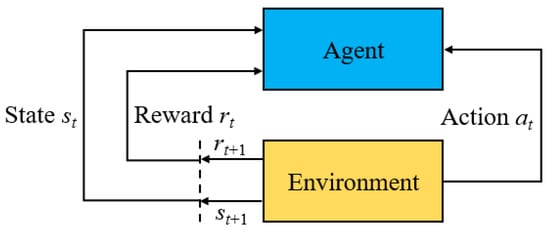
Figure 3.
A typical framework for MDPs.
- (1)
- States S: a finite set of environmental states.
- (2)
- Actions A: a finite set of actions taken by the reinforcement learning agent.
- (3)
- State transition model P (s, a, s′): representing the probability of transitioning from state s Є S to the next state, s′ Є S, when action a Є A is taken.
- (4)
- Reward function R (s, a): representing the numerical reward for taking action a Є A in state s Є S. This reward can be positive, negative, or zero.
The goal of an MDP is to find a policy π that maximizes the total accumulated numerical reward. The expression for the total cumulative reward is as follows:
where γ represents the reward discount factor, t denotes the time step, and r represents the reward value at time step t. The state value function Vπ(s) in an MDP is defined as the expected reward value of state s under policy π, as defined in Equation (5).
In this context, Eπ represents the expected value of the reward function under policy π. Similarly, the state–action value function Qπ (s, a) is the expected reward value when action a is taken in state s under policy π, defined as follows:
4.1. The MDP Framework for Solving Floorplanning Problems
In floorplanning problems, the agent in reinforcement learning interacts with the environment by selecting a perturbation to iteratively generate new floorplan solutions. The objective is to minimize the total area and total wirelength, which serve as rewards to encourage the agent to learn better strategies and ultimately find an optimal floorplan solution. To explore better floorplan solutions, the following MDP is defined:
- (1)
- State space S: for the floorplanning problem, a state s Є S represents a floorplan solution, including a complete sequence of gates (Г+, Г−), and the orientation of each module.
- (2)
- Action space A: A neighboring solution of a floorplan is generated by predefined perturbations in the action space. The following five perturbations are defined:
- (a)
- Swap any two modules in the Г+ sequence.
- (b)
- Swap any two modules in the Г− sequence.
- (c)
- Swap one module from the Г+ sequence with one module from the Г− sequence.
- (d)
- Randomly move a module to a new position in both Г+ and Г−.
- (e)
- Rotate any module in the sequence pair by 90°.
- (3)
- State transition P: given a state, applying any of the above perturbations will result in the agent transitioning to another state, simplifying the probabilistic setting in the MDP.
- (4)
- Reward R: Allocating rewards for actions taken in a state is crucial in reinforcement learning. In this floorplanning problem, the objective is to minimize the area and wirelength. Thus, the reward is assigned as the reduction in the objective cost. A positive reward is assigned whenever the agent discovers a better solution, while no reward is assigned otherwise. The reward function is defined as follows:
The reward r in this context refers to a local reward, representing the reward value obtained when the current floorplan transitions from state s to state s′ through a perturbation. Here, F represents the optimization objective function defined in Equation (3).
4.2. Deep Reinforcement Learning Algorithm
After defining the MDP framework for solving the floorplanning problem, we choose to utilize the deep reinforcement learning algorithm to train the agent. In this paper, we employ the policy gradient (PG) algorithm based on Actor–Critic (AC) architecture, which is a model-free policy-based algorithm. In comparison to value-based methods, policy-based methods ensure a faster convergence. The gradient method utilizes gradient descent to optimize the policy π. Specifically, the parameter θ is associated with the policy π that is to be optimized. We define an objective function J(θ), as illustrated in Equation (8), where the objective function J(θ) represents the target of obtaining the expected discounted total reward by following the parameterized policy π. Hence, our objective is to learn an θ that maximizes the function J(θ).
Reinforcement learning algorithms are a type of Monte Carlo method, allowing them to learn from a sequence of episodes or a series of steps taken by an agent during its exploration, without prior knowledge of the transition function in the MDP framework. The parameter vector θ is learned through a deep neural network. This network is referred to as the policy gradient network, and its weights represent the θ parameters. The policy network, or agent, is a deep neural network with a set of hidden layers. The activation function of the last layer of this network is “Softmax”, as the network’s output is a probability distribution of environmental actions. The policy gradient algorithm updates the parameters θ in the direction of actions with the highest rewards. The weights are then updated using the computed gradient, defined as follows:
α represents the learning rate. By taking the derivative of Formula (8), Formula (10) is derived, which will be utilized to update the values of the θ parameters. The definition of this formula is as follows:
This is the calculation of the expected trajectory τ obtained by sampling the policy πθ. R(τ) represents the reward accumulated over a single episode.
To train the policy network, the deep reinforcement learning algorithm is employed as shown in Algorithm 1, At each step of the episode, the policy network will predict a probability distribution assigned to the different actions available in the environment given the state description. The set of state, action, reward and next state in each episode are recorded. The set of discounted rewards are employed to calculate the gradient and update the weights of the policy network.
| Algorithm 1: Deep Reinforcement Learning Algorithm |
| Input: number of episodes, number of steps Output: Policy π 1: Initialize θ (policy network weights) randomly |
| 2: for e in episodes do |
| 3: for s in steps do |
| 4: Perform an action as predicted by the policy network |
| 5: Record s, a, r, s′ |
| 6: Calculate the gradient as per Equation (10) |
| 7: end |
| 8: Update θ as per Equation (9) |
| 9: end |
After numerous experiments for parameter tuning and optimization, the hyperparameters settings of the algorithm in this paper are presented in Table 1.

Table 1.
Reinforcement learning hyperparameters.
5. Experimental Results
5.1. Experimental Environment and Test Data
The experiment was conducted on a computer with a 12th Gen Intel(R) Core(TM) (Intel(R), Santa Clara, CA, USA) i5-12500 3.00 GHz CPU and 16.00 GB of RAM memory. The algorithm we proposed was implemented in Python3.8 using the PyTorch library [44], with the Adam optimizer [45] applied to train the neural network model. During training, to save time and prevent overfitting, we employed a stopping mechanism where the training process would halt if no better solution was found in the final 50 steps. For the simulated annealing algorithm, we adjusted its parameters through multiple experiments and selected the best parameter set based on the floorplan results.
Our algorithm was tested on two standard test circuit sets, MCNC and GSRC, and compared with the simulated annealing algorithm and the deep Q-learning algorithm proposed by He et al. [36]. The MCNC benchmark comprises five hard modules and five soft modules, while the GSRC benchmark consists of six hard modules and six soft modules. Hard modules allow rotation but cannot change their shape, whereas soft modules provide area and aspect ratio, allowing multiple shapes. In this experiment, our test circuits consisted of fixed-size hard modules. The basic information about the three test circuits in the MCNC and GSRC test circuit sets is shown in Table 2 and Table 3, respectively.

Table 2.
Basic information about MCNC test circuit.

Table 3.
Basic information about GSRC test circuit.
5.2. Experimental Results and Analysis
We conducted experiments using a reinforcement learning-based VLSI floorplanning algorithm on two internationally standardized test circuit sets, MCNC and GSRC. The experimental results were compared with the deep Q-learning algorithm and simulated annealing algorithm presented in Ref. [36]. Additionally, floorplan visualization experiments were performed. Building upon these experiments, we extended our study by incorporating an additional experiment. The proposed algorithm and the simulated annealing algorithm were tested on the MCNC and GSRC standard test circuit sets. Three blocks, namely RAM, ROM, and CPU, were selected from each test circuit and placed as fixed modules in predetermined locations. Subsequently, the placement results of our algorithm were compared with those of the simulated annealing algorithm, followed by floorplan visualization experiments.
5.2.1. Experimental Results of MCNC and GSRC Test Sets
First, a synergistic optimization of area and wirelength was performed on the MCNC test set, and the experimental results are presented in Table 4. The dead space (DS) represents the proportion of gaps between macro-modules within the floorplan border to the total floorplan area. As shown in the table, the proposed algorithm generated a floorplan in the MCNC test circuits with a smaller area, DS, and wirelength compared to the simulated annealing algorithm. In terms of layout area and DS, the proposed algorithm also outperformed the approach described in Reference [36]. However, a direct comparison of wirelength was not made due to the different estimation method used in Reference [36]. Regarding DS and wirelength, the proposed algorithm achieved an average improvement of 2.7% and 9.1%, respectively, compared to the simulated annealing algorithm. Furthermore, compared to Reference [36], the proposed algorithm achieved an average improvement of 1.1% in DS. Therefore, the proposed algorithm demonstrates certain advantages over the simulated annealing algorithm and Reference [36] in area optimization for small-scale circuits, as well as outperforming the simulated annealing algorithm in wirelength optimization.

Table 4.
Comparison of experimental results of MCNC test circuit.
Table 5 presents the experimental results comparison for three GSRC test circuits, revealing that the proposed algorithm outperforms the simulated annealing algorithm and Reference [36] in terms of floorplan area and DS and is also superior to the simulated annealing algorithm in wirelength. In comparison with the simulated annealing algorithm, the proposed algorithm achieves an average improvement of 7.0% in DS and 8.8% in wirelength. Furthermore, when compared to Reference [36], the proposed algorithm obtains an average improvement of 3.7% in DS. From both tables, it can be observed that, as the size of the test circuits increases, the DS for all three methods also increases, indicating an increased difficulty in floorplan placement. However, the proposed algorithm demonstrates a further improvement in performance compared to the simulated annealing algorithm and Reference [36] for large-scale circuits, offering more pronounced advantages in floorplan area and wirelength optimization.

Table 5.
Comparison of experimental results of GSRC test circuit.
5.2.2. Experimental Results of MCNC and GSRC Test Sets with Obstacles
The optimization of area and wirelength for MCNC benchmark circuits was conducted, and the experimental results are presented in Table 6. Since the fixed module placement constraint was employed, the proposed algorithm is only compared with the simulated annealing algorithm in this context. It can be observed from the table that, for all five test circuits, the proposed algorithm achieves a smaller floorplan area, DS, and wirelength than the simulated annealing algorithm. The proposed algorithm demonstrates an average improvement of 9.2% in wirelength and 3.4% in DS compared to the simulated annealing algorithm. Therefore, regarding the MCNC benchmark circuits under the fixed placement constraint of three modules, the proposed algorithm exhibits more significant advantages in optimizing the floorplan area and wirelength compared to the simulated annealing algorithm.

Table 6.
Comparison of experimental results of MCNC test circuits with obstacles.
Table 7 compares the experimental results of three GSRC benchmark circuits, under the constraint of fixed module placement. It can be observed that the proposed algorithm in this paper outperforms the simulated annealing algorithm in terms of planar floorplan area, wirelength, and DS. Compared to the simulated annealing algorithm, the proposed algorithm achieves an average improvement of 11.2% in wirelength and 8.5% in DS. From Table 5 and Table 6, it can be seen that, as the size of the test circuits increases, both methods experience an increase in wirelength and DS, making the floorplan and routing more challenging. However, under the constraint of pre-placing three fixed modules, the proposed algorithm in this paper demonstrates superior performance compared to the simulated annealing algorithm in large-scale circuit testing. Lastly, comparing the experimental results of pre-placing fixed modules in the MCNC and GSRC benchmark circuits, we can observe that the former outperforms the latter, indicating that pre-placing fixed modules makes the floorplanning problem more complex and challenging.

Table 7.
Comparison of experimental results of GSRC test circuits with obstacles.
5.3. Floorplan Visualization
5.3.1. Visualization of MCNC and GSRC Circuit Floorplan
Comparison of MCNC circuit floorplan results are shown in Figure 4. The DS of the floorplan generated by the algorithm in this paper is only 5.0%, while the simulated annealing algorithm produces a floorplan with a DS of 8.8%. Comparison of GSRC circuit floorplan results are shown in Figure 5. The DS of the floorplan generated by the algorithm in this paper for the n100 test circuit is 7.0%, which is lower than the 9.9% DS achieved by the simulated annealing algorithm. From the figures, it is evident that the floorplans generated by the algorithm in this paper have a lower DS and overall floorplan areas than the floorplans generated by the simulated annealing algorithm, both in the small-scale and large-scale test circuits in both benchmark sets. This confirms the superior performance of the algorithm proposed in this paper.
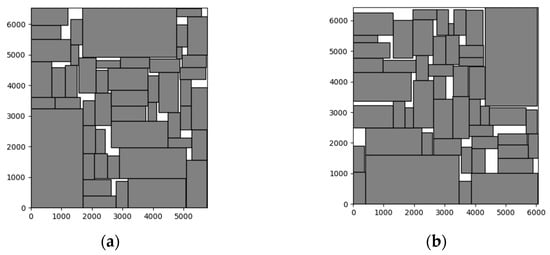
Figure 4.
The floorplans generated by the algorithm proposed in this paper (a) and the simulated annealing algorithm (b) for the ami49 test circuit.
Figure 5.
The floorplan generated by the algorithm proposed in this paper (a) and the simulated annealing algorithm (b) for the n100 test circuit.
5.3.2. Visualization of MCNC and GSRC Circuit Floorplan with Obstacles
Comparison of MCNC circuit floorplan results with obstacles are shown in Figure 6. The DS of the planar floorplan generated by the algorithm in this paper is only 9.0%, while the DS of the simulated annealing algorithm is 14.6%. Comparison of GSRC circuit floorplan results with obstacles are shown in Figure 7. The DS of the floorplan generated by the algorithm in this paper is only 9.1%, whereas the DS of the simulated annealing algorithm is 19.3%. This demonstrates the effectiveness of the algorithm proposed in this paper.
Figure 6.
The floorplans of the ami49 test circuit generated by the algorithm proposed in this paper (a) and the simulated annealing algorithm (b).
Figure 7.
The floorplans of the n100 test circuit generated by the algorithm proposed in this paper (a) and the simulated annealing algorithm (b).
6. Conclusions
In this paper, we investigate the floorplanning problem in the integrated circuit design flow and propose a sequence pair-based deep reinforcement learning floorplanning algorithm. Experimental results on the MCNC and GSRC benchmark circuit sets demonstrate that our algorithm outperforms the deep Q-learning algorithm and the simulated annealing algorithm in terms of both DS and wirelength. Moreover, as the circuit size increases and the difficulty of the floorplan and wiring grows, the advantages of our algorithm become more pronounced. In recent years, machine learning-based methods have been increasingly applied in the EDA field. However, the algorithm in this paper also has some limitations, such as the long optimization time of the algorithm. Next, we aim to explore novel approaches, such as graph neural networks, within deep learning algorithms to address floorplanning problems. This integration may potentially enhance the intelligence and precision of algorithms, thereby significantly improving the quality of the floorplan optimization results.
Author Contributions
Conceptualization, S.Y.; methodology, S.Y.; software, S.Y.; validation, C.Y.; formal analysis, C.Y.; investigation, S.D.; data curation, S.D.; writing—original draft preparation, S.Y.; writing—review and editing, S.D.; visualization, S.Y.; project administration, S.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Natural Science Foundation of China (grant no. 61871244, 61874078, 62134002), the Fundamental Research Funds for the Provincial Universities of Zhejiang (grant no. SJLY2020015), the S&T Plan of Ningbo Science and Technology Department (grant no. 202002N3134), and the K. C. Wong Magna Fund in Ningbo University of Science.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to further study.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the existing affiliation information. This change does not affect the scientific content of the article.
References
- Fleetwood, D.M. Evolution of total ionizing dose effects in MOS devices with Moore’s law scaling. IEEE Trans. Nucl. Sci. 2017, 65, 1465–1481. [Google Scholar] [CrossRef]
- Wang, L.T.; Chang, Y.W.; Cheng, K.T. (Eds.) Electronic Design Automation: Synthesis, Verification, and Test; Morgan Kaufmann: San Francisco, CA, USA, 2009. [Google Scholar]
- Sherwani, N.A. Algorithms for VLSI Physical Design Automation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Adya, S.N.; Chaturvedi, S.; Roy, J.A.; Papa, D.A.; Markov, I.L. Unification of partitioning, placement and floorplanning. In Proceedings of the IEEE/ACM International Conference on Computer Aided Design, ICCAD-2004, San Jose, CA, USA, 7–11 November 2004; pp. 550–557. [Google Scholar]
- Markov, I.L.; Hu, J.; Kim, M.C. Progress and challenges in VLSI placement research. In Proceedings of the International Conference on Computer-Aided Design, San Jose, CA, USA, 5–8 November 2012; pp. 275–282. [Google Scholar]
- Gubbi, K.I.; Beheshti-Shirazi, S.A.; Sheaves, T.; Salehi, S.; Pd, S.M.; Rafatirad, S.; Sasan, A.; Homayoun, H. Survey of machine learning for electronic design automation. In Proceedings of the Great Lakes Symposium on VLSI 2022, Irvine, CA, USA, 6–8 June 2022; pp. 513–518. [Google Scholar]
- Garg, S.; Shukla, N.K. A Study of Floorplanning Challenges and Analysis of macro placement approaches in Physical Aware Synthesis. Int. J. Hybrid Inf. Technol. 2016, 9, 279–290. [Google Scholar] [CrossRef]
- Subbulakshmi, N.; Pradeep, M.; Kumar, P.S.; Kumar, M.V.; Rajeswaran, N. Floorplanning for thermal consideration: Slicing with low power on field programmable gate array. Meas. Sens. 2022, 24, 100491. [Google Scholar]
- Tamarana, P.; Kumari, A.K. Floorplanning for optimizing area using sequence pair and hybrid optimization. Multimed. Tools Appl. 2023, 1–23. [Google Scholar] [CrossRef]
- Nakatake, S.; Fujiyoshi, K.; Murata, H.; Kajitanic, Y. Module packing based on the BSG-structure and IC layout applications. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1998, 17, 519–530. [Google Scholar] [CrossRef]
- Guo, P.N.; Cheng, C.K.; Yoshimura, T. An O-tree representation of non-slicing floorplan and its applications. In Proceedings of the 36th annual ACM/IEEE Design Automation Conference, New Orleans, LA, USA, 21–25 June 1999; pp. 268–273. [Google Scholar]
- Lin, J.M.; Chang, Y.W. TCG-S: Orthogonal coupling of P*-admissible representation with worst case linear-time packing scheme. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2004, 23, 968–980. [Google Scholar] [CrossRef]
- Chang, Y.C.; Chang, Y.W.; Wu, G.M.; Wu, S.-W. B*-trees: A new representation for non-slicing floorplans. In Proceedings of the 37th Annual Design Automation Conference, Los Angeles, CA, USA, 5–9 June 2000; pp. 458–463. [Google Scholar]
- Yu, S.; Du, S. VLSI Floorplanning Algorithm Based on Reinforcement Learning with Obstacles. In Proceedings of the Biologically Inspired Cognitive Architectures 2023—BICA 2023, Ningbo, China, 13–15 October 2023; Springer Nature: Cham, Switzerland, 2023; pp. 1034–1043. [Google Scholar]
- Zou, D.; Wang, G.G.; Sangaiah, A.K.; Kong, X. A memory-based simulated annealing algorithm and a new auxiliary function for the fixed-outline floorplanning with soft blocks. J. Ambient. Intell. Humaniz. Comput. 2017, 15, 1613–1624. [Google Scholar] [CrossRef]
- Liu, J.; Zhong, W.; Jiao, L.; Li, X. Moving block sequence and organizational evolutionary algorithm for general floorplanning with arbitrarily shaped rectilinear blocks. IEEE Trans. Evol. Comput. 2008, 12, 630–646. [Google Scholar] [CrossRef]
- Fischbach, R.; Knechtel, J.; Lienig, J. Utilizing 2D and 3D rectilinear blocks for efficient IP reuse and floorplanning of 3D-integrated systems. In Proceedings of the 2013 ACM International symposium on Physical Design, Stateline, NV, USA, 24–27 March 2013; pp. 11–16. [Google Scholar]
- Fang, Z.; Han, J.; Wang, H. Deep reinforcement learning assisted reticle floorplanning with rectilinear polygon modules for multiple-project wafer. Integration 2023, 91, 144–152. [Google Scholar] [CrossRef]
- Tang, X.; Tian, R.; Wong, D.F. Fast evaluation of sequence pair in block placement by longest common subsequence computation. In Proceedings of the Conference on Design, Automation and Test in Europe, Paris, France, 27–30 March 2000; pp. 106–111. [Google Scholar]
- Tang, X.; Wong, D.F. FAST-SP: A fast algorithm for block placement based on sequence pair. In Proceedings of the 2001 Asia and South Pacific design automation conference, Yokohama, Japan, 2 February 2001; pp. 521–526. [Google Scholar]
- Dayasagar Chowdary, S.; Sudhakar, M.S. Linear programming-based multi-objective floorplanning optimization for system-on-chip. J. Supercomput. 2023, 1–24. [Google Scholar] [CrossRef]
- Tabrizi, A.F.; Behjat, L.; Swartz, W.; Rakai, L. A fast force-directed simulated annealing for 3D IC partitioning. Integration 2016, 55, 202–211. [Google Scholar] [CrossRef]
- Tung-Chieh, C.; Yao-Wen, C. Modern floorplanning based on B*-tree and fast simulated annealing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 25, 637–650. [Google Scholar] [CrossRef]
- Sadeghi, A.; Lighvan, M.Z.; Prinetto, P. Automatic and simultaneous floorplanning and placement in field-programmable gate arrays with dynamic partial reconfiguration based on genetic algorithm. Can. J. Electr. Comput. Eng. 2020, 43, 224–234. [Google Scholar] [CrossRef]
- Chang, Y.F.; Ting, C.K. Multiple Crossover and Mutation Operators Enabled Genetic Algorithm for Non-slicing VLSI Floorplanning. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Tang, M.; Yao, X. A memetic algorithm for VLSI floorplanning. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2007, 37, 62–69. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, S.; Li, B. Combining the ant system algorithm and simulated annealing for 3D/2D fixed-outline floorplanning. Appl. Soft Comput. 2016, 40, 150–160. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3389–3396. [Google Scholar]
- Bello, I.; Pham, H.; Le, Q.V.; Norouzi, M.; Bengio, S. Neural combinatorial optimization with reinforcement learning. arXiv 2016, arXiv:1611.09940. [Google Scholar]
- Zhou, C.; Wu, W.; He, H.; Yang, P.; Lyu, F.; Cheng, N.; Shen, X. Deep reinforcement learning for delay-oriented IoT task scheduling in SAGIN. IEEE Trans. Wirel. Commun. 2020, 20, 911–925. [Google Scholar] [CrossRef]
- Nazari, M.; Oroojlooy, A.; Snyder, L.; Takac, M. Reinforcement learning for solving the vehicle routing problem. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Huang, J.; Patwary, M.; Diamos, G. Coloring big graphs with alphagozero. arXiv 2019, arXiv:1902.10162. [Google Scholar]
- Mirhoseini, A.; Goldie, A.; Yazgan, M.; Jiang, J.W.; Songhori, E.; Wang, S.; Lee, Y.-J.; Johnson, E.; Pathak, O.; Nazi, A.; et al. A graph placement methodology for fast chip design. Nature 2021, 594, 207–212. [Google Scholar] [CrossRef]
- He, Z.; Ma, Y.; Zhang, L.; Liao, P.; Wong, N.; Yu, B.; Wong, M.D.F. Learn to floorplan through acquisition of effective local search heuristics. In Proceedings of the 2020 IEEE 38th International Conference on Computer Design (ICCD), Hartford, CT, USA, 18–21 October 2020; pp. 324–331. [Google Scholar]
- Cheng, R.; Yan, J. On joint learning for solving placement and routing in chip design. Adv. Neural Inf. Process. Syst. 2021, 34, 16508–16519. [Google Scholar]
- Agnesina, A.; Chang, K.; Lim, S.K. VLSI placement parameter optimization using deep reinforcement learning. In Proceedings of the 39th International Conference on Computer-Aided Design, Virtual, 2–5 November 2020; pp. 1–9. [Google Scholar]
- Vashisht, D.; Rampal, H.; Liao, H.; Lu, Y.; Shanbhag, D.; Fallon, E.; Kara, L.B. Placement in integrated circuits using cyclic reinforcement learning and simulated annealing. arXiv 2020, arXiv:2011.07577. [Google Scholar]
- Xu, Q.; Geng, H.; Chen, S.; Yuan, B.; Zhuo, C.; Kang, Y.; Wen, X. GoodFloorplan: Graph Convolutional Network and Reinforcement Learning-Based Floorplanning. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 41, 3492–3502. [Google Scholar] [CrossRef]
- Shahookar, K.; Mazumder, P. VLSI cell placement techniques. ACM Comput. Surv. (CSUR) 1991, 23, 143–220. [Google Scholar] [CrossRef]
- Gaon, M.; Brafman, R. Reinforcement learning with non-markovian rewards. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3980–3987. [Google Scholar] [CrossRef]
- Bacchus, F.; Boutilier, C.; Grove, A. Rewarding behaviors. Proc. Natl. Conf. Artif. Intell. 1996, 13, 1160–1167. [Google Scholar]
- Zimmer, L.; Lindauer, M.; Hutter, F. Auto-pytorch: Multi-fidelity metalearning for efficient and robust autodl. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3079–3090. [Google Scholar] [CrossRef]
- Zhang, Z. Improved adam optimizer for deep neural networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; pp. 1–2. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).