Optimization Study of Water Interval Charge Structure Based on the Evaluation of Rock Damage Effect in Smooth Blasting
Abstract
1. Introduction
2. Establishment of a Method for Evaluating Rock Damage Effects
2.1. Basis of Evaluation
2.1.1. Evaluation of Rock Damage Effects Based on Classical Strength Theory
2.1.2. Evaluation Method Based on Damage Fracture Theory
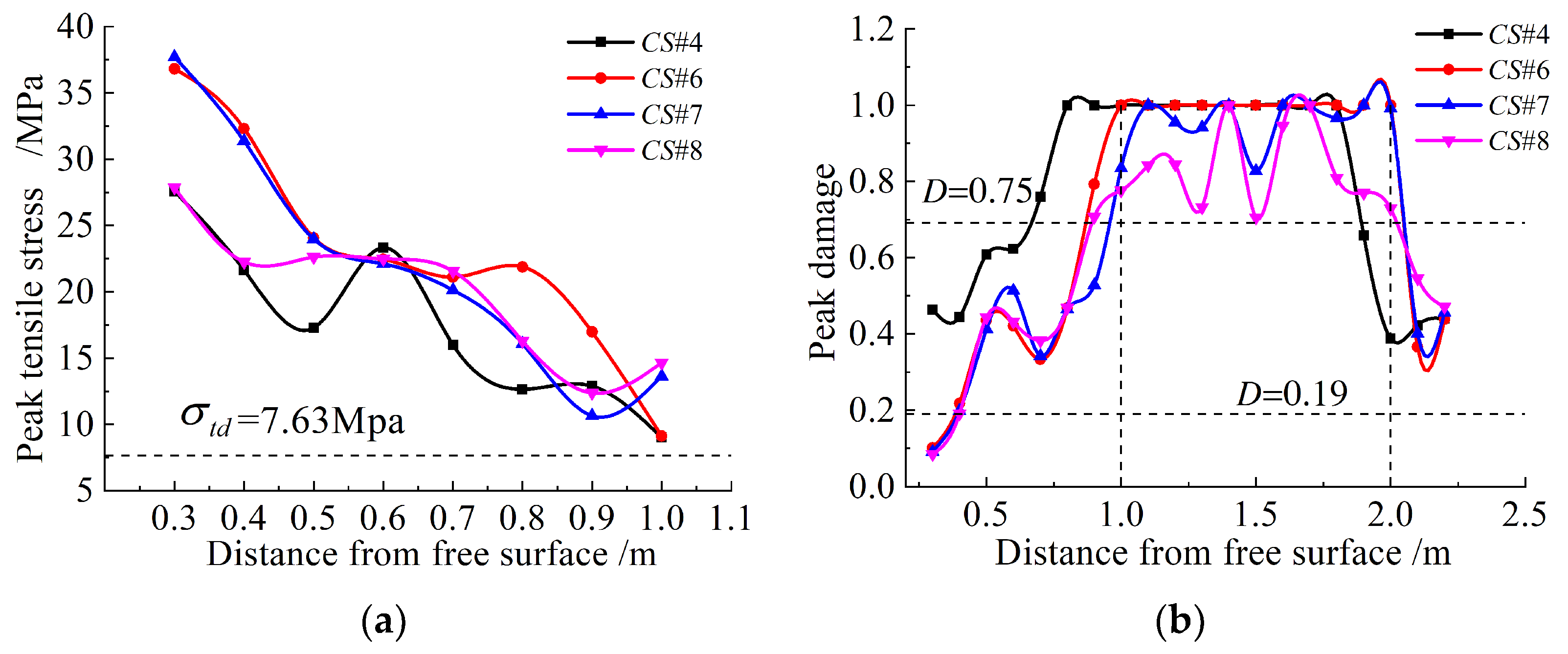
2.2. Determination of Evaluation Indicator Thresholds
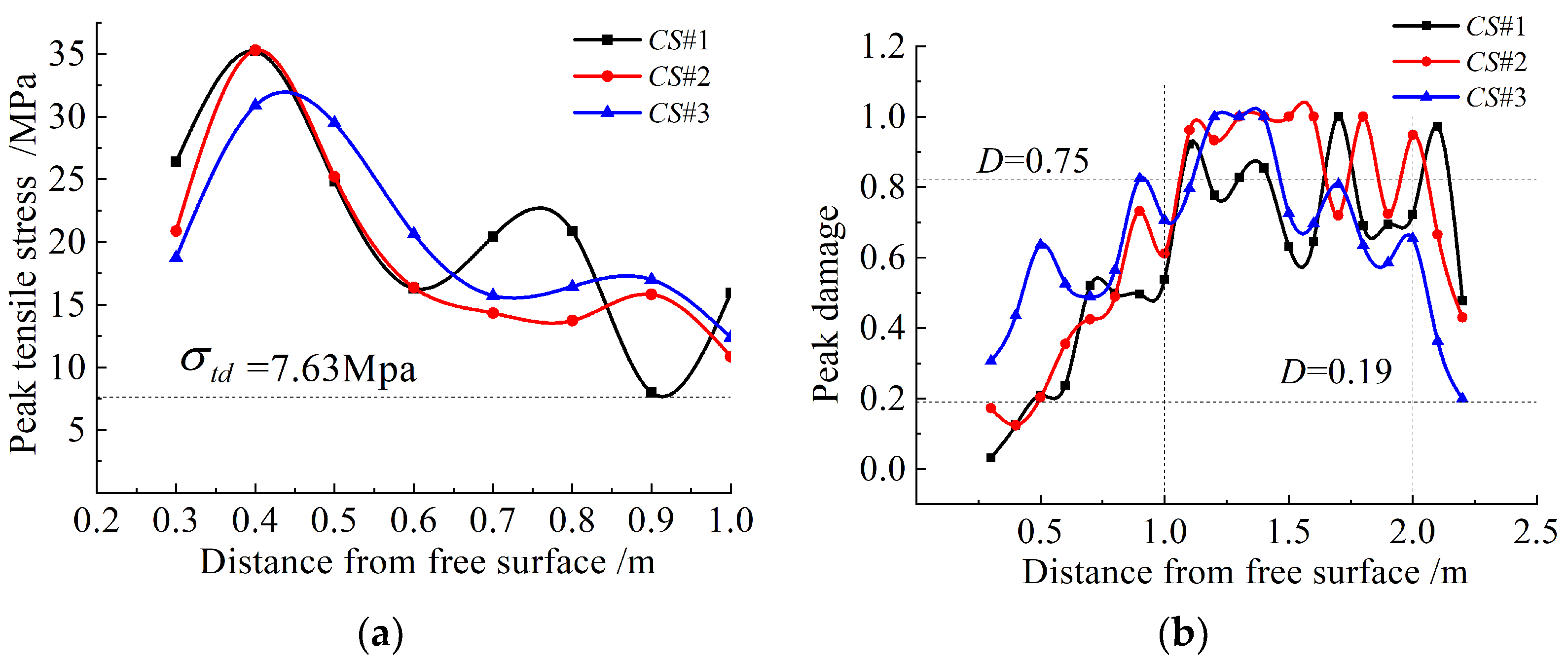
2.2.1. Dynamic Tensile Strength Threshold
2.2.2. Damage Factor Threshold
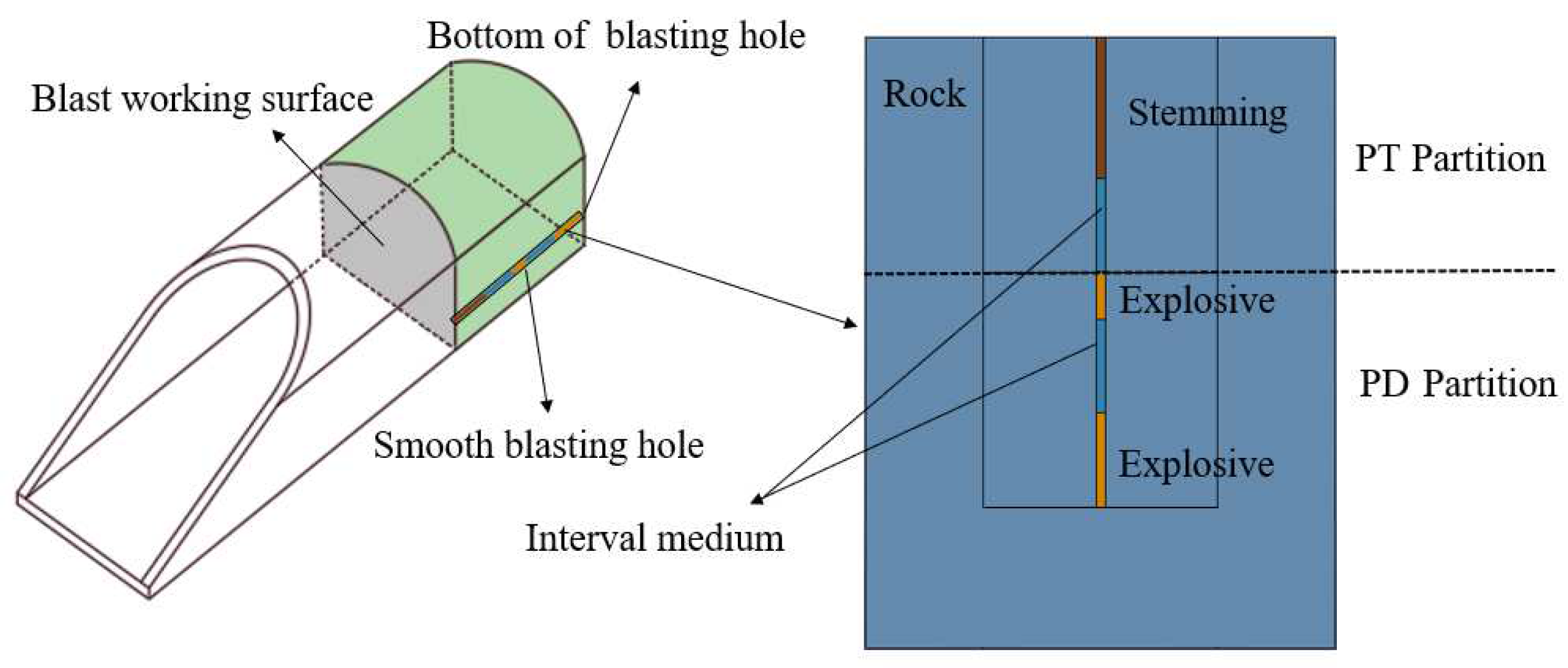
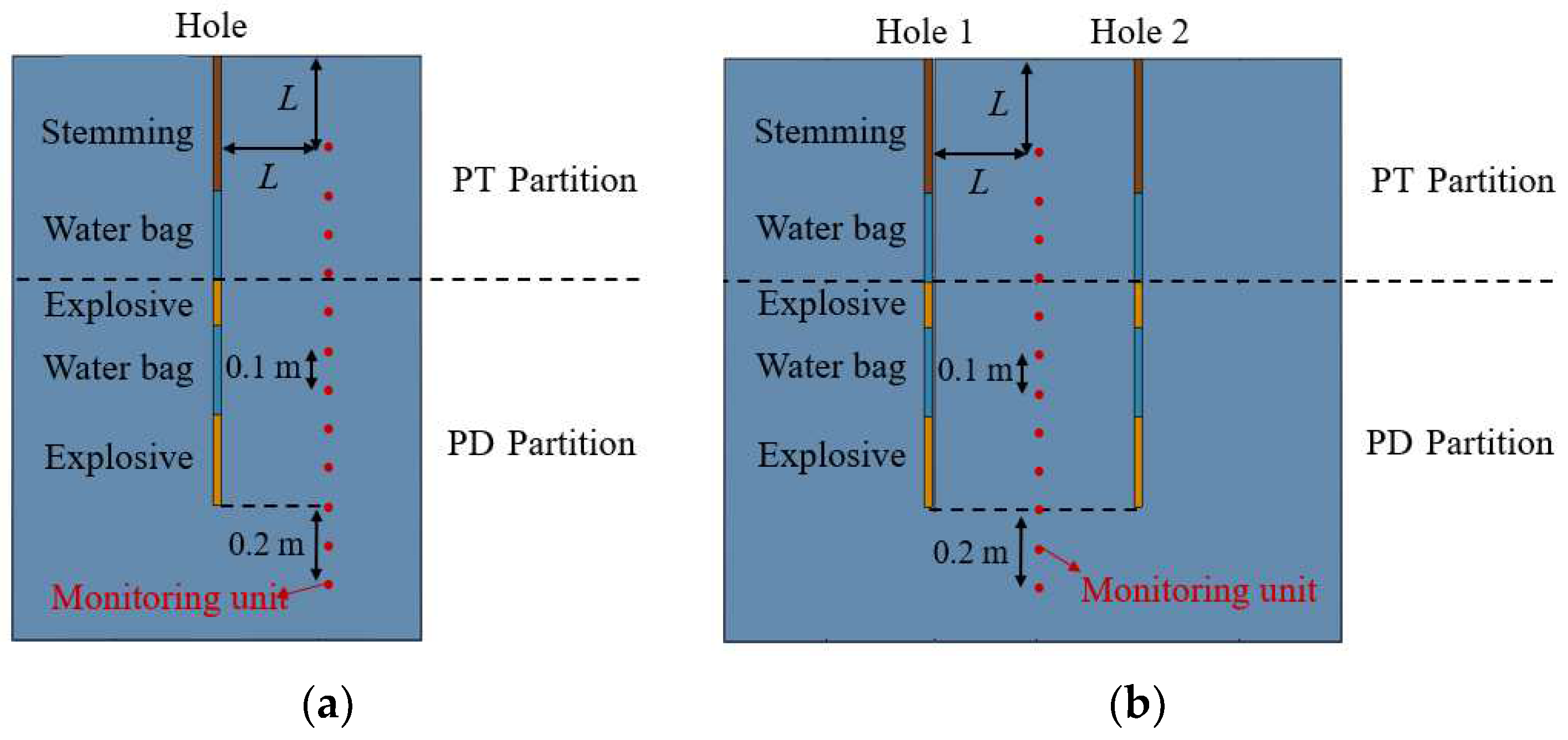
2.3. Principles for Selecting Monitoring Locations
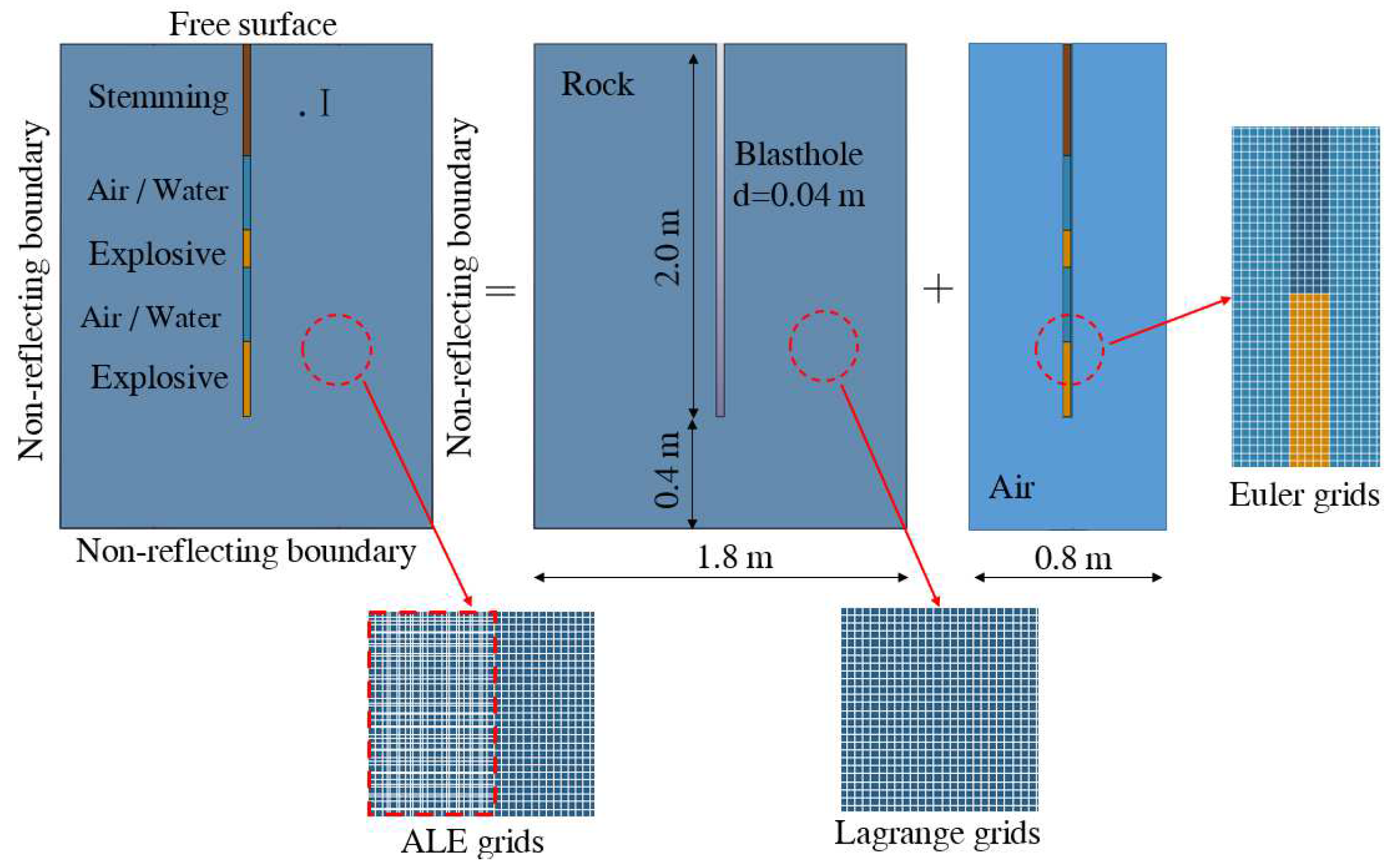
3. Numerical Models and Parameter Selection
3.1. Numerical Model
3.2. Sandstone Material Parameters
3.3. Material Parameters of ALE
3.3.1. Explosives Material
3.3.2. Water and Air Material
3.3.3. Stemming Material
4. Results and Discussion
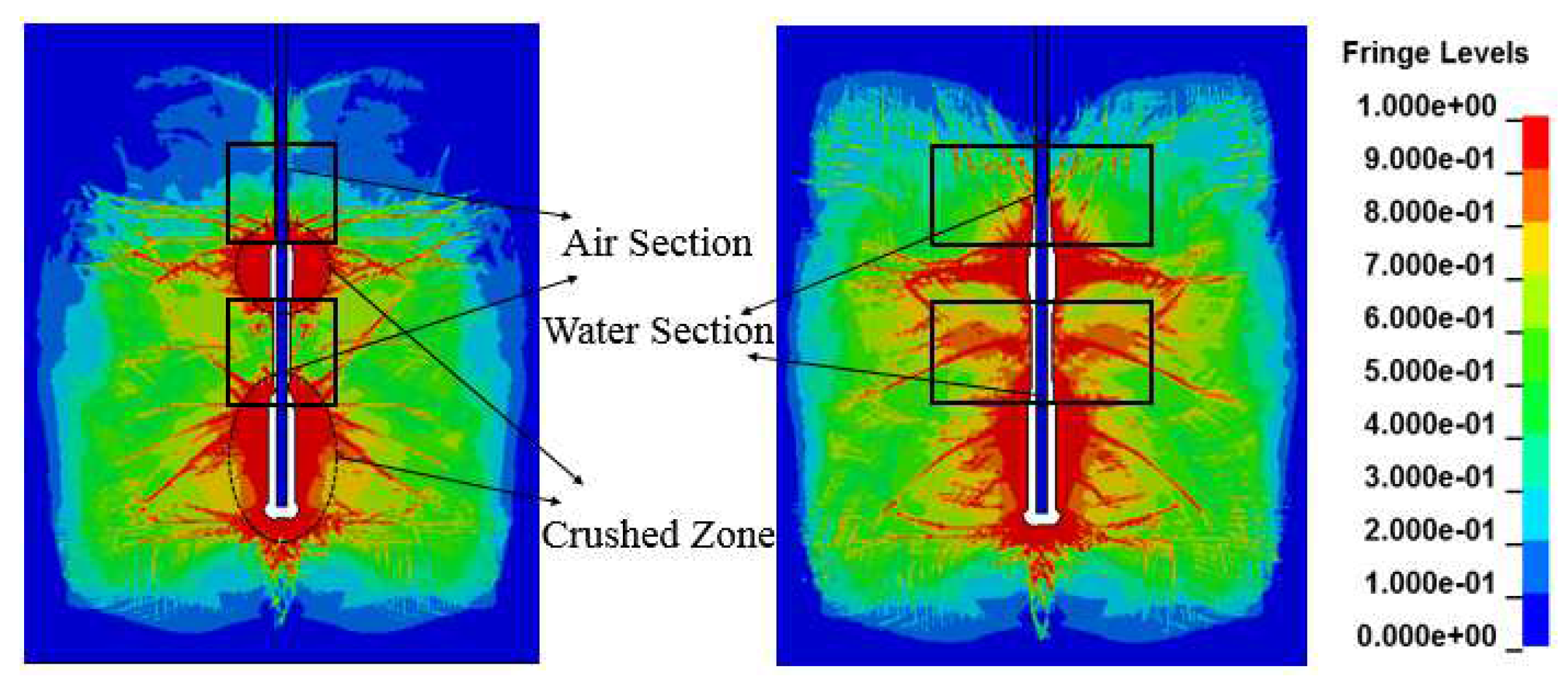
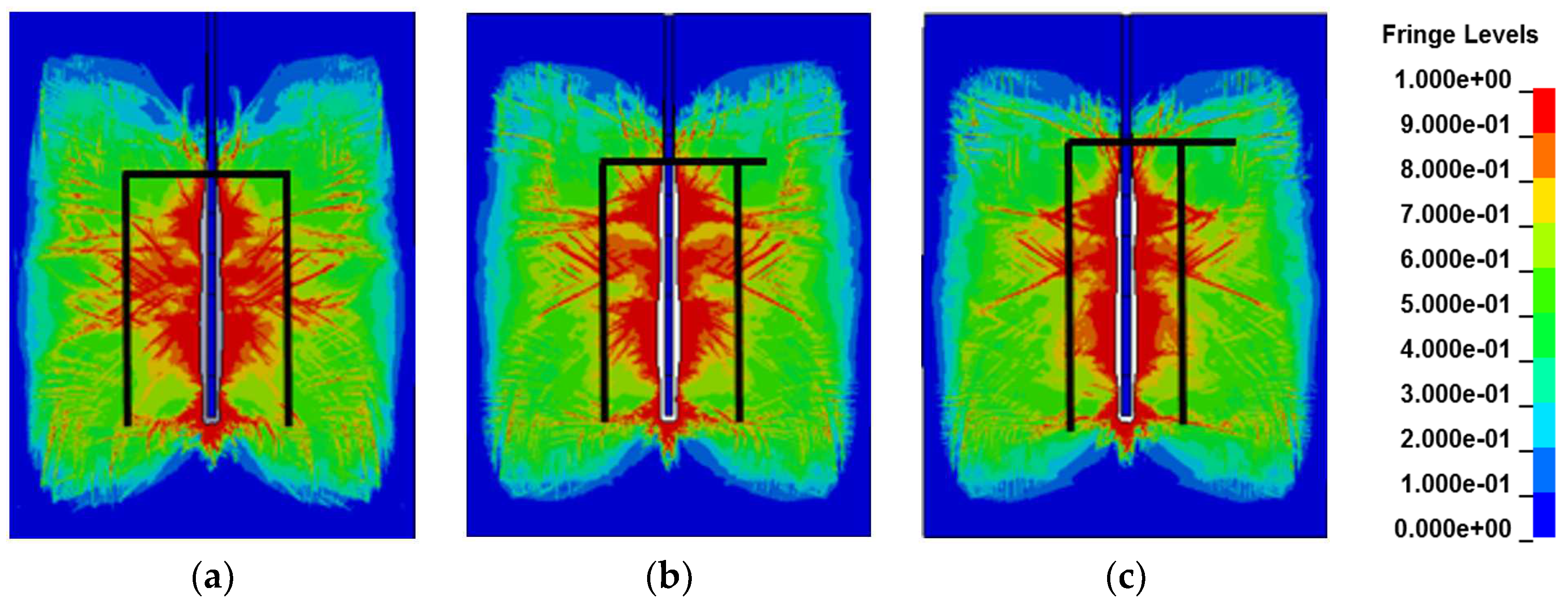
4.1. Rock-Damaging Effects of Different Interval Medium
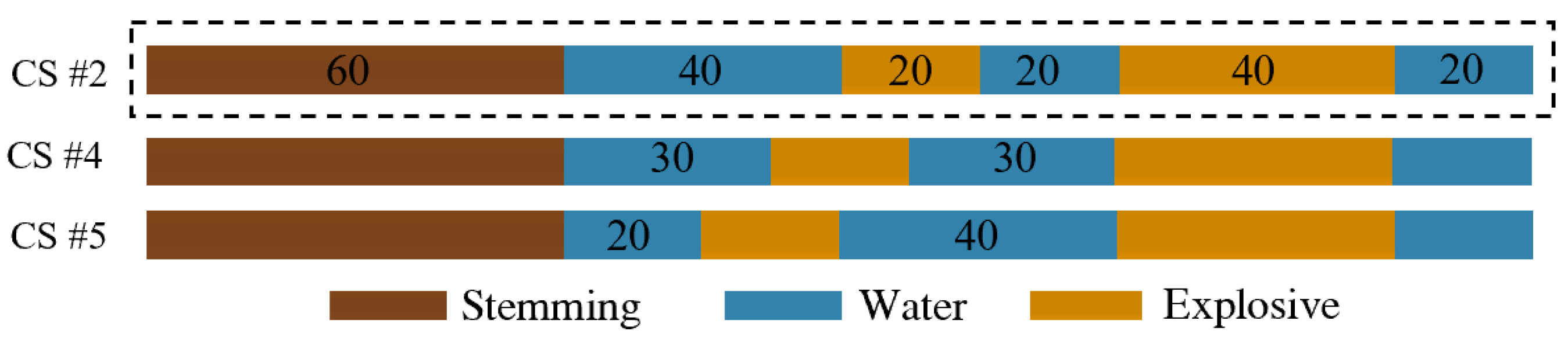
4.2. Damage Effects of Rocks under Different Water Interval Charge Configurations
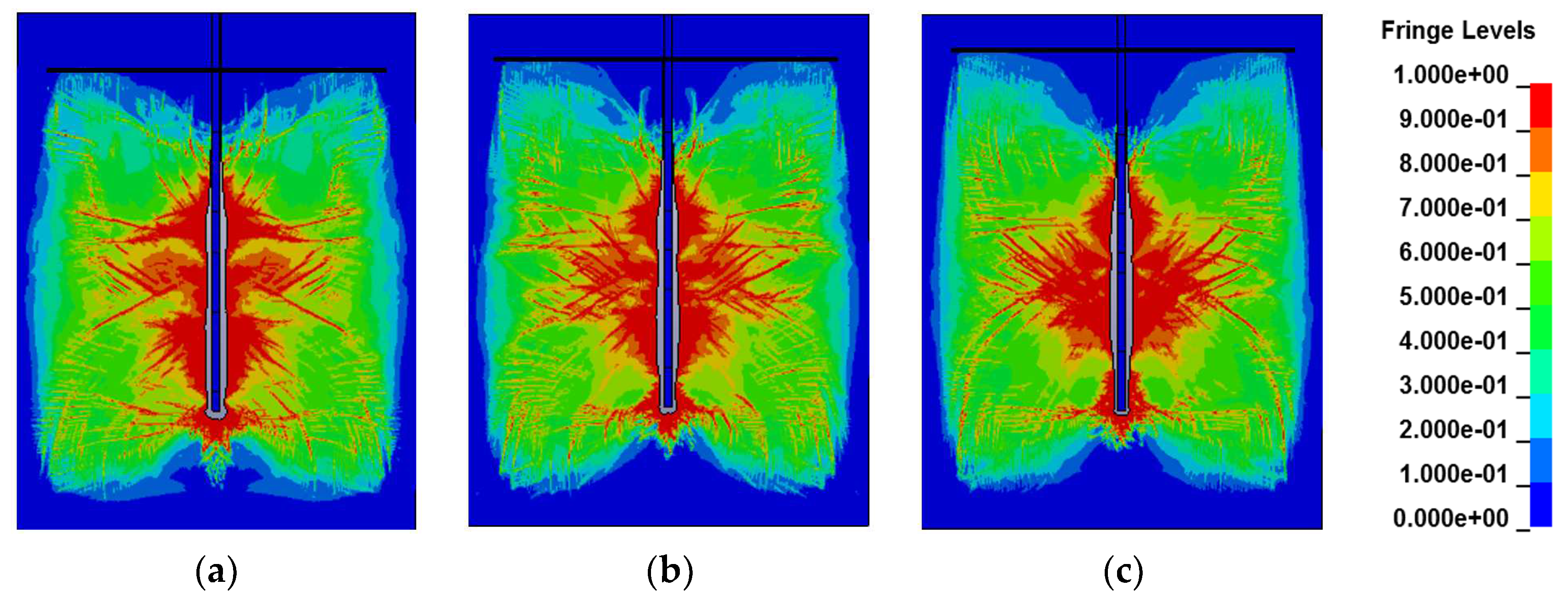
4.2.1. Length of Water Interval at the Bottom of the Blast Hole
4.2.2. Length of Water Interval at the Top of the Blast Hole
4.3. Damage Effect of Rock under Different Eplosive Quantities
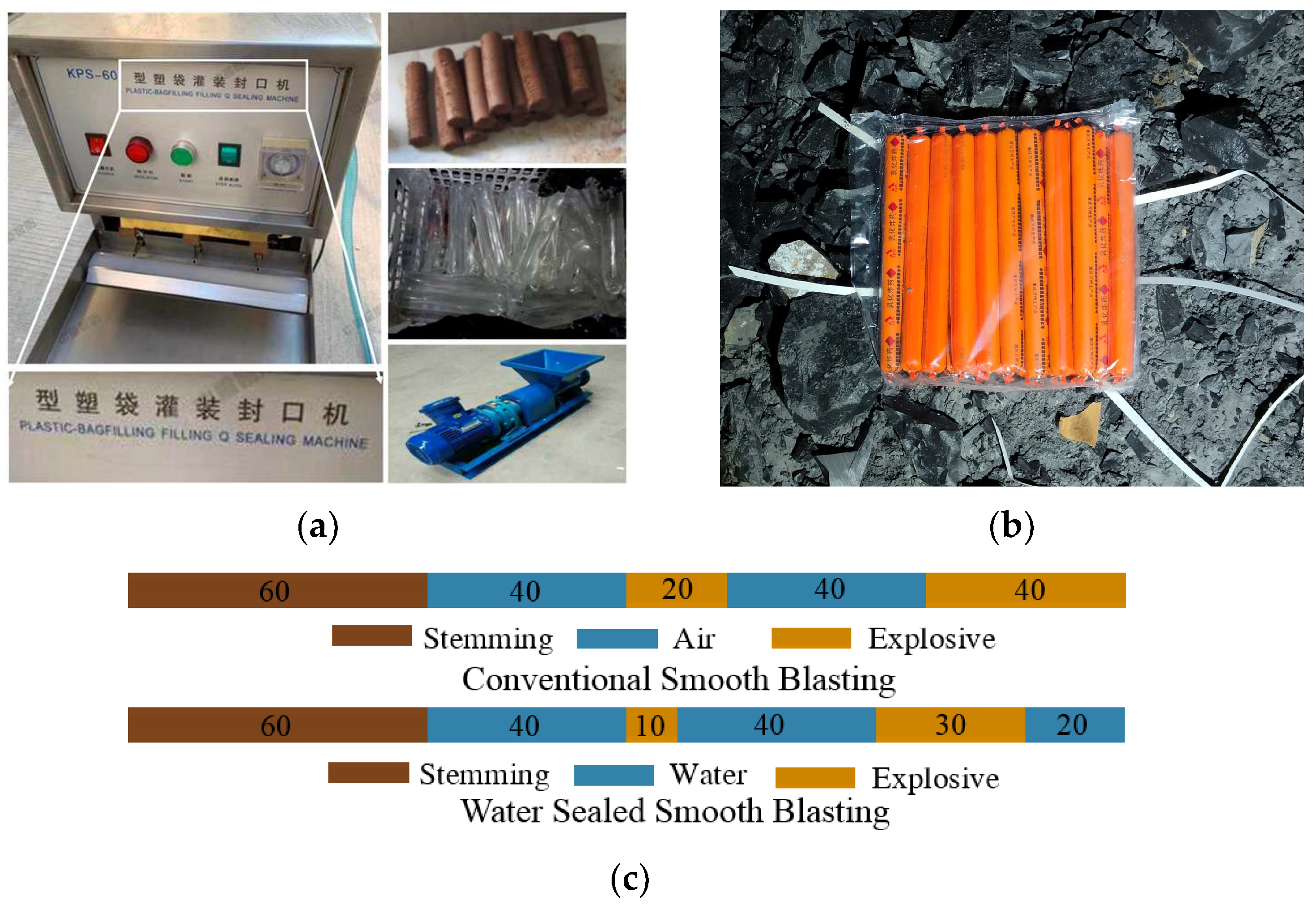
4.4. Field Test
5. Conclusions
- (1)
- A method for evaluating the damaging effect of rock has been established based on the classical strength theory and damage fracture theory. The method divides the damaged area into two parts, takes dynamic tensile stress and damage variables as the key indexes, evaluates the numerical simulation results, and selects the preferred loading structure. Field tests verified the feasibility and accuracy of the method.
- (2)
- In the water interval charge structure, when the length of the water medium at the bottom of the hole is 20 cm, the damage range of the retained rock can be controlled while ensuring rock fragmentation. The length of the water medium at the orifice and in the middle of the hole is greater than 30 cm, which will affect the superimposed effect of the blasting stress wave, resulting in underdigging.
- (3)
- According to the evaluation results of the preferred charge structure, the length ratio of the upper and lower sections of explosives can reach 1:3, while the length ratio of the water medium is 2:2:1. In soft rock tunneling projects, the preferred charge structure reduces the amount of drugs by about 26% compared with the air-spaced charge structure, and the rate of half-hole traces is increased to 75%, which reduces the phenomenon of over-undercutting and the work of the secondary blasting, and significantly improves the operational efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| σvm | Mises effective stress |
| σcd | Dynamic compressive strength |
| σtd | Dynamic tensile strength |
| σ1/σ2/σ3 | Three principal stresses |
| ∆εp | Equivalent plastic strain increment |
| ∆μp | Equivalent plastic volume strain increment |
| εpf | Equivalent plastic strain |
| μpf | Equivalent plastic volume strain |
| D1, D2 | Material damage parameters |
| p* | Normalized pressure |
| T* | Maximum characteristic tensile stress |
| EFmin | Minimum plastic strain at which material breaks |
| ∆εij | Strain increment |
| σij’ | Stress bias |
| ∆λ | Instantaneous constant |
| ∆ε1/∆ε2/∆ε3 | Plastic strain increment under principal stress |
| Dc | Compressive damage variable |
| Dt | Tensile damage variable |
| σt | Tensile stress |
| σtd | Dynamic tensile strength |
| σst | Uniaxial static tensile strength |
| Loading rate | |
| E0 | Original elastic modulus |
| E | Post-blast elastic modulus |
| v | Post-blast rock longitudinal wave velocity |
| η | Rock wave velocity reduction rate |
| D | Damage variable |
| Dmax | Peak damage variable |
| σtmax | Peak tensile stress |
References
- Mandal, S.K.; Singh, M.M.; Dasgupta, S. Theoretical concept to understand plan and design smooth blasting pattern. Geotech. Geol. Eng. 2008, 26, 399–416. [Google Scholar] [CrossRef]
- Park, D.; Jeon, S. Reduction of blast-induced vibration in the direction of tunneling using an air-deck at the bottom of a blasthole. Int. J. Rock Mech. Min. Sci. 2010, 47, 752–761. [Google Scholar] [CrossRef]
- Fourney, W.; Bihr, S.; Leiste, U. Borehole pressures in an air decked situation. Fragblast 2006, 10, 47–60. [Google Scholar] [CrossRef]
- Jang, H.; Handel, D.; Ko, Y.; Yang, H.; Miedecke, J. Effects of water deck on rock blasting performance. Int. J. Rock Mech. Min. Sci. 2018, 112, 77–83. [Google Scholar] [CrossRef]
- Huang, B.; Li, P. Experimental investigation on the basic law of the fracture spatial morphology for water pressure blasting in a drillhole under true triaxial stress. Rock Mech. Rock Eng. 2015, 48, 1699–1709. [Google Scholar] [CrossRef]
- Kutter, H.; Fairhurst, C. On the fracture process in blasting. Int. J. Rock Mech. Min. Sci. 1971, 8, 181–202. [Google Scholar] [CrossRef]
- Oh, T.; Cho, G.; Ji, I. Effects of free surface using waterjet cutting for rock blasting excavation. J. Korean Tunn. Undergr. Space Assoc. 2013, 15, 49–57. [Google Scholar] [CrossRef]
- Yan, S.; Xu, Y. Numerical simulation of water-coupled charge rock blasting mechanism. Chin. J. Undergr. Space Eng. 2005, 1, 921–924+943. [Google Scholar]
- Zong, Q.; Meng, D. Blasting technieal optimization of rock tunnel digging in stratum of kaolin among coal. Rock Soil Mech. 2004, 25, 984–987. [Google Scholar]
- Feng, H.; Zhang, X.; Wang, L.; Huang, Q.; Ou, X.; Zhang, C.; Zhou, X. Calculation and analysis for water-sealed charge structure blasting vibration in tunnel drilling and blasting construction. J. Vib. Shock 2020, 39, 93–100+124. [Google Scholar]
- Liu, J.; Gao, W.; Zhang, S.; Xu, H. Numerical Analysis and Application of Uncoupled Coefficient of Water Sealed Blasting on Blasting Effect. IOP Conf. Ser. Earth Environ. Sci. 2021, 719, 032035. [Google Scholar] [CrossRef]
- Ishchenko, O.; Konoval, V.; Ishchenko, K. Physical and simulation modelling of solid media fracturing by means of explosive charges of different cross-sectional shapes. Min. Miner. Deposits 2022, 16, 122–131. [Google Scholar] [CrossRef]
- Li, S.; Ling, T.; Liu, D.; Liang, S.; Zhang, R.; Huang, B.; Liu, K. Determination of rock mass parameters for the RHT model based on the Hoek–Brown Criterion. Rock Mech. Rock Eng. 2023, 56, 2861–2877. [Google Scholar] [CrossRef]
- Donzé, F.; Bouchez, J.; Magnier, S. Modeling fractures in rock blasting. Int. J. Rock Mech. Min. Sci. 1997, 34, 1153–1163. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, C.; Remennikov, A.; Wu, T.; Xia, Y. Dynamic response and safety control of civil Air defense tunnel under excavation blasting of subway tunnel. Tunn. Undergr. Space Technol. 2021, 112, 103879. [Google Scholar] [CrossRef]
- Choo, J.; Sun, Y.; Fei, F. Size effects on the strength and cracking behavior of flawed rocks under uniaxial compression: From laboratory scale to field scale. Acta Geotech. 2023, 18, 3451–3468. [Google Scholar] [CrossRef]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown failure criterion—2002 edition. In Proceedings of the Fifth North American Rock Mechanics Symposium, Toronto, ON, Canada, 7–10 July 2002; Volume 1, pp. 267–273. [Google Scholar]
- Costamagna, E.; Oggeri, C.; Segarra, P.; Castedo, R.; Navarro, J. Assessment of contour profile quality in d&b tunnelling. Tunn. Undergr. Space Technol. 2018, 75, 67–80. [Google Scholar]
- Holmquist, T.; Johnson, G.; Cook, W. A Computational Constitutive Model for Concrete Subjected to Large Strains, High Strain Rates and High Pressures. In Proceedings of the Fourteenth International Symposium on Ballistics, Quebec City, QC, Canada, 26–29 September 1993; Volume 2, pp. 591–600. [Google Scholar]
- Polanco-Loria, M.; Hopperstad, O.; BØ, T.; Berstad, T. Numerical predictions of ballistic limits for concrete slabs using a modified version of the hjc concrete model. Int. J. Impact Eng. 2008, 35, 290–303. [Google Scholar] [CrossRef]
- Yang, X.; Wang, S. Meso-mechanism of damage and fracture on rock blasting. J. Vib. Shock 2000, 20, 247–252. [Google Scholar]
- Liu, K.; Wu, C.; Li, X.; Li, Q.; Fang, J.; Liu, J. A modified HJC model for improved dynamic response of brittle materials under blasting loads. Comput. Geotech. 2020, 123, 103584. [Google Scholar] [CrossRef]
- Grady, D.E.; Kipp, M.E. Continuum modeling of explosive fracture in Oil shale. Int. J. Rock Mech. Min. Sci. 1980, 17, 147–157. [Google Scholar] [CrossRef]
- Taylor, L.M.; Chen, E.P.; Kuszmaul, J.S. Microcrack-induced damage accumulation in brittle rock under dynamic loading. Comput. Methods Appl. Mech. Eng. 1986, 55, 301–320. [Google Scholar] [CrossRef]
- Kuszmaul, J.S. A new constitutive model for fragmentation of rock under dynamic loading. In Proceedings of the 2nd International Symposium on Rock Fragmentation by Blasting, Keystone, CO, USA, 23 August 1987. [Google Scholar]
- Liu, L.; Katsabanis, P.D. Development of a continuum damage model for blasting analysis. Int. J. Rock Mech. Min. Sci. 1997, 34, 217–231. [Google Scholar] [CrossRef]
- Thorne, B.J. A Damage Model for Rock Fragmentation and Comparison of Calculations with Blasting Experiments in Granite; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 1990; pp. 1–52. [Google Scholar]
- Yang, R.; Bawden, W.; Katsabanis, P. A new constitutive model for blast damage. Int. J. Rock Mech. Min. Sci. 1996, 33, 245–254. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J. An improved computational constitutive model for brittle materials. AIP Conf. Proc. 1994, 309, 981–984. [Google Scholar]
- Kong, X.; Fang, Q.; Li, Q.; Wu, H.; Crawford, J.E. Modified K&C model for cratering and scabbing of concrete slabs under projectile impact. Int. J. Impact Eng. 2017, 108, 217–228. [Google Scholar]
- Xia, X. Study of Damage Characteristics and Safety Threshold of Rock Vibration by Blast. Ph.D. Thesis, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, China, 2006. [Google Scholar]
- Liu, L.; Lu, W.; Chen, M.; Yan, P.; Wang, G. Statistic damage threshold of critical broken rock mass under blasting load. Chin. J. Rock Mech. Eng. 2016, 35, 1133–1140. [Google Scholar]
- Chafi, M.; Karami, G.; Ziejewski, M. Numerical analysis of blast-induced wave propagation using FSI and ALE multi-material formulations. Int. J. Impact Eng. 2009, 36, 1269–1275. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R. A computational constitutive model for glass subjected to large strains, high strain rates and high pressures. J. Appl. Mech. 2011, 78, 051113. [Google Scholar] [CrossRef]
- Ling, T.; Wu, S.; Liu, D.; Liang, S.; Li, C.; Ma, J. Determination of Holmquist-Johnson-Cook model parameters for sandstone. J. China Coal Soc. 2018, 43, 2211–2216. [Google Scholar]
- Kury, J.; Honig, H.; Lee, E.; Mcdonnel, J.; Wilkins, M. Metal acceleration by chemical explosives. In Proceedings of the Fourth Symposium (International) on Detonation, White Oak, MD, USA, 12–15 October 1965. [Google Scholar]
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual; LSTC: Livermore, CA, USA, 2020. [Google Scholar]
- Hagan, T.N. Rock breakage by explosives. In Proceedings of the 6th Colloquium, Stockholm, Sweden, 22–26 August 1977. [Google Scholar]
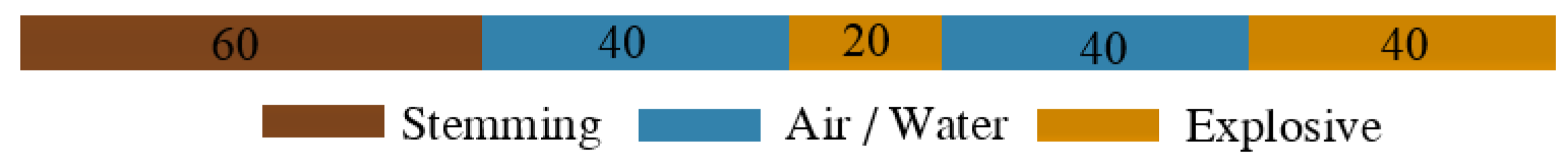






| Parameter | Unit | Value |
|---|---|---|
| Density, ρ | kg/m3 | 2010 |
| Shear modulus, G | GPa | 5.6 |
| Normalized cohesive strength, A | 0.32 | |
| Normalized pressure hardening, B | 1.76 | |
| Strain rate coefficient, C | 0.0127 | |
| Pressure hardening exponent, N | 0.79 | |
| Maximum tensile hydrostatic pressure, T | MPa | 7.63 |
| Quasi-static uniaxial compressive strength, fc | MPa | 33.7 |
| Quasi-static threshold strain rate, EPS0 | s−1 | 1 |
| Amount of plastic strain before fracture, EFMIN | 0.01 | |
| Normalized maximum strength, SFMAX | 7 | |
| Crushing pressure, Pcrush | MPa | 25.38 |
| Crushing volumetric strain, µcrush | 0.00167 | |
| Locking pressure, Plock | GPa | 0.8 |
| Locking volumetric strain, µlock | 0.08 | |
| Damage constant, D1 | 0.04 | |
| Damage constant, D2 | 1 | |
| Pressure constant, K1 | GPa | 81 |
| Pressure constant, K2 | GPa | −91 |
| Pressure constant, K3 | GPa | 89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Gong, M.; Wu, H.; Wu, X.; Liu, X. Optimization Study of Water Interval Charge Structure Based on the Evaluation of Rock Damage Effect in Smooth Blasting. Appl. Sci. 2024, 14, 2868. https://doi.org/10.3390/app14072868
Wang S, Gong M, Wu H, Wu X, Liu X. Optimization Study of Water Interval Charge Structure Based on the Evaluation of Rock Damage Effect in Smooth Blasting. Applied Sciences. 2024; 14(7):2868. https://doi.org/10.3390/app14072868
Chicago/Turabian StyleWang, Sijie, Min Gong, Haojun Wu, Xiaodong Wu, and Xiangyu Liu. 2024. "Optimization Study of Water Interval Charge Structure Based on the Evaluation of Rock Damage Effect in Smooth Blasting" Applied Sciences 14, no. 7: 2868. https://doi.org/10.3390/app14072868
APA StyleWang, S., Gong, M., Wu, H., Wu, X., & Liu, X. (2024). Optimization Study of Water Interval Charge Structure Based on the Evaluation of Rock Damage Effect in Smooth Blasting. Applied Sciences, 14(7), 2868. https://doi.org/10.3390/app14072868






