Field and Numerical Investigation of Taihu Resort Cut Slope Failure in Suzhou, China

Abstract

This study aims to determine the cause of a landslide located at Taihu Resort in Suzhou, Jiangsu Province, China. Field monitoring has been conducted, including two-dimensional finite element method (FEM) numerical analyses to examine slope stability under different working conditions. The monitoring data indicated that the slope deformation was triggered in two phases: at a certain period when the slope was cut and moderate rainfall occurred in November; and afterward, when a continuous heavy rainfall intensity hit during the monsoon rainfall, which accelerated sliding of the slope. Numerical simulations show that stress and maximum displacement distributions formed and redistributed during the excavation process, where the shear strain occurred mainly in the front layer of soil. Additionally, the factor of safety of the slope decreases gradually with the increase in the excavation rate. During 15 days of continuous rainfall infiltration, the slope under heavy rainfall indicates a minimum factor of safety (FoS). Specifically, the slope excavation followed by heavy rainfall intensities contributed significantly to the landslide.

1. Introduction

Landslides triggered by human excavation or rainfall are among the most common geological disasters and are the core issue of slope engineering research around the world. During the period 2004–2016, the total cases of landslide events show that there were 4862 landslides around the world [1,2,3], of which 409 occurred only during the monsoon rainfall. In China, from 1994 to 2018, 126 landslides were recorded after construction under rainfall, which represents 74.1% of all failure cases, and 22.4% of failures after 8 days of heavy rainfall intensity [4]. These landslide disasters caused great loss of life and property. Many research investigations have discovered that failure on slopes is mainly caused by excavations [5,6,7,8,9], rainfall infiltration [10,11,12,13], or by human excavations accompanied by rainfall [14,15,16]. To avoid costly losses from sudden landslides, it is of great significance to conduct a comprehensive stability analysis of slopes under different scenarios. Methods such as finite elements have become a widely applied research topic in the field of geotechnical engineering for the estimation of slope stability. Further, the safety factor is considered the key indicator of slope stability. Over the previous decades, the strength reduction technique in finite element slope stability analysis has been employed by many authors, due to its efficiency in estimating slope stability [17,18,19,20,21,22,23,24,25]. At present, the technique has been developed to analyze the stability of complex geometries such as excavation slope models [26,27,28,29,30]. This method provides unique safety factor results by using the Mohr–Coulomb (MC) failure criterion [31,32]. Recently, the authors have examined the influence of rainfall intensities on slope safety factors [33,34,35,36].

Many factors lead to slope instability. In excavation slope engineering, the failure of cut slopes may be related to factors such as inadequate drainage, erosion control measures, slope angle, irregular monitoring of the cut slope, and geological setting, which is an important component of the cut slope’s stability. A lack of geological investigation prior to design may increase the possibility of failure on the cut slope [37]. Many scholars have investigated excavation-induced landslide cases in China [38,39]. They found that the failure was caused by the excavation of the slope toe with an inadequate slope geological investigation. Chen J. et al. (2022) [40] found that the excavation of the slope in Sichuan Province was performed without a proper understanding of the geological condition of the slope. W.Y. Xu et al. (2013) [41] analyzed a case study of a slope failure induced by excavation near Xiluodu Dam. According to the results, the damage was primarily caused by excavation that activated the ancient slip zone, thereby allowing external factors to impact the slope and cause a shallow slide. Therefore, as a precaution against future failures of cut slopes, it is usually necessary to study the cut slope failure after a landslide, obtain an adequate interpretation of the causes of collapses, and conduct a series of comprehensive landslide examinations [42,43,44,45,46]. As a result, the above-mentioned authors adopted different approaches and instruments to monitor landslide conditions. These studies provide a substantial contribution to the investigation of the complex structure of landslide areas. Hence, such investigations provide ideal guidance for land-slide emergencies. The recent research on the landslide mechanism caused by human excavations has been advanced by introducing different work conditions to reveal the instability mechanism after and before excavation, which provides an early warning measure for slopes exposed to cutting. For example, Xie et al. (2021) [47] and Yuan, L. et al. (2022) [48] analyzed a different landslide case in China. Based on the field investigation analysis, landslide activation was highly correlated with the reduction in safety factors caused by rainfall. Wang et al. (2013) [49] and Tao et al. (2023) [50] found that excavation followed by rainfall was a direct cause of collapses; therefore, excavation was the main exciting reason for landslides and a major trigger factor for the instability of slope problems.

A major cause of slope instability is rainfall infiltration quantity and duration, which can lead to a series of influences such as soil strength reductions, matric suction, and an increase in pore pressure on soil surfaces. Moreover, the rainfall amount, duration, intensity, and terrain slope have serious impacts on slope stability [24], making the slope more prone to failure; therefore, many scholars have carried out research on this problem, focusing on the stability of slope under different rainfall patterns [51,52,53] and different rainfall durations [54,55,56,57]. The scholars found a large proportion of landslides are caused by high pore-water pressure occurring under heavy rainfall or lengthy periods of moderately intense rainfall. Dhanai, P. et al. (2022) and X. Gu, L. Wang, Q. Ou et al. (2023) [58,59] found that an increase in rainfall intensity is a significant impact factor on the development of soil slope damage, which reduces the matric suction, while the increase in water saturation in the slope has a significant effect on the factor of safety (FoS). Q. Li et al. (2020) [60] studied slope instability induced during the construction of the expressway in Guangdong Province under excavation and rainfall conditions. Their results revealed the main cause was the continued rainfall infiltration, which significantly increased the pore pressure of the slope and triggered the collapse.

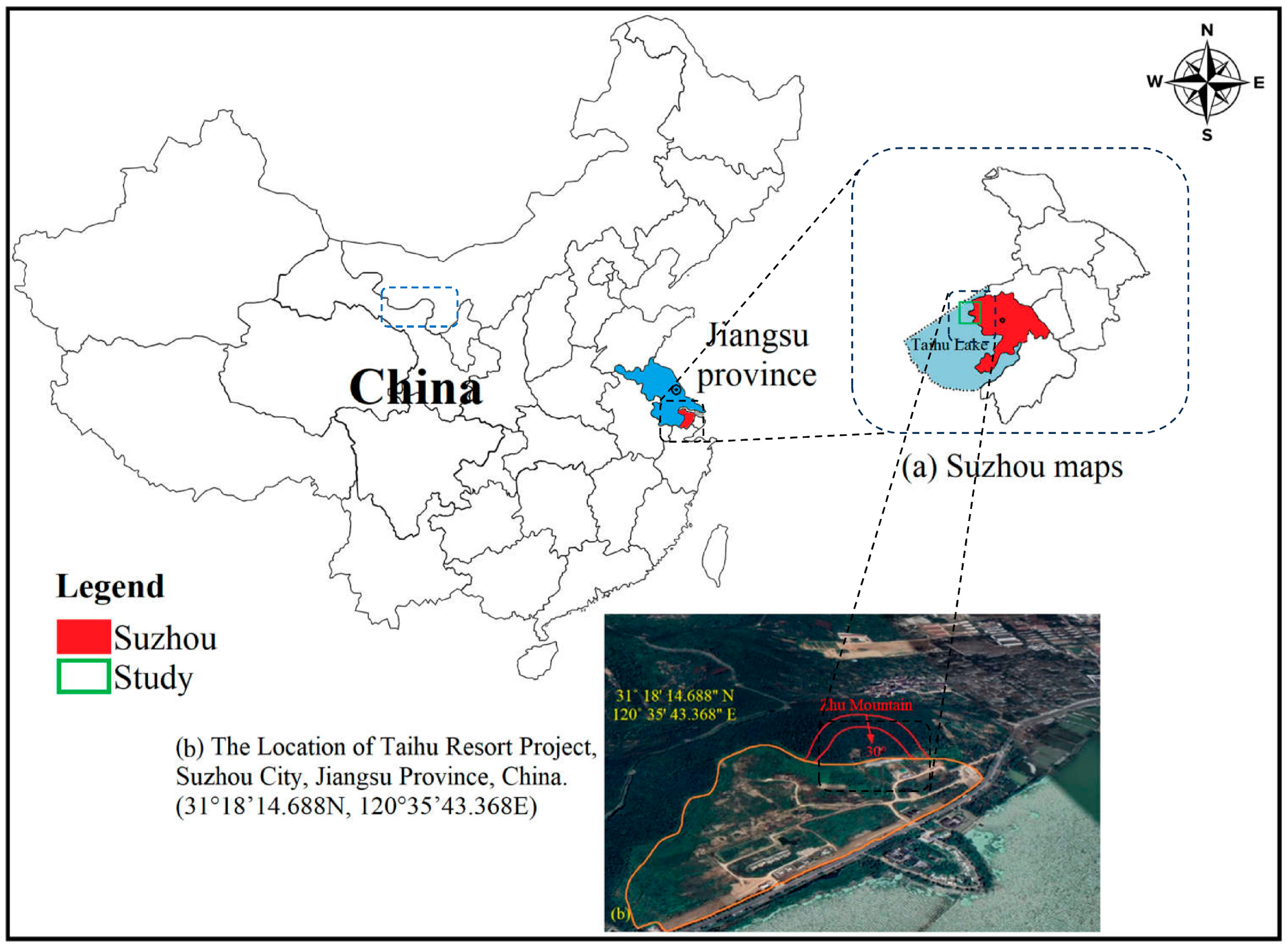
These studies have provided varying advice and guidance for the ideal excavation of slopes to a certain extent, including some investigations of slope stability and rainfall-induced failure. However, less attention has been paid to systematically studying the slope stability of gradually excavating slopes based on different parameters and working conditions. In this paper, a case study investigation of the Taihu cut slope along the Taihu Lake in Suzhou, Jiangsu Province, China, is taken as the engineering object (Figure 1). Therefore, a comprehensive field investigation of the slope has been carried out first. Following that, two-dimensional numerical modeling was developed based on the finite element method using MIDAS GTS V1.1 software to estimate slope stability influenced by excavation and rainfall scenarios using strength reduction FEM. According to the field investigation and numerical analysis of the slope failure mechanism, this study provides the strength reduction mechanism of slopes, thereby contributing to the literature on the effect of excavating slopes and soil-water interaction on slope stability.

2. Project Overview of the Taihu Resort Landslide

The slope project is located in Taihu Resort along Taihu Lake in western Suzhou, Jiangsu Province, China. The slope area location coordinates are 31°18′14.688 N and 120°35′43.368 E. The northwest corner of the site is about 1800 m from the main peak of Tan Mountain, with a height of 253 m. The northeast corner of the site is about 2400 m from the main peak of Xuanmu Mountain, with a height of 231 m (Figure 2). According to a field survey, the soil and rock masses in the Taihu area are composed mainly of mixed limestone and quartz sandstone. The slope area belongs to the monsoon ocean climate zone; the annual rainfall is 1076 mm; and the precipitation period is concentrated from 26 February to 10 September. The precipitation in June and July is estimated to account for 48% of the annual rainfall [China Meteorological Data Sharing Service System]. Furthermore, the increase in the lake water level has a big impact on the slope during monsoon rainfall, and there are no springs or valleys that cut the slope or at the foot. In March 2012, the construction of Taihu Resort (Zhu Mountain) began, and the slope was excavated on the east side of the project with a width of 34 m and a length of 55 m according to the design requirements. In all, 1690 m² of slope excavation surface area was required. 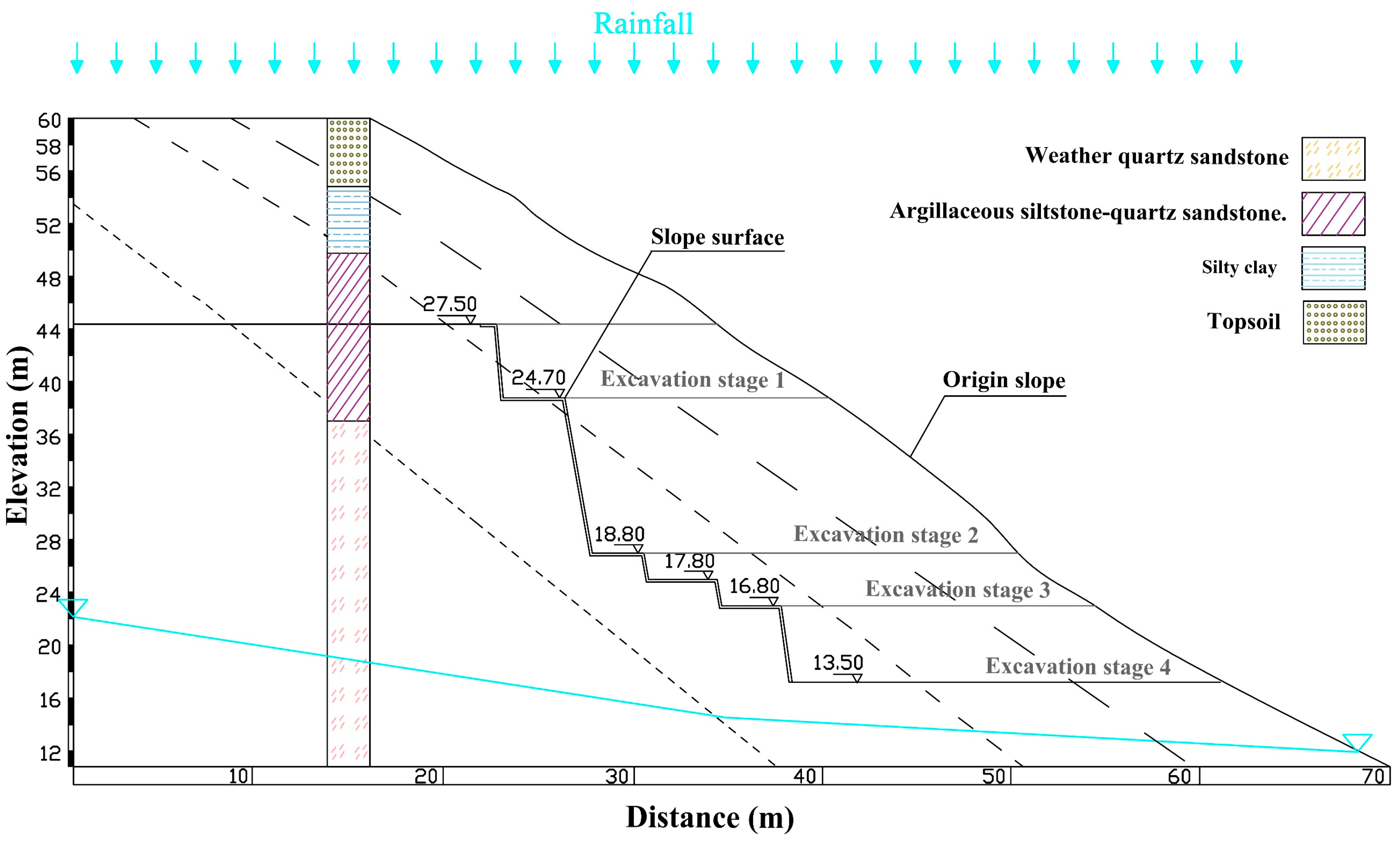The geology and topographical map of the study area of the Taihu slope are shown in Figure 2 and Figure S1. The slope design of the top elevation is approximately 13.93~15.11 m (Figure 3), and the slope direction is east–west and inclined to the south.

The topography of the southern Taihu slope at the middle part is inclined about 10°~20°, while the slope foot has a gentler angle of about 5°~10°, and the project terrain is relatively flat. Photos of the original and the cut slope failure are shown in Figure 3. According to drilling holes and a field geological survey, the stratigraphic structure of the slope body is relatively simple. The strata within the depth range revealed by drilling at the site are divided into four engineering geological strata as follows: The top and second soil slope layers are mainly composed of cohesive soil and silty clay, respectively, with medium dry strength and medium compressibility (gray-yellow, gray-white, plastic). The third layer is composed of medium-thick layered argillaceous siltstone intercalated with argillaceous quartz sandstone and silty mudstone (brown-red, gray-yellow, and gray-white), which is mainly composed of cohesive soil and gravel. The base layer of the slope is composed of strongly weathered quartz sandstone (brown-red, gray-yellow, fine-grained structure, and calcareous cementation). The slope location is in a low, mountainous, and hilly area. Figure 3 shows the scheme of the geological model and the revised design (excavation scheme) of the Taihu slope.

3. Study Landslide Area

In the previous section, the geotechnical profile of the Taihu slope of Section 6 (S6) before and after excavation was presented in Figure 3. Hence, after the excavation process, the base layer of the slope consists of strongly weathered quartz sandstone, while the overtop layer consists of soil interbedded with clayey silt layers. After a detailed investigation of the Taihu landslide and a comprehensive study of the monitoring data to understand the failure mechanism, the final damage occurred mainly in the silty clay layer of the slope, which was caused during the monsoon rainfall in 2013. Further, the failure of the slope is divided into two phases. The first collapse phase was caused by local slumping at the toe of Section 6 (S6) of the slope in November 2012, with cracks occurring along the slope body. The second overall failure phase of the slope was caused during the monsoon rainfall in June and July 2013, which led to the total failure, including the shotcrete cover on the slope at Section 6 (S6).

Figure 4 illustrates the landslide in Taihu slope photos and a cross-section at the first collapse phase. According to the field investigation, two months after completing the excavations and treatment of the slope, the first collapse occurred over the toe on the middle portion of the slope (S6) after moderate rainfall (20 mm/day ≤ rainfall ≤ 70). It should be noted that heavy rainfall was recorded with a precipitation intercity of 130.9 mm in three days at the end of November 2012, and the groundwater table rose near the slope toe, which caused swelling in the slope body and cracks in the shotcrete (Figure 4a). The tension cracks occurred along the slope body, 7–15 m long, with openings of 10–15 mm at the middle portion of the slope surface, and continued to propagate. Accordingly, a collapse at the toe of the slope was triggered. As shown in a close-up view (Figure 4b,c), it can be seen that the first slip surface failure mainly occurred within the argillaceous siltstone layer, including a critical crack along the slope toe.

Before the slope failure occurred, there were many intermittent tension cracks in the slope surface. After the constant rain of 20 mm/day ≤ rainfall ≤ 180 mm/day during the monsoon rainfall from March 2013 to July 2013, with maximum daily precipitation occurring in May, the groundwater table level rose significantly. A seepage occurred along the whole slope surface, as shown in Figure 5a. 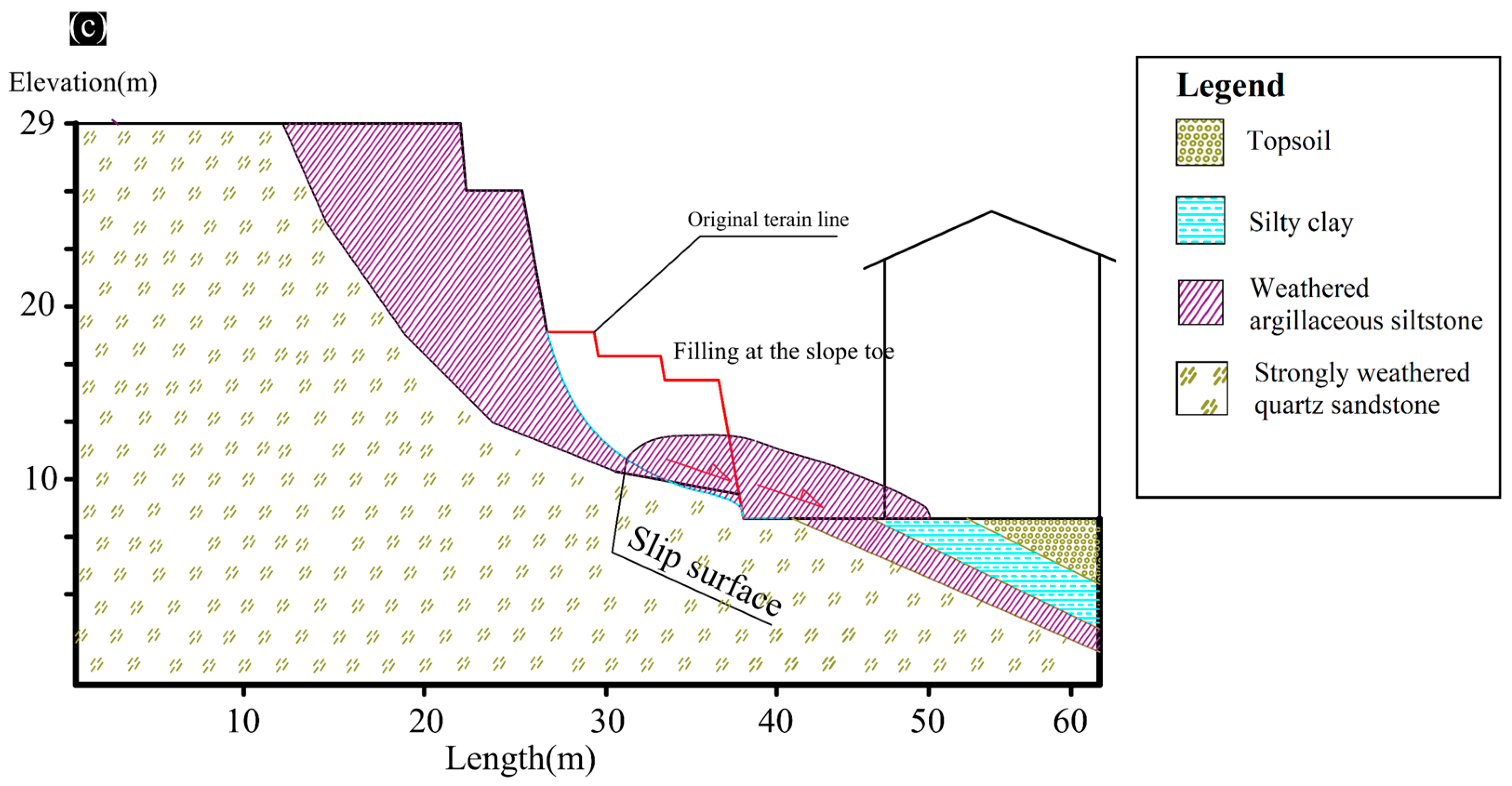Therefore, the tension cracks expanded in the following days significantly at Section 6 (S6), which led to the occurrence of the second failure phase of the slope (Figure 5a,b). Thus, a gully with a thickness of about 5–7 m was formed in the slope body. The scheme of the failure mechanism and the slip surface along Section 6 (S6) based on the measurement data and the final collapse at the end of June 2013 can be observed in Figure 5c. Accordingly, the geotechnical investigation showed that the total displacement of the sliding mass was about 11 m with an inclined angle of 70°–75°. Hence, the damage to the slope body was significant.

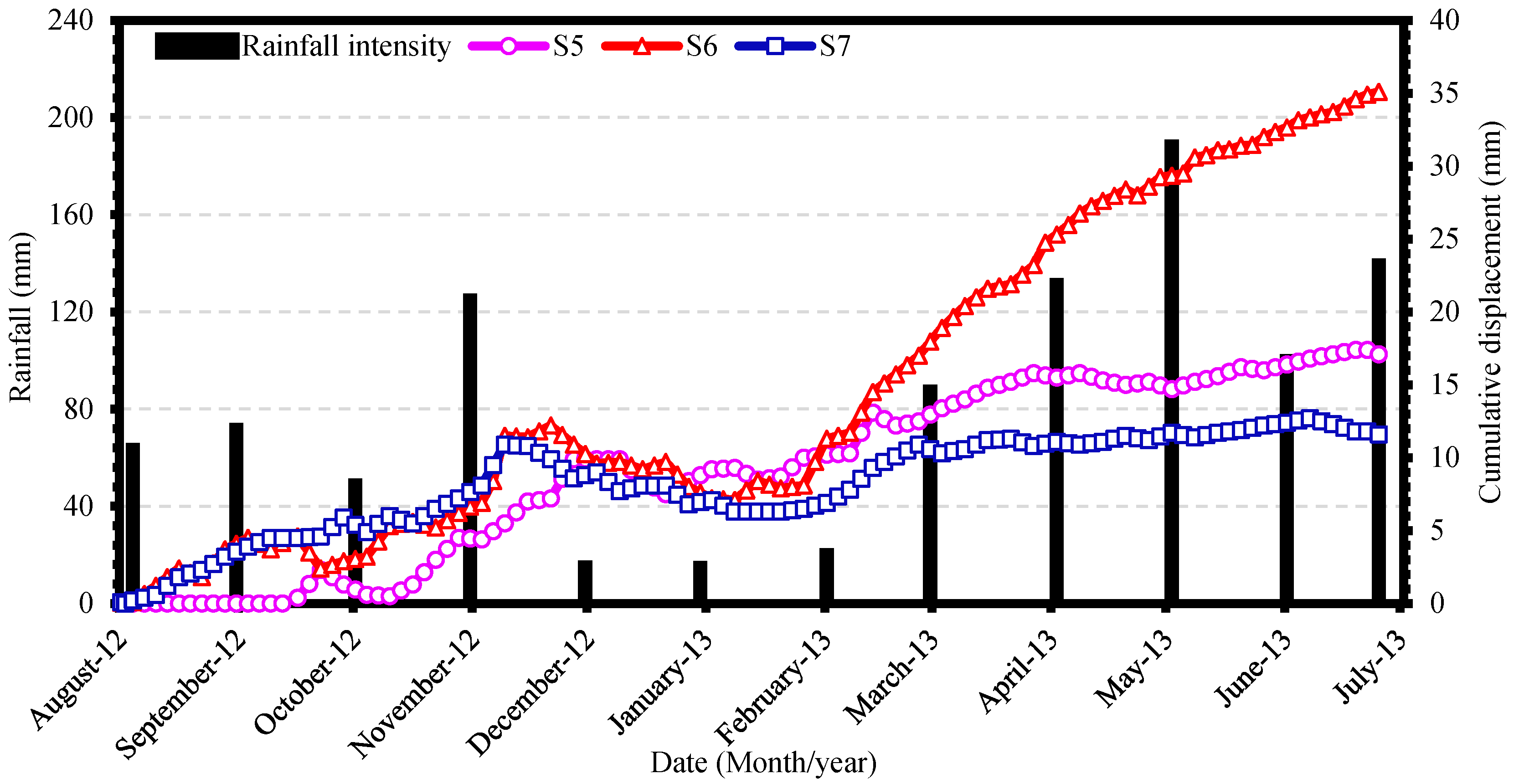
Relationship between Slope Displacement and Precipitation Amount

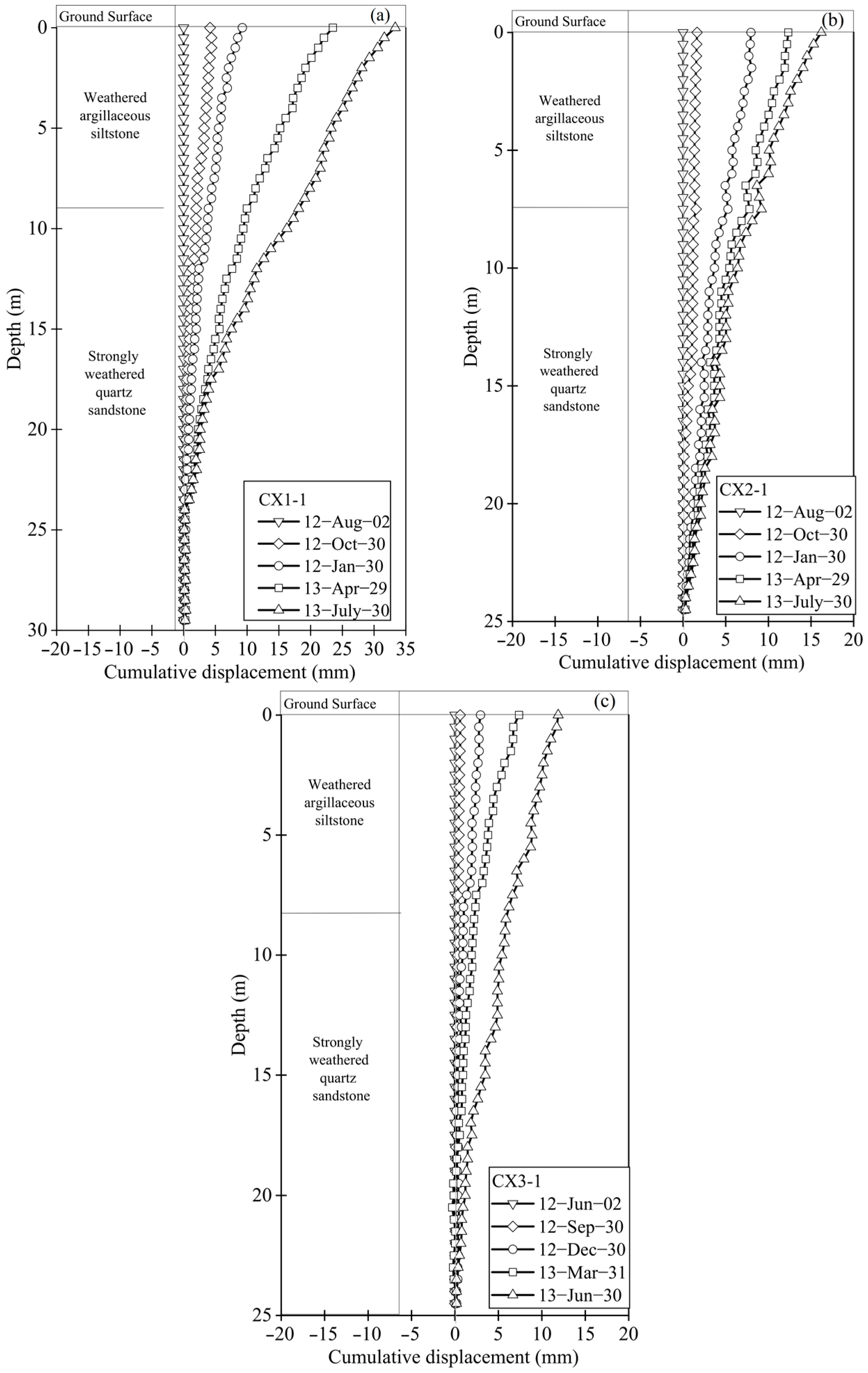
In order to investigate the relationship between slope displacement and rainfall, slope displacement monitoring data were collected by the Suzhou Civil Architecture Design Institute (SCADI), and precipitation data were obtained from the China Meteorological Data Sharing Service System. The cumulative displacements in depth are illustrated in Figure 6a–c, and the horizontal displacement and meteorological records are illustrated in Figure 7, whereas the displacements were monitored during the period from August 2012 to July 2013. The evolution of the ground displacement values could be divided into three periods as follows. In the first period, from August to November, the monitoring point of Section S5 recorded very small displacements as a straight line during August and September, except for the Section S6 and S7 displacements, which started increasing irregularly from August to the middle of November. Heavy rainfall occurred at the beginning of November, with 110 mm of precipitation. The displacement of the three sections started increasing significantly in November with an intensity of rainfall of 10 mm/day ≤ rainfall ≤ 80 mm/day, with total accumulated displacement values of 10 mm, 12 mm, and 11 mm in Sections S5, S6, and S7, respectively. In the next period, from December to February, the slope remained stable, and a small decrease in the cumulated displacement was recorded from December to February. In the third period, from the end of February to July, based on the meteorological data, the monitoring area entered the monsoon rainfall in March. Therefore, the slope was affected by heavy rainfall, as can be seen from the monitoring points at Sections S6 and S7, which developed at a rate of 0.31 mm/day (Figure 7). Section S6 recorded an increase of 0.23 mm/day with an intensity of rainfall 50 mm/day ≤ rainfall ≤ 120 mm/day. Until July 2013, under the influence of continuous rainfall, the maximum cumulative displacements at Sections S5–S7 reached 14 mm and 17 mm, respectively. Accordingly, the slope stability at Section 6 (S6) and CX1–1 reached a critical state in July. Hence, the process went into global failure almost eight months after the completion of remedial work. Through a detailed field investigation, it was determined that rainfall was one of the main factors that induced failure on the Taihu slope.

4. Methods

4.1. Strength Reduction Method

The stability analysis used the strength reduction method (SRM) to estimate the safety factor by gradually reducing the soil strength until the slope reaches a stable strength reduction factor or until the calculation does not converge. Zienkiewicz et al. (1975) [61] proposed the shear strength reduction (SSR) technique to enhance the method for estimating the factor of safety. Typically, the strength reduction method (SRM) is used with the Mohr–Coulomb (MC) failure criteria. The safety factor is estimated using the following formula:

$$C^{\prime }=\frac{C^{\prime }}{FoS}$$

(1)

$${\varphi }^{\prime }={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left[\frac{\mathrm{t}\mathrm{a}\mathrm{n}{\varphi }^{\prime }}{FoS}\right]$$

(2)

where the shear strength parameters “C’” and “$\varphi$’” are used in SRM processes, and are defined as the actual shear strength indexes and the strength reduction factor of the rock and soil. The SRM technique is considered a precise method for identifying the critical failure surface based on the localized shear strain by decreasing in shear strength until the slope reaches the critical state.

4.2. Hydraulic Model

The finite element code, Midas GTS, is used to investigate the failure of the Taihu Resort’s cut slope in Suzhou. In this study, the slope model was simulated based on actual on-site measurements and mechanical property data. The numerical calculation enables us to measure the volume of infiltration water. The soil–water retention curve (SWRC) is used to determine the volumetric water content curve, which has the capability to describe the changes in the pore-water pressure. Therefore, in order to predict or estimate the volume of infiltration water for soil and rock slopes, a fitting formula obtained from field or laboratory tests of water retention was developed by Van Genuchten (1980) [62]. The model was applied to this study as follows:

$$S=\frac{{{\theta }_w-\theta }_r}{{\theta }_s-{\theta }_r}={\left(\frac{1}{1+{\left(a\times h\right)}^n}\right)}^m \left\{\begin{array}{c}{\theta }_{\left(h\right)}={\theta }_s\\ h\ge 0\end{array}\right.$$

(3)

$$k_w=k_s\frac{{\left\{1-\left(a\times h^{\left(n-1\right)}\right){\left[1+{\left(a\times h\right)}^n\right]}^{-m}\right\}}^2}{{\left\{\left(1+{\left(a\times h\right)}^n\right)\right\}}^{\frac{m}{2}}}$$

(4)

$$m=1-\frac{1}{n}\begin{array}{c} \end{array}$$

(5)

where $S$ is the saturation, θ_w is the volumetric water content, and θr and θs represent residual and saturated volumetric water content, respectively. h is the pressure head, a, n, and m are fitting parameters, and $k_s$ and $k_w$ represent the saturated coefficient of permeability and the coefficient of hydraulic conductivity, respectively.

Based on the van Genuchten model, a typical soil–water retention curve (SWRC) is illustrated in Figure 8.

5. Simulation of Sequential Slopes under Excavation and Rainfall Scenarios

Although the treated slopes that are exposed to intense weather conditions are generally able to withstand them, it is important to study the techniques that suit the nature of the slope in support of geotechnical engineers. In cases where slopes have complex shapes, an extensive geological examination is required before cutting the slope. In addition, geotechnical engineers should pay attention to the possibility of subsequent failure occurring in a large area once localized damage has occurred on the slope. Therefore, based on the geological profile of the Taihu slope, a two-dimensional numerical analysis of the Taihu slope under excavation and different rainfall scenarios is simulated effectively for slope stability assessment. The elastic–plastic constitutive model is adopted in this study and is based on the Mohr–Coulomb (MC) criterion. Midas GTS was used to simulate the slope Section (S6) as a representative landslide area. In order to study the results of the deformation and stability of the slope, this section presented an effective analysis of the slope failure subject. The slope excavation was carried out in stages and at different heights, starting at 3 m, 6.5 m, 2 m, and 4.5 m. The selected rainfall intensities are 170 mm/day (heavy rainfall) and 60 mm/day (moderate rainfall), and the surface flux was applied at the top of the slope.

5.1. Establishment of Slope Finite Element Model

The numerical model is simulated based on the actual cut slope project size described in Section 3. Therefore, the surrounding environment of the slope, inclination angles, and influence range of the size must all be taken into consideration while establishing the size of the numerical model. Finite element mesh is used in this study to establish a two-dimensional numerical model that is discretized into a finite element mesh of quadrilateral elements to simulate and investigate the stability of the slope, which was selected as an excavation model with four excavation stages. The gradually excavated depths and angles are presented in

Table 1. Taihu slope excavation design parameters.

Slope Excavation Stages	Slope Ratio	Height (m)	Width (m)
Stage 1	1:0.09	3	2.5
Stage 2	1:0.17	6.5	2
Stage 3	1:0.17	1	2
	1:0.17	1	2
Stage 4	1:0.17	4.5	-

. A suitable mesh size model was selected and varied between 0.8–1.1. The boundary condition in the numerical analysis is set mainly in terms of displacement, as shown in Figure 9. The physical and mechanical parameters were obtained by experiments, as seen in

Table 2. Mechanical parameters of each geologic layer.

Soil Parameters	C (kPa)	φ (°)	E (kN/m2)	γ (kN/m3)	v	${\mathit{\theta }}_{\mathit{s}}$	${\mathit{\theta }}_{\mathit{r}}$	${\mathit{k}}_{\mathit{s}}$
Topsoil	10	12	4.9 × 105	18.5	0.2	-	-	5.00 × 10−3
Silty clay	25	18	4.0 × 104	20	0.25	0.32	0.049	2.68 × 10−5
Weathered argillaceous siltstone	26	14	32 × 103	19.5	0.3	0.38	0.03	7.15 × 10−8
Strongly weathered quartz sandstone	34	26	1.0 × 107	22	0.22	0.42	0.07	4.00 × 10−6

.

5.2. Influence of Excavation on the Slope Stability

Excavation of the slope is one of the main factors affecting slope stability and plays a significant role in attenuating its mechanical characteristics. In slope engineering, a stress disturbance occurs near the slope surface in the soil and rock slope under excavation. This causes a redistribution of stress near the slope surface and directly affects the strain distribution zone. In addition, during the excavation of a slope at a certain depth, the slope’s safety factor may be seriously reduced. This may threaten its stability, which can cause the slope to collapse. Therefore, the simulation of excavation impact on slope stability is demonstrated by slope excavation carried out in four stages. In this way, the distributions of shear strain and stress in the slope after each excavation stage can be analyzed in detail. On the one hand, the safety factors of the slope can also be estimated based on the strength reduction method (SRM).

5.2.1. Shear Strain Analysis

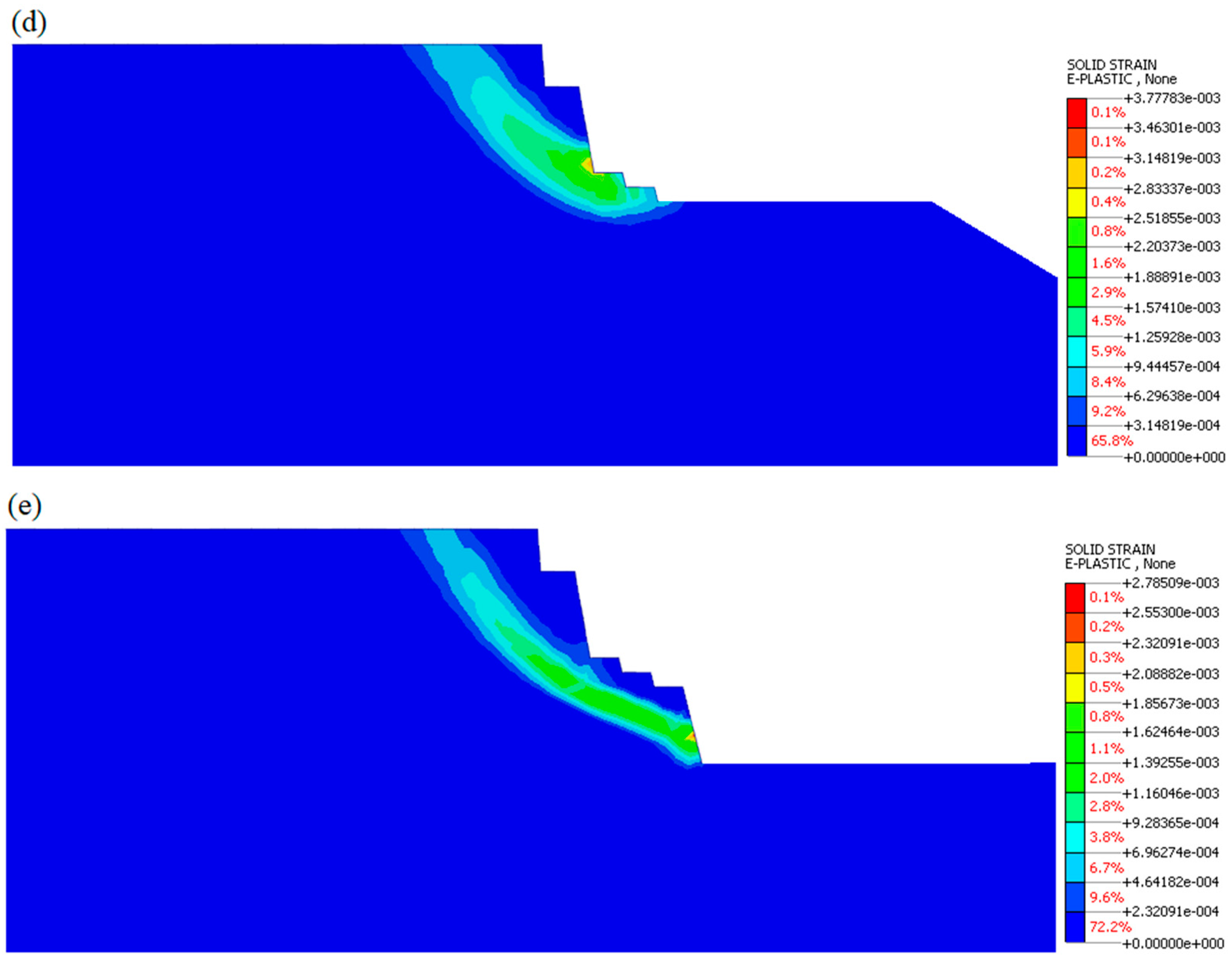
The overall observed maximum shear strain distribution trends of the slope were analyzed during the excavation process. These trends are illustrated in sequence in Figure 10. Accordingly, the numerical analysis indicated that gradual excavation is the main factor affecting shear strain. Therefore, the shear strain distribution is generated and transformed downward gradually to the new toe position of the slope surface after each excavation stage. Here, it should be mentioned that for the first excavation stage, the maximum shear strain occurred in different locations compared with the second excavation stage. As indicated in the figures, beginning with the second excavation stage, the shear strain continues to transform downward to the new toe position of the slope formed after each excavation stage. Lastly, at the final excavation stage, the shear strain surface was generated at the junction between soil and rock layers and extended till the top of the slope (Figure 10d). In addition, the maximum shear strain value increases with the increase in the excavation rate. At the fourth excavation stage, the shear strain occurred mainly above the toe of the slope into the third layer of the slope body, indicating that the failure of the slope occurred mainly in the argillaceous siltstone layer.

This analysis was conducted to investigate the deformation behavior of slopes based on the shear strain distribution. As a result, we found that the numerical simulation indicates that an obvious internal deformation occurs at the foot of the slope and propagates toward the crest of the slope. In addition, the inclination of the soil and rock layers layout in the slope plays a significant influence on the path and shape of the slope failure. Overall, slope excavation has proven that it is the major factor affecting slope stability. Therefore, the FoS value is greatly reduced from 4.103 of the original slopes to 1.241 after the final excavation stage. Consequently, the slope stability coefficient of the fourth stage excavation decreased significantly. As displayed in Figure 10d, the excavation slope has a huge effect on the factor of safety (FoS). Therefore, the slope stability coefficient indicates that the slope is stable.

5.2.2. Stress Analysis

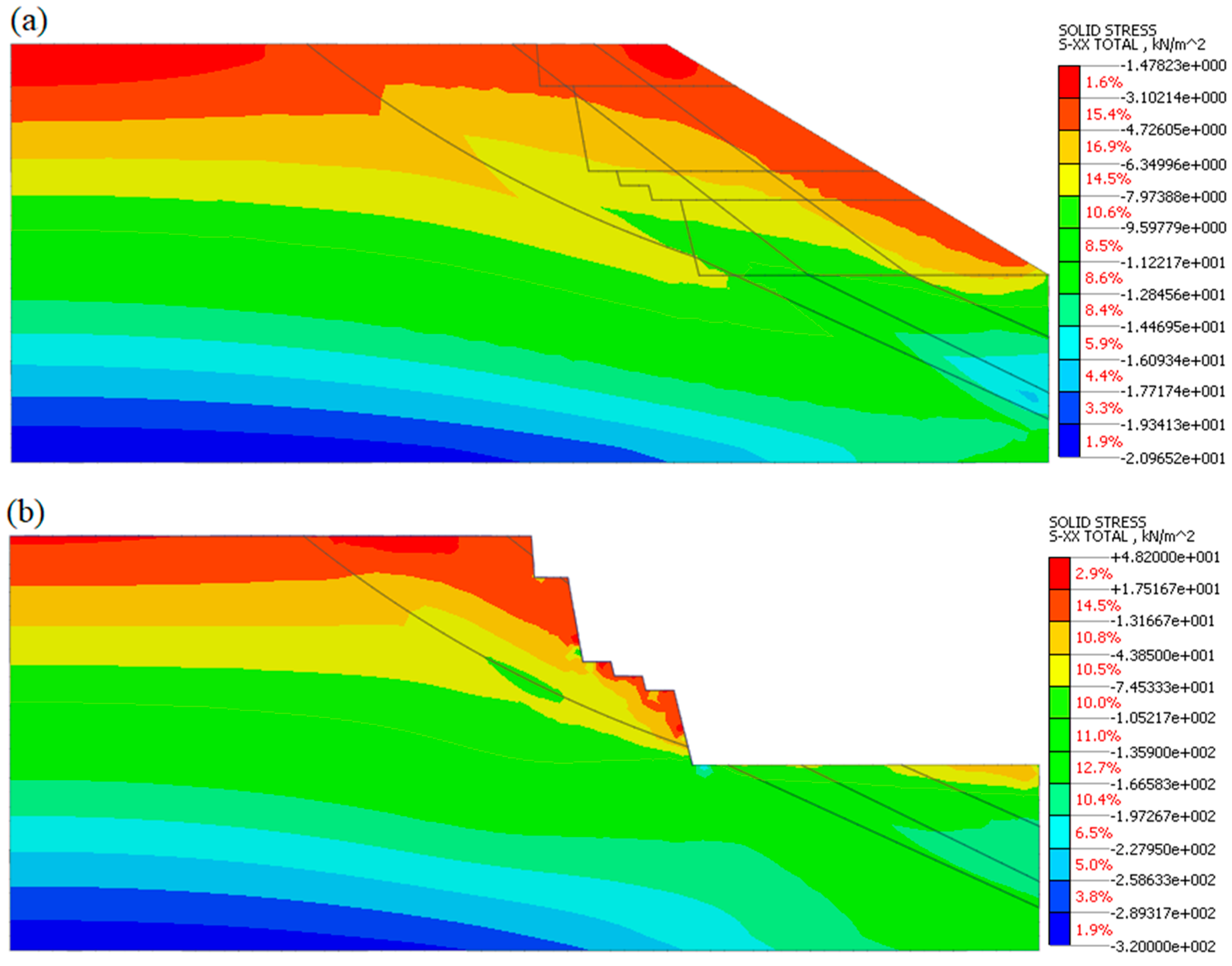
The height of the excavation on the slope greatly impacts the stress distribution and stability of the slope. In the previous section, numerical simulations of the slope ensured that the excavations resulted in an increase in the distribution of shear strain within the slope body. In order to analyze the stress changes within the slope during the process of excavation, a detailed comparison is carried out to evaluate the effect of excavation on the distribution of horizontal stress. Additionally, a detailed analysis is conducted of the horizontal stress development at two selected points at the mid-toe and mid-top along the shear strain of the slope. The Midas GTS software defines negative stress as compressive stress and positive as tensile stress. Before excavations proceeded, it can be observed from the horizontal stress distribution of the original slope in Figure 11a that the stress distribution zone within the original slope indicated compressive stress and diffused over the entire slope. When the fourth slope excavation stage occurred at 10 m of elevation, as can be seen in (Figure 11b), the horizontal stress distribution within the initial slope was redistributed and increased at the final excavation stage, where the slope excavation significantly affected the stress distribution and also led to demolishment in the stresses within the slope body, which the horizontal stress redistributed after the newly excavated slope surface. In detail, the height of the tensile stress distribution range is about 4 to 6 m along the argillaceous siltstone layer, and it extends partially over the slope toe. Therefore, the tensile stress of the excavated slope was substantially higher in the soil slope layer compared to the original slope. Therefore, the fourth excavation stage resulted in an opposite reaction to the stability of the slope, which affected the stability of the slope negatively.

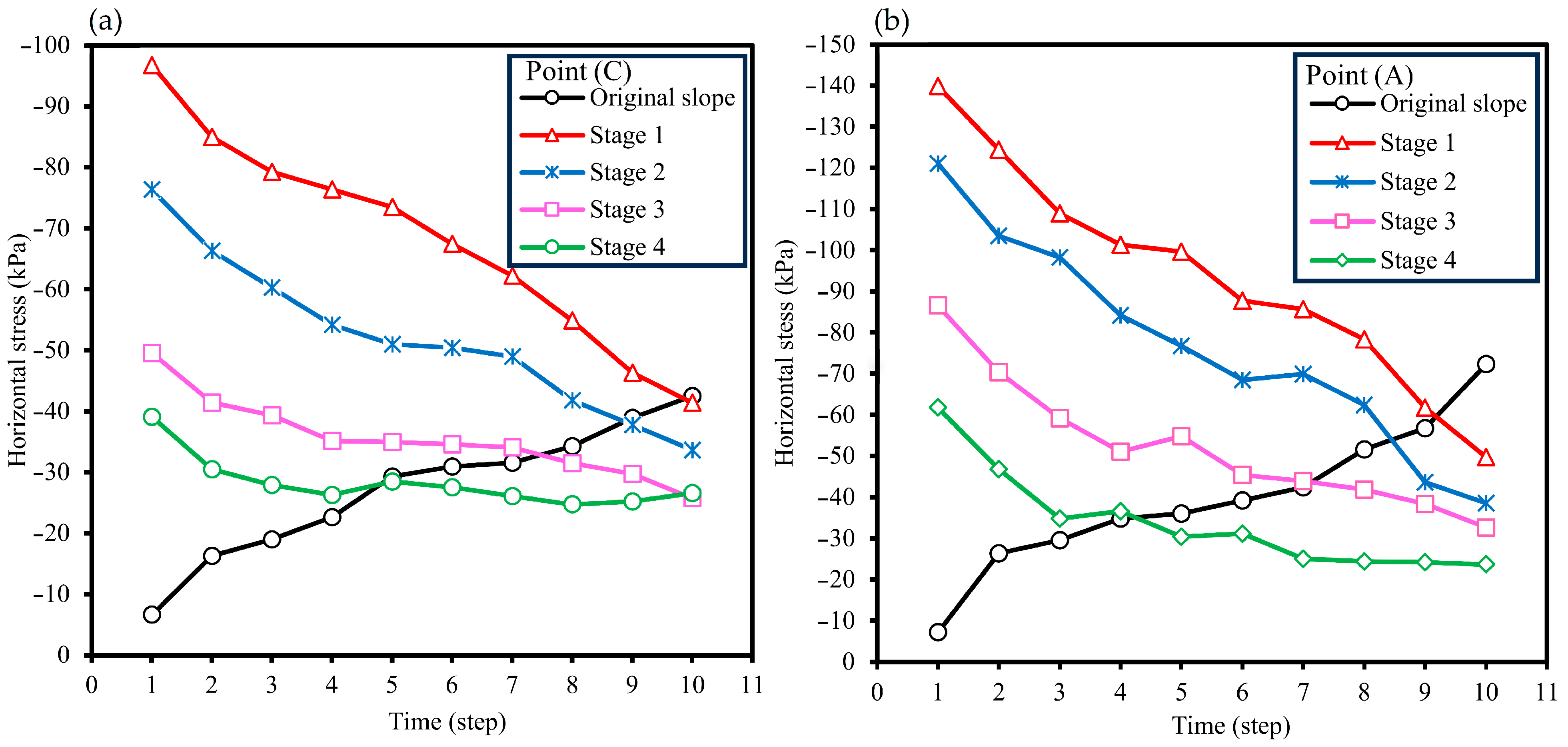
The change in the horizontal stress of the slope during the excavation process has a great influence on the slope’s stability. To determine the horizontal stress variation within the slope from the original slope to the fourth excavation stage, two points at the middle-top and middle-lower of the slope were set to observe the changes. Figure 12a,b show the horizontal stress development at each excavation stage of the middle and top of the slope, respectively. It can be seen from Figure 12 that the horizontal compressive stress for all excavation stages decreases gradually with the progress of the excavation rate for both the top and middle selected points, except for the original slope horizontal stress, which indicates that the horizontal compressive stress increases gradually with time. Moreover, the horizontal compressive stress at the middle-lower values is greater than the horizontal compressive stress of the mid-top values.

5.3. Influence of Rainfall Condition on Slope Stability

Previous Section 5.2 have demonstrated the stability analysis of the slope under excavation conditions based on stress and strain distribution. Section 4 investigated Taihu slope failure in Suzhou based on monitoring data. It became clear that heavy rainfall in June 2013 caused a significant failure in Section 6 (S6) of the Taihu slope. In this section, the finite element calculation models of the cut slope under rainfall conditions are established using Midas GTS. This would provide a feasible approach for a more accurate analysis of the effect of rainwater infiltration on slope stability. According to the field survey results of the landslide, considering meteorological data of the Suzhou area, two classified rainfall amounts are selected to determine the effect of rainfall on soil water retention and slope stability: 60 mm/day is regarded as moderate rainfall and 180 mm/day as heavy rainfall. In practical soil engineering implementations, the saturation and volumetric water content of soil often change due to the increase in rainwater infiltration, or other causes. Due to the unavailability of data on the volumetric water content of the slope, the influence of different rainfall intensities on the pressure head and slope stability factor are studied in detail. The rainfall infiltration based on the soil-water retention and tendencies of slope stability under moderate and heavy rainfall intensities were analyzed and compared. In order to study the extent of influence of rainwater infiltration on slope stability, a numerical analysis of the rainfall impact on the pore-water pressure of the slope under rainfall conditions was presented and analyzed. The influence of rainfall conditions on the simulation model was determined over 15 consecutive days of rainwater infiltration. These are presented in four steps: 1 day of rainfall, 5 days of rainfall, 9 days of rainfall, and 15 days of rainfall. The numerical simulation results of the pore pressure head are illustrated in the following figures.

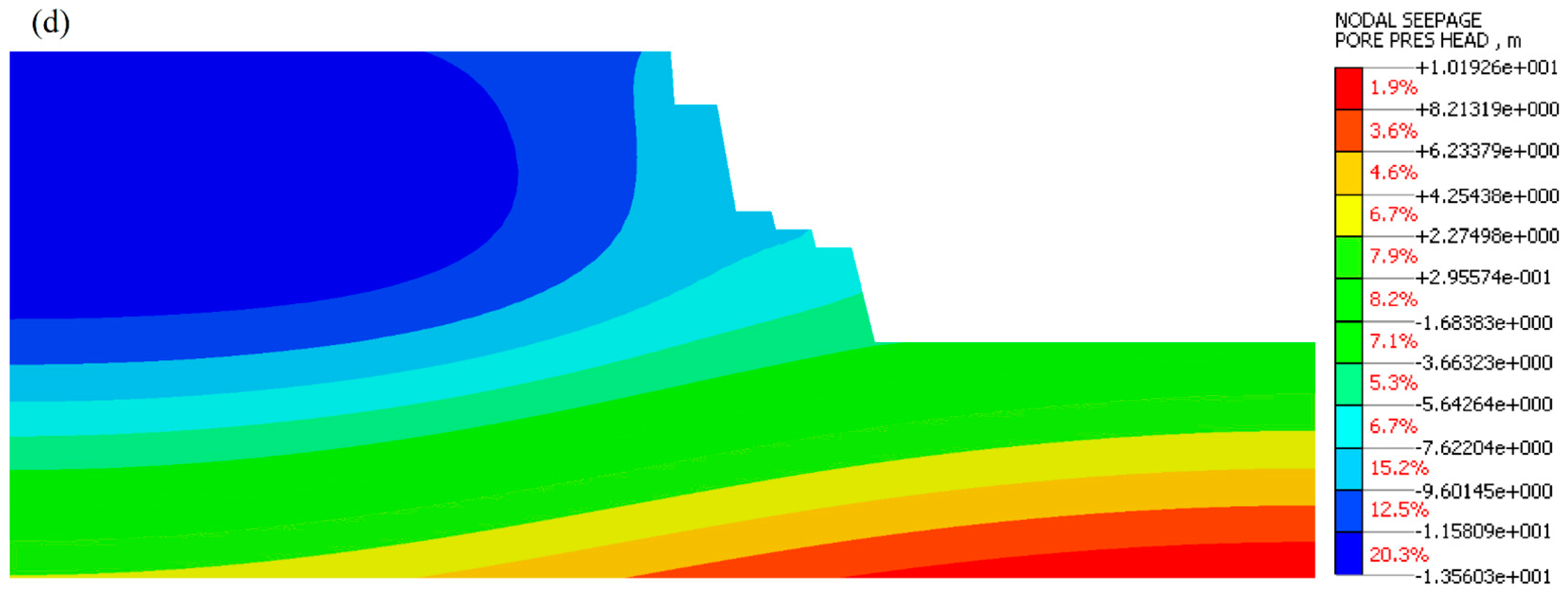
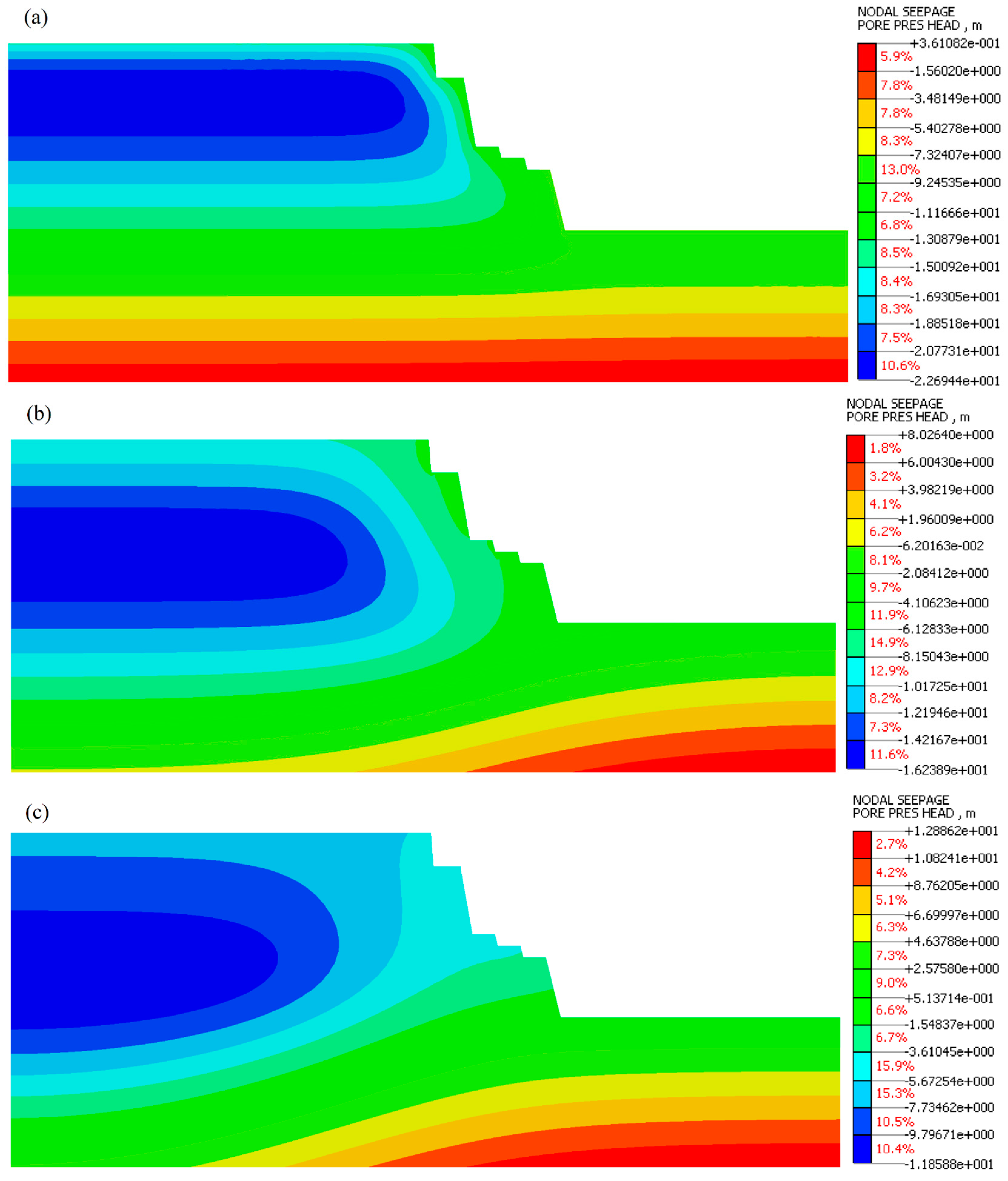
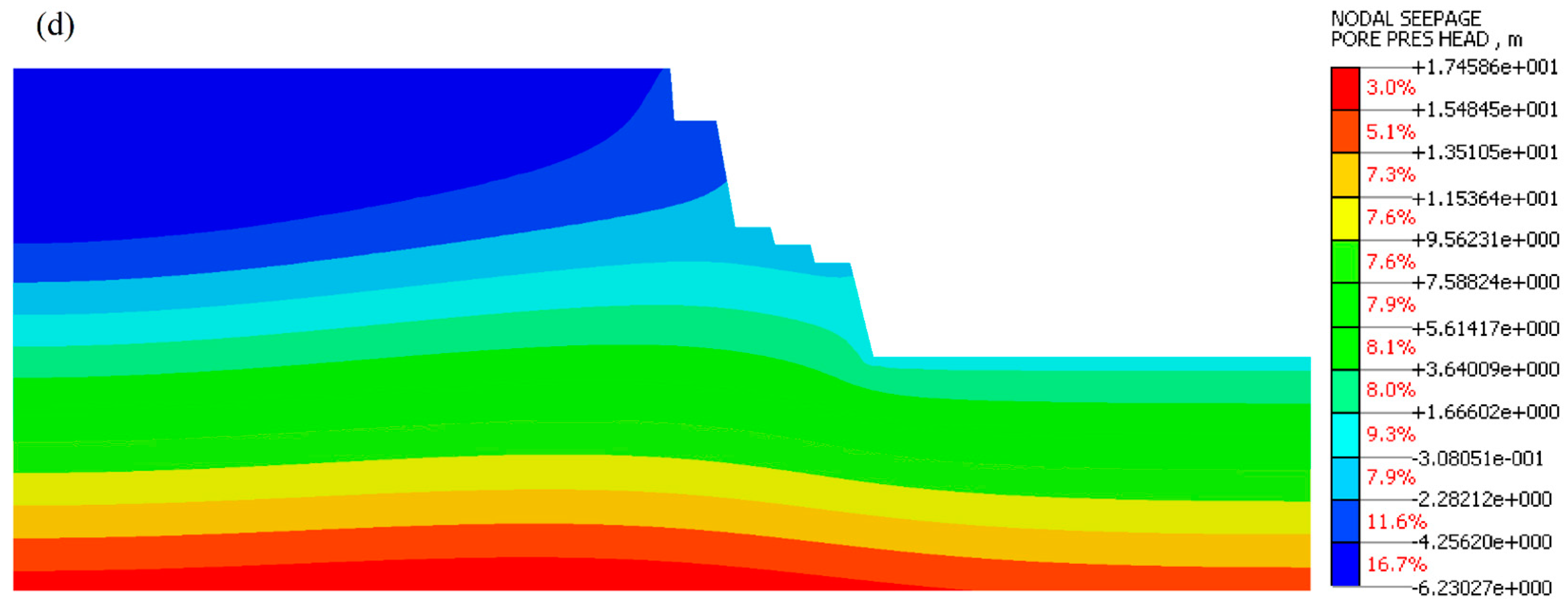
Figure 13 and Figure 14 illustrate the distribution of the pressure head of slope induced under different rainfall intensities. During the numerical modeling, as illustrated in Figure 13a and Figure 14a, the pressure head distribution within the slope depicts certain changes at the top and surface of the slope after one day of heavy and moderate rainfall. However, it can be observed that the pressure head is relatively small, including the contour of the pressure head that starts shrinking gradually into the slope body. With continued rainfall, rainwater infiltration influences the pressure head significantly, which continues to shrink after 5 and 9 days, respectively; as a result, the pore pressure distribution increases over time at the toe with the continuous rainfall infiltration. With the increase in groundwater level of the slope after 9 days of heavy rainfall, the pressure head increased significantly at the toe surface of the slope, indicating that the toe of the slope was the first slope part eroded by rainfall. Similarly, this increased the slope’s body weight, which affected the slope stability. Otherwise, the slope was unstable. After this, it can be noted that only a tiny part of the slope was observed in the pressure head distribution under heavy rainfall compared to moderate rainfall intensities. In this part, the unsaturated zone has shrunk considerably in a heavy rainfall scenario, and the pore water pressure area of the slope has expanded at the weathered argillaceous siltstone layer. This resulted in the front layer of the cut slope under heavy rainfall being severely less stable than when the slope was under moderate rainfall.

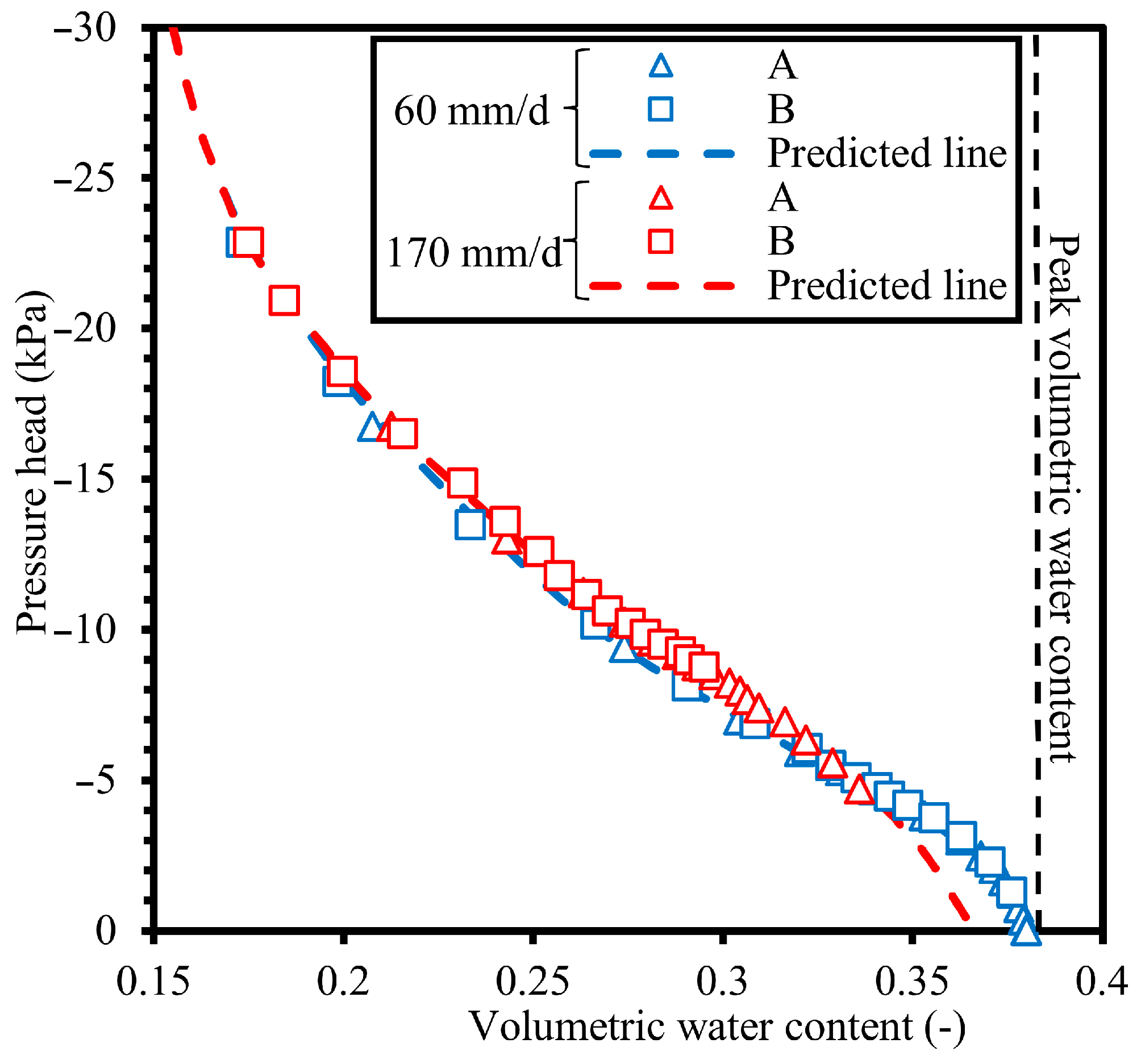
The greatest change in the soil and water retention curve (SWRC) shows the relationship between soil water at the argillaceous siltstone layer selected points (A, B) under different rainfall intensities, as illustrated in Figure 15 and Figure 16. The plotted curves display hysteretic behavior during the wetting stage until it reaches the peak value of volumetric water content and saturation degree, thus increasing the pressure head. It can be observed from the figures that the pressure head of the slope increased gradually with the increase in the initial saturation degree and the volumetric water content. Additionally, the degree of saturation and the volumetric water content of the slope were higher during heavy rainfall compared to moderate rainfall intensity. Therefore, an increase in the degree of saturation and volumetric water content of the slope typically leads to an increase in the tension crack in the slope, thus decreasing the stress and shear strength of the slope.

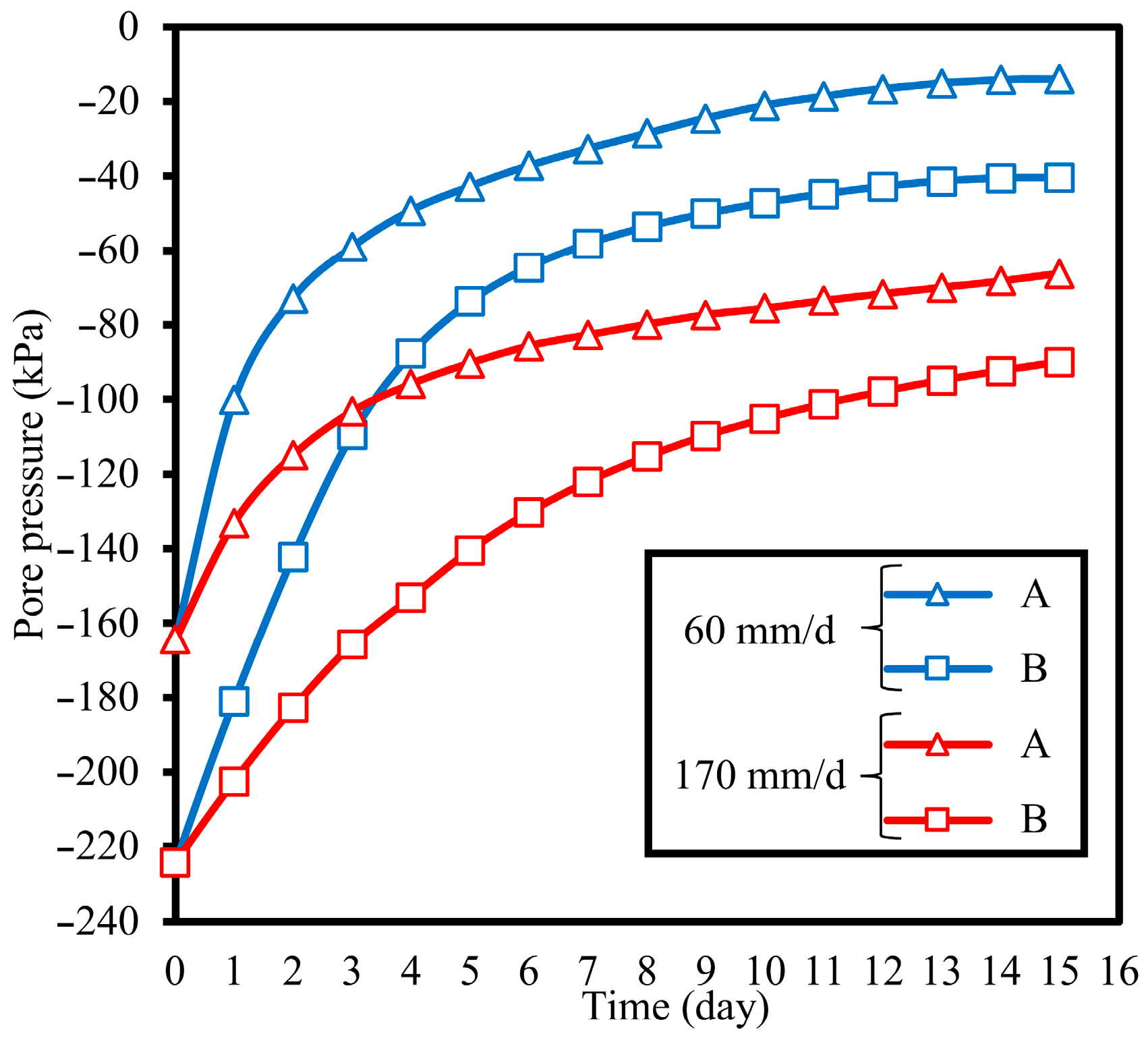
Figure 17 displays the evolution of the pore water pressure over time at the argillaceous siltstone layer under different rainfall intensities. The pore pressure under both selected rainfall intensities was observed in two stages. In the first stage, under the heavy rainfall intensity, the pore pressure increased sharply in the first four days compared to moderate rainfall, which increased slightly. Afterward, as the infiltration of rainwater continues, the pore-water pressure increases slowly until it reaches the maximum value under the rainfall intensity of 170 mm/day. Therefore, an increase in the pore water pressure of the slope generally leads to a reduction in the slope stability. 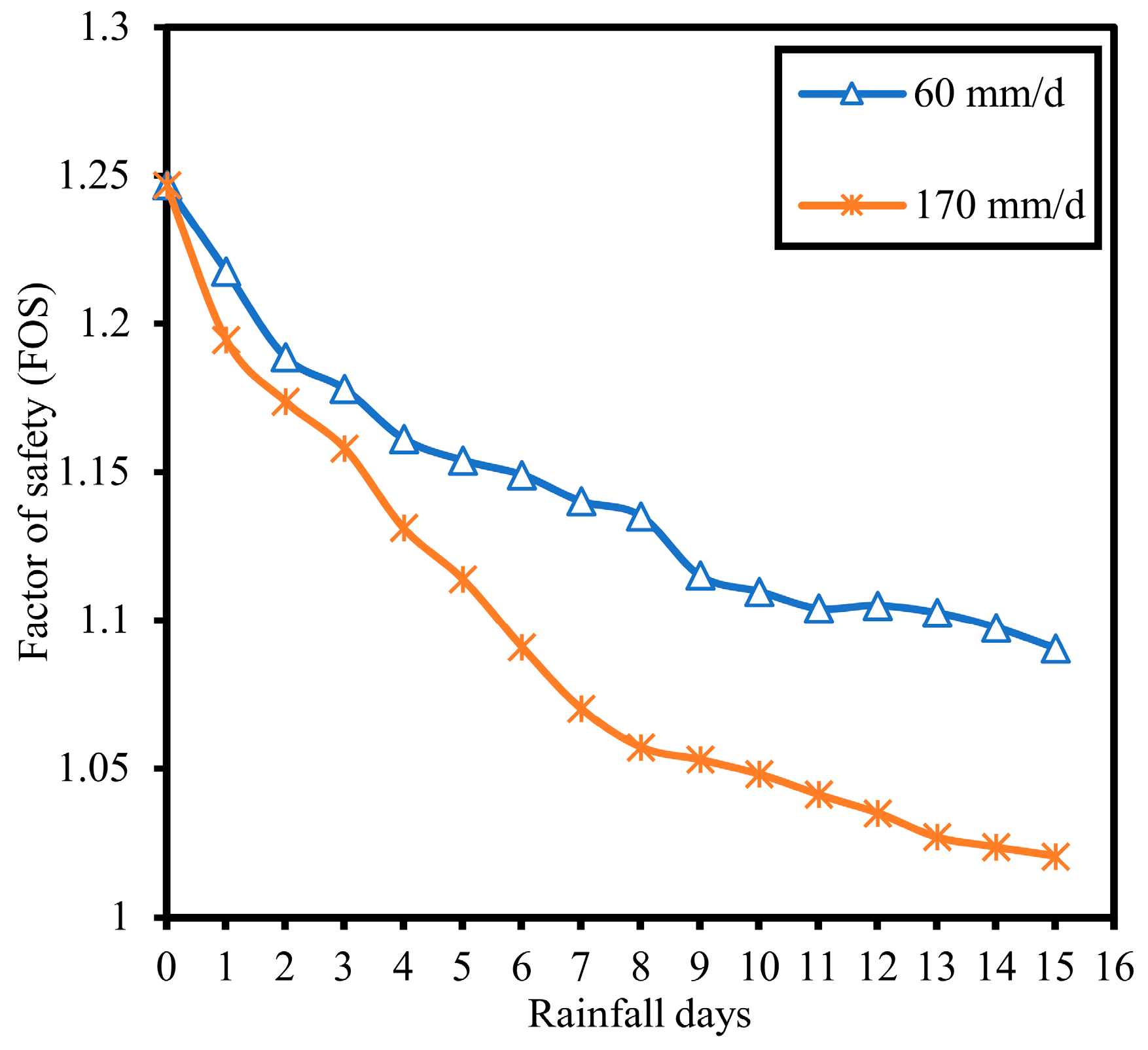Figure 18 illustrates the evolution of the factor of safety of slopes over time under different rainfall intensities. It can be seen that the FoS of the slope at heavy and moderate rainfall intensities decreases with continuous rainfall. Accordingly, comparing the safety factors of the slope under different rainfall intensities, the slope under heavy rainfall intensity reached the minimum factor of safety after 15 days of the rainfall process.

6. Discussion

In the tourist cities located in eastern China with large populations, resorts and hotels are considered fundamental infrastructures that are expected to be built in safe areas. Inappropriately excavated slopes can become one of the causes of landslides, which contradicts the core objective of safety. Therefore, while the excavation of hillslopes for buildings or resorts continues to expand in many countries due to urbanization, there is a need to understand and investigate the main causes of landslides. Previous research on the stability of slopes has often mainly focused on simulation analysis or geotechnical monitoring examination statistics based on a single working condition or a specific parameter, disregarding the possibility of any further invisible factor that may have a detrimental effect that contributes to slope instability without executing an overall verification analysis under different conditions. By considering a case study of a typical landslide induced by excavation, the temporal and spatial Taihu slope failures were analyzed first based on the monitoring data. An investigation was carried out first in this paper, and two-dimensional numerical simulations were conducted under excavation by stages and different rainfall scenarios.

The analysis of the investigated Taihu slope failure during the monsoon rainfall in the Suzhou area found that the slope collapse that occurred at the soil layer of weathered argillaceous siltstone was induced by the cut of the slope at an angle that did not fit the design safety requirements, which led to a significant reduction in shear strength. The rainfall infiltration into the slope caused a gradual increase in the volumetric water content, which caused cracks and abrasion at the slope surface due to plugging the drainage out. Therefore, the investigation results indicated that the main reason for the Taihu cut slope failure is related to the heavy rainfall. Through the analysis of the numerical simulation, the FoS of the slope was effectively reduced during the excavation progress. During the excavation process, the stress, strain, and displacement distributions were significantly affected, and the stress was redistributed to every newly formed surface. On the other hand, the maximum shear strain distribution appears at the toe of the new excavation slope.

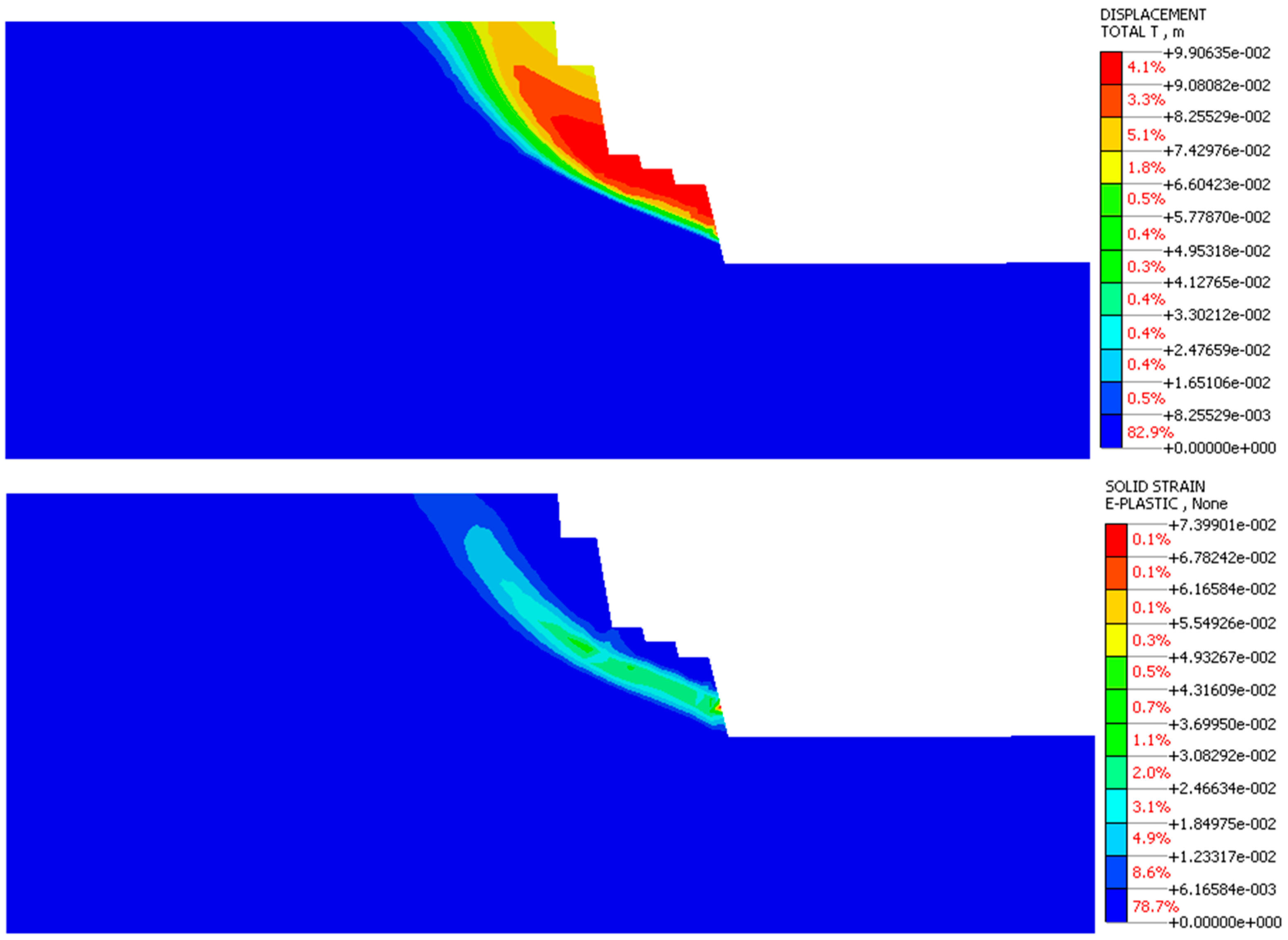
Due to the deformation analysis, the application of a rainfall condition has a huge effect on the shear strain and displacement distributions of the slope. Figure 19 and Figure 20 show the maximum shear strain and displacement distribution after 15 days of rainfall with different precipitations of moderate and heavy rainfall. Overall, the distribution of shear strain occurs above the toe of the slope and gradually shifts the top of the slope in the form of an upward arc under both rainfall intensities. Clearly, the damage began at the junction (layers contact), continued propagating to the middle of the slope, and continued expanding toward the top of the slope. However, the circular slip surface underwent no change under heavy and moderate rainfall. The displacement characteristic of the slope is particularly large compared with moderate rainfall. The failure surface only occurred beginning along the contact in the front layer of weathered argillaceous siltstone, indicating a large displacement.

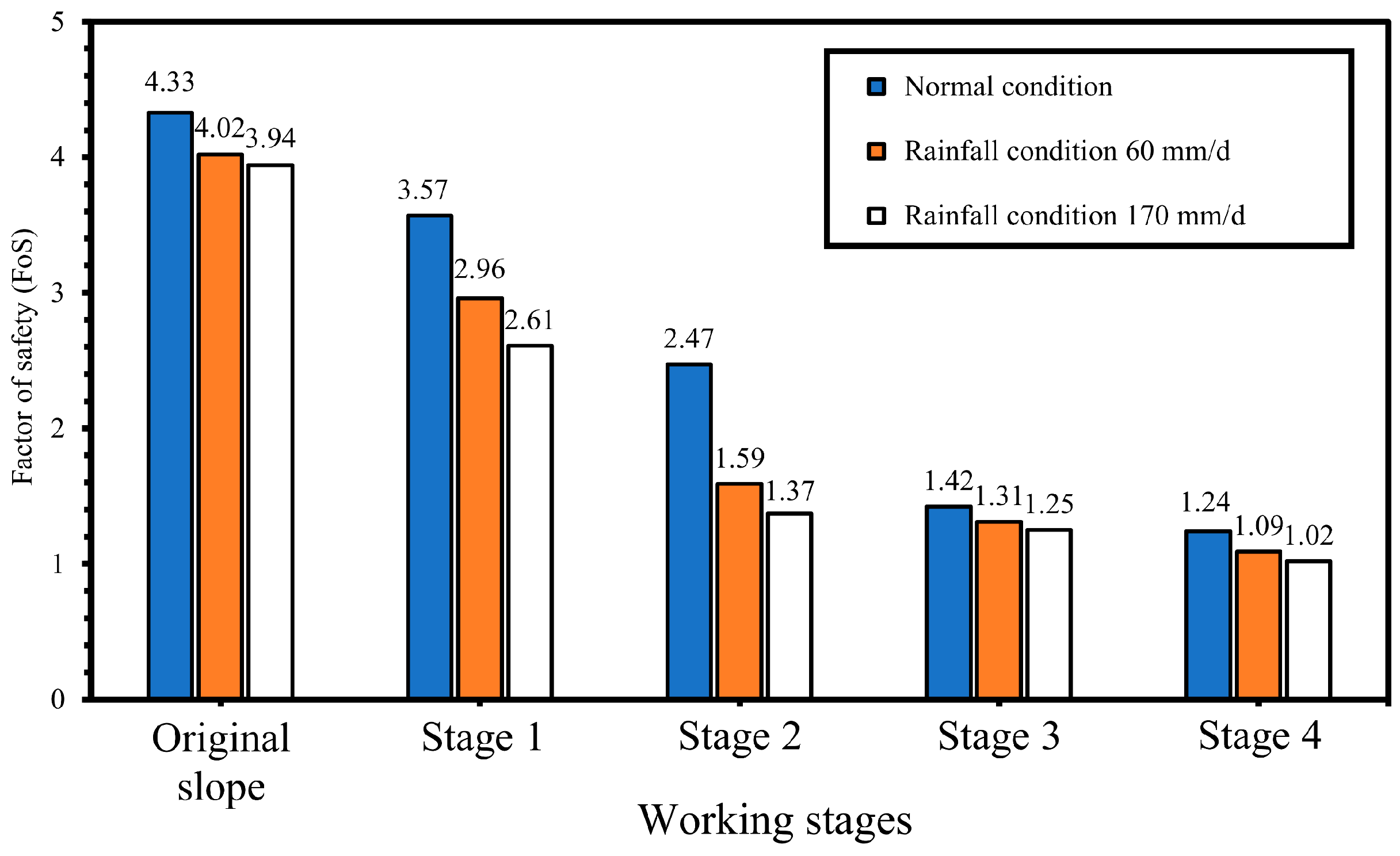
The soil water retention and stability of the slope with continued rainfall infiltration for 15 days were simulated. It was found that the pore-water pressure, degree of saturation, and volumetric water content increased with the increase in rainfall time and intensity. Additionally, the effect of heavy rainfall on the slope stability was higher than under moderate rainfall for identical rainfall duration, and the slope stability under heavy rainfall reached the minimum safety factor. Therefore, the Taihu landslide was caused by the irrational excavation followed by continuous heavy rainfall. As slope stability assessments based on numerical analysis, a different safety factor is given for the slope under the various excavation stages and rainfall intensities, as illustrated in Figure 21. As defined in the “Technical Code for Building Slope Engineering” (GB50330-2002) [63], the minimum slope stability factor is FOS > 1.35; therefore, the slope stability indicates that the slope in the final excavation stage reaches the instability state. Consequently, the slope indicates that it is unstable under both selected conditions.

7. Conclusions and Recommendations

The failure mechanism of slopes associated with excavation or rainfall has received much attention from various soil researchers globally in the last two decades. A landslide often results from inadequate geological examination prior to the final design, poor soil structure conditions, or steep slope geometry, which can increase the possibility of failure under external conditions. In this paper, a comprehensive instability investigation of the Taihu slope located in Suzhou was carried out. According to the results of the analyses, the main conclusions are as follows:

• According to the collected monitoring data analysis, the investigation results showed that the collapse was related to two factors: the poor soil structure after excavation, which destroyed the balance of the slope, and the continuous rainfall infiltration during the monsoon rainfall that raised the groundwater table, which increased earth pressure and caused a decrease in shear strength. Therefore, an abrasion at the toe slope surface occurred, which triggered a sliding zone that formed in the body of the slope and led to the failure.
• Numerical simulation results show that during the slope excavation process, the horizontal stress distribution was gradually demolished, which is redistributed after each excavation stage and changes over time as more material is removed. As continuous excavation progresses, horizontal compressive stress increases gradually, and tensile stress appears within the slope body in the weathered argillaceous siltstone strata. This effectively reduces the factor of safety. Thus, the excavation of the slope has an enormous impact on stress distribution and the stability of the slope.
• On the other hand, after every formed excavation, the shear strain and displacement distributions are redistributed and transferred to the revised toe position of the slope surface. Therefore, at the final excavation stage, the shear strain generated above the toe of the slope precisely at the junction of the soil and rock zone and shifted upward into the middle of the soil layer in the form of an upward arc until the crest of the slope. The displacement distribution mainly exhibited a concentrated pattern at the weathered argillaceous siltstone. Through the analysis, it was found that the inclination of the soil and rock strata on the slope had a considerable influence on the shear strain distribution, including the slope failure path. Additionally, the slope stability factor dropped from 4.103 at the original slope to 1.241 at the fourth excavation stage, which put the whole slope in an unstable state.
• Under various rainfall scenarios, the continuous rainwater infiltration increases the volumetric water content, thus gradually increasing the pore-water pressure in 15 days of heavy rainfall, moving the pressure head toward the front layer of the weathered argillaceous siltstone layer. Therefore, the rainfall intensity has a great impact on the pressure head, which reduces the slope stability factor dramatically, which obviously causes a weakening in the shear strength, resulting in large displacement. Consequently, the FoS of the slope decreased from 1.241 to 1.02 in 15 days of heavy rainfall, which was the minimum safety factor indicated, and the slope is highly qualified to fail.

In this study, the stability assessments indicated that the excavations had an influence on the stability of the slope, which caused a huge reduction in the shear strength. Combining the field monitoring and numerical analysis results, the heavy rainfall after the excavation of the slope affected slope stability, which shows a remarkable reduction in the safety factor. Unfortunately, such poor structure excavation of the Taihu cut slope went against the slope stability. Therefore, it is necessary to conduct reinforcement with an accurate drainage system to protect the slope from the risk of failure and erosion. In future work, it is strongly recommended to apply appropriate remedial measures to protect slope stability by using anti-slide piles with anchor cables, including a drainage system to reduce groundwater levels and prevent damage to the slope.