Abstract
This article addresses the often overlooked but critical long-term factors of creep, shrinkage, ageing and corrosion in civil engineering structures. The paper emphasizes their substantial impact on structural mechanical resistance and safety, drawing attention to key examples like the Civic Tower in Pavia, the Koror-Babeldaob Bridge and dams in the USA. By exploring the challenges faced in modern engineering, the article sheds light on the need to consider these effects. Various models for predicting creep and shrinkage in concrete structures are introduced as potential solutions. In conclusion, the paper highlights the necessity for engineers to navigate the intricacies of material behaviour for successful construction amidst evolving challenges.
1. Introduction
Material parameters are generally time-dependent; that is, they change their properties over period of time. In some cases, this change is positive (for example, concrete increases its strength over time), but in some cases, change can induce the weakening of material and overall structure. That kind of negative change can lead to structural collapse.
When discussing long-term effects on masonry and concrete structures, considerations include creep, shrinkage, aging and corrosion. The goal of this paper is to provide insight into these processes, accompanied by examples that underscore their significance and the potential consequences of neglecting them. Concrete is a mixture of cement, aggregate and water with additives. Cement is a mixture of calcium silicates and aluminates. After adding water in dry mixture of cement and aggregate, a number of exothermic chemical reactions start simultaneously. This process is commonly denoted with the term hydration. Hydration begins immediately after the cement comes in contact with water, but lasts for a very long period of time. During prolonged hydration, concrete increases its strength and modulus of elasticity and this process is called aging.
Over time, concrete can be affected by reactive liquids and gases which can cause chemical, physical–chemical or colloidal deterioration and disintegration of concrete components. This process is known as concrete corrosion. Also, there is another type of corrosion—corrosion of reinforcement—which will not be discussed in this paper. Creep is the process of structure deformation under long-term (sustained) load.
It is well established that body deforms under the influence of force. When a force is applied, the change is immediate. In addition, if the force is applied over an extended period, the material attempts to adapt, changing its shape and volume to redistribute stress.
Generally, creep in concrete is defined as a time-dependent deformation due to long-term actions [1,2]. These definitions imply that creep will lead to an increase in initial deformation over time, while in the absence of creep, the initial deformation will decrease as a function of aging, shrinkage of concrete and relaxation of steel [3]. Structure stability can be seriously threatened if progression of shrinkage and creep deformation is neglected. Thus, the obligation to take creep into account when designing and dimensioning reinforced and prestressed structures is even more important. Therefore, considering creep is crucial when designing and dimensioning reinforced and prestressed structures, as it can cause stress redistribution in structures, which leads to a reduction in the load-bearing capacity.
Concrete shrinkage can be described by defining a decreasing function of volume concerning moisture change in the concrete mixture. In the case of restrained deformations of concrete, shrinkage will initiate further stresses in the concrete, which will be accounted for by reinforcement. Therefore, reinforcement accounts for the reduction in shrinkage deformation [4,5]. Displacement decreases over time [3] if shrinkage is present. Also, the influence of creep diminishes with time.
The change in the strain in concrete over time is illustrated below (Figure 1). Shrinkage starts immediately after concrete mixture is prepared. At time t0, the structure is loaded, causing immediate strain (εm). Subsequently, creep develops, a process that gradually diminishes over time (Figure 1). Upon unloading, the structure immediately recovers a part of the strain, while another part recovers over a more extended period. The irreversible part of the strain is impossible to recover.
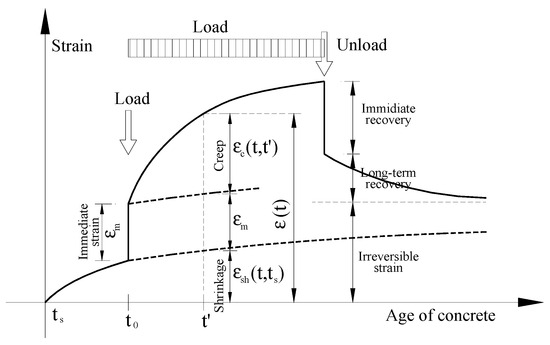
Figure 1.
Age-dependent strain change in concrete.
As mentioned earlier, concrete aging contributes to the improvement of strength as well as other mechanical properties which are considered positive. On the other side, concrete corrosion occurs only in direct contact with water.
2. Motivation
As mentioned in the Introduction, in most cases, long-term effects such as corrosion, aging, shrinkage and creep can be neglected. In the design of simple residential buildings, using approximate solutions (or completely neglecting mentioned effects) is a common practice. However, the neglect of the long-term effects in more complex structures can lead to reduction in mechanical resistance and stability. Three illustrative cases will be mentioned, with structures that had failed due to one or more already mentioned long-term effects.
2.1. The Civic Tower in Pavia, Italy
The Civic Tower (city of Pavia, Italy) was built near Pavia Cathedral in 11th century, from brickwork masonry (Figure 2). The tower had a rectangular footprint, and its height was 72 m.

Figure 2.
Civic Tower in Pavia, Italy, before the collapse [6].
The Civic Tower suddenly collapsed on 17 March 1989 killing four and injuring fifteen people. All that was left of the tower was 8000 cubic meters of brick, sand and granite rubble (Figure 3) [7,8].

Figure 3.
Remains of the Civic Tower in Pavia after the collapse [8].
The collapse stunned engineering community and officials. The tower was solidly built, there was not an indication of chemical–physical damage of the bricks (main building material), or the settlement. The collapse of the tower made the Italian government close the Leaning Tower of Pisa over concerns that the popular tourist site might also be at risk of collapse [7,8].
To fully understand the cause of the collapse numerous experimental and numerical investigations were conducted, leading to several identified factors [7,8]:
- The tower was built in several phases, starting from 1060. The steeple, built with granite blocks, was added 500–600 years later;
- The thick bearing walls (2.8 m) were made of two thin external faces in regular brickwork and the internal core was made (filled with) with some kind of soft concrete containing mixture of broken bricks and stone pebbles with thick layers of mortar;
- The total estimated mass of the tower was 12,000 tons, with the steeple alone weighing 3000 tons.
An investigation showed that the bottom part of the tower was under very high compression stresses caused by its own weight: maximum values of 1.7 to 2.0 MPa were found according to the FE elastic model, and between 1.8 and 3.5 MPa according to experimental measurements. These values are significantly high compared to the material’s compressive strength [7,8]. This likely resulted in the gradual development of tiny fissures, which, over centuries, might have contributed to the sudden collapse of the material without any obvious immediate cause or evident warning signs, such as significant cracks or spalling, even in the days leading up to the collapse. A careful review of the photographs captured by archaeologists for the Civic Museums in 1968 indicates that, even then, there were fine vertical cracks spread widely across the exterior surface of the tower wall. These cracks were exceptionally challenging to observe and resembled those observed on the specimens during testing [9].
Identifying the sole cause of the collapse proved challenging, but the elevated compressive stress induced by the dead load of the tower was undoubtedly one of the main contributing factors to the disaster.
2.2. The Koror-Babeldaob Bridge, Palau
The Koror-Babeldaob Bridge was a bridge in Palau that was connecting islands Koror and Babeldaob. The bridge was a balanced cantilever prestressed concrete box girder bridge with a total length of 385.6 m and a main span of 240.8 m. It was primarily constructed for carrying traffic, but it also carried water-supply piping and electrical conduits [10].
Sagging in the bridge’s centre began almost immediately after its completion. After a decade of use, concrete creep led to a sag of approximately 1.2 m in the main span’s middle section, causing driver anxiety and government concern (Figure 4). Therefore, the Palau government commissioned two independent studies to determine if the bridge was safe to use. Both studies concluded that the safety of the bridge was sufficient, despite an expected additional sag of 1 m. Encouraged by these studies, the government decided to take only a couple of cosmetic interventions with resurfacing and reinforcement of the bridge.

Figure 4.
The Koror-Babeldaob Bridge, sagging of the middle point [10].
The bridge collapsed abruptly and catastrophically on 26 September 1996 during the nice weather and practically unloaded (Figure 5). This disaster occurred only 18 years after construction, 6 years after engineers declared the bridge safe, and less than 3 months after all the reinforcements were made to address the escalating sagging [10].

Figure 5.
(a,b) The Koror-Babeldaob Bridge collapse [11].
The main cause of the collapse of Koror-Babeldaob Bridge remains unexplained, despite various studies having been conducted. The most likely theory is that the collapse occurred due to excessive long-time deflections of the prestressed box girders [12]. This could be due to factors such as inadequate design assumptions, material properties, construction practices, or environmental conditions, leading to unexpected deformation and ultimately structural failure. However, as the lawsuit regarding the demolition was settled out of court, the final cause has never been disclosed [10,11].
2.3. Concrete Dams in the USA
In the design and construction of the first modern concrete dams, relatively little attention had been paid to the materials and their behaviour over time. However, even the engineers at the time were aware of certain shortcomings and attempted to solve them. The works of Abrams [13] from 1918 on concrete mixture and determination of water–cement factor are likely among the earliest in this field. Understanding the processes created by hydration of cement was encouraged in the late 1920s, when engineers tried to understand the phenomenon of hydration heat that creates unwanted cracks in massive concrete dams.
The design and construction of the Hoover Dam in the 1930s (Figure 6), the largest dam in the world at that time, with an extremely large amount of concrete, led to advancement in concrete mix design, transportation, installation and cooling of concrete. Strict controls of the installed concrete enabled the reduction in the water–cement factor, which led to significantly better quality of the concrete. Low hydration heat concrete, originally developed for the Hoover Dam, also showed very high resistance to the sulphate environment. At the same time, these successes encouraged researchers into further development of the concrete resistant to all types of degradation [14,15].
In the years that followed, various concrete mixes with different additives were proposed for concrete dams. Some concrete dams met expectations, and some did not. Comparing the results on individual dams has proven highly beneficial in designing durable and resistant concrete mixture. For example, concrete in direct contact with water at the Arrowrock Dam (Boise River, ID, USA) and the Lahontan Dam (Carson River, NV, USA) required significant repairs after 20 years of use, with concrete on the overflows proving particularly sensitive. In contrast, the Elephant Butte Dam (Elephant Butte, NM, USA) remained completely undamaged (Figure 7) [14,15].

Figure 6.
The Hoover Dam on Colorado river, USA [16].

Figure 7.
Dams in the USA: (a) Arrowrock; (b) Lahontan; (c) Elephant Butte [17,18,19].
One extreme example is the American Falls Dam, built in 1927, which exhibited significant signs of degradation and had to be replaced in 1977.
Systematic studies of the physical properties of dams, considering chemical changes in the concrete over time, have provided invaluable insights into estimating changes in compressive strength and modulus of elasticity of the concrete in contact with water.
Various improvements in the concrete durability over time are evident: from the first concrete with a reduced water–cement factor, through concrete with additives such as pozzolani, to the concrete with the addition of polymer and silicate dust (silica fume) (Figure 8) [14]. This development continues to this day.

Figure 8.
Timeline of various improvements in concrete durability [12].
3. Long-Term Effects in Concrete
In the Introduction, the effects of creep, shrinkage, ageing and corrosion on concrete are highlighted.
Observing creep and shrinkage separately is the simplest and most convenient approach. The disadvantage of this approach is evident since mentioned effects are not independent from one another [20,21].
It should also be noted that a number of different alternating external influences make it impossible for the model calculations to completely coincide with the measured results. The coefficient of variation for laboratory-measured shrinkage on samples from a single concrete mix was approximately 8% [22,23,24,25,26,27,28,29]. Hence, it is unrealistic to expect that the predicted and experimental results will be in the range of less than 20%. For creep, deviation is even greater. In structures where creep and shrinkage might cause critical deformation or stresses, conducting test specimens and extrapolating the results is advisable.
3.1. Concrete Shrinkage
Concrete shrinkage occurs during the process of concrete hardening due to hydration of cement, as well as the process of drying concrete due to loss of moisture to the environment. The volume of hardened concrete decreases. Shrinkage obtains its maximum on surfaces of the element exposed to drying and decreases towards the inside of the element. The main factors affecting shrinkage are as follows [28,29,30,31]:
- (1)
- Mechanical effects from temperature changes;
- (2)
- Thermal effects of cement hydration;
- (3)
- Hydrological effects related to hydration;
- (4)
- Hydrological effects related to climate;
- (5)
- Compressive strength of concrete;
- (6)
- Consistency of the fresh mix;
- (7)
- Type and content of cement;
- (8)
- Water–cement (w/c) factor;
- (9)
- Ratio of fine aggregate according to the total amount of aggregate;
- (10)
- Air content;
- (11)
- Effective element thickness.
According to the literature [32,33], shrinkage can be divided into four main types:
- Autogenous shrinkage—reduction in volume of the mixture of water and cement during hydration;
- Plastic shrinkage—created by the vacuum which occurs when water evaporates from the pores of the capillaries;
- Drying shrinkage—due to the loss of moisture from the concrete, i.e., the release of water from the concrete into the environment; this occurs with hardened concrete;
- Carbonization shrinkage—a reduction in volume by carbonization as a consequence of chemical reactions in cement stone caused by carbon dioxide from the environment.
Each type of shrinkage is schematically illustrated concerning concrete age (Figure 9), along with ratios between each type of shrinkage [34].
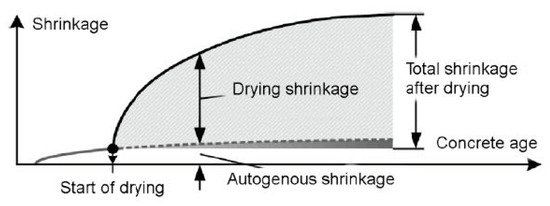
Figure 9.
Shrinkage strain components for normal concrete [34].
A large number of factors affecting shrinkage makes it impossible to generalize one universal model. Researchers have adopted a phenomenological approach, collecting data over long period of time. A contribution in this area was made by numerous authors, some of whom are listed below [21].
One of the earliest models describing concrete shrinkage originates from Michaelis and Menten [5] (1913). It explains the phenomenon of shrinkage by physical-chemical processes at the beginning of the hardening of concrete. After World War II, research on concrete shrinkage intensified. Several models were proposed, based on the phenomenological parameters: Miller (1958), Branson (1977) and Corley & Sozen (1978) [21].
From the mid-1990s, several significant studies were conducted. Hua, Erlacher and Acker (1995) proposed a macroscopic-scale analytical model of autogenous shrinkage and two years later improved this model. Koenders and Breugel (1997) used thermodynamic approach to determine autogenous shrinkage of hardening cement paste. Ishida et al. (1998) proposed a model which is based on micro-mechanical influence of water in pore structure of the concrete [21,31].
It can be shown that reduction in the shrinkage strain would substantially diminish initials cracks too [35,36,37,38]. Achieving this could involve replacing Portland cement with Sulfoaluminate cement (SAC), which can be combined with shrinkage-reducing admixture. Assuming regular concrete strength, autogenous shrinkage as well as the early-age strength of concrete, will decrease with the addition of fly ash [39,40]. Conversely, high-strength concrete will exhibit increased shrinkage under the same conditions [41].
Current research on shrinkage primarily focuses on a deeper understanding of autogenous and drying shrinkage [31], particularly in construction stages [42], using new types of cement [43], or with different types of concrete mixtures with different admixtures: various types of aggregate, fibres, etc. [44].
Despite numerous theories, shrinkage remains incompletely explored, and not all causes of this physical phenomenon have been explained. Over the last 5 years, Web of Science has registered over 80 papers dedicated specially to concrete shrinkage.
3.2. Concrete Creep
Creep is a time-dependent deformation of concrete under constant load, which can be several times greater than the initial deformation [1,2]. Concrete creep can be divided into two components:
- (1)
- Basic creep occurs in conditions without movement of moisture;
- (2)
- Creep by drying: the part of creep that occurs when there is movement of moisture from or into the environment.
For the purpose of practical design, it is not necessary to distinguish between basic creep and creep by drying [3]. Creep by drying, in addition to opening cracks, has the most significant impact on the nonlinear behaviour of structures, while the impact of basic creep on nonlinearity is almost negligible [45].
According to [2], there are three main groups of factors affect the occurrence of creep:
- (1)
- The composition of the concrete mix;
- (2)
- The impact of the environment in which the observed structure is located;
- (3)
- The design of the system.
Although the mechanism of creep is still not fully known, it can be said that creep depends on the properties and amount of cement paste and on the properties of the aggregate within the concrete mix. Generally, a concrete mix with a larger volume of aggregate (and a corresponding reduction in the content of cement paste) will lead to less creep deformation in contrast to a mix with a larger volume of cement paste. Also, the “stiffer” unit will try to “restrain” more time-dependent deformation behaviour, and thus reduce the creep effect. If aggregate is (partly) made from recycled concrete, its increasing in the concrete mix will lead to an increase in creep and shrinkage [46,47]. It has also been observed that the creep deformation is inversely proportional to the degree of cement hardening [48]. It is also known that an increase in water content [48] and air in the concrete mix causes an increase in creep deformation, which is approximately proportional to the square of the water–cement factor [48,49]. Fresh concrete with better properties ensures a lower degree of creep and shrinkage development. A study in the literature [49] deals with this issue and proposes a new numerical approach to predict time-dependent flow of fresh concrete based on the discrete element method.
The next group of factors influencing creep behaviour are the environmental conditions in which the concrete is prepared, installed and loaded. The creep size is particularly sensitive to the relative humidity conditions of the concrete sample. An increase in relative humidity causes a slower creep development and thus decline in the final amount of creep. The development of concrete creep over time also depends on the duration and type of curing of the concrete. Thus, increasing the curing period of wetting concrete is directly related to lower creep development, while curing concrete reduces the size of the final creep deformation up to 30% [2]. Creep is also very sensitive to temperature conditions; an increase in the degree of creep development is related to higher temperatures.
An important factor influencing the development of creep deformation is the adopted design solution. The magnitude of the stress in the concrete element is linearly related to the creep deformation for stress values up to approximately 40 to 60% of the compressive strength [2]. The creep deformation is inversely proportional to the strength of the concrete at the moment of loading [48]. The size and the shape of the concrete element is another key factor. Thinner concrete elements will more easily allow the loss of moisture to the environment, and will thus experience greater creep deformation than thicker concrete elements [48]. Also, load time is very important. Concrete loaded in the later period is exposed to less total creep deformation. For instance, the same concrete loaded on the first day has an 18% higher creep deformation than concrete loaded on the third day [50].
Numerous researchers, including Z.P. Bažant [22,23,24,25,26,27], have studied the phenomena of shrinkage and creep of concrete over the years. Despite many proposed models, none provide a complete description of the creep phenomenon, each having advantages, disadvantages and specific applications. More recently, many articles [51,52,53] have focused on the time-dependent behaviour of fibre-reinforced concrete or artificial materials such as AFRP (aramid fibre-reinforced polymer), CFRP (carbon fibre-reinforced polymer), or GFRP (glass fibre-reinforced polymer), although the time-dependent behaviour of “normal” concrete has not been fully tested and defined.
3.3. The Models for Prediction of Creep and Shrinkage
Over the past three decades, numerous models have been proposed to estimate the creep and shrinkage. In the majority of cases, those two phenomena are treated together. These models aim to strike a balance between reliability and ease of use, and they mainly differ in the number and type of parameters they take into account. The reliance of the engineering community, which typically possesses limited knowledge of concrete creep and shrinkage, on simplified models underscores the importance of such models in the field.
Despite a level of uncertainty such simplifications bring into the model, the right choice of parameters can much accelerate the calculations while preserving model predictions.
Some of the most commonly used models in engineering practice are as follows:
- ACI-92 (American Concrete Institute) [2];
- The Eurocode-2 model, based on Fib Model Code 1990 with its revision in 1999;
- Australian Standard AS 3600 Model Code of 1988 [7];
- South African Standard SABS 0100 2000 [54];
- The model of British Standard BS 8110 from 1985 [5];
- The new Fib Model Code Model, from 2010;
- The model of the Japanese Society of Civil Engineers.
Some engineers use strictly scientific models, such as the Gardner–Lockman model GL2000 and the B3 or B4 models suggested by Bažant and his co-workers and approved by Recommendation of RILEM (The International Union of Laboratories and Experts in Construction Materials, Systems and Structures).
With the exception of the last three models (GL2000, B3 and B4), all others are based on norms for structures design and express creep strain as the product of the concrete elastic deformation and the creep coefficient. The creep coefficient can be calculated according to several intrinsic and/or extrinsic variables [55]. Some of the mentioned codes with factors which were accounted for in calculations are listed below (Table 1) [55].

Table 1.
Models of creep and shrinkage predictions and factors accounted for [55].
All mentioned models would give significant differences in determining the creep coefficient and the relative shrinkage, so one has to be very careful in which cases to use them. A comparative study about model usage can be found in [55].
3.4. Aging of the Concrete
Concrete, widely utilized in infrastructure such as buildings, bridges and dams, is subjected to various environmental and mechanical factors that contribute to its deterioration over time. As concrete ages, it undergoes changes in mechanical and physical properties that can impact its structural integrity. Over time, factors such as moisture ingress, chemical reactions and mechanical loading contribute to deterioration. Creep, a gradual deformation under sustained loads, increases with age, leading to potential structural deformation. Shrinkage, caused by moisture loss, can result in cracking and reduced durability. Additionally, the porosity of concrete may increase over time, making it more susceptible to moisture penetration and chemical attacks. These changes in mechanical and physical properties highlight the importance of proactive maintenance and rehabilitation efforts to ensure the long-term performance of concrete structures [59,60,61].
While aging can lead to some deterioration in concrete structures, there are indeed positive aspects as well. With proper curing and aging, concrete can experience improvements in strength and modulus of elasticity over time. This phenomenon is often attributed to the ongoing hydration process, which continues even after the initial setting of the concrete. As hydration progresses, the cementitious matrix becomes more compact and dense, resulting in enhanced mechanical properties. Additionally, chemical reactions within the concrete can contribute to the development of additional bonding between particles, further increasing strength and stiffness. Therefore, aging can have beneficial effects on the mechanical properties of concrete under certain conditions.
The existing evaluations on the influence of and aging on the mechanical properties focus on compressive strength, along with elastic modulus and splitting tensile strength. Estimating the elastic modulus and splitting tensile strength is crucial since stress calculations rely on the elastic modulus, while the initiation of cracks is assessed based on the tensile strength. Often, these models take temperature into account in addition to concrete ageing [62]. Prediction models for aging concrete, like most, exhibit several shortcomings: simplified assumptions, lack of validation, limited accuracy, difficulty in accounting for combined effects, and sensitivity to input parameters.
Nowadays, many methods have been developed which involves establishing a functional relationship between concrete’s mechanical properties and its age through data fitting from early experimental data. This method aims to derive a functional equation that enables the calculation of concrete’s mechanical parameters at any given time [63].
3.5. Corrosion
The corrosion of embedded steel stands as a primary cause behind the premature deterioration of reinforced concrete structures globally [64].
The causes of corrosion in reinforced concrete (RC) structures can be attributed to several factors, including the following:
- Carbonation: Carbon dioxide (CO2) from the atmosphere reacts with calcium hydroxide in concrete, reducing its pH and neutralizing its alkalinity. As the pH level decreases to a critical point, the passive layer becomes unstable, leading to potential steel corrosion. Throughout the propagation stage, the corrosion rate is contingent upon various factors, including the presence of water and oxygen. Carbonation-induced corrosion results in general corrosion of steel when it comes into contact with carbonated concrete [65].
- Chloride Attack: Chloride ions, often present in seawater, or marine environments, can penetrate concrete and reach the embedded steel reinforcement. Chloride attack can initiate and accelerate corrosion by breaking down the passive film on the steel surface.
- Moisture and Oxygen: Corrosion of steel reinforcement in concrete requires the presence of moisture and oxygen. Water ingress through cracks or pores in the concrete provides the necessary electrolyte for the electrochemical corrosion process, while oxygen facilitates the oxidation of iron in the steel.
- Cracks and Poor Concrete Cover: Cracks in concrete structures can provide pathways for aggressive substances such as chlorides and carbon dioxide to reach the embedded steel reinforcement, accelerating corrosion. Inadequate concrete cover over the reinforcement also increases the risk of corrosion by reducing the protective barrier between the steel and external corrosive agents [66].
- Microorganisms (bacteria): Microbiologically influenced corrosion occurs when microorganisms, such as colonize the concrete surface and create conditions conducive to corrosion. These microorganisms produce metabolic by products that can degrade the protective passive film on embedded steel reinforcement and promote localized corrosion.
With respect to the abovementioned factors, carbonation and chloride attack are the most common cause of corrosion [67]. Various analytical methods for predicting basic corrosion mechanisms in reinforced concrete are proposed. Estimating the depth of carbonation in concrete can be accomplished using classical approach from CEB [68] and modified [69] diffusion models. The composition of concrete plays a significant role in the diffusion of CO2, while humidity strongly influences the rate of carbonation. Surface materials with high compactness and impermeability can noticeably delay the carbonation process of concrete. Similarly, chloride concentration within the concrete can be determined using diffusion models [69]. Various models have been proposed to incorporate the time-dependent diffusion coefficient for concretes [70,71,72,73]. It is important to account for variations in the diffusion coefficient due to concrete cracking and changes in the water-to-cement ratio. Detailed discussions on models are provided in [74].
4. Discussion
The history of engineering in the construction of permanent structures goes back to ancient civilizations, where marvels such as the pyramids in Egypt, the Great Wall of China, Roman bridges and the intricate urban planning of Macedonian and Aztec cities demonstrated early engineering prowess. From grand temples to revered churches and mosques, these structures stand as tangible testaments to the enduring ambition of engineers throughout history. The initial impetus for the development of concrete stemmed from the desire to emulate the longevity associated with natural stone while simultaneously achieving cost-effectiveness and ease of use. However, this ambitious vision has encountered challenges in its realization.
Since its inception, concrete has presented engineers with certain limitations. In response, the field has witnessed a continuous quest for innovation, leading to transformative technologies such as reinforced concrete, pre-stressed concrete, high-strength concrete, self-compacting concrete and various additive-enhanced concretes. While these advancements may not always provide cost-efficient or simplified solutions, they undeniably represent a significant advance in the field of civil engineering and push the boundaries of what is feasible. Today’s engineering is grappling with a variety of complex challenges, from the construction of towering skyscrapers and expansive bridges to the engineering of tunnels beneath the sea. Moreover, the prospect of constructing futuristic projects in space and on other planets looms on the horizon. In this landscape, understanding material behaviour, particularly under extreme loading conditions, is no longer a luxury but an essential requirement for engineers. Aspects of concrete behaviour that were once overlooked in common engineering practice, such as temperature variations, creep, shrinkage, ageing, corrosion and distinct performance phases, have now become key considerations in the planning and execution of construction projects.
5. Conclusions
Concrete, which started as a simple mix of cement, water and aggregates, has transformed into a versatile, high-tech material with the addition of fibres and other substances. This evolution demonstrates its ability to tackle various challenges. Understanding how these new materials behave is now crucial for researchers, emphasizing the importance of grasping how materials react in today’s complex construction environments.
In the modern lexicon, an “Engineer” is defined as a “skilful contriver or originator of something”. In today’s era, engineers are tasked with embodying this definition, serving as adept contrivers who can navigate and address the intricate demands posed by contemporary construction challenges. The evolution of concrete and the corresponding innovations in engineering practices reflect the dynamic nature of the field, where continual adaptation and ingenuity are indispensable to meet the evolving requirements of construction in the modern world.
Funding
This research is partially supported through project KK.01.1.1.02.0027, a project co-financed by the Croatian Government and the European Union through the European Regional Development Fund—the Competitiveness and Cohesion Operational Programme.
Data Availability Statement
Not applicable.
Conflicts of Interest
Author Neda Bebekwas employed by the company HERING d.d. for Design and Construction. The remaining authors declare that the re-search was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Naaman, A.E. Prestressed Concrete Analysis and Design: Fundamentals, 2nd ed.; Techno Press 3000: Ann Arbor, MI, USA, 2004. [Google Scholar]
- ACI Committee 209. Guide for Modeling and Calculating Shrinkage and Creep of Concrete (ACI 209.2R-08); American Concrete Institute: Farmington Hills, MI, USA, 2008. [Google Scholar]
- Mante, D.M. Improving Camber Predictions for Precast, Prestressed Concrete Bridge Girders. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 2016. [Google Scholar]
- Chow, C.O.; Hinton, E.; Abdel Rahman, H.H. Analysis of Creep and Shrinkage Effect in Reinforced Concrete Beams. In Proceedings of the International Conference on Computer-Aided Analysis and Design of Concrete Structures, Split, Yugoslavia, 17–21 September 1984. [Google Scholar]
- Ghali, A.; Favre, R.; Elbadry, M. Concrete Structures: Stresses and Deformations, 3rd ed.; Spon Press: London, UK, 2002. [Google Scholar]
- Available online: https://en.wikipedia.org/wiki/Civic_Tower_(Pavia) (accessed on 31 January 2024).
- Binda, L.; Anzani, A.; Saisi, A. Failures due to long-term behaviour of heavy structures: The Pavia Civic Tower and the Noto Cathedral. Trans. Built Environ. 2003, 66, 99–108. [Google Scholar]
- Binda, L.; Saisi, A.; Tiraboschi, C. Investigation procedures for the diagnosis of historic masonries. Constr. Build. Mater. 2000, 14, 199–233. [Google Scholar] [CrossRef]
- Binda, L. Learning from Failure Long-Term Behaviour of Heavy Masonry Structures; WIT Press: Southampton, UK; Boston, MA, USA, 2008; ISBN 9781845640576. [Google Scholar]
- Koror–Babeldaob Bridge—Wikipedia. Available online: https://en.wikipedia.org/wiki/Koror%E2%80%93Babeldaob_Bridge (accessed on 31 January 2024).
- Koror-Babeldaob Bridge|Koror, Palau|WJE. Available online: https://www.wje.com/projects/detail/koror-babeldaob-bridge (accessed on 31 January 2024).
- Bažant, Z.P.; Yu, Q.; Li, G.H. Excessive long-time deflection of prestressed boxgirder. I: Record-span bridge in Palau and other paradigms. J. Struct. Eng. ASCE 2012, 138, 676–686. [Google Scholar] [CrossRef]
- Abrams, D.A. Design of Concrete Mixtures, Structural Materials Research Laboratory; Lewis Institute: Chicago, IL, USA, 1918. [Google Scholar]
- Dolen, T.P. Materials Properties Model of Aging Concrete; Report DSO-05-05; U.S. Department of the Interior Bureau of Reclamation, Technical Service Center: Denver, CO, USA, 2005.
- Dolen, T.P.; Scott, G.; von Fay, K.; Hamilton, R. The Effects of Concrete Deterioration on Safety of Dams; Dam Safety Research Report No. DSO-03-05; Dam Safety Office (DSO), US Department of Interior: Washington, DC, USA, 2003.
- Available online: http://www.history.com/topics/hoover-dam (accessed on 31 January 2024).
- Available online: http://www.usbr.gov/projects/Facility.jsp?fac_Name=Arrowrock+Dam (accessed on 31 January 2024).
- Available online: https://en.wikipedia.org/wiki/Lahontan_Dam (accessed on 31 January 2024).
- Available online: http://elephantbuttelake.net/photos.php (accessed on 31 January 2024).
- Gribniak, V.; Kaklauskas, G.; Kliukas, R.; Jakubovskis, R. Shrinkage effect on short-term deformation behavior of reinforced concrete—When it should not be neglected. Mater. Des. 2013, 51, 1060–1070. [Google Scholar] [CrossRef]
- Gribniak, V.; Kaklauskas, G.; Bacinskas, D. Shrinkage in Reinforced Concrete Structures: A Computational Aspect. J. Civ. Eng. Manag. 2008, 14, 49–60. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Kim, S.S. Nonlinear creep of concrete—Adaptation and flow. J. Eng. Mech. Div. 1979, 105, 429–445. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Prasannan, S. Solidification theory for concrete creep. Part II: Verification and Application. J. Eng. Mech. 1989, 115, 1704–1725. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Asghari, A.A. Constitutive law for nonlinear creep of concrete. J. Eng. Mech. Div. 1977, 103, 113–124. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Panula, L. Creep and shrinkage characterization for analyzing prestressed concrete structures. PCI J. 1980, 25, 86–122. [Google Scholar]
- Bažant, Z.P.; Chern, J.C. Log-double-power law for concrete creep. ACI J. 1985, 82, 665–675. [Google Scholar]
- Bažant, Z.P.; Kim, J.K. Improved prediction model for time—Dependent deformations of concrete: Part 2—Basic creep. Mater. Struct. 1991, 24, 409–421. [Google Scholar] [CrossRef]
- Bažant, Z.P. Theory of creep and shrinkage in concrete structures: A precise of recent developments. In Mechanics Today; Nemat-Nasser, S., Ed.; Pergamon Press: New York, NY, USA, 1975; Volume 2. [Google Scholar]
- Bažant, Z.P. Mathematical models for creep and shrinkage of concrete. In Creep and Shrinkage in Concrete Structures; Bazant, Z.P., Wittmann, F.H., Eds.; John Wiley and Sons: New York, NY, USA, 1982. [Google Scholar]
- Wyffels, T.A.; Frenc, C.E.; Shield, C.K. Effects of Pre-Release Cracks in High-Strength Prestressed Concrete; Final Project Report; Minnesota Department of Transportation Office of Research Administration, University of Minnesota: St. Paul, MN, USA, 2000. [Google Scholar]
- Kovler, K.; Zhutovsky, S. Overview and future trends of shrinkage research. Mater. Struct. 2006, 39, 827–847. [Google Scholar] [CrossRef]
- Aslani, F. Experimental and Numerical Study of Time Dependet Behaviour of Reinforced Self-Compacting Concrete Slabs. Ph.D. Thesis, School of Civil and Environmental Engineering, University of Technology Sydney, Sydney, Australia, 2014. [Google Scholar]
- Gilbert, R.I.; Ranzi, G. Time-Dependent Behaviour of Concrete Structures; Spon Press: London, UK; New York, NY, USA, 2011. [Google Scholar]
- Sakata, K.; Shimomura, T. Recent progress in research on and evaluation of concrete creep and shrinkage in Japan. J. Adv. Concr. Technol. 2004, 2, 133–140. [Google Scholar] [CrossRef][Green Version]
- Gilbert, G.I. Shrinkage and early-age temperature induced cracking and crack control in concrete structures. In Proceedings of the Second International Conference on Performance-Based and Life-Cycle Structural Engineering (PLSE 2015), Brisbane, Australia, 9–11 December 2015; Fernando, D., Teng, J.-G., Torero, J.L., Eds.; pp. 591–599. [Google Scholar]
- Klemczak, B.; Knoppik-Wrobel, A. Early age thermal and shrinkage cracks in concrete structures—Description of the problem. Archit. Civ. Eng. Environ. 2011, 4, 35–48. [Google Scholar]
- Klemczak, B.; Knoppik-Wrobel, A. Early age thermal and shrinkage cracks in concrete structures—Influence of geometry and dimension of a structure. Archit. Civ. Eng. Environ. 2011, 4, 55–70. [Google Scholar]
- Safiuddin, M.; Amrul Kaish, A.B.M.; Woon, C.N.; Raman, S.N. Early—Age cracking in concrete: Causes, consequence, remedial measures, and recommendations. Appl. Sci. 2018, 8, 1730. [Google Scholar] [CrossRef]
- Biolzi, L.; Cattaneo, S.; Crespi, P.; Giordano, N. Damage in glass-concrete composite panels. Constr. Build. Mater. 2016, 116, 235–244. [Google Scholar] [CrossRef]
- Sarkar, S.; Halder, A.; Bishnoi, S. Shrinkage in concretes containing fly ash. In Proceeding of the UKIERI Concrete Congress; Jalandhar: Bella Vista, Australia, 2013; pp. 1–11. [Google Scholar]
- Kate, G.K.; Murnal, P.B. Effect of addition of fly ash on shrinkage characteristics in high strength concrete. Int. J. Adv. Technol. Civ. Eng. 2013, 2, 11–16. [Google Scholar] [CrossRef]
- Xia, D.; He, M.; Tang, Y.J.; Shi, L.W. Experimental study on concrete’s dry-shrinkage stress in construction stage. In Proceedings of the International Conference on Applied Materials and Electronics Engineering (AMEE), Hong Kong, China, 18–19 January 2012; pp. 200–203. [Google Scholar]
- Li, Y.H.; Bai, J.B.; Liu, L.M.; Wang, X.Y.; Yu, Y.; Li, T. Micro and macro experimental study of using the new cement-based self-stress grouting material to solve shrinkage problem. J. Mater. Res. Technol. 2022, 17, 3118–3137. [Google Scholar] [CrossRef]
- Frayyeh Qais, J.; Kamil Mushtaq, H. The Effect of Adding Fibers on Dry Shrinkage of Geopolymer Concrete. Civ. Eng. J. Tehran 2021, 12, 2099–2108. [Google Scholar] [CrossRef]
- Havlasek, P.; Jirasek, M. Multiscale modeling of drying shrinkage and creep of concrete. Cem. Concr. Res. 2016, 85, 55–74. [Google Scholar] [CrossRef]
- Geng, Y.; Wang, Y.; Chen, J. Creep behaviour of concrete using recycled coarse aggregates obtained from source concrete with different strengths. Constr. Build. Mater. 2016, 128, 199–213. [Google Scholar] [CrossRef]
- Seara-Paz, S.; Gonzales-Fonteboa, B.; Martinez-Abella, F.; Gonzales-Taboada, I. Time-dependent behaviour of structural concrete made with recycled coarse aggregates. Creep and shrinkage. Constr. Build. Mater. 2016, 122, 95–109. [Google Scholar] [CrossRef]
- Neville, A.M.; Brooks, J.J. Time-Dependent behaviour of concrete containing a plasticiser. Concrete 1975, 9, 33–35. [Google Scholar]
- Li, Z.; Cao, G.; Tan, Y. Prediction of time-dependent flow behaviors of fresh concrete. Constr. Build. Mater. 2016, 125, 510–519. [Google Scholar] [CrossRef]
- Polivka, M.P. Studies of creep in mass concrete, Paper 12. In Symposium on Mass Concrete; ACI Special Publication: Baltimore, MD, USA, 1964; Volume 6. [Google Scholar]
- Jeong, Y.; Lee, J.; Kim, W.S. Modeling and Measurement of Sustained Loading and Temperature-Dependent Deformation of Carbon Fiber-Reinforced Polymer Bonded to Concrete. Materials 2015, 8, 435–450. [Google Scholar] [CrossRef] [PubMed]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. Time-dependent behavior of concrete beams prestressed with bonded AFRP tendons. Compos. Part B Eng. 2016, 97, 1–8. [Google Scholar] [CrossRef]
- Zawam, M.; Soudki, K.; West, J.S. Effect of Prestressing Level on the Time-Dependent Behavior of GFRP Prestressed Concrete Beams. J. Compos. Constr. 2017, 21, 04017001. [Google Scholar] [CrossRef]
- SABS 0100 2000; The Structural Use of Concrete Part 1: Design. South African Bureau of Standards: Pretoria, South Africa, 2000.
- Usibe, B.E.; Iniobong, I.E.; Ushie, E.O.J. Prediction of Creep Deformation in Concrete Using Some Design Code Models. Lat. Am. J. Phys. Educ. 2012, 6, 375. [Google Scholar] [CrossRef]
- CEB-FIP. Design Manual Application of the CEB-FIP Model Code 1978 for Concrete Structures; CEB-FIP: Lausanne, Switzerland, 1984. [Google Scholar]
- CEB-FIP. Model Code 1990 Design Code, Thomas Telford; CEB-FIP: Lausanne, Switzerland, 1999. [Google Scholar]
- Bažant, Z.P.; Baweja, S. Creep and shrinkage prediction model for analysis and design of concrete structures—Model B3. Mater. and Struct. 1995, 28, 357–365, 415–430, 488–495. [Google Scholar]
- Pijaudier-Cabot, G.; Haidar, K.; Loukili, A.; Omar, M. Ageing and durability of concrete structures, International Centre for Mechanical Sciences. CISM 2017, 461, 255–286. [Google Scholar]
- Soutsos, M.N. Concrete Durability: A Practical Guide to the Design of Durable Concrete Structures; Thomas Telford Ltd.: London, UK, 2009. [Google Scholar]
- Wan-Wendner, R. Aging concrete structures: A review of mechanics and concept. Die Bodenkult. J. Land Manag. Food Environ. 2018, 69, 175–199. [Google Scholar] [CrossRef]
- Kim, J.-K.; Han, S.H.; Park, S.K. Effect of temperature and aging on the mechanical properties of concrete: Part II. Prediction model. Cem. Concr. Res. 2002, 32, 1095–1100. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, X.; Peng, X.; Qin, F. General Curve Model for Evaluating Mechanical Properties of Concrete at Different Ages. Coatings 2023, 13, 2002. [Google Scholar] [CrossRef]
- Bamforth, P. Enhancing reinforced concrete durability: Guidance on selecting measures for minimising the risk of corrosion of reinforcement in concrete. In Concrete Society Technical Report; Concrete Society: Camberley, UK, 2004; Volume 61. [Google Scholar]
- Bertolini, L.; Elsener, B.; Pedeferri, P.; Redaelli, E.; Polder, R. Corrosion of Steel in Concrete: Prevention, Diagnosis, Repair, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Wu, J.; He, Y.; Xu, C.; Jia, X.; Huang, Y.; Chen, Q.; Huang, C.; Dadras Eslamlou, A.; Huang, S. Interpretability Analysis of Convolutional Neural Networks for Crack Detection. Buildings 2023, 13, 3095. [Google Scholar] [CrossRef]
- Revert, A.B.; De Weerdt, K.; Hornbostel, K.; Geiker, M.R. State-of-the-Art Report: Service Life Modelling, Carbonation of Concrete and Corrosion in Carbonated Concrete; Report No. R-1-2017; Norwegian University of Science and Technology: Trondheim, Norway, 2017. [Google Scholar]
- Comité Euro-International du Béton (CEB). New Approach to Durability Design—An Example for Carbonation Induced Corrosion; Bulletin No. 238; Comité Euro-International du Béton (CEB): Lausanne, Switzerland, 1997. [Google Scholar]
- Yoon, I.-S.; Copuroglu, O.; Park, K.-B. Effect of global climatic change on carbonation progress of concrete. Atmos. Environ. 2007, 41, 7274–7285. [Google Scholar] [CrossRef]
- Roa-Rodriguez, G.; Aperador, W.; Delgado, A. Calculation of chloride penetration profile in concrete structures. Int. J. Electrochem. Sci. 2013, 8, 5022–5035. [Google Scholar] [CrossRef]
- Leber, I.; Blakey, F.A. Some effects of carbon dioxide on mortars and concrete. ACI Mater. J. 1956, 28, 295–308. [Google Scholar] [CrossRef][Green Version]
- Bentz, E.C.; Thomas, M.D.A. Life-365 Service Life Prediction Model, Life-365 Consortium III; The Silica Fume Association: Lovettsville, VA, USA, 2013. [Google Scholar]
- Kwon, S.J.; Na, U.J.; Park, S.S.; Jung, S.H. Service life prediction of concrete wharves with early-aged crack: Probabilistic approach for chloride diffusion. Struct. Saf. 2009, 31, 75–83. [Google Scholar] [CrossRef]
- Zhou, Y.; Gencturk, B.; Willam, K.; Attar, A. Carbonation-Induced and Chloride-Induced Corrosion in Reinforced Concrete Structures. J. Mater. Civ. Eng. 2014, 27, 04014245. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).