Abstract
Gas drainage radius is the most important parameter for determining reasonable well spacing. However, the drainage radius of both single-layer and multi-layer commingled gas production wells cannot be directly obtained through reservoir well tests. In order to address the above challenge, for single-layer gas production wells in a closed constant-volume gas reservoir, a calculation model for drainage radius is derived using the modified flowing material balance method. The results indicate that the calculated error of this model is only 0.73% and much smaller than that of the flowing material balance method (5.78%), implying its high accuracy. For multi-layer commingled gas production wells, another calculation model of drainage radius is established by coupling the pseudo-steady-state production capacity equation with the material balance principle. The research results demonstrate that the novel calculation model has a maximum relative error of only 2.33% and requires only two production profile tests to rapidly calculate the drainage radius of each layer within the gas reservoir, suggesting its satisfactory simplicity, significant efficiency and high precision. The proposed calculation models of drainage radius achieve a convenient and rapid calculation for both single-layer and multi-layer commingled gas production wells, and fill the theoretical gap in efficient calculation of drainage radius for a closed constant-volume gas reservoir.
1. Introduction
The radius of investigation is an important parameter for evaluating the controlled reserve of a gas well [1,2,3]. When a production well starts producing, the distribution profile of reservoir pressure becomes a funnel shape (i.e., a pressure drop funnel). The distance from the production well to the edge of the pressure drop funnel is known as the radius of investigation [1]. For a closed constant-volume gas reservoir, when the pressure reaches the boundary, the pressure wave no longer propagates outward, and the flow status of the gas reservoir becomes pseudo-steady state. In this scenario, the radius of investigation does not increase with time, which is commonly referred to as the drainage radius of a gas well [1].
Extensive studies have been conducted on the calculation models of the radius of investigation. Van Poollen [2] first proposed the calculation method for the radius of investigation of a homogeneous, uniformly thick, infinite and single-phase flow oil reservoir. Earlougher [3] established a calculation equation for the radius of investigation considering different reservoir shapes. Daungkaew et al. [4] derived a calculation formula of the radius of investigation of a vertical well in a homogeneous reservoir with a closed boundary. Whittle and Gringarten [5] suggested that the radius of investigation can be calculated using the intersection of the unit slope representing pseudo-steady flow and the horizontal slope corresponding to infinite radial flow on the pressure derivative curve. By considering oil production, reservoir thickness and pressure gauge resolution, Kuchuk [6] proposed a calculation formula of the radius of investigation of a radial cylindrical oil reservoir. Additionally, for naturally fractured reservoirs, Aguilera [7] successfully obtained a method to calculate the radius of investigation using real well-test data. For the dual-porosity gas reservoir, Wang et al. [8] derived a calculation model of the radius of investigation by considering the matrix and fractures. Nie et al. [1] first derived the calculation formula of the radius of investigation of a multi-zone composite gas reservoir. Galvao and Guimaraes [9] developed the delta transient method (DTM) to obtain the permeability and skin coefficient of each layer of a multi-layered infinite formation, and extended the method to multiple flow-rate schemes [10]. Bela et al. [11] extended the DTM method to the horizontal wellbore model in order to obtain individual layer permeabilities and skin factors of stratified reservoirs with multilateral wells. Sallam and El-Banbi [12] and Juell and Whitson [13] attempted to analyze multi-layered commingled gas reservoirs using an iterative workflow. Although they achieved history in the matching of gas wells or gas reservoirs through continuous iteration, these methods have multiple solutions.
In the process of calculating the radius of investigation, besides utilizing suitable calculation models for different oil and gas reservoirs, a large quantity of well test data is also required. Common methods for measuring well test data include the pressure drawdown test and pressure buildup test. However, the accuracy of well test data from the pressure drawdown test is easily affected by factors such as sensor specifications, instrument resolution [14], abnormal reservoir properties, flow geometry, the magnitude of applied flow rate, test duration time [15,16,17], production fluctuations and wellbore flow states [4]. Therefore, it is often recommended to use the pressure buildup test in industrial gas field case studies. However, the pressure buildup test requires shutting in the gas well for a long period, which can significantly impact field gas production, especially for low-permeability/tight gas reservoirs.
In summary, previous research on the calculation models of investigation radius has primarily focused on deriving calculation formulas suitable for different types of oil and gas reservoirs. However, the above models could only compute the average drainage radius for the gas well with a single layer [2,3,4,5,6,7,8]. Although some studies [9,10,11,12,13] have involved multi-layer commingled gas production wells, a clear calculation formula of the drainage radius of these wells was not proposed. In addition, although the well test data required for calculation of the drainage radius can be obtained by using the pressure drawdown test and pressure buildup test, its accuracy from pressure drawdown test is easily affected by many factors, while the long shut-in time required for pressure buildup test can seriously impact the production of gas field and the economic feasibility of gas reservoir development [14,15,16,17]. Therefore, it remains unknown how to calculate the drainage radius of each layer of a multi-layer commingled gas production well. In order to address these issues, this study proposes a new, convenient and rapid calculation method of the drainage radius in a closed constant-volume gas reservoir. For a single-layer gas well, this study utilizes a modified material balance method to derive a calculation model of the drainage radius in a closed constant-volume gas reservoir. This obtained model provides a quick and efficient calculation method needing only two flow pressure tests, and resolves the drawbacks of previous calculation methods requiring extensive well test data and the adverse effects of a long shut-in period during pressure buildup test on gas production. For a multi-layer commingled gas production well, this paper establishes a calculation model and solution method of the drainage radius in a closed constant-volume gas reservoir by coupling production capacity equation with the material balance principle. By using only two gas production profile tests, this proposed calculation model can address the current challenge of obtaining the drainage radius of each layer of a multi-layer commingled gas production well. The main purpose of this study is to calculate the drainage radius of single-layer/multi-layer commingled gas production wells in a closed constant-volume gas reservoir, providing a theoretical basis for determining reasonable well spacing.
2. Calculation Model of Drainage Radius of Single-Layer Gas Well
2.1. Modified Flowing Material Balance Method
Mattar and Mcneil [18] firstly proposed the flowing material balance equation, stating that when a gas reservoir is in a pseudo-steady state, the bottomhole flowing pressure and the average reservoir pressure decrease at the same rate. Also, they further concluded that the straight line of is parallel to that of . However, this method did not consider the pressure’s impact on natural gas viscosity and its compressibility, assuming these properties remain constant. Figure 1 shows the relationship curve between the product of natural gas viscosity and its compressibility and reservoir pressure in the Yanan gas field in Shaanxi Province, China. It can be seen that the product of natural gas viscosity and its compressibility increases rapidly as pressure decreases, which is contrary to the assumption of previous research. Therefore, we propose the modified flowing material balance method, and the specific method is as follows.
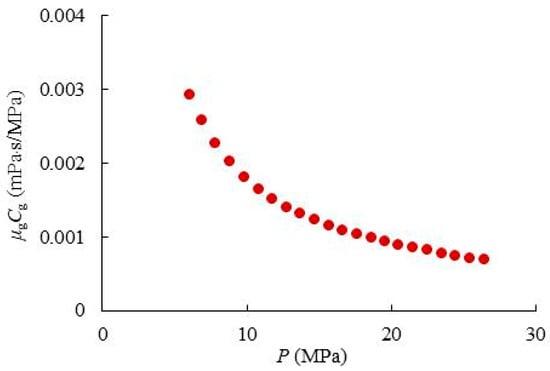
Figure 1.
Relationship curve between the product of natural gas viscosity and its compressibility and reservoir pressure.
For a single-layer gas reservoir, the following assumptions are made: (1) the gas reservoir is circular and enclosed, and a vertical production well is located in the center; (2) the gas reservoir is a uniformly thick, isothermal and horizontal medium; (3) the single-phase compressible gas satisfies Darcy’s Law; (4) the effects of gravity and capillary forces are neglected; (5) the development of the gas reservoir relies solely on elastic expansion energy.
When the flow phase of gas reservoir satisfies the pseudo-steady state:
where ΨR is the pseudo-pressure function of reservoir pressure (PR), MPa2/(mPa·s); Ψwf is the pseudo-pressure function of bottomhole flowing pressure (Pwf), MPa2/(mPa·s); t is the production time, day.
According to the definition of the compressibility of natural gas, the relationship of pseudo-pressure function (Ψ) and pseudo-pressure (P/Z) can be determined as:
where Ψ is the pseudo-pressure function of pressure P, MPa2/(mPa·s); P is the pressure at any point in the reservoir, MPa; Z is gas compressibility factor at pressure P; P/Z is the pseudo-pressure, MPa; μg is the gas viscosity, mPa·s; Cg is the compressibility of natural gas, MPa−1.
When the gas well maintains constant production, the daily gas production remains constant, so:
where Gp is the cumulative gas production, 108 m3; qsc is the daily gas production, m3/d.
Substituting Equations (2) and (3) into Equation (1) yields the flowing material balance equation for a closed constant-volume gas reservoir:
where PR is the reservoir pressure, MPa; ZR is the gas compressibility factor corresponding to PR; μgR is the gas viscosity corresponding to PR, mPa·s; CgR is the compressibility corresponding to PR, MPa−1; Pwf is the bottomhole flowing pressure, MPa; Zwf is the gas compressibility factor corresponding to Pwf; μgwf is the gas viscosity corresponding to Pwf, mPa·s; Cgwf is the compressibility corresponding to Pwf, MPa−1.
Assuming a correction factor λ and , then:
where is the correction factor for flowing material balance method.
As PR is unknown, the value of is difficult to obtain. PR can be derived by converting the production pressure drop and bottomhole flowing pressure during the pseudo-steady stage, so:
where is the production pressure drop.
From Equation (5) and the physical properties of natural gas at high pressure (as shown in Figure 1), we can obtain , so . Also, the following characteristics can be obtained: (1) at the same production pressure drop, the lower the reservoir pressure, the greater the difference between and ; (2) at the same reservoir pressure, the larger the production pressure drop, the greater the difference between them.
The modified flowing material balance method is as follows: (1) plot the relationship curve between and using known bottomhole flowing pressure and cumulative gas production data, as shown in Figure 2; (2) conduct linear fitting for the data points showing a linear trend to determine the slope of the fitted line (−m); (3) calculate the value of by Equation (6); (4) calculate the value of , and then use this value as the slope to draw a straight line through the point , the intercept of this straight line on the horizontal coordinate is the original gas in place () calculated using the modified material balance method (Equation (7) is the formula for this straight line); (5) substitute the value of into the volumetric method formula (Equation (8)) [19] to obtain the gas well’s drainage radius ():
where m is the slope of the straight line section of , MPa/108 m3; Pi is the original formation pressure, MPa; Zi is the gas compressibility factor corresponding to Pi.
where re is the drainage radius, m; Gi is the original gas in place, 108 m3; Pi is the reservoir temperature, MPa; Ti is the reservoir temperature, K; h is the reservoir thickness, m; Sgi is the initial gas saturation; is the porosity of production layer j; Tsc is the standard condition temperature, 293.15 K; Psc is the standard condition pressure, 0.1013 MPa.
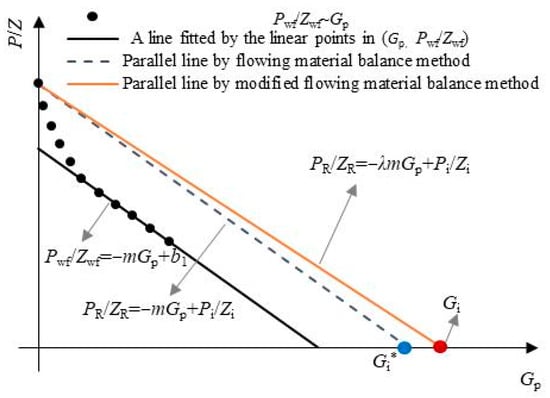
Figure 2.
Schematic diagram of the determination of original gas in place using modified flowing material balance method.
2.2. Method Validation
In order to validate the accuracy of the above flowing material balance method, a circular and enclosed gas reservoir model with a central vertical production well is established using Eclipse (Version 2010) numerical simulation software. The physical properties of the gas reservoir model are listed in Table 1 and this model is used to simulate the entire production process of the gas reservoir with a single layer. The gas well is operated under a constant gas rate, and the numerical simulation results during the pseudo-steady stage are shown in Figure 3.

Table 1.
Physical properties of the gas reservoir model.
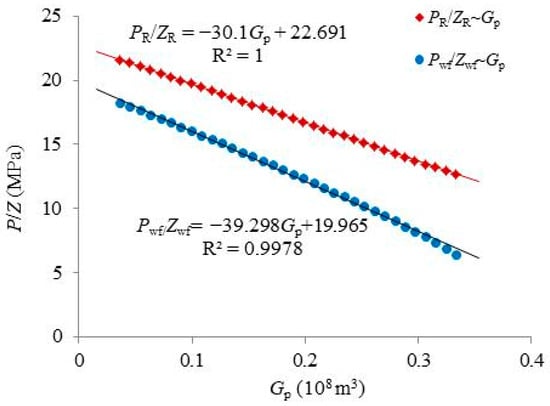
Figure 3.
The relationship of pseudo-reservoir pressure and cumulative gas production.
From Figure 3, it can be seen that and the slope of (i.e., m) is −39.298. Also, the value of can be determined as 22.691 by the mathematical formula of the regression trend line using the red points. The value of λ can be obtained using Equation (6) and is approximately 0.78. And then, using Equation (7), when P/Z = 0, the original gas in place can be calculated as = 22.691/(0.78 × 39.298) = 0.7403 × 108 m3. Using this value and Equation (8), we can obtain the value of the drainage radius as 494.1 m.
Table 2 compares the calculation results of different methods. It can be seen that the calculation error of the drainage radius using flowing material balance method is very large (12.72%), while that of the modified flowing material balance method is only 1.18%, suggesting that our proposed modified flowing material balance method is more accurate.

Table 2.
Comparison of calculation results for different methods.
2.3. Practical Application
There is a gas well X1 in a gas reservoir, the production layer is s2, the effective gas layer thickness is 8.2 m, reservoir porosity is 7.3%, initial gas saturation is 70.87%, reservoir temperature is 90.68 °C and original reservoir pressure is 20.956 MPa. Well X1 undergoes multiple pressure recovery tests and flowing pressure tests. And then, these test data are used to plot the relationship of and . The relationships of and and and are shown in Figure 4. Table 3 compares the calculated results of original gas in place and the drainage radius for well X1 using the material balance method, flowing material balance method, and modified flowing material balance method. From Table 3, it can be observed that compared to the material balance method, the relative errors of original gas in place and drainage radius obtained by modified flowing material balance method is much smaller than that calculated by flowing material balance method. These results demonstrate that the calculation model of drainage radius derived from the proposed modified flowing material balance method has high precision and lower relative error.
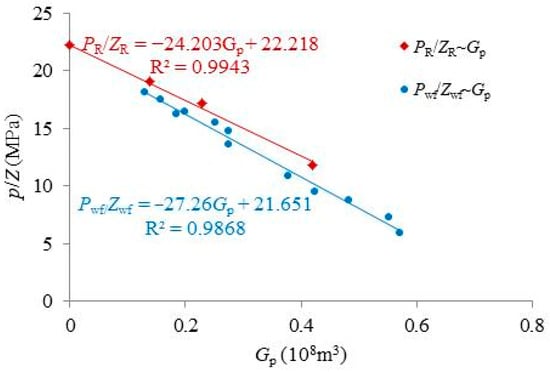
Figure 4.
Relationship of and for well X1.

Table 3.
Comparison of calculation results for different methods for well X1.
3. Calculation Model of Drainage Radius of Multi-Layer Commingled Gas Production Well and Its Application
3.1. Calculation Model of Drainage Radius of Multi-Layered Gas Well
For a multi-layered gas reservoir, the following assumptions are made: (1) the gas reservoir is circular and enclosed, and a vertical production well is located in the center and produces from multiple layers; (2) the gas reservoir is a uniformly thick, isothermal, and horizontal medium; (3) the single-phase compressible gas satisfies Darcy’s Law; (4) the effects of gravity and capillary forces are neglected; (5) the development of the gas reservoir relies solely on elastic expansion energy; (6) inter-layer crossflow is not considered. The productivity equation of the gas well when the j-th layer stays in pseudo-steady flow is given by:
where the coefficient of productivity equation, Aj, is defined as:
where j is the layer number, j = 1, …, n; n is the number of layers in the gas well, dimensionless; ΨRj is the pseudo-reservoir pressure function of layer j, MPa2/(mPa·s); Ψwfj is the pseudo-bottomhole flowing pressure function of layer j, MPa2/(mPa·s); Aj is the productivity coefficient of layer j, MPa2/(mPa·s)/(m3/d); qscj is the daily gas production of layer j, m3/d; Tj is the temperature of layer j, K; rej is the drainage radius of layer j, m; rw is the wellbore radius, m; Sj is the skin factor of layer j, dimensionless; Kj is the permeability of layer j, 10−3μm2; hj is the thickness of layer j, m.
Take the derivative of Equation (9) with respect to time t, and then substitute Equation (2) into it, yielding the following equation:
where PRj is the reservoir pressure of layer j, MPa; ZRj is the gas compressibility factor corresponding to PRj, dimensionless; μgRj is the gas viscosity corresponding to PRj, mPa·s; CgRj is the compressibility corresponding to PRj, MPa−1; Pwfj is the bottomhole flowing pressure of layer j, MPa; Zwfj is the gas compressibility factor corresponding to Pwfj, dimensionless; μgwfj is the gas viscosity corresponding to Pwfj, mPa·s; Cgwfj is the compressibility corresponding to Pwfj, MPa−1.
For a constant-production gas well, if the production ratio of each layer remains unchanged, the second term on the right side of Equation (11) is 0, and Equation (11) can be transformed into Equation (4) which represents the flowing material balance equation for a closed constant-volume gas reservoir.
The material balance principle for a closed constant-volume gas reservoir [20,21,22] is given by:
where Pij is the original reservoir pressure of layer j, MPa; Zij is the deviation factor corresponding to Pij; Tij is the temperature of the reservoir, K; Gpj is the cumulative gas production of layer j, 108 m3; Gij is the controlled reserves of layer j, 108 m3; Sgij is the initial gas saturation of layer j; is the porosity of layer j.
Substitute Equation (12) into Equation (11):
where is the average daily gas production of layer j, m3/d.
Assuming and , Equation (13) can be simplified as:
where is the change rate of the pseudo-bottomhole flowing pressure in layer j, MPa/d; is the change rate of the gas rate in layer j, m3/d2.
From Equations (10) and (14), it can be observed that the two terms on the right side of Equation (14) are related to the drainage radius. Moreover, if the change rate of the gas rate in layer j is smaller, the second term on the right side of Equation (14) is smaller, and the impact of Aj on the calculation results of the drainage radius is smaller.
The calculation procedures for the drainage radius of a multi-layer commingled gas production well are as follows: (1) obtain bottomhole flowing pressures Pwfj(t1) and Pwfj(t2) and gas rates qscj(t1) and qscj(t2) at two arbitrary times t1 and t2 through gas production profile tests; (2) use the data from step (1) and the definition formulas of and to calculate their values; (3) assume an initial value for the drainage radius and substitute it into Equation (14), and then calculate the value of the right side of Equation (14); (4) compare the values of the left and right sides of Equation (14), if the error between them is less than 1 × 10−4, the initial value of is the drainage radius of multi-layer commingled gas production well; if the error is larger than 1 × 10−4, re-assume an initial value of and repeat steps (3) and (4) until the error between the values on the left and right sides of Equation (14) meets the setting requirements; then, the obtained is the drainage radius of multi-layer commingled gas production well. The procedure used in the model calculations is shown in the flowchart of Figure 5.
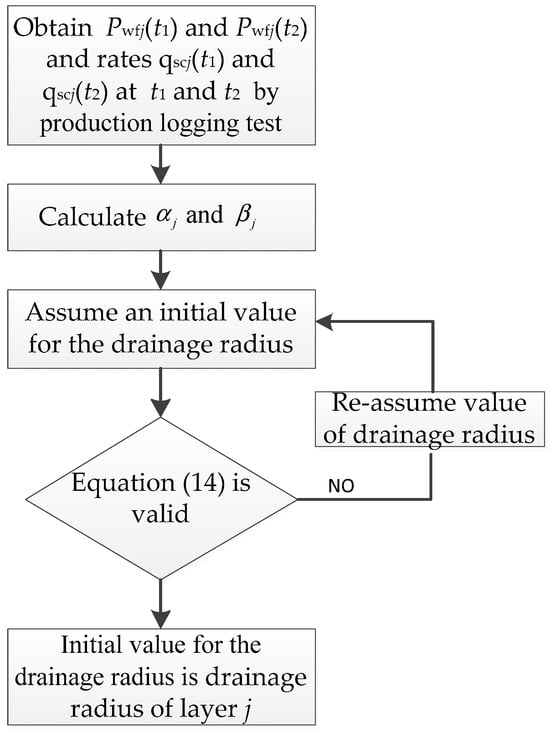
Figure 5.
Flowchart of calculation model of drainage radius.
3.2. Method Validation
The drainage radius of multi-layer commingled gas production wells cannot be directly measured through reservoir well tests, so it is difficult to verify the accuracy of the proposed calculation model through the measured value of drainage radius. Therefore, in order to validate the accuracy of the calculation model of drainage radius, Eclipse numerical simulation software is applied to create a circular and enclosed gas reservoir model with a vertical production well in the center, which is used to simulate the entire production process of a multi-layer commingled gas production well. Specific properties of the gas reservoir model are shown in Table 4. Radial grids are adopted in the gas reservoir model and the grid block sizes in the radial direction, the theta direction and the vertical direction are 10 m, 11.25° and 1 m, respectively. Figure 6 and Figure 7 show the gas–water relative permeability curve and gas PVT data for different layers in the model, respectively. The gas well is operated under a constant gas rate. As shown in Table 4, drainage radii of different layers in the gas reservoir model are given. Using the above data, reservoir simulation can be conducted to obtain production data (such as gas rate and bottomhole flowing pressure). Figure 8 presents the production data for three layers resulting from the numerical reservoir simulation. The calculated value of the drainage radius can be obtained by using the proposed calculation model and the obtained production data. And then, the derived calculation model can be verified by comparing the calculated values with the given values in the gas reservoir model.

Table 4.
Properties of gas reservoir model.
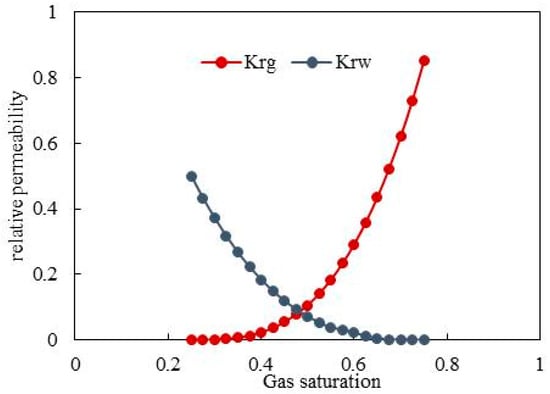
Figure 6.
Gas–water relative permeability curves.
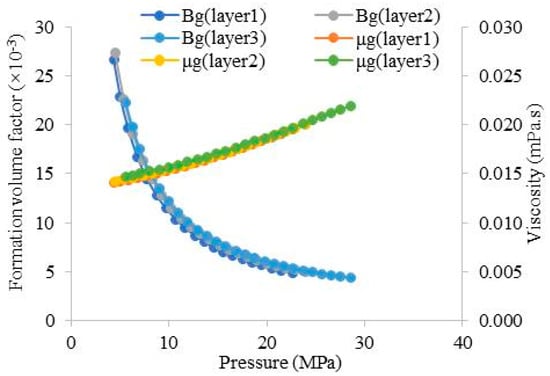
Figure 7.
Gas PVT for every layer.
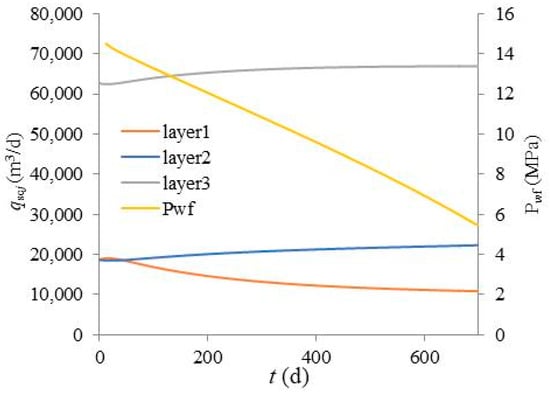
Figure 8.
Gas rates and bottomhole flowing pressure in a commingled gas reservoir model.
The aforementioned calculation procedures of drainage radius and the data of bottomhole flowing pressure and gas rate at 300 days and 600 days are applied to calculate drainage radius. Table 5 shows the calculated results for each layer. From Table 5, it can be observed that the drainage radius for layers 1 to 3 in gas reservoir are 295.7 m, 492.3 m and 716.3 m, respectively. The maximum relative error between the calculated values and the actual values of drainage radius from the Eclipse numerical gas reservoir model (Table 4) is 2.33%. These results suggest that the proposed calculation model of drainage radius of multi-layer commingled gas production well is significantly accurate. Also, it enables quick calculation of the drainage radius only using bottomhole flowing pressure and gas rate from two arbitrary time points. In summary, the proposed model is simple, efficient and highly accurate, meeting the engineering calculation requirements of on-site gas fields.

Table 5.
Calculation results of drainage radius for three layers.
3.3. Sensitivity Analysis
From Equation (14), it can be seen that the parameters influencing the calculation results of drainage radius primarily include the change rate of the pseudo-bottomhole flowing pressure (), natural gas properties (such as and ), coefficient of productivity equation (Aj) and change rate of the gas rate (). Bottomhole flowing pressure during gas well production is relatively easy to obtain and has high accuracy. Therefore, the values of and are relatively accurate. However, Aj is determined by formation coefficient (Kh) and skin factor (S). Thus, the parameters affecting the calculation results of drainage radius are primarily natural gas properties (), formation coefficient (Kh), skin factor (S) and change rate in the gas rate ().
In the actual production process of gas wells, there is a certain uncertainty in the values of each parameter. In order to analyze the impact of the uncertainty of each parameter on drainage radius, a sensitivity analysis of various parameters is conducted. Figure 6 illustrates the impact of four parameters on the drainage radius within different ranges of variation. From Figure 9, it can be seen that natural gas properties has the greatest impact on calculation results of drainage radius, while formation coefficient, skin factor and change rate in the gas rate have relatively small effects. Therefore, the values of natural gas properties are the most important.
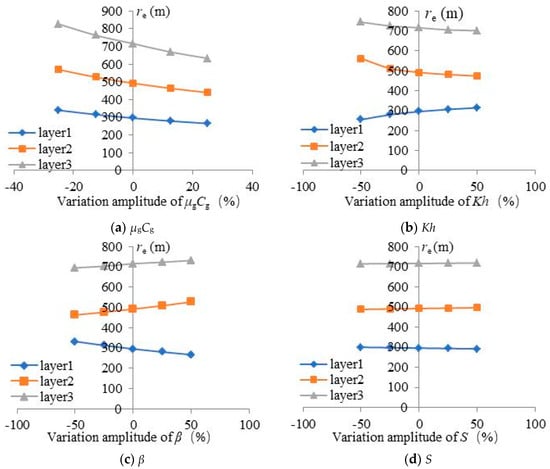
Figure 9.
Impact of four parameters on drainage radius.
3.4. Case Study of Calculation Model of Drainage Radius
There is a gas reservoir belonging to the Yanchang Petroleum (Group), where the multi-layer commingled gas production well is X6. The main three production layers of the gas reservoir are the layer of h8, s1 and s2. Well X6 began gas production in February 2015, and two production profile tests were conducted on 3 December 2015 and 25 September 2019. The reservoir properties and the results of production profile tests for each layer are presented in Table 6.

Table 6.
Reservoir properties and results of production logging tests of well X6.
Utilizing the aforementioned proposed calculation model to obtain the drainage radius of well X6, the calculated results of layer h8, s1 and s2 are 327.9 m, 129.1 m and 394.3 m, respectively. Since the drainage radius of a multi-layer commingled gas production well cannot be directly obtained through well testing, a numerical simulation model for the gas reservoir is established using Eclipse reservoir numerical simulation software to validate the reliability of the proposed calculation model of drainage radius. The grid settings, gas–water relative permeability curve and gas PVT data used in numerical model of the gas reservoir are the same as that of Section 3.2.
After using the calculated radii of drainage of three layers in the reservoir numerical model, the reliability of the proposed calculation model is validated through history matching of the bottomhole flowing pressure and comparison of the gas rate splitting coefficients of each layer in well X6. Figure 10 displays the history matching of the measured and simulated bottomhole flowing pressure of well X6. Figure 11 illustrates the comparison between the measured and simulated gas rate splitting coefficients of each layer in well X6.
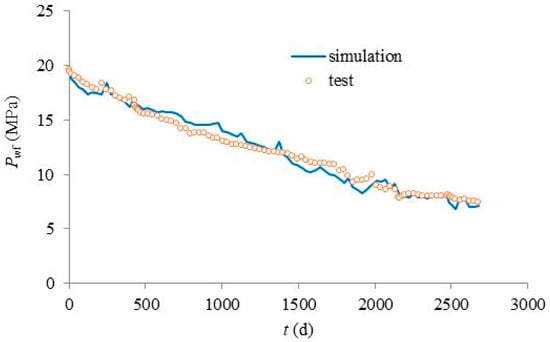
Figure 10.
History matching of bottomhole flowing pressure of well X6.
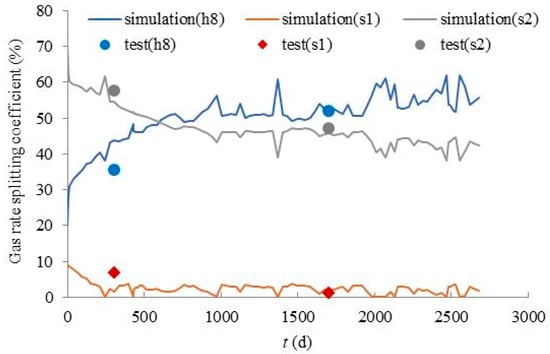
Figure 11.
Comparison of measured and simulated gas rate splitting coefficients of each layer in well X6.
From Figure 10 and Figure 11, it can be seen that the simulated bottomhole flowing pressure and gas rate splitting coefficients of each layer of well X6 are well-fitted to the measured data. This confirms the reliability of the proposed calculation model of drainage radius of multi-layer commingled gas production well.
4. Discussion
The results of the reservoir numerical simulation and the case study of the real gas field show that the proposed calculation models of drainage radius are very simple, efficient and highly accurate. However, it should be pointed out that these novel calculation models are derived by using the assumption of pseudo-steady flow. Also, the derived calculation models in this paper are suitable for a closed constant-volume gas reservoir with pseudo-steady flow. Like previous research [13], this study assumes that the boundary is circular. When the boundary is another shape, further research is needed. In addition, from Equations (5) and (14), it can be found that the calculation models all involve the physical properties of natural gas (i.e., μg and Cg). Through the sensitivity analysis in Section 3.3, it can be seen that the impact of natural gas physical properties on the calculation results is greater than that of the formation coefficient (Kh), skin factor (S) and change rate in the gas rate (). Therefore, PVT testing of natural gas is very important and has a significant impact on the calculation results. Moreover, for gas reservoirs with large changes in natural gas components, certain uncertainties will be brought to the calculation models.
By observing the calculation procedures, it is clear that the calculation models of drainage radius of commingled gas production wells require at least two gas production profile tests. However, the accuracy of the tests is limited by the precision of test instruments. At the same time, sand production and liquid accumulation in the wellbore increase the difficulty in interpreting the test data, leading to certain errors in calculation results. Fortunately, according to the sensitivity analysis in Section 3.3, it is proved that the change rate of the gas rate () has relatively little impact on the calculation results drainage radius.
5. Conclusions
In this study, the calculation methods of drainage radius of single-layer/multi-layer commingled gas production wells in a closed constant-volume gas reservoir are investigated. Based on the results of analytical studies, the following conclusions can be drawn:
- (1)
- The novel calculation model of the drainage radius of a single-layer gas well is proposed and proven to be effective and accurate. Results from the case study indicate that the error of calculated drainage radius is only 0.73%, significantly lower than that of the flowing material balance method (5.78%).
- (2)
- The newly derived calculation model of the drainage radius of multi-layer commingled gas production well is established by coupling a production capacity equation with the principle of mass balance in the closed constant-volume gas reservoir. This model is significantly concise and efficient, requiring only two gas production profile tests to swiftly calculate the drainage radius for each layer within the gas reservoir.
- (3)
- The proposed calculation model of the drainage radius of the multi-layer commingled gas production well is validated using reservoir numerical simulation. The results indicate that a maximum relative error of this model is only 2.33%, demonstrating that it has good simplicity, significant efficiency and high precision and meets the engineering calculation demands in gas fields.
- (4)
- Sensitivity analysis reveals that the calculation model of drainage radius is most sensitive to the physical properties of natural gas, while the influences of formation coefficient, skin factor and change rate of the gas rate are comparatively small.
- (5)
- The case study of a closed constant-volume gas reservoir with multi-layer commingled gas production well demonstrates the proposed calculation model of drainage radius has satisfactory accuracy and reliability. It can achieve a good history-match of the actual measured bottomhole flowing pressure and gas rate splitting coefficients for each layer with the simulated data.
Author Contributions
Conceptualization, C.X., W.Z., L.Z. and X.Q.; methodology, C.X., W.Z., X.Q. and Y.W.; software, L.Z. and Y.X.; validation, C.X., W.Z., L.Z., X.Q. and Y.X.; formal analysis, C.X. and W.Z.; investigation, X.Q. and Y.W.; resources, L.Z.; data curation, L.Z. and Y.X.; writing—original draft preparation, C.X. and W.Z.; writing—review and editing, W.Z., L.Z., X.Q. and Y.W.; visualization, Y.W. and W.Z.; supervision, X.Q. and W.Z.; project administration, Y.W. and X.Q.; funding acquisition, W.Z, X.Q. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the West Light Foundation of the Chinese Academy of Sciences (Grant No. XAB2021YW03), the Natural Science Foundation of Shaanxi Province of China (Grant No. 2023-JC-YB-368), the National Natural Science Foundation of China (Grant No. 51804036), the Key Research and Development Program of Shaanxi Province (Grant No. 2023-YBGY-308) and Fundamental Research Funds for the Central Universities (Grant No. 300102271205).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, C.X., upon reasonable request.
Acknowledgments
The authors would like to thank the Research Institute of Shaanxi Yanchang Petroleum (Group) Co., Ltd. for its support.
Conflicts of Interest
Authors C.X., L.Z., X.Q. and Y.W. were employed by the company Research Institute of Shaanxi Yanchang Petroleum (Group) Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Nie, R.-S.; Zhou, H.; Chen, Z.; Guo, J.-C.; Xiong, Y.; Chen, Y.-Y.; He, W.-F. Investigation radii in multi-zone composite reservoirs. J. Pet. Sci. Eng. 2019, 182, 106262. [Google Scholar] [CrossRef]
- Van Poollen, H.K. Radius of drainage and stabilization-time equations. Oil Gas J. 1964, 62, 138–164. [Google Scholar]
- Earlougher, R.C. Advances in Well Test Analysis, Monograph Series; SPE Press: Richardson, TX, USA, 1977; pp. 5–15. [Google Scholar]
- Daungkaew, S.; Hollaender, F.; Gringarten, A.C. Frequently Asked Questions in Well Test Analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Whittle, T.M.; Gringarten, A.C. The Determination of Minimum Tested Volume from the Deconvolution of Well Test Pressure Transients. In Proceedings of the Society of Petroleum Engineers, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Kuchuk, F.J. Radius of Investigation for Reserve Estimation from Pressure Transient Well Tests. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 15–18 March 2009. [Google Scholar]
- Aguilera, R. Radius and linear distance of investigation and interconnected pore volume in naturally fractured reservoirs. J. Can. Pet. Technol. 2006, 45, 729–734. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, T.; Ma, X. Modeling the nonlinear flow for a multiple fractured horizontal well with multiple finite-conductivity fractures in triple media carbonate reservoir. J. Porous Media 2018, 21, 1283–1305. [Google Scholar] [CrossRef]
- Galvao, M.S.C.; Guimaraes, C.S. A New Method for Calculating Individual Layer Permeability and Skin in a Multilayered Reservoir Using Production Logging Data: The Delta Transient Method. In Proceedings of the SPE Latin America and Caribbean Mature Fields Symposium, Salvador, Brazil, 15–16 March 2017. [Google Scholar]
- Guimaraes, C.S.; Galvao, M.S.C. Application of the Delta Transient Method to Multi-Rate Tests: A Method for Calculating Individual Layer Permeability and Skin in a Multilayered Reservoir using Production Logging Data. In Proceedings of the Offshore Technology Conference, Rio de Janeiro, Brazil, 24–26 October 2017. [Google Scholar]
- Bela, R.V.; Pesco, S.; Barreto, A.B.; Onur, M. Assisted history matching and graphical methods for estimating individual layer properties from well testing data in stratified reservoirs with multilateral wells. J. Pet. Sci. Eng. 2022, 208, 109326. [Google Scholar] [CrossRef]
- Sallam, M.A.; El-Banbi, A.H. Analysis of multi-layered commingled and compartmentalized gas reservoirs. J. Pet. Explor. Prod. Technol. 2018, 8, 1573–1586. [Google Scholar] [CrossRef]
- Juell, A.; Whitson, C.H. Backpressure equation for layered gas reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Ramakrishnan, T.S.; Prange, M.D.; Kuchuk, F.J. Radius of investigation in pressure transient testing. Transp. Porous Media 2020, 12, 106–112. [Google Scholar] [CrossRef]
- Wang, Y.; Yi, X. Flow modeling of well test analysis for a multiple-fractured horizontal well in triple media carbonate reservoir. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 439–457. [Google Scholar] [CrossRef]
- Wei, M.; Duan, Y.; Dong, M.; Fang, Q.; Dejam, M. Transient production decline behavior analysis for a multi-fractured horizontal well with discrete fracture networks in shale gas reservoirs. J. Porous Media 2019, 22, 343–361. [Google Scholar] [CrossRef]
- Blasingame, T.A.; Johnston, J.L.; Lee, W.J. Type-Curve Analysis Using the Pressure Integral Method. In Proceedings of the SPE California Regional Meeting, Bakersfield, CA, USA, 5–9 April 1989. [Google Scholar]
- Mattar, L.; Mcneil, R. The flowing gas material balance. J. Can. Pet. Technol. 1998, 37, 52–55. [Google Scholar] [CrossRef]
- Shariff, A.J. An Approach for Determining the Drainage Boundary of the Gas Wells Producing from Low-Permeability Gas Reservoirs. In Proceedings of the SPE Unconventional Gas Technology Symposium, Louisville, KY, USA, 18–21 May 1986. [Google Scholar]
- Schilthuis, R.J. Active Oil and Reservoir Energy. Trans. Aime 1936, 118, 33–52. [Google Scholar] [CrossRef]
- Havlena, D.; Odeh, A.S. The Material Balance as an Equation of a Straight Line? Part II, Field Cases. J. Can. Pet. Technol. 1964, 16, 815–822. [Google Scholar] [CrossRef]
- Hirakawa, S. Gas Reservoir Material Balance. J. Jpn. Assoc. Petrol. Technol. 1959, 24, 1–2. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).