Abstract
The algorithmic complexity vulnerability (ACV) that may lead to denial of service attacks greatly disrupts the security and availability of applications, and due to the widespread use of third-party libraries, its impact may be amplified through the software supply chain. The existing work in the field is dedicated to abstract loop or iterative patterns and fuzzing the entire application to discover algorithm complexity vulnerabilities, but they still face efficiency and effectiveness issues. Our research focuses on: (1) proposing a representation and extraction method for code features related to algorithmic complexity vulnerabilities, helping analysts quickly understand program logic; (2) providing a new ACV detecting model, focusing on the spatial complexity anomalies caused by deep recursion structures, and proposing a new filtering method; and (3) aiming at the difficulty of efficiently generating complex-data-type-related payloads using existing symbol execution techniques, a call-chain-guided payload construction method is proposed. We tested third-party components in the open-source Java Maven Repository, identified many unexposed vulnerabilities, and eight of them received Common Vulnerabilities and Exposures (CVE) identifiers, and demonstrated that our method can discover more algorithmic complexity vulnerabilities compared to existing tools with better performance.
1. Introduction
An algorithmic complexity vulnerability is an inappropriate design or implementation of algorithmic logic that can lead to attackers carefully constructing malicious inputs, triggering abnormal resource consumption or time consumption, and resulting in a denial of service [1]. The most typical such kind of denial of service (DoS) attack is Zip bomb [2], such as 42.zip [3], which may appear to be only 42 KB, but after decompression, it can scale to several PB of data, causing enormous pressure on the decompression program and resources, resulting in spatial ACV. The Regular Expression Denial of Service (ReDoS) vulnerability [4,5,6,7,8,9], is another type of vulnerability caused by improper filtering rules on regular expressions, allowing attackers to consume a significant amount of time and resources for software or library regular matching operations by submitting specific inputs. The recent occurrence in Ruby, such as CVE-2023-36617 [10], is a typical example.
As above, compared to traditional memory crash vulnerabilities that can be tested through blind fuzzing methods, algorithm complexity vulnerabilities are more closely integrated with algorithm design and implementation, which leads to traditional blind fuzzing methods being more inefficient. At the same time, due to the extensive use of open-source components including logging framework and blockchain smart contrast provided by third-party repositories in modern software development, such as Maven and GitHub, software developers unintentionally introduce code with algorithmic complexity vulnerabilities developed by others, further expanding the threats of ACV. This also makes it difficult for existing analysis methods to analyze algorithmic complexity vulnerabilities hidden in open-source components.
At present, researchers have proposed solutions to the above problems. Liu et al., proposed Acquirer [11], which combines static and dynamic methods to generate control flow and data flow graphs of the program, identify potential algorithm complexity issues, and use dynamic testing techniques to verify the resource consumption of the program, thereby discovering and verifying temporal ACVs. Awadhutkar et al. proposed DISCOVER [12], a static analysis tool that calculates the time complexity of a loop by analyzing the number of iterations in the loop, internal operations in the loop body, and nested structures. Blair et al., proposed HotFuzz [13], which compensates for the shortcomings of traditional fuzzing methods in discovering ACVs by introducing temporal and spatial guidance, in order to discover more spatial and temporal features associated with different inputs. Through directional fuzzing testing, more ACVs are discovered. Li et al., proposed a dynamic path search approach that combines dynamic symbol execution and constraint-based path exploration techniques to explore the execution path of a program, and detects ACVs based on path coverage information and pathological inputs [14].
In order to address the challenges faced by detecting ACV and address the gap in related field mentioned above, we propose a three-step ACV detection and verification workflow. First, we propose a static analysis method based on analyzing Java bytecode, analyzing various complex iterations and other conditional operations, APIs such as I/O, exception handling mechanisms, etc., in order to provide detailed information for analysts to perform high-level abstraction and filter suspicious vulnerability code call chains. Secondly, to compensate for the shortcomings of existing ACV detecting models, a brand new Java ACV model related to exception handling mechanism in deep recursion process is proposed. The existing methods have strong randomness and require a large amount of manual verification, ignore the underlying causes of vulnerabilities, such as Java language features, which reduces the efficiency of analysis. Finally, we propose a ACV verification and payload generation method. Most existing symbolic execution techniques are used in the stage of initial filtering suspicious code with ACVs. However, applying symbolic execution to the payload generation stage also has certain limitations, such as lack the ability to support complex data types. A call-chain-based and manually assisted payload generation method is proposed, which can more efficiently accelerate the vulnerability verification and payload generation.
To demonstrate the ability of our proposed method to detect ACVs in open-source repositories, we conducted an analysis on Maven, the most popular third-party component repository in Java. During the experiment, we identified a large number of vulnerability call chains with algorithmic complexity risks and conducted manual verification. We constructed corresponding payloads and provided vulnerability reports to the project maintainers. Among them, eight were officially recognized and assigned CVE numbers. In addition, other vulnerability call chains have been manually confirmed to affect the reliable operation of the algorithm, but have not yet been submitted to the maintainers. Compared to the State-of-the-Art (SOTA), it has also achieved significant improvements.
In summary, the main contributions of our work are listed as follows:
- A static analysis method for filtering program call chain. We provide optional static analysis methods, including sensitive call chain filtering based on the Root framework and graph based analysis, supporting abstract understanding of program algorithm and logic, and supporting the construction and application of vulnerability models.
- A new model for detecting algorithm complexity vulnerabilities. An ACV model related to Java deep recursion and exception handling mechanisms has been proposed, and a call chain filtering and analysis method has also been proposed. This model have been overlooked in existing research, but still remain an important cause of spatial algorithm complexity vulnerabilities.
- Payload generation guided by vulnerable call chains. Applying symbolic execution and constraint solving to payload generation instead of path solving still has certain shortcomings. A vulnerable call chains guided payload generation method is proposed to achieve faster vulnerability verification, and improve the efficiency of vulnerability exploitation.
- New algorithm complexity vulnerabilities. Based on the above work, detailed testing was conducted on third-party components in the Maven Repository, discovering many new 0-day vulnerabilities and obtaining eight CVE numbers.
The remaining parts of our paper are organized as follows: Section 2 summarizes the work in related fields, Section 3 introduces the background and threat model of this research, Section 4 introduces the main innovations of this paper, Section 5 describes and introduces the experimental results, and Section 6 summarizes and prospects for the future.
2. Related Work
Awadhutkar et al. [12,15] noted that fully automated detection of algorithmic complexity vulnerabilities is not feasible. Therefore, they proposed a tool named DISCOVER to assist in detecting these vulnerabilities. Their workflow mainly consists of three stages: First, they automate loop feature description based on the Termination Dependence Graph (TDG) and Loop Projected Control Graph (LPCG). Subsequently, they filter for suspicious loop patterns and further provide a catalog of loops to users for interactive auditing.
Blair et al. [13] introduced HotFuzz, a Guided Micro-Fuzzing method designed to discover Algorithm Denial-of-Service vulnerabilities. They utilized genetic algorithms to evolve arbitrary Java objects, aiming to trigger the worst-case performance of target methods. They defined Small Recursive Instantiation (SRI) to derive seed inputs represented as Java objects for micro-fuzzing. Additionally, they employed EyeVM to track and analyze the root causes of these vulnerabilities.
Wei et al. [16] introduced a pattern fuzzing method named Singularity, aimed at uncovering the worst-case scenarios in given applications. The authors initially proposed a Domain Specific Language-style approach, namely the Recurrent Computation Graph (RCG) computational model, to express input patterns. Furthermore, they utilized a genetic programming (GP) algorithm to manipulate RCGs for solving optimization problems, thus generating more effective input patterns that trigger the worst performance. They discovered availability vulnerabilities in real-world applications such as Google Guava and JGraphT.
Liu et al. [11] proposed a hybrid method for detecting algorithmic complexity vulnerabilities. This approach initially employs static methods to analyze loops and recursive structures in the target Java source code, identifying potentially vulnerable loop constructs. It then utilizes context information to guide critical path instrumentation, and constructs test cases based on branch strategies. By employing dynamic selective symbolic execution for path searching, it discovers cases that exhibit abnormal resource consumption, thereby uncovering time complexity-related algorithmic complexity vulnerabilities.
Noller et al. [17] proposed a hybrid method that combines fuzz testing and symbolic execution to detect time and space complexity algorithmic vulnerabilities. The main contribution of this method lies in its initial development of a fuzz testing approach, aimed at enhancing coverage and exploring paths with high resource consumption. To improve the efficiency of fuzz testing, a symbolic execution technique is employed. On the one hand, this technique explores potential high resource consumption paths through symbolic execution. On the other hand, it guides fuzz testing to generate samples that satisfy branch conditions, thereby enhancing the effectiveness of the approach.
Liu et al. [18] proposed a method for detecting and exploiting vulnerabilities related to ReDoS. They developed a tool named Revealer, which also combines static and dynamic analyses. Initially, they use static analysis tools to locate potentially vulnerable structures in regular expressions. Subsequently, they dynamically validate whether these vulnerable structures can be triggered. The dynamic method employed by the authors differs from fuzz testing and is a relatively precise method of generating regular expressions. They achieved performance improvements and detected a large number of new vulnerabilities.
To sum up, current work in analyzing algorithmic complexity vulnerabilities mainly includes two major approaches, i.e., static method and dynamic method. Static methods are exemplified by loop characteristic analysis, which involves modeling and analyzing loop features in algorithms to identify vulnerable loop patterns [12,15,19,20]. Dynamic methods are represented by fuzzing techniques, which utilize input mutations and resource consumption tracking to identify test cases that trigger abnormal resource usage [13,16,21,22,23]. Hybrid methods, combining static and dynamic analysis, has been proven to enhance the efficiency of algorithmic complexity vulnerability detection and achieve better results [11,17,18,24].
However, most of these efforts face the following issues: insufficient abstraction of the causes of algorithmic complexity vulnerabilities by dynamic methods, resulting in relatively poor efficiency and capability in vulnerability detecting; inadequate support for vulnerability detecting by static methods, requiring more subsequent manual analysis for support; challenges in comprehensive vulnerability detection due to immature symbolic execution tools by hybrid methods. In comparison to these efforts, the advantages of our work lie in a generic workflow for detecting algorithmic complexity vulnerabilities, as well as a specific, efficient spatial algorithmic complexity vulnerability detection model related to recursive structures and exception handling. Based on this model, we can achieve rapid vulnerability detection and validation.
3. Background
This section mainly describes the definition of ACV and the threat models we concern about.
3.1. Algorithm Complexity Vulnerability
- Algorithm complexity. Algorithmic complexity (AC) [25,26] is a measure of how an algorithm performs as the size of its input, denoted as ‘n’, increases. It is typically divided into time complexity, which refers to the growth rate of the algorithm’s execution time with respect to the input size, and space complexity, which relates to the memory requirements of the algorithm. The analysis of algorithmic complexity mainly focuses on the worst-case scenario as ‘n’ approaches infinity. This theoretical evaluation helps in understanding the efficiency of algorithms, though actual execution time may vary due to factors like processor speed and compiler optimizations.
- Algorithmic Complexity Attack. An Algorithmic Complexity Attack (ACA) [27,28,29] is a form of cyber attack that exploits the worst-case performance of an algorithm to exhaust system resources, leading to Denial of Service (DoS). Attackers can craft inputs that trigger the most complex behavior of the backend algorithm, causing the exhaustion of CPU, memory, or disk space. Examples of such attacks include Zip bombs or specially crafted regular expressions causing ReDoS. These attacks are efficient as they do not require substantial server resources, relying instead on technical strategies to effectively disrupt services.
- Algorithmic complexity vulnerability. Algorithmic complexity vulnerabilities caused by design flaws in program construction stage are exploited for complexity attacks, triggering abnormal consumption of time or space resources. These vulnerabilities often occur because developers focus on average-case performance during algorithm selection and testing, overlooking potential resource exhaustion in worst-case scenarios. Temporal complexity vulnerabilities can lead to Central Processing Unit (CPU) exhaustion, while spatial complexity issues may consume all available Random Access Memory (RAM) or disk space. Such vulnerabilities are relatively common in software development due to a lack of consideration for extreme performance cases under certain inputs. A simple example of ACV is shown in Listing 1, in which the regex “(a+)+$” can perform poorly on certain inputs.
| Listing 1. A brief sample of ACV. |
 |
3.2. Threat Model
Here, we mainly talk about two aspects, i.e., the threat for algorithm design and implementation, and the threat for Java language features.
3.2.1. ACV Threat for Algorithm Design and Implementation
The safe and reliable design of the program and the reliable operation of the application system have several elements:
- Appropriate algorithm implementation. Due to the wide application of third-party libraries, the same algorithm logic may have different code implementations. Due to the different programming abilities of developers, it is inevitable that artificial or unintentional security problems may occur in the algorithm implementation.
- Use input sanitization. Sanitization involves removing any potentially dangerous characters from user inputs, while validation ensures that the data conforms to the expected format and type. By constraining the range of user inputs, the risk of exploiting vulnerabilities can be effectively diminished [30,31].
- Implementation hard resource limits. In some cases, input sanitization is not always effective, because some functions need to be more flexible to accept user input, and it is difficult to fully limit the user’s input space. Therefore, hard resource constraints, which specifically refers to limiting the size of user input data, can sometimes have a better effect.
Therefore, the violation of the above principles may lead to ACV, which inspires our ACV threat model.
- Threat for third-party components in the supply chain. A large number of components in the supply chain implement similar functions or contain similar algorithm fragments, but vulnerable code fragments may be introduced by developers intentionally or unintentionally.
- Threat for input sanitization. Input sanitization defines the type of user input space and discards or accepts certain types of characters. Within the limited scope, the attacker can construct malicious samples and trigger unexpected algorithm logic, resulting in abnormal consumption of time and space resources.
- Threat for hard resource constraints. Even if the type and size of user input space are limited, it is still possible for attackers to use the complex algorithm call chain to trigger the abnormal execution, circulation, and nesting of branches, resulting in unexpected resource consumption.
3.2.2. Java Language Features
- Java recursion, Java method recursion and stack overflow. In particular. In the design of algorithm, there will be many structures such as loop, iteration, recursion, and so on [32]. These structures facilitate software development and program understanding, but at the same time, they also bring some hidden dangers of security and reliability. There may be many problems with the loop structure, such as undefined boundaries [15]. In our work, we focus on the problem of recursive reference, because compared with other loop structures, its code is simpler, and it will consume more resources and have greater impact in case of problems, which is also relatively neglected by existing work. The default method stack size of Java generally only supports about 2000 method recursion calls, beyond which the stack overflow exception will be triggered. If the class methods are recursive methods, by constructing specific parameters, class methods can perform deep recursion and trigger stack overflow.
- Java exception and error handling mechanism. In Java, the program may encounter various exceptions when running, such as divide by zero exception, null pointer exception, array out of bounds exception, etc. [33]. When these exceptions occur, the program will stop execution and throw exceptions. If the exception is not handled, the program will terminate execution. Such handling mechanism is a very important part of Java, for it can help us catch and handle various exceptions in programs. Although errors should not be captured in general, but for some web applications, security frameworks and custom exception handlers, developers may need to capture and handle errors when developing some frameworks or underlying components to better handle errors and ensure program stability, especially components on third-party repositories and the cloud. Apache Tomcat and Spring framework are the two typical examples. However, there are still many programs in open-source repositories that have not considered catching and handling possible ACVs during the design phase.
As shown in Figure 1, this is our overall threat model, with the bolded parts representing the concepts and threat types provided in this paper. Open-source code repositories such as Maven provide third-party components for developers to download and customize to build applications. Suppose the average AC of a certain algorithm in such a component is O(nlogn). However, due to careless coding or malicious tampering by developers, the component may have ACV. Attackers can exploit this vulnerability by initiating ACA, constructing malicious inputs, satisfying input sanitization conditions, and leveraging programming language features to trigger the vulnerability. This could lead to direct attacks on the component or the entire application through the component. The attacker could reach the upper limit of hard resource constraints or exhaust all resources without limits, resulting in an actual algorithmic complexity far exceeding O(nlogn).
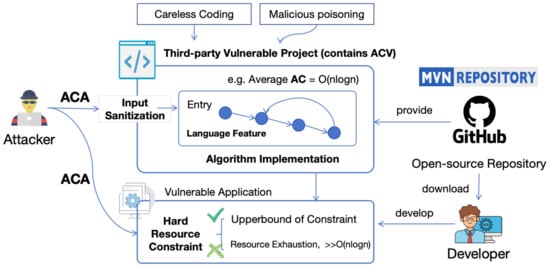
Figure 1.
Threat model described based on concepts we proposed.
4. Methodology
The above background leads to our method design as follows:
- The analysis method for the third-party components of the supply chain. Statically analyze the supply chain components, and then pave the way for the subsequent vulnerability analysis. The analysis should include various features of the program, including language independent features (intermediate representation, IR) and language related features (such as exception handling mechanisms of Java languages).
- The filter method for vulnerable recursion structure. Based on the previous step, the function call chain is filtered with the function entry accessible to user data and ACV sensitive language processing mechanism as key retrieval principles. The obtained call chain reveals the algorithm call logic that users may trigger ACV by constructing malicious inputs.
- The exploitation method for ACV. Based on the control of input sanitization for user input type and field, and the control of hard resource limits for input size, we verify the vulnerability and generate the corresponding payload guided by the comprehension of algorithm logic and the vulnerable call chain.
4.1. Overall Architecture
Our overall architecture as shown in Figure 2 includes three main parts: processing, analysis, and verification. The processing part handles the third-party components of Java (e.g., Maven Java Archive (JAR) files) and constructs the call chain. The analysis part is based on our vulnerability model to detect the vulnerability code, including filtering the recursion structure, analyzing the termination conditions and exception handling mechanism. In the verification phase, the vulnerability is verified and exploited by generating payload based on vulnerable call chain and the comprehension of language features.

Figure 2.
Overall architecture.
4.2. Analysis Base Construction
Algorithm complexity vulnerability is a vulnerability related to algorithm logic design. This vulnerability has nothing to do with specific programming language features, so this type of vulnerability may appear in different languages, such as Java, Python, etc. Here, we mainly discuss Java language, for other program languages, simply replacing the JAR file with the corresponding source code or other code files, following the same follow-up process and method, ACV detection can also be achieved. Language-independent intermediate representation is an abstract and programming language-independent representation of programming code. By converting the source code into a language-independent intermediate representation, we can eliminate the characteristics strongly related to the language, focus on the language independent algorithm logic and call structure, and help analysts analyze vulnerabilities more efficiently.
We propose two ways to support the analysis of ACV:
- Code analysis based on the Soot framework [34,35].
- Using the Soot framework as a foundation, we proposed a new intermediate representation analysis framework to support the visualization of function call structures in graph format. Our framework supports the analysis of bytecode in JAR files, generating language-independent intermediate representations, and constructs dependency and call relationship lists. These relations are then stored and represented using a graph database. By leveraging the code graph, we can easily identify structural features associated with ACVs, such as direct recursion and indirect recursion as shown in Figure 3, aiding in the construction and summarization of vulnerability models, further supporting the transfer of models to different programming languages [36].
 Figure 3. (a) Direct recursion and (b) indirect recursion (for readability, we use PowerPoint to redraw the vulnerable recursion examples according to the generated call graph).
Figure 3. (a) Direct recursion and (b) indirect recursion (for readability, we use PowerPoint to redraw the vulnerable recursion examples according to the generated call graph).
4.3. Model-Based Vulnerable Call Chain Search
Here, we mainly introduce our new ACV detecting model. On the basis of fully understanding the principle of vulnerability and the features of the programming language, we propose a new spatial algorithm complexity vulnerability detecting model. Our main design basis includes three parts: (1) aiming at the language-independent ACV features, an analysis method for class methods is proposed; (2) according to the characteristics of recursive structure, the analysis and judgment method of unsafe termination condition is proposed; and (3) for the Java language features, we discover the vulnerable recursion fragment that are not captured and processed by Java language-dependent exception and error handling mechanism.
4.3.1. Class Method Recursive Structure
In order to improve the simplicity, efficiency and maintainability of the code, Java introduces class methods. Furthermore, class methods have two designs: recursive and non recursive. Recursive design can handle a large number of algorithmic logic problems with simple code by calling itself (as shown in Listing 2). However, because each recursive call needs to save the context information, when the recursive depth is too large, it may lead to frequent method calls and stack operations, resulting in stack overflow ACVs.
| Listing 2. Java class method recursion structure. |
 |
Most of the existing ACV detecting and even most vulnerability detecting methods only support basic data types. Taking the vulnerability detecting method based on symbolic execution technology as an example, most of the existing symbolic execution vulnerability detecting methods for Java language only support basic data types, such as int and char, while it is difficult to solve constraints for complex data types such as String or Object, thus is not possible to better detect vulnerabilities related to class methods. Therefore, at this stage, we mainly adopt static call chain feature analysis instead of symbolic execution, supplementing the analysis of class methods recursion and then supporting the subsequent vulnerability verification and utilization.
Our algorithm, as outlined in the pseudocode in Algorithm 1, is implemented using the Soot framework. We start by acquiring all ActiveBodies from the JAR file. For each unit within an ActiveBody, we analyze its type of call (Line 5). If these calls are of the InvokeStmt type or the AssignStmt type, and contain a method call (Line 6), we then conduct further analysis: we examine the method call, and if it is not within an exception handling block (Line 9, will be detailed described in Section 4.3.3), we proceed to check the stack used for storing method calls. If recursive calls are detected (Line 12), and there are no limits on recursion depth (Line 13, will be detailed described in Section 4.3.2), we record the current call stack. If no recursive calls are found, we push non-basic class methods and non-abstract methods onto the stack and recursively analyze the called method (Line 19).
| Algorithm 1 Discovering all vulnerable recursive structures. |
|
At the same time, our method supports the analysis of direct and indirect recursion. On the call chain, direct recursion and indirect recursion have the following characteristics: direct recursion has the characteristic of explicit self-calling in the figure, and indirect recursion may achieve self calling through complex indirect calls. Figure 2a shows “methodB()” directly recursively calling itself, while Figure 2b shows “methodA()” indirectly recursively calling itself by calling “methodB()” and “methodC()”.
4.3.2. Unsafe Recursion Termination Conditions
The termination condition is the key part of the recursive algorithm, which determines when the recursion stops and returns the result. In recursive algorithms, the termination condition is usually a conditional statement. When the condition is met, the recursion will no longer continue to execute, but start to return results or perform other operations. The existence of termination conditions is to prevent recursion from entering an infinite loop and ensure that recursion ends eventually.
In general, termination conditions have two important characteristics:
- The termination condition must be attainable. That is to say, in the process of recursion, after a series of recursive calls, the termination condition should be met finally.
- The termination condition should not include a recursive call, otherwise the recursion will not end. The termination condition should be a explicit case without further recursion.
To match and detect whether there is a limit on the number of recursive levels, software developers commonly use two methods to record and judge the recursion depth:
- Define a class attribute in the class corresponding to the recursive method to record the recursion depth. Each time the recursive method proceeds to the next level, increment this class attribute to update the recursion depth. Before executing the next recursive method, compare this class attribute with a constant representing the maximum depth. The recursive method can proceed to the next level if the depth is less than this constant value.
- Include a variable to record the recursion depth as a parameter in the recursive method. Each time the method recurses to the next level, increment this depth variable and pass it to the next level of recursion. Before executing the next recursive method, compare this variable with a constant representing the maximum depth. The recursive method can proceed to the next level if it is less than this constant value.
The common features of these two methods are: (1) There is a variable that records the depth of recursion, which increases in synchronism with each recursion level. (2) This variable is compared with a constant value, and the next level of recursion is only allowed if the variable is less than this constant value. Hence, the logic for judgment is as follows, and the algorithm pseudocode is shown in Algorithm 2.
- Identify the variable in the recursive method that has ‘+1’ increment (Line 7).
- Determine whether this variable is a formal parameter of the recursive method or comes directly or indirectly from a class attribute (Line 7).
- Check if this variable is compared with a constant value, and ensure that the call to the next level of recursion is within the judgment logic that checks for the variable being less than this constant value (Line 5).
4.3.3. Uncaptured Error
Based on the Java exception handling mechanism mentioned above, if a method’s nested call does not capture errors such as “java.lang.throwable”, 7 “java.lang.error”, or “java.lang.stackoverflowerror”, it may indicate the presence of error types that are unforeseen or unhandled by the developer. This is particularly critical in the case of “StackOverflowError”, as such uncaught errors can lead to algorithmic complexity vulnerabilities, potentially causing runtime errors that are not anticipated by the developers.
By utilizing Soot or our proposed method to analyze the call chains of all public methods in Java third-party libraries, we can detect whether there are instances of recursion without catching the aforementioned types of errors. With the help of our proposed method, we can clearly identify the presence of recursive paths in the program (i.e., cases where class methods reference themselves). If these recursive methods do not show try-catch captures for errors like “java.lang.throwable”, “java.lang.error”, and “java.lang.stackoverflowerror” at the statement level within the call chain context, it indicates that errors in recursion are not foreseen and handled by the developer but are thrown by the JVM, which are worth our analysis and utilization.
| Algorithm 2 Judging if there is constraint for recursion depth in a method body. |
|
As illustrated in Algorithm 3, Line 1 iterates over each exception handling block (trap) in the body and use a flag “isInTrap” to track whether the current iteration is inside a trap (Line 4). Then, iterate over each unit (Line 5) in the body for checking whether the unit is inside the exception and error handling block (Line 6–14). This function is further used in Algorithm 1 mentioned in Section 4.3.1.
| Algorithm 3 Determine if a recursion structure is captured by error handling mechanisms. |
|
4.4. Recursion-Guided Payload Generation
Most current automated payload generation methods rely on symbolic execution and constraint solving [37,38]. However, these techniques are more mature in the context of C language, while symbolic execution technology for Java is still in a developmental and exploratory stage. There is an urgent need for reliable and efficient test case generation techniques and tools specifically for Java programs. At present, most Java symbolic execution tools [39] can only support basic and simple data types, such as symbolic representation of int and char. However, they are still unable to fully symbolize complex data types like string and object. This limitation restricts the use of symbolic execution for constraint solving on specified vulnerability paths.
To address our targeted vulnerability types, i.e., spatial ACV, we propose a semi-automatic, procedural, and standardized payload generation method to support rapid vulnerability verification and exploitation. Our method process mainly includes:
- Analyzing the recursive method’s parameter processing logic. First, identify and extract all statements involved in processing the parameters within the recursive method according to the automatically filtered call chain. This includes all operations from the start of the recursive method until the parameters are passed to the next level of recursive calls.
- Constructing the initial actual parameter (argument). Based on the extracted parameter processing logic, generate an initial actual parameter (the initial value of the parameter) that should satisfy the conditions for at least one recursive call.
- Automatically iterative processing of actual parameters. Apply the extracted parameter processing logic to the initial actual parameter, repeating multiple times (e.g., 10,000 iterations). Each iteration simulates the changes in the arguments during a recursive call.
- Generating the final payload. After numerous iterations, the final value of the obtained actual parameter is used as the payload. This payload represents the final state of the argument after multiple recursive analysis and can be used for further verification or exploitation.
5. Evaluation
In this section, we mainly discuss and evaluate our proposed method around the following three research questions:
- RQ1: Effectiveness: can our method better detect algorithm complexity vulnerabilities?
- RQ2: Superiority: does our tool perform better than existing tools?
- RQ3: Verification and exploitation: can our method better support vulnerability verification and exploitation?
5.1. Experiment Setup and Description of Dataset
All our experimental data comes from the real world. Due to the close-source nature of previous research datasets and the poor availability of them, we selected real-world open-source projects to verify the effectiveness of vulnerability mining methods, such as the popular Maven repository project and the high star project of GitHub, including org.apache.pdfbox (version 2.0.27), org.apache.sling.commons.json (version 2.0.20), Jettison (version 1.5.1), Hutool-json (version 5.8.10), Ini4j (version 0.5.2). All experiments were conducted on Ubuntu 16.04, 32 GB memory, 4 vCPUs, 128 GB disk space, and the JDK (Java Development Kit) version is 1.8.
5.2. Result and Analysis
We will provide a detailed description of our experimental results around the three research questions mentioned above.
5.2.1. RQ1: Effectiveness
In our research, due to the limitations of existing datasets and our ultimate goal of detect new algorithmic complexity vulnerabilities, we have opted to analyze real-world projects. To obtain representative results for our analysis, we primarily search for popular projects in the Maven repository and conduct in-depth analyses of these popular repositories. Our primary targets for analysis include projects such as Jettison, Ini4j, org.apache.pdfbox, etc. Jettison is a well-received Java library that facilitates the conversion between Extensible Markup Language (XML) and JavaScript Object Notation (JSON) using Streaming API for XML (StAX). Ini4j is a Java API designed for handling configuration files in the Windows .ini format. The org.apache.pdfbox is an open-source Java tool dedicated to working with PDF documents.
We ran our tool on these popular Maven projects for testing, obtaining the experimental results as shown in Table 1. The column from left to right shows the project name (Benchmark), the number of stars obtained by the project on GitHub (Stars), the number of forks (Forks), the number of other project that reference this project (Usage), the total number of classes in the corresponding JAR file (TotalClasses), the number of call paths that meet the filtering criteria (VulnerablePath), and the number of verified external-accessible paths (VerifiedPath).

Table 1.
The experimental results of our approach on popular projects in the Maven repository.
For example, the hutool-json project has gained 27.2 k stars and 7.3 k forks on GitHub, and is used by 95 downstream projects in the Maven repository. Upon analysis, we found that hutool-json contains a total of 74 classes. There are 30 paths that meet our filtering criteria, i.e., specific recursive structure, unsafe termination conditions, and unhandled error calling structure, of which 12 are externally accessible. It is worth noting that these 30 paths are all unsafe paths related to vulnerabilities, but due to some class methods being externally unreachable (i.e., non-usage methods), a total of 12 exploitable vulnerability paths have been decided. Among these 12 vulnerability exploitation paths, due to the similar principles of some vulnerabilities, only three CVE numbers were authorized by the official during the reporting process. However, in fact, these 12, and even these 30 paths are the real paths with vulnerabilities.
Our effectiveness is primarily reflected in the following aspects: Firstly, we can perform detailed analysis of JAR files, extracting all classes and methods, without the need to manipulate the source code. Secondly, we are able to conduct a thorough analysis of the call chain of the JAR files, filtering out all our ACV model-related potential vulnerability paths. Additionally, due to the multifaceted constraints of our model, all identified potential vulnerabilities actually pose security issues. The only uncertainties lie in aspects such as external accessibility and similarity in the structure of the vulnerability principles. Lastly, all discovered paths are verified or officially recognized as vulnerabilities.
For the comparative experiments, we compared our tool with Google’s open-source fuzzing tool, oss-fuzz [40] (GitHub 9.4 k stars). The oss-fuzz supports fuzzing Java source code to discover vulnerabilities such as crashes and memory leaks (the final effect achieved is the same as our targeted spatial ACV). As oss-fuzz requires specific method as fuzzing entry and necessitates extensive time for execution, we selected the vulnerable method, i.e., XML.toJSONObject method of org.json, JSONObject.<init> method of org.json and JSONObject.<init> method of org.codehaus.jettison.json as the example entries for oss-fuzz and our tool. As shown in Table 2, the column for left to right shows the entry method, the tool, the testing results, the number of generated test cases, the time consumption and the average memory consumption, respectively. The results demonstrate that our method can identify complete vulnerable call chains, such as org.json.XML.toJSONObject →org.json.XML.parse→ org.json.XML.parse, while oss-fuzz fuzzing engine, libfuzzer, despite generating a large number of test inputs within a limited time frame (658300271 test inputs in 74 h), still failed to detect these vulnerabilities. This is because ACVs are closely related to the design and implementation of algorithms logic, while oss-fuzz adopts a random seed generation approach, which cannot trigger deep recursive logic. Additionally, oss-fuzz cannot handle complex object types, resulting in low coverage and inability to discover the target vulnerabilities.

Table 2.
The comparison experiment between our tool and oss-fuzz. Note that in this table, jettison.json.JSONObject.<init> is used to represent org.codehaus.jettison.json.JSONObject.<init> due to space constraints.
5.2.2. RQ2: Superiority
The superiority of our method and tool is primarily demonstrated through comparison with other tools. We have chosen the most representative research achievements in recent years, and compared them from various perspectives, including applicability scenarios and range, types of vulnerabilities that can be analyzed, supported data types, and the effort required for exploitation stage. This comparison is conducted to analyze the advanced nature of the tool we propose. It is noteworthy that in our experimental process, most tools opted not to be open-source. The DARPA Space and Time Analysis for Cybersecurity (STAC) program dataset, which has been commonly used for results evaluation in many studies, also can no longer be found in an officially public way. The specific details are as follows, as shown in Table 3.

Table 3.
The comparison between our tool and state-of-the-art tools in the related field.
Compared to the most advanced tools recently proposed in the field, the type of vulnerabilities we focus on is more targeted towards current weak points, specifically spatial ACV. Our approach starts with bytecode analysis, eliminating the need to access the source code, thus offering a broader applicability. Our method is static, which brings it closer to the essence of vulnerability occurrence than other hybrid or dynamic methods. Due to the precision of our proposed model, our results can almost certainly detect all spatial algorithmic complexity vulnerabilities that meet our criteria without false positive. For payload generation, we employ a manually assisted approach, leveraging an understanding of the call chain to rapidly construct payloads, supporting both basic and complex data types.
We also conducted experiments to compare the performance of our tool with oss-fuzz. As shown in Table 2, our tool can complete the analysis from a method entry within several seconds, while oss-fuzz requires hours to complete the testing for merely one method (for method XML.toJSONObject of org.json, the test was still not completed after 74 h, so we set a two-hour testing duration for the other two methods). It must be acknowledged that static methods have a natural advantage in terms of efficiency compared to dynamic methods, so comparing our tool with oss-fuzz may not be entirely fair. However, our experimental results aim to demonstrate that as a type of vulnerability closely related to specific program design logic, our proposed model for detecting it not only has a higher detection rate and lower false positive rate, but also has extremely high efficiency. The detected call chains are almost all real vulnerabilities (no false positives have been found so far), which can significantly reduce the double-check cost for analysts. This is very helpful for rapid vulnerability discovery and verification. Additionally, this also suggests that existing dynamic fuzzing tools should place greater emphasis on testing program logic.
5.2.3. RQ3: Verification and Exploitation
As mentioned earlier, the vulnerability analysis method and detection model we propose can detect vulnerabilities related to recursive structures with almost no false positives. This is because the vulnerability chains we filter meet the following characteristics: they have the potential to directly or indirectly trigger an unending recursion, are externally reachable, and are not captured by the exception and error handling mechanism. Therefore, based on the understanding of the conditions that trigger recursion and the argument processing context, it is possible to rapidly construct and exploit payloads for these vulnerabilities.
Following our proposed Recursion-Guided payload generation method, and using our publicly disclosed vulnerability CVE-2022-45685 [41] shown in Listing 3 as an example, we illustrate the rapid construction of a payload. In the vulnerability source code, “JSONTokener” in Line 3 acts as the cursor for the input string. First, we analyze the logic of the recursive method’s parameter processing by examining the call chain from new “JSONObject” to the next new “JSONObject”, which involves all the processing statements for “JSONTokener” as shown in Line 8–Line 22 and Line 32–42. Next, based on these processing statements, we construct the initial actual parameter that can trigger the recursive loop, which is “{1{”. Then, we iteratively process this actual parameter. Following the characteristics of function recursion in Java, we construct a method that can trigger recursion 10,000 times, which is achieved by repeating “{1{” ten thousand times. This results in the final payload.
Overall, our method of vulnerability payload generation is capable of rapid construction based on the characteristics of recursive structures in call chains and the conditions that trigger recursion. Analysts with a fundamental understanding of code can quickly verify vulnerabilities and write the corresponding payloads. All 8 publicly disclosed CVE vulnerabilities can be found in references [40,41,42,43,44,45,46,47,48].
| Listing 3. The source code fragment of our discovered vulnerability in Jettison—CVE-2022-45685. |
 |
6. Conclusions
Algorithmic complexity vulnerabilities are prevalent in various applications and programming languages, and have a significant impact on a multitude of downstream software, especially with the widespread use of open-source code repositories in today’s era. Recent works in the field have mostly focused on algorithmic complexity vulnerability detection based on fuzzing testing, which involves generating initial and mutated samples either randomly or based on limited understanding of the program. This approach monitors the program’s execution time or resource consumption to detect vulnerabilities. Some studies also provide interactive views to support auxiliary analysis. Compared to existing methods, our tool offers the following advantages: precise vulnerability model that accurately identify spatial algorithmic complexity vulnerabilities related to recursive structures; higher efficiency and accuracy with almost no false positives in specific vulnerability type; and support for rapid vulnerability verification and exploitation, with an analysis process that more closely aligns with the nature of vulnerability occurrence.
Of course, our research method has certain limitations and future development opportunities. First, we have not fully explored the potential of our vulnerability call chain discovery method. We have only proposed an accurate model for detecting algorithmic complexity vulnerabilities in recursive structures. In the future, we could develop more models to discover more exploitation patterns of algorithmic complexity vulnerabilities, even other vulnerabilities. Secondly, regarding the generation of vulnerability payloads, we currently employ a semi-automated method limited by the lack of Java dynamic symbolic execution tools, requiring significant manual intervention. In the future, we could consider delving into fully automated payload generation to improve the efficiency of vulnerability verification and exploitation. Finally, we will continue to delve deeper into our research on the same type of vulnerability detecting methods between different programming languages, utilizing a unified intermediate representation to detect ACVs and other type of vulnerabilities related to program logic.
Author Contributions
Supervision, B.C.; methodology, Z.W., D.B. and W.T.; writing—original draft preparation, Z.W.; writing—review and editing, Z.W., W.T. and D.B.; software, D.B.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found here: https://mvnrepository.com/ (accessed on 8 January 2024), including org.apache.pdfbox, org.apache.sling.commons.json, jettison, hutool, ini4j. The algorithm pseudocode and proof of authorized CVE identifiers are publicly available at https://github.com/BIngDiAn-s/ACV_Find_Method (accessed on 8 January 2024). The authorized CVEs mentioned in this study are openly available in [41,42,43,44,45,46,47,48], other data presented in this article are not readily available because the data are part of an ongoing study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Algorithmic Complexity Vulnerabilities: An Introduction. Available online: https://twosixtech.com/blog/algorithmic-complexity-vulnerabilities-an-introduction/ (accessed on 8 January 2024).
- Zip Bomb. Available online: https://en.wikipedia.org/wiki/Zip_bomb (accessed on 8 January 2024).
- 42.zip. Available online: https://www.unforgettable.dk/ (accessed on 8 January 2024).
- Regular Expression Denial of Service—ReDoS. Available online: https://owasp.org/www-community/attacks/Regular_expression_Denial_of_Service_-_ReDoS (accessed on 8 January 2024).
- Kirrage, J.; Rathnayake, A.; Thielecke, H. Static Analysis for Regular Expression Denial-of-Service Attacks. In Proceedings of the International Conference on Network and System Security, Madrid, Spain, 3–4 June 2013; Lopez, J., Huang, X., Sandhu, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 135–148. [Google Scholar]
- Wüstholz, V.; Olivo, O.; Heule, M.J.; Dillig, I. Static Detection of DoS Vulnerabilities in Programs That Use Regular Expressions. In Proceedings of the 23rd International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Uppsala, Sweden, 22–29 April 2017, Proceedings, Part II; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10206, pp. 3–20. [Google Scholar] [CrossRef]
- Davis, J.; Coghlan, C.; Servant, F.; Lee, D. The impact of regular expression denial of service (ReDoS) in practice: An empirical study at the ecosystem scale. In Proceedings of the 2018 26th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Lake Buena Vista, FL, USA, 4–9 November 2018; pp. 246–256. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, C.; Li, Y.; Xu, Z.; Huang, S.; Liu, Y.; Yao, Y.; Xiao, Y.; Zou, Y.; Liu, Y.; et al. Effective ReDoS Detection by Principled Vulnerability Modeling and Exploit Generation. In Proceedings of the 2023 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 22–24 May 2023; pp. 2427–2443. [Google Scholar] [CrossRef]
- Staicu, C.A.; Pradel, M. Freezing the web: A study of ReDoS vulnerabilities in Javascript-based web servers. In Proceedings of the 27th USENIX Conference on Security Symposium (SEC’18), Baltimore, MD, USA, 15–17 August 2018; pp. 361–376. [Google Scholar]
- CVE-2023-36617 Detail. Available online: https://nvd.nist.gov/vuln/detail/CVE-2023-36617 (accessed on 8 January 2024).
- Liu, Y.; Meng, W. Acquirer: A Hybrid Approach to Detecting Algorithmic Complexity Vulnerabilities. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security (CCS ’22), Los Angeles, CA, USA, 7–11 November 2022; pp. 2071–2084. [Google Scholar] [CrossRef]
- Awadhutkar, P.; Santhanam, G.R.; Holland, B.; Kothari, S. DISCOVER: Detecting Algorithmic Complexity Vulnerabilities. In Proceedings of the 2019 27th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering (ESEC/FSE 2019), Tallinn, Estonia, 26–30 August 2019; pp. 1129–1133. [Google Scholar] [CrossRef]
- Blair, W.; Mambretti, A.; Arshad, S.; Weissbacher, M.; Robertson, W.; Kirda, E.; Egele, M. HotFuzz: Discovering Temporal and Spatial Denial-of-Service Vulnerabilities Through Guided Micro-Fuzzing. ACM Trans. Priv. Secur. 2022, 25, 1–35. [Google Scholar] [CrossRef]
- Li, W.; Chen, Z.; He, X.; Duan, G.; Sun, J.; Chen, H. CVFuzz: Detecting Complexity Vulnerabilities in OpenCL Kernels via Automated Pathological Input Generation. Future Gener. Comput. Syst. 2022, 127, 384–395. [Google Scholar] [CrossRef]
- Awadhutkar, P.; Santhanam, G.R.; Holland, B.; Kothari, S. Intelligence amplifying loop characterizations for detecting algorithmic complexity vulnerabilities. In Proceedings of the 2017 IEEE 24th Asia-Pacific Software Engineering Conference (APSEC), Nanjing, China, 4–8 December 2017; pp. 249–258. [Google Scholar]
- Wei, J.; Chen, J.; Feng, Y.; Ferles, K.; Dillig, I. Singularity: Pattern Fuzzing for Worst Case Complexity. In Proceedings of the 2018 26th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering (ESEC/FSE 2018), Lake Buena Vista, FL, USA, 4–9 November 2018; pp. 213–223. [Google Scholar] [CrossRef]
- Noller, Y.; Kersten, R.; Păsăreanu, C.S. Badger: Complexity Analysis with Fuzzing and Symbolic Execution. In Proceedings of the 27th ACM SIGSOFT International Symposium on Software Testing and Analysis (ISSTA 2018), Amsterdam, The Netherlands, 16–21 July 2018; pp. 322–332. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.; Meng, W. Revealer: Detecting and Exploiting Regular Expression Denial-of-Service Vulnerabilities. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 1468–1484. [Google Scholar] [CrossRef]
- Xie, X.; Chen, B.; Liu, Y.; Le, W.; Li, X. Proteus: Computing Disjunctive Loop Summary via Path Dependency Analysis. In Proceedings of the 2016 24th ACM SIGSOFT International Symposium on Foundations of Software Engineering (FSE 2016), Seattle, WA, USA, 13–18 November 2016; pp. 61–72. [Google Scholar] [CrossRef]
- Parolini, F.; Miné, A. Sound Static Analysis of Regular Expressions for Vulnerabilities to Denial of Service Attacks. In Theoretical Aspects of Software Engineering, Proceedings of the 16th International Symposium (TASE 2022), Cluj-Napoca, Romania, 8–10 July 2022; Aït-Ameur, Y., Crăciun, F., Eds.; Springer: Cham, Switzerland, 2022; pp. 73–91. [Google Scholar]
- Toffola, L.D.; Pradel, M.; Gross, T.R. Synthesizing programs that expose performance bottlenecks. In Proceedings of the 2018 International Symposium on Code Generation and Optimization (CGO 2018), Vienna, Austria, 24–28 February 2018; pp. 314–326. [Google Scholar] [CrossRef]
- Nguyen, T.; Ishimwe, D.; Malyshev, A.; Antonopoulos, T.; Phan, Q.S. Using dynamically inferred invariants to analyze program runtime complexity. In Proceedings of the 3rd ACM SIGSOFT International Workshop on Software Security from Design to Deployment (SEAD 2020), Virtual, 9 November 2020; pp. 11–14. [Google Scholar] [CrossRef]
- Shen, Y.; Jiang, Y.; Xu, C.; Yu, P.; Ma, X.; Lu, J. ReScue: Crafting regular expression DoS attacks. In Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering (ASE ’18), Montpellier, France, 3–7 September 2018; pp. 225–235. [Google Scholar] [CrossRef]
- Holland, B.; Santhanam, G.R.; Awadhutkar, P.; Kothari, S. Statically-Informed Dynamic Analysis Tools to Detect Algorithmic Complexity Vulnerabilities. In Proceedings of the 2016 IEEE 16th International Working Conference on Source Code Analysis and Manipulation (SCAM), Raleigh, NC, USA, 2–3 October 2016; pp. 79–84. [Google Scholar] [CrossRef]
- Algorithmic Complexity. Available online: https://devopedia.org/algorithmic-complexity (accessed on 8 January 2024).
- Algorithmic Complexity. Available online: https://viterbi-web.usc.edu/~adamchik/15-121/lectures/Algorithmic%20Complexity/complexity.html (accessed on 8 January 2024).
- Algorithmic Complexity Attack. Available online: https://en.wikipedia.org/wiki/Algorithmic_complexity_attack (accessed on 8 January 2024).
- Crosby, S.A.; Wallach, D.S. Denial of Service via Algorithmic Complexity Attacks. In Proceedings of the 12th Conference on USENIX Security Symposium (SSYM’03), Washington, DC, USA, 4–8 August 2003; Volume 12, p. 3. [Google Scholar]
- Czubak, A.; Szymanek, M. Algorithmic Complexity Vulnerability Analysis of a Stateful Firewall. In Information Systems Architecture and Technology, Proceedings of the 37th International Conference on Information Systems Architecture and Technology—ISAT 2016—Part II, Karpacz, Poland, 18–20 September 2016; Grzech, A., Świątek, J., Wilimowska, Z., Borzemski, L., Eds.; Springer: Cham, Switzerland, 2017; pp. 77–97. [Google Scholar]
- How to Use Input Sanitization to Prevent Web Attacks. Available online: https://www.esecurityplanet.com/endpoint/prevent-web-attacks-using-input-sanitization/ (accessed on 8 January 2024).
- Barlas, E.; Du, X.; Davis, J.C. Exploiting input sanitization for regex denial of service. In Proceedings of the 44th International Conference on Software Engineering (ICSE ’22), Pittsburgh, PA, USA, 25–27 May 2022; pp. 883–895. [Google Scholar] [CrossRef]
- Recursion in Java. Available online: https://www.geeksforgeeks.org/recursion-in-java/ (accessed on 8 January 2024).
- Exceptions in Java. Available online: https://www.geeksforgeeks.org/exceptions-in-java/ (accessed on 8 January 2024).
- Vallée-Rai, R.; Co, P.; Gagnon, E.; Hendren, L.; Lam, P.; Sundaresan, V. Soot: A Java Bytecode Optimization Framework. In Proceedings of the CASCON First Decade High Impact Papers (CASCON ’10), Toronto, ON, Canada, 1–4 November 2010; pp. 214–224. [Google Scholar] [CrossRef]
- soot-oss/soot. Available online: https://github.com/soot-oss/soot (accessed on 8 January 2024).
- Dietrich, J.; Jezek, K.; Rasheed, S.; Tahir, A.; Potanin, A. Evil Pickles: DoS Attacks Based on Object-Graph Engineering. In Proceedings of the 31st European Conference on Object-Oriented Programming (ECOOP 2017), Barcelona, Spain, 19–23 June 2017; Müller, P., Ed.; Leibniz International Proceedings in Informatics (LIPIcs). Leibniz-Zentrum für Informatik: Dagstuhl, Germany, 2017; Volume 74, pp. 10:1–10:32. [Google Scholar] [CrossRef]
- Burnim, J.; Juvekar, S.; Sen, K. WISE: Automated test generation for worst-case complexity. In Proceedings of the 2009 IEEE 31st International Conference on Software Engineering, Vancouver, BC, Canada, 16–24 May 2009; pp. 463–473. [Google Scholar] [CrossRef]
- Luckow, K.; Kersten, R.; Păsăreanu, C. Symbolic Complexity Analysis Using Context-Preserving Histories. In Proceedings of the 2017 IEEE International Conference on Software Testing, Verification and Validation (ICST), Tokyo, Japan, 13–17 March 2017; pp. 58–68. [Google Scholar] [CrossRef]
- Luckow, K.; Dimjašević, M.; Giannakopoulou, D.; Howar, F.; Isberner, M.; Kahsai, T.; Rakamarić, Z.; Raman, V. JDart: A Dynamic Symbolic Analysis Framework. In Tools and Algorithms for the Construction and Analysis of Systems, Proceedings of the 22nd International Conference, TACAS 2016, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2016, Eindhoven, The Netherlands, 2–8 April 2016; Chechik, M., Raskin, J.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 442–459. [Google Scholar]
- oss-fuzz. Available online: https://github.com/google/oss-fuzz (accessed on 8 January 2024).
- CVE-2022-45685. Available online: https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2022-45685 (accessed on 8 January 2024).
- CVE-2022-45690. Available online: https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2022-45690 (accessed on 8 January 2024).
- CVE-2022-45688. Available online: https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2022-45688 (accessed on 8 January 2024).
- CVE-2022-41404. Available online: https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2022-41404 (accessed on 8 January 2024).
- CVE-2022-47937. Available online: https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2022-47937 (accessed on 8 January 2024).
- CVE-2022-45687. Available online: https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2022-45687 (accessed on 8 January 2024).
- CVE-2022-45693. Available online: https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2022-45693 (accessed on 8 January 2024).
- CVE-2022-45689. Available online: https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2022-45689 (accessed on 8 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).