Method for Determining Design Heating Load of Rural Residential Buildings Considering Indoor Temperature Uncertainty

Abstract

In rural locations, the application of clean heating technologies requires an appropriate design heating load. However, the variation characteristics of indoor temperatures in rural residential buildings are rarely taken into consideration by traditional techniques of calculating the design heating load, which may result in over- or under-design. As a result, a new method that took the uncertainty of the indoor temperature into account was presented to calculate the design heating load for rural residential buildings. First, for the “part-time, part-space” heating mode in rural residential buildings, an indoor temperature stochastic model was established to generate multiple indoor temperature scenarios; on the basis of this, heating loads under these scenarios were simulated and their probability distributions were counted; lastly, the design heating load was selected from the load probability distribution based on a predetermined confidence level. When the new method and the traditional method were compared, it was discovered that the new method can offer a more thorough guide to the determination of the design load value for the design of heating systems in rural residential buildings, while the traditional method’s result might not satisfy the reliability requirements.

1. Introduction

Coal is widely utilized for heating rural residential buildings in northern China, which is thought to be one of the primary causes of air pollution [1,2]. The Chinese government promotes the use of heat pumps, solar energy, and other clean heating technologies to meet heating demands in rural residential buildings in order to reduce air pollution [3]. Rural inhabitants’ acceptance of clean heating technologies has greatly risen as a result of the substantial government subsidies. Nevertheless, when it comes to designing clean heating systems, the methodological system for urban residential buildings is primarily used to determine the design load for rural residential buildings, which means that the consumption characteristics of rural residential buildings are not fully taken into account.

Compared to urban residential buildings, which operate on an “all-time, all-space” basis, rural residential buildings have a different heating mode. The bulk of homes in rural areas are single-story and multi-room buildings. Each room in a rural residential building serves a certain function, and the use of each space is influenced by the activities of its residents [4]. For instance, people use their bedrooms for sleeping at night and leave other spaces, like the hall, unoccupied; similarly, people use the hall for daytime entertaining and leave the bedrooms empty. In this case, human activity causes non-continuous occupancy in each room throughout the course of one day. Different from large-scale centralized heating found in urban residential buildings, rural residential buildings often receive small-scale decentralized heating. Because of this, heating equipment in rural residential buildings can be easily turned on and off at any time by people, creating a unique “part-time, part-space” heating mode [5,6].

The two most popular methods for figuring out the design heating load are the load index method and the design parameter method [7]. The load index method is the most user-friendly of them all since it enables designers to determine the design heating load based directly on the building area. Nevertheless, this method finds it difficult to take into consideration the impacts of many elements on the design load outcomes, such as the building envelope’s performance. Consequently, the design parameter method, a more refined technique, was released. In this method, the designer must first specify the indoor and outdoor design conditions, then it is possible to perform load simulations to obtain the design heating load value.

The design parameter method is commonly employed for urban residential buildings because of the well-established applicable codes, which facilitate the determination of indoor and outdoor design conditions. However, the determination of indoor design conditions for rural residential buildings is more difficult. Due to the “part-time, part-space” heating mode, the indoor temperatures in rural residential buildings have a large uncertainty in both temporal and spatial dimensions. There are multiple options for the indoor temperature scenario in each room in rural residential buildings, due to the variety of some factors like the occupancy schedule [8,9,10], type of activity [11], and preferred temperature [12,13,14], but designers are unable to empirically determine which option can meet the requirements for design reliability. Regretfully, there are inadequate standards governing heating system design in rural residential buildings, making it difficult for designers to obtain reliable information about the design scenarios of indoor temperatures. As a result, the inability to accurately assess indoor design conditions limits the application of the design parameter method in rural residential buildings.

When the reliable indoor temperature scenario cannot be entirely established, how can the design heating load of a rural residential building be calculated? A workable answer is offered by the recently created probabilistic design load calculation method (also known as the probabilistic method) [15,16,17]. This method permits the load computation to include some uncertain parameters. The following is its basic procedure: initially, the uncertain parameters are quantified using some probabilistic models [18]; the building heating or cooling loads are then simulated under various samples of uncertain parameters; lastly, the probabilistic characteristics of the loads are statistically obtained and the design load values are selected in accordance with certain rules [19]. Using the probabilistic method, Fernando et al. [20] determined the design capacity of the air-conditioning system of an office building in Spain, taking into account the uncertainty of the building thermal parameters and internal disturbance parameters. Taking a residential building in Hong Kong as an example, An et al. [21] proved that the design load values of the building determined based on the probabilistic method were extremely close to its actual peak load demand. The probabilistic method was used by Wu et al. [22] to determine the design capacity of the air conditioning systems in three kinds of buildings, and all of the results were favorable. The aforementioned research shows how the probabilistic method may effectively address the challenge of determining design loads rationally when there are uncertain parameters.

In conclusion, indoor temperatures in rural residential buildings exhibit notable uncertainty in both temporal and spatial dimensions because they operate on a “part-time, part-space” heating mode. The traditional design load calculation methods (such as the design parameter method) mainly serve buildings with “full-time, full-space” heating mode, so it is usually assumed that the indoor temperature of the buildings is constant. This assumption is inconsistent with the actual situation of rural buildings, so the design load calculated by these traditional methods can not accurately reflect the real heating load of rural residential buildings. Therefore, considering the uncertainty of indoor temperatures due to changes in the occupancy schedule, type of activity, and preferred temperature, this study suggested a probabilistic method for calculating design heating loads for rural residential buildings.

The paper is organized as follows: Section 2 introduces the design heating load determination method for rural residential buildings considering indoor parameter uncertainty; Section 3 shows the design load results for a typical rural residential building in Harbin; Section 4 analyzes the advantages of applying the method of this study, using the traditional method as a control; and Section 5 concludes the article.

2. Method

In order to address the need for heating system design in rural residential buildings, this study suggested a probabilistic method for determining the design heating load, taking into account the indoor temperature uncertainty. The three steps of the probabilistic method are as follows:

(1)

A stochastic model of indoor temperature in rural residential buildings was developed, to reflect the uncertainty of the indoor temperature in both temporal and spatial dimensions;

(2)

Stochastic load simulations were performed to obtain the probability distribution of the design heating load under multiple uncertain indoor temperature scenarios;

(3)

Based on the probability distribution of the design heating load in a rural residential building, the final design load value was selected according to a certain confidence level.

2.1. Method for Constructing the Stochastic Model of Indoor Temperature

First, a stochastic model of indoor temperature for rural residential buildings must be created. A rural residential building’s indoor temperature is mostly determined by the occupancy and activity situations in each room. There are two types of occupancy situations: occupied states and vacant states. In occupied states, there are two types of activity situations: sleeping states and active states. Various occupancy and activity situations translate into varying preferences for interior temperature.

To characterize the indoor temperature uncertainty in rural residential buildings in both temporal and spatial dimensions, it is first necessary to describe the random occupancy behavior of each room. To this end, this study described the state change in each room between “occupied ($O_p=1$)” and “vacant ($O_p=0$)” with the help of a Markov chain model [23], to obtain the corresponding random occupancy schedules. In this model, the next moment state of a room depends only on the current state, which is represented by the transfer probability using the following equation:

$$p\left\{X_{t+1}=j|X_t=i\right\}=p_{ij}$$

(1)

where $X_t$ denotes the occupancy situations at moment $t$, and $p_{ij}$ denotes the transfer probability.

According to the Markov chain model, it is possible to generate random occupancy schedules for each room in a rural residential building. Based on this, the activity situations in occupied states can be analyzed. This study combined the function of the room and the moments at occupied states to jointly determine the activity situations. According to the literature [24], the judgment rules are formulated as follows: (1) When a bedroom is occupied at night, the occupants are judged to be in a sleeping state; and when a bedroom is occupied during the day, the occupants are judged to be in an active state; (2) All other rooms except bedrooms will be judged to be in an active state by default when occupied. The mathematical representation of the judgment rules are as follows:

When $O_p=1$:

Bedrooms:

$$S_p=\left\{\begin{array}{ll}0,& \mathrm{if} 1\le t<t_u \mathrm{or} t_l<t\le 24\mathrm{h}\\ 1,& \mathrm{if} t_u\le t\le t_l\end{array}\right.$$

(2)

Other rooms:

$$S_p=1, \mathrm{i}\mathrm{f} 1\le t\le 24 \mathrm{h}$$

(3)

where $S_p$ denotes the activity situations. Among them, $S_p=0$ represents sleeping states; and $S_p=1$ represents active states. $t_u$ and $t_l$ denote the upper and lower bounds of time when $S_p=1$ in bedrooms.

Finally, according to the occupancy and activity situations, the preference for setting the indoor temperature can be determined. In rural residential buildings, people move between indoors and outdoors more frequently, and therefore prefer to set indoor temperatures low (only 11~18 °C) to avoid the discomfort caused by drastic temperature changes. At the same time, there are some differences in indoor temperature preferences depending on occupancy and activity situations [25]. In general, when the occupants are active, the corresponding room’s indoor temperature will be set higher (such as 16 °C). However, when the occupants are sleeping, the corresponding room’s indoor temperature will be set relatively low (such as 12 °C) due to the habit of covering up. When a room is unoccupied, the corresponding heating unit stops working, at which point its indoor temperature is kept at a lower value by default. Based on the above guidelines, the mathematical representation of the indoor temperature are as follows:

$$T_{in}=\left\{\begin{array}{c}\mathrm{U}\left(a_1,b_1\right), \mathrm{if} O_p=1,S_p=1\\ \mathrm{U}\left(a_2,b_2\right), \mathrm{if} O_p=1,S_p=0\\ c, \mathrm{if} O_p=1\end{array}\right.$$

(4)

where $T_{in}$ denotes the indoor temperature; $\mathrm{U}$ denotes a uniform distribution; $a_1$ and $a_2$ denote the lower bounds of the uniform distribution, $a_1>a_2$; $b_1$ and $b_2$ denote the upper bounds of the uniform distribution, $b_1>b_2$; and $c$ is a constant.

2.2. Method for Generating the Probability Distribution of Design Heating Loads

Then, it is necessary to obtain the probability distribution of the design load in a rural residential building under the influence of the indoor temperature uncertainty. Based on the stochastic model of indoor temperature proposed in Section 2.1, the stochastic simulation of design heating load can be carried out for each room in a rural residential building, and then the probability distribution of the design heating load for the building can be determined, and the specific technical route is shown in Figure 1. The method is divided into the following four steps:

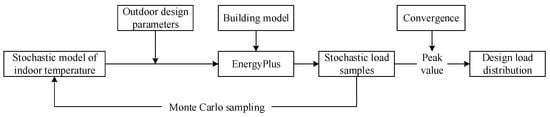
Figure 1. Technical route for stochastic simulation of design heating load.

(1)

The random indoor temperature scenarios for each room were generated by Monte Carlo sampling based on the stochastic model in Section 2.1, and the outdoor design conditions are a design day on which the outdoor temperature is fixed within 24 h and this fixed value is equal to the design dry-bulb temperature provided in the standard. Based on these, the 24 h loads of different rooms were simulated with the help of EnergyPlus software [26]. The results were as follows:

$$Q_{1,t}, Q_{2,t}, \cdots , Q_{n,t}$$

(5)

where $Q_{n,t}$ denotes the heating load of the $n$th room in a rural residential building at moment $t$, $t=1, 2, \cdots , 24$.

(2)

The hourly load results for each room were superimposed to obtain the hourly load results for the building, and its daily peak value was used as the design load sample. The specific formula of the design load sample was as follows:

$$Q_t=Q_{1,t}+Q_{2,t}+\cdots +Q_{n,t}$$

(6)

$$Q_d=\mathrm{M}\mathrm{a}\mathrm{x}\left\{Q_t\right|\mathrm{t}=\mathrm{1,2},\cdots ,24\}$$

(7)

where $Q_t$ denotes the heating load of the building at moment $t$, and $Q_d$ denotes the design load sample.

(3)

The rate of change in the mean value of the design load samples $S\left(N\right)$ was taken as an indicator parameter to determine whether the probabilistic characteristics of the building heating load were stable or not. The minimum number of simulations $N_{min}$ was determined by using $S\left(N\right)<0.2\%$ as a criterion for simulation convergence [22]. S(N) was calculated by the following equation:

$$S\left(N\right)=\frac{\left|Q_{d,mean}\right(N+∆N)-Q_{d,mean}(N\left)\right|}{Q_{d,mean}\left(N\right)}$$

(8)

where $Q_{d,mean}\left(N\right)$ denotes the mean value of all design load samples in the previous $N$ simulations; $N$ denotes the number of simulations; and $S\left(N\right)$ denotes the rate of change in the mean value of the design load samples.

(4)

The probability distribution of all design load samples at the minimum number of simulations was counted to characterize the uncertainty of design heating loads in the rural residential building.

2.3. Method for Determining Design Heating Load Value for Rural Residential Buildings

Finally, it is necessary to determine the heating design load value for rural residential buildings. Based on the probability distribution of design heating loads in Section 2.2, the design load value was selected in accordance with a certain confidence level to guide the design capacity determination of the building heating system. The specific process is shown in Figure 2. Here, the confidence level indicates the probability that the selected design value is not exceeded in the probability distribution of design heating loads, which is calculated as follows:

$$h\left(N\right)=\left\{\begin{array}{c}1, Q_d\left(N\right)<Q_{d,f}\\ 0, Q_d\left(N\right)\ge Q_{d,f}\end{array}\right.$$

(9)

$$N_{un}={\sum }_{N=1}^{N_{min}}h\left(N\right)$$

(10)

$$\beta =\frac{N_{un}}{N_{min}}\times 100\%$$

(11)

where $Q_d\left(N\right)$ denotes the design load value in the $N$th simulation, $Q_{d,f}$ denotes the selected design value, $N_{un}$ denotes the number of times that $Q_{d,f}$ is not exceeded, and $\beta$ denotes the confidence level.

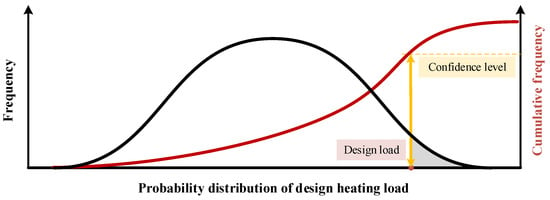
Figure 2. Schematic diagram of determining the design heating load. (Note: The black curve represents the probability distribution of the design heating load, the red curve represents the cumulative distribution of the design heating load, and the yellow double-arrow line represents the confidence level of a design load value).

3. Results

Harbin is located in the northern part of China, where there is strong demand for heating in rural residential buildings during the winter. In this study, an example of a rural residential building in Harbin was used to demonstrate the results of using the probabilistic design heating load calculation method, taking into account the indoor temperature uncertainty.

3.1. Building Model

In this study, a typical rural residential building was constructed on EnergyPlus software. It consists of four rooms: the master bedroom, hall, second bedroom, and kitchen. The spatial layout of these four rooms is shown in Figure 3. On this basis, the thermal parameters of the rural residential building were determined with reference to the Ministry of Housing and Urban–Rural Development of the People’s Republic of China (GB/T 50824-2013) [27] and related literature [28,29]. The specific information is shown in Table 1.

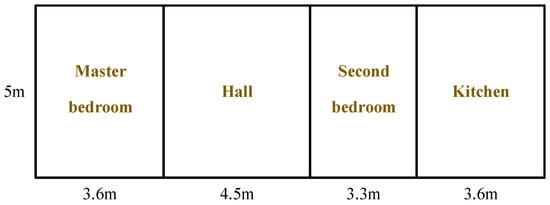
Figure 3. The spatial layout of the rural residential building.

Table 1. Information about the building parameters.

Parameter Type	Parameter		Value
Geometric parameter	Length/width/m		15/5
	Number of floors		1
	Floor height/m		4.0
Thermal performance parameters	Roof heat transfer coefficient/W/(m2·K)		0.80
	Wall heat transfer coefficient/W/(m2·K)		1.20
	Window heat transfer coefficient/W/(m2·K)		2.0
	Window-wall ratio	East	0.30
		South	0.40
		West	0.30
		North	0.25

3.2. Stochastic Load Simulation

In order to implement the stochastic load simulation for the rural residential building, it is first necessary to determine the specific parameters corresponding to the stochastic model of indoor temperature in Section 2.1. Among them, the setting of transfer probability in the Markov chain model mainly referred to the literature [30], which has been studied in detail for the use of rural residential buildings in northern China. The range of values for the indoor temperature in each room corresponding to different occupancy and activity situations is shown in Table 2.

Table 2. The parameters of the stochastic model of indoor temperature.

Occupancy Scenario	Room	Temperature Settings
$\mathrm{i}\mathrm{f} O_p\left(t\right)=1:$	Master bedroom, second bedroom	$T\left(t\right)~U\left(11, 14\right) ℃, \mathrm{if} 1\le t<8 \mathrm{o}\mathrm{r} 22<t\le 24\mathrm{h}$
		$T\left(t\right)~U\left(15, 18\right) ℃,\mathrm{i}\mathrm{f} 8\le t\le 22\mathrm{h}$
	Hall	$T\left(t\right)~U\left(15, 18\right) ℃, 0\le t\le 24\mathrm{h}$
	Kitchen	$T\left(t\right)~U\left(15, 18\right) ℃, 0\le t\le 24\mathrm{h}$
$\mathrm{i}\mathrm{f} O_p\left(t\right)=0:$	All rooms	$T\left(t\right)=5 ℃, 0\le t\le 24\mathrm{h}$

Based on the stochastic model of indoor temperature, random indoor temperature scenarios in each room were obtained by sampling. The results of a single simulation are shown in Figure 4. As can be seen from Figure 4, the simulation results of the stochastic model of indoor temperature in this study can reasonably reflect the usage characteristics of the four rooms in the rural residential buildings. Among them, the hall and kitchen, which take on the functions of daily activities and cooking, respectively, are occupied mainly during the day, so their indoor temperatures are set lower at night. The second bedroom, which takes on the function of sleeping, is mostly occupied at night, so its indoor temperature is generally set lower during the day. And the master bedroom, which simultaneously performs the functions of sleeping and daily activities, may be occupied throughout the day. At the time of occupancy, the indoor temperature at night is lower than that in the daytime, reflecting the distinction between sleeping and daily activities.

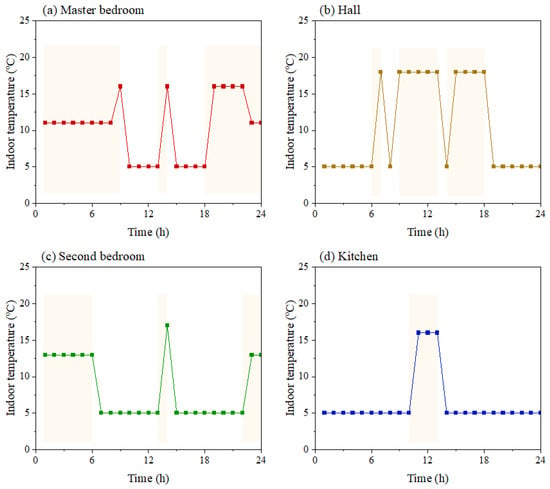
Figure 4. Simulation results from the stochastic model of indoor temperature in rural residential buildings. (Note: Light yellow area indicates that the room is occupied at this time).

In order to implement the stochastic load simulation for the rural residential building, it is also necessary to determine the 24 h outdoor design conditions. Harbin’s wintertime indoor–outdoor temperature difference is so great that variations in the outdoor temperature has little effect on the building’s peak load. Thus, it is assumed in this study that the outdoor dry bulb temperature will remain constant over time. On this basis, the 24 h outdoor design conditions were determined based on the extreme value of the dry bulb temperature in Harbin provided by the code [7].

Following the steps in Section 2.2, a stochastic simulation of the heating load in the rural residential building was carried out in combination with the indoor temperature scenarios and outdoor design conditions. In order to determine the minimum number of simulations, the rate of change in the mean value of the design load samples at different simulation times was calculated according to Equation (8), and the specific results are shown in Figure 5. From Figure 5, it can be seen that when the number of simulations reaches 550, the rate of change $S\left(N\right)$ is less than 0.2%. At this point, the convergence criterion is reached.

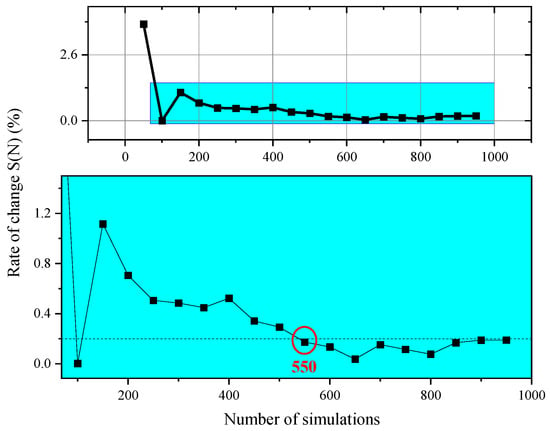
Figure 5. Minimum number of simulations in the stochastic simulation.

3.3. Probabilistic Design Heating Load

Based on the minimum number of simulations in Section 3.2, the corresponding number of random load samples are selected and their probability distributions are statistically obtained, and the specific results are shown in Figure 6.

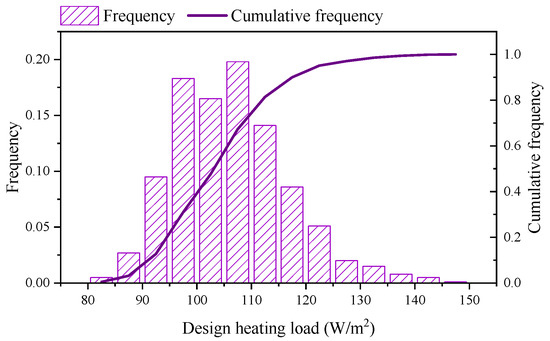
Figure 6. Probability distribution of the design heating load in the rural residential building.

As can be seen in Figure 6, the design load of the building is mainly distributed between 80 and 150 W/m², and this variation is due to the indoor temperature uncertainty. Based on the probability distribution of the design heating load, the final design load value can be chosen according to a certain confidence level. In this process, the higher the confidence level, the larger the selected design load value, but this variation is not uniform. For example, at the 100% confidence level, the design load of the building is 145 W/m²; at the 90% confidence level, the design load of the building is 120 W/m², which is 17.2% lower than the value of the design load corresponding to the 100% confidence level; and at the 80% confidence level, the design load of the building is 114 W/m², which is 5% lower than the value of the design load corresponding to the 90% confidence level. It can be found that the change in design load from the 100% to 90% confidence level is much larger than the change in design load from the 90% to 80% confidence level.

Therefore, within the confidence level between 90% and 100%, the design loads corresponding to the smaller confidence levels are recommended, to achieve a larger reduction in the design capacity of the building heating system by sacrificing a small design reliability. Within the confidence level of 80% to 90%, the design loads corresponding to the larger confidence levels are recommended, to achieve a large increase in the design reliability by a small increase in the design capacity of the building heating system.

4. Discussion

In order to verify the effectiveness of the new method in this study, a traditional design load calculation method corresponding to the “all-time, all-space” heating mode was used as a control. In this traditional method, the indoor temperatures of the master bedroom, hall, second bedroom, and kitchen were kept constant at 18 °C, as shown in Figure 7.

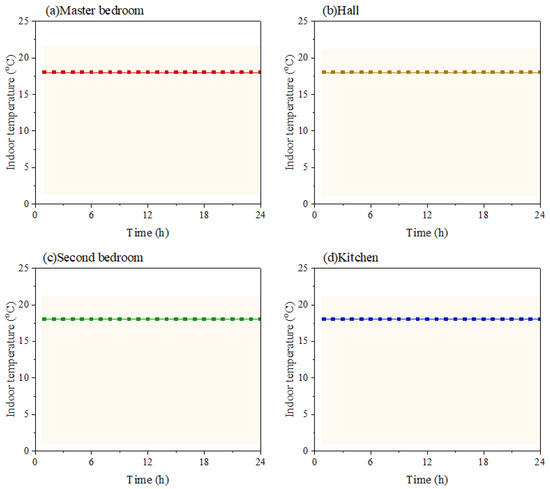
Figure 7. Indoor temperature setting in the rural residential building under the “all-time, all-space” heating mode. (Note: Light yellow area indicates that the room is occupied at this time).

Then, combining the outdoor design conditions introduced in Section 3.2, the 24 h heating loads of the building were simulated, whose peak value was used as the design load value for the traditional method. Finally, the results of the traditional method were compared with those of the new method, as shown in Figure 8.

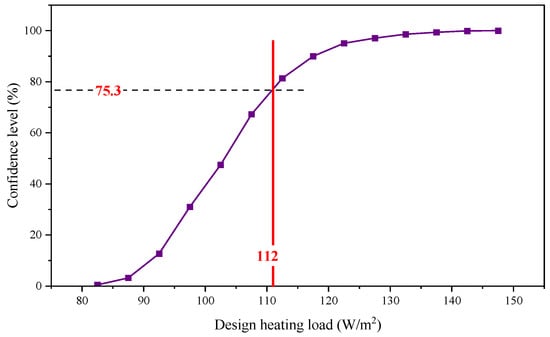
Figure 8. Comparison of the design heating loads of the new method with the traditional method. (Note: The purple line indicates the results of the new method in this study, and the red line indicates the results of the traditional method).

As can be seen in Figure 8, the design load of the traditional method is 112 W/m². This value is within the range of the new method of this study, and therefore the corresponding confidence level can be calculated, which is 75.3%. This means that the design capacity of the heating system for this rural residential building using the traditional method only ensures a 75.3% chance that the system will be reliable in actual operation. Such a low level of reliability may not be expected by the designer, but the designer is not able to propose a reasonable improvement based on the traditional method. In contrast, the new method in this study provides a confidence level for each design load value, which guides the designer in making specific decisions to reduce or increase the design capacity based on reliability and economic needs.

5. Conclusions

To meet the demand for heating system design in rural residential buildings, this study proposed a probabilistic design heating load calculation method that takes into account the indoor temperature uncertainty. The results of this new method are demonstrated using a rural residential building in Harbin as an example. The specific conclusions are as follows:

(1)

A refined method for determining the design heating load of rural residential buildings was proposed. In this method, an indoor temperature stochastic model was established for the usage characteristics of rural residential buildings to generate multiple possible scenarios for the indoor temperature, to ensure the reasonableness of the design load determination.

(2)

Using a rural residential building in Harbin as an example, the results of the application of the new method in this study were analyzed, and guiding principles for design load selection were found. Specifically, within the confidence level of 90% to 100%, design load values corresponding to lower confidence levels were recommended to reduce the design capacity; within the confidence degree of 80% to 90%, design load values corresponding to higher confidence levels were recommended to enhance the design reliability.

(3)

The advantages of this new method were analyzed by using the traditional method as a control. The results showed that while the traditional method might not be able to meet the reliability requirements of heating system design for rural residential buildings, the new method can guide the designer to reduce or increase the design capacity based on reliability and economic needs.

In the new method, whether the design heating load result is reasonable or not depends on whether the stochastic model of indoor temperature can accurately reflect the uncertainty of indoor temperature. In this study, the parameters of this stochastic model were determined by referring to the existing literature. Due to the difference in the level of economic development, the indoor temperature regulation habits of rural buildings in different regions will also be different. Therefore, the model parameters set in this study are not necessarily applicable to rural buildings in all regions. In future work, we will improve the problem of model parameter determination through a lot of field investigation to apply this research method to cases in diverse countries and regions.