Time-Varying Meshing Stiffness and Dynamic Parameter Model of Spiral Bevel Gears with Different Surface Roughness
Abstract
1. Introduction
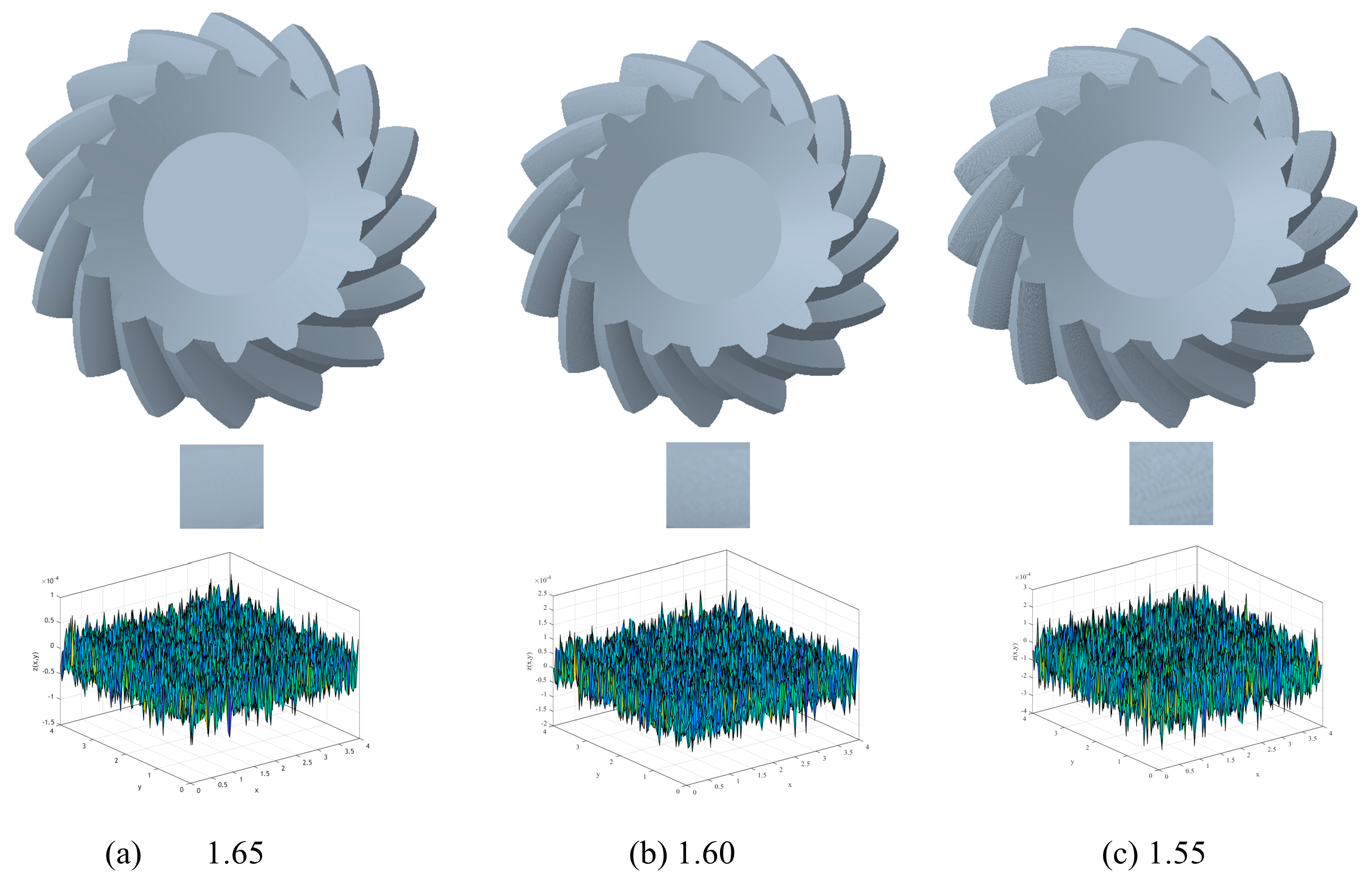
2. Establishment of Tooth Surfaces with Different Roughness
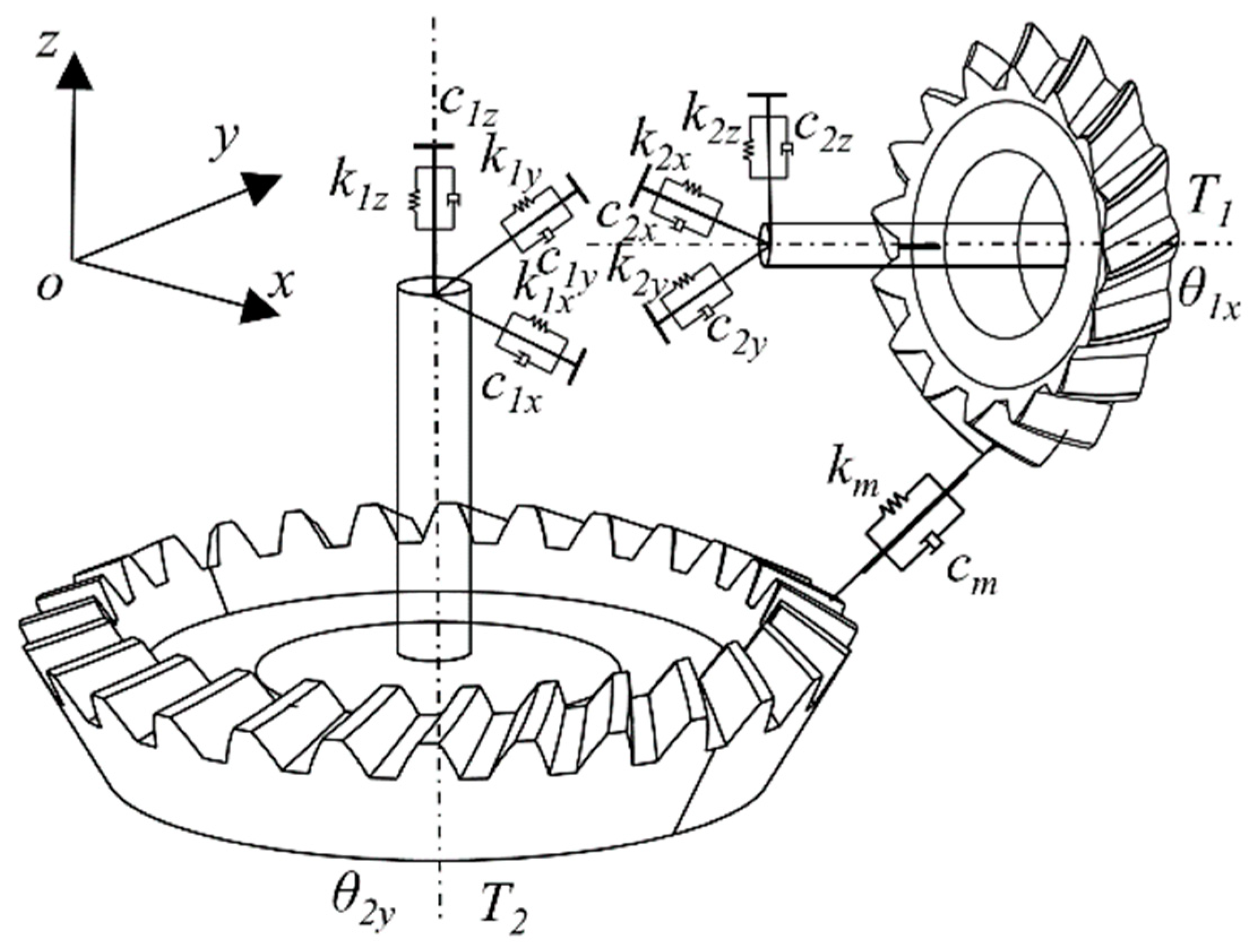
3. Establishment of the Dynamic Model for Spiral Bevel Gears
3.1. Dynamic Transmission Error
3.2. Tooth Flank Normal Clearance
3.3. Loaded Tooth Contact Analysis (LTCA)
4. Calculating Time-Varying Mesh Stiffness
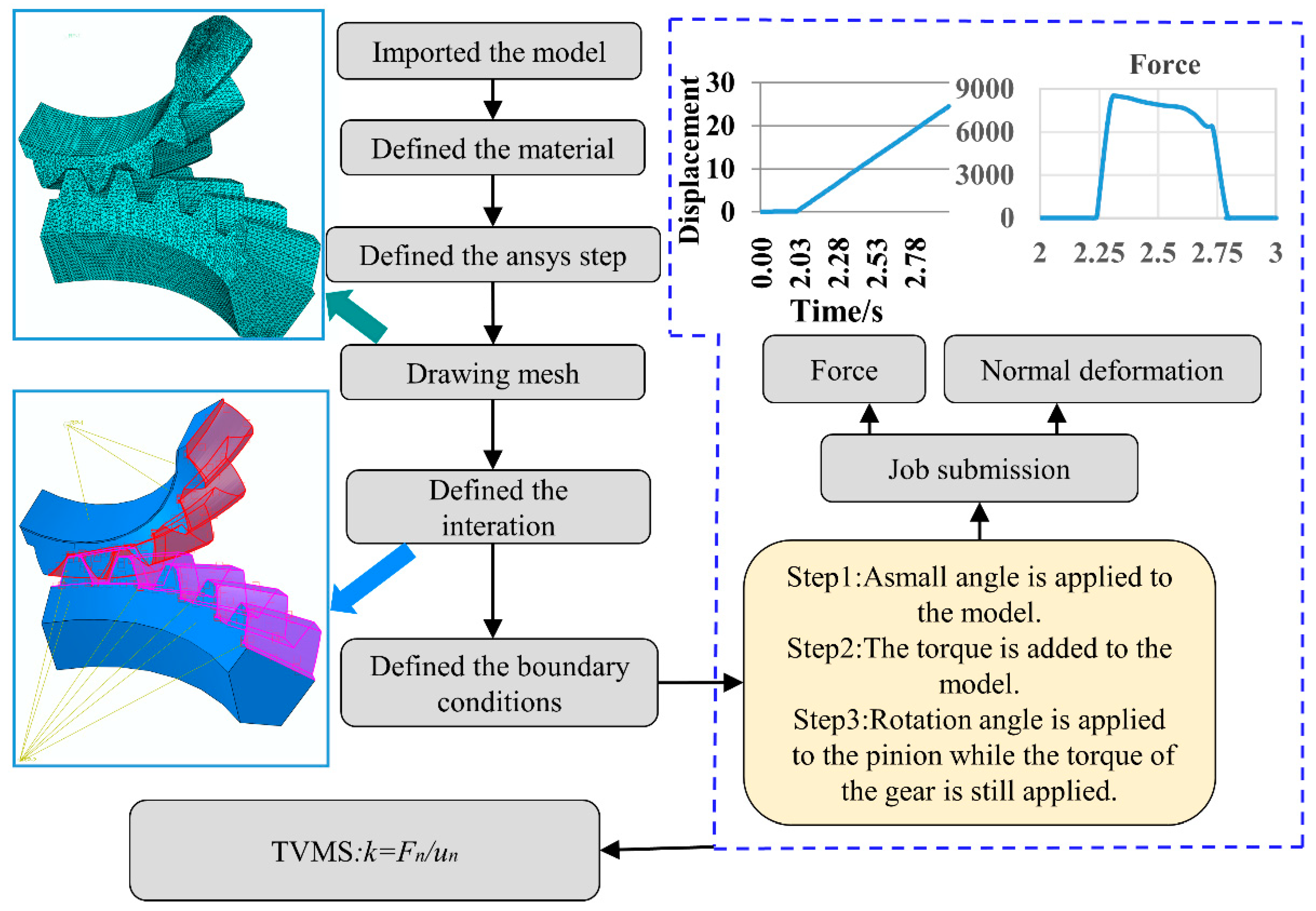
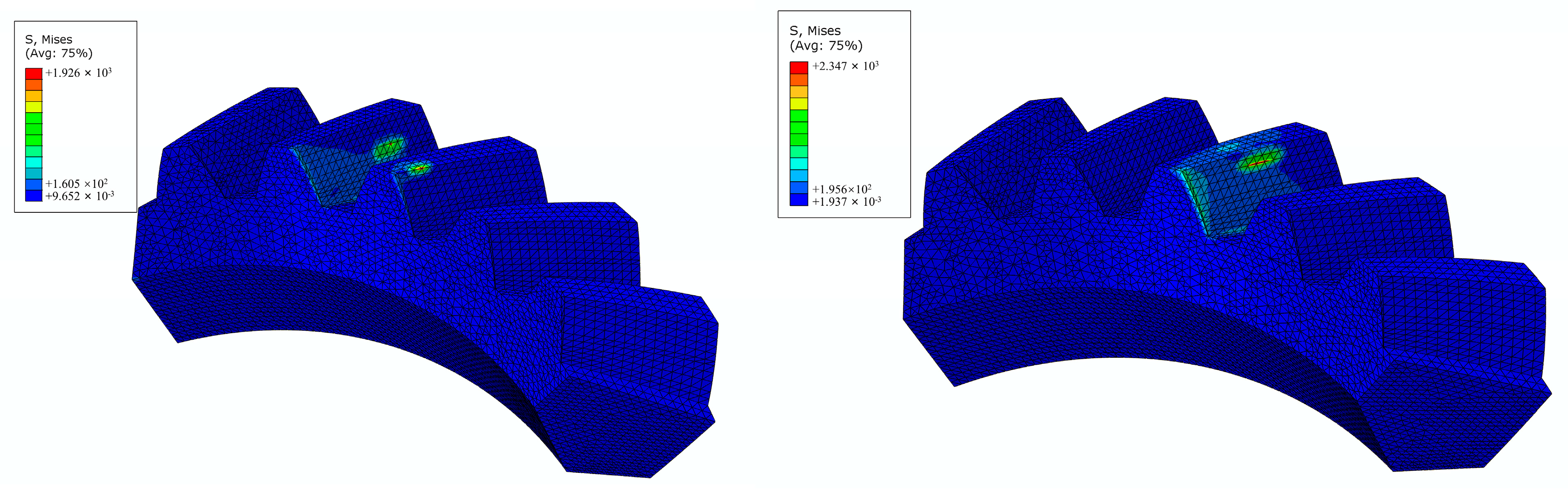
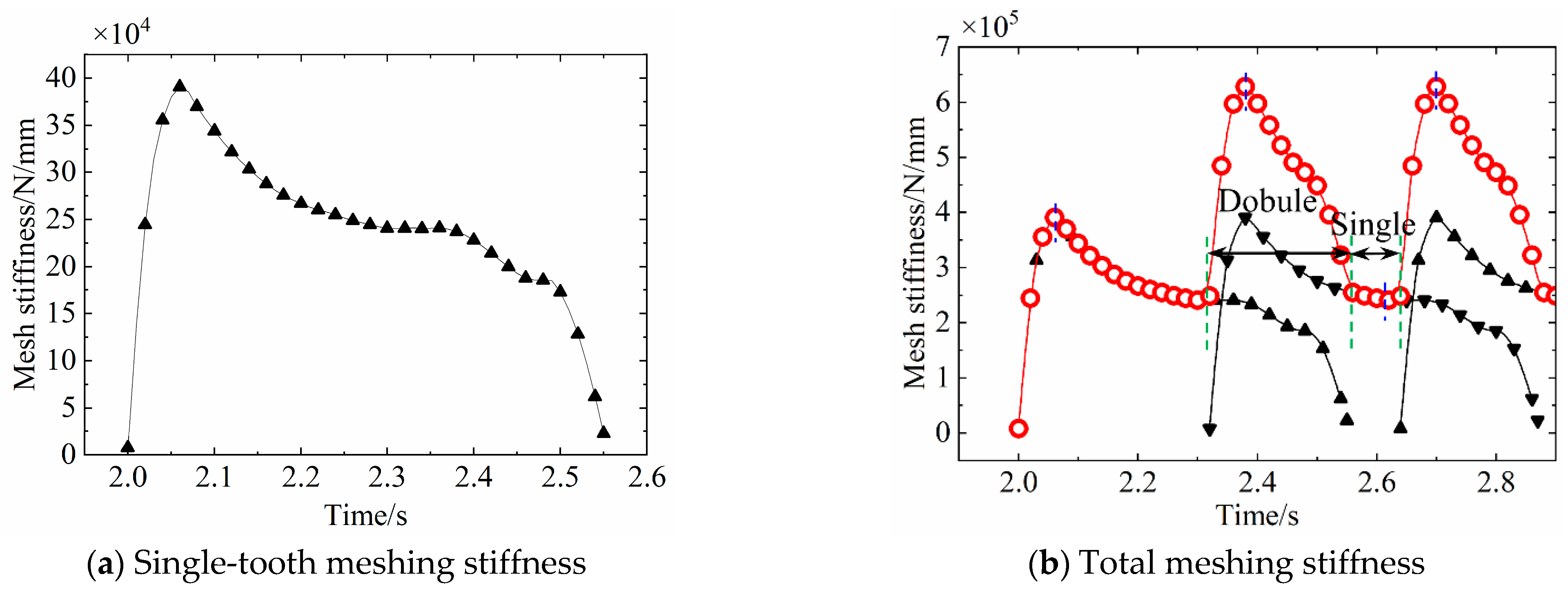
4.1. Model Establishment and Stiffness Analysis
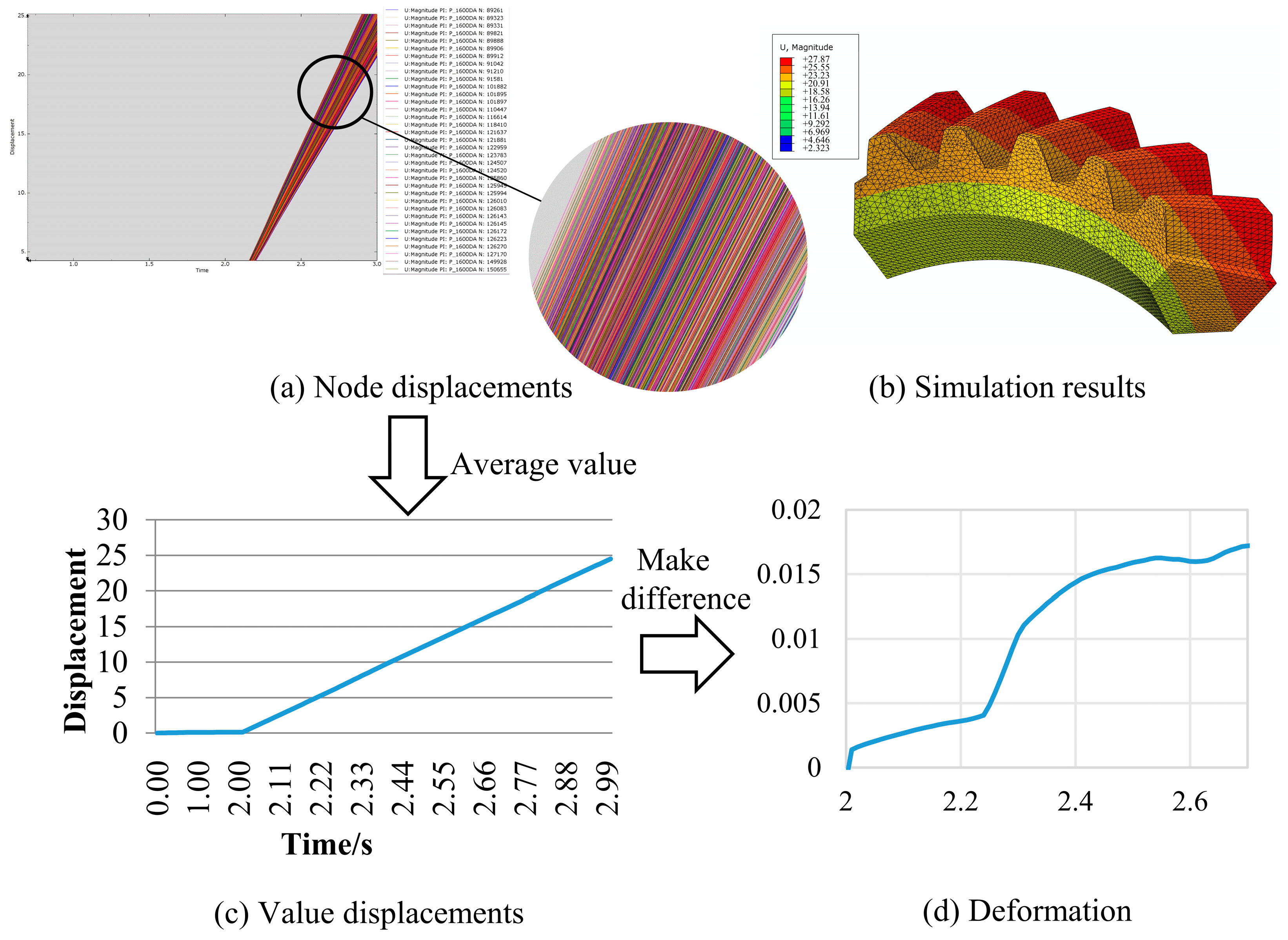
4.2. Finite Element Preprocessing
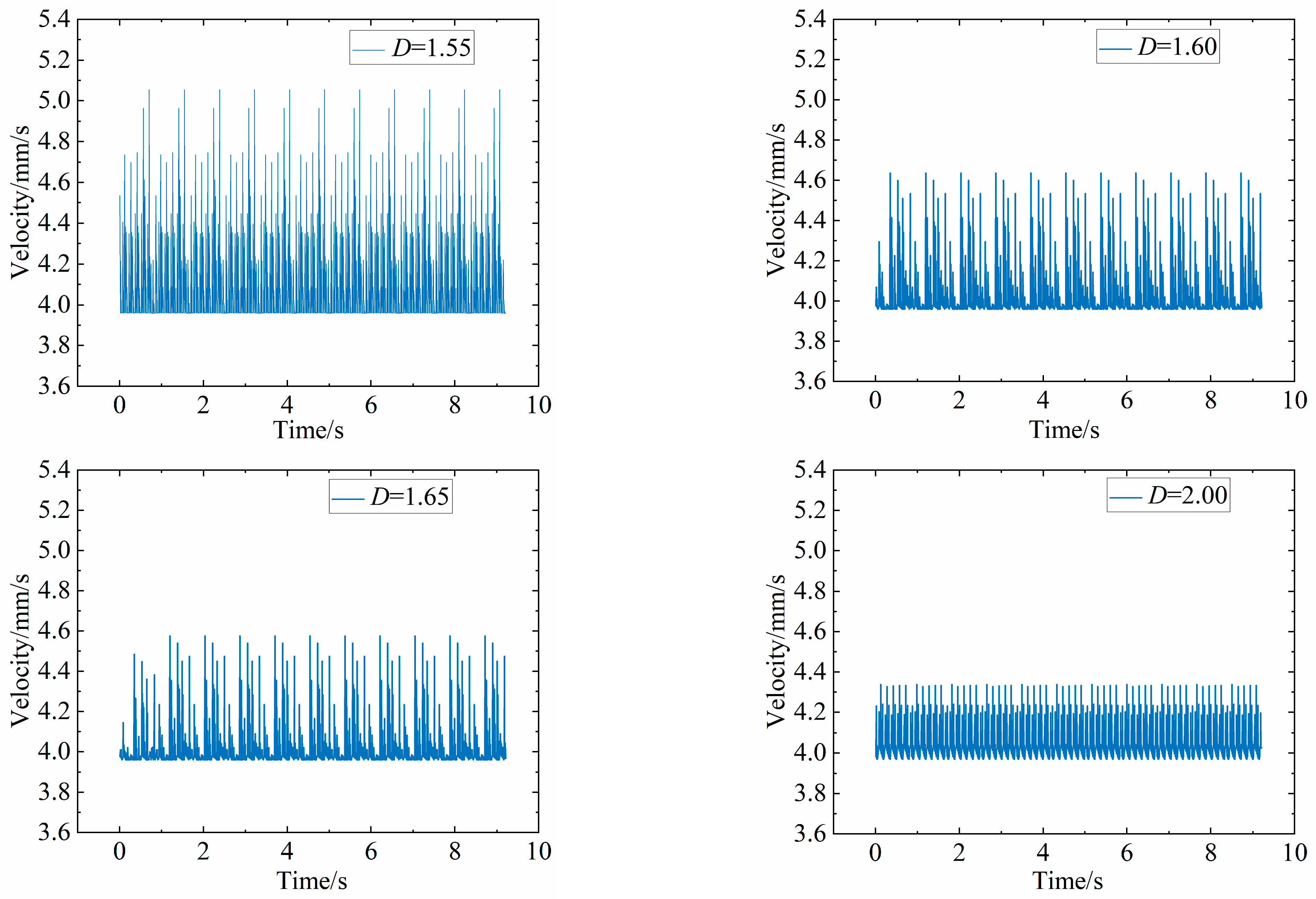
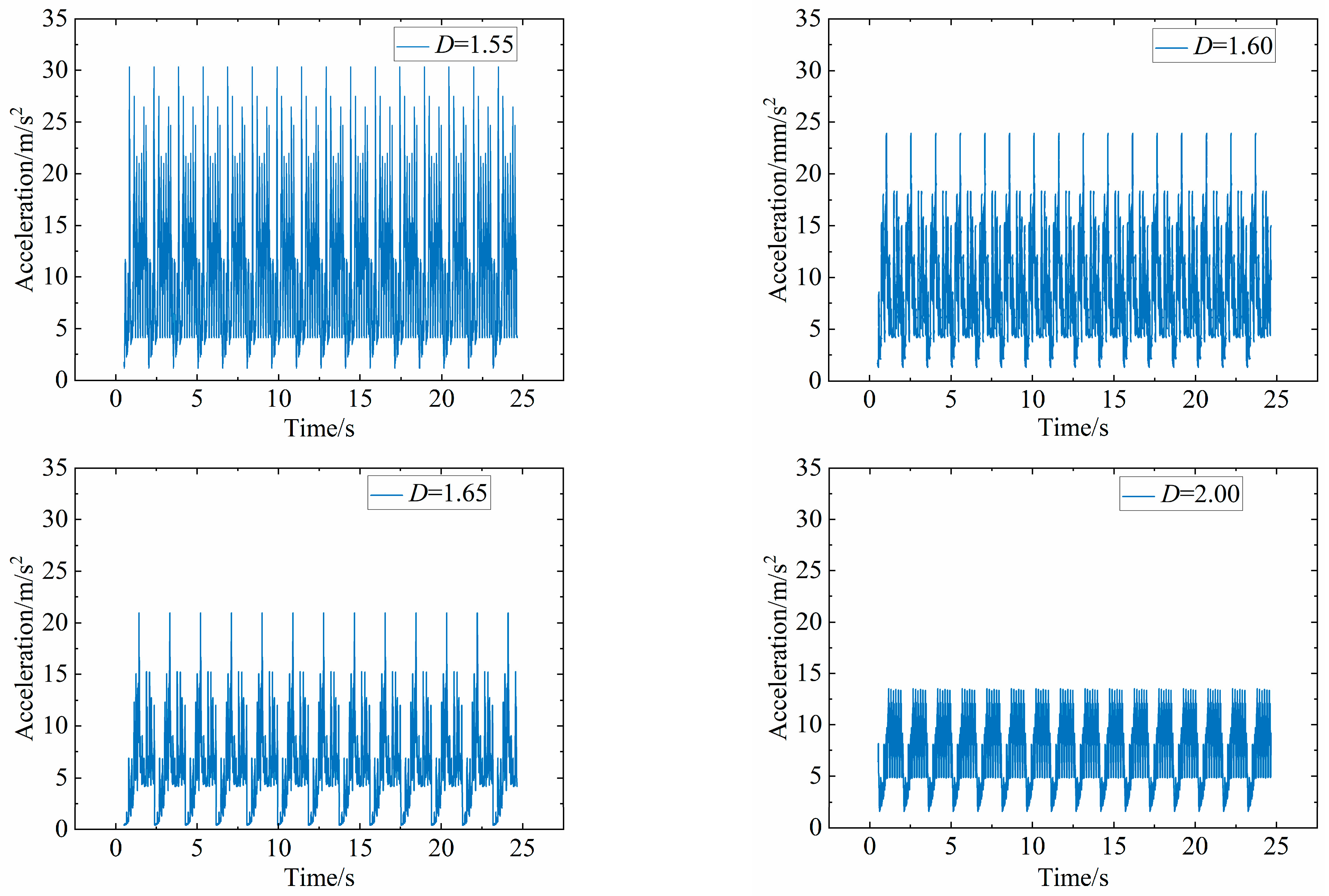
4.3. Experiment Result Analysis
5. Conclusions
- (1)
- Fractal dimensions are introduced into the involute equation. The MATLAB software is utilized to calculate the involute profiles under different roughness levels. By establishing the relationship between fractal dimensions and tooth surface roughness, the tooth profiles under varying roughness conditions are determined. The three-dimensional models of spiral bevel gears under different surface roughness levels are obtained using the principle of tooth cutting with a gear hob.
- (2)
- A novel model is proposed for calculating the mesh stiffness of spiral bevel gears under different fractal dimensions. Fractal dimensions are introduced into the differential dynamic equations of spiral bevel gears to determine the factors influencing the dynamic characteristics due to fractal dimensions and surface friction. Finite element analysis is employed to investigate the models of spiral bevel gears under various fractal dimensions, resulting in the determination of the time-varying mesh stiffness under different fractal dimensions. The results indicate that as the fractal dimension decreases, the time-varying mesh stiffness continuously decreases. Therefore, reducing the fractal dimension to some extent contributes to decreasing the time-varying mesh stiffness of the gears, thereby enhancing the smoothness of motion.
- (3)
- After establishing an experimental setup for spiral bevel gears, tests showed that the errors under two operating conditions were found to be 3.22% and 6.11%, respectively, indicating a small margin of error and validating the accuracy of the model. Through dynamic analysis using the developed model, the vibration characteristics of gears under different fractal dimensions were examined.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pei, X.; Pu, W.; Wang, Z. Contact stiffness and dynamic behavior caused by surface defects of spiral bevel gear in mixed lubrication. Eng. Fail. Anal. 2021, 121, 105129. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, A.; Wei, J.; Lim, T.C. Nonlinear excitation and mesh characteristics model for spiral bevel gears. Int. J. Mech. Sci. 2023, 257, 108541. [Google Scholar] [CrossRef]
- Li, S. A thermal tribo-dynamic mechanical power loss model for spur gear pairs. Tribol. Int. 2015, 88, 170–178. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Li, K.; Qiao, B.; Shen, Z.; Chen, X. An analytical method to calculate the time-varying mesh stiffness of spiral bevel gears with cracks. Mech. Mach. Theory 2023, 188, 105399. [Google Scholar] [CrossRef]
- Yin, L.; Deng, C.; Yu, W.; Shao, Y.M.; Wang, L.M. Dynamic characteristics of gear system under different micro-topographies with the same roughness on tooth surface. J. Cent. South Univ. 2020, 27, 2311–2323. [Google Scholar] [CrossRef]
- Wang, X.; Xiang, C.; Li, C.; Li, S.; Shao, Y.; Wang, L. Effect of roughness on meshing power loss of planetary gear set considering elasto-hydrodynamic lubrication. Adv. Mech. Eng. 2020, 12, 1687814020908422. [Google Scholar] [CrossRef]
- Patir, N. A numerical procedure for random generation of rough surfaces. Wear 1978, 47, 263–277. [Google Scholar] [CrossRef]
- Watson, W.; Spedding, T.A. The time series modelling of non-Gaussian engineering processes. Wear 1982, 83, 215–231. [Google Scholar] [CrossRef]
- Ausloos, M.; Berman, D.H. A multivariate Weierstrass–Mandelbrot function. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 331–350. [Google Scholar]
- Meng, F.; Xia, H.; Zhang, X.; Wang, J.; Jin, Y. Study on nonlinear dynamic characteristics of gear system with 3D anisotropic rough tooth surface based on fractal theory. Int. J. Non-Linear Mech. 2023, 150, 104366. [Google Scholar] [CrossRef]
- Ding, H.; Rong, S.; Rong, K.; Tang, J. Semi-FEM dynamic meshing impact forecasting model for spiral bevel and hypoid gear transmission. Appl. Math. Model. 2022, 104, 279–305. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Zhai, J.; Han, Q. Research on nonlinear dynamic performance of the central bevel gear transmission system in aero-engine with complex excitation. Mech. Based Des. Struct. Mach. 2023, 51, 6680–6703. [Google Scholar] [CrossRef]
- Heingartner, P.; Mba, D. Determining power losses in helical gear mesh: Case study. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2003; pp. 965–970. [Google Scholar]
- Anderson, N.E.; Loewenthal, S.H. Efficiency of nonstandard and high contact ratio involute spur gears. J. Mech. Transm. Autom. Des. 1986, 108, 119–126. [Google Scholar] [CrossRef]
- Anderson, N.E.; Loewenthal, S.H. Design of spur gears for improved efficiency. J. Mech. Des. 1982, 104, 767–774. [Google Scholar] [CrossRef]
- Britton, R.D.; Elcoate, C.D.; Alanou, M.P.; Evans, H.P.; Snidle, R.W. Effect of surface finish on gear tooth friction. J. Trib. 2000, 122, 354–360. [Google Scholar] [CrossRef]
- Schleich, B.; Anwer, N.; Mathieu, L.; Wartzack, S. Skin Model Shapes: A new paradigm shift for geometric variations modelling in mechanical engineering. Comput. Aided Des. 2014, 50, 1–15. [Google Scholar] [CrossRef]
- Chen, Q.; Ma, Y.; Huang, S.; Zhai, H. Research on gears’ dynamic performance influenced by gear backlash based on fractal theory. Appl. Surf. Sci. 2014, 313, 325–332. [Google Scholar] [CrossRef]
- Sayles, R.S.; Thomas, T.R. Surface topography as a nonstationary random process. Nature 1978, 271, 431–434. [Google Scholar] [CrossRef]
- Bonori, G.; Pellicano, F. Non-smooth dynamics of spur gears with manufacturing errors. J. Sound Vib. 2007, 306, 271–283. [Google Scholar] [CrossRef]
- Inalpolat, M.; Handschuh, M.; Kahraman, A. Influence of indexing errors on dynamic response of spur gear pairs. Mech. Syst. Signal Process. 2015, 60, 391–405. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W. A Proposed Model for Stochastic Vibration Analysis of Gear Transmission Systems. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers: New York, NY, USA, 1996; Volume 97584, p. V02BT02A012. [Google Scholar]
- Chang, L.; Liu, G.; Wu, L. Determination of composite meshing errors and its influence on the vibration of gear system. J. Mech. Eng. 2015, 51, 123–130. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Kang, Y.; Lin, J.C. Comprehensive dynamics model and dynamic response analysis of a spur gear pair based on gear pair integrated error. J. Mech. Eng. 2010, 46, 55–61. [Google Scholar] [CrossRef]
- Kang, H. Research on gear dynamics considering influence of tooth surface roughness. J. Plast. Eng. 2019, 26, 234–239. [Google Scholar]
- Papadopoulou, S.; Pressas, I.; Vazdirvanidis, A.; Pantazopoulos, G. Fatigue failure analysis of roll steel pins from a chain assembly: Fracture mechanism and numerical modeling. Eng. Fail. Anal. 2019, 101, 320–328. [Google Scholar] [CrossRef]
- Ge, S.R.; Tonder, K. The fractal behavior and fractal characterization of rough surfaces. Tribology 1997, 17, 73–80. [Google Scholar]
- Kleemola, J.; Lehtovaara, A. Experimental simulation of gear contact along the line of action. Tribol. Int. 2009, 42, 1453–1459. [Google Scholar] [CrossRef]
- Mu, Y.M.; He, X.M.; Fang, Z.D. Design and dynamic performance analysis of high-contact-ratio spiral bevel gear based on ease-off technology. Int. J. Precis. Eng. Manuf. 2021, 22, 1963–1973. [Google Scholar] [CrossRef]
- Simon, V. Design of face-hobbed spiral bevel gears with reduced maximum tooth contact pressure and transmission errors. Chin. J. Aeronaut. 2013, 26, 777–790. [Google Scholar] [CrossRef]
- Deng, X.Z.; Fan, M.; Yang, H.B. Relationship between contact ratio and load of spiral bevel gears. China Mech. Eng. 2002, 12, 878–880. [Google Scholar]
- Simon, V. Load distribution in spiral bevel gears. ASME J. Mech. Des. 2007, 129, 2406090. [Google Scholar] [CrossRef]
- Simon, V. FEM stress analysis in hypoid gears. Mech. Mach. Theory 2000, 35, 1197–1220. [Google Scholar] [CrossRef]
- Qu, W.; Ding, H.; Tang, J. An innovative semi-analytical determination approach to numerical loaded tooth contact analysis (NLTCA) for spiral bevel and hypoid gears. Adv. Eng. Softw. 2020, 149, 102892. [Google Scholar] [CrossRef]
- ISO 6336-21:2017; Calculation of Load Capacity of Spur and Helical Gears. Calculation of Scuffing Load Capacity (also Applicable to Bevel and Hypoid Gears). Integral Temperature Method. ISO: Geneva, Switzerland, 2017.
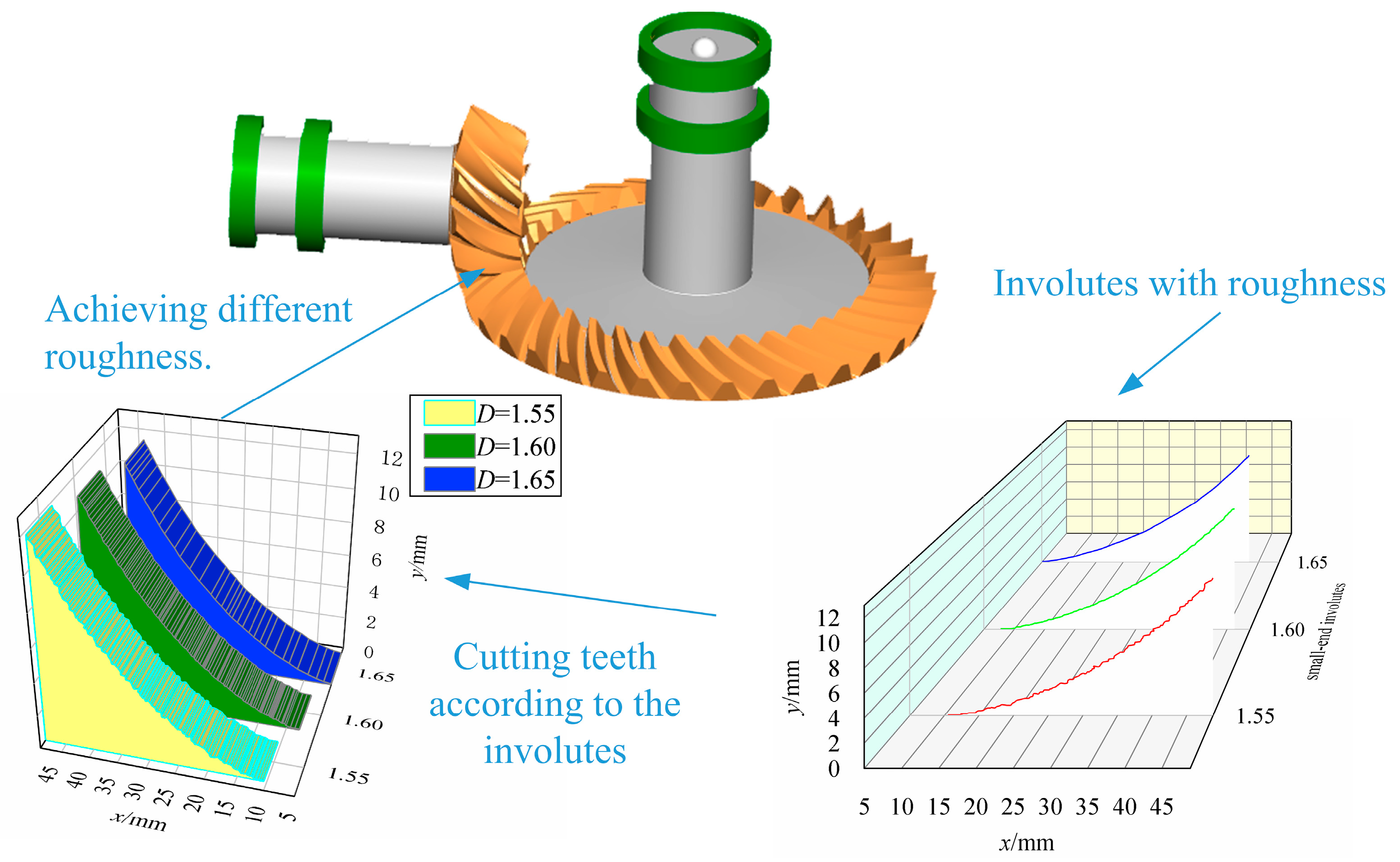
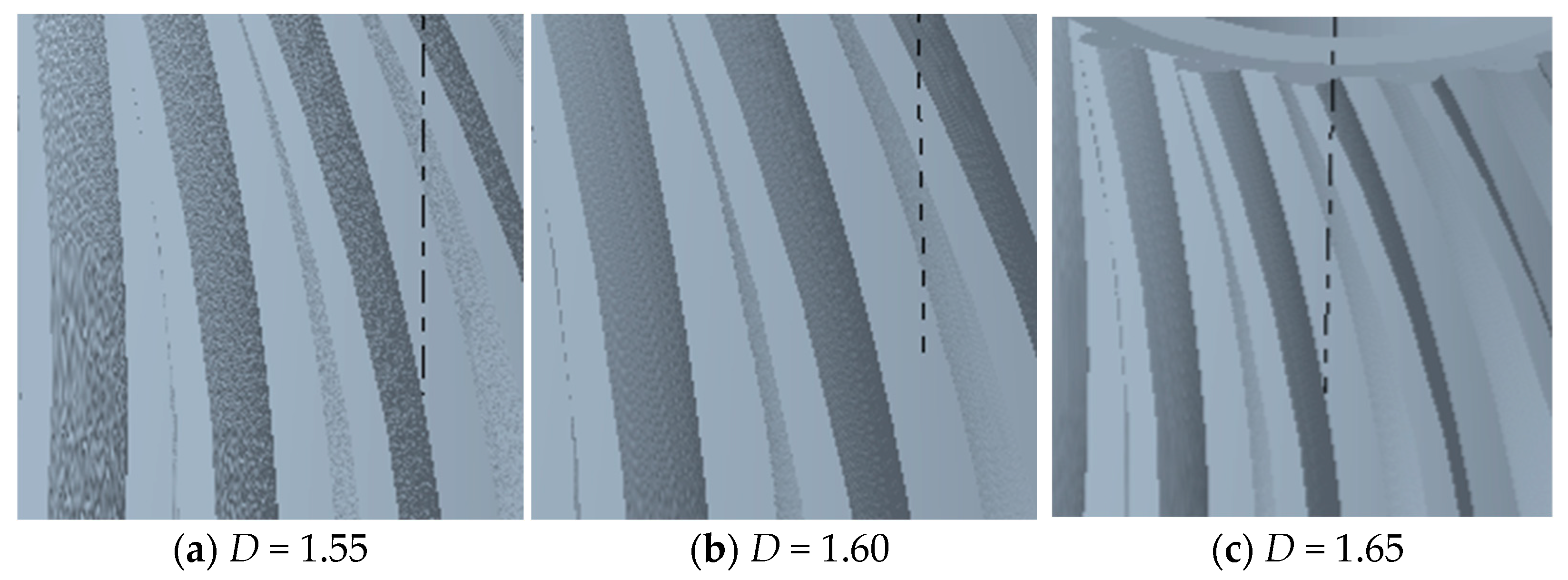
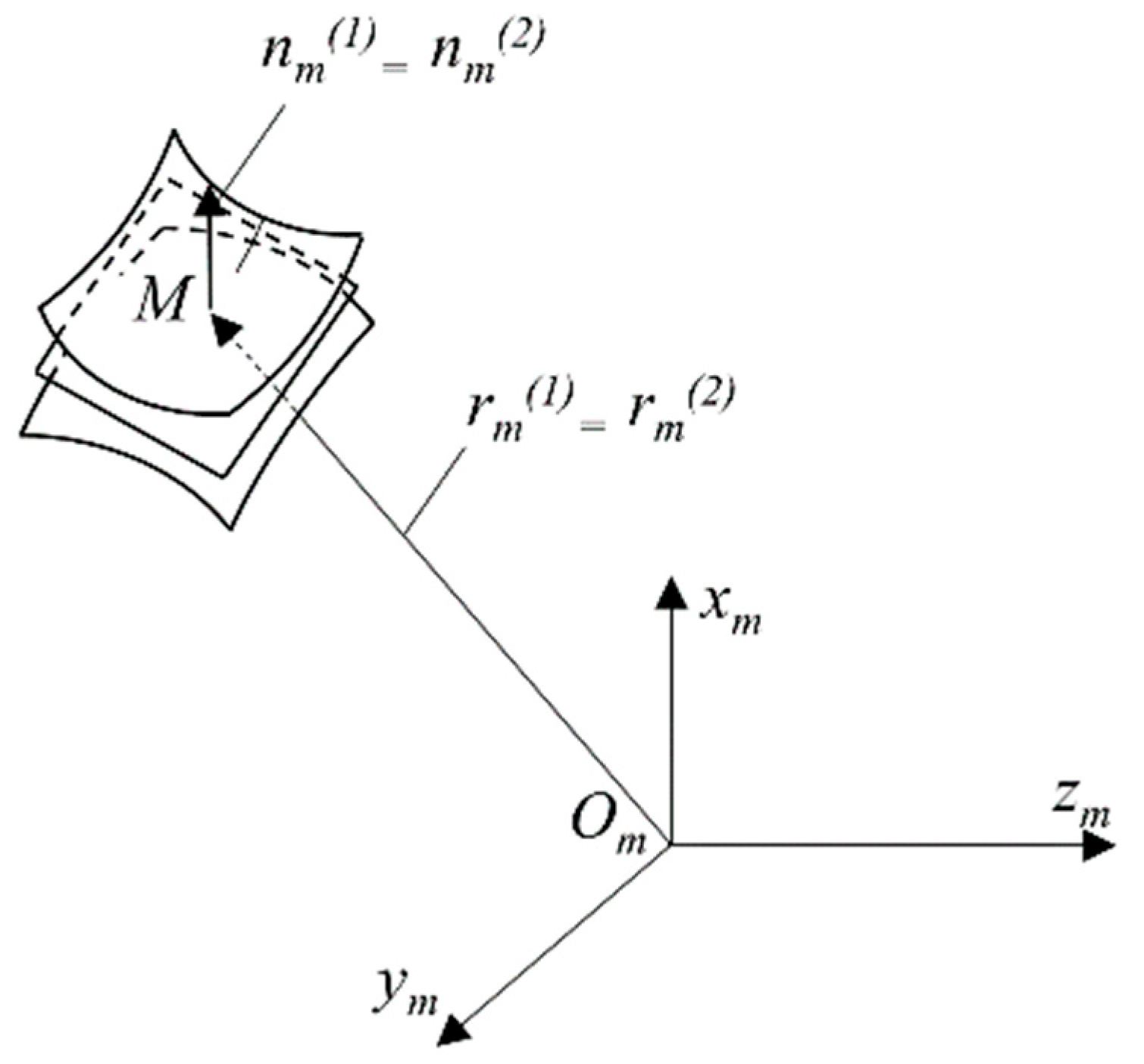
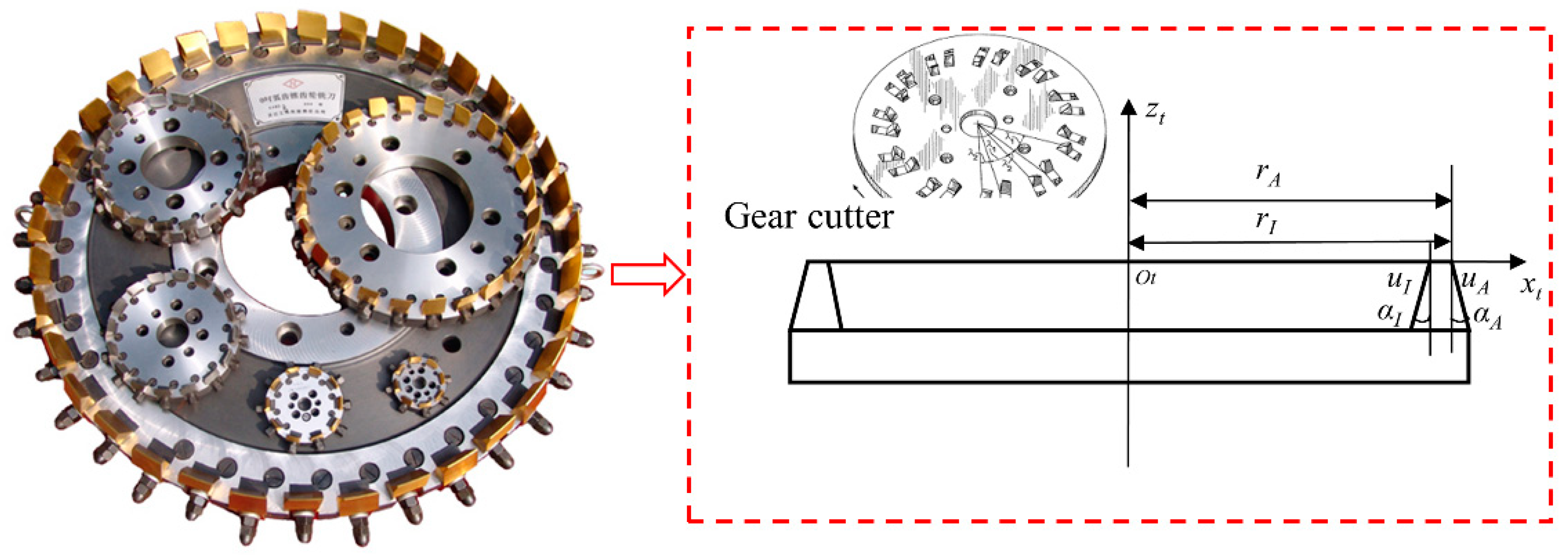




| Postprocessing Operation | Roughness/μm |
|---|---|
| Unground machining | 0.8 |
| Grinding machining | 0.4 |
| Polishing | 0.2 |
| Postprocessing Operation | Surface Roughness/μm | Fractal Dimension | Characteristic Scale Coefficient |
|---|---|---|---|
| Unground machining | 0.8 | 1.55 | 5 × 10−6 |
| Grinding machining | 0.4 | 1.60 | 3 × 10−6 |
| Polishing | 0.2 | 1.65 | 2 × 10−6 |
| Pinion | Gear | |
|---|---|---|
| Number of teeth | 16 | 27 |
| Module (mm) | 4.25 | |
| Face width (mm) | 12 | |
| Pressure angle (°) | 20 | |
| Spiral angle (°) | 30 | |
| Shaft angle (°) | 90 | |
| Hand of spiral | Left hand | Right hand |
| Time/s | Simulation Data under 77 N·m (mm/s) | Experimental Data under 77 N·m (mm/s) | Simulation Data under 105 N·m (mm/s) | Experimental Data under 105 N·m (mm/s) |
|---|---|---|---|---|
| 1 | 3.97 | 3.98 | 3.94 | 4.53 |
| 2 | 4.13 | 4.09 | 3.95 | 4.55 |
| 3 | 3.96 | 4.07 | 3.96 | 4.55 |
| 4 | 4.04 | 4.12 | 4.19 | 4.62 |
| 5 | 3.96 | 4.10 | 3.96 | 4.49 |
| 6 | 3.97 | 4.10 | 3.95 | 4.44 |
| 7 | 4.01 | 4.04 | 3.96 | 4.41 |
| 8 | 4.02 | 4.09 | 4.58 | 4.41 |
| 9 | 4.21 | 4.19 | 3.96 | 4.35 |
| 10 | 4.02 | 4.18 | 4.17 | 4.33 |
| 11 | 4.07 | 4.18 | 3.96 | 4.42 |
| 12 | 4.01 | 4.24 | 5.00 | 4.45 |
| 13 | 4.34 | 4.21 | 3.96 | 4.39 |
| 14 | 3.99 | 4.13 | 4.63 | 4.39 |
| 15 | 4.08 | 4.15 | 3.96 | 4.33 |
| 16 | 3.98 | 4.15 | 4.53 | 4.29 |
| 17 | 4.23 | 4.17 | 3.96 | 4.37 |
| 18 | 3.97 | 4.23 | 4.21 | 4.39 |
| 19 | 4.03 | 4.22 | 3.96 | 4.39 |
| 20 | 3.96 | 4.15 | 3.95 | 4.42 |
| 21 | 3.98 | 4.15 | 3.96 | 4.40 |
| 22 | 4.01 | 4.17 | 3.95 | 4.30 |
| 23 | 4.02 | 4.23 | 4.40 | 4.35 |
| 24 | 4.20 | 4.19 | 3.95 | 4.35 |
| 25 | 4.02 | 4.16 | 4.06 | 4.35 |
| 26 | 4.07 | 3.98 | 3.96 | 4.41 |
| 27 | 4.00 | 3.98 | 4.73 | 4.42 |
| 28 | 4.33 | 3.99 | 3.96 | 4.44 |
| 29 | 3.99 | 4.01 | 4.38 | 4.44 |
| 30 | 4.09 | 4.05 | 3.96 | 4.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.-J.; Zheng, X.-Q.; Lan, H.-Q.; Wang, L.-N.; Yang, S.-W.; Sheng, R. Time-Varying Meshing Stiffness and Dynamic Parameter Model of Spiral Bevel Gears with Different Surface Roughness. Appl. Sci. 2024, 14, 1533. https://doi.org/10.3390/app14041533
Cai Z-J, Zheng X-Q, Lan H-Q, Wang L-N, Yang S-W, Sheng R. Time-Varying Meshing Stiffness and Dynamic Parameter Model of Spiral Bevel Gears with Different Surface Roughness. Applied Sciences. 2024; 14(4):1533. https://doi.org/10.3390/app14041533
Chicago/Turabian StyleCai, Zhi-Jie, Xi-Qing Zheng, Hui-Qing Lan, Liu-Na Wang, Si-Wei Yang, and Rui Sheng. 2024. "Time-Varying Meshing Stiffness and Dynamic Parameter Model of Spiral Bevel Gears with Different Surface Roughness" Applied Sciences 14, no. 4: 1533. https://doi.org/10.3390/app14041533
APA StyleCai, Z.-J., Zheng, X.-Q., Lan, H.-Q., Wang, L.-N., Yang, S.-W., & Sheng, R. (2024). Time-Varying Meshing Stiffness and Dynamic Parameter Model of Spiral Bevel Gears with Different Surface Roughness. Applied Sciences, 14(4), 1533. https://doi.org/10.3390/app14041533






