Joint Entity and Relation Extraction Model Based on Inner and Outer Tensor Dot Product and Single-Table Filling

Abstract

Joint relational triple extraction is a crucial step in constructing a knowledge graph from unstructured text. Recently, multiple methods have been proposed for extracting relationship triplets. Notably, end-to-end table-filling methods have garnered significant research interest due to their efficient extraction capabilities. However, existing approaches usually generate separate tables for each relationship, which neglects the global correlation between relationships and context, producing a large number of useless blank tables. This problem results in issues of redundant information and sample imbalance. To address these challenges, we propose a novel framework for joint entity and relation extraction based on a single-table filling method. This method incorporates all relationships as prompts within the text sequence and associates entity span information with relationship labels. This approach reduces the generation of redundant information and enhances the extraction capability for overlapping triplets. We utilize the internal and external multi-head tensor fusion approach to generate two sets of table feature vectors. These vectors are subsequently merged to capture a wider range of global information. Experimental results on the NYT and WebNLG datasets demonstrate the effectiveness of our proposed model, which maintains excellent performance, even in complex scenarios involving overlapping triplets.

1. Introduction

Extracting entity pairs and their relationships from unstructured text and constructing relationship triplets are important steps in building knowledge graphs [1,2] and question-answering systems [3,4]. Early relational triple extraction tasks were mainly carried out using a pipeline approach [5] consisting of two subtasks: entity extraction [6] and relationship classification [7]. However, such extraction methods often suffer from the problem of cascading errors and efficiency, making it difficult to capture the dependencies between entities and relationships. Therefore, researchers have primarily focused on the joint extraction approach, attempting to extract triplets in an end-to-end manner to reduce the issues of cascading errors and exposure bias. For example, [8] proposed a two-stage extraction network, first extracting the subject and then extracting the corresponding relationship and object.

In recent years, end-to-end table-filling methods [9,10,11,12] have demonstrated their powerful extraction capabilities, especially in extracting triplets from complex sentences containing overlapping triplets. For instance, [10] divided joint extraction into three parts and completed the extraction in one stage, thereby avoiding exposure bias. Due to the complexity of human language, the number of entities and their relationships in a sentence is uncertain, which increases the difficulty of extracting relationship triplets [13], specifically, the problem of relationship overlap [14]. The overlapping problem refers to situations where multiple triplets share common entities or relations. Specifically, it involves cases where the boundaries of entities or relations overlap, creating ambiguity in the extraction process. The cases of triplet overlap can generally be classified into three categories: SEO, EPO, and SOO, as shown in Figure 1. If several triples in a sentence share the same entity, it is SEO; for example, the triples (Thomas Davies, graduated, University of London) and (England, contains, University of London) share the entity “University of London”. It is EPO if there are multiple relationships between certain entity pairs; for example, the triples (France, contains, Paris) and (Paris, capital, France) both exist for the same entity pair “France” and “Paris”. A triple is SOO if the subject and object are nested entities of each other; for example, if the object “Thomas” in the triple (Thomas Davies, first name, Thomas) is a nested entity of the subject “Thomas Davies”. The design of table-filling schemes also affects the ability to extract complex entities and relationships. Designing an efficient and highly generalizable table-filling method has become a research focus.

Figure 1. Overall cases of normal, EPO, SEO, and SOO overlapping triples. Different colors represent different entities in the case sentence.

Currently, models based on table-filling methods for extracting triplets usually maintain a separate table for each relationship, where each entry in the table represents the existence of a certain relationship between token pairs [11,12]. However, this approach presents three issues: (1) It generates many useless relationship tables, and the number of positive samples in the tables with relationships is much smaller than the number of blank labels, making the model easily affected by negative samples during the learning process. (2) When extracting entity spans, it often relies on complex multi-class labels or additional tables to map the head and tail markers. The former requires a complex decoding mechanism to achieve triplet extraction, whereas the latter introduces more redundant information. (3) It fails to fully utilize the semantic information of relationships. These relationships are often mapped to an ID and cannot establish intrinsic connections with the context and relevant entities, making it difficult to capture fine-grained semantic information between relationships.

Inspired by ref. [15], in this paper, we propose a single-table-filling framework model, which no longer maintains multiple relational tables but instead uses a shared representation to express the relationship between entities. Specifically, the relationships are first extracted as words with a special meaning. These relationship words are then concatenated with the original text and transformed into word embeddings, which are input into the BERT [16] language model for uniform encoding. Unlike the table-filling approach in ref. [15], we rely on the entity span information within the relationship labels. This means that we construct continuous subject–relation pair labels and object–relation pair labels to identify the spans of subject and object entities, thereby addressing the problem of complex triple overlap. To capture more global information, BiGRU [17] is employed to extract additional hidden layer information, and a multi-head tensor dot-product operation is employed to encode table features. These encoded features are subsequently fused with the output of the self-attention mechanism within the transformer [18] to iteratively acquire the intermediate encoding of table cells. Finally, the sigmoid function is employed to obtain the probability table for the final result. To address the extreme imbalance of positive and negative samples, as well as difficult samples, we employ the focal loss [19] as a loss function to replace the traditional binary cross-entropy, as it exhibits better training performance in situations with imbalanced sample difficulty and positive-negative sample distribution.

The main contributions of this work are as follows:

(1)

We propose a novel table-filling scheme, which can extract entities with multiple relations and tokens end to end. Even when applied to a simple network architecture, it achieves high accuracy.

(2)

We propose a new framework model that combines the attention mechanism inside the transformer with the multi-head tensor dot-product results of sentence representations, enriching the feature vectors of the table and improving accuracy compared to extracting results using only the attention mechanism.

(3)

We apply the focal loss function to entity relation extraction table-filling methods. To the best of our knowledge, most current relation extraction models based on table-filling methods use cross-entropy as the loss function for training.

(4)

We evaluate the proposed model on two public datasets, NYT [20] and WebNLG [21], and select classic models from the past three years as baselines. Our model achieves the best accuracy on the NYT dataset and demonstrates higher training efficiency.

2. Related Works

Relation triplet extraction is an important process in constructing a knowledge graph [1,2], which mainly involves two entities and the relationship between them. Early studies typically used a pipeline approach [5], which involved two steps. Firstly, named entity recognition was used to extract all entities from the text. Then, relation classification was used to identify the relationships between them. These two steps used two completely independent encoders. However, this extraction method introduces two problems. Firstly, it does not utilize the potential connections between entities and relationships, treating them completely separately. Secondly, there is a cascading error problem, where errors generated during the entity extraction step directly affect the accuracy of the relation classification task. In order to address these challenges, researchers have conducted collaborative studies focusing on joint entity and relation extraction [22,23].

Early research on joint extraction mainly focused on feature engineering [24], using random discrete variables to represent the results of local entity recognition and relation extraction. However, errors often occur when extracting features using NLP tools, which reduces the overall performance of the model. In recent years, deep neural networks have achieved success in various fields, and researchers have attempted to use a shared encoder for both entity extraction and relation classification in joint learning [22,23]. Currently, end-to-end [14] extraction methods have demonstrated powerful performance, leading to various branches in the task of joint relational triple extraction. Based on different methods and extraction processes, we categorize the joint extraction task into the following types:

Tagging-based methods. These approaches typically employ binary labeling sequences to identify the start and end positions of entities, taking into account the interrelationships between entities across various relationship types. The authors of ref. [8] proposed a cascaded framework called CasRel, which first extracts the subject and then extracts the corresponding object based on the subject for relationship classification prediction. In ref. [25], the authors decomposed the joint extraction of triplets into three sub-tasks and used a relationship prioritization method to filter redundant relationships, leading to significant improvements in computational efficiency and extraction accuracy compared to the CasRel model. Despite the good performance achieved by these methods, they involve multiple sub-modules or steps, which leads to exposure bias and insufficient batching capability. Additionally, the integration of relationship information into the sentence to assist entity recognition tasks has not been well applied.

Generation-based methods. These approaches generally utilize RNN models as a foundation and adopt the Seq2Seq [26] framework to transform the extraction task into a generation task, generating triplets in a fixed format. In ref. [27], the authors proposed an end-to-end language generation model called REBEL for relation extraction. This model is flexible in adapting to new domains and longer document data without the need to train specific modules from scratch, making the training process more efficient. However, this method struggles with handling long-distance dependency issues and also considers the context when generating triplets, leading to higher computational efficiency and model complexity.

Table-filling-based methods. These approaches transform the extraction task into a table-filling task, where each relationship is represented by a table, and each item in the table indicates whether the corresponding token pair in the row and column has that specific relationship. Some models use the diagonal as the vector space for NER tasks, such as those in refs. [28,29], but such labeling schemes struggle with nested entities and complex sentence structures. The advantage of the table-filling method lies in its ability to introduce prior knowledge about relationships through preconstructed relationship tables. These relationship tables can contain rich domain knowledge and semantic rules, aiding the model in understanding the potential connections between entities and relationships. In recent years, many efficient models for triplet extraction have been developed. The TPLinker model was proposed in ref. [10], which considers the joint extraction problem as an end-to-end token-pair linking task. This approach effectively avoids exposure bias. However, for each relationship, it requires two token-link matrices mapping entity boundaries, resulting in a large amount of redundant information. Consequently, the model convergence speed is slow and the decoding efficiency is low. In ref. [11], the authors proposed the OneRel model, which is an improvement on the TPlinker model, introducing the one-module one-step approach. They reduced the number of required label matrices to m, where m is the number of predefined relationships, to improve decoding efficiency and reduce information redundancy. The authors of ref. [12] proposed the GRTE model, which increases the types of labels and incorporates two valuable global features. They used a transformer-based approach to capture more global information through iterative processes, achieving good results. Despite the state-of-the-art performance of these two methods, the scope of triplet extraction still requires $(n\times n\times m)$, where n is the sentence length, resulting in a large number of useless relationship tables. Additionally, both of these approaches require multi-label classification when extracting entity spans, increasing the difficulty of entity recognition. The authors of ref. [15] introduced the UniRel model, which encodes both relationships and entities as sequences to construct a unified representation. This method is similar to the prompt approach in relation classification and successfully unifies the representation of relationships and entities, reducing the relation matrix to one and further minimizing redundancy. However, this model has some issues. It can only extract single tokens, and its architecture is relatively simple, not fully utilizing the rich feature information provided by language models. Although the relation matrix is reduced to one, the cost is that the number of negative samples generated by this type of relation matrix far exceeds that in previous studies using individual tables. The differences in the table-filling methods are shown in Table 1:

Table 1. Comparisonof different table-filling methods.

Model Approach	Number of Label Types	Supports Multiple Words	Number of Tables
TPlinker	2	Yes	$2\times m+1$
OneRel	4	Yes	m
GRTE	8	Yes	m
UniRel	2	No	1
Ours	2	Yes	1

3. Methodology

In this section, we first present the definition of the joint relational triple extraction problem, followed by an introduction to our table annotation strategy and decoding algorithm. Finally, we provide a detailed description of the model architecture.

3.1. Problem Definition

Given a text sequence $X=\left\{x_1{,x}_2,{\dots x}_n\right\}$, where $x_i,i=1,\dots ,n$ is the word in the text sequence and n is the length of the text sequence, our objective is to extract a relational triple $T={\displaystyle \bigcup _{i=1}^N}\left\{h_i,r_i,t_i\right\}$, where $h_i,r_i,$ and $t_i$ represent the subject, relationship between the two entities, and object, respectively. N is the number of triplets in the sequence. The subjects and objects are derived from the entities $E=\left\{e_1,e_2\dots ,e_k\right\}$ in text X, where E is the set of all entities in the sentence, and k is the number of entities in the text. $r_iϵR$, where R is the predefined set of relationships.

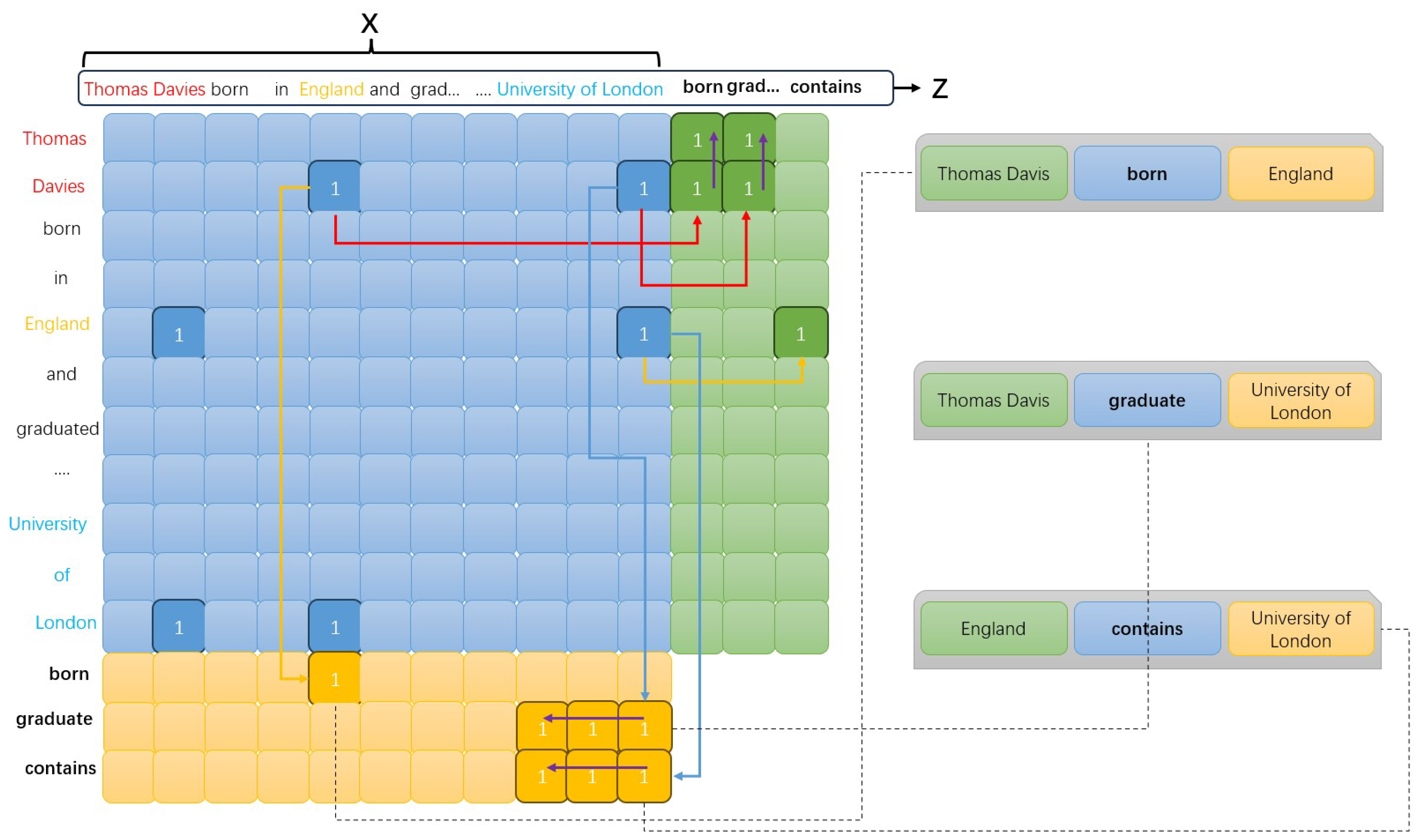
3.2. Table-Filling Schemes

Firstly, we map all relationships to a single token, allowing this word to carry potential semantic information about the existence of the relationship. Then, we concatenate all word relationships from the set R with the sequence X to form the complete text sequence $Z=\left\{x_1,\dots {,x}_n{,x}_{n+1},\dots {,x}_{n+m}\right\}$. The length of Z is $(n+m)$, where m represents the size of the set R.

Based on the input S, we construct a table with a size of ${(n+m)}^2$, as shown in Figure 2. For each cell indexed by the i-th row and j-th column, it has a label t representing the token pair $\left(x_i,x_j\right)\in Z\times Z$. If $t\ne 0$, it indicates the existence of a relation for that token pair. The table is primarily divided into three parts, with the blue section representing the entity–entity extraction. If the label t of $\left(x_i,x_j\right)$ in this section is non-zero, it means there is a predefined relationship between the entities with $x_i$ and $x_j$ as the tail tokens (or a single token representing an entity). For example, the label for (Davies, England) is 1, which means that there is a relationship between the entity ending with “Davies” and the entity ending with “England”.

Figure 2. Example of the scheme. The bold part represents the relation sequence. The purple arrow represents searching the entire entity from back to front. The green area represents the entity of the object, the orange area represents the entity of the subject, and the blue area represents the aligned tokens at the tails of the subject and object. The lower triangle is symmetrical to the upper triangle. On the right are three triplets obtained based on this table.

The green section represents the extraction section of subject relations. If the label t of $\left(x_i,x_j\right)$ in this section is 1, it indicates an association between the word $x_i$ and the relation $r_j$. It is important to note that in this case, $x_j$($j>n$) is no longer a word from X but represents a word relationship in Z. When there are vertical consecutive labels of 1 in this section, they signify that the consecutive tokens in the corresponding row form a subject entity. For example, the label for (Davies, born) is 1, and it is observed that the label for the previous token pair (Thomas, born) is also 1, which indicates that “Davies Thomas” is a subject, and “born” is the corresponding relation.

The orange section represents the extraction section of object relations. This section follows a similar principle to the extraction section of subject relations. When there are horizontally consecutive labels of 1 in this section, they indicate that the entity formed by the continuous tokens in the corresponding column is an object, and it is associated with the relation $r_j$. For example, if the label for (born, England) is 1, it means that “England” is an object, and the corresponding relation is “born”. The row corresponds to “graduate” and “contains”, whereas the column corresponds to “University of London” with six labels, indicating the association between “University of London” and the “graduate” and “contains” relations.

For the extraction of triplets, we integrate the extraction results of these three components. First, we save the tokens extracted from the entity–entity extraction into the set $\epsilon$. The subject-relation extraction results are saved in the dictionary $D_s$, and the object-relation extraction results are saved in the dictionary $D_o$. Note that a dictionary is a variable type; its format is (key: value), where key and value represent a mapping relationship. The keys of these two dictionaries are the positions of the entity tokens, and the values are the relations corresponding to the tokens. Next, we iterate through the set $\epsilon$ to search the two dictionaries. Using the set $\epsilon$, we map each tail position to the corresponding entity ending with that position. If the mapped subject and object ($h_i$ and $t_i$) have the same relation ($r_i$), they can form a triplet. Finally, based on the tail positions, we traverse the dictionaries $D_s$ and $D_o$ from back to front to find all the tokens of the entity, complete the entity, and form the final relation triplet. The specific decoding process is shown in Algorithm 1.

Finally, the three parts of the label are integrated, and after our decoding algorithm, we can obtain the triplets (Davies Thomas, born, England), (Davies Thomas, graduate, University of London), and (England, contains, University of London). Our padding strategy has the following three main advantages:

(1)

All relations are unified in one table, reducing a large number of redundant samples. For form-filling strategies such as GRTE [12] and OneRel [11], $\left(n^2\times m\right)$ cells need to be filled, whereas our filling strategy only requires ${(m+n)}^2$ cells.

(2)

It can solve the complex overlapping problems of EPO, SEO, and SOO.

(3)

The labels for each part of the relationship not only provide the relative position information of the corresponding entity (i.e., whether the entity is the subject or object) but also provide the span information of the entity (i.e., the specific position of the entity in the sentence). This allows our model to achieve a one-module one-step extraction process, further avoiding exposure bias.

Algorithm 1 Table decoding strategy

Input: Table probability matrix $L\in {\mathbb{R}}^{\left(n+m\right)\ast (n+m)}$, threshold t Output: Triplet T extracted from sentence Z 1: $D_s=dict\left(\right),D_o=dict\left(\right),\epsilon =set\left(\right)$ // Used to store subject-relation, object-relation, and entity pairs, respectively. The $dict\left(\right)$ function creates a new dictionary, and the $set\left(\right)$ function creates a new set. 2: $L^{row},L^{col}=torch.where\left(L_{i,j}\ge t\right)$ // This is a function in the Python programming language that extracts the positions of all cells in the probability matrix L with values greater than the threshold t. It saves the positions of all rows in $L^{row}$ and the positions of all columns in $L^{col}$. 3: for  $each\left(row,col\right)\in \left(L^{row},L^{col}\right)$ do 4:     if $row\ne 0$ and $col\ne 0$ and $row\le n$ then 5:         if $col<n+1$ then 6:            add $(row,col)$ to $\epsilon$ 7:         end if 8:     else if $col\ge n+1$ then 9:         $col=row-n-2$ 10:         if $row\notin D_s$ then 11:            $D_s\left[row\right]=\left[\right]$ 12:         end if 13:         add $col$ to $D_s\left[row\right]$ 14:     end if 15: end for 16: Replace the dictionary $D_s$ with the dictionary $D_o$, and transpose the input probability matrix. Repeat steps 3–15 to extract the relationship-tail entity part and store it in the dictionary $D_o$ 17: $D_r=set\left(\right)$ // A set storing relations in a sentence 18: for  $each(sub\_t,obj\_t)\in D_r$ do 19:     if $sub\_t\in D_s$ and $obj\_t\in D_o$ then 20:         $D_r\leftarrow D_s\left[sub\_t\right]\&D_o\left[obj\_t\right]$ 21:         for $rel\in D_r$ do 22:            $sub\_h=sub\_t$ //Set a variable to find the beginning of a subject 23:            $obj\_h=obj\_t$ //Set a variable to find the beginning of an object 24:            for $sub\_h\in D_s\left[rel\right]$ do 25:                $sub\_h=sub\_h-1$ 26:            end for 27:            for $obj\_h\in D_o\left[rel\right]$ do 28:                $obj\_h=obj\_h-1$ 29:            end for 30:            $T\leftarrow \left\{\left(sub\_h,sub\_t\right),rel,\left(obj\_h,obj\_t\right)\right\}$ 31:         end for 32:     end if 33: end for 34: return T

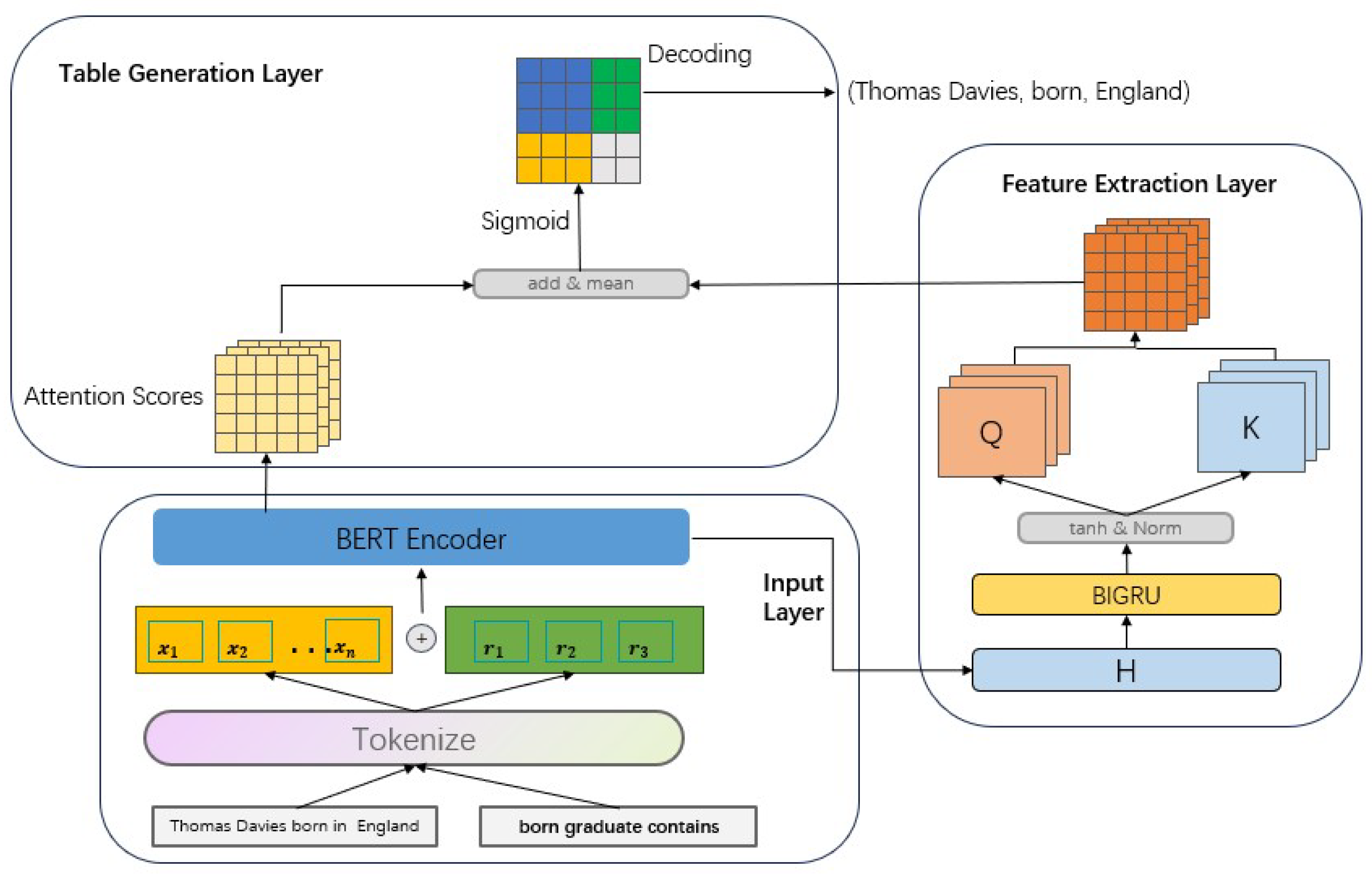
3.3. The Model Framework

The overall architecture of the model in this paper is shown in Figure 3. It mainly consists of three parts: the input layer, feature extraction layer, and table-generation layer.

Figure 3. The overall architecture of the model, which is divided into three parts: the input layer, feature extraction layer, and table-generation layer.

Input Layer. We use a pre-trained BERT-based model as the encoder for sentences. The concatenated sentence Z is input to obtain the token-level sentence representation $H\in {\mathbb{R}}^{\left(n+m\right)\times d_n}$:

$$H=\left\{t_1,t_2\dots t_n,t_{n+1}\dots t_{n+m}\right\}=BERT\left(\left\{x_1,x_2\dots x_n,r_1\dots r_m\right\}\right)$$

(1)

where $x_i$ is a word in the text sequence Z. After passing through the BERT encoder, it is converted into a word vector and then input into the BERT model to calculate the word embedding. $t_i$ represents the encoded word embedding, and $d_n$ represents the dimension of the word embedding (768 at the base level). We also extract the scores from the self-attention mechanism in the BERT encoder, originating from the multi-head self-attention computation in the encoder of the 12-layer transformer. The output of each BERT encoder layer is based on the output of the previous layer. The specific formula [18] is as follows:

$${Attention(Q,K,V)}_i=softmax\left(S_i\right)V=softmax\left(\frac{\left.{\left(H\right.}_{i-1}{W}^Q\right){\left(H_{i-1}{W}^K\right)}^T}{\sqrt{d_k}}\right)\left(H_{i-1}{W}^V\right)$$

(2)

where $S_i$ represents the scores of the multi-head self-attention mechanism in the i-th layer of the BERT encoder. $W^Q,W^K$, and $W^V$, respectively, represent the learnable mapping matrices for the query matrix Q, key matrix K, and value matrix V in the attention mechanism. $H_{i-1}$ represents the hidden layer output of the previous encoder layer, and $d_k$ is the embedding dimension in the attention computation. Here, we focus on the attention scores of the final layer, denoted as $S_{12}\in {\mathbb{R}}^{\left(n+m\right)\left(n+m\right)d_h}$, where $d_h$ represents the number of heads. Note that the attention scores taken here are the unnormalized results, which means they have not undergone the operation of softmax normalization.

Feature Extraction Layer. We use the representation H from BERT’s final layer output as input to the BiGRU [17] model, which enables capturing more semantic information, enhancing token-level representations, and obtaining the vector representation Y:

$$Y=BiGRU\left(H\right)$$

(3)

After the BiGRU update, we normalize Y horizontally, apply a tanh activation layer, and apply dropout, resulting in the input U for the multi-head tensor dot-product operation. The specific formula is as follows:

$$U=tanh\left(LayerNorm\left(Y\right)\right)$$

(4)

Through our experiments, we found that in our model, the multi-head tensor dot-product and multi-head self-attention mechanisms exhibit similar performance when extracting table features. However, the computational cost of the multi-head tensor dot product is lower. Its computation is similar to that of self-attention but omits the operations involving the value matrix and the multiplication of feature vectors after linear transformation. Firstly, we map U to the Q and K vectors through two linear transformations. Then, we transpose the K vector and perform matrix multiplication. Finally, we divide the result by the square root of $\sqrt{d_k}$ to obtain the table feature $R\in {\mathbb{R}}^{{\left(n+m\right)}^2\times d_h}$. The specific formulas are as follows:

$$Q_i=U_i{W}_q+b_q$$

(5)

$$K_i=U_i{W}_k+b_k$$

(6)

$$P_i=\frac{Q_i{K}_i^T}{\sqrt{d_k}}$$

(7)

$${\mu }_i\left(x,y\right)=q_{i,x}{k}_{i,y}^T$$

(8)

Formulas (9) and (10) represent the linear transformation operations. $W_q$ and $W_k$ are learnable parameter matrices, $b_q$ and $b_k$ are bias values, and $Q,K\in {\mathbb{R}}^{\left(n+m\right)\times d_h\times d_k}$ are the query matrix and key matrix, respectively. Here, $i\in \left\{1,\dots {,d}_h\right\}$ denotes the head position of the mapping. Formula (7) represents the overall result, whereas Formula (8) represents the specific calculation result ${\mu }_i(x,y)$ for each cell in the table. x and y denote the rows and columns of the table, respectively. $q_{i,x}$ and $k_{i,y}$ represent the query vector and key vector at the mapping position of the corresponding time step.

Table-Generation Layer. We add the result of Formula (7) to the $S_i$ of Formula (2), take the average of all the heads, and compute the final probability matrix $L\in {\mathbb{R}}^{{\left(n+m\right)}^2}$ using the sigmoid function. The specific formula is as follows:

$$L=sigmoid\left(\frac{1}{\tau }\sum _i^{\tau }\left(P_i+S_i\right)\right)$$

(9)

where $\tau$ is the number of heads. In contrast to the UniRel [15] model, which only recognizes discrete single-token labels, it is sufficient for UniRel to utilize the attention mechanism within BERT to capture information. However, our model needs to capture continuous labels, requiring more global information and entity feature information. Compared to the GRTE [12] model, ours can effectively reduce model complexity by only requiring binary classification to extract all entities, thus improving the precision of triple extraction.

3.4. Model Optimization

We adopt a joint training approach and apply methods such as dropout and horizontal regularization to the BiGRU layer and multi-head tensor dot-product layer to enhance the model’s generalization performance and prevent overfitting. Due to the table-filling method used in this work, the tables used are often larger than those used in conventional table-filling methods, resulting in a much larger number of negative samples compared to positive samples within a single table. Additionally, the majority of samples are easy to classify (i.e., predicted probabilities close to 0 or 1), with difficult-to-classify samples constituting a small portion (i.e., predicted probabilities around 0.5). Traditional binary cross-entropy loss treats these samples equally. Therefore, we utilize the focal loss function for training, which performs better in cases of imbalanced sample categories and uneven distribution of easy and difficult samples. The specific cross-entropy loss function is shown in Equation (10), and the focal loss function is shown in Equation (11):

$${\mathcal{c}}_b=-\frac{1}{{(n+m)}^2}\sum _i^{n+m}\sum _j^{n+m}\left(p_{i,j}log\left(p_{i,j}^{\prime }\right)+\left(1-p_{i,j}\right)log\left(1-p_{i,j}^{\prime }\right)\right)$$

(10)

$${\mathcal{c}}_f=-\frac{1}{{\left(n+m\right)}^2}\sum _i^{n+m}\sum _j^{n+m}\left(p_{i,j}\alpha {\left(1-p_{i,j}^{\prime }\right)}^{\gamma }log\left(p_{i,j}^{\prime }\right)+\left(1-p_{i,j}\right)\left(1-\alpha \right){p_{i,j}^{\prime }}^{\gamma }log\left(1-p_{i,j}^{\prime }\right)\right)$$

(11)

where $\alpha$ is the weight that adjusts the balance between positive and negative samples, and $\gamma$ is the weight that adjusts the balance for hard examples. $p_{i,j}^{\prime }$ represents the predicted value of the token-level cell $(i,j)$, whereas $p_{i,j}$ represents its ground-truth label value.

4. Experiments

This section begins by introducing the two datasets employed in this research. Subsequently, it elaborates on the experimental setup and the specific hyperparameter settings. Next, a comparative analysis is performed, pitting the proposed table-filling method and model against existing approaches to showcase their superior effectiveness. Finally, the impact of individual model components on the results is thoroughly investigated.

4.1. Datasets

We evaluate our method on two benchmark datasets, NYT [20] and WebNLG [21]. These two datasets have been widely used in the study of joint relational triple extraction. The NYT dataset consists of over 60,000 sentences, and the training set, test set, and validation set include 56,195, 5000, and 500 sentences, respectively, including 24 relations. It was generated using a distant supervision approach by extracting articles from the New York Times. On the other hand, the WebNLG dataset is sourced from articles in Wikipedia and comprises over 6000 sentences with 171/216 relations. Among them, 5019 sentences are used as the training set, 500 sentences are used as the validation set, and 703 sentences are used as the test set. Many sentences in these datasets exhibit overlapping relationships or contain multiple triples, which enables us to evaluate the performance of our model in handling overlapping and multiple triple problems. There are two different versions of each dataset. NYT* and WebNLG* only require matching the last word of the entity, whereas NYT and WebNLG require matching the entire entity span. Specific information on the datasets is shown in Table 2.

Table 2. Statistics of the datasets.

Dataset	Train	Valid	Test	Relations
NYT*	56,195	4999	5000	24
NYT	56,195	5000	5000	24
WebNLG*	5019	500	703	171
WebNLG	5019	500	703	216

Following a previous work [11], we divide the test set into three categories—SEO, EPO, and SOO—based on the overlap type. Additionally, we divide it into one or more triples based on the number of triples. Note that a sentence may have multiple overlaps. The details are shown in Table 3.

Table 3. Statistics on the number of triples in the test set, where N represents the number of triples in a sentence.

Dataset	Triples in Test Set				Number of Triplets
	Normal	SEO	EPO	SOO	N = 1	N > 1
NYT*	3266	1297	978	45	3244	1756
NYT	3222	1273	969	117	3089	1911
WebNLG*	245	457	26	84	266	437
WebNLG	239	448	6	85	256	447

4.2. Parameter Settings

Our model is implemented in PyTorch and runs on an NVIDIA GeForce RTX 3090 24G GPU. For fairness, we use the BERT case-based model as the pre-trained language model. We employ the cosine annealing algorithm as the learning rate adjustment strategy, with an initial learning rate of $3\times {10}^{-5}$/$5\times {10}^{-5}$ for NYT and WebNLG, respectively. AdamW is used for parameter optimization. On NYT and WebNLG, the batch size is set to 32/16, and the threshold values are 0.53/0.48, respectively. The model is trained for 100 epochs, and the dropout rates are 0.1. For the weight setting of the focal loss function, $\alpha$ is set to 0.5 for the NYT dataset and 0.6/0.75 for the WebNLG/WebNLG* dataset, whereas $\gamma$ is set to 2 for both datasets. Following previous works [8,10,11,12,25], we set the maximum sentence length for testing to be within 100.

4.3. Main Results

Table 4 summarizes the results of our model compared to other baseline methods on the two datasets. We evaluated the models using precision, recall, and $F1$ score, considering the extracted triples were correct only when the subject, object, and relationship matched the gold standard annotations completely. We selected several classic and efficient models from the past three years for comparison:

Table 4. Performance comparison of different methods on the NYT and WebNLG datasets. The best is bold, and the next best is underlined.

Model	NYT*			NYT			WebNLG*			WebNLG
	Prec.	Rec.	F1	Prec.	Rec.	F1	Prec.	Rec.	F1	Prec.	Rec.	F1
CasRel	89.7	89.5	89.6	-	-	-	93.4	90.1	91.8	-	-	-
TPLinker	91.3	92.5	91.9	91.4	92.6	92.0	91.8	92.0	91.9	88.9	84.5	86.7
PRGC	93.3	91.9	92.6	93.5	91.9	92.7	94.0	92.1	93.0	89.9	87.2	88.5
EmRel	91.7	92.5	92.1	92.6	92.7	92.6	92.7	93.0	92.9	90.2	87.4	88.7
GRTE	92.9	93.1	93.0	93.4	93.5	93.4	93.7	94.2	93.9	92.3	87.9	90.0
OneRel	92.8	92.9	92.8	93.2	92.6	92.9	94.1	94.4	94.3	91.8	90.3	91.0
Ours	93.7	92.9	93.3	94.0	93.3	93.7	94.7	93.6	94.1	89.4	88.1	88.8

• CasRel [8] uses a cascaded framework for sequential extraction, which is relatively slow. Our model can extract all triplets in the text at once.
• TPLinker [10] uses a one-stage token-linking approach for joint relation triplet extraction but requires multiple supporting modules. Our model only needs one module to extract complete triplets.
• PRGC [25] divides joint relation triplet extraction into three subtasks, which can lead to exposure bias. In contrast, our model treats it as a holistic table-filling task, avoiding exposure bias.
• EmRel [30] represents relations as embedding vectors but still requires multiple components. It refines the representation of entities and relations through an attention-based fusion module.
• GRTE [12] is the state-of-the-art method for the NYT dataset, but it requires multiple class labels to determine a complete entity pair. Our method only requires binary classification.
• OneRel [11] is the state-of-the-art method for the WebNLG dataset, achieving improved triplet recognition efficiency through a one-stage single-model approach. However, it still requires triplet extraction in a three-dimensional table, whereas ours only requires extraction in a two-dimensional table, reducing memory usage.

All the experimental results of the baselines were directly sourced from the original literature, and the performance of each model was compared using precision (Prec.), recall (Rec.), and $F1$ score. Their calculation formulas are as follows:

$$Precision=\frac{TP}{TP+FP}$$

(12)

$$Recall=\frac{TP}{TP+FN}$$

(13)

$$F1=\frac{2\times Precision\times Recall}{Precision+Recall}$$

(14)

where $TP$ represents instances correctly predicted as positive by the model, $FP$ represents instances incorrectly predicted as positive by the model but are actually negative, and $FN$ represents instances incorrectly predicted as negative by the model but are actually positive.

The experimental results show that our model achieved the highest $F1$ score and precision on the NYT and WebNLG datasets, outperforming the $F1$ score of the second-highest GTRE model by 0.3% and its precision by 0.8% and 0.6%, respectively. However, recall was slightly lower than the GTRE model. This indicates that our model performed best when the number of relations was relatively small. On the WebNLG dataset, our model achieved a slightly lower $F1$ score by 0.2% compared to the previous best model, OneRel, but achieved higher precision by 0.6%, maintaining competitiveness. We believe that the main reason for this is that the model’s prediction accuracy primarily comes from the attention mechanism, both internal and external to the BERT encoder. The WebNLG* dataset contains up to 171 relations, and when combined with the original input text, the total sequence length exceeds 300. However, the attention calculation and multi-head tensor dot-product methods did not excel in handling long texts. Moreover, larger tables also introduced more negative samples, and although we used focal loss to mitigate this, the problem remained. On the WebNLG dataset, although our model did not achieve better results than the OneRel and GRTE models, it still exhibited good triple extraction ability. We believe there may be two reasons for this: (1) Similar to the WebNLG* dataset, the increase in the number of relations led to overly long synthetic text sequences, where the attention mechanism could not exert its advantage. (2) The relationship prompt information was composed of individual tokens, and when there were too many relations, similar prompts caused confusion and led to misjudgment.

The above results demonstrate that our model exhibits satisfactory performance in extracting triplet accuracy when the number of predefined relations in the dataset is relatively small. But as the number of relations increases, the effectiveness of our model suffers.

4.4. Detailed Results on Complex Scenarios

In this section, we evaluate the extraction capability of our model in cases where there are overlapping triplets and single sentences containing multiple triplets. For comparison with previous models, we conducted experiments on two different subsets: NYT* and WebNLG*. The specific extraction results are shown in Table 5 and Table 6. We can observe that our model achieved the best $F1$ scores on 11 out of 20 subsets and the second-best scores on 3 subsets. Particularly, on the NYT* dataset with a smaller number of relations, our model achieved the best scores in all overlapping situations. On the WebNLG dataset, our model still obtained the four best results, indicating its excellent performance on datasets with a large number of relations. However, as the number of predefined relations increases, the model’s ability to recognize similar semantic relationships decreases, making it more challenging to handle sentences with multiple triplets. Overall, our model is able to handle complex sentence structures well. However, as the number of relations increases, its recognition ability is also affected. Compared to other baseline models, our model can still effectively extract triplets in complex scenarios.

Table 5. $F1$ values of different models for sentences with different numbers of triples. The best is bold, and the next best is underlined.

Model	NYT*					WebNLG*
	N = 1	N = 2	N = 3	N = 4	N > 4	N = 1	N = 2	N = 3	N = 4	N > 4
CasRel	88.2	90.3	91.9	94.2	83.7	89.3	90.8	94.2	92.4	90.9
TPlinker	90.0	92.8	93.1	96.1	90.0	88.0	90.1	94.6	93.3	91.6
PRGC	91.1	93.0	93.5	95.5	93.0	89.9	91.6	95.0	94.8	92.8
GRTE	90.8	93.7	94.4	96.2	93.4	90.6	92.5	96.5	95.5	94.4
OneRel	90.5	93.4	93.9	96.5	94.2	91.4	93.0	95.9	95.7	94.5
Ours	91.4	93.4	94.7	95.6	94.9	91.7	93.3	95.4	94.1	95.3

Table 6. $F1$ values of different models for sentences with different overlapping patterns. The best is bold, and the next best is underlined.

Model	NYT*				WebNLG*
	Normal	SEO	EPO	SOO	Normal	SEO	EPO	SOO
CasRel	87.3	91.4	92.0	77.0	89.4	92.2	94.7	90.4
TPlinker	90.1	93.4	94.0	90.1	87.9	92.5	95.3	86.0
PRGC	91.0	94.0	94.5	81.8	90.4	93.6	95.9	94.6
GRTE	91.1	94.4	95.0	-	90.6	94.5	96.0	-
OneRel	90.6	94.8	95.1	90.8	91.9	94.7	95.4	94.9
Ours	91.1	94.8	95.3	93.2	91.6	94.5	94.9	96.6

4.5. Detailed Results on Different Subtasks

We further explored the results of our model on different subtasks, dividing the extraction of relation triples into two subtasks: entity pair recognition and relation classification. In this context, h represents the head, t represents the tail, and r represents the relation. Only when both the head and tail entities in $(h,r,t)$ are correct can it be counted as a correct prediction. The specific results are shown in Table 7.

Table 7. Experimental results on subtasks, where $(h,t)$ represents an entity pair, r represents a relation contained in a sentence, and $(h,r,t)$ represents a complete relation triple. The best is bold.

Model	Element	NYT*			WebNLG*
		Prec.	Rec.	F1	Prec.	Rec.	F1
CasRel	(h, t)	89.2	90.1	89.7	95.3	91.7	93.5
	r	96.0	93.8	94.9	96.6	91.5	94.0
	(h, r, t)	89.7	89.5	89.6	93.4	90.1	91.8
PRGC	(h, t)	94.0	92.3	93.1	96.0	93.4	94.7
	r	95.3	96.3	95.8	92.8	96.2	94.5
	(h, r, t)	93.3	91.9	92.6	94.0	92.1	93.0
OneRel	(h, t)	93.3	93.4	93.3	96.2	96.5	96.3
	r	96.7	96.9	96.8	96.7	97.0	96.8
	(h, r, t)	92.8	92.9	92.8	94.1	94.4	94.3
Ours	(h, t)	93.9	93.5	93.7	96.2	94.6	95.4
	r	97.0	95.7	96.3	96.9	95.7	96.3
	(h, r, t)	93.7	92.9	93.3	94.7	93.6	94.1

Most of our model’s test results on NYT were better than the baseline. Interestingly, our method often achieved higher precision at the expense of recall. In relation extraction, our model’s precision was 1.3% higher than recall. We analyze the specific reasons for this in Section 4.8. For the two subtasks of WebNLG, our model obtained the best precision scores but comparativelyower recall and $F1$ scores. This is the main bottleneck of our model.

4.6. Efficiency of the Model

The model’s number of parameters, training time, required memory for training, and inference time on the NYT dataset were evaluated, as shown in Table 8. Our model has slightly more parameters than TPLinker and OneRel, mainly due to the large number of parameters in the BiGRU model. In terms of training time, our model trained 1.5 times faster than TPLinker and 1.6 times faster than the OneRel model. We believe a possible reason for this is that our model is trained as a single module, allowing for batch processing of samples and faster tensor dot-product computation. Although OneRel is also trained as a single module, each linear layer requires a large number of parameters $\left(n^2\times d_n\times 3\right)$ to calculate, where $d_n$ is the embedding dimension of the encoder and n is the sentence length, resulting in more time consumption. TPLinker trains its head, tail, and relation separately as three models, which takes a relatively longer time. Regarding training memory, our tensor space was limited to a two-dimensional plane, requiring less memory. In terms of inference speed, TPLinker required the most time, mainly because it needs to iterate over all token pairs and use token linking to determine the head and tail entities. Therefore, it has the highest computational complexity, whereas our model and OneRel only need to iterate over tokens with specific markers. Our inference time was higher than that of OneRel, mainly because complete triplet decoding in OneRel usually only needs three labels, whereas our labels are relatively dense, requiring more iterations.

Table 8. The efficiency comparison of the model on the NYT dataset. Params represents the number of parameters of the encoder in the model. Training time refers to the time required to train an epoch, inference indicates the time required to infer a sentence, and memory indicates the video memory occupied during training. The batch size is set to 8. The best is bold.

Model	NYT
	Params	Training Time(s)	Memory (M)	Inference (ms)
TPLinker	109,602,962	1641	4388	47.6
OneRel	112,072,800	1758	21,254	14.4
Ours	114,810,624	1078	4246	28.3

4.7. Ablation Study

In this section, we conduct ablation experiments on the NYT dataset to demonstrate the effectiveness of various components in the proposed method. The specific results are shown in Table 9.

Table 9. Ablation experiments on the NYT dataset, where w/o indicates removing the module, ours refers to the proposed complete model, and BiLSTM indicates replacing the BiGRU module with a BiLSTM module. The best is bold.

Model	Prec.	Rec.	F1
Ours	94.0	93.3	93.7
w/o multi-head tensor dot product	93.3	93.7	93.5
w/o inside multi-head self-attention of BERT	93.3	93.6	93.4
w/o focal loss	92.1	93.5	93.3
BiLSTM	93.4	93.5	93.5

We conducted five sets of experiments, with the first set being our proposed complete model. In the second set, we removed the multi-head tensor dot-product operation and only used the scores obtained from the multi-head self-attention as the final result. Compared to the first group, the $F1$ score decreased by 0.2%. Although a simpler structure improved the efficiency of the model, it could not fully utilize the semantic information in the language model, resulting in fewer identifiable triples. This was also the reason for the decrease in precision and the increase in recall. Therefore, the addition of additional sentence features is beneficial to this model. In the second group, we removed the multi-head self-attention module from the encoder, resulting in a decrease of 0.3% in the $F1$ score. This indicates that the internal attention mechanism in the BERT encoder plays an important role in the filling framework. In the third group, we did not use the focal loss function but instead used the traditional binary loss function, resulting in a decrease of 0.4% in the $F1$ score. In Figure 4, we can observe that whether using the focal loss or the cross-entropy loss, the models converged after around 10,000 steps. However, training with cross-entropy loss (green line) resulted in a significantly slower convergence speed. This is because focal loss assigns more weight to hard samples, making the model pay more attention to them, which is very helpful for this table-filling method. In the fourth group, we replaced the BiGRU [17] model with the BiLSTM model and found that compared to the BiLSTM model, BiGRU worked better in combination with the attention mechanism, resulting in better performance.

Figure 4. The model training process of different ablation experiments. The x-axis represents the number of training iteration steps in thousands, with a batch size of 32.

Figure 4 shows shows the convergence process of various ablation models on the NYT dataset. “ATT” represents using only the internal attention calculation within the encoder, and “tensor” represents using only the external tensor dot-product operation. The entire model converged after approximately 10,000 steps, but it can be clearly seen that the full framework converged the fastest. The next fastest was when using the BiLSTM module, followed by using only the internal attention mechanism and then using only the external tensor dot product. The slowest convergence was observed when using cross-entropy training.

4.8. Case Study

In this section, we selected three sentences from the NYT dataset to analyze our model. The first sentence contained normal triplets, the second sentence contained EPO overlapping triplets, and the third sentence contained SEO overlapping triplets. We compared the recognition results of the different models in the ablation experiments, as shown in Table 10. In the first sentence, we compared the use of different loss functions and found that both models recognized incorrect entities due to insufficient information in the sentences. However, the model trained with cross-entropy recognized more incorrect relationships, possibly because of the semantic similarity between “lived” and “birth,” which are difficult to distinguish, resulting in lower precision. During training, focal loss can assign more weight to this situation.

Table 10. Examples of normal, EPO, and SEO in the NYT dataset. Orange represents misrecognized relations, red represents misrecognized entities, and blue represents correctly recognized triples.

Instance
Sentence #1	There were readings about New Orleans from Mark Twain, Tennessee Williams, Truman Capote and others.
Ground truth	(Truman Capote, /people/person/place_of_birth, New Orleans)
w/o focal loss	(Mark Twain, /people/person/place_of_birth, New Orleans) (Truman Capote, /people/person/place_lived, New Orleans)
Ours	(Mark Twain, /people/person/place_of_birth, New Orleans)
Sentence #2	ON Christmas Eve, 1989, a small force of about 100 men led by an obscure former Liberian government official crossed the border from Ivory Coast into Nimba County in northern Liberia.
Ground truth	(Liberia, /location/country/a_d *, Nimba County) (Nimba County, /location/a_d/country, Liberia) (Liberia, /location/location/contains, Nimba County)
w/o inside attention of BERT	(Liberia, /location/country/a_d, Nimba County)
Ours	(Liberia, /location/country/a_d, Nimba County) (Nimba County, /location/a_d/country, Liberia) (Liberia, /location/location/contains, Nimba County)
Sentence #3	A Felton diploma would cost $2000,minusa$ 500 scholarship; we could graduate for $500 from Glenndale -LRB- not to be confused with the Glendale colleges in Arizona and California -RRB-.
Ground truth	(California, /location/location/contains, Felton) (California, /location/location/contains, Glendale)
w/o tensor dot product	(California, /location/location/contains, Glenndale) (California, /location/location/contains, Felton)
Ours	(California, /location/location/contains, Felton) (California, /location/location/contains, Glendale)

* a_d is the abbreviation of administrative_divisions.

In the second sentence, we compared a model lacking internal attention in the encoder with the proposed complete model. It can be observed that the deficient model did not recognize all triplets, possibly due to insufficient global information. In the third sentence, we compared the results of the model without auxiliary tensor dot-product operations with the proposed complete model. It can be observed that the model incorrectly identified “Glendale” as “Glenndale.” This might be because the overly simplistic architecture failed to fully capture the inherent correlation between entities and relationships in complex scenes. In conclusion, our model is relatively rigorous and comprehensive, predicting fewer triplets but with higher accuracy. This explains the high precision and low recall of the model.

4.9. Parameter Analysis

We further explored the influence of hyperparameters on the model. We set the candidate values of $\alpha =\left\{0.5,0.55,0.6,0.65\right\}$, with a fixed decay rate of 0.2 and a threshold of 0.5. The results are shown in Figure 5 and Figure 6. On the NYT dataset, when the values of $\alpha$ were 0.55 and 0.65, precision and recall tended to be stable, and when the values of $\alpha$ were 0.5 and 0.6, precision and recall decreased and increased, respectively. On the WebNLG* dataset, sample inhomogeneity was more pronounced, so our optimal $\alpha$ value was higher than that of the NYT dataset.

Figure 5. Comparison of different values of the $\alpha$ value of the $F1$ score on the NYT dataset.

Figure 6. Comparison of different values of the $\alpha$ value of the $F1$ score on the WebNLG* dataset.

5. Conclusions

In this paper, we propose a new method for joint relational triple extraction using table filling. By transforming relations into prompt information and making entity spans dependent on this information, complex triple extraction tasks can be accomplished with only one table, effectively reducing redundant information and memory consumption during training. Based on this, we integrate the internal attention calculation of the BERT language model with the sentence feature-based multi-head tensor dot product to extract more table features. We also introduce a simple and effective loss function to address the problem of sample imbalance in tables. Experimental results on two benchmark datasets demonstrate that our model is competitive in terms of efficiency and accuracy. In the future, we plan to explore solutions for addressing the limitation of attention mechanisms in long text sequences. We also plan to introduce other neural architectures, such as graph neural networks [31], through ensemble learning [32,33] to improve the model’s extraction capability in long texts and multi-relational scenarios. Additionally, relationship-prioritized [34] approaches can be experimented with to reduce the relationship sequence and enhance our model. And we think that the method based on table filling can not only be applied to the task of joint triple extraction but also extended to other tasks in the future [35].