Mechanical Behavior of Hollow Corrugated Sandwich Cylinders Under Inner Pressure Loading
Abstract
1. Introduction
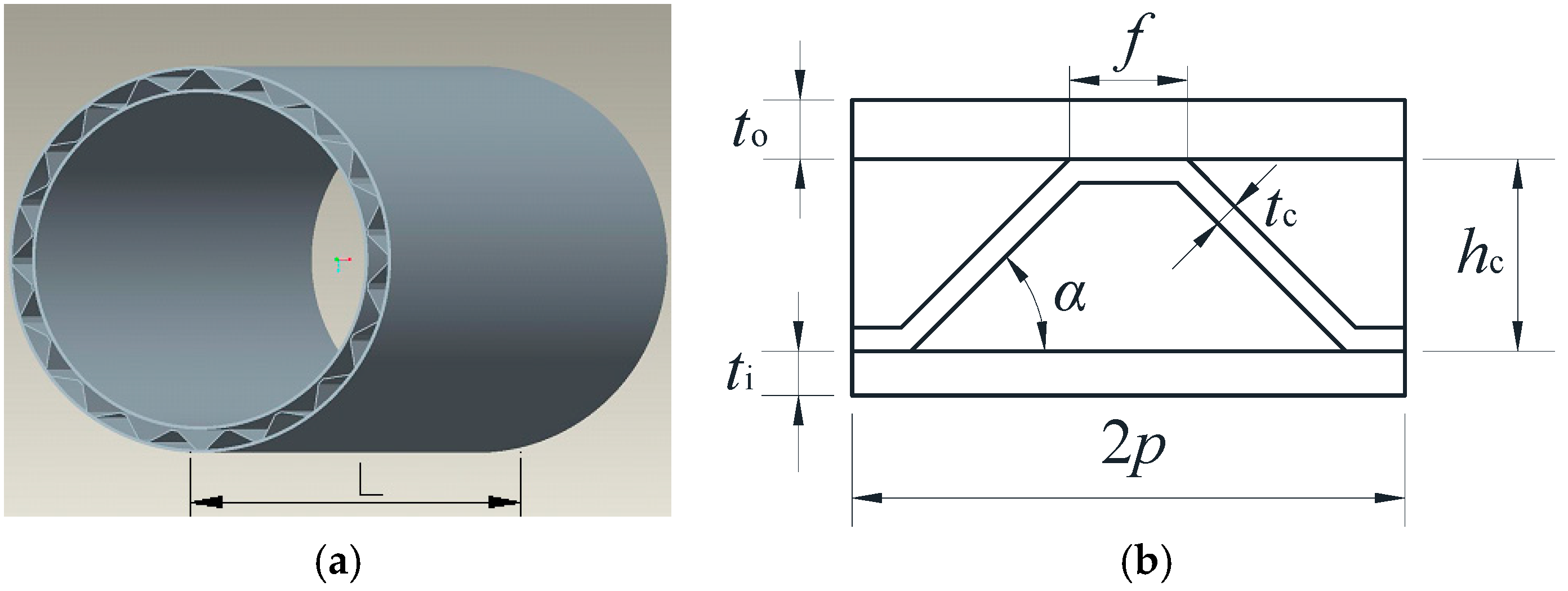
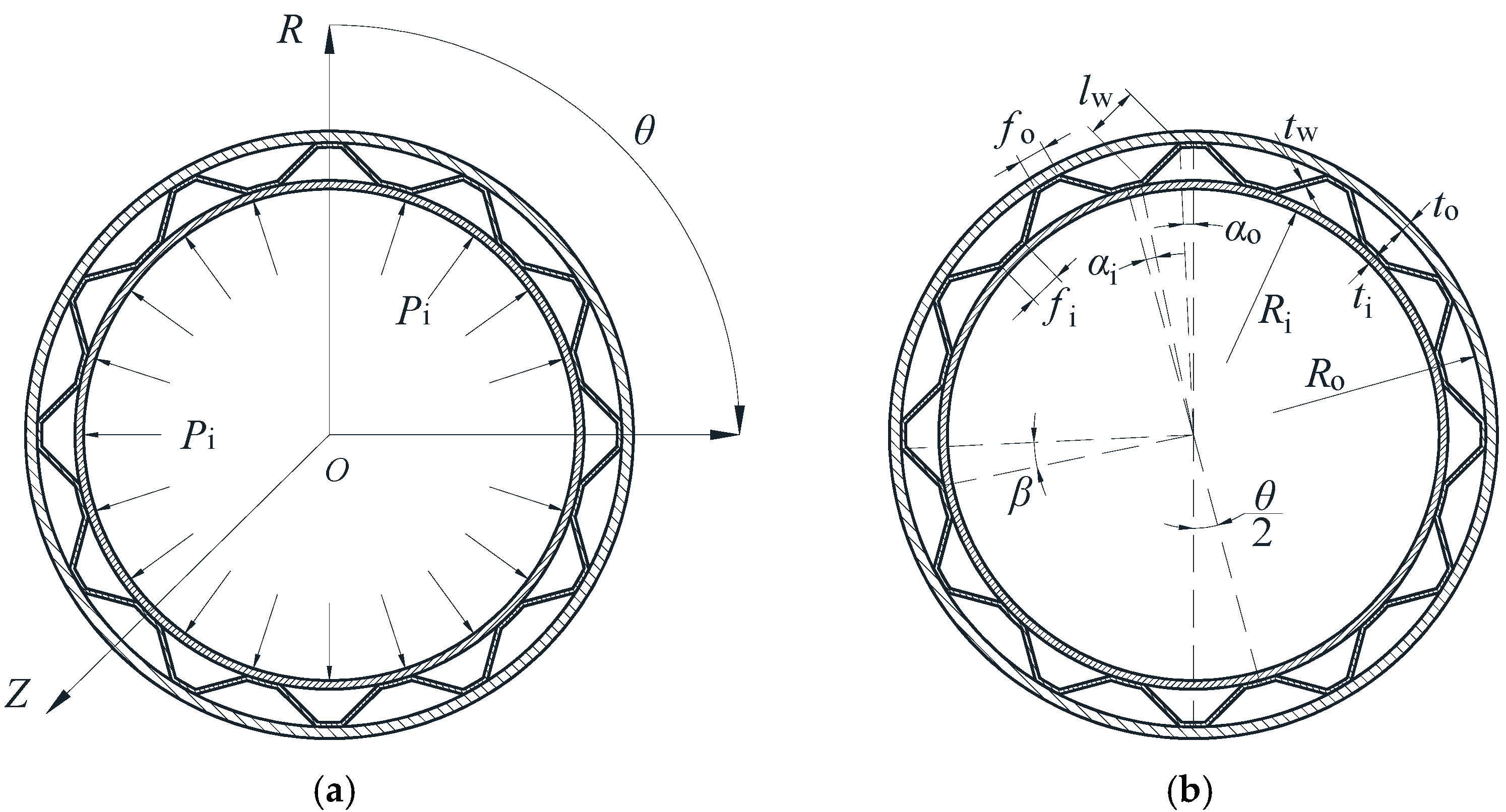
2. Description of Problems
2.1. Structure Model
2.2. Loading and Mass Expression
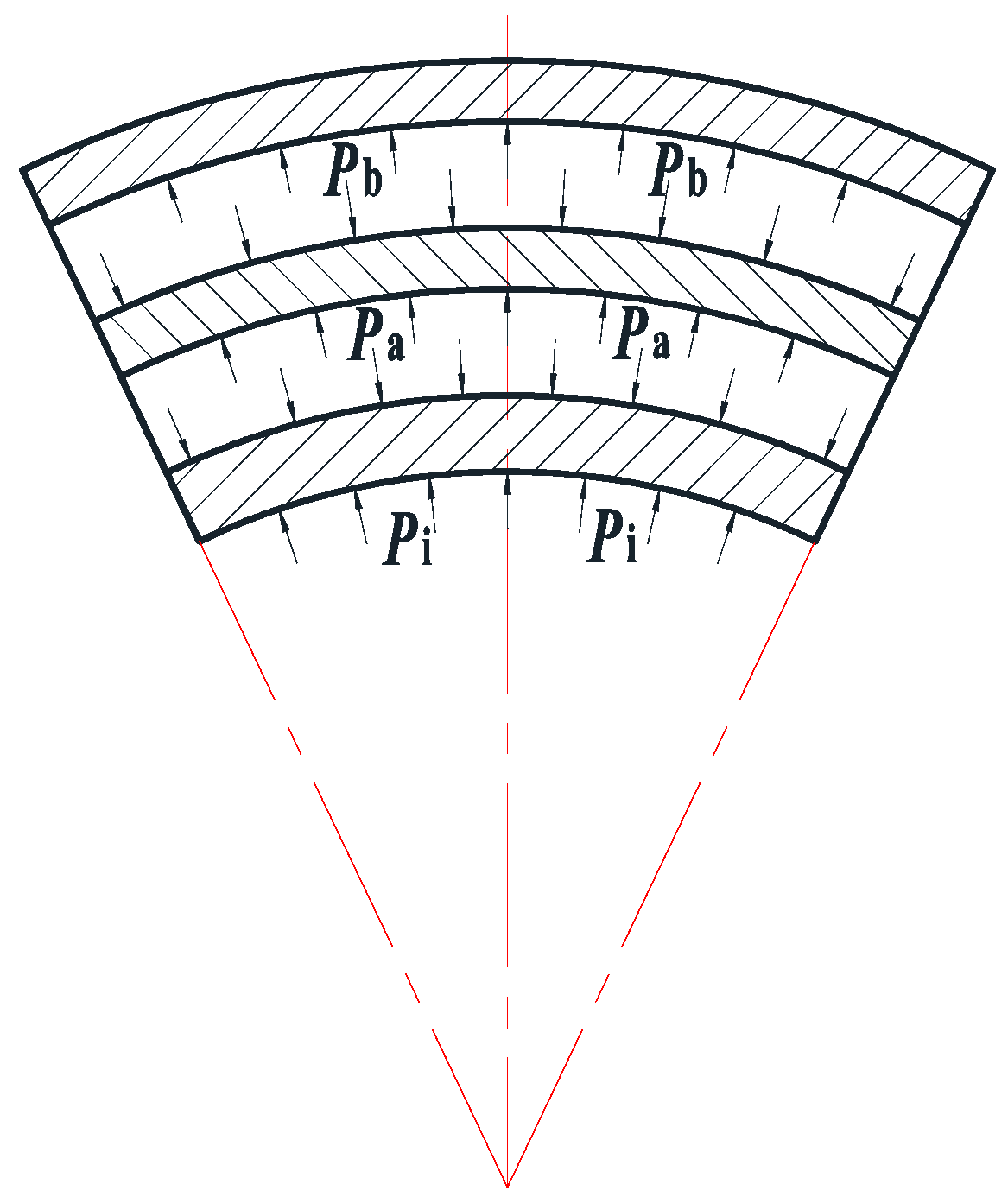
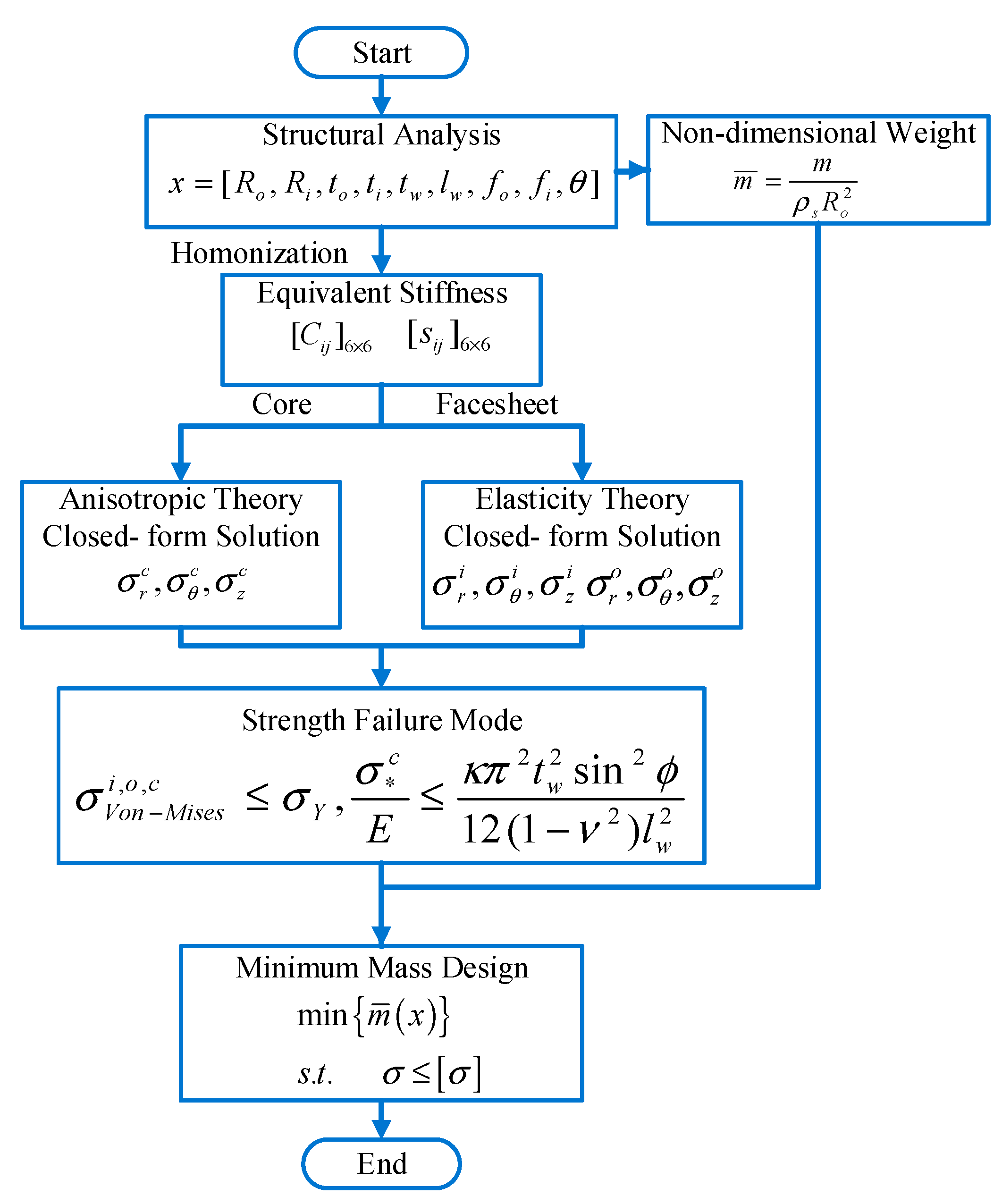
3. Structural Analysis
3.1. Closed-Form Solution for Corrugated Core Panel
3.2. Closed-Form Solutions of the Inner and Outer Facesheets
3.3. Displacement Compatibility Conditions
3.4. Model Validation of the Closed-Form Solution
4. The Minimum Weight Design Model
4.1. Dimensionless Expression of Mass
4.2. Failure Mode
4.3. Minimum Weight Design Model
5. Results and Discussion
5.1. Stress Distribution of Typical Corrugated Cylinder Shell
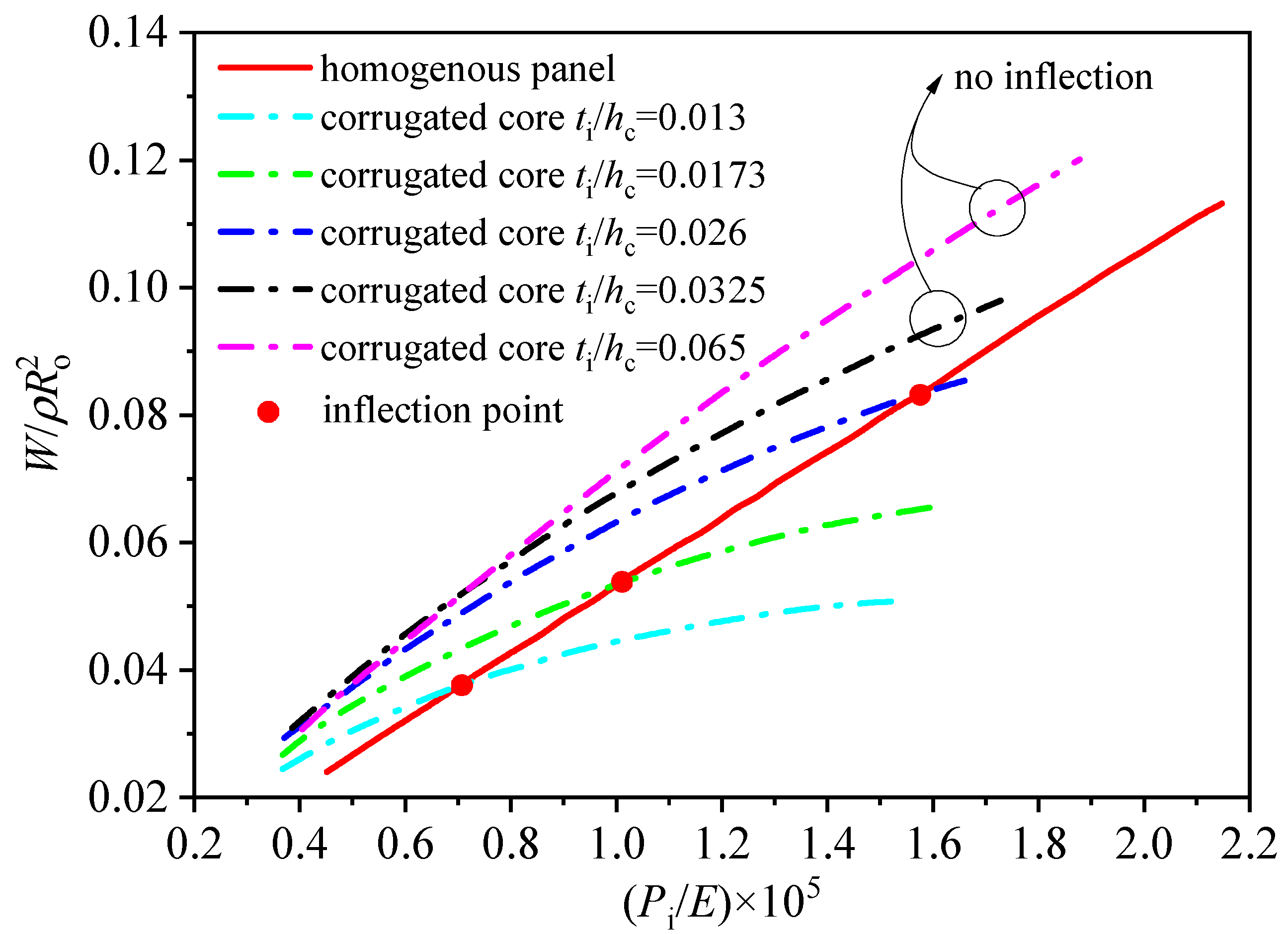
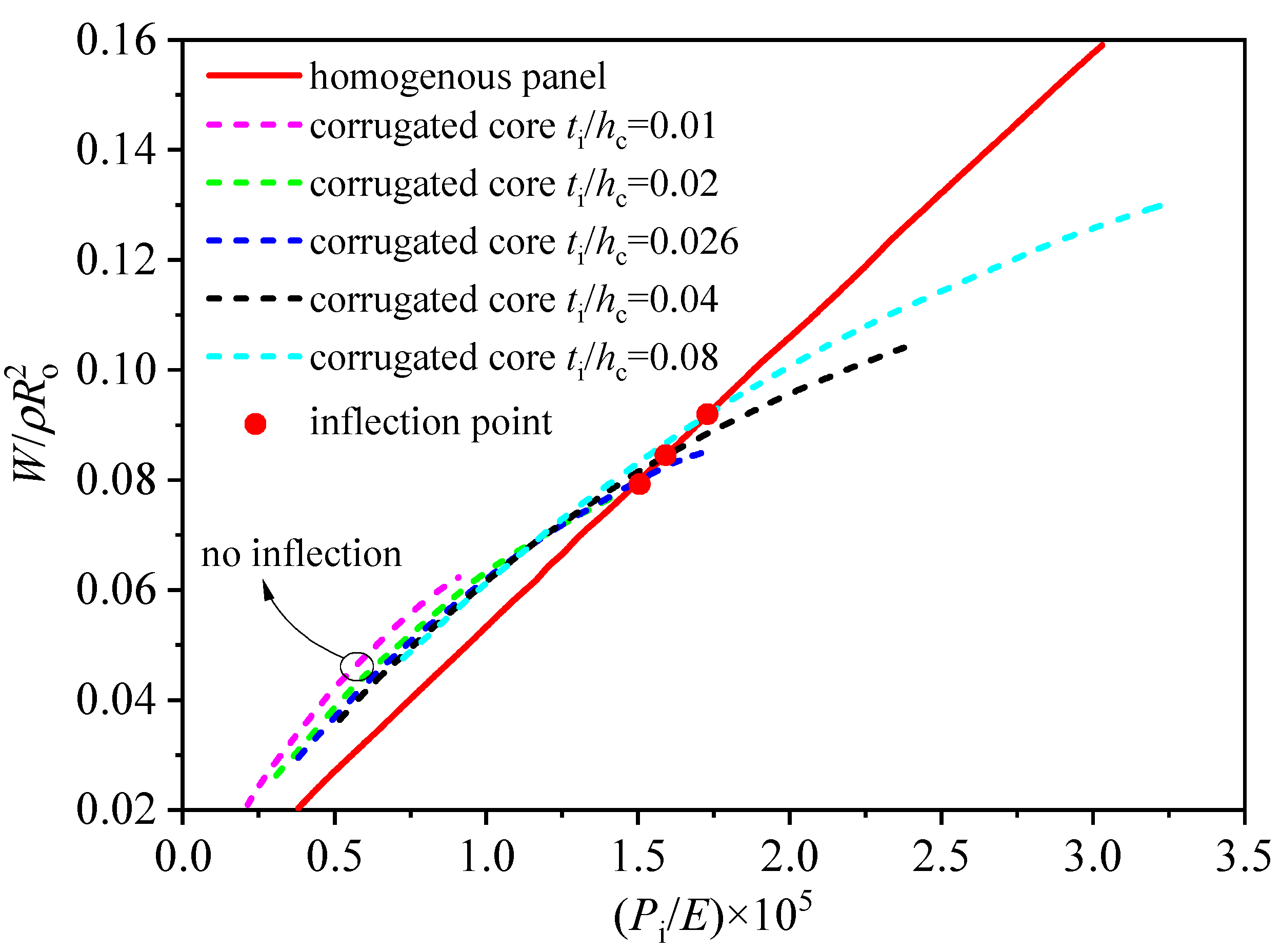
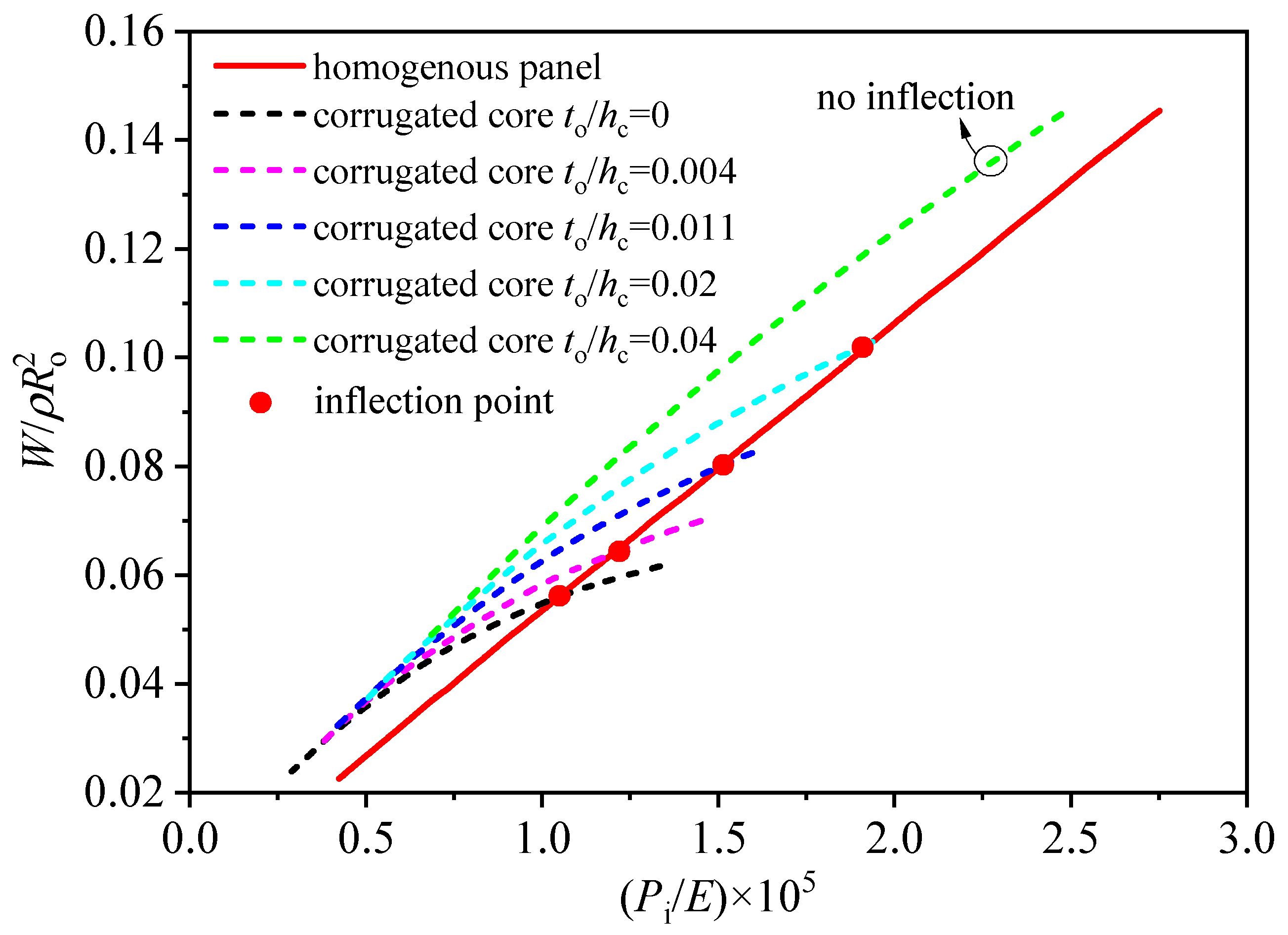
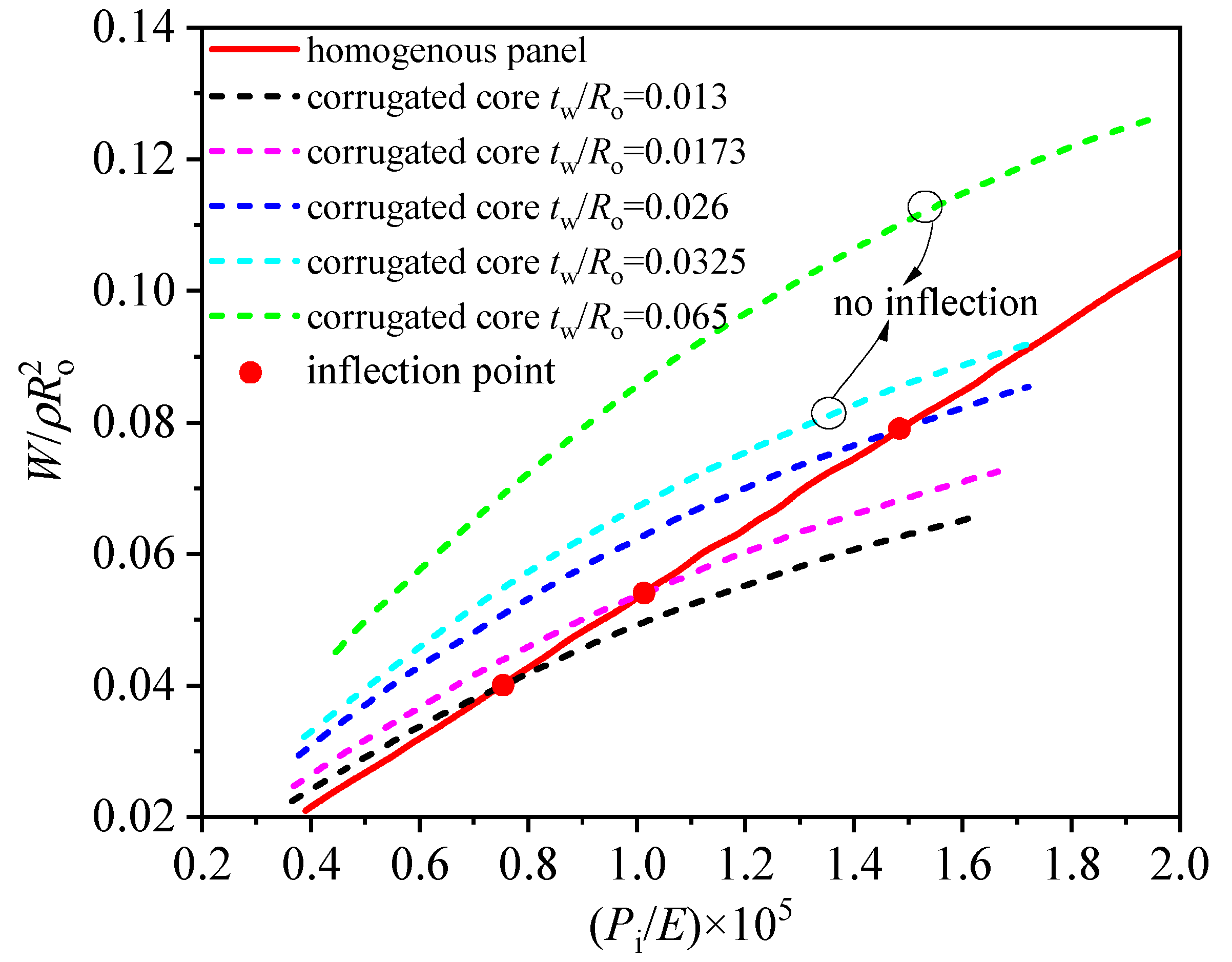
5.2. Minimum Weight Analysis of Hollow Corrugated Cylinder Shell
- (1)
- The minimum weight of the hollow homogeneous panel cylinder exhibits approximately linear growth with respect to the limit load, whereas the hollow corrugated sandwich cylinder undergoes a gradual change in weight;
- (2)
- Compared to the homogeneous panel cylinder, when the inner pressure is relatively low (Pi < ), a higher minimum weight is required for the hollow corrugated sandwich cylinder to withstand the same inner pressure load. However, as the limit inner pressure load exceeds this threshold, there is a notable improvement in structural efficiency, resulting in the hollow corrugated sandwich cylinder having a lighter minimum weight than the homogeneous panel cylinder for the same inner pressure load;
- (3)
- Furthermore, when the thickness of the hollow corrugated sandwich cylinder hc is varied, it is observed that the parameter hc significantly influences the emergence of the inflection point. At relatively small thicknesses (), the structural efficiency of the hollow corrugated sandwich cylinder is minimal. However, as the thickness increases to a certain value (), the structural efficiency of the hollow corrugated sandwich cylinder becomes notably superior to that of the homogeneous panel structure. Moreover, as the thickness of the corrugated core increases, the structural efficiency also increases.
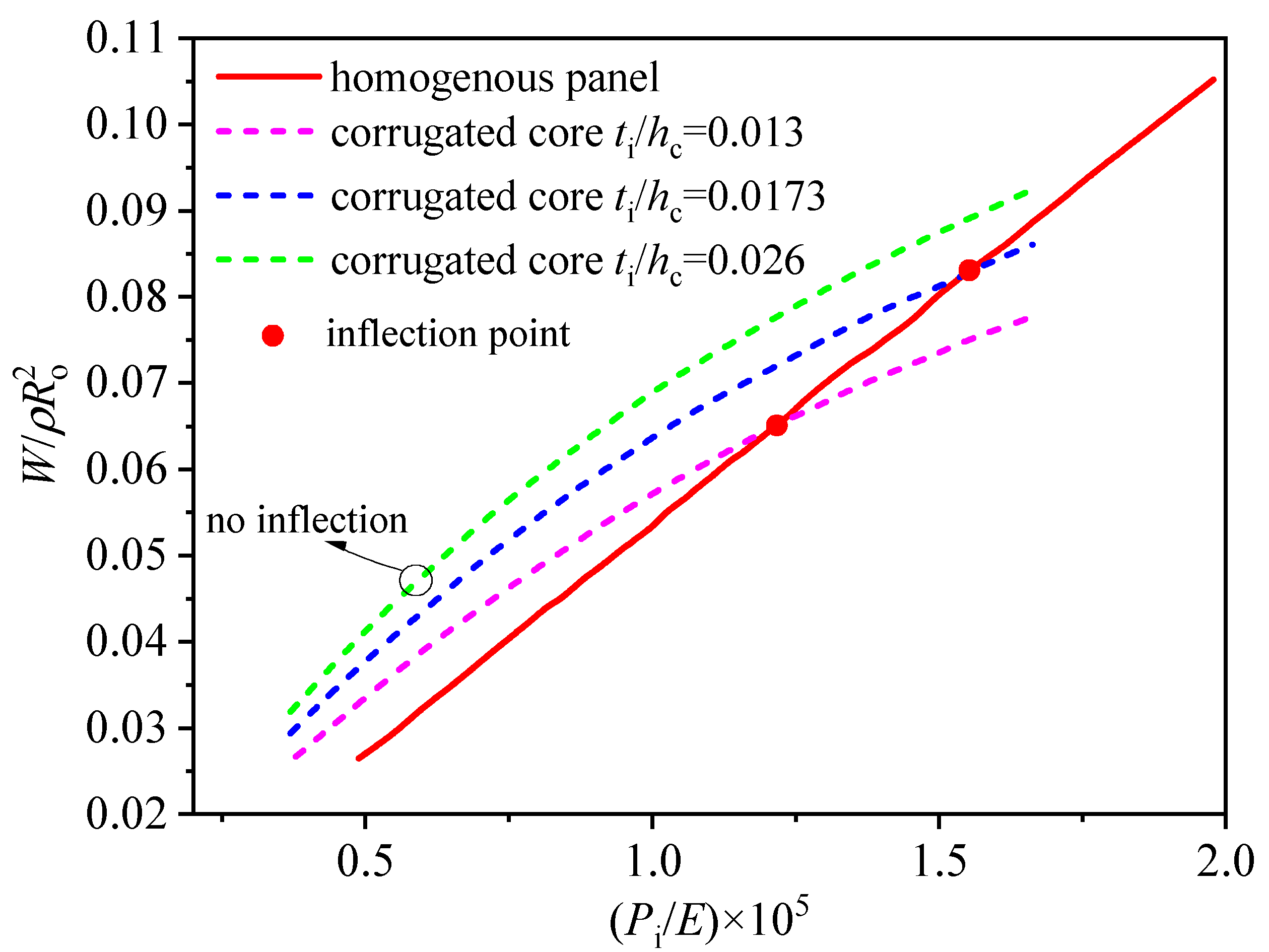
5.3. Minimum Weight Comparison of Different Hollow Corrugated Sandwich Cylinders
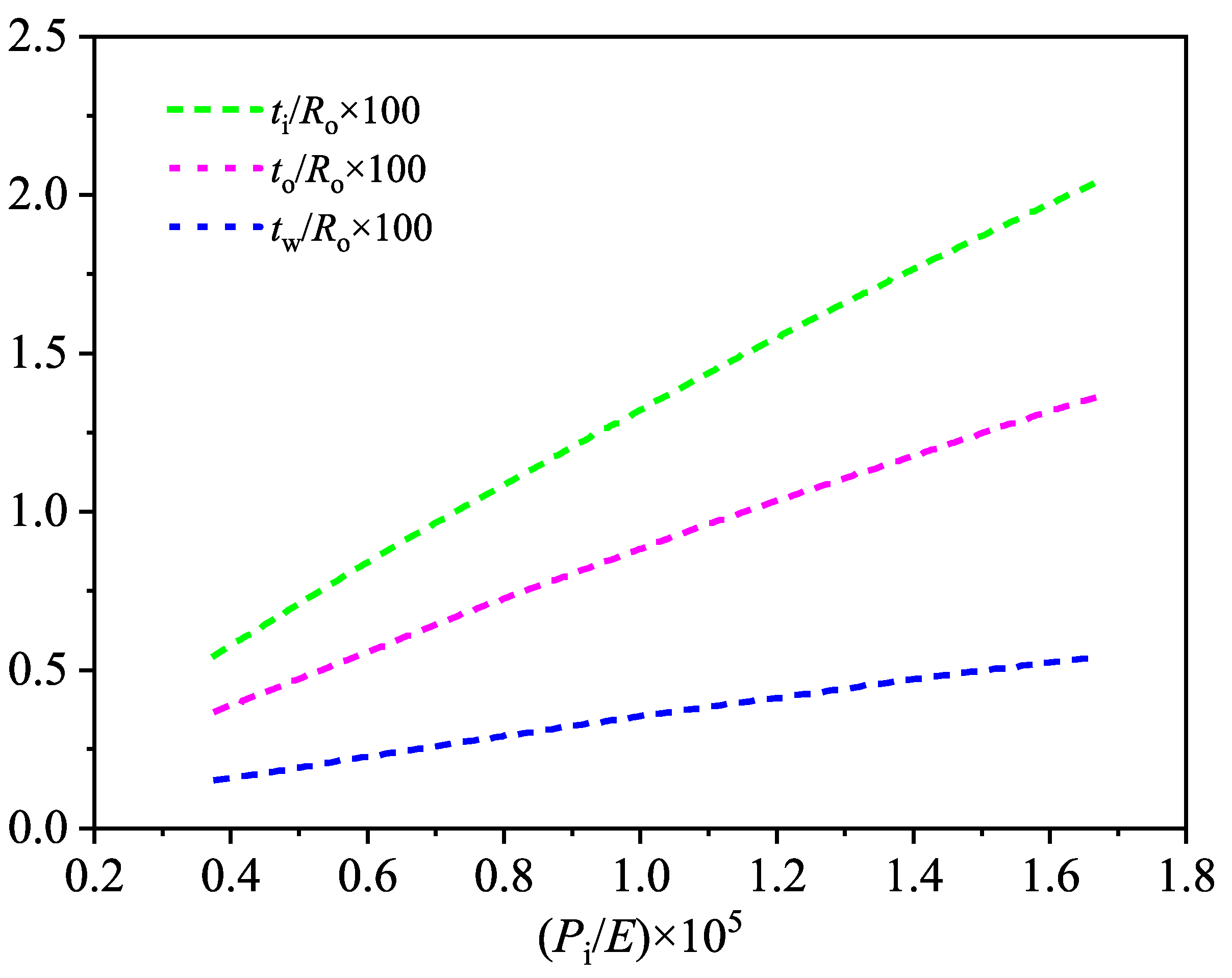
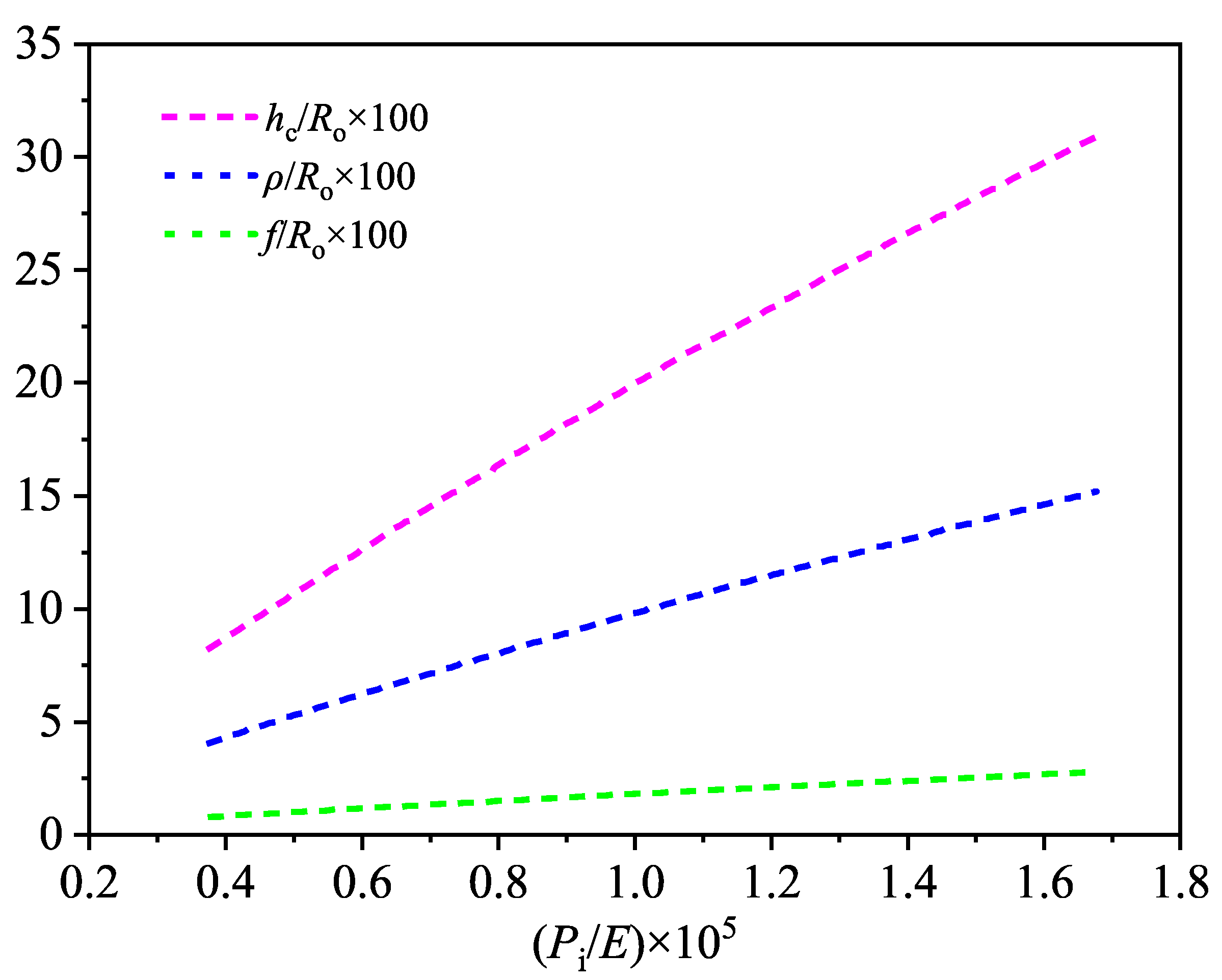
5.4. Sensitivity Analysis of Structural Parameters
6. Conclusions
- (1)
- Concerning the long, hollow sandwich cylinder without column caps, an elastic closed-form solution and the minimum weight design model of the hollow corrugated sandwich cylinder were proposed with the homogenization method.
- (2)
- The stress distribution of the hollow corrugated sandwich cylinder with different topological structural parameters was compared and analyzed. It is found that there is an inflection point of the structural efficiency during the increase in the pressure. Notably, the hollow corrugated sandwich cylinder demonstrates a relatively pronounced structural advantage only when subjected to significant internal pressure.
- (3)
- The optimal structural efficiency of the hollow corrugated sandwich cylinder is closely related to its topological parameters. With the increase in the topological parameters, including core thickness, inner facesheet thickness, outer facesheet thickness, core thickness, and core inclining angle, both the minimum weight and the limit load increase accordingly, leading to a relative advancement of the inflection point in the structural efficiency curve.
- (4)
- The model did not consider the influence of the failure between the core and facesheets, which should be further investigated to improve the accuracy and practicability of the model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moss, D.R. Pressure Vessel Design Manual; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Su, W. Research on Some Problems About Numerical Simulation of Pressure Equipment and Its Engineering Application. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2003. (In Chinese). [Google Scholar]
- Lu, T.J.; He, D.P.; Chen, C.Q.; Zhao, C.Y.; Fang, D.N.; Wang, X.L. The multi-functionality of ultra-light porous metals and their applications. Adv. Mech. 2006, 36, 517–535. (In Chinese) [Google Scholar]
- Lu, T.J.; Zhang, Q.C.; Jin, F. Recent progress in the development of lightweight porous materials and structures. Mater. China 2012, 31, 13–35. [Google Scholar]
- Alankaya, V.; Alarçin, F. Using sandwich composite shells for fully pressurized tanks on liquefied petroleum gas carriers. J. Mech. Eng. 2016, 62, 32–40. [Google Scholar] [CrossRef]
- Arunkumar, M.; Pitchaimani, J.; Gangadharan, K.; Babu, M.L. Sound transmission loss characteristics of sandwich aircraft panels: Influence of nature of core. J. Sandw. Struct. Mater. 2017, 19, 26–48. [Google Scholar] [CrossRef]
- Shaban, M.; Alibeigloo, A. Three-dimensional elasticity solution for sandwich panels with corrugated cores by using energy method. Thin-Walled Struct. 2017, 119, 404–411. [Google Scholar] [CrossRef]
- Timoshenko, S. Strength of Materials, 3rd ed.; Van Nostrand Reinhold: New York, NY, USA, 1958. [Google Scholar]
- Timoshenko, S.; Goodier, J.N. Theory of elasticity. In Engineering Societies Monographs, 3rd ed.; McGraw-Hill: Tokyo, Japan; London, UK, 1970. [Google Scholar]
- Boressi, A.P.; Schmidt, R.J.; Sidebottom, O.M. Advanced Mechanics of Materials, 5th ed.; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Mendelson, A. Plasticity: Theory and Application; Macmillan Series in Applied Mechanics; Macmillan: New York, NY, USA, 1968. [Google Scholar]
- Parker, A.P. Autofrettage of open-end tubes-pressures, stresses, strains, and code comparisons. ASME J. Press. Vessel Technol. 2001, 123, 271–281. [Google Scholar] [CrossRef]
- Perry, J.; Aboudi, J. Elasto-plastic stresses in thick walled cylinders. ASME J. Press. Vessel Technol. 2003, 125, 248–252. [Google Scholar] [CrossRef]
- Lekhniëtìskiæi, S.G. Theory of Elasticity of an Anisotropic Body; Mir Publishers: Moscow, Russia, 1981; p. 430. [Google Scholar]
- Luo, Z.D.; Li, S.J. Mechanics of Anisotropic Materials; Shanghai Jiaotong University Press: Shanghai, China, 1994. [Google Scholar]
- Khalili, S.M.R.; Azarafza, R.; Davar, A. Transient dynamic response of initially stressed composite circular cylindrical shells under radial impulse load. Compos. Struct. 2009, 89, 275–284. [Google Scholar] [CrossRef]
- Rizzetto, F.; Jansen, E.; Strozzi, M.; Pellicano, F. Nonlinear dynamic stability of cylindrical shells under pulsating axial loading via Finite Element analysis using numerical time integration. Thin-Walled Struct. 2019, 143, 106213. [Google Scholar] [CrossRef]
- Semenyuk, N.P.; Zhukova, N.B. Stability of a sandwich cylindrical shell with core subject to external pressure and pressure in the inner cylinder. Int. Appl. Mech. 2020, 56, 40–53. [Google Scholar] [CrossRef]
- Kardomateas, G.A.; Chung, C.B. Buckling of Thick Orthotropic Cylindrical Shells Under External Pressure Based on Non-Planar Equilibrium Modes. Int. J. Solids Struct. 1994, 31, 2195–2210. [Google Scholar] [CrossRef]
- Kardomateas, G.A. Elasticity Solutions for Sandwich Orthotropic Cylindrical Shells Under External/Internal Pressure or Axial Force. AIAA J. 2001, 39, 713–719. [Google Scholar] [CrossRef]
- Kardomateas, G.A.; Simitses, G.J. Buckling of Long Sandwich Cylindrical Shells Under External Pressure. J. Appl. Mech. 2005, 72, 493–499. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Z.C.; Lu, T.J. Minimum weights of pressurized hollow sandwich cylinders with ultralight cellular cores. Int. J. Solids Struct. 2007, 44, 3231–3266. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Z.C.; Lu, T.J. Bi-functional optimization of actively cooled, pressurized hollow sandwich cylinders with prismatic cores. J. Mech. Phys. Solids 2007, 55, 2565–2602. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to Grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
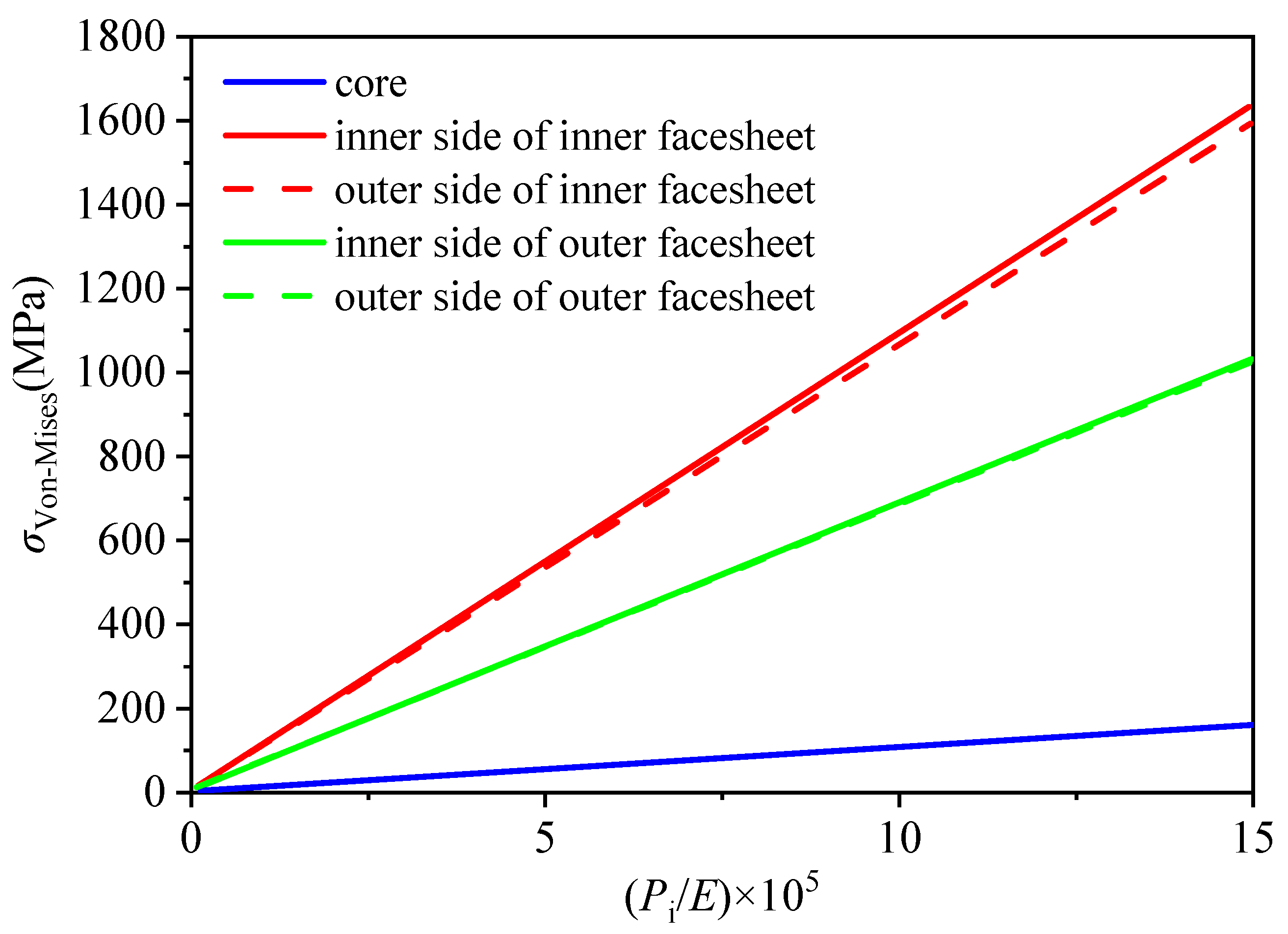
| Case | Ro (m) | p/Ro | hc/Ro | f/Ro | To/Ro | Ti/Ro | Tc/Ro | Pi/E |
| 1 | 0.15 | 0.0837 | 0.333 | 0.0533 | 0.00367 | 0.00867 | 0.0026 | 15 × 10−5 |
| Case | Results in [23] | Closed-Form Solution in This Paper | Error (%) | ||
|---|---|---|---|---|---|
| 1 | Inner Facesheet | (Pa) | −3.01 × 107 | −3.09 × 107 | 2.66 |
| (Pa) | 1.89 × 109 | 1.81 × 109 | 4.23 | ||
| (Pa) | 5.54 × 108 | 5.32 × 108 | 3.97 | ||
| (Pa) | 1.69 × 109 | 1.63 × 109 | 3.55 | ||
| 2 | Outer Facesheet | (Pa) | −4.3 × 106 | −4.22 × 106 | 1.86 |
| (Pa) | 1.17 × 109 | 1.15 × 109 | 1.71 | ||
| (Pa) | 3.5 × 108 | 3.45 × 108 | 1.43 | ||
| (Pa) | 1.05 × 109 | 1.03 × 109 | 1.90 | ||
| 3 | Core | (Pa) | −6.23 × 107 | −6.58 × 107 | 5.62 |
| (Pa) | −2.08 × 108 | −1.82 × 108 | 12.50 | ||
| (Pa) | 1.84 × 108 | 1.60 × 108 | 13.04 | ||
| Parameters | Relevance | |
|---|---|---|
| Size design variables | ti | 0.6133 |
| to | 0.6087 | |
| tw | 0.5720 | |
| Shape design variables | hc | 0.6954 |
| ρ | 0.6873 | |
| f | 0.6690 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wu, J.; Chen, C.; Cui, H.; Yang, Y.; Guo, R.; Zhou, H. Mechanical Behavior of Hollow Corrugated Sandwich Cylinders Under Inner Pressure Loading. Appl. Sci. 2024, 14, 12011. https://doi.org/10.3390/app142412011
Zhang L, Wu J, Chen C, Cui H, Yang Y, Guo R, Zhou H. Mechanical Behavior of Hollow Corrugated Sandwich Cylinders Under Inner Pressure Loading. Applied Sciences. 2024; 14(24):12011. https://doi.org/10.3390/app142412011
Chicago/Turabian StyleZhang, Li, Junan Wu, Changfa Chen, Hao Cui, Yongliang Yang, Rui Guo, and Hao Zhou. 2024. "Mechanical Behavior of Hollow Corrugated Sandwich Cylinders Under Inner Pressure Loading" Applied Sciences 14, no. 24: 12011. https://doi.org/10.3390/app142412011
APA StyleZhang, L., Wu, J., Chen, C., Cui, H., Yang, Y., Guo, R., & Zhou, H. (2024). Mechanical Behavior of Hollow Corrugated Sandwich Cylinders Under Inner Pressure Loading. Applied Sciences, 14(24), 12011. https://doi.org/10.3390/app142412011






