1. Introduction
With the rapid development of network devices and the surge in network traffic, these devices now combine multiple functions and can provide various services simultaneously to mobile users. This results in multiple concurrent data flows. When a mobile device moves, the data transmission path in the wired network may need to be updated due to a change in the device’s access switch. It is important to note that, in this paper, the term “wired network” refers to a static network composed of switches and links. Traditional mobility management schemes, whether anchor-based or non-anchor-based, typically select a single switching path. However, when this path cannot accommodate all the mobile data flows, it may lead to network congestion, resulting in increased packet delays and higher packet loss rates. Such issues severely degrade the user experience, especially for real-time services like Voice over Internet Protocol (VoIP) and online gaming, which require low transmission delays, and for video live streaming, where high packet loss rates can cause audio–video synchronization issues.
Recent research has explored providing multiple switching paths for mobile data flows by selecting different late-binding nodes for each flow [
1]. However, this approach does not take into account the potential overlap of links between paths, which limits its effectiveness in complex networks. To address this limitation, multi-topology routing can be employed. This approach generates multiple logical topologies as subsets of the physical network topology. When the mobility management process is triggered and a new network address of the mobile device is obtained, a logical topology is selected for each mobile data flow. This method enables the distribution of flows across multiple paths, reducing the possibility of congestion caused by relying on a single switching path. In this scheme, the construction of logical topologies plays a critical role, as it provides the foundation for the subsequent topology selection process. Well-designed topologies can provide high-bandwidth, low-latency paths to all possible destination nodes, significantly improving the final performance of mobile users. Conversely, poorly designed topologies fail to provide such paths and waste the limited flow entry capacity of switches.
Previous studies on multi-topology construction have mainly focused on other objectives. Some are motivated by node or link failure recovery [
2,
3,
4,
5]. These studies aim to quickly restore transmission by switching topologies when failures occur. Others focus on traffic engineering [
6,
7,
8,
9], aiming to maximize link utilization by increasing path diversity or employing other strategies. Other studies aim to isolate different types of flows and allocate them to separate topologies to provide varying levels of Quality of Service (QoS) [
10,
11,
12]. However, these methods are not suitable for providing multiple switching paths specifically for mobile data flows.
Mobile devices may move in and out of the coverage area of access points connected to various access switches. Therefore, the multi-topology construction must consider multiple paths from the source node (e.g., the switch connected to a content server) to each access switch. Moreover, the handover mechanism in wireless networks is outside the scope of this study. We focus solely on optimizing switching paths in wired networks. The number of logical topologies deployed in the physical network must also be limited, as it impacts both switch capacity utilization and the computational complexity of selecting topologies for data flows, ultimately affecting the performance of mobile users. For a given source–destination node pair, multiple paths may exist within different logical topologies. If adding a new path does not increase the total available bandwidth between the node pair, it is considered redundant. Including such paths unnecessarily increases the number of logical topologies and wastes switch capacity. Existing multi-topology construction methods fail to optimize and balance the transmission capacity to all destination nodes while considering switch flow entry constraints. This shortfall prevents them from providing efficient switching paths for mobile data flows. This highlights the need for a new method that specifically targets these issues.
In this paper, we focus on multi-topology construction to provide efficient paths with high-bandwidth, low packet loss rates, and low data transmission delays for mobile data flow scheduling. The main contributions of this paper are as follows:
We propose a multi-topology deployment scheme based on software-defined networking (SDN) and analyze the constraints and requirements involved in efficient multi-topology construction for scheduling mobile data flows within SDN.
We model the multi-topology construction problem and divide it into two subproblems, for which we propose two algorithms. The first algorithm introduces a novel path-ranking method based on contributions to overall transmission capacity. The second algorithm constructs a multi-topology to maximize and balance transmission capacity between node pairs, considering the path rankings and switch flow entry constraints.
We implement the proposed multi-topology construction method on Mininet [
13] and compare its performance with the AMPLE [
6] method, the k-shortest path method, and the baseline single-path switching method. The results show that our approach reduces the average packet delay, decreases the average packet loss rate, and improves throughput, regardless of the mobile device’s new location.
The structure of this paper is as follows.
Section 2 reviews related work on multi-topology construction.
Section 3 provides details on the deployment of multi-topology routing in SDN.
Section 4 models the problem and introduces our multi-topology construction method for scheduling mobile data flows in SDN.
Section 5 presents experimental results and a comparative analysis against three other methods. Finally,
Section 6 concludes the paper and outlines directions for future work.
2. Related Work
The number of flow entries in an SDN switch is limited for several reasons. Firstly, there are limitations of hardware. Flow entries are stored in a switch, which is commonly implemented with Ternary Content Addressable Memory (TCAM) technology [
14]. However, TCAM is power-hungry, expensive, and available in limited space or capacity that can only accommodate between 750 and 20,000 flow entries [
15]. Secondly, the number of flow entries can affect the performance of a switch. Managing and querying flow entries require computational resources. Having too many flow entries can lead to increased processing time and querying time, thereby affecting the speed of packet forwarding. Additionally, when events such as topology changes, network reconfigurations [
16], and the creation of rerouting rules [
17] occur, the routing update operation must be completed within 25 milliseconds to meet the stringent QoS requirements of real-time applications [
18]. Fast routing updates rely on the number of flow entries. Due to these reasons, network designers need to configure flow entries reasonably based on actual needs and hardware capabilities.
There are some studies on multi-topology construction methods. They can be divided into three categories. The first category aims at fast recovery from link/node failures. Wójcik [
2] proposed an approach called FAMTAR. It uses the optimal path between two endpoints in the physical topology and automatically finds new paths in case of congestion by setting the cost of the congested link to a high value, forming logical topologies. Menth [
3] described a network design principle that emphasized redundancy and resilience through multi-topology routing. This approach ensures that even if one link or node fails, there remains at least one available route between any two nodes. Similarly, Gardner [
4] proposed a method based on multi-topology routing for pre-planning for geographically correlated failures. It constructs logical topologies with a network-wide coverage approach. Cevher [
5] implemented an IP fast reroute method based on multi-topology routing for SDN. It constructs a multi-topology on the data plane of SDN and relies on the existing failure detection mechanisms of the controller. These methods do not take into account the distribution of data flows across different logical topologies, which makes them fail to support simultaneous transmission across multiple paths.
Another category focuses on traffic engineering, which aims to maximize link utilization or maximize throughput. Wang [
6] proposed a method called AMPLE. It computes the link weights in different sub-topologies to maximize intra-domain path diversity across a multi-topology construction. Based on AMPLE, Jaron [
7] introduced a QoS-aware cost function for topology state monitoring. Additionally, the method establishes a policy-based routing scheme to select the optimal logical topology, ensuring QoS for new users while enhancing overall network performance. Mihailovic [
8] constructed a multi-topology based on minimum set cover to enhance path diversity and introduced novel offline optimization features using a dynamic cost function. Wang [
9] proposed a multi-topology construction method that removes each link from exactly one logical topology, continuing until either all links are isolated within a single topology or the removal of a link would disconnect the topology. To prevent congestion, the algorithm aims to balance the number of links removed from each logical topology. Although these methods construct multi-topologies with good path diversity and reasonably distribute data flows across different logical topologies, they fail to ensure balanced bandwidth from the source node to each destination node.
The third category aims to provide different QoS levels to various flows. Bhandari [
10] proposed constructing logical topologies over a physical network using different objective functions designed to meet different QoS requirements of IoT applications, while adhering to the features of Directed Acyclic Graph (DODAG). Demir [
11] constructed logical topologies for Audio Video Bridging (AVB) streams to reduce interference with the transmission of Time-Triggered (TT) streams while satisfying their delay requirements. Similarly, Pop [
12] aimed to determine the routing of both TT and AVB streams, as well as the scheduling of TT flows, ensuring that all frames are schedulable and the worst-case end-to-end delay of AVB is minimized. These methods provide varying transmission quality for different types of services, but they do not address the overall bandwidth maximization between node pairs, nor do they limit the number of paths a node can be traversed.
Regarding the studies on multi-topology construction mentioned above, none of them consider maximizing the overall bandwidth between every node pair while limiting the number of paths that each node can be traversed. In other words, they do not account for the flow entry capacity limitations of switches when constructing multi-topologies in SDN networks. Therefore, it is necessary to explore a new method for constructing a multi-topology that addresses these challenges.
3. System and Scenario Description
In essence, the goal of any method for constructing multi-topology routing is to ensure that there are multiple transmission paths between a node pair. In traditional networks, switches are responsible for both data forwarding and control logic, which limits the flexibility of packet forwarding in a top–down manner. That is, multiple logical topologies are first established, and then, for each logical topology, the switches calculate the shortest path to each destination node based on the link weights in that topology and stores the results in the forwarding table. Each forwarding table corresponds to a logical topology. From this perspective, a logical topology corresponds to a single path for each node pair in the network.
Software-defined networking is an emerging network architecture. It separates the control layer from the data layer of the network, providing a more flexible and programmable network management method. In SDN, switches are only responsible for packet forwarding, while the control logic is managed by the controller. An SDN controller installs packet forwarding rules in switches using protocols such as P4 [
19] and OpenFlow [
20] to control how data packets are processed. Each switch has one or more flow tables, and each flow table contains a set of flow entries, where each entry defines the matching conditions and actions for packet processing. The switch forwards packets according to these rules. Given the flexible forwarding characteristics of SDN, the controller can directly specify the path between two nodes in different logical topologies and install the corresponding flow forwarding rules as flow entries in the relevant switches. This eliminates the need for each router or switch in traditional networks to independently determine the path. As a result, this approach is more flexible, intelligent, and efficient, enabling rapid adaptation to dynamic traffic demands. Similarly, each flow table corresponds to a logical topology.
In an SDN switch, flow tables are arranged in order. Data packets first match the flow table with the highest priority. After a data packet is processed in a flow table, it is forwarded to another flow table if the action is “Goto Table”. This mechanism allows us to implement multi-topology routing in SDN. The controller generates multiple logical topologies based on the physical topology through certain strategies and installs the packet forwarding rules for each topology as flow entries in the relevant switches. Each switch stores multiple flow tables corresponding to each topology. In addition, there is a flow table with the highest priority known as the “topology selection table”, which is configured for selecting topologies for mobile data flows. It is updated in the relevant switches when a mobility event occurs. In real-world networks, there are multiple mobile users that may connect to the network through different switches. Additionally, the content requested by users may vary, leading to different bandwidth and delay requirements. Flow Table 0 can change dynamically based on user demands and the network situation. It allocates topologies for the multiple data flows. By using a certain strategy to dynamically construct Flow Table 0, it can meet the requirements of multiple mobile users. While a multi-topology provides multiple paths, not all topologies must be used. The specific topologies to be used, and the assignment of data flows to these topologies, are determined by Flow Table 0. The construction of the topology selection table is not the focus of this paper. When a data packet enters a switch, it first matches the topology selection table, then proceeds to the corresponding flow table for forwarding.
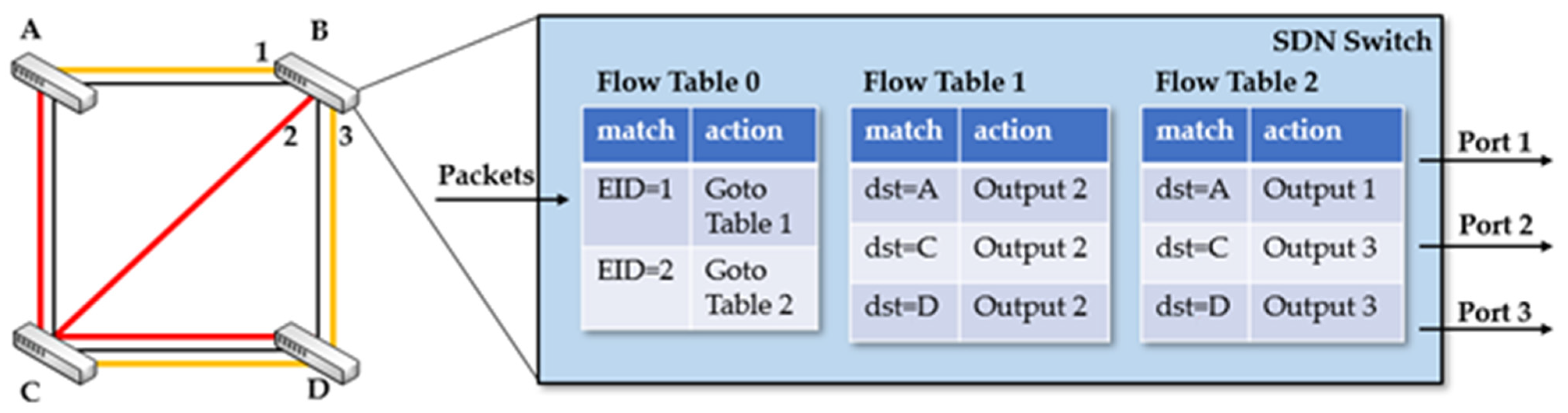
Figure 1 shows an example of multi-topology routing in SDN and the processing logic in a switch.
As shown in
Figure 1, there are four switches. The black connections represent the physical topology. The red connections represent Logical Topology 1, and the yellow connections represent Logical Topology 2. Let us take Switch B as an example. The flow tables in Switch B are shown in the figure. Flow Table 0, with the highest priority, is the “topology selection table”. Flow Table 1 stores the forwarding rules for packets in Topology 1, while Flow Table 2 stores the forwarding rules for packets in Topology 2. It is assumed that a data packet contains a field that stores the content identifier (EID) of the content it belongs to. Packets belonging to the same content form a data flow. When Switch B receives a data packet, it first matches Flow Table 0. It identifies which data flow the packet belongs to by matching the EID field of the data packet. The packet is then forwarded to either Flow Table 1 or Flow Table 2 according to the corresponding action. Finally, it is forwarded through the corresponding port according to the matching destination address. This enables the data packets belonging to a specific data flow to be directed to the specified topology, and the path between a node pair in a logical topology is configured by the controller. It is assumed that the new network address of a mobile device can be obtained within a precise delay from a distributed on-site resolution system [
21], and the packets’ destination addresses can be updated to the new network address in some way.
If a switch is part of a logical topology, the corresponding flow table needs to be installed in the switch. The number of flow entries in the flow table is equal to the number of paths from the source node to the destination node that traverse the switch in the topology. It should be noted that in a logical topology, there is at most one path between any source–destination node pair.
4. Problem Modeling and Solution
4.1. Overall Problem Description
As mentioned earlier, in SDN, we can specify paths between node pairs within a logical topology. This allows us to construct each flow table (logical topology) by combining paths. In a complex mesh network, there are many paths between a source node
and a destination node
. All simple paths from s to t can be obtained using Depth-First Search (DFS) or Breadth-First Search (BFS) algorithms. However, since these paths may share overlapping links, having more paths does not necessarily increase the overall transmission capacity. Given that mobile devices may move to various nearby locations, the constructed multi-topology should include multiple paths from the source node to multiple destination nodes. Our goal is to construct a multi-topology consisting of a subset of all possible paths between node pairs that ensures high and balanced transmission capacity for each node pair. We formulate the multi-topology construction problem as a mathematical model. The main symbols used in the model are shown in
Table 1.
Objective Function: The goal of efficient multi-topology construction for scheduling mobile data flows is to maximize the average total flow capacity that can be transmitted through multiple paths from the source node
to each destination node
within a unit of time.
where
is the set of all destination nodes,
is the set of all simple paths from node
to node
,
is the amount of traffic transmitted by path
in a unit of time, and
is the number of destination nodes.
Constraints:
Link Bandwidth Constraint: For each link
, the amount of traffic that can be transmitted in a unit of time must not exceed its available bandwidth.
where
is the set of all links in the physical topology,
is the available bandwidth of link
, and
is the set of links contained in path
.
Non-Negativity Constraint: Ensure that the amount of traffic is non-negative.
It should be noted that may equal 0, indicating that path is not in use.
Flow Entry Capacity Constraints: For each switch node, the number of active paths traversing it cannot exceed its flow entry capacity constraint.
where
is the set of all paths traversing switch node
, and
is the flow entry capacity constraint for switch node
.
It should be noted that the multi-topology is generated based on a static physical topology. The construction of the multi-topology does not take into account the future demands and specific mobility of devices, as these are unknown at the time of its creation. However, this limitation can be addressed by dynamically allocating mobile data flows across different logical topologies. The goal of the multi-topology construction is to maximize the average transmission capacity from the source node to all possible destination nodes, thus achieving a certain level of scalability and universality. Additionally, it provides a solid foundation for the dynamic allocation of mobile data flows.
4.2. A Ranking Method Based on Path Contribution
This section introduces a novel path contribution ranking approach to identify and select paths based on their contribution to the overall transmission capacity, rather than relying solely on simple metrics like hop count or bottleneck link bandwidth. The method works by selecting paths that maximize overall transmission capacity and ranking them according to the order in which they are selected. This process eliminates redundant paths and ensures that high-contribution paths are prioritized. The earlier a path is selected, the greater its contribution and the higher its rank. These path rankings then serve as a reference for the subsequent multi-topology construction. A mathematical model for this problem is established as follows:
Objective Function: Maximize the flow capacity
that can be transmitted through multiple paths from node
to node
in a unit of time:
Constraints:
Link Bandwidth Constraint: For each link
, the amount of traffic that can be transmitted in a unit of time must not exceed its available bandwidth.
Non-Negativity Constraint: Ensure that the amount of traffic is non-negative.
where
may equal 0, indicating that path
is not in use. From this mathematical model, we can see that, compared to the overall problem model, we have not considered the flow entry constraints of the switches as they are difficult to define using the variable
. We will address this issue later. Additionally, in the overall problem model, the objective is to maximize the average transmission capacity from the source node to all destination nodes. In contrast, this problem aims to maximize the transmission capacity from the source node to a single destination node. Therefore, the number of variables in this problem is the number of paths between one node pair, while the number of variables in the overall problem is the sum of the number of paths of all node pairs. This problem is a subproblem of the original problem. In most multipath selection schemes, such as those in [
22,
23], if two paths share an overlapping node or link, one of them is typically removed. This aims to avoid the situation where both paths become unavailable due to the failure of the shared node or link. However, this requirement is too strict for maximizing network transmission capacity in this algorithm. The bottleneck link
of path
is defined as follows:
If the shared link of two paths is not the bottleneck link of them, including the other path can still increase network transmission capacity. Therefore, the focus should be on ensuring that the selected paths do not overlap on bottleneck links; that is, if multiple paths have the same bottleneck link, only one of them can be selected. In this case, the shorter path is retained, as shorter paths generally result in lower data transmission delays. The details of the ranking method are given below Algorithm 1.
| Algorithm 1 Rank paths while maximizing transmission capacity |
1: Input: Paths P
2: Output: Total flow, Paths selected according to the rank order
3: Function find_max_min_bandwidth_path(paths):
−1
None
6: for path in paths do
7: if path.min_bandwidth() > max_min_bandwidth then
path.min_bandwidth()
path
10: else if path.min_bandwidth() = max_min_bandwidth then
11: if path.length() < best_path.length() then
path
13: end if
14: end if
15: end for
16: Return (best_path, max_min_bandwidth)
17: Function update_bandwidth(path, min_bw):
18: for link in path.links do
link.capacity—min_bw
20: end for
21: Main Program:
0
[]
24: while True do
find_max_min_bandwidth_path(paths)
26: if best_path = None or min_bw <= 0 then
27: break
28: end if
29: update_bandwidth(best_path, min_bw)
total_flow + min_bw
31: path_results.append((best_path, min_bw))
32: end while
33: Return total_flow, path_results |
The input to this Algorithm 1 is the set of all simple paths between a source–destination node pair, along with parameters such as the available bandwidth of each link in the path and the path length.
The algorithm selects the path from the path set that has the maximum minimum link bandwidth and is the shortest. For all links contained in path , the available bandwidth is reduced by , making the available bandwidth of the bottleneck link of path equal to 0. The path is then removed from the set , and the next path with the maximum minimum link bandwidth and shortest length is selected. This process is repeated until set is empty or the maximum minimum link bandwidth is less than or equal to 0. The time complexity of the algorithm is , where represents the number of links, and represents the number of paths.
The output of this algorithm is the maximum transmission capacity between the node pair and the selected paths ranked by contribution. Higher-ranked paths can transmit greater amounts of traffic. The output path set is the minimal set of paths that achieves the maximum transmission capacity from the candidate paths. Removing any path from this minimal set would lead to a decrease in overall transmission capacity, while adding another path would not increase it. This ensures that the multiple paths selected between the node pair are non-redundant. It is important to note that the shortest path between the node pair is always selected in this algorithm. If the bottleneck link of the shortest path overlaps with the bottleneck links of other paths, the shortest path is still selected due to its minimal length. If the bottleneck link of the shortest path does not overlap with the bottleneck links of other paths, it will be selected sooner or later during one of the iterations in the loop from line 24 to line 32.
4.3. Logical Topologies Construction
If all paths between node pairs are installed in switches as flow entries, the number of entries in some switches may exceed their flow entry capacity. Existing multi-topology construction methods do not consider the limitations of switches’ flow entry capacity. In this section, we propose a multi-topology construction method to maximize and balance the transmission capacity between every node pair, while considering both path rankings and the switch flow entry capacity. The method aims to incorporate as many paths as possible into the multi-topology to enhance the overall transmission capacity. Following the path contribution rankings, the algorithm prioritizes higher-ranked paths and alternates the path selection between node pairs, ensuring a balanced distribution of transmission capacity across the network.
Using the ranking method above, we obtain the maximum transmission capacity and the selected paths’ rankings for each node pair. Therefore, it is necessary to discard some paths during the multi-topology construction process, while also adhering to the ranking order of the paths. The construction problem can be modeled as follows:
Objective Function: Maximize the number of the paths kept in switches:
where
is a binary variable.
if path
is selected, and
otherwise.
Constraints:
Flow Entry Capacity Constraints of the Switch: For each switch node, the number of the selected paths traversing it cannot exceed its capacity constraint.
Path Ranking Constraint: For each path with a ranking number of
, it can only be considered after all paths with a ranking number lower than
have been checked. The following constraint is introduced:
where
is the set of all paths with a ranking number of
, and
is the set of all switch nodes that path
traverses.
To solve this problem, we propose Algorithm 2 as follows:
| Algorithm 2 Construct multi-topology |
1: Input:
2: nodes: List of Nodes(switches)
3: node_pairs: List of NodePairs
4: Output:
5: Multi-topology constructed according to the rank of paths
6: Function construct_multi_topology(nodes, node_pairs):
7: for node in nodes do
[]
9: end for
{}
11: for pair in node_pairs do
12: for path in pair.paths do
13: if path.rank not in topos then
[]
15: end if
16: topos[path.rank].append(path)
17: end for
18: end for
19: for (rank, paths) in sorted(topos.items()) do
20: for path in paths do
True
22: for node in path.nodes do
23: if node.path_limit <= len(node.selected_paths) then
False
25: break
26: end if
27: end for
28: if can_select then
29: for node in path.nodes do
30: node.selected_paths.append(path.id)
31: end for
32: else
33: topos[rank].remove(path)
34: end if
35: end for
36: end for
37: Return topos |
In this algorithm, paths with lower ranking numbers are prioritized for each node pair. Paths with the same ranking number are kept in the same logical topology. In the relevant switches, paths to different destinations with the same ranking number are placed in the tables with the same table ID. When each path is added, the algorithm ensures that all switches traversed by this path satisfy the flow entry capacity constraints. The time complexity of the algorithm is , where represents the maximum number of ranks, and represents the number of nodes. Combining the time complexity of Algorithm 1, the overall computational complexity of the problem is which can also be written as . Since the multi-topology construction process is performed offline as a pre-processing step, it does not affect the real-time performance of mobile users. This approach balances the number of paths in each logical topology, thereby balancing the transmission capacity from the source node to each destination node. It is important to note that if the shortest path between a node pair has a high ranking number, it may not be selected. A higher ranking number for the shortest path indicates that its bottleneck bandwidth is smaller, making it more prone to congestion under heavy traffic. Our goal is to maximize the average transmission capacity, so we may need to discard the shortest path if its transmission capacity is poor. Even so, each selected path is the shortest among the multiple paths that share the same bottleneck link. Overall, the paths we select tend to be shorter.
5. Performance Evaluation
5.1. Evaluation Metrics
In the previous section, we introduced a method for multi-topology construction based on path ranking, referred to as the RANK method. This section presents a series of experiments aimed at evaluating the impact of the RANK method on mobile user performance. In our research on routing strategies, we found that choosing an algorithm depends on the objectives intended to be achieved for a specific network [
24]. Therefore, we used three well-established performance metrics to quantify mobile user performance: average packet delay, average packet loss rate, and throughput.
5.2. Simulation Setup
The experimental platform was set up on Ubuntu 20.04 and included Mininet 2.3.0, Open vSwitch 2.17.9, and the Ryu 4.34 controller [
25]. Mininet [
13] is a network simulator widely used for developing, testing, and evaluating SDN applications. It creates a realistic virtual network, running real kernel, switch, and application code on a single machine, emulating the behavior of a real network. For a performance comparison, we employed two other multi-topology construction methods: AMPLE [
6] and the k-shortest paths approach, along with a single-path switching method as the baseline. The single-path switching method routes all mobile data flows through the shortest path from the source node to the new destination node. For multi-topology routing, each intermediate node (excluding the source and destination nodes) was assigned a flow entry capacity constraint of four, corresponding to the constraint in Algorithm 2. Using the AMPLE method, we constructed four logical topologies and removed some paths to meet the flow entry capacity constraints of each node. Similarly, with the k-shortest paths method, we selected four shortest paths for each node pair to construct four logical topologies, and then deleted some paths to satisfy the flow entry capacity constraints of each node.
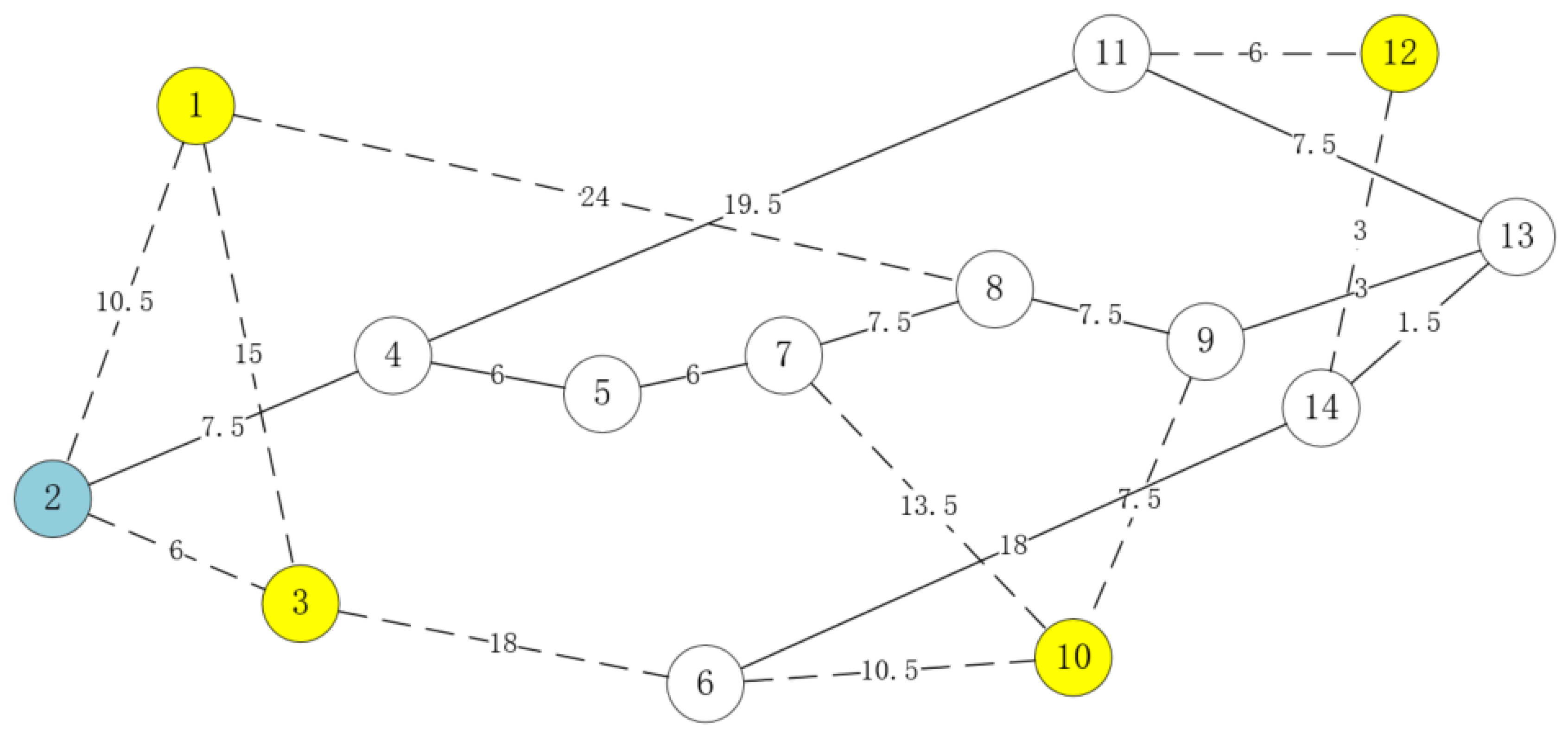
In a typical network architecture, switches are organized into three layers: the core layer, the aggregation layer, and the access layer. They form an efficient and reliable network together. The access layer may consist of multiple switches connecting to devices accessed by mobile users (such as base stations or wireless access points). The aggregation switches are responsible for aggregating the traffic from the access layer and forwarding it to the core layer. Access switches are typically connected to multiple aggregation switches to achieve load balancing. To simulate a complex network topology with many paths between node pairs, this experiment employed a mesh topology. We generated a network topology containing 14 nodes based on the National Science Foundation Network (NSFNET) backbone [
26], as shown in
Figure 2 below.
In this experiment, we assume that the transmission delay of a link is proportional to its length. Based on the distances between nodes, the link delays were calculated and are presented in the figure (in milliseconds). This topology served as the physical topology, and logical topologies were constructed based on it.
In this network, each node represents a switch, and each line represents a link. The network consists of 14 switches and 21 links. The blue node represents Switch S2, which is the source node. The content server is connected to it. The yellow nodes represent Switches S1, S3, S10, and S12, which serve as destination nodes. The mobile device accesses the network through these switches. There are two types of links: dashed lines represent links with a bandwidth of , while solid lines represent links with a bandwidth of . The mobile device initially connects to the network through Switch S3, which serves as the access switch. It is assumed that Switches S1, S10, and S12 cover the entire range of device movement. Regardless of the device’s location, it can only access the network through one of these three switches.
We generated varying numbers of data flows, each with a sending rate of
and a packet size of 1000 bytes. Based on the multi-topologies constructed using the three methods, we employed a genetic algorithm [
27] to create the “topology selection table” (Flow Table 0), allocating mobile data flows to specific topologies for path switching. The fitness of individuals in the genetic algorithm was evaluated based on the average packet delay:
where
represents the number of data flows, and
is a Boolean variable such that if data flow
selects topology
, then
; otherwise,
. The variable
denotes the length of the path from the source node to the new destination node in topology
selected for data flow
. An individual represents a data flow allocation plan, which can be described as an
matrix, where each element
indicates whether data flow
is assigned to topology
. Since each data flow can only be assigned to one topology, each row in the matrix contains exactly one “1” and
“0” s. The crossover points are selected randomly, defined by a row of the matrix. Crossover involves swapping the upper and lower parts of the rows between two matrices. In practical terms, this means altering the topology selection of certain data flows. The mutation points are also selected randomly, defined by a row of the matrix. Mutation involves changing the position of the “1” within that row. In practical terms, this means altering the topology selection of a specific data flow. Introducing randomness in genetic algorithms helps increase population diversity. This prevents premature convergence to local optima. It also enhances the algorithm’s global search ability, allowing it to explore more areas of the solution space. Ultimately, this improves the algorithm’s ability to find better solutions. Each experiment was repeated three times, and the average results were recorded. The detailed experimental results are presented in the following section.
5.3. Results and Discussions
In this section, we present the experimental results and provide a discussion and analysis of them.
5.3.1. Average Packet Delay
We captured the data packets sent by the content server and received by the mobile device at its new location. The average packet delay for each flow was calculated by measuring the time difference between the sending and receiving of packets within the flow. The overall average packet delay was then obtained by dividing the sum of these delays by the number of data flows. The figures below compare the average packet delay achieved by different multi-topology construction methods and the single-path switching method in relation to the number of contents requested by the mobile device. Results are presented for cases where the mobile device moves to S1, S10, and S12.
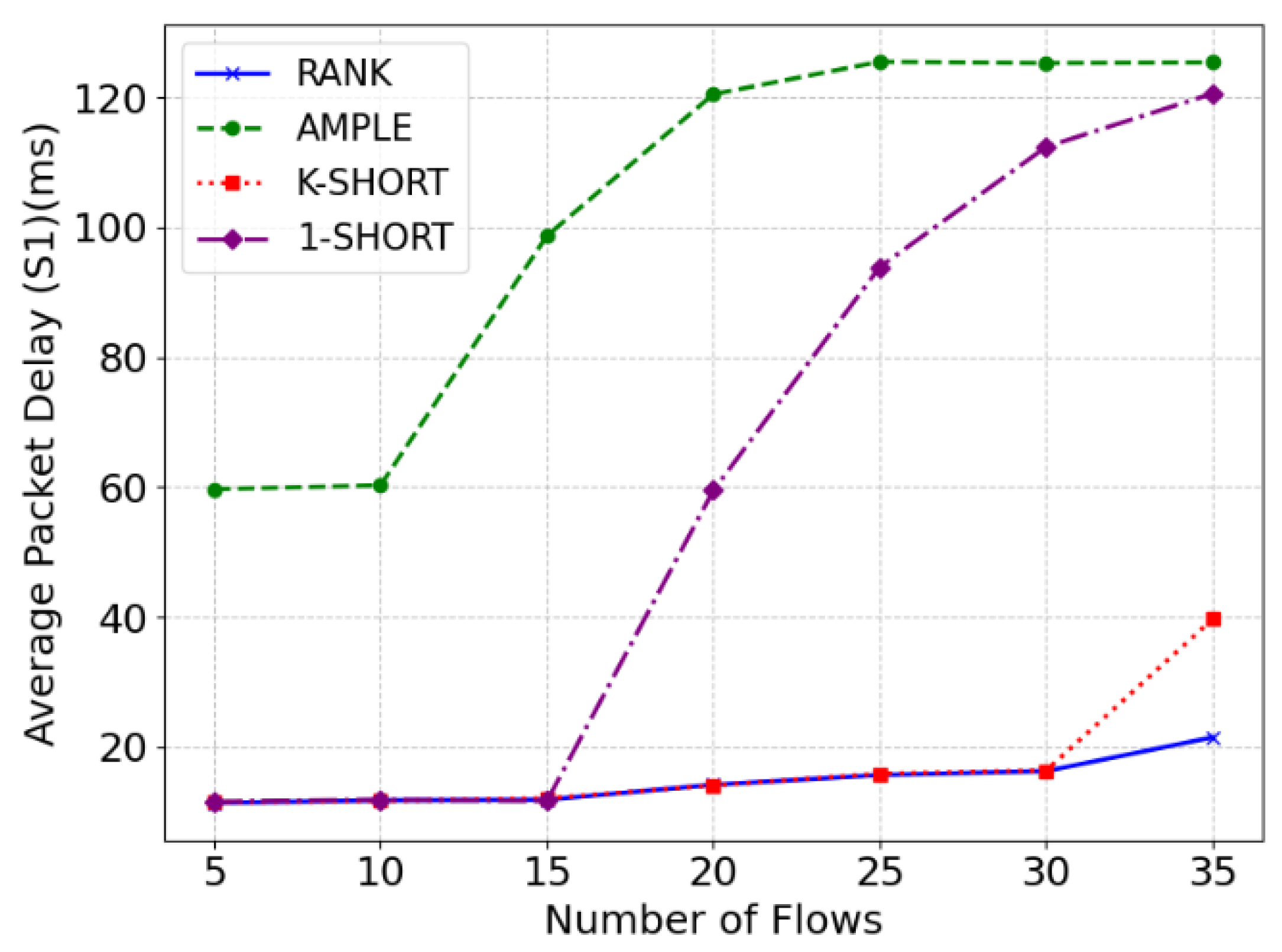
It can be seen from
Figure 3 that when the device moves to S1, the RANK method achieves the lowest average packet delay. When the number of data flows ranges from 5 to 15, the performance of the RANK, k-shortest, and single-path methods is similar, as all of them can provide the shortest path, and the available bandwidth of the shortest path is sufficient for all data flows. When the number of data flows increases to 20, the single-path method experiences congestion, leading to a significant increase in the average packet delay. As the number of data flows continues to grow, congestion worsens, resulting in further increases in the average packet delay. In contrast, for the RANK and k-shortest methods, the average packet delay increases slowly as the number of data flows grows from 15 to 30. This is because the bandwidth of the shortest path is exhausted, and longer paths are used. However, when the number of data flows reaches 35, the k-shortest method begins to experience congestion, causing a noticeable increase in the average packet delay to 39.7 milliseconds (ms). The RANK method, on the other hand, continues to provide paths that can accommodate all data flows, avoiding congestion and keeping a lower average packet delay of 21.5 ms.
Among the four methods, the AMPLE method performs the worst. It provides longer paths with a lower overall bandwidth, resulting in the highest average packet delay even when the bandwidth is sufficient. When the number of data flows reaches 15, severe congestion occurs. It is worth noting that as the number of data flows increases, congestion worsens. However, since the link queue size is fixed, the average packet delay does not increase indefinitely; instead, more packets are directly dropped.
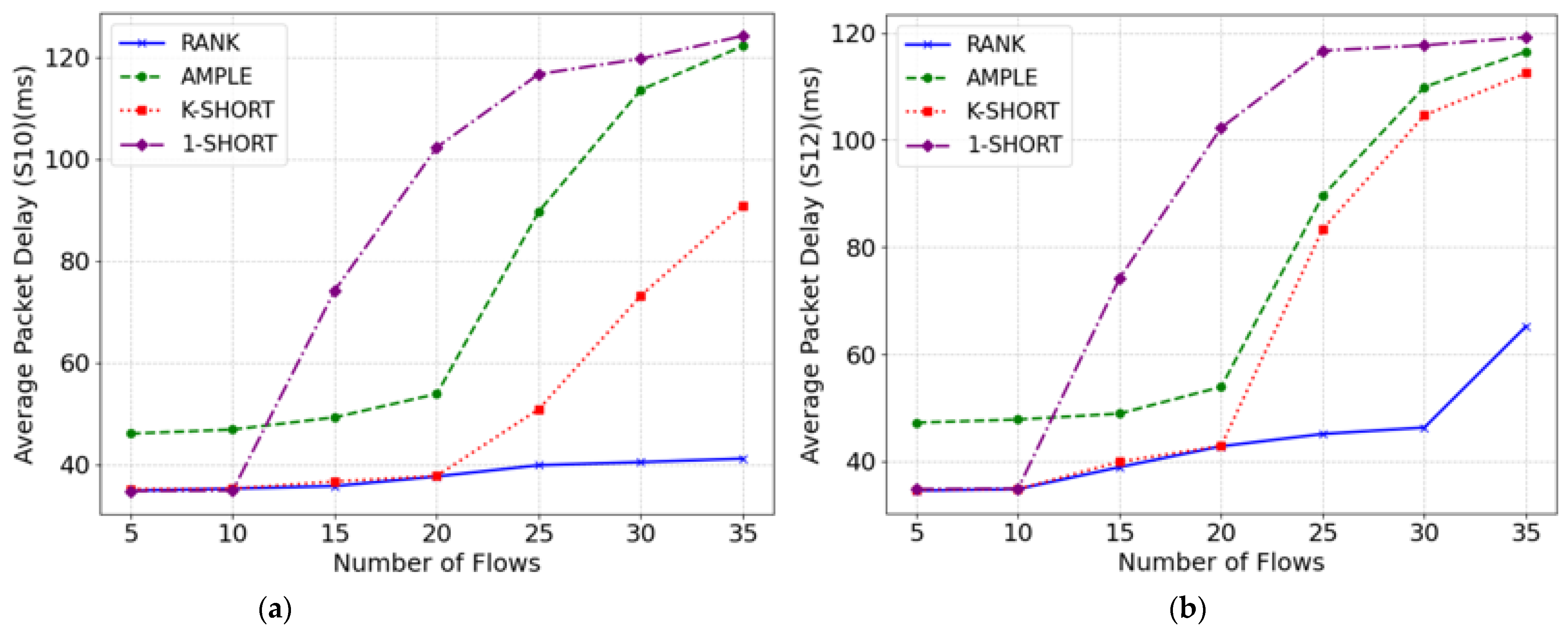
Figure 4a shows how the four methods perform when the device moves to S10. When the number of data flows is between 5 and 10, all four methods provide paths that can accommodate all data flows. Among them, the RANK, k-shortest, and single-path methods provide the shortest paths, resulting in lower average packet delays around 35 ms. In contrast, the AMPLE method provides longer paths, leading to a higher average packet delay of around 46 ms. As the number of data flows increases to 15, the single-path method experiences congestion, causing a significant increase in average packet delay. When the data flow number reaches 25, both the k-shortest and AMPLE methods also encounter congestion. However, the RANK method avoids congestion, maintaining a low average packet delay of 41.2 ms even as the data flow number grows to 35.
Figure 4b shows the performance of the four methods when the device moves to S12, which is similar to the last case. As the number of data flows increases, the RANK method consistently maintains a lower average packet delay. When the number of data flows reaches 35, congestion occurs in the RANK method, but the level of congestion is lighter compared to the other three methods. The average packet delay rises to 65.2 ms, which is 42% lower than the second-lowest k-shortest method.
Overall, regardless of the access switch the device moves to, the RANK method achieves a lower average packet delay. This is because the RANK method ranks paths to maximize transmission capacity while prioritizing shorter paths, which reduces delay. Additionally, while satisfying the flow entry capacity constraints of each node, the RANK method ensures a balance in the number of paths between each node pair. As a result, the RANK method provides shorter paths under low-traffic conditions, thereby reducing average packet delay, and helps alleviate congestion in high-traffic conditions.
5.3.2. Average Packet Loss Rate
Figure 5 shows the impact of the four methods on the average packet loss rate when the device moves to S1.
When the number of data flows is between 5 and 10, all four methods provide paths that can accommodate all data flows without congestion, resulting in a packet loss rate of 0. As the number of data flows increases to 15, the AMPLE method experiences congestion, causing the average packet loss rate to rise to 0.19. When the number of data flows reaches 20, the single-path method becomes congested, and the average packet loss rate increases to 0.22. As the number of data flows grows to 35, the k-shortest method also experiences congestion, with the average packet loss rate rising to 0.14. Throughout the experiment, the RANK method consistently provides sufficient paths for mobile data flows, effectively avoiding congestion and maintaining a packet loss rate of 0.
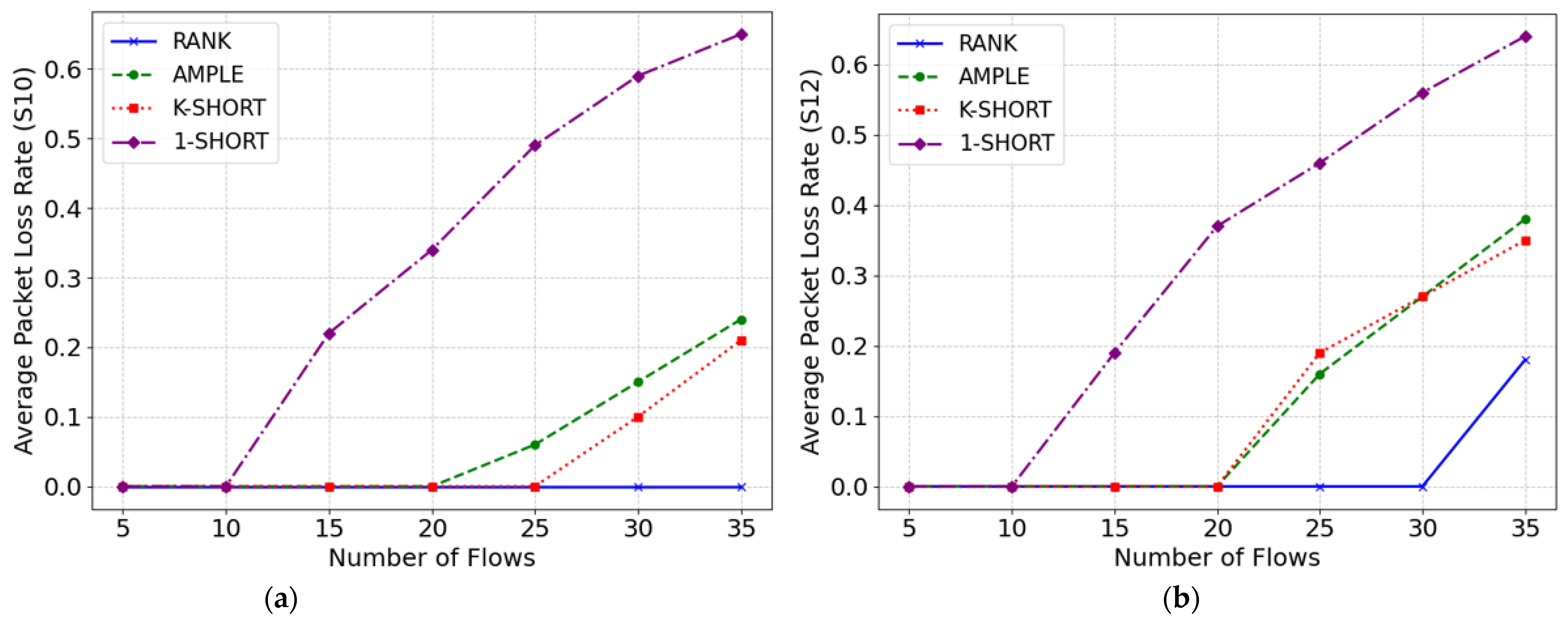
Figure 6a shows the performance of the four methods on the average packet loss rate when the device moves to S10. Similar to the previous case, the RANK method experienced no congestion throughout the experiment, maintaining a packet loss rate of 0.
Figure 6b shows the performance of the four methods on the average packet loss rate when the device moves to S12. When the number of data flows is between 5 and 30, the RANK method performs well, maintaining a packet loss rate of 0. As the number of data flows increases to 35, the RANK method experiences congestion, but the level of congestion is lower compared to the other three methods. The average packet loss rate for RANK is 0.18, which is 48% lower than k-shortest, 53% lower than AMPLE, and 72% lower than the single-path method.
Overall, the RANK method performs the best in terms of the average packet loss rate. As the number of flows increases, RANK continues to provide paths that can accommodate all the flows, thereby maintaining a stable packet loss rate of 0. Even when traffic reaches levels that cause congestion, the RANK method mitigates congestion severity by providing distinct paths that avoid overlap on bottleneck links. The RANK method effectively reduces congestion, leading to a significantly lower average packet loss rate.
5.3.3. Throughput
Figure 7 illustrates the impact of the four methods on throughput when the device moves to S1, S10, and S12. From the figure, it is evident that regardless of the device’s location, the RANK method provides the highest transmission capacity, resulting in the highest throughput compared to the other three methods. Specifically, when the device moves to S1, the throughput achieved by the RANK method reaches 26.32 Mbps, which is 17.8% higher than the k-shortest method, 306.2% higher than AMPLE, and 164.2% higher than the single-path method.
This is because the RANK method maximizes and balances the transmission capacity to each destination node. A higher average transmission capacity typically leads to higher overall throughput. However, it is important to note that maximizing the average transmission capacity does not necessarily ensure that the transmission capacity from the source node to every individual destination node is also maximized. In Algorithm 2, due to the flow entry constraints of the switches, we must discard certain paths. This means that the transmission capacity from the source node to the destination nodes along the discarded paths cannot be maximized. In contrast, other algorithms that select all paths from the source to those destination, while still respecting the flow entry constraints of the switches, could potentially offer higher transmission capacity between the source node and those destinations. However, such algorithms may consume more flow entry capacity, which restricts their ability to include paths for other destination nodes. This could result in imbalanced resource distribution across the network.
6. Conclusions
This paper presents a method for constructing a multi-topology to provide efficient switching paths for mobile data flows in software-defined networking (SDN). We proposed a multi-topology deployment scheme tailored for SDN. Additionally, we modeled the multi-topology construction problem with the objective of maximizing the average transmission capacity from the source node to each destination node. To solve this problem, we developed a method consisting of two algorithms. To evaluate its performance, we implemented the method in Mininet and compared it against existing solutions, including AMPLE, the k-shortest paths method, and the single-path switching method. The simulation results show that our method consistently outperforms the alternatives across key performance metrics. It reduces the average packet delay, lowers the packet loss rate, and improves throughput when a mobile device moves to different access switches. These results highlight the effectiveness of our approach in providing multiple efficient paths to each possible destination node and in balancing the transmission capacity across them. In future work, we will explore the dynamic management of a multi-topology. We plan to monitor current mobile devices’ demands and network conditions at regular intervals. Based on these data, we will adjust the multi-topology accordingly. For example, we will increase the number of paths from the source node to destination nodes with high device density. We will also discard paths related to link or node failures and select alternative paths. Additionally, we will investigate efficient dynamic mobile data flow allocation algorithms to handle real-time network traffic and varying link conditions. Ultimately, we aim to develop more robust and optimized multipath routing solutions.
Author Contributions
Conceptualization, C.Z. and R.H.; investigation, C.Z.; methodology, C.Z.; software, C.Z.; validation, C.Z.; writing—original draft preparation, C.Z.; writing—review and editing, H.D. and R.H.; supervision, H.D. and R.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Basic and Frontier Exploration Project Independently Deployed by the Institute of Acoustics, Chinese Academy of Sciences: Research on Wide-Area RDMA Transmission Acceleration Technology Based on SEANet (Project No. JCQY202407).
Data Availability Statement
All of the necessary data are included in the article.
Acknowledgments
We would like to express our gratitude to Haojiang Deng and Rui Han for their meaningful support for this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| SDN | Software-defined networking |
| VoIP | Voice over Internet Protocol |
| QoS | Quality of service |
| AMPLE | Adaptive Multi-toPoLogy traffic Engineering |
| TCAM | Ternary Content Addressable Memory |
| DODAG | Directed Acyclic Graph |
| AVB | Audio Video Bridging |
| TT | Time-Triggered |
| FAMTAR | Flow-Aware Multi-Topology Adaptive Routing |
| EID | Entity Identification |
| BFS | Breadth-First Search |
| DFS | Depth-First Search |
| RANK | Multi-topology construction based on path ranking |
| NSFNET | National Science Foundation Network |
| Mbps | Megabits per second |
| ms | Milliseconds |
References
- Xing, M.; Deng, H.; Han, R. ICN-Oriented Mobility Support Method for Dynamic Allocation of Mobile Data Flows. Electronics 2023, 12, 1701. [Google Scholar] [CrossRef]
- Wójcik, R.; Domżał, J.; Duliński, Z. Flow-aware multi-topology adaptive routing. IEEE Commun. Lett. 2014, 18, 1539–1542. [Google Scholar] [CrossRef]
- Menth, M.; Martin, R. Network resilience through multi-topology routing. In Proceedings of the Fifth International Workshop on Design of Reliable Communication Networks, Naples, Italy, 16–19 October 2005; pp. 271–277. [Google Scholar]
- Gardner, M.T.; May, R.; Beard, C.; Medhi, D. Using multi-topology routing to improve routing during geographically correlated failures. In Proceedings of the 2014 10th International Conference on the Design of Reliable Communication Networks (DRCN), Ghent, Belgium, 1–3 April 2014; pp. 1–8. [Google Scholar]
- Cevher, S.; Ulutas, M.; Altun, S.; Hokelek, I. Multi topology routing based IP fast re-route for software defined networks. In Proceedings of the 2016 IEEE Symposium on Computers and Communication (ISCC), Messina, Italy, 27–30 June 2016; pp. 1224–1226. [Google Scholar]
- Wang, N.; Ho, K.H.; Pavlou, G. AMPLE: An adaptive traffic engineering system based on virtual routing topologies. IEEE Commun. Mag. 2012, 50, 185–191. [Google Scholar] [CrossRef]
- Jaron, A.; Mihailovic, A.; Aghvami, A.H. Qos-aware multi-plane routing method for OSPF-based IP access networks. Comput. Netw. 2016, 99, 1–14. [Google Scholar] [CrossRef][Green Version]
- Mihailovic, A.; Abrishamchi, B.; Farhoudi, M.; Aghvami, A.H. A comprehensive multi-topology minimum set cover link-state routing approach for emerging random all-IP access network topologies. Comput. Netw. 2012, 219, 109418. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Li, L. Robust traffic engineering using multi-topology routing. In Proceedings of the GLOBECOM 2009-2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Bhandari, K.S.; Ra, I.H.; Cho, G. Multi-topology based QoS-differentiation in RPL for internet of things applications. IEEE Access 2020, 8, 96686–96705. [Google Scholar] [CrossRef]
- Demir, Ö.K.; Cevher, S. Multi-Topology Routing based traffic optimization for IEEE 802.1 Time Sensitive Networking. Real-Time Syst. 2023, 59, 123–159. [Google Scholar] [CrossRef]
- Pop, P.; Raagaard, M.L.; Craciunas, S.S.; Steiner, W. Design optimisation of cyber-physical distributed systems using IEEE time-sensitive networks. IET Cyber-Phys. Syst. Theory Appl. 2016, 1, 86–94. [Google Scholar] [CrossRef]
- Mininet. Available online: http://mininet.org/ (accessed on 12 November 2024).
- Isyaku, B.; Mohd Zahid, M.S.; Bte Kamat, M.; Abu Bakar, K.; Ghaleb, F.A. Software defined networking flow table management of openflow switches performance and security challenges: A survey. Future Internet 2020, 12, 147. [Google Scholar] [CrossRef]
- Al-Fares, M.; Radhakrishnan, S.; Raghavan, B.; Huang, N.; Vahdat, A. Hedera: Dynamic flow scheduling for data center networks. In Proceedings of the 7th USENIX conference on Networked systems design and implementation, San Jose, CA, USA, 28–30 April 2010; pp. 89–92. [Google Scholar]
- Jain, S.; Kumar, A.; Mandal, S.; Ong, J.; Poutievski, L.; Singh, A.; Vahdat, A. B4: Experience with a globally-deployed software defined WAN. ACM SIGCOMM Comput. Commun. Rev. 2013, 43, 3–14. [Google Scholar] [CrossRef]
- Qiu, K.; Yuan, J.; Zhao, J.; Wang, X.; Secci, S.; Fu, X. Fastrule: Efficient flow entry updates for tcam-based openflow switches. IEEE J. Sel. Areas Commun. 2019, 37, 484–498. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y.; Zhu, Z.; Li, H.; Jiang, Y. BOND: Flexible failure recovery in software defined networks. Comput. Netw. 2019, 149, 1–12. [Google Scholar] [CrossRef]
- Bosshart, P.; Daly, D.; Gibb, G.; Izzard, M.; McKeown, N.; Rexford, J.; Walker, D. P4: Programming protocol-independent packet processors. ACM SIGCOMM Comput. Commun. Rev. 2014, 44, 87–95. [Google Scholar] [CrossRef]
- McKeown, N.; Anderson, T.; Balakrishnan, H.; Parulkar, G.; Peterson, L.; Rexford, J.; Turner, J. OpenFlow: Enabling innovation in campus networks. ACM SIGCOMM Comput. Commun. Rev. 2008, 38, 69–74. [Google Scholar] [CrossRef]
- Wang, J.; Chen, G.; You, J.; Sun, P. SEANet: Architecture and Technologies of an On-site, Elastic, Autonomous Network. J. Netw. New Media 2020, 9, 1–8. [Google Scholar]
- Ruby, R.; Zhong, S.; ElHalawany, B.M.; Luo, H.; Wu, K. SDN-enabled energy-aware routing in underwater multi-modal communication networks. IEEE/ACM Trans. Netw. 2021, 29, 965–978. [Google Scholar] [CrossRef]
- Arbelaez, A.; Mehta, D.; O’Sullivan, B.; Quesada, L. A constraint-based parallel local search for the edge-disjoint rooted distance-constrained minimum spanning tree problem. J. Heuristics 2018, 24, 359–394. [Google Scholar] [CrossRef]
- Tache, M.D.; Păscuțoiu, O.; Borcoci, E. Optimization Algorithms in SDN: Routing, Load Balancing, and Delay Optimization. Appl. Sci. 2024, 14, 5967. [Google Scholar] [CrossRef]
- Ryu Controller. Available online: https://github.com/faucetsdn/ryu (accessed on 2 December 2024).
- Mills, D.L.; Braun, H.W. The NSFNET backbone network. In Proceedings of the ACM workshop on Frontiers in computer communications technology, Stowe, VT, USA, 11–13 August 1987; pp. 191–196. [Google Scholar]
- Mitchell, M. An introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998; ISBN 978-0-262-53237-6. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).