An Enhanced Crowned Porcupine Optimization Algorithm Based on Multiple Improvement Strategies
Abstract
1. Introduction
2. Crowned Porcupine Optimization Algorithm
2.1. Exploration Stage
2.2. Exploitation Stage
3. Improved Crowned Porcupine Optimization Algorithm
3.1. Logistic Chaotic Mapping for Population Initialization
3.2. Elite Preservation Strategy
- Initialize population .
- For each iteration : (a) Evaluate the fitness for all . (b) Sort the population: . (c) Select the elite set: . (d) Generate new solutions: Update using ICPO. (e) Update the population: .
- Repeat the above steps until the termination criteria are met.
3.3. Enhanced Population Diversity
3.4. Adaptive Step Size Strategy
- Time-dependent Factor: The time-dependent factor, is calculated using Equation (13):
- 2.
- Fitness-based Factor: The fitness-based factor is computed in two different ways, depending on the defense mechanism used:
- 3.
- Chaotic Factor: The chaotic factor is calculated using Equation (16):
4. Simulation Experiments
4.1. Simulation Environment and Parameter Settings
4.2. Test Results
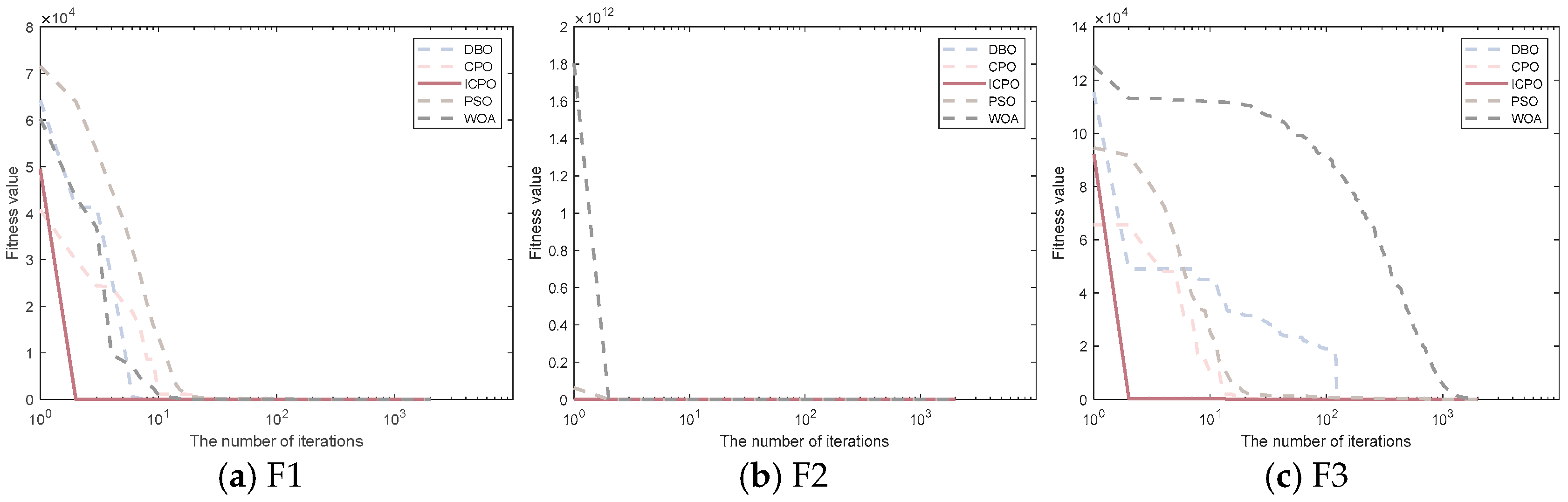
4.2.1. Analysis of Unimodal Function (F1–F7) Test Results
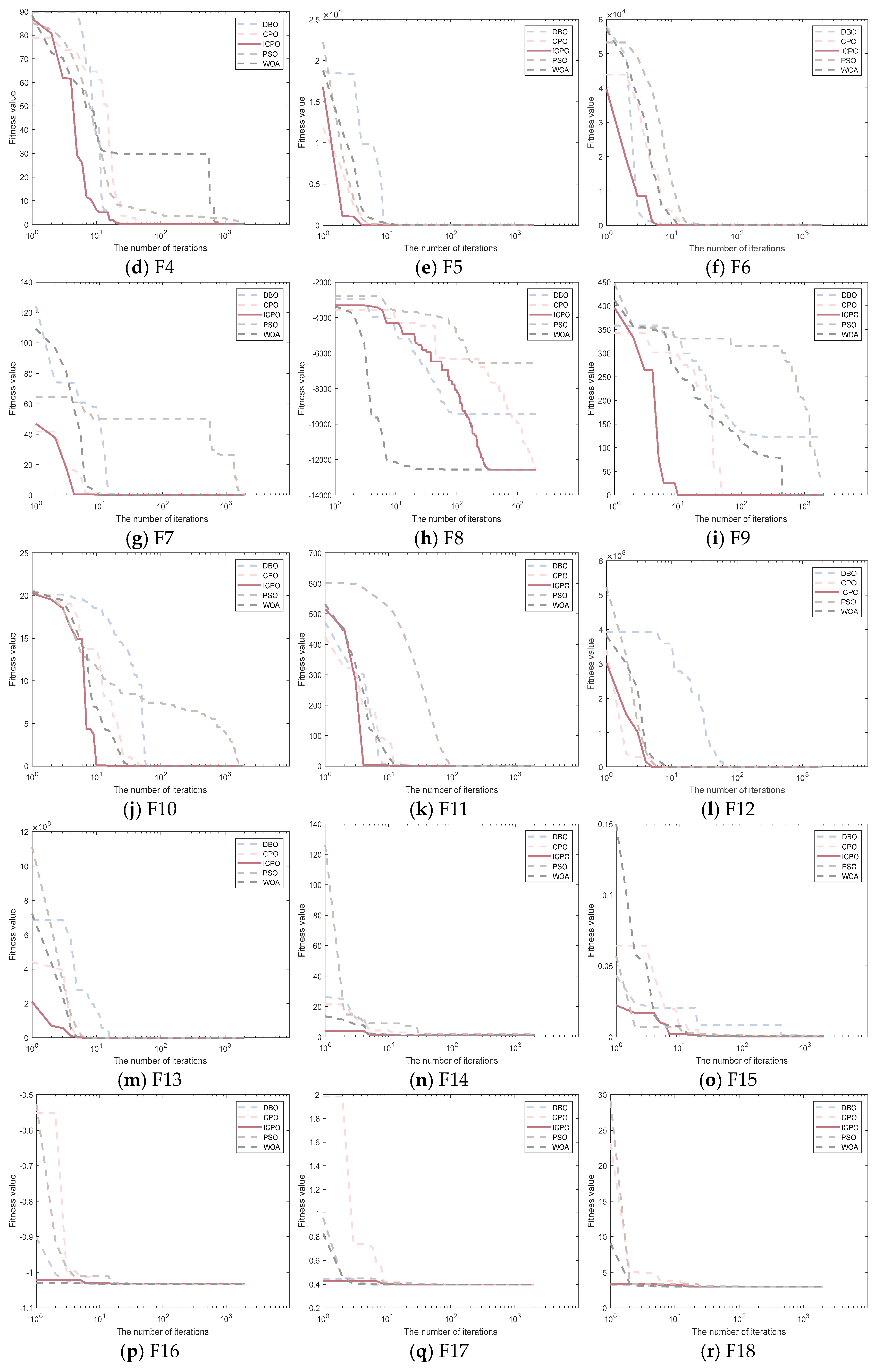
4.2.2. Analysis of Multimodal Function (F8–F13) Test Results
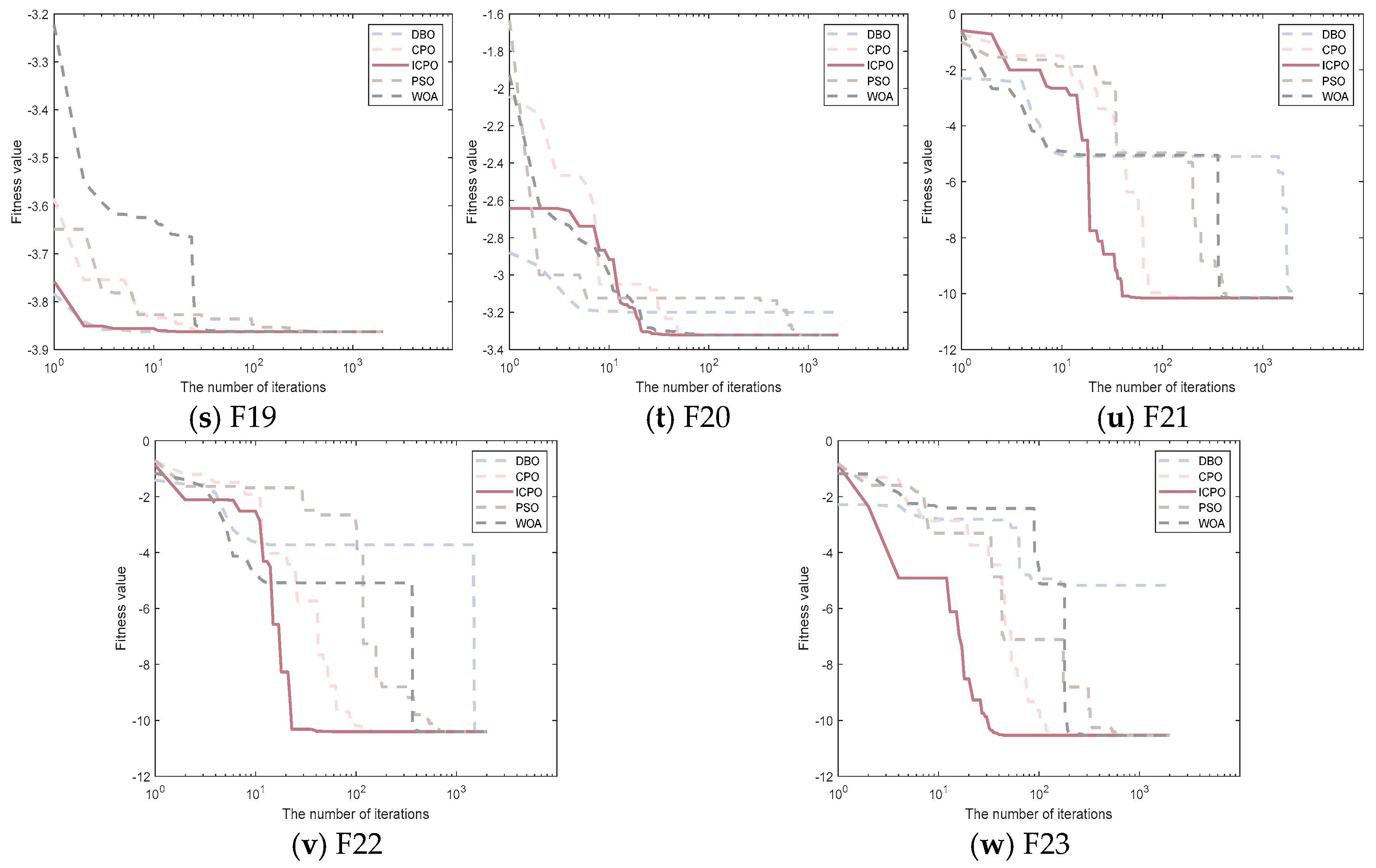
4.2.3. Analysis of Fixed-Dimensional Function (F14–F23) Test Results
4.3. Convergence Curves of the Improved Crowned Porcupine Optimization Algorithm
4.4. Wilcoxon Rank-Sum Test
5. Engineering Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boussaid, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Akinola, O.O.; Ezugwu, A.E.; Agushaka, J.O.; Zitar, R.A.; Abualigah, L. Multiclass feature selection with metaheuristic optimization algorithms: A review. Neural Comput. Appl. 2022, 34, 19751–19790. [Google Scholar] [CrossRef] [PubMed]
- Salgotra, R.; Sharma, P.; Raju, S.; Gandomi, A.H. A Contemporary Systematic Review on Meta-heuristic Optimization Algorithms with Their MATLAB and Python Code Reference. Arch. Comput. Methods Eng. 2024, 31, 1749–1822. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst.-Int. J. Escience 2019, 97, 849–872. [Google Scholar] [CrossRef]
- El Aziz, M.A.; Ewees, A.A.; Hassanien, A.E. Whale Optimization Algorithm and Moth-Flame Optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.J.; Qu, B.Y.; Chen, X.; Wang, H. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Dorfler, F.; Sandberg, H.; Low, S.H.; Chakrabarti, S.; Baldick, R.; Lavaei, J. A Survey of Distributed Optimization and Control Algorithms for Electric Power Systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A Survey on Demand Response Programs in Smart Grids: Pricing Methods and Optimization Algorithms. Ieee Commun. Surv. Tutor. 2015, 17, 152–178. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Hou, Y.; Gao, H.; Wang, Z.; Du, C. Improved Grey Wolf Optimization Algorithm and Application. Sensors 2022, 22, 3810. [Google Scholar] [CrossRef] [PubMed]
- Li, M.-W.; Wang, Y.-T.; Geng, J.; Hong, W.-C. Chaos cloud quantum bat hybrid optimization algorithm. Nonlinear Dyn. 2021, 103, 1167–1193. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Guo, Q. Modified Whale Optimization Algorithm Based on Tent Chaotic Mapping and Its Application in Structural Optimization. Ksce J. Civ. Eng. 2020, 24, 3703–3713. [Google Scholar] [CrossRef]
- Bai, Y.; Cao, L.; Chen, B.; Chen, Y.; Yue, Y. A Novel Topology Optimization Protocol Based on an Improved Crow Search Algorithm for the Perception Layer of the Internet of Things. Biomimetics 2023, 8, 165. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Cao, L.; Chen, Y.; Chen, C.; Yue, Y.; Zhu, W. Gorilla optimization algorithm combining sine cosine and cauchy variations and its engineering applications. Sci. Rep. 2024, 14, 7578. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Yu, H.; Fang, X.; Tian, L.; Han, P. A Path Planning Method Based on Multi- Objective Cauchy Mutation Cat Swarm Optimization Algorithm for Navigation System of Intelligent Patrol Car. IEEE Access 2020, 8, 151788–151803. [Google Scholar] [CrossRef]
- Juang, C.-F. A hybrid of genetic algorithm and particle swarm optimization for recurrent network design. IEEE Trans. Syst. Man Cybern. Part B Cybern. A Publ. IEEE Syst. Man Cybern. Soc. 2004, 34, 997–1006. [Google Scholar] [CrossRef] [PubMed]
- Mafarja, M.M.; Mirjalili, S. Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. Ieee Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Demir, F.B.; Tuncer, T.; Kocamaz, A.F. A chaotic optimization method based on logistic-sine map for numerical function optimization. Neural Comput. Appl. 2020, 32, 14227–14239. [Google Scholar] [CrossRef]
- Wang, L.; Gao, Y.; Li, J.; Wang, X. A Feature Selection Method by using Chaotic Cuckoo Search Optimization Algorithm with Elitist Preservation and Uniform Mutation for Data Classification. Discret. Dyn. Nat. Soc. 2021, 2021, 7796696. [Google Scholar] [CrossRef]
- Han, M.; Du, Z.; Yuen, K.F.; Zhu, H.; Li, Y.; Yuan, Q. Walrus optimizer: A novel nature-inspired metaheuristic algorithm. Expert Syst. Appl. 2024, 239, 122413. [Google Scholar] [CrossRef]
- Lei, W.; Jia, K.; Zhang, X.; Lei, Y. Research on Chaotic Chimp Optimization Algorithm Based on Adaptive Tuning and Its Optimization for Engineering Application. J. Sens. 2023, 2023, 5567629. [Google Scholar] [CrossRef]
| Description | Dim | Range | fmin |
|---|---|---|---|
| d | [−100,100] | 0 | |
| d | [−10,10] | 0 | |
| d | [−100,100] | 0 | |
| d | [−100,100] | 0 | |
| d | [−30,30] | 0 | |
| d | [−100,100] | 0 | |
| d | [−128,128] | 0 | |
| d | [−500,500] | −418.989d | |
| d | [−5.12,5.12] | 0 | |
| d | [−32,32] | 0 | |
| d | [−600,600] | 0 | |
| d | [−50,50] | 0 | |
| d | [−50,50] | 0 | |
| 2 | [−65.536,65.536] | 0.998 | |
| 4 | [−5,5] | 0.0003075 | |
| 2 | [−5,5] | −1.0316 | |
| 2 | [−5,5] | 0.398 | |
| 2 | [−2,2] | 3 | |
| 3 | [−1,2] | −3.86 | |
| 6 | [0,1] | −3.32 | |
| 4 | [0,1] | −10.1532 | |
| 4 | [0,1] | −10.4028 | |
| 4 | [0,1] | −10.5363 |
| Algorithm | Parameters |
|---|---|
| PSO | |
| DBO | |
| WOA | |
| CPO | |
| ICPO |
| Function | Comparative Algorithms | |||||
|---|---|---|---|---|---|---|
| PSO | DBO | WOA | CPO | ICPO | ||
| F1 | Best | 2.05 × 10−5 | 0.00 | 0.00 | 0.00 | 0.00 |
| Median | 3.42 × 10−6 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Time(s) | 4.68 × 10−1 | 1.54 | 7.68 × 10−1 | 7.76 × 10−1 | 1.16 | |
| F2 | Best | 1.82 × 10−4 | 0.00 | 1.43 × 10−322 | 0.00 | 0.00 |
| Median | 4.56 × 10−4 | 0.00 | 1.98 × 10−322 | 4.88 × 10−158 | 0.00 | |
| Time(s) | 3.04 × 10−1 | 6.08 × 10−1 | 3.23 × 10−1 | 3.43 × 10−1 | 3.82 × 10−1 | |
| F3 | Best | 6.40 | 0.00 | 6.15 × 10−1 | 0.00 | 0.00 |
| Median | 1.04 × 10 | 0.00 | 3.58 × 10 | 0.00 | 0.00 | |
| Time(s) | 1.25 | 1.72 | 1.26 | 1.32 | 1.47 | |
| F4 | Best | 5.02 × 10−1 | 4.94 × 10−324 | 1.37 × 10−11 | 0.00 | 0.00 |
| Median | 6.45 × 10−1 | 4.94 × 10−324 | 1.47 × 10−1 | 4.04 × 10−161 | 0.00 | |
| Time(s) | 2.81 × 10−1 | 5.42 × 10−1 | 2.60 × 10−1 | 3.26 × 10−1 | 3.57 × 10−1 | |
| F5 | Best | 2.10 × 10 | 1.82 × 10 | 2.41 × 10 | 1.10 × 10 | 9.43 |
| Median | 7.79 × 10 | 1.95 × 10 | 2.42 × 10 | 1.12 × 10 | 1.10 × 10 | |
| Time(s) | 4.14 × 10−1 | 6.74 × 10−1 | 3.96 × 10−1 | 4.45 × 10−1 | 4.71 × 10−1 | |
| F6 | Best | 3.88 × 10−7 | 1.85 × 10−32 | 2.75 × 10−6 | 0.00 | 0.00 |
| Median | 4.19 × 10−6 | 1.00 × 10−31 | 5.19 × 10−6 | 0.00 | 0.00 | |
| Time(s) | 2.87 × 10−1 | 5.25 × 10−1 | 2.73 × 10−1 | 3.19 × 10−1 | 3.39 × 10−1 | |
| F7 | Best | 3.62 × 10−2 | 4.25 × 10−5 | 1.07 × 10−5 | 1.24 × 10−4 | 3.94 × 10−5 |
| Median | 7.25 × 10−2 | 1.61 × 10−4 | 1.52 × 10−5 | 2.59 × 10−4 | 8.36 × 10−5 | |
| Time(s) | 1.00 | 1.29 | 1.00 | 1.02 | 1.04 | |
| F8 | Best | −7.83 × 103 | −1.12 × 104 | −1.26 × 104 | −1.26 × 104 | −1.23 × 104 |
| Median | −6.73 × 103 | −9.74 × 103 | −1.26 × 104 | −1.26 × 104 | −1.20 × 104 | |
| Time(s) | 5.04 × 10−1 | 7.09 × 10−1 | 3.98 × 10−1 | 4.95 × 10−1 | 4.66 × 10−1 | |
| F9 | Best | 2.23 × 10 | 0.00 | 0.00 | 0.00 | 0.00 |
| Median | 3.93 × 10 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Time(s) | 4.12 × 10−1 | 5.67 × 10−1 | 2.91 × 10−1 | 3.59 × 10−1 | 3.78 × 10−1 | |
| F10 | Best | 5.68 × 10−4 | 4.44 × 10−16 | 3.98 × 10−15 | 4.44 × 10−16 | 4.44 × 10−16 |
| Median | 1.42 × 10−3 | 4.44 × 10−16 | 3.98 × 10−15 | 4.44 × 10−16 | 4.44 × 10−16 | |
| Time(s) | 4.13 × 10−1 | 5.80 × 10−1 | 3.12 × 10−1 | 3.57 × 10−1 | 3.70 × 10−1 | |
| F11 | Best | 7.40 × 10−3 | 0.00 | 0.00 | 0.00 | 0.00 |
| Median | 7.40 × 10−3 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Time(s) | 4.45 × 10−1 | 6.58 × 10−1 | 3.91 × 10−1 | 4.59 × 10−1 | 4.70 × 10−1 | |
| F12 | Best | 6.05 × 10−9 | 1.65 × 10−32 | 4.46 × 10−7 | 1.57 × 10−32 | 1.57 × 10−32 |
| Median | 2.43 × 10−8 | 2.04 × 10−32 | 8.43 × 10−7 | 1.57 × 10−32 | 1.57 × 10−32 | |
| Time(s) | 2.16 | 2.55 | 2.13 | 2.14 | 2.16 | |
| F13 | Best | 6.50 × 10−8 | 2.58 × 10−32 | 2.79 × 10−6 | 1.35 × 10−32 | 1.35 × 10−32 |
| Median | 1.13 × 10−6 | 5.22 × 10−31 | 1.21 × 10−5 | 1.35 × 10−32 | 1.35 × 10−32 | |
| Time(s) | 2.20 | 2.58 | 2.16 | 2.15 | 2.20 | |
| F14 | Best | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 |
| Median | 1.10 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | |
| Time(s) | 3.10 | 3.71 | 3.22 | 3.17 | 3.18 | |
| F15 | Best | 3.08 × 10−4 | 3.08 × 10−4 | 3.08 × 10−4 | 3.08 × 10−4 | 3.08 × 10−4 |
| Median | 3.45 × 10−4 | 3.66 × 10−4 | 3.10 × 10−4 | 3.08 × 10−4 | 3.08 × 10−4 | |
| Time(s) | 1.57 × 10−1 | 4.95 × 10−1 | 2.30 × 10−1 | 2.70 × 10−1 | 2.83 × 10−1 | |
| F16 | Best | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| Median | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | |
| Time(s) | 2.76 × 10−1 | 1.37 | 6.24 × 10−1 | 7.47 × 10−1 | 7.85 × 10−1 | |
| F17 | Best | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| Median | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | |
| Time(s) | 1.08 × 10−1 | 4.52 × 10−1 | 1.97 × 10−1 | 2.31 × 10−1 | 2.35 × 10−1 | |
| F18 | Best | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 |
| Median | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | |
| Time(s) | 1.02 × 10−1 | 4.33 × 10−1 | 1.86 × 10−1 | 2.23 × 10−1 | 2.35 × 10−1 | |
| F19 | Best | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 |
| Median | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | |
| Time(s) | 1.81 × 10−1 | 5.39 × 10−1 | 2.64 × 10−1 | 3.08 × 10−1 | 3.23 × 10−1 | |
| F20 | Best | −3.32 | −3.32 | −3.32 | −3.32 | −3.32 |
| Median | −3.32 | −3.26 | −3.20 | −3.32 | −3.32 | |
| Time(s) | 1.97 × 10−1 | 5.41 × 10−1 | 2.68 × 10−1 | 3.13 × 10−1 | 3.20 | |
| F21 | Best | −1.02 × 10 | −1.02 × 10 | −1.02 × 10 | −1.02 × 10 | −1.02 × 10 |
| Median | −1.02 × 10 | −1.00 × 10 | −1.02 × 10 | −1.02 × 10 | −1.02 × 10 | |
| Time(s) | 2.27 × 10−1 | 5.82 × 10−1 | 3.03 × 10−1 | 3.48 × 10−1 | 3.51 × 10−1 | |
| F22 | Best | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 |
| Median | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | |
| Time(s) | 2.73 × 10−1 | 6.51 × 10−1 | 3.57 × 10−1 | 3.98 × 10−1 | 4.15 × 10−1 | |
| F23 | Best | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 |
| Median | −9.73 | −7.86 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | |
| Time(s) | 3.35 × 10−1 | 7.16 × 10−1 | 4.19 × 10−1 | 4.62 × 10−1 | 4.65 × 10−1 | |
| Function | DBO-ICPO | PSO-ICPO | WOA-ICPO | CPO-ICPO | ||||
|---|---|---|---|---|---|---|---|---|
| p-Value | H | p-Value | H | p-Value | H | p-Value | H | |
| F1 | N/A | = | 1.21 × 10−12 | + | 1.35 × 10−4 | + | 1.93 × 10−10 | + |
| F2 | 2.25 × 10−4 | + | 1.44 × 10−11 | + | 1.44 × 10−11 | + | 1.44 × 10−11 | + |
| F3 | N/A | = | 1.21 × 10−12 | + | 1.21 × 10−12 | + | 1.93 × 10−10 | + |
| F4 | 9.93 × 10−8 | + | 1.62 × 10−11 | + | 1.62 × 10−11 | + | 1.58 × 10−7 | + |
| F5 | 3.02 × 10−11 | + | 3.02 × 10−11 | + | 3.02 × 10−11 | + | 4.31 × 10−8 | + |
| F6 | 2.78 × 10−11 | + | 1.67 × 10−11 | + | 1.67 × 10−11 | + | 1.67 × 10−11 | + |
| F7 | 1.43 × 10−8 | + | 3.02 × 10−11 | + | 1.41 × 10−1 | − | 3.26 × 10−7 | + |
| F8 | 3.65 × 10−11 | + | 2.98 × 10−11 | + | 1.99 × 10−4 | + | 8.41 × 10−9 | + |
| F9 | 1.10 × 10−2 | + | 1.21 × 10−12 | + | N/A | = | N/A | = |
| F10 | N/A | = | 1.21 × 10−12 | + | 6.53 × 10−7 | + | N/A | = |
| F11 | N/A | = | 1.21 × 10−12 | + | 3.33 × 10−1 | − | N/A | = |
| F12 | 1.10 × 10−10 | + | 1.99 × 10−11 | + | 1.99 × 10−11 | + | 1.99 × 10−11 | + |
| F13 | 1.82 × 10−6 | + | 5.31 × 10−5 | + | 1.42 × 10−5 | + | 5.31 × 10−5 | + |
| F14 | 3.34 × 10−1 | + | 1.10 × 10−2 | + | 4.50 × 10−12 | + | N/A | = |
| F15 | 3.70 × 10−9 | + | 5.40 × 10−10 | + | 3.36 × 10−10 | + | 4.72 × 10−7 | + |
| F16 | 1.61 × 10−1 | − | 1.61 × 10−1 | − | 3.56 × 10−12 | + | 5.97 × 10−1 | − |
| F17 | N/A | = | N/A | = | 1.21 × 10−12 | + | N/A | = |
| F18 | 3.78 × 10−4 | + | 3.62 × 10−4 | + | 2.06 × 10−11 | + | 1.72 × 10−6 | + |
| F19 | N/A | = | N/A | = | 1.21 × 10−12 | + | N/A | = |
| F20 | 2.78 × 10−3 | + | 5.10 × 10−3 | + | 2.03 × 10−4 | + | 1.20 × 10−1 | − |
| F21 | 1.05 × 10−8 | + | 4.24 × 10−5 | + | 1.72 × 10−12 | + | 3.34 × 10−1 | − |
| F22 | 8.84 × 10−2 | − | 9.00 × 10−1 | − | 1.25 × 10−11 | + | 1.07 × 10−6 | + |
| F23 | 2.61 × 10−3 | + | 8.54 × 10−2 | − | 1.04 × 10−11 | + | 6.36 × 10−4 | + |
| Algorithms | Best | ||||
|---|---|---|---|---|---|
| ICPO | 0.7782 | 0.3846 | 40.3196 | 200.0000 | 5885.332774 |
| PSO | 0.8001 | 0.3955 | 41.4561 | 184.7623 | 5923.891842 |
| WO | 0.7782 | 0.3846 | 40.3197 | 199.9991 | 5885.335002 |
| WOA | 0.8014 | 0.4072 | 41.4696 | 184.5874 | 5967.191023 |
| CPO | 0.7782 | 0.3846 | 40.3196 | 200.0000 | 5885.332775 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, W.; Gu, Y.; Huang, J. An Enhanced Crowned Porcupine Optimization Algorithm Based on Multiple Improvement Strategies. Appl. Sci. 2024, 14, 11414. https://doi.org/10.3390/app142311414
Lei W, Gu Y, Huang J. An Enhanced Crowned Porcupine Optimization Algorithm Based on Multiple Improvement Strategies. Applied Sciences. 2024; 14(23):11414. https://doi.org/10.3390/app142311414
Chicago/Turabian StyleLei, Wenli, Yifan Gu, and Jianyu Huang. 2024. "An Enhanced Crowned Porcupine Optimization Algorithm Based on Multiple Improvement Strategies" Applied Sciences 14, no. 23: 11414. https://doi.org/10.3390/app142311414
APA StyleLei, W., Gu, Y., & Huang, J. (2024). An Enhanced Crowned Porcupine Optimization Algorithm Based on Multiple Improvement Strategies. Applied Sciences, 14(23), 11414. https://doi.org/10.3390/app142311414






